2048点FFT在定点DSP上的实现
DSP下FFT的实现

DSP下快速FFT的实现侯凯(吉林大学通信工程学院吉林长春130012)试验中用计算机软件CCStudio仿真FFT的过程中需要四个文件,分别是.dat、.asm、.cmd和.inc文件。
.inc文件里存放的是FFT用到的正弦和余弦系数;.dat文件是进行FFT的输入数据,在这里由C程序生成;.cmd为汇编程序分配空间;.asm文件是执行程序的源代码。
COEFF.INC文件一般可从网上下载得到。
1生成.dat文件的C程序如下:#include "stdio.h"#include "conio.h"main(){FILE *fw;int i,j,t;fw=fopen("d:fft.dat","wt");fprintf(fw," .data\n");fprintf(fw,"d_input1: ");t=0x5000;for(i=0;i<1024;i=i+16){if(i%32==0){ for(j=0;j<16;j++)fprintf(fw," .word 0x%04x\n",t); /*输出字段长度为4,不足补0*/ }else{ for(j=0;j<16;j++)fprintf(fw," .word 0x%04x\n",0);}}fclose(fw);}生成文件含1024个数值,相邻两个数值构成一个输入量,分别为实部和虚部,即输入数据共512个。
2.cmd文件MEMORY{PAGE 0: //共16K的片内存储空间EPROM: org=3000h, len=1000hPAGE 1:SPRAM: org=0060h, len=0020hDARAM: org=0100h, len=1000hRAM : org=1500h, len=1400h}SECTIONS{.text : > EPROM PAGE 0.data : > EPROM PAGE 0STACK : > SPRAM PAGE 1.bss : > SPRAM PAGE 1sine : > DARAM PAGE 1cosine : > DARAM PAGE 1d_input : > RAM PAGE 1 //输入数据起始地址1500hfft_data : > RAM PAGE 1fft_out : > RAM PAGE 1}3.asm文件.title "fft.asm".mmregs.global _c_int00.copy "coeff.inc" ;加载含sin和cos数值的文件.copy "3fft512.dat" ;加载输入数据的文件sine: .usect "sine",512 ;sin函数sin(pai*k/512) k=0~511 故预留空间512个cosine: .usect "cosine",51 ;cos函数cos(pai*k/512) k=0~511 故预留空间512个d_input: .usect "d_input",2048 ;为输入文件预留2048个单元空间,最多输入1024个数据fft_data: .usect "fft_data",2048 ;为处理后的数据分配2048个单元fft_out: .usect "fft_out",1024 ;为最终结果分配1024个单元STACK .usect "STACK",10 ;分配堆栈K_DATA_IDX_1 .set 2 ;定义一些常量K_DATA_IDX_2 .set 4K_DATA_IDX_3 .set 8K_TWID_TBL_SIZE .set 512K_TWID_IDX_3 .set 128K_FLY_COUNT_3 .set 4K_FFT_SIZE .set 512 ;512个数据=2的9次方K_LOGN .set 9 ;共9级运算.bss d_twid_idx,1 ;给变量分配1个空间.bss d_data_idx,1.bss d_grps_cnt,1****** *** 位倒序*** *** *** .asg AR2,REORDERED ;REORDERED即为AR2,下同.asg AR3,ORIGINAL_INPUT.asg AR7,DATA_PROC_BUF.text_c_int00: ;程序初始化及位倒序SSBX FRCTSTM #STACK+10,SPSTM #d_input,AR1 ;将输入文件的数据从程序区传送到数据区RPT #2*K_FFT_SIZE-1 ;重复执行2*K_FFT_SIZE次MVPD d_input1,*AR1+STM #sine,AR1 ;将coeff.inc文件中sin函数传到数据区RPT #511MVPD sine1,*AR1+STM #cosine,AR1 ;将coeff.inc文件中cos函数传到数据区RPT #511MVPD cosine1,*AR1+STM #d_input,ORIGINAL_INPUT;ORIGINAL_INPUT=AR3 AR3=#d_input首地址STM #fft_data,REORDERED;DATA_PROC_BUF=AR2 AR2=#fft_data首地址STM #K_FFT_SIZE-1,BRC;BRC=#K_FFT_SIZE-1 BRC寄存器决定RPTBD的执行次数RPTBD bit_rev_end-1 ;块循环STM #K_FFT_SIZE,AR0 ;AR0=#K_FFT_SIZEMVDD *ORIGINAL_INPUT+,*REORDERED+;fft_data=d_input 且#d_input++ #fft_data++MVDD *ORIGINAL_INPUT-,*REORDERED+;fft_data=d_input 且#d_input--#fft_data++MAR *ORIGINAL_INPUT+0B;#d_input与AR0的值位码倒序相加,可实现位倒序bit_rev_end: ;循环执行,最后在fft_data中的是d_input位倒序后的数据* * * ** * * FFT 代码* * * * * * * * .asg AR1,GROUP_COUNTER.asg AR2,PX.asg AR3,QX.asg AR4,WR.asg AR5,WI.asg AR6,BUTTERFLY_COUNTER.asg AR7,STAGE_COUNTER* * * stage 1 * * * ;第一级蝶运算STM #0, BKLD #-1,ASM ;存储时右移1位,防止数据溢出STM #fft_data,PX ;PX=#fft_data PX指向实部记PR指向虚部记PILD *PX,16,A ;AH=PRSTM #fft_data+K_DATA_IDX_1,QX;QX=#fft_data+2 即第二个数实部STM #K_FFT_SIZE/2-1,BRCRPTBD stage1end-1STM #K_DATA_IDX_1+1,AR0SUB *QX,16,A,B ;BH=PR-QRADD *QX,16,A ;AH=PR+QRSTH A,ASM,*PX+ ;PR变为(PR+QR)/2 PR++ST B,*QX+ ;QR变为(PR-QR)/2 QR++||LD *PX,A ;AH=PISUB *QX,16,A,B ;BH=AH-QI=PI-QIADD *QX,16,A ;AH=AH+QI=PI+QISTH A,ASM,*PX+0 ;PI变成(PI+QI)/2 PI+AR0ST B,*QX+0% ;QI变成(PI-QI)/2 QI+AR0||LD *PX,Astage1end:* * * Stage 2 * * * ;第二级蝶运算STM #fft_data,PXSTM #fft_data+K_DATA_IDX_2,QXSTM #K_FFT_SIZE/4-1,BRC ;共含碟群数目为#K_FFT_SIZE/4LD *PX,16,ARPTBD stage2end-1STM #K_DATA_IDX_2+1,AR0;1st ;第二级碟运算中每个碟群由两个碟运算构成;每个碟群的第一个蝶运算时乘数为1SUB *QX,16,A,BADD *QX,16,ASTH A,ASM,*PX+ST B,*QX+||LD *PX,ASUB *QX,16,A,BADD *QX,16,ASTH A,ASM,*PX+STH B,ASM,*QX+;2nd ;每个碟群的第二个蝶运算时乘数为-jMAR *QX+ADD *PX,*QX,ASUB *PX,*QX-,BSTH A,ASM,*PX+SUB *PX,*QX,AST B,*QX||LD *QX+,BST A,*PX||ADD *PX+0%,AST A,*QX+0%||LD *PX,Astage2end: ;第二级蝶运算完成* * * Stage 3 through Stage logN * * * ;第三级到最后一级(logN)STM #K_TWID_TBL_SIZE,BKST #K_TWID_IDX_3,d_twid_idxSTM #K_TWID_IDX_3,AR0STM #cosine,WRSTM #sine,WISTM #K_LOGN-2-1,STAGE_COUNTER;STAGE_COUNTER运算的级数ST #K_FFT_SIZE/8-1,d_grps_cnt;d_grps_cnt为每级运算中碟群数STM #K_FLY_COUNT_3-1,BUTTERFLY_COUNTER;BUTTERFLY_COUNTER为蝶群中蝶数ST #K_DATA_IDX_3,d_data_idx stage:STM #fft_data,PXLD d_data_idx,AADD *(PX),ASTLM A,QXMVDK d_grps_cnt,GROUP_COUNTER group:MVMD BUTTERFLY_COUNTER,BRCRPTBD butterflyend-1LD *WR,TMPY *QX+,AMACR *WI+0%,*QX-,AADD *PX,16,A,BST B,*PX||SUB *PX+,BST B,*QX||MPY *QX+,AMASR *QX,*WR+0%,AADD *PX,16,A,BST B,*QX+||SUB *PX,BLD *WR,TST B,*PX+||MPY *QX+,Abutterflyend:; 为下一级运算更新数据PSHM AR0MVDK d_data_idx,AR0MAR *PX+0MAR *QX+0BANZD group,*GROUP_COUNTER-POPM AR0MAR *QX-LD d_data_idx,ASUB #1,A,BSTLM B,BUTTERFLY_COUNTERSTL A,1,d_data_idxLD d_grps_cnt,ASTL A,ASM,d_grps_cntLD d_twid_idx,ASTL A,ASM,d_twid_idxBANZD stage,*STAGE_COUNTER-MVDK d_twid_idx,AR0fft_end: ;FFT变换完成* * * Compute the power spectrum * * *STM #fft_data,AR2 ;AR2=#fft_dataSTM #fft_out,AR4 ;AR4=#fft_outSTM #K_FFT_SIZE*2-1,BRCRPTB power_end-1SQUR *AR2+,A ;A=AR2的平方AR2++SQURA *AR2+,A;A=A+AR2的平方即实部与虚部平方的和STH A,*AR4+ ;#fft_out=Apower_end:here: B here.end4实验结果图1 输入数据图2 FFT结果。
2048点FFT在定点DSP上的实现

新 用汇编语言编写, 但是在各子程序的入口和出口都考 虑了与 C 语言的兼容性, 使得各子程序能够直接被 C
语言调用。
1 汇编模块 fft_brev.asm, 此模块的功能是把 2048
点实数数据打包成为 1024 点复数数据 , 并把复数数
据进行倒位序排列。在 C 函数中, 通过 FFT_brev()来调
据, 并完成复数数据的位反转操作;
2 计算 1024 点基 2 复数 FFT;
3 劈分还原计算, 获得 2048 点实数 FFT 结果;
技
4 计算幅值的平方, 获得频谱的幅度谱。
术
根据实际需要, 还可以对数据进行加窗函数处理。 1.2 具体函数介绍
创
根据上面的程序流程, 介绍具体的函数模块。考
虑到 程序的效率 和代码的精 简, FFT 算法函数 全部 采
考虑到 CCD 是 2160 像元, 为了方便运用基 2 算
1 程序介绍与实现
1.1 程序流程 FFT 的计算量比傅 立叶变换的 计 算 量 减 少 了 , 但 是 FFT 要 做 到 大 点 数 , 实 时 运 算 , 对 于 普 通 的 单 片 机 来说还是一件比较困难的事。一方面, FFT 需要对原始 自然序列进行码位倒序排列; 另一方面, 蝶形运算是 复数运算, 需要多次查表相乘运算才能实现。DSP 控制 器就是针对这些需求而设计的专用芯片: 具有专为 FFT 算法而设计的反序间接寻址; 可实现增/减 1 或增/
DS P 开 发 与 应 用
204 8 点 F F T 在定点 DS P 上的实现
Acco m p lis h m e n t o f 2048 p o in ts FFT in TMS 320C240x fixe d - p o in t DS P
FFT算法的DSP实现

FFT 算法的DSP 实现对于离散傅里叶变换(DFT)的数字计算,FFT是一种有效的方法。
一般假定输入序列是复数。
当实际输入是实数时,利用对称性质可以使计算DFT 非常有效。
一个优化的实数FFT算法是一个组合以后的算法。
原始的2N个点的实输入序列组合成一个N 点的复序列,之后对复序列进行N 点的FFT 运算,最后再由N 点的复数输出拆散成2N点的复数序列,这 2 N点的复数序列与原始的2N点的实数输入序列的DFT输出一致。
使用这种方法,在组合输入和拆散输出的操作中,FFT 运算量减半。
这样利用实数FFT 算法来计算实输入序列的DFT的速度几乎是一般FFT算法的两倍。
下面用这种方法来实现一个256 点实数FFT(2N=256 )运算。
1. 实数FFT 运算序列的存储分配如何利用有限的DSP 系统资源,合理的安排好算法使用的存储器是一个比较重要的问题。
本文中,程序代码安排在0x3000 开始的存储器中,其中0x3000~0x3080 存放中断向量表,FFT程序使用的正弦表和余弦表数据(.data段)安排在OxcOO开始的地方,变量(.bss段定义)存放在0x80 开始的地址中。
另外,本文中256 点实数FFT 程序的数据缓冲位Ox23OO~Ox23ff , FFT 变换后功率谱的计算结果存放在Ox22OO~Ox22ff 中。
连续定位.cmd 文件程序如下:MEMORY {PAGE O: IPROG: origin = Ox3O8O,len=Ox1F8OVECT: lorigin=Ox3OOO,len=Ox8OEPROG: origin=Ox38OOO,len=Ox8OOOPAGE 1:USERREGS: origin=Ox6O,len=Ox1cBIOSREGS: origin=Ox7c,len=Ox4IDATA: origin=Ox8O,len=OxB8O}SECTIONS{EDATA: origin=OxCOO,len=Ox14OO{.vectors: { } > VECT PAGE O.sysregs:.trcinit:.gblinit: { } > BIOSREGS PAGE 1 { } > IPROG PAGE O { } > IPROG PAGE O.bios:frt:{ } > IPROG PAGE O { } > IPROG PAGE O.text: { } > IPROG PAGE O.cinit: { } > IPROG PAGE O.pinit: { } > IPROG PAGE O.sysinit: { } > IPROG PAGE O.data: .bss: .far:.const: { } > EDATA PAGE 1 { } > IDATA PAGE 1 { } > IDATA PAGE 1 { } > IDATA PAGE 1.switch: { } > IDATA PAGE 1 .sysmem: { } > IDATA PAGE1•cio:{ } > IDATA PAGE1.MEM$obj: { } > IDATA PAGE1.sysheap: { } > IDATA PAGE1}2.基2实数FFT运算的算法该算法主要分为以下四步进行:1)输入数据的组合和位排序首先,原始输入的2N=256个点的实数序列复制放到标记有“ d_input_addr "的相邻单元,当成N=128点的复数序列d[n],其中奇数地址是d[n]实部,偶数地址是d[n]的虚部,这个过程叫做组合(n为序列变量,N为常量)。
调用DSP库函数实现FFT的运算

通信与信息工程学院2013 /2014 学年第二学期软件设计实验报告模块名称调用DSP库函数实现FFT的运算专业通信工程学生班级B110107学生学号学生姓名指导教师王奇报告内容一、实验目的(1)了解FFT 的原理;(2)了解在DSP 中FFT 的设计及编程方法;(3)了解在DSP 中CFFT 的设计及编程方法;(4)熟悉对FFT 的调试方法;(5)了解用窗函数法设计FFT 快速傅里叶的原理和方法;(6)熟悉FFT 快速傅里叶特性;(7)了解各种窗函数对快速傅里叶特性的影响。
二、实验原理1,,1,0,][][10-==∑-=N m W k x m X km NN k 1,,1,0,][1][10-==--=∑N k W m X N k x km N N m如果利用上式直接计算DFT,对于每一个固定的m,需要计算N 次复数乘法,N-1次加法,对于N 个不同的m,共需计算N 的2次方复数乘法,N*(N-1)次复数加法.显然,随着N 的增加,运算量将急剧增加, 快速傅里叶算法有效提高计算速度,利用FFT 算法只需(N/2)logN 次运算。
FFT 并不是一种新的变换,它是离散傅立叶变换(DFT )的一种快速算法。
由于我们在计算DFT 时一次复数乘法需用四次实数乘法和二次实数加法;一次复数加法则需二次实数加法。
每运算一个X (k )需要4N 次复数乘法及2N+2(N-1)=2(2N-1)次实数加法。
所以整个DFT 运算总共需要4N^2 次实数乘法和N*2(2N-1)=2N(2N-1)次实数加法。
如此一来,计算时乘法次数和加法次数都是和N^2 成正比的,当N 很大时,运算量是可观的,因而需要改进对DFT 的算法减少运算速度。
根据傅立叶变换的对称性和周期性,我们可以将DFT 运算中有些项合并。
我们先设序列长度为N=2^L,L 为整数。
将N=2^L 的序列x(n)(n=0,1,……,N-1),按N 的奇偶分成两组,也就是说我们将一个N 点的DFT 分解成两个N/2 点的DFT,一般来说,输入被假定为连续的。
快速傅里叶变换(FFT)的DSP实现

快速傅里叶变换(FFT)的DSP实现(天津大学电子信息工程学院)摘要:本文介绍了快速傅里叶变换(FFT)的快速高效的原理及实现方法,对快速傅立叶变换(FFT)的特点进行了研究和总结.对于快速傅立叶变换(FFT)在TMS320C54X系列数字信号处理器(DSP)实现中出现的计算溢出等问题进行了分析并提出了解决方法,同时据此使用DSP实现了快速傅立叶变换(FFT).关键词:数字信号处理;快速傅立叶变换;反序;计算溢出1引言:傅里叶变换是一种将信号从时域变换到频域的变换方式,在语音处理、图像处理、信号处理领域中都发挥了极大的作用,是一种重要的分析工具。
离散傅里叶变换(DFT)是连续傅里叶变换在离散系统中的表现形式,具有非常广泛的应用.但是由于DFT的计算量很大,因此在很长一段时间里其应用受到限制。
快速傅里叶变换(FFT)是实现普通离散傅里叶变换的一种高效方法,快速傅里叶变换(FFT)的出现使得傅里叶变换在实际中得到了广泛的应用.快速傅里叶变换并不是一种新的变换,它是离散傅里叶变换的一种快速算法。
它是DSP领域中的一项重大突破.由于考虑了计算机和数字硬件实现的约束条件,研究了有利于机器操作的运算结构,使DSP的计算时间缩短了一到两个数量级,还有效的减少了计算所需的存储容量,FFT技术的应用极大的推动了DSP的理论的技术的发展。
本文中使用的是由TI公司生产的TMS320C54系列的DSP。
C54x系列DSP具有很高的操作灵活性和速度。
它具有一个先进的修正哈佛结构、专门硬件逻辑的CPU、片内存储器、片内外设和专用的指令集、将C54xCPU 和片内存储器与外设配置组合在一起的螺旋结构。
这使得该系列可以满足电子市场众多领域的应用要求.2DSP在数字信号处理中的优势:数字信号处理是一门广泛应用于许多领域的新兴学科.20世纪60年代以来,随着计算机和信息技术的飞速发展,数字信号处理技术应用而生并得到迅速广泛的应用。
基于DSP的FFT实现

基于DSP的FFT实现傅里叶变换(Fourier Transform)是一种将信号在时间和频率域之间进行转换的数学工具。
它可以将信号从时域转换为频域,使我们能够分析信号的频率成分。
离散傅里叶变换(Discrete Fourier Transform,DFT)是一种计算机算法,用于对离散信号进行傅里叶变换。
离散信号是由一系列采样点组成的,并且在实际应用中,离散信号更常见于数字信号处理(Digital Signal Processing,DSP)系统。
FFT(Fast Fourier Transform)是一种高效的算法,用于计算DFT。
它通过利用信号的对称性和周期性,以O(nlogn)的时间复杂度计算DFT,相比于直接计算的O(n^2)时间复杂度更为高效。
因此,FFT在数字信号处理中被广泛使用,并且是很多DSP系统中实现频谱分析的核心算法。
基于DSP的FFT实现通常采用固定点数格式进行计算,以适应数字信号的要求。
固定点数格式将浮点数表示为带有整数和小数部分的定点数,其中小数部分的位数是固定的。
这允许在硬件实现中使用更简单和更高效的运算器,并且减少了计算过程中的存储需求。
在前向变换中,基于DSP的FFT实现通常采用蝶形运算器结构,该结构通过并行计算减少了计算量。
蝶形运算器将复数乘法和加法运算相结合,以高效地计算傅里叶变换的结果。
在反向变换中,基于DSP的FFT实现使用相同的蝶形运算器结构,但需要调整一些参数来恢复时域信号。
这些参数通常是指数项,用于将频域信号的幅度和相位信息与原始时域信号进行组合。
由于DSP系统通常具有固定的计算能力和存储容量,基于DSP的FFT 实现需要考虑对资源的高效利用。
这可能包括通过流水线技术实现并行计算,使用分块技术减少存储需求,并使用低功耗算法来减少计算负载。
总结起来,基于DSP的FFT实现是一种高效的数字信号处理技术,用于将时域信号转换为频域信号。
它通过利用固定点数格式和蝶形运算器结构,以高效和准确的方式计算傅里叶变换。
快速傅里叶变换的DSP实现

快速傅里叶变换的DSP实现FFT的基本原理是将N点的时间域信号转换为频域信号,其中N为2的幂。
FFT通过将DFT变换分解为递归处理的子问题,大大提高了计算效率。
下面将介绍FFT的DSP实现步骤。
第一步是将输入信号分解为偶数位和奇数位部分。
即将输入信号的下标为偶数和奇数的采样点分为两个序列。
第二步是对这两个序列分别进行FFT变换。
对于每个序列,不断递归地将其分解为更小的序列进行FFT变换。
第三步是将两个FFT变换的结果结合起来。
通过将奇数位序列的结果乘以旋转因子(Wn)与偶数位序列的结果相加,得到FFT的结果。
第四步是重复第二和第三步,直到最后得到完整的FFT结果。
在DSP实现FFT时,需要注意以下一些优化技巧。
首先是采用位逆序(bit-reversal)算法。
位逆序算法对输入序列进行重新排列,使得后续计算可以利用FFT的特殊结构进行高效处理。
其次是使用查表法计算旋转因子。
旋转因子是FFT中的关键部分,计算量很大。
通过将旋转因子预先计算并存储在查找表中,可以大大提高计算效率。
另外,可以采用并行计算的方法,同时处理多个子序列,以进一步提高计算速度。
此外,在实际应用中,还需要注意处理FFT的边界条件和溢出问题,以及对频谱结果进行解释和处理。
综上所述,FFT在DSP中的实现需要考虑算法的效率和优化技巧。
通过采用递归分解、位逆序、查表法和并行计算等方法,可以实现高效的FFT计算。
在实际应用中,还需要注意处理边界条件和溢出问题,以及对频谱结果的处理和解释。
希望本文的介绍能帮助读者更好地理解和应用FFT在DSP中的实现。
dsp的fft的设计与实现
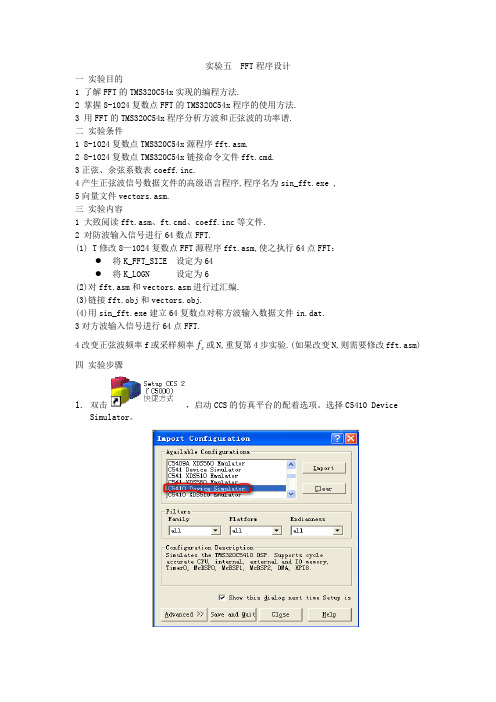
实验五 FFT程序设计一实验目的1 了解FFT的TMS320C54x实现的编程方法.2 掌握8-1024复数点FFT的TMS320C54x程序的使用方法.3 用FFT的TMS320C54x程序分析方波和正弦波的功率谱.二实验条件1 8-1024复数点TMS320C54x源程序fft.asm.2 8-1024复数点TMS320C54x链接命令文件fft.cmd.3正弦、余弦系数表coeff.inc.4产生正弦波信号数据文件的高级语言程序,程序名为sin_fft.exe ,5向量文件vectors.asm.三实验内容1 大致阅读fft.asm、ft.cmd、coeff.inc等文件.2 对防波输入信号进行64数点FFT.(1) T修改8—1024复数点FFT源程序fft.asm,使之执行64点FFT:●将K_FFT_SIZE 设定为64●将K_LOGN 设定为6(2)对fft.asm和vectors.asm进行过汇编.(3)链接fft.obj和vectors.obj.(4)用sin_fft.exe建立64复数点对称方波输入数据文件in.dat.3对方波输入信号进行64点FFT.f或N,重复第4步实验.(如果改变N,则需要修改fft.asm) 4改变正弦波频率f或采样频率s四实验步骤1.双击,启动CCS的仿真平台的配着选项。
选择C5410 DeviceSimulator。
2.点击project菜单栏的new选项,新建一个fft64的工程注意存储的路径。
2.把下图中用到的文件拷到工程文件目录的文件路径下。
3.在ccs平台中将用到的程序导入到平台中,点击project—>add file to project。
选择多个文件时,可以按住ctrl键。
4.将所有的程序段中的start改为_main,将fft.Asm中的K_FFT_SIZE .set 32 ;NK_LOGN .set 5 ;LOG(N)改为K_FFT_SIZE .set 64 ;NK_LOGN .set 6 ;LOG(N)5,对源文件进行编译(注意先对每个.asm文件先进行编译,以防止程序有错误),没有错误时进行链接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
芯片 特有的反序 间接寻址等 功能, FFT 算法程 序采 用
汇编语言编写, 主程序采用 C 语言, 因此程序具有良
好的接口性能和可扩展性能。
一般计算 N 点实数 FFT 时, 简单的把 N 点实数数
据当作 N 点虚部为 0 的复数数据来处理, 直接计算 N
点复数 FFT。这样不仅浪费了 DSP 片内资源, 还影响了
2 汇编模块 fft1024c.asm, 此模块的功能是计算 1024
点基 2 复数 FFT。输入的数据必须是 Q15 格式的数据。
3 汇编模块 fft2048.asm, 此模块的功能是劈分 1024
点复数 FFT 的结果, 得到 2048 点实数 FFT 的真正结果。
4 汇 编 模 块 fft_mag.asm, 此 模 块 的 功 能 是 计 算
图 1 系统结构框图
而言, 用于工 业探测的线 阵 CCD 像素不高 , 但在光谱 响 应 范 围 、几 何 精 度 、动 态 范 围 有 自 己 独 特 的 优 势 。比 如我们所用的 TCD1208 CCD 就是一款面 向光谱探测 用的线阵 CCD, 有 2160 像元, 光谱响应范围 400 纳 米- 1100 纳米, 并且动态范围大, 灵敏度高, 稳定可靠。 整个嵌入 式线阵 CCD 光谱 探测系统的 结构框图如 图 1 所示, 在 DSP 上要完成 CCD 驱动 、A/D 转换、FFT 运 算、控制液晶显示等功能, 其中 FFT 运算是重点。
计算的实时性, 尤其是点数比较大时, 这种影响更加明
显。为了提高实数 FFT 的计算效率, 利用 FFT 计算的特
点, 把 N 点实数数据打包成 N/2 点复数数据, 通过计算
N/2 点复数 FFT 来获得 N 点实数 FFT, 这样可以把 FFT
的计算速度提高近一倍。实数 FFT 的计算流程为:
1 把 2048 点 实 数 数 据 打 包 成 为 1024 点 复 数 数
2 在 FFT 计算的蝶形运算和劈分计算中, 涉及到 正弦和余弦计算。因此需要预先制好正弦和余弦表。
3 简单改变几个参数值和扩展一下正弦和余弦表, 就可以用此程序计算 4096 以及更大点数的实数 FFT。 但需要注意扩展存储空间以及防止结果精度的降低。
1.3 抗干扰设计 为防止各种干扰使得程序不能正常运行, 我们从 软硬件两个方面采取抗干扰措施。从硬件方面, 我们 采用 TI 的专用电源芯片 TPS7333, 为 DSP 提供稳定电 源; 在集成芯片的电源与地之间放置 0.01μF 和 0.1μF 的去耦电容, 并让去耦电容尽量靠近集成芯片; 模拟 地与数字地分开, 只在一点共接等。在软件方面, 为了 使程序跑飞的 DSP 回到正常状态, 加入看门狗功能。
图 3 频谱的幅度谱
(转 247 页)
- 160 - 360元 / 年 邮局订阅号: 82-946
《 现场总线技术应用 200 例》
您的论文得到两院院士关注
电子设计
先把满量程基 准 电 压 先 分 为 2m 个 区 间 , 用(2m- 1) 个比较器进行第一步 A/D 转换, 得到 m 位的二进制编 码作为 MSB。再把每个区间都分成 2n-m 个子区间, 用 (2n-m- 1)个比较器对 2m 个区间中的某一区间进行第二步 A/D 转换, 这一区间的选择由前面所得的 m 位的编码作 为图中开关控制信号得以确定。第二步 A/D 转换得到 ( n- m) 位二进制编码作为 LSB, 最终得到 n 位编码。
技 it has the features of easy realization, high efficiency, good expansibility and compatibility. It had run in the embedded system for
linear CCD spectral detection successfully.
DS P 开 发 与 应 用
中 文 核 心 期 刊《 微 计 算 机 信 息 》( 嵌 入 式 与 S OC )2006 年 第 22 卷 第 5-2 期
为工业控制、电机控制和数字信号处理等用途而设 计
的 DSP, 具 备 单 周 期 乘 加 指 令 , 具 有 FFT 反 序 间 接 寻
址功能, 最高运行速度为 40MIPS。为了充分利用 DSP
2048 点实数 FFT 的结果的幅值平方, 得到幅度谱, 输
出的数据格式为 Q14 格式。
主函数调用示例:
void main(void) {… … fft.ipcbptr=ipcb; fft.magptr=mag;
//FFT 计算缓冲区 //存 放 幅 度 谱
fft.init1(); 转因子
//复制 计 算复 数 FFT 所 需 的 旋
目前, 由于线阵 CCD 在光谱探测 、光 学 传 感 等 方 数据处理。
面的广泛应用, 常需要嵌入式芯片( 如 DSP) 对 CCD 输
出的数据进行实时分析处理。用于工业探测的线阵
CCD 与我们通常认识的面阵 CCD 有所 不同。我们日
常生活中出现的面阵 CCD 少说也有几十万像素, 高的 可达上千万像素, 常用在数码相机等设备上。相比较
文献标识码: A
Abstr act: Because of the demand of data processing in linear CCD, this paper introduces the realization of 2048 points FFT in
TMS320C240x fixed- point DSP. Arithmetic program of FFT is programmed in assembly code, and it can be called by C function. So
文其林:硕士研究生
减一个变址量的间接寻址方式, 为各种查表运算提供
基金项目:北京市优秀人才培养专项经费资助
方便; 能在一个指令周期完成乘和累加操作, 提高了
基金编号: 20041D0501511
乘法运算的速度。TMS320LF2407 定点 DSP 是一款专
《 P LC 技术应用 200 例》
邮局订阅号: 82-946 360 元 / 年 -159-
您的论文得到两院院士关注 文章编号:1008- 0570(2006)05- 2- 0159- 02
DS P 开 发 与 应 用
204 8 点 F F T 在定点 DS P 上的实现
Acco m p lis h m e n t o f 2048 p o in ts FFT in TMS 320C240x fixe d - p o in t DS P
新 用汇编语言编写, 但是在各子程序的入口和出口都考 虑了与 C 语言的兼容性, 使得各子程序能够直接被 C
语言调用。
1 汇编模块 fft_brev.asm, 此模块的功能是把 2048
点实数数据打包成为 1024 点复数数据 , 并把复数数
据进行倒位序排列。在 C 函数中, 通过 FFT_brev()来调
语 言 编 写 , 可 通 过 C 语 言 函 数 调 用 , 因 此 具 有 实 现 简 单 、高 效 的 特 点 , 且 扩 展 性 和 兼 容 性 强 , 可 运 行 于 嵌 入 式 线 阵 CCD 光 谱
探测系统中。
关键词: FFT; DSP; 劈分算法; 位反转算法
中图分类号: TP391
(北京工业大学)文 其 林 白 晓 东 周 洪 直 贾 宝 敦
Wen , Qilin Bai, Xiaodong Zhou , Hongzhi J ia , Baodun
摘要: 针 对 线 阵 CCD 输 出 数 据 的 处 理 需 要 , 介 绍 了 2048 点 FFT 在 TMS320C240x 定 点 DSP 上 的 实 现 。 FFT 算 法 程 序 采 用 汇 编
据, 并完成复数数据的位反转操作;
2 计算 1024 点基 2 复数 FFT;
3 劈分还原计算, 获得 2048 点实数 FFT 结果;
技
4 计算幅值的平方, 获得频谱的幅度谱。
术
根据实际需要, 还可以对数据进行加窗函数处理。 1.2 具体函数介绍
创
根据上面的程序流 简, FFT 算法函数 全部 采
考虑到 CCD 是 2160 像元, 为了方便运用基 2 算
1 程序介绍与实现
1.1 程序流程 FFT 的计算量比傅 立叶变换的 计 算 量 减 少 了 , 但 是 FFT 要 做 到 大 点 数 , 实 时 运 算 , 对 于 普 通 的 单 片 机 来说还是一件比较困难的事。一方面, FFT 需要对原始 自然序列进行码位倒序排列; 另一方面, 蝶形运算是 复数运算, 需要多次查表相乘运算才能实现。DSP 控制 器就是针对这些需求而设计的专用芯片: 具有专为 FFT 算法而设计的反序间接寻址; 可实现增/减 1 或增/
用。具体声 明 形 式 为 : void FFT_brev (int *source, int
*done, int size), 其中指针 source 指向的数组存放未经
倒位序排列的数据, 指针 done 指向的数组存放倒位序
排列后的数据, size 是数组的大小, 为了节省空间, 指
针 source 和 done 可以指向同一数组。
2 实验结果及分析
图 2 2048 点正弦数据波形
整个程序是在 集成开发环 境 CC4.1 下开发完 成 , 为了方便程序运行结果的说明, 用此程序去计算一组 2048 点 正 弦 数 据 , 频 率 为 1 赫 兹 , 采 样 频 率 为 128 赫 兹。数据采用 Q15 格式。
正弦数据波形如图 2 所示。一般情况下, 我们只 关心信号频域的幅度谱。幅度谱|X( k) |2 的计算: X( k) = Xr( k) +jXi( k) , |X( k) |2=|Xr( k) |2+|Xi( k) |2, FFT 计 算 结 果 的信号幅度谱|X( k) |2 如图 3 所示。
