4高斯分布
1-4 高斯定理class - 副本
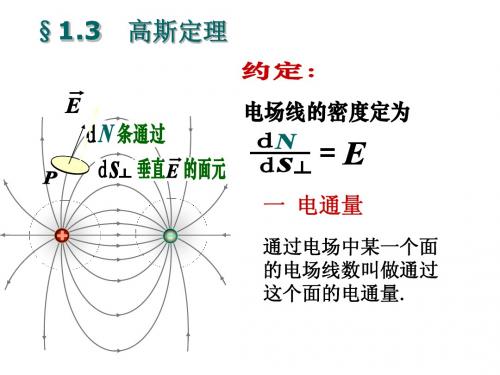
高斯定理 高斯定理的应用
(Gauss’ Law)
(用高斯定理求解的静电场必须具有一定的对称性) 其步骤为 对称性分析;
根据对称性选择合适的高斯面;
应用高斯定理计算.
1
高斯定理
(Gauss’ Law)
例1
均匀带电球壳的电场强度 一半径为 R , 均匀带电 Q 的薄 球壳 . 求球壳内外任意点的电场强 度. 解(1) 0 r R
高斯定理 8 – 4 电场强度通量 高斯定理
第八章静电场
8 – 4 电场强度通量
高斯定理 续32
第八章静电场
三
高斯定理
在真空中,通过任一闭合曲面的电场强度通量, 等于该曲面所包围的所有电荷的代数和除以 0 . (与面外电荷无关,闭合曲面称为高斯面)
1 Φe E dS
r
s2
+ + +
+
S1 +
O
+ + +
R
r
+
+ + +
(2) r
R
Q 2 4π 0R
E
o
R
r
例2:求均匀带电球体的电场分布。已知球体的半径 为R,所带总电量为Q。
1
高斯定理
(Gauss’ Law)
例3 无限长均匀带电直线的电场强度 无限长均匀带电直线,单位长度上的电荷,即 电荷线密度为 ,求距直线为 处的电场强度.
3)穿进高斯面的电场强度通量为负,穿出为正.
4)仅高斯面内的电荷对高斯面的电场强度通量有贡献.
5)静电场是有源场.
1
高斯定理
(Gauss’ Law)
5-4 电场强度通量 高斯定理

5-4 电场强度通量
高斯定理
正点电荷与负点电荷的电场线
+
-
5-4 电场强度通量
高斯定理
一对等量正点电荷的电场线
+
+
5-4 电场强度通量
高斯定理
一对等量异号点电荷的电场线
-
+
5-4 电场强度通量
高斯定理
一对不等量异号点电荷的电场线
2q
-q
5-4 电场强度通量
高斯定理
带电平行板电容器的电场线
+ + + + + + + + + + + + +
i 1 n
3 高斯定理的讨论 (1) 高斯面:闭合曲面. (2) 电场强度:所有电荷的总电场强度. (3) 电通量:穿出为正,穿进为负.
(4) 仅面内电荷对电通量有贡献.
5-4 电场强度通量
四 高斯定理应用举例 用高斯定理求电场强度的一般步骤为 对称性分析; 根据对称性选择合适的高斯面; 应用高斯定理计算.
高斯定理
1 Φe E dS ε0 S
q in i
i 1
n
5-4 电场强度通量
高斯定理
例2 设有一半径为R , 均匀带电Q 的球面. 求球面内外任 意点的电场强度. 解 高斯面:闭合球面 对称性分析:球对称 (1) 0 r R E dS 0 E 0
in ei
E
1 n in SE dS ε0 qi i 1
dS
s
qi
5-4 电场强度通量
高斯定理
2 高斯定理 在真空中静电场,穿过任一闭合曲面的电场强度通量,
4高斯最小拘束原理

n
3
证:将拘束改写为 1 n 1 Z = ( Fi − m i a i ) ⋅ ( Fi − m i a i ) 2 i =1 m i
∑
设真实运动的加速度为 && ,约束允许的可能加速度 r 为 && + δ&& ,则拘束Z的变化: r r
1 n 1 ∆ Z = ∑ {[ Fi − m i ( && + δ &&)] ⋅ [ Fi − m i ( && + δ &&)] − r r r r 2 i =1 m i ( Fi − m i &&) ⋅ ( Fi − m i &&)} r r 1 n 1 = ∑ [ m i2δ && ⋅ δ && − 2 m i ( Fi − m i &&)δ &&] r r r r 2 i =1 m i n 1 n = ∑ m i δ && ⋅ δ && − ∑ ( Fi − m i &&)δ && r r r r 2 i =1 i =1
16
根据高斯原理: ∂Z ∂Z ∂Z & && + && + δZ = δx δy δϕ& = 0 && ∂&& x ∂&& y ∂ϕ
∂Z ∂Z ∂Z = 0, = 0, =0 && ∂&& x ∂&& y ∂ϕ
即:
∂&&1 x ∂&&2 x m1 ( &&1 − g sin α ) x + m2 ( &&2 − g sin α ) x = 0 (6) ∂&& x ∂&& x ∂&&1 y ∂&&2 y m1 &&1 y y + m2 &&2 = 0 (7) y y ∂&& ∂&& ∂&&1 x ∂&&1 y ∂&&2 x ∂&&2 y m1 ( &&1 − g sin α ) x + m1 &&1 y + m2 ( &&2 − g sin α ) x + m2 &&2 y =0 && && && && ∂ϕ ∂ϕ ∂ϕ ∂ϕ
大学物理高斯定理

第11章 静电场
11-4 高斯定理
2 点电荷在任意形状的高斯面内 通过球面 S 的电场线也必通 过任意曲面S‘ ,即它们的电 通量相等。 为 q / o
S'
S +
q E Φ E d dS e e SS o
第11章 静电场
11-4 高斯定理
3 电荷q在闭合曲面以外
0
dV E d S 若电荷连续分布,则为 e: E d S s V
0
第11章 静电场
11-4 高斯定理
讨论
1 闭合面内、外电荷 对
S
E 都有贡献
对电通量 E dS 的贡献有差别
只有闭合面内的电量对电通量有贡献 2 静电场性质的基本方程
非匀强电场
E
dS
en
Φ dΦ S E dS
第11章 静电场
11-4 高斯定理
讨论
1
dΦ E dS 的正、负取决于面元的法线方向与
电场强度方向的关系
如图所示: 若面元法向相反:
E dS 0
E dS ' 0
E
dS
dS '
第11章 静电场
11-4 高斯定理
11-4 高斯定理
描述电场的两种方法:电力线和电通量。 11.4.1 电场线 1 曲线上各点的切线方向都与该点处的场强方向一致 2 电场线密度
EP
dN E dS
第11章 静电场
EQ
Q
P
dN
dS
11-4 高斯定理
电场线的性质: 电场线起自于正电荷或无穷远,止于负电荷或无穷 远 ,没有电荷处不中断。 对于静电场不可能出现单一绕向的闭合电力线。 两条电场线不会相交,不能相切。
e4高斯分布的星像点精确模拟及质心计算

第7期王海涌,等:基于高斯分布的星像点精确模拟及质心计算卜2一盯‰c薏,一丢<(8)I缸一2--0,2ln(堕)一1。
g。
22即参照公式(7)和(8)的同行(或同列)对称像素,取灰度值较大的一个,一方面可以提高解算精度,另一方面在像点较暗及阈值较高的情况下,避免灰度为零出现奇异值。
最后,根据z。
一△z+z,,Y。
一△j,+y,,得到星像点的精确质心估计坐标(z。
,Y。
)。
这种高斯像点质心提取算法是无偏的,参与运算的像元灰度取相对较大的值,信噪比高,这是该新型算法优势所在。
4仿真结果4.1理论仿真选定某一像素对角线上等距排列的20个点作为某导航星在CCD坐标平面上的映射坐标(z。
,Y。
),即z。
和Y。
都以间距0.05pixel分布在半开区间[一0.5,0.45)pixel内,仿真条件:A=500,盯=0.671,依次按照公式(1)进行4pixel×4pixel灰度扩散分配,加入高斯噪声N(0,1.22)后取整,然后依据公式(6)~(8)进行像点质心解算,针对每个映射坐标点做50次测量,基于真值求其(a)两种高斯算法RMS值的比较(a)RMSoftwoGaussmethods缈(b)三种算法RMS值的比较(b)RMSofthreemethods图4算法标准差的比较Fig.4ComparisonofRMSresultsofdifferentalgo—rithms标准差,并与灰度重心法和加权灰度重心法的运算结果进行标准差的比较。
从以上仿真条件可知,对于Ax和Ay的处理是等价的,因而可以只分析Ay的仿真结果,从图4(a)可以看到,当偏差Ay∈[一0.15,0.15]时,涉及像元对角线上中心点及左右各3个点,对这7个点的位置进行估计采用第一种算法即公式(6)最好;当Ay(壬[一o.15,0.15]时,涉及到上述7个点之外的其它位置点,选用第二种算法即公式(7)和(8)最好,两种算法可以分3段区间合成一个分段函数:fformula(6)样一0.15≤Aye0.15Iformula(7)。
静电4-高斯定理 (1)

1) 通过包围点电荷q 的同心球面的电通量都等于q/0 在该场中任取一包围点电荷的闭合球面(如图示)
穿过S的电通量 = 穿过S的电力线条数
Φe S E dS EdS E dS
q 4 0 r
2
4r
2
Φe
q
0
S
q E
E
dS
这一结论是库仑平方反比关系的必然结果 电量为q 的点电荷产生的电力线总条数为: N q / 0 2 4 r 以q为球心、半径为r 的整个 4 4球面度 2 球面对球心张开的立体角为: r 任意闭合曲面对曲面内任一点所张 开的总立体角均为4球面度:
3.3 高斯定理的表述和证明
1.表述: 在真空中的静电场内,通过一个任意闭合曲面 的电通量e等于该闭合面所包围的所有电荷量的代 数和qi 除以0 ,与闭合面外的电荷无关 。
e= E dS
S
q
i
i内
0
闭合面S习惯上 称为高斯面
2.高斯定理的明
库仑定律 + 叠加原理
一般电荷分布的场
3.4 从高斯定理看电力线的性质
看书自学
3.5. 高斯定理在解场方面的应用
E dS
S
q
i
i
0
Q 分布具有某种对称性的情况,高斯定理求 E较方便
步骤
1. 对称分析 2. 选取适当高斯面
3. 计算电通量
4. 让它等于面内自由电荷的
1/ 0
9
常见的电量分布的对称性:
球对称 均匀带电的 轴对称 无限长 柱体 柱面 带电线 面对称 无限大
E
均匀带电球体
E内 0 E外
Q 4 0 r
matlab 高斯分布算概率 -回复

matlab 高斯分布算概率-回复【Matlab 高斯分布算概率】引言:高斯分布,也被称为正态分布,是统计学领域中最常见的一种概率分布。
在很多实际应用中,高斯分布被广泛用于模拟和分析数据。
本文将介绍如何使用Matlab来计算和分析高斯分布概率。
一、高斯分布的定义与特点:高斯分布是一个连续概率分布,其特点是呈钟形曲线,中心对称,两边逐渐向下趋近于零。
高斯分布由两个参数决定:均值μ(表示分布的中心位置)和标准差σ(表示数据分布的离散程度)。
高斯分布的概率密度函数可以用数学公式表示为:p(x) = (1 / sqrt(2π*σ^2)) * exp(-((x-μ)^2) / (2σ^2))其中,sqrt表示开平方,exp表示指数函数。
二、Matlab中的高斯分布函数:在Matlab中,用于计算高斯分布概率的函数是normpdf(x, μ, σ),其中x是要计算概率的点,μ是均值,σ是标准差。
通过该函数,我们可以直接计算给定均值和标准差下的概率。
三、使用Matlab计算高斯分布概率:下面我们通过一个具体的例子来演示如何使用Matlab计算高斯分布概率。
例子:假设有一组数据x = [1, 2, 3, 4, 5, 6, 7, 8],我们希望计算在均值为4,标准差为1的条件下,各个数据点的概率。
以下是具体的计算步骤:1. 打开Matlab,并定义数据x、均值μ和标准差σ:x = [1, 2, 3, 4, 5, 6, 7, 8];μ= 4;σ= 1;2. 使用normpdf函数计算每个数据点的概率:prob = normpdf(x, μ, σ);3. 输出结果:disp(prob);运行上述代码后,将会得到以下结果:0.2419 0.0539 0.0044 0.0001 0.0044 0.05390.2419 0.3989结果表示在给定均值为4和标准差为1的条件下,各个数据点的概率。
四、Matlab绘制高斯分布曲线:除了计算高斯分布概率,Matlab还提供了绘制高斯分布曲线的功能,通过绘制曲线可以更直观地观察数据分布情况。
高斯简介及主要事迹(3篇)

第1篇一、高斯简介卡尔·弗里德里希·高斯(Carl Friedrich Gauss,1777年4月30日-1855年2月23日),德国数学家、物理学家、天文学家。
高斯是数学史上最伟大的数学家之一,被誉为“数学王子”。
他的研究成果涵盖了数学的各个分支,对现代数学的发展产生了深远的影响。
二、高斯的主要事迹1. 数论领域的贡献(1)证明了代数基本定理:高斯在1801年发表的论文《算术研究》中,证明了代数基本定理,即每一个非零的复系数多项式都有至少一个复根。
这一成果为复数理论的发展奠定了基础。
(2)提出了高斯整数:高斯在1801年的论文中,首次提出了高斯整数的概念,即形如a+bi的数,其中a、b为整数,i为虚数单位。
高斯整数在数论研究中具有重要的地位。
(3)解决了二次互反律:高斯在1801年发现了二次互反律,即对于任意的两个整数m和n,当n不等于0且m的奇偶性与n的奇偶性相同时,存在整数x和y,使得m^2 = nx^2 + ny^2。
这一成果为解决丢番图方程奠定了基础。
2. 几何学领域的贡献(1)非欧几何的萌芽:高斯在1827年发表了论文《关于曲面的一般研究》,提出了非欧几何的基本思想。
他认为,几何学的研究对象不仅仅是平面,还包括曲面。
这一观点为后来的非欧几何发展奠定了基础。
(2)最小二乘法:高斯在1795年提出了最小二乘法,这是一种处理数据误差和不确定性问题的数学方法。
最小二乘法在统计学、物理科学等领域有着广泛的应用。
3. 天文学领域的贡献(1)高斯-塞德尔迭代法:高斯在1809年提出了高斯-塞德尔迭代法,这是一种求解线性方程组的迭代方法。
该方法在数值计算中具有重要的地位。
(2)地球椭球形的计算:高斯在1821年计算出了地球椭球形的参数,为后来的地球物理研究和地理信息系统的发展提供了重要的数据基础。
4. 物理学领域的贡献(1)电磁学:高斯在电磁学领域的研究成果为麦克斯韦方程组的建立奠定了基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
uur uur
已知线性变换 Y A X,其中高斯矢量X ~ N ur
证明:随机矢量Y也是高斯矢量。
M X ,CX
,A
aij
为常系数矩阵。
mn
ur
思路:求Y的特征函数。
Y特征函数定义 线性变换代入 A放入括号中
X特征函数定义
QY u1,L ,un E exp
ur T ur jU Y
u1
M ,
xn
un
uur MX
m1
M ,
mn
C11 C12 L
uur DX
CX
C21 M
C22 M
L O
Cn1 L L
C1n
C2n
M
Cnn
fX x1,L , xn
1
n
1 exp
2 2 CX 2
r uur xMX
T CX1 2
r uur xMX
QX
u1,L
3 条件数学期望
新
随机变量关于某 个给定值的条件
数学期望
随机变量关于另 一个随机变量的 条件数学期望
随机矢量的数字特征
数学期望 矩
相关理论 特征函数
数学期望 方差 互相关
协方差
随机矢量的数字特征
数学期望
矩 相关理论 特征函数
相关系数的引入
不相关、正交
不相关、正交、独 立之间的关系
随机矢量的数字特征
内容组织
描述 方法
特殊 性质
概率密度
一维
特征函数
n维
独立与不相关等价 线性变换
一维高斯分布
fX
x
1
e
(
xm)2 2 2
2
相应的特征函数为
QX
u
exp
jum
u 2
2
2
方差 2 D[X ]
数学期望 m EX
要牢记 求解过程见P55例1.30
n维高斯分布
r x
x1 M,
ur U
一元特征函数的性质
5、相互独立变量和的特征函数等于特征函数之积。
n
n
X1,K , Xn相互独立,Y Xi,则 QY u QXi u
i 1
i 1
QY
u
E e juY
E e ju( X1 X2 L
Xn )
n E
i1
e juXi
n i 1
E e j Xi
n
QXi
i 1
6、若随机变量X的n阶绝对矩存在,
rect( t ) ƒ
Sa
2
1
1
1e
jux dx
1 e jux
1
e ju-1
0
ju 0 ju
rect(t)
1 0
, ,
t 1 2 t 1 2
1 ju
e
ju
2 e ju
2 e ju
2
2 j sin (u ju
2) e ju
2
e ju 2 Sa(u ) 2
思考: 2系数体现在哪里?
E Y kP Y k kCnk pk 1 p nk L
k 1
k 1
计 算
DY (k EY )2 Pk (k mY )2 Cnk pk 1 p nk L
k 1
k 1
很 难
n
n
QY e jk P Y k e jkCnk pk qnk L
k 1
k 1
exp k 1
jmk uk
n k 1
uk2 2
2 k
exp
n k 1
jmk uk
uk2
2 k
2
n
exp jmkuk
k 1
uk2 2
2 k
n
QX k
k 1
uk
特殊性质2——线性变化
高斯分布的线性变换后仍服从高斯分布。
uur X
X1 M
X n
ur Y
Y1
M
Ym
ur uur
n
QX
u1,L ,un
ur T QX U
E
e
uur T jU
uur X
E[e k1
juk
Xk
]
对应关系
1
2
n
QX
u1,L ,un
噲垐nn维 维垐垐傅 傅立 立垐垐叶 叶正 逆垐垐变 变换 换垎垐 f X
x1,L , xn
特征函数的性质(n维)
1、 QX (u1,...,un ) QX (0,...,0) 1
新
随机变量关于某 个给定值的条件
数学期望
随机变量关于另 一个随机变量的 条件数学期望
随机矢量的数字特征
数学期望 矩
相关理论 特征函数
数学期望 方差 互相关
协方差
随机矢量的数字特征
数学期望
矩 相关理论 特征函数
相关系数的引入
不相关、正交
不相关、正交、独 立之间的关系
随机矢量的数字特征
数学期望
矩
相关理论
新
特征函数
定义 性质
一维 n维
高斯分布
☆ 概率论的总结和应用 ☆
重要地位
在实际应用中,常常遇到大量随机变量的问 题。中心极限定理已证明,在满足一定条件 下,大量随机变量和的极限分布是高斯分布。 因此,高斯分布占有特殊的地位,是科学技 术领域中最常遇到的分布,也是无线电技术 理论(包括噪声理论,信号检测理论,信息 理论等)中最重要的概率分布。
,un
E
e
uur T jU
r x
exp
j
uur M
T X
ur U
ur U
T
CX
ur U
2
举例(多维高斯) CX 6
CX1
1 6
5 2
2
2
r uur
xMX
T CX1
r uur xMX
x1
x2
1 6
5 2
2
2
x1
x2
1 6
(5x12
2x22
4x1x2 )
fX
x1, x2
整理,A和U分开
特殊性质2——线性变化
uur
ur
uur
uur uur
MY E[Y] E AX A E[X ] AM X
CY
ur D[Y
数学期望
矩
相关理论
新
特征函数
定义 性质
一维 n维
特征函数的定义(一维)
1
2
QX
u 噲 垐傅 傅垐垐立 立叶 叶垐正 逆垐变 变换 换垎垐
f
x
变换是唯一的
存在2系数, 不是傅立叶变换
QX u E[e juX ]
f
xe juxdx
2
1
2
f
x
e
jux
dx
2 F 1
4
u,v0
CXY RXY E[ X ]E[Y ] 4 0 4
XY
CXY
XY
CXY 4 1 DX DY 4
线性相关 Y X 1
随机矢量的数字特征
数学期望 矩
1
一维随机变量 二维随机变量 n维随机变量
随机矢量的函数
离散型 连续型
相关理论 特征函数
2 数学期望的性质
3 条件数学期望
举例(一元特征函数的性质)
1
QXi u E e juXi e juk P Xi k q pe ju k 0
QY u n QXi u q pe ju n
i 1
性质5
举例(一元特征函数的性质)
EY j d pe ju q n np
du
u0
E
Y
2
j
2
d2 du 2
ur Y的特征函数为:QY (u1,...,uk ) QX (u1,...,uk , 0,..., 0)
7、E
X1n
X
k 2
j
nk
nk QX u1,u2 u1nu2k
E XY 2QXY u,v
uv u 0,v 0
u1 0,u2 0
8、QX
(u1,u2 )
E[
X1n
X
k 2
n0 k0
随机信号分析
南京航空航天大学 信息科学与技术学院
常建平 李海林
概率论
概率空间 高斯分布
随机变量
多维随机变量
(随机矢量)
概率论
随机变量的 数字特征
随机变量 函数的分布
随机矢量的数字特征
数学期望 矩
1
一维随机变量 二维随机变量 n维随机变量
随机矢量的函数
离散型 连续型
相关理论 特征函数
2 数学期望的性质
b1 M
ur Y
uur AX
ur B
a1X1 M
b1
an nn
bn n1
多元
an X n bn
n
可得:QY (u1,u2,L
j ukbk , un ) e k1
QX
a1u1,L , anun
ur
2、已知r 1,A a1,L ,an 1n , B b(常数)
一维随机变量
E[X ] ( j) dQX (u)
E[X k ] ( j)k d kQX (u) duk
u0
du u0
E[
X
2
]
d
2QX (u) du2
u0
举例(一元特征函数的性质)
例1.31 求二项分布的数学期望、方差和特征函数?
解:① 方法一:二项分布的分布律为
