电力变压器的参数与数学模型
电机学变压器的运行原理(空载、负载、数学模型)

第8章 变压器
28
2、T型等效电路 T型等效电路的形成过程,见下图。
I&1 R1
X 1
R2
I&0
Rm
U&1
E&2 E&1E&2 E&1
E&2
Xm
X 2 I&2
U&2
Z L
T型等效电路的形成过程
第8章 变压器
29
Γ型等效电路
对于电力变压器,一般 I1NZ1<0.08U1N,且 I1NZ1 与 -E1是相量相加,因此可将励磁支路前移与电源并 联,得到Γ型等效电路。
1、空载电流的波形
电网电压为正弦波,铁 心中主磁通亦为正弦波。若 铁心不饱和(Bm < 1.3T), 空载电流 i0 也是正弦波。
电力变压器,Bm= 1.4T ~1.73T,铁心都是饱和的 。其励磁电流呈尖顶波,除 基波外,还有较强的三次谐 波和其它高次谐波。
第8章 变压器
11
2、空载电流与主磁通的相量关系
问题:一般电力变压器 的变比 k 较大,一、二 次侧的电压、电流差别
很大,计算不便,画相
量图更加困难。因此,
下面介绍分析变压器的 一个重要方法——等效 电路、折算。
第8章 变压器
19
四、绕组归算(折算)及数学模型
所谓把二次侧折算到一次侧,就是用一个匝数为N1 的等效绕组,去替代变压器匝数为N2二次侧绕组,折 算后的变压器变比 N1/ N1=1 。
第8章 变压器
30
4、简化等效电路和相量图
对于电力变压器,由于 I0<0.03I1N,故在分析变压器满载及负 载电流较大时,可以近似地认为 I0=0,将励磁支路断开,等效电 路进一步简化成一个串联阻抗,如图所示。
电力网络等值电路_图文

一.双绕组变压器的参数和数学模型
.
RT jXT
Io
.. U1N Ig
.BT GT Ib
短路实验Βιβλιοθήκη 空载实验铭牌参数:SN 、
UIN/UⅡN
、
Pk、Uk% 、
P0、I0%
阻抗(短路实验:在原边加I1N)
1.电阻
变压器的电阻是通过变压器的短路损耗Pk ,其近似等于额定总铜耗PCu。
五个基准值中只有两个可任意选择,其余派生。 一般选功率和电压。
功率的基准值:选取某一整数,如:100MVA
电压的基准值:取参数和变量都将向其归算的该级额定 电压。如拟将参数归算到220kV侧,则 基准电压取220kv
当选定各变量的基准值时,可表示出相应的标么值 。如:
结论::线电压和相电压的标幺值数值相等; 三相功率和单相功率的标幺值数值相等。
Io
.. U1N Ig
.BT GT Ib
电导
变压器电导对应的是变压器的铁耗,近似等 于变压器的空载损耗,因此变压器的电导可 如下求解:
电纳
在变压器中,流经电纳的电流和空载 电流在数值上接近相等,其求解如下:
二.三绕组变压器的参数和数学模型
ZT2
高
中
ZT1
2
1
ZT3
3
低
YT
三绕组变压器电气结 线图
由于所选变比不同,可分为准确计算法和近似 计算法
基准值改变后标么值的换算
求多电压级网络标么值等值电路的两种方法
1)参数归算法(先有名值归算,后求标么值) ①取基本级(SB=SN,UB=UN); ②参数折算(将各级电压折算到基本级侧); ③求标幺值。 2)基准值归算法(先基准值归算,后求标么值) ①取基本级(SB=SN,UB1=UN1); ②基本级折算(将基本级SB、UB1折算到各电压级 ,分别求出UB2、UB3、……、UBn); ③求标幺值。
电力系统各元件的数学模型

推导过程:从1-1’,2-2’之间等值,将导纳支路拿出去
ZT 1:k
I1 1 I2 k
U2
k
U1
I1
ZT
1 I1
U1
ZT
1:k I2
2 U2
I1
U1 ZT
U2
1’
ZT k
U1 (y10
y) 12
2’
U2
y 12
I2
U1 ZT k
U2 ZT k2
U1 y12
U2 (y20
y) 12
§2.5 电力系统的等值电路
一些常用概念
1. 实际变比 k
k=UI/UII UI、UII :分别为与变压器高、低压绕组实际 匝数相对应的电压。 2. 标准变比kN
• 有名制:归算参数时所取的变比 • 标幺制:归算参数时所取各基准电压之比
3. 非标准变比 k* k*= k /kN=UIIN UI /UII UIN
U
U UB
I S Z
I IB S SB Z ZB
P jQ SB
R jX ZB
P SB R ZB
j
Q SB
P
jQ
j
X ZB
R
jX
§2.5 电力系统的等值电路
2、基准值的选取 1) 基准值的单位与对应有名值的单位相同 2) 各种量的基准值之间应符合电路的基本关系
SB 3 UB IB UB 3 IB ZB
§2.5 电力系统的等值电路
四、电力系统的等值电路制订
1、决定是用有名值,还是用标幺值
容量不相同时 2、变压器的归算问题
电压等级归算
采用Γ型和T型 采用π型—不归算
3、适当简化处理
第二章电力系统各元件的数学模型

试验时小绕组不过负荷,存在归算问题,归算到SN
2) 对于(100/50/100)
2
Pk (12)
P' k (12)
IN 0.5IN
P 4 ' k (12)
2
Pk ( 23)
P' k (23)
IN 0.5IN
P 4 ' k ( 23 )
3) 对于(100/100/50)
2
Pk (13)
P' k (13)
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
§2.3 电力线路的参数和数学模型
一次整循环换位:
A B
C
换位的目的:为了减 少三相参数的不平衡
§2.3 电力线路的参数和数学模型
Xd
§2.1 发电机的数学模型
受限条件
定子绕组: IN为限—S园弧
转子绕组: Eqn ife 励磁电流为限—F园弧 Xd
原动机出力:额定有功功率—BC直线
其它约束: 静稳、进相导致漏磁引起温升—T弧
进相运行时受定 子端部发热限制 受原动机出力限制
定子绕组不超 过额定电流
励磁绕组不超 过额定电流 留稳定储备
2、由短路电压百分比求XT(制造商已归算,直接用)
U U U U 1 k1(%) 2
k(12) (%) k(13) (%) (%) k(23)
XT1
Uk
1(%
)U2 N
100SN
U U U U 1 k2 (%) 2
k(12) (%) k(23) (%) (%) k(13)
2.3-电力变压器的参数与数学模型

2.3-电力变压器的参数与数学模型电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器,假定:绕组电阻为零;因此绕组损耗I2R为零。
铁心磁导率是无穷大,所以铁心磁阻为零。
不计漏磁通;即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。
不计铁心损耗。
图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:(2-46)磁场强度矢量Hc 为(2-47)其中,磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大,则磁阻R c近似为零。
(2-48)上式可写为:图2-21为双绕组变压器的示意图。
(2-49)或者图2-21中的标记点表示电压E1和E2,在标记点侧是+极,为同相。
如果图2-21中的其中一个电压极性反向,那么E1与E2相位相差180o。
匝数比k定义如下:理想单相双绕组变压器的基本关系为(2-50)(2-51)由推导可得两个关于复功率和阻抗的关系如下。
图2-21中流进一次侧绕组的复功率为(2-52)代入(2-50)和(2-51)(2-53)可见,流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。
即理想变压器没有有功和无功损耗。
如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连,那么(2-54)这个阻抗,当折算到一次侧时,为(2-55)因此,与二次侧绕组相连的阻抗Z2折算到一次侧,需将Z2乘以匝数比的平方k2。
2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器,与理想变压器的区别如下:计及绕组电阻;铁心磁导率为有限值;磁通不完全由铁心构成;计及铁心有功和无功损耗。
图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组,用于计及该绕组损耗I2R。
电抗为一次绕组的漏电抗,串联于一次绕组用于计及一次绕组的漏磁通。
这个漏磁通是仅与一次绕组交链的磁通的组成部分,它引起电压降落,对应且超前。
漏电抗引起无功损耗。
类似的,二次绕组中串联了电阻和电抗。
电力系统的模型和参数_变压器的数学模型

电力系统的模型与参数
变压器的等值电路
带变比的等值电路
电力系统的模型与参数
变压器的等值电路
Π型等值
例题
例1.
有一台SFL20000/110型的降压变压器 向10kV电网供电,铭牌参数: ΔPS = 135kW,VS% = 10.5,ΔP0 = 22kW, I0% = 0.8 试计算归算到高压侧的变压器参数并画出忽 略励磁支路的Π型等值电路
三绕组变压器的参数计算
三绕组变压器的空载试验
与双绕组变压器相同
作业
一台220/121/10.5kV,120MVA,容量比
100/100/50的三相三绕组变压器,I0% = 0.9 ,P0 = 123.1kW,短路损耗和短路电压如下 表所示。试计算励磁支路的导纳,各绕组的 电阻和等值电抗。各参数归算到中压侧。
高压-中压 短路损耗(kW) 短路电压(%) 660 24.7 高压-低压 256 14.7 中压-低压 227 8.8 未归算到SN 已归算
变压器并列运行的条件
连接组别相同
接线组别不同在并列变压器的二次绕组中会出现电压差 ,在变压器的二次侧内部产生循环电流。 变比相同 变压器比不同,二次电压不等,在二次绕组中也会产生 环流,并占据变压器的容量,增加变压器的损耗。 短路电压值相同 变压器短路电压与变压器的负荷分配成反比。 容量相近 容量不同的变压器短路电压不同,负荷分配不平衡,运 行不经济。
例题
例题
例题
例2.
额定电压为110/11kV的三相变压器折算 到高压侧的电抗为100Ω,忽略励磁支路。给 定原边相电压为 110 / 3 kV,当I1 = 50A时, 利用Π型等值电路计算副边的电压和电流。
2.2变压器的数学模型

2.2 变压器的数学模型z变压器正负序参数与等值电路z变压器零序阻抗与等值电路变压器正序参数与等值电路一、变压器的用途与分类z变压器是一种静止电机,将电能从一种电压形式(等级)转换成另一种电压形式(等级)。
z根据用途不同,变压器可以分为:电力变压器与特种变压器。
9电力变压器:在电力系统中传输和分配电能。
9特种变压器:其他用途的变压器,包括电炉变压器、试验变压器(互感器),等。
变压器正序参数与等值电路z根据相数,分为:单相、三相、多相变压器等。
z根据绕组数目,分为:双绕组、自耦、三绕组、多绕组变压器等。
z根据铁心型式,分为:心式、壳式变压器等。
z根据冷却方式,分为:干式、油浸式变压器等。
心式、壳式变压器变压器正序参数与等值电路二、电力变压器的结构z变压器主要部件是绕组和铁心:绕组是变压器的电路,铁心是变压器的磁路,两者构成变压器的核心即电磁部分。
9铁心的型式包括心式(结构简单,工艺简单,应用广泛)和壳式(用在小容量变压器)两种,通常由0.35mm或0.5mm硅钢片叠成。
9绕组用绝缘铜线在绕线模上绕制而成,套装在变压器铁心柱上,为了提高绝缘性能,通常将低压绕组置于在内层,而高压绕组套装在低压绕组外层。
z除了电磁部分,还有油箱、冷却装置、绝缘套管、调压和保护装置等部件。
变压器正序参数与等值电路三、变压器的基本工作原理z 当一次绕组接交流电压后,励磁电流在铁心中产生交变的主磁通Φ。
z Ф在两个绕组中分别产生感应电势e 1和e 2 。
dtd Ne Φ−=11dtd Ne Φ−=22变压器正序参数与等值电路z不计绕组电阻和漏抗压降,则:U1/U2≈ (-e1)/(-e2)=N1/N2=k9k定义为变压器的变比9N2>N1,为升压变压器9N2<N1,为降压变压器四、变压器空载运行z 变压器的一次绕组接交流电源,二次绕组开路,负载电流为零,称为变压器的空载运行。
z 一次绕组电流i 0产生励磁磁势F 0= N 1i 09F 0产生的磁通分为两部分:大部分以铁心为磁路,同时与一次绕组N 1和二次绕组N 2匝链,在两个绕组中产生电势e 1和e 2,称为主磁通Ф;另一部分磁通仅与一次绕组匝链,通过油或空气形成闭路,称为一次绕组的漏磁通Ф1σ变压器正序参数与等值电路变压器正序参数与等值电路z一次绕组电流i 0分为两部分,i μ和i Fe :i μ用于激励主磁通,称为磁化电流,与电势e 1之间的相位差是90°,是无功电流;i Fe 与铁心损耗相对应,与-e 1同相位,是有功电流9i 0即是励磁电流9X m 反映了变压器铁心的导磁性能,代表了主磁通Φ对电路的电磁效应,称为励磁电抗;R m 是用来代表铁耗的等效电阻,称为励磁电阻。
1 电力系统各元件数学模型
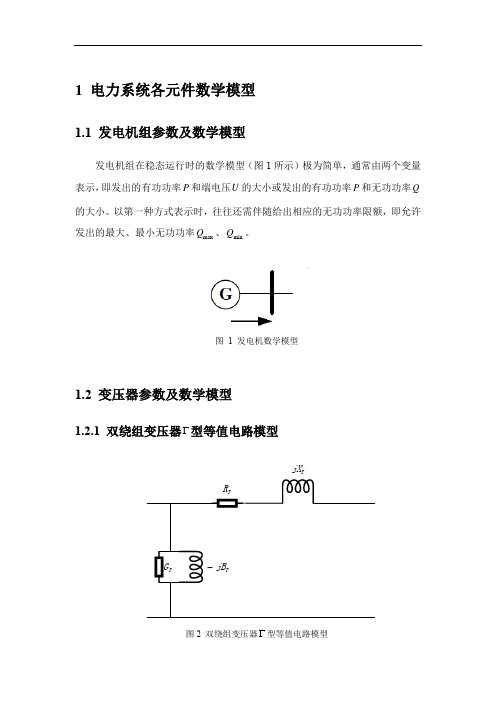
1 电力系统各元件数学模型1.1 发电机组参数及数学模型发电机组在稳态运行时的数学模型(图1所示)极为简单,通常由两个变量表示,即发出的有功功率P 和端电压U 的大小或发出的有功功率P 和无功功率Q 的大小。
以第一种方式表示时,往往还需伴随给出相应的无功功率限额,即允许发出的最大、最小无功功率max Q 、min Q 。
图 1 发电机数学模型1.2 变压器参数及数学模型1.2.1双绕组变压器Γ型等值电路模型TjX 图2 双绕组变压器Γ型等值电路模型双绕组变压器Γ型等值电路模型如图2所示,电路参数通过以下公式计算。
注意,公式中N U 取不同绕组的额定电压,表示将参数归算到相应绕组所在的电压等级(所得所得阻抗/导纳参数都是等值为Y/Y 接线的单相参数);公式中各参数由变压器厂家提供,采用实用单位。
22020210001001000%100k N T Nk NT N T NN T N P U R S U U X S P G U I S B U ⎧∙=⎪⎪⎪%∙=⎪⎪⎨⎪=⎪⎪⎪=∙⎪⎩(1-1) 其中,k P 为短路损耗,k U %为短路电压百分数,0P 为空载损耗,0%I 为空载电流百分数,N U 为归算侧的额定电压,N S 为额定容量 该电路模型一般用于手算潮流中。
1.2.2 双绕组变压器T 型等值电路模型1jX '图 3 双绕组变压器T 型等值电路模型其中,1R 和1X 为绕组1的电阻和漏抗,'2R ,'2X 为归算到1次侧的绕组2 的电阻和漏抗,m R 和m X 为励磁支路的电阻和电抗。
该电路模型一般用于电机学中加深对一二次侧和励磁支路电阻电抗的理解以及手算潮流计算中。
1.2.2 三绕组变压器Z 图4三绕组变压器的等值电路三绕组变压器的等值电路如图3所示,图中,变压器的励磁支路也以导纳表示。
该电路模型一般用于手算潮流计算中。
三绕组变压器的参数计算如下: 电阻:由短路损耗计算()()()1(12)(31)(23)2(23)(12)(31)3(31)(23)(12)121212k k k k k k k k k P P P P P P P P P P P P ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-2) 211222233100010001000k N T Nk N T Nk NT N P U R S P U R S P U R S ⎧∙=⎪⎪⎪∙⎪=⎨⎪⎪∙⎪=⎪⎩(1-3) 其中,k P 为短路损耗,N U 为归算侧的额定电压,N S 为额定容量对于容量比为100/100/50和100/50/100的变压器,厂家提供的短路损耗是小容量绕组达到自身额定电流()/2N I 时的试验数据,计算时应首先将短路损耗折算为对应于变压器额定电流()N I 的值例如,对于100/100/50型变压器,厂家提供的是未经折算的短路损耗'(23)k P -,'(31)k P -,'(12)k P -首先应进行容量归算'(23)(23)'(31)(31)44k k k k P P P P ----⎧=⎪⎨=⎪⎩(1-4) 按新标准,厂家仅提供最大短路损耗max k P ,按以下公式计算电阻:2max (100%)2(50%)(100%)20002k N T N T T P U R S RR ⎧=⎪⎨⎪=⎩(1-5) 其中max k P 为最大短路损耗,N U 为归算侧的额定电压,N S 为额定容量 电抗:由短路电压百分数计算()()()1(12)(31)(23)2(12)(23)(31)3(23)(31)(12)1%%%%21%%%%21%%%%2k k k k k k k k k k k k U U U U U U U U U U U U ---------⎧=+-⎪⎪⎪=+-⎨⎪⎪=+-⎪⎩(1-6) 211222233100100100k N T Nk N T N k NT N U U X S U U X S U U X S ⎧%=⎪⎪⎪%⎪=⎨⎪⎪%⎪=⎪⎩(1-7) 其中,k U %为短路电压百分数,N U 为归算侧的额定电压,N S 为额定容量 注意,厂家提供的短路电压是经过额定电流折算后的数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.-电力变压器的参数与数学模型————————————————————————————————作者:————————————————————————————————日期:电力变压器的参数与数学模型2.3.1理想变压器对于理想变压器,假定:绕组电阻为零;因此绕组损耗I2R为零。
铁心磁导率是无穷大,所以铁心磁阻为零。
不计漏磁通;即整个磁通为铁心和一次侧绕组、二次侧绕组相交链的磁通。
不计铁心损耗。
图2-20双绕组变压器内部结构图2-21 双绕组变压器示意图从安培和法拉第定律知:(2-46)磁场强度矢量Hc 为(2-47)其中,磁场强度、磁感应强度和磁通量的关系为由于理想变压器铁心磁导率为无限大,则磁阻R c近似为零。
(2-48)上式可写为:图2-21为双绕组变压器的示意图。
(2-49)或者图2-21中的标记点表示电压E1和E2,在标记点侧是+极,为同相。
如果图2-21中的其中一个电压极性反向,那么E1与E2相位相差180o。
匝数比k定义如下:理想单相双绕组变压器的基本关系为(2-50)(2-51)由推导可得两个关于复功率和阻抗的关系如下。
图2-21中流进一次侧绕组的复功率为(2-52)代入(2-50)和(2-51)(2-53)可见,流进一次侧绕组的复功率S1与流出二次侧绕组的复功率S2相等。
即理想变压器没有有功和无功损耗。
如果阻抗Z2与图2-21中理想变压器的二次侧绕组相连,那么(2-54)这个阻抗,当折算到一次侧时,为(2-55)因此,与二次侧绕组相连的阻抗Z2折算到一次侧,需将Z2乘以匝数比的平方k2。
2.3.2实际双绕组变压器1.简化条件实际单相双绕组变压器,与理想变压器的区别如下:计及绕组电阻;铁心磁导率为有限值;磁通不完全由铁心构成;计及铁心有功和无功损耗。
图2-22实际单相双绕组变压器的等效电路图电阻串联于图中一次侧绕组,用于计及该绕组损耗I2R。
电抗为一次绕组的漏电抗,串联于一次绕组用于计及一次绕组的漏磁通。
这个漏磁通是仅与一次绕组交链的磁通的组成部分,它引起电压降落,对应且超前。
漏电抗引起无功损耗。
类似的,二次绕组中串联了电阻和电抗。
由于变压器铁心磁导率为有限值,式(2-48)中磁阻为非零。
除以,化简后得到,(2-56)定义等式(2-56)右侧项为,称为磁化电流,相位滞后,可以通过并联电感元件-电纳描述西。
另外,实际上还有另外一个并联支路,通过电阻器-电导西描述,输送电流为铁心损耗电流。
与同相位。
当包含铁心损耗电流时,上式变为(2-57)图2-22中的等效电路,包括并联导纳。
注意当二次绕组开路(),一次绕组输入为正弦电压,I1包括两个部分:铁心损耗电流和磁化电流。
与相关联的有功损耗W,有功损耗为铁心损耗,包括磁滞和涡流两个部分。
磁滞损耗的产生是因为铁心中磁通变化一个循环需要消耗热能。
采用高品质的钢合金作为铁心材料可以减少磁滞损耗。
涡流的产生是因为磁铁心的感应电流(涡流)与磁通正交。
同样可以通过采用合金钢薄片作为铁心使涡流损耗降低。
与相关联的无功损耗为var。
这个无功功率用于磁化铁心。
向量和称为励磁电流。
(a)二次侧的电阻和漏电抗归算到一次侧;(b)忽略并联支路;(c)忽略励磁电流和内阻图2-23变压器等值电路图(2-23)为工程中单相双绕组变压器的三种等效电路。
图(2-23)(a),二次侧的电阻和漏电抗归算到一次侧后的等值电路。
图(2-23)(b)忽略并联支路,即忽略励磁电流。
因为励磁电流通常低于额定电流的5%,在系统研究中不计励磁电流,除非特殊考虑到变压器效率或者励磁现象。
对于额定容量超过500kVA 的大型电力变压器,绕组电阻比漏电抗小,可忽略,见图(2-23)(c)。
因此,工程变压器运行在正弦稳态状态,等效电路由一个理想变压器、外部阻抗和导纳支路构成。
2.参数计算1)阻抗计算在电力系统中,变压器短路试验中所测得的短路损耗P k近似等于额定电流流过变压器时绕组中的总铜损P cu,即P k≈P cu而铜耗与电阻之间有如下关系:(2-58)即得:(2-59)式中,RT为变压器每相绕组的总电阻,I N、S N、U N分别为变压器的额定电流、额定功率和额定线电压。
其中S N、U N、以VA、V为单位,P k以W为单位。
如果P k改以kW,S N、U N改以MVA、kV为单位,则上式可写成在短路计算实验中,短路电压等于变压器阻抗在额定电流下产生的压降,即(2-60)大容量变压器电抗值接近阻抗值,式中XT为变压器绕组漏抗归算到U N侧的电抗值,通常下式关系:(2-61)式中,S N单位为MVA,U N单位为kV。
2)导纳计算在电力系统中,变压器励磁支路以导纳表示时,变压器空载试验所得变压器空载损耗P0近似等于铁耗P fe,因此,电导G T可由空载损耗求得(2-62)式中,G T为变压器的电导;P0为变压器空载损耗;U N为变压器额定电压。
由于(2-63)(2-64)即得(2-65)式中,为变压器的电纳;为变压器的空载电流百分值;表示变压器的励磁功率损耗,U N,S N分别为变压器额定电压、额定容量。
变压器的数学模型有两种,即型或T型等值电路模型,或型等值电路模型,它们分别用于手算和计算机计算。
例(2-3)有一台121/10.5kV、容量为31.5MVA的三相双绕组变压器,其短路损耗为200kW,空载损耗为47W,短路电压百分数为10.5,空载电流百分数为2.7,试计算变压器等值阻抗与导纳。
解:计算变压器阻抗1)串联电阻(归算到121kV高电压侧)归算到10.5kV低压侧:2)串联电抗3)励磁回路(并联)导纳电导:电纳:(a)等效参数在高压侧(b)等效参数在低压侧(a)等效参数在高压侧;(b)等效参数在低压侧图2-24 例2-3变压器等值电路2.3.3三绕组变压器三绕组变压器等值电路中的参数计算原则与双绕组变压器的相同,等值电路如图(2-25)所示,下面分别确定各参数的计算公式。
图2-25 三绕组变压器等值电路1.电阻我国目前生产的变压器三个绕组的容量比按国家标准一般有三种类型:即:第Ⅰ类,100/100/100,三绕组容量都等于变压器的额定容量;第II 类,100/100/50,第三绕组容量仅为变压器额定容量的50%;第III 类:100/50/100,第二绕组容量为变压器额定容量的50%。
为了确定三个绕组的等值阻抗,要有三个方程,为此需要有三种短路试验的数据。
三绕组变压器的短路试验是依次让一个绕组短路,按双绕组变压器来作的。
如该变压器三个绕组容量都等于变压器额定容量,属于第Ⅰ类变压器,可由提供的三绕组间的短路损耗,,,直接按下式求取各绕组的短路损耗。
(2-66)(2-67)然后按与双绕组变压器相似的公式计算各绕组的电阻(2-68)如该变压器三个绕组容量不同,即第三绕组容量仅为变压器容量的50%,或第二绕组容量仅为变压器容量的50%,属第II、III类变压器时,则制造厂提供的短路损耗是一对绕组中容量较小的一方达到它的额定电流,这时,应首先将各绕组间的短路损耗数据归算为额定电流下的值,再运用上述公式求取各绕组的短路损耗和电阻。
例如,对100/50/100类型变压器,制造厂提供的短路损耗为,,其中是在第二绕组中流过它本身的额定电流,即二分之一变压器额定电流时测得的数据。
因此,应首先将它们归算到对应于变压器的额定电流下的短路损耗:(2-69)之后利用以及归算后得到的短路损耗,按式(2-68)(2-69)计算各绕组电阻短路损耗及等值电阻。
有时,三绕组变压器只给出一个最大短路损耗P kmax,最大短路损耗是指两个100%容量绕组中流过额定电流,另一个100%或50%容量绕组空载时的损耗。
由P kmax可求得两个100%容量绕组的电阻,另一绕组电阻就等于这两个绕组之一电阻的两倍。
(变压器的设计原则:按同一电流密度选择各绕组导线截面积)计算公式为:(2-70)2.电抗三绕组变压器按其三个绕组排列方式的不同有两种不同结构——升压结构和降压结构。
升压结构变压器的中压绕组最接近铁芯,低压绕组居中,高压绕组在最外层。
降压结构变压器的低压绕组最靠近铁芯,中压绕组居中,高压绕组仍在最外层。
各绕组排列方式虽有不同,但求取两种结构变压器电抗的方法并无不同,即由各绕组两两之间的短路电压、、求出各绕组的短路电压,(2-71)(2-72)再按与双绕组变压器相似的计算公式求各绕组的电抗(2-73)应该指出,求电抗和求电阻时不同,无论按新旧标准,制造厂提供的短路电压百分数总是归算到各绕组中通过变压器额定电流的数值。
因此,第II、III类变压器对于短路电压不需要再进行归算了。
求取三绕组变压器导纳的方法和求取双绕组变压器导纳方法相同。
例(2-4),一台220/121/10.5kV,120MVA,容量比100/100/50的Y0/Y0/△三相三绕组变压器(升压型),I0%=0.9,P0=123.1kW,短路损耗和短路电压百分数见下表。
试计算励磁支路的导纳,各绕组电阻和等值漏抗。
各参数归算到中压侧。
高压-中压高压-低压中压-低压短路损耗(kW)660 256 227 未归算到S N短路电压(%)24.7 14.7 8.8 已归算解:高中低压侧分别编号为1、2、3侧1)励磁支路导纳计算:2)各绕组电阻计算:从而3)各绕组等值漏抗计算:于是结果说明:低压绕组等值电抗呈现负值,由于变压器属降压结构,使得计算得到短路电压百分数为负值,但并不表示这种低压绕组具有容性漏抗。
三绕组变压器中压绕组或低压绕组等值电抗为负值是常见现象,近似计算时可取为零。
2.3.4自耦变压器自藕变压器可完全等值于普通变压器,如图2-26所示。
自藕变压器的短路试验又和普通变压器的相同,自耦变压器的等值电路及参数求取与普通变压器相同,需要说明的是,三绕组自藕变压器的容量归算问题,因三绕组自藕变压器第三绕组的容量总是小于变压器的额定容量SN。
而且,制造厂提供的短路试验数据中,不仅短路损耗Pk,甚至短路电压百分数Uk%有时也是未经归算的数值。
如需这种归算,由前面已知,可将短路损耗及短路电压百分数进行归算。
(a)自藕变压器;(b)等值的三绕组变压器图2-26自藕变压器可完全等值于普通变压器短路损耗折算方法如下:(2-74)短路电压百分数应按下式折算:(2-75)例(2-5),一台三相三绕组(升压型)自藕变压器220/121/10.5kV,120MVA,容量比100/100/50的Y0/Y0/△,I0%=0.5,P0=90kW,短路损耗和短路电压百分数见下表。
高压-中压高压-低压中压-低压短路损耗(kW)430 228.8 280.3 未归算到S N短路电压(%)12.8 11.8 17.58 已归算试计算(1)励磁支路的导纳,各绕组电阻和等值漏抗,各参数归算到中压侧。
