讲座中科大SHPB实验技术短训班(6)SHPB实验技术概要
SHPB实验技术-力学基础实验课件-中国科技大学-10

硬材料实验技术
采用硬质垫块
采用小尺寸试件 将导致: 几何二维效应 物理二维效应
几何二维效应和物理二维效应
几何二维效应:
1 1* 2 2*
物理二维效应:
1 1*
2 2*
数值模拟结果表明,几何二维效应的影响不大 物理二维效应引起的端面(弹性)凹陷需要分析
硬质聚氨酯泡沫应力-应变曲线
3、高速CCD:测变形,测层裂,测裂纹扩展;
……
谢
谢!
起点难确定 大尺寸 波形严重弥散 频移明显
脆
性
max 0.5% 100 / s
混凝土是SHPB实验技术最难对付的材料
混凝土冲击压缩试验
撞击杆 v 输入杆 输入杆应变计 试件应变计 输出杆应变计 输出杆 a2 a3 波形整形器 万向头 试件 PVDF
120o a1 120o
超动态应变仪
0 t
AE s ( i (t ) r (t ) t (t )) 2 A0
基本公式(二波法)
均匀假定
2C0 s r (t ) l0 s s dt A s E t (t ) A0
面临的挑战
常规SHPB实验技术规范化 复杂材料SHPB实验技术的研究
超高应变率试验
10 5 ~ 10 6 / s) (
平板撞击试验(一维应变) 试件厚 <<压板厚 类似于SHPB
10 5 ~ 10 6 / s) 超高应变率试验 (
平板斜撞试验(压剪试验)
材料动态力学性能实验
落锤实验和冲击摆实验 均未考虑惯性效应 不能测量材料的动态
~ 曲线
Along Fiber Direction
霍普金森压杆实验报告
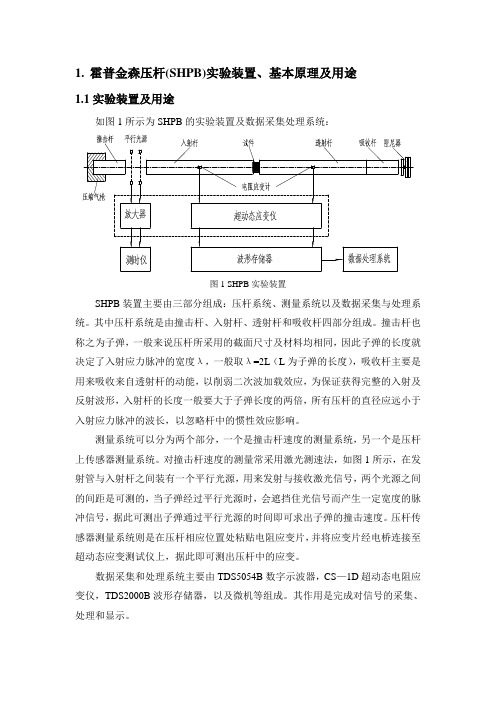
(1)
νⅠ = ν2 = ν i +ν r = −c(ε i − ε r )
′ = ν t = −cε t νⅡ = ν 2
(t= ε )
νⅡ −νⅠ
l0 c l0
=
t
c (ε i − ε r − ε t ) l0 − ε r − ε t )dt
ε= (t )
∫ (ε
0
i
(2)
由 (1) 、 (2) 式进而可得试件材料的应力应变关系。根据均匀假定,可得
图 2 应力波波速测量原理图
鉴于弹性波在自由端反射的异号波形具有相同的传播速度, 还可以采用如图 3 所示的更为简单的测试方法。这时,应变片所记录的是拉压相间的应力波,同 一相位间隔距离代表应力波行走了一个来回,即杆长的二倍距离,据此也可以确 定应力波在细长杆中的传播速度。
图 3 应力波波速测量原理图
图 9 试样的工程应变率曲线
工程应力-应变曲线:
图 10 试样的工程应力-应变曲线
万试屋 – 材料测试仪器方法资源小站/test_house
εi + εr = ε t ,代入公式后则可得到更为简单的形式:
ε (t ) = −
σ (t ) =
2c t ε r dt l0 ∫0
A Eε t A0 万试屋 – 材料测试仪器方法资源小站/test_house
2. 霍普金森压杆(SHPB)实验的操作过程
2.1 实验问题描述
常规的拉伸(或压缩)实验测得的是材料在低应变率( 力应变曲线。本实验测得的是材料在高应变率(
)下的应
)下的应力-应变曲线,
其原理如图 4 所示。 当枪膛内的子弹以某速度撞击输入杆时,在杆内产生一个入 射脉冲 ,试件在该应力作用下产生高速变形,与此同时,在压杆中分别产生往 和向前的透射脉冲 。
讲座中科大SHPB实验技术短训班(3)半无限长杆中的弹性波

或者
σ = −ρ0C0v
冲击力与打击速度成正比
冲击力与 ρ0C0 成正比 ρ0C0 为弹性波阻抗(声阻抗),又称动态硬度。
二、讨论 1、一维假定的有效性 由于二维效应(横向泊桑效应)的作用,将导致平截面的扭屈。
y
B A
x z
以圆杆为例,由于泊桑效应,在 A 点的质点速度只有 x 分量
B 点的质点速度除 x 分量外还有泊桑效应引起的 y 分量
ρ0
仅与材料性质有关,又称内秉速度。
(Ι)区应力波尚未传到,状态保持不变,称为恒值区
(Π)区内的应力波在传播过程中
状态量 v 和ε 值保持不变,称为简单波
(Π)区称为简单波区
在状态平面(v, ε )中
恒值区对应于一个点
简单波对应于一个点
简单波区对应一条线。
2 在(Π)区中
v
=
−C0ε
=
−
σ ρ0C0
= =
R2 R1
= v(R) + C0ε (R) = v(Q) − C0ε (Q)
≡ ≡
0 0
⇒
⎧v( ⎩⎨ε (
p) p)
= =
0 0
结果表明:Ι 区保持原状(静止,未变形)
此时(Ι)区对应于状态平面(v, ε )上的一个点(0,0)
在(Π)区,任取一点 S,其左、右特征线分别为 VS,TS 。
其特征线上的相容关系分别为:
C0
结果表明:在(Π)区,任意点上的 v 和ε 值分别为:
v( X ,t) = v* (τ ) = v* (t − X ) C0
v* (t − X )
ε(X,t) = −
C0
C0
即(Π)区中的状态(扰动)是由杆端以 C0 速度传递过来的
材料动态特性实验报告,SHPB实验报告

机械工程学院研究生研究型课程考试答卷课程名称:材料动态特性实验(SHPB实验)考试形式:□专题研究报告□论文√大作业□综合考试评阅人:时间:年月日材料动态特性实验实验目的:1、了解霍普金森杆的实验原理和实验步骤;2、会用霍普金森杆测试材料动态力学性能。
1.SHPB 组成:Kolsky 在Hopkinson 压杆技术的基础上提出采用分离式 Hop-kinson 压杆 SHPB )技术来测定材料在一定应变率范围的动态应力 ── 应变行为 ,该实验的理论基础是一维应力波理论, 它通过测定压杆上的应变来推导试样材料的应力 ── 应变关系, 是研究材料动态力学性能最基本的实验方法之一。
为了测出A3钢(又称Q235钢)的屈服极限、弹性模量以及其他性能参数。
用SHPB 实验就行数据测量。
SHPB 的实现装置如下图:分离式Hopkinson 压杆装置示意图它由压缩气枪、撞击杆、测时仪、输入杆(入射杆)、超动态应变仪、试件、透射杆、吸收杆、阻尼器和数据处理系统组成。
2.实验原理:SHPB 技术建立在两个基本假定的前提上:(1)杆中应力波是一维波;(2)试件应力/应变沿其长度均匀分布。
根据垂直入射应力波在界面出的反射、透射原理和上述假定由:应力相等:)()()(t t t T R I σσσ=+ (1)应变相等:)()()(t t t T R I εεε=+ (2)式中()I t σ和()R t σ分别为入射杆的入射应力和反射应力,()T t σ为透射杆的透射应力,()I t ε和()R t ε为入射杆的入射应变和反射应变,()Tt ε为透射杆的透射应变。
图1 输入杆-试件-输出杆相对位置如图2所示,在满足一维应力波假定的条件下,一旦测得试件与输入杆的界面X 1处的应力,可理论推导得: []112()(,)(,)(,)2S I R T SA t X t X t X t A σσσσ=++ (3) SR I T S S L t X v t X v t X v L t X v t X v t ),(),(),(),(),()(11212--=-=ε (4) []⎰⎰--==t R I T S t S S dt t X v t X v t X v L dt t 01120),(),(),(1)(εε (5)式中:A 为压杆的横截面积,s A 为试件的横截面积,S L 为试件的长度。
讲座中科大SHPB实验技术短训班(2)杆运动的控制方程

第二讲 杆运动的控制方程一、物质坐标和空间坐标以质点为坐标的参考系称为物质坐标,也称Lagrange 坐标。
以位置为坐标的参考系称为空间坐标,也称Euler 坐标。
描述力学问题的两种处理方法:○1 L 氏法:研究的是物质团(流体力学中的橡皮袋;球场中的人盯人)。
○2 E 氏法:研究的是空间场(流体力学中的鼠笼;球场中的打位置)。
固体力学中常采用L 氏法,因为固体材料变形小,又,测点都固定在质点上。
流体力学中常采用E 氏法,因为流体介质易流动,又,测点都安置在空间场。
在爆炸力学中,则两种方法都采用。
在连续介质力学中,空间位置x⇔材料质点X即 x=x(X,t) 或者 X=X(x,t)物理量F 既可以用空间坐标描述 F=F(x,t)也可以用物质坐标描述 F=F(X,t)。
在我们的讨论中,均采用物质坐标来描述二、控制方程等截面 均质 细长杆 1、基本假定:○1、一维假定: v ,σ,ε仅仅是X ,t 函数。
○2、应变率无关假定: σ=σ(ε) 2、基本方程: ○1、连续方程:XZ YtX v X t u t X u ∂∂=∂∂⇒∂∂∂=∂∂∂ε22 ○2、运动方程:()()t X P t dX X P tvdXA ,,00−+=∂∂ρ Xt v ∂∂=∂∂⇒σρ0 ○3、本构方程: )(εσσ= (弹性杆: εσE =) 3、控制方程⎪⎩⎪⎨⎧===εσσρεE v v X t tX 0 形式三种控制方程的 ○1ε~v : ⎪⎩⎪⎨⎧===X X t t X C E v v εερε200 中 020ρE C = (以下同) ○2σ~v : ⎪⎪⎩⎪⎪⎨⎧==X t t X v C v σρσρ020011 ○3 u : XX tt u C u 20= 典型的波动方程以上三种形式完全等价()t dX X P ,+(X P ,XX+dX三、特征线和特征线上的相容关系求解波动方程的一种好方法:特征线法。
SHPB实验技术应注意的几类问题

S P 实验技术受到挑战 。 HB 传统 S P H B实验 中. 结果分析 以一维平面假定 为 基础 。 根据一维假定 , 任意一个应力 脉冲在压杆中的传播速度为定 值, 仅 与材料性质有关 。但是这一假定忽略 了压杆 中质点的横向惯性 运动。
即忽略 了压杆的横 向收缩 或膨胀对动能 的贡献 。由于该近似假定 。 造成
的基本思路 与方法。
关键词:H B 实 S P ; 验技术; 动态力学性雒
中图分类号 :H107 T 4. 文献标识码 : A
反射波 、 透射波的应变信号 。
材料 在冲击载荷下的力学响应往往与静载 荷下的力学响应有显 著 不同, 因此研究材料在各种冲击载荷下 的力学行 为已经成为相关设 计部 门日 益关注 的问题 。准确地获得材料 的本构特性 , 是合理进行 工程设计 的基础 , 也为模拟仿真技术提供 了正确 的材料模 型和可靠的材料属性数 据f。 ”同时也是研究地壳岩石动力学特性的基础工作 。 分离式霍普金 森压杆 (D t ok s r s e a, sl pi o Pe u r简称 S P ) iH n n s r B H B 实验技术 自 14 年 由 99 Kl ys ok [发明至今 已有 5 s 】 O多年的历史 , 已成为测量材料动态力学性能的 主要手段 之一 。 国内有关科研单位为了不同的研究 目的相继建立起不同
是减小压杆 的直径 . 要求半径 r 与脉冲宽度 A之 比小于 01这样压杆中 .,
S P 实验的基本原理是细长杆 中弹性应力波传播 理论 ,是建立在 HB 两个基本假定的基础上 。 即一维假定( 又称平面假定 ) 和应 力均匀假定。
一
维假定 就是认为应力波在 细 杆 中传播过 程中 , 弹性杆 中的每个横截
SHPB原理范文

SHPB原理范文SHPB(Split Hopkinson Pressure Bar)是一种应用广泛的高速冲击试验技术,用于研究材料在高速冲击载荷作用下的力学行为。
SHPB原理基于冲击波的传播和反射,通过试验装置中的冲击杆和样品,将冲击力传导到试件中,并测量其动态响应。
SHPB试验装置由多个组件组成,包括冲击杆、样品和检测设备。
冲击杆通常由两根长杆和一个短杆组成,它们被放置在一个冲击器中。
样品则被夹持在两根长杆之间,以使冲击力传递到样品上。
检测设备包括应变计和压力传感器,用于测量样品表面的应变和冲击力。
在SHPB试验中,首先通过冲击器对短杆施加冲击力,产生冲击波。
冲击波通过长杆向样品传播,当它到达样品的一端时,一部分冲击波会反射回来,另一部分则会继续传播到另一根长杆上。
这种传播和反射的过程将冲击力传递到样品中,并引起样品的动态响应。
通过在样品上放置应变计,可以测量样品表面的应变响应。
通过压力传感器,可以同时测量冲击杆中的冲击力。
结合所施加的冲击力和样品的应变响应,可以计算出主要的应力-应变行为,从而研究材料在高速冲击载荷下的力学特性。
SHPB原理的关键在于冲击波的传导和反射。
传导过程中的波速计算依赖于速度匹配条件,即波速在相邻材料中保持一致。
反射相对复杂,取决于材料的应力-应变关系和波速的差异。
通过测量反射波的幅值和相位,可以计算样品的冲击特性,如应力、应变和变形等。
SHPB技术的应用十分广泛。
它可以用于研究各种材料,如金属、陶瓷、复合材料和生物材料等的高速冲击响应。
通过改变冲击能量、冲击载荷速度和样品尺寸等参数,可以模拟不同冲击条件,并研究材料的损伤与断裂行为。
例如,SHPB技术可以用于评估材料的冲击韧性、应力波传播特性、动态断裂行为和高速变形机制等。
总的来说,SHPB原理是利用冲击波的传导和反射,通过冲击杆和样品传递冲击力,并测量样品的动态响应。
它是一种重要的高速冲击试验技术,已广泛用于研究材料在高速冲击载荷下的力学行为。
讲座中科大SHPB实验技术短训班(4)一维弹性波的相互作用

X
2 X
1
例:人摔倒,自由端反射,速度加倍。 以上两个特例表明: 1、应力波反射与否取决于边界条件是否满足
反射后的结果应满足边界条件。 2、图解法比较好。
三、有限长杆的共轴打击
过去已有的知识
动量守恒
○1 、只有最终结果,无中间过程。
动能守恒
○2 、有局限性,需引入恢复系数。
1、两杆一样硬( (ρ0C0 )1 = (ρ0C0 )2 ),或者相同材料的杆撞击。 子弹撞击相同材料的无限长杆。
在撞击处,若两边速度不等,
⎧ 分离 ⎩⎨或二次撞击
。
四、弹性波的反射和透射
自由端的固壁端是边界的两个特例
波是否反射透射,取决于边界
波在界面处反射透射的原则是:
⎧V ' = V '' = V ⎩⎨σ ' = σ '' = σ
速度连续 应力相等
1 在不同介质界面上的反射和透射
σr 2
σt
1
σi
σi σr
[σ ]21 = ρ0C0[V ]21
σ 2 − σ 1 = ρ0C(0 V2 − V1)
⇒
⎧σ ⎨ ⎩
2
−σ1 = σ2
− ρ 0 C 0V1 = 2σ 1
=
σ1
即固壁端反射,应力加倍。
○2 、图示法:
σ
0
V1
V
σ1
1
2 例:砸核桃
3 自由端 V1
t
2 1
0
图解法: σ 0
σ (l,t) = 0
+σ2 + V2
弹性波相互作用满足线性叠加原理:
○2 图解法: σ 1
V3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SHPB实验技术短训班
第六讲: SHPB实验技术
一、前言
SHPB
技术最为成熟 应用最为广泛 实验手段
设计思想新颖 一维假定 均匀假定
结构简单
测量方法巧妙 间接测量 应变片技术
方便成熟
应变率范围 (102~104/s) 令人关注
研究对象
金属 橡胶 岩石 冻土
聚合物 多孔介质 陶瓷 混凝土 炸药 等等
SHPB的推广型 拉 、压、弯、扭试验 动屈曲试验 动三点弯曲试验
ε& 可用于中 试验
ε& 可用于超高 试验 (1)减小压杆尺寸 (2)直接撞击试件
Kolsky(1949)提出 SHPB实验装置
众人(50年代~70年代)讨论了相关问题 波形弥散, 应力不均匀性 试件惯性 端面摩擦 截面不匹配
促进了SHPB实验技术的发展和推广 面临的挑战:1.常规SHPB实验技术规范化
2.复杂材料SHPB实验技术的研究
二 、常规SHPB实验技术规范化
测定 KIc 等有规范
测定动态 σ ~ ε 曲线无规范
存在问题: (1)拥有设备的很多,了解原理的不 多; (2)动态测试技术基础差; (3)实验经费限制,有一定难度,又无
规范约束,实验精度难以保证。
一维假定(不计横向泊桑效应)又 τ << L0 / C0
ε&s
=
Co l0
(εi (t) |x=x1
−εr (t) |x=x1
−εt (t) |x=L1+l0+x2 )
∫ ;
εs
=
t 0
ε&sdt
σs
=
AE 2A0
(εi (t) |x=x1
+εr (t) |x=x1
+εt (t) |x=L1+l0+x2 )
这里已经认定贴片处的应变信号与试件端 面处的信号完全一样
实际情况
二维效应
高频振荡 波形弥散
存在升时tr
σ ~ ε 曲线有振荡 εi ,ε r ,εt 振荡有偏差
屈服应力 σ y ? 弹性模量 E ?
均匀假定:εi + ε r = εt
ε&s
=
−
2C0 l0
ε r (t) |x=x1
ε s = ∫ ε&sdt
σs
=
A A0
εE
(t) | t
x=L1 +l0 + x2
前期(t < 4τ )不均匀
E?
σ y?
端面摩擦,截面不匹配,压杆不对中
均会影响一维假定
就规范化提出几点看法:
硬件(装置)方面: (1) 压杆系列长径比、强度、光洁度、
准直度、端面垂直度及压杆支架的可 调性等 (2) 测量仪器 超动态应变仪(频响)
数字示波器(精度) 弹速测量系统(精度) (3) 试件的长径比及加工精度等
软件(实验技术)方面:
(1)干扰信号 电磁波干扰 钢杆的压磁效应
(2)应变片输出信号的检验及标定等 (3)杆件的对中及试件端面的润滑等
举行研讨会,逐步形成共识,提出规范草案
三 、复杂材料 SHPB实验技术研究
软材料 : 橡胶 多孔介质 复杂材料 脆材料: 岩石,陶瓷
复合材料:混凝土
软材料
ρ0s = 0.1 ~ 1g / cm3,
C0s = 101 ~ 102 m / s << C0B (= 5×103 m / s)
(ρ0C0 )s << (ρ0C0 )B
C0s
↓⇒ τ
(=
l0 C0s
)
↑⇒
应力不均匀时间加长
变形量大 ε max ≥ 80%
减薄试件厚度 改进数据处理
(ρ0C0 )s ↓↓
σ t 很小
空心杆 波形弥散
粘弹性杆 压杆失稳 双片测量法
石英晶体片 半导体应变片
脆材料
εb < 0.5%
ε&max
=
ε b受限制 4τ
Δt ≥ 4τ
σ 不能太大 0
pulse shaper
减缓脉冲升时,消除高频振荡 有利于应力均匀化,减少波形弥散
冲击拉伸
混凝土材料
非均匀性(骨料粒径大) 大尺寸SHPB
φ 76,φ100,200 × 200
束形SHPB
φ 74
大尺寸
脆性
直锥变截面SHPB 波形严重弥散 升时大
振荡 起点难确定 频移明显
εmax < 0.5% ⇒ ε& < 100 / s
混凝土材料:
实验技术的难度最大 需要波形弥散的修正 需在试件表面(中点处)贴应变片 拟在试件两端放压电薄膜
子弹
v
φ37
60
变截面杆
半导体应变片 电阻应变片 混凝土试件
φ74 3200
AB C 500
超动态应变仪
PC机
瞬态波形记录仪
实验装置简图
。
