光学玻璃的特殊色散机理_王衍行
光学中的光的色散

光学中的光的色散在我们日常生活中,当阳光穿过三棱镜时,会在墙上形成一条色彩斑斓的光带,这美丽而神奇的现象就是光的色散。
光的色散不仅是一种引人入胜的自然现象,更是光学领域中的一个重要概念,它为我们揭示了光的本质和特性。
要理解光的色散,首先得明白光是一种电磁波。
光是由不同波长的电磁波组成的,而这些不同波长的光在我们眼中就呈现出了不同的颜色。
比如,红光的波长较长,紫光的波长较短。
那么,为什么光在通过三棱镜时会发生色散呢?这是因为光在不同介质中的传播速度是不同的。
当光从一种介质进入另一种介质时,会发生折射现象。
而三棱镜的特殊形状使得光在穿过它时,不同波长的光折射的程度不一样。
波长较长的红光折射程度较小,而波长较短的紫光折射程度较大。
这样,原本混合在一起的各种波长的光就被分开了,从而形成了我们看到的色散现象。
光的色散在自然界中有着广泛的表现。
比如,彩虹就是最常见的光的色散现象之一。
当阳光照射到空气中的雨滴时,光线在雨滴内部发生折射和反射,多次折射和反射后的光线从雨滴中射出,就形成了彩虹。
彩虹中从外到内依次排列着红、橙、黄、绿、蓝、靛、紫七种颜色,这正是光的色散的结果。
光的色散在科学研究和实际应用中也具有重要的意义。
在天文学中,通过对恒星发出的光进行色散分析,科学家们可以了解恒星的组成成分和温度等信息。
在光学仪器中,如分光镜,就是利用光的色散原理来分析物质的成分和结构。
在通信领域,光的色散现象也会带来一些问题。
在光纤通信中,由于光信号在光纤中传输时会发生色散,导致信号的失真和衰减,从而影响通信质量。
为了解决这个问题,科学家们研发了各种技术来补偿光的色散,比如色散补偿光纤和色散补偿模块等。
此外,光的色散还与我们的日常生活息息相关。
在摄影中,摄影师们需要了解光的色散原理,以便更好地控制色彩和光线,拍摄出高质量的照片。
在显示技术中,如液晶显示器和等离子显示器,也需要考虑光的色散问题,以提供清晰、准确的色彩显示。
总之,光的色散是光学中一个非常重要的概念,它不仅让我们看到了美丽的彩虹和多彩的世界,还为科学研究和技术发展提供了重要的理论基础和应用价值。
红外光学玻璃及红外晶体材料光学特性
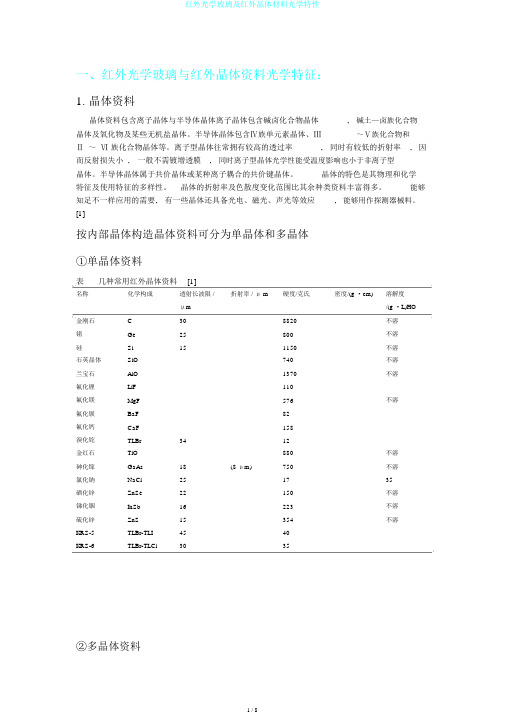
一、红外光学玻璃与红外晶体资料光学特征:1. 晶体资料晶体资料包含离子晶体与半导体晶体离子晶体包含碱卤化合物晶体,碱土—卤族化合物晶体及氧化物及某些无机盐晶体。
半导体晶体包含Ⅳ族单元素晶体、Ⅲ~Ⅴ族化合物和Ⅱ~Ⅵ族化合物晶体等。
离子型晶体往常拥有较高的透过率,同时有较低的折射率,因而反射损失小 ,一般不需镀增透膜,同时离子型晶体光学性能受温度影响也小于非离子型晶体。
半导体晶体属于共价晶体或某种离子耦合的共价键晶体。
晶体的特色是其物理和化学特征及使用特征的多样性。
晶体的折射率及色散度变化范围比其余种类资料丰富得多。
能够知足不一样应用的需要,有一些晶体还具备光电、磁光、声光等效应,能够用作探测器械料。
[1]按内部晶体构造晶体资料可分为单晶体和多晶体①单晶体资料表几种常用红外晶体资料[1]名称化学构成透射长波限 /折射率 / μ m硬度/克氏密度/(g ·cm)溶解度μm/(g ·L)HO金刚石C308820不溶锗Ge25800不溶硅Si151150不溶石英晶体SiO740不溶兰宝石AlO1370不溶氟化锂LiF110氟化镁MgF576不溶氟化钡BaF82氟化钙CaF158溴化铊TLBr3412金红石TiO880不溶砷化镓GaAs18(8 μm)750不溶氯化钠NaCl251735硒化锌ZnSe22150不溶锑化铟InSb16223不溶硫化锌ZnS15354不溶KRS-5TLBr-TLI4540KRS-6TLBr-TLCl3035②多晶体资料表红外多晶资料[1]资料透射范围 / μm折射率 /5 μm硬度/克氏熔点/℃密度/(g ·m)在水中溶解度MgF~5761396不溶ZnS~3541020不溶MgO~6402800不溶CaF~2001403微溶ZnSe~22150不溶CdTe2~30401045不溶常用的红外单晶资料包含Ge、Si 、金红石、蓝宝石、石英晶体、ZnS、 GaAs、 MgF、 NaCl 、TlBr 、KHS-6(TlBr-TlCl)和KHS-5(TlBr-TlI)等,拥有熔点高、热稳固性好、硬度高、折射率和色散化范围大等长处,但晶体尺寸受限、成真相对较高。
高考物理一轮复习讲义光学专题(二)光的色散干涉衍射和偏振

光的色散、干涉、衍射和偏振一、光的色散1.光的色散(1)现象:一束白光通过三棱镜后在屏上会形成彩色光带。
(2)成因:棱镜材料对不同色光的折射率不同,对红光的折射率最小,红光通过棱镜后的偏折程度最小,对紫光的折射率最大,紫光通过棱镜后的偏折程度最大,从而产生色散现象。
2.各种色光的比较分析颜色红橙黄绿青蓝紫频率ν低→高同一介质中的折射率小→大同一介质中的速度大→小同一介质中的波长大→小通过同一棱镜的偏折角小→大同一介质中的临界角大→小同一装置的双缝干涉条纹间距大→小平行玻璃砖三棱镜圆柱体(球)结构玻璃砖上下表面是平行的横截面为三角形的三棱镜横截面是圆对光线的作用通过平行玻璃砖的光线不改变传播方向,但要发生侧移通过三棱镜的光线经两次折射后,出射光线向棱镜底面偏折圆界面的法线是过圆心的直线,光线经过两次折射后向圆心偏折应用测定玻璃的折射率全反射棱镜,改变光的传播方向改变光的传播方向二、光的干涉1.产生干涉的条件两列光的频率相同,振动方向相同,且具有恒定的相位差,才能产生稳定的干涉图样。
2.杨氏双缝干涉(1)原理如图所示。
(2)形成亮、暗条纹的条件①单色光:形成明暗相间的条纹,中央为亮条纹。
光的路程差r2-r1=kλ(k=0,1,2,…),光屏上出现亮条纹。
光的路程差r2-r1=(2k+1)λ2(k=0,1,2,…),光屏上出现暗条纹。
①白光:光屏上出现彩色条纹,且中央亮条纹是白色(填写颜色)。
①条纹间距公式:Δx=ldλ。
3.薄膜干涉的理解和应用(1)形成:如图所示,竖直的肥皂薄膜,由于重力的作用,形成上薄下厚的楔形。
光照射到薄膜上时,在膜的前表面AA′和后表面BB′分别反射回来,形成两列频率相同的光波,并且叠加。
(2)亮、暗条纹的判断①在P1、P2处,两个表面反射回来的两列光波的路程差Δr等于波长的整数倍,即Δr=nλ(n =1,2,3,…),薄膜上出现亮条纹。
①在Q处,两列反射回来的光波的路程差Δr等于半波长的奇数倍,即Δr=(2n+1)λ2(n=0,1,2,3,…),薄膜上出现暗条纹。
五、光的色散(王新)
第五节 光的色散
第五节 光的色散
1.了解光的色散现象。
2.知道色光的三原色和颜料的三原 色。
3.了解物体的颜色。
一、 色散
1666年,英国物理学家牛顿用玻璃三棱镜使太阳光(白光)发生了色散。
白光由 红
橙 黄 绿 蓝 靛 紫
七种色光混合而成。
一、 色散
1
2
3
4
空气Biblioteka 玻璃空气一、 色散
三、 物体的颜色
红光照射下
蓝光照射下
彩虹是太阳光在传播中被空中水滴
色散
而产生的.
二、 色光的混合与颜料的混合
二、 色光的混合与颜料的混合
二、 色光的混合与颜料的混合
色光的三原色:红、绿、蓝。
颜料的三原色是品红、黄、青。
三、 物体的颜色
三、 物体的颜色
不透明物体的颜色由它反射的色光决定.
三、 物体的颜色
透明物体的颜色由它透过的色光决定.
光学现象色散和衍射的特性

光学现象色散和衍射的特性色散和衍射是光学中常见的现象,它们具有一些特殊的特性。
下面就分别介绍色散和衍射的特性。
一、色散的特性色散是指光在经过透明介质时,由于不同波长的光在介质中传播速度不同,产生分散现象。
色散的特性主要包括以下几个方面:1. 色散与光的波长有关:不同波长的光在介质中传播时速度不同,因此产生色散现象。
光的波长越大,色散效应越明显。
2. 色散与介质的折射率有关:介质的折射率越高,光的传播速度越慢,色散效应越明显。
不同介质的色散程度也不同。
3. 色散与入射角有关:光线在介质中入射角度不同,色散现象的程度也不同。
当光线垂直入射时,色散效应最小。
4. 色散与光的波形有关:不同的光波形在介质中传播时,色散的程度也会不同。
例如,白色光在经过三棱镜时,被分解成七种不同颜色的光。
二、衍射的特性衍射是指光通过一个有限孔径或者遇到障碍物时,发生弯曲和扩散的现象。
衍射的特性主要包括以下几个方面:1. 衍射现象与光的波长有关:波长越短,衍射效果越明显。
例如,紫外线的衍射现象比可见光更为显著。
2. 衍射现象与光的传播环境有关:在光线通过狭缝或者孔径时,会发生衍射现象。
例如,光线通过窄缝时,会出现衍射现象,产生衍射图样。
3. 衍射与障碍物的大小有关:障碍物的尺寸越大,衍射效应越显著。
例如,光线通过一个大孔洞时,会出现较明显的衍射现象。
4. 衍射与光的波前有关:光的波前形状会影响衍射现象。
当波前是平面或球面时,衍射程度较小;而当波前是锯齿形或不规则形状时,衍射程度较大。
综上所述,色散和衍射作为光学现象,都具有一些独特的特性。
了解这些特性有助于我们更好地理解和应用光学知识,在实际生活和科学研究中发挥更大的作用。
光学玻璃的折射率和色散

DATE May 2004 PAGE 1/15TIE-29: Refractive Index and Dispersion0. IntroductionThe most important property of optical glass is the refractive index and its dispersion behavior.This technical information gives an overview of the following topics:- Dispersiono Principal dispersion (page 2) o Secondary spectrum (page 3)o Sellmeier dispersion equation (page 4)- Temperature dependence of refractive index (page 6)- Influence of the fine annealing process on the refractive index and Abbe number(page 9)- Tolerances (page 12)- Refractive index measurement (page 13)1. Refractive IndexIf light enters a non-absorbing homogeneous materials reflection and refraction occurs at the boundary surface. The refractive index n is given by the ratio of the velocity of light in vacuum c to that of the medium vvc n =(1-1)The refractive index data given in the glass catalogue are measured relative to the refractive index measured in air. The refractive index of air is very close to 1.Practically speaking the refractive index is a measure for the strength of deflection occurring at the boundary surface due to the refraction of the light beam. The equation describing the amount of deflection is called Snell’s law:)sin()sin(2211αα⋅=⋅n n (1-2)The refractive index is a function of the wavelength. The most common characteristic quantity for characterization of an optical glass is the refractive index n in the middle range of the visible spectrum. This principal refractive index is usually denoted as n d – the refractive index at the wavelength 587.56 nm or in many cases as n e at the wavelength 546.07 nm.2. Wavelength Dependence of Refractive Index: DispersionThe dispersion is a measure of the change of the refractive index with wavelength. Dispersion can be explained by applying the electromagnetic theory to the molecular structure of matter. If an electromagnetic wave impinges on an atom or a molecule the bound charges vibrate at the frequency of the incident wave.DATE May 2004 PAGE 2/15The bound charges have resonance frequency at a certain wavelength. A plot of the refractive index as a function of the wavelength for fused silica can be seen in Figure 2-1. It can be seen that in the main spectral transmission region the refractive index increases towards shorter wavelength. Additionally the dotted line shows the absorption coefficient as a function of the wavelength.Figure 2-1: Measured optical constants of fused silica (SiO 2 glass) [1]2.1 Principal DispersionThe difference (n F – n C ) is called the principal dispersion. n F and n C are the refractive indices at the 486.13 nm and 656.27 nm wavelengths.The most common characterization of the dispersion of optical glasses is the Abbe number. The Abbe number is defined as)/()1(C F d d n n n −−=ν (2.1-1)Sometimes the Abbe number is defined according to the e line as)/()1(C F e e n n n ′′−−=ν (2.1-2).Traditionally optical glasses in the range of νd > 50 are called crown glasses, the other ones as flint glasses.Glasses having a low refractive index in general also have a low dispersion behaviour e.g. a high Abbe number. Glasses having a high refractive index have a high dispersion behaviour and a low Abbe number.DATE May 2004 PAGE 3/152.2. Secondary SpectrumThe characterization of optical glass through refractive index and Abbe number alone is insufficient for high quality optical systems. A more accurate description of the glass properties is achievable with the aid of the relative partial dispersions.The relative partial dispersion P x,y for the wavelengths x and y is defined by the equation:)/()(,C F y x y x n n n n P −−= (2.2-1)As Abbe demonstrated, the following linear relationship will approximately apply to the majority of glasses, the so-called ”normal glasses”d xy xy y x b a P ν⋅+≈, (2.2-2)a xy andb xy are specific constants for the given relative partial dispersion.In order to correct the secondary spectrum (i.e. color correction for more than two wavelengths) glasses are required which do not conform to this rule. Therefore glass types having deviating partial dispersion from Abbe’s empirical rule are especially interesting.As a measure of the deviation of the partial dispersion from Abbe’s rule the ordinate difference ∆P is introduced. Instead of relation (2.2-2) the following generally valid equation is used:y x d xy xy y x P b a P ,,∆+⋅+=ν (2.2-3)The term ∆P x,y therefore quantitatively describes a dispersion behavior that deviates from that of the ”normal glasses.”The deviations ∆P x,y from the ”normal lines” are listed for the following five relative partial dispersions for each glass type in the data sheets.)/()()/()()/()()/()()/,,,,C F g i g i C F F g F g C F e F e F C F s C s C C F t C C,t n n n n P n n n n P n n n n P n n n n P n (n )n (n P −−=−−=−−=−−=−−= (2.2-4)The position of the normal lines is determined based on value pairs of the glass types K7 and F2. The explicit formulas for the deviations ∆P x,y of the above-mentioned five relative partial dispersions are:DATE May 2004 PAGE 4/15)008382.07241.1()/()()001682.06438.0()/()()000526,04884.0()/()()002331.04029.0()/()()004743.05450.0()/()(,,,,,d C F g i g i d C F F g F g d C F e F e F d C F s C s C d C F t C t C n n n n P n n n n P n n n n P n n n n P n n n n P ννννν⋅−−−−=∆⋅−−−−=∆⋅−−−−=∆⋅+−−−=∆⋅+−−−=∆ (2.2-5)Figure 2.2-1 shows the P g,F versus the Abbe number νd diagram.Figure 2.2-1: P g,F as a function of the Abbe number for Schott’s optical glass sortiment.Additionally the normal line is given.The relative partial dispersions listed in the catalog were calculated from refractive indices to 6 decimal places. The dispersion formula (2.3-1) can be used to interpolate additional unlisted refractive indices and relative partial dispersions (see chapter 2.3).2.3. Sellmeier Dispersion EquationThe Sellmeier Equation is especially suitable for the progression of refractive index in the wavelength range from the UV through the visible to the IR area (to 2.3 µm). It is derived from the classical dispersion theory and allows the description of the progression of refractive index over the total transmission region with one set of data and to calculate accurate intermediate values.DATE May 2004 PAGE 5/15)()()(1)(3223222212212C B C B C B n −⋅+−⋅+−⋅=−λλλλλλλ (2.3-1)The determination of the coefficients was performed for all glass types on the basis of precision measurements by fitting the dispersion equation to the measurement values. The coefficients are listed in the data sheets.The dispersion equation is only valid within the spectral region in which refractive indices are listed in the data sheets of each glass. Interpolation is possible within these limits. The wavelengths used in the equation have to be inserted in µm with the same number of digits as listed in Table 2.3-1. For practical purposes Equation 2.3-1 applies to refractive indices in air at room temperature. The achievable precision of this calculation is generally better than 1·10-5 in the visible spectral range. The coefficients of the dispersion equation can be reported for individual glass parts upon request. This requires a precision measurement for the entire spectral region, provided the glass has sufficient transmission.Table 2.3-1: Wavelengths for a selection of frequently used spectral linesDATE May 2004 PAGE 6/153. Temperature Dependence of Refractive IndexThe refractive indices of the glasses are not only dependent on wavelength, but also upon temperature. The relationship of refractive index change to temperature change is called the temperature coefficient of refractive index. This can be a positive or a negative value. The data sheets contain information on the temperature coefficients of refractive index for several temperature ranges and wavelengths. The temperature coefficients of the relative refractive indices ∆n rel /∆T apply for an air pressure of 0.10133·106 Pa. The coefficients of the absolute refractive indices dn abs /dT apply for vacuum.The temperature coefficients of the absolute refractive indices can be calculated for other temperatures and wavelengths values with the aid of equation (3-1).)232(),(21),(),(22102210002TKabs TE E T D T D D T n T n dT T dn λλλλλ−∆⋅⋅++∆⋅⋅+∆⋅⋅+⋅⋅−= (3-1)Definitions:T 0 Reference temperature (20°C) T Temperature (in °C) ∆T Temperature difference versus T 0 λ Wavelength of the electromagnetic wave in a vacuum (in µm) D 0, D 1, D 2, E 0, E 1 and λTK : constants depending on glass typeThis equation is valid for a temperature range from -40°C to +80°C and wavelengths between 0.6438 µm and 0.4358 µm. The constants of the dispersion formula are also calculated from the measurement data and listed on the test certificate.The temperature coefficients in the data sheets are guideline values. Upon request, measurements can be performed on individual melts in the temperature range from -100°C to +140°C and in the wavelength range from 0.3650 µm to 1.014 µm with a precision better than ± 5·10-7/K. The accuracy at the limits of the measurement range is somewhat less than in the middle of this interval.The temperature coefficients of the relative refractive indices ∆n rel /∆T and the values for ∆n abs can be calculated with the help of the equations listed in Technical Information TI Nr. 19 (available upon request).Figures 3-1 to 3-4 show the absolute temperature coefficient of refractive index for different glasses, temperatures and wavelengths.DATE May 2004 PAGE 7/15DATE May 2004PAGE 8/15SF 6.DATE May 2004 PAGE 9/154. Influence of the Fine Annealing Process on the Refractive Index and Abbe numberThe optical data for a glass type are chiefly determined by the chemical composition and thermal treatment of the melt. The annealing rate in the transformation range of the glass can be used to influence the refractive index within certain limits (depending on the glass type and the allowable stress birefringence). Basically slower annealing rates yield higher refractive indices. In practice, the following formula has proven itself.)/log()()(00h h m h n h n x nd d x d ⋅+= (4-1) h 0 Original annealing rate h x New annealing rate m nd ? Annealing coefficient for the refractive index depending on the glass typeThe refractive index dependence on annealing rate is graphically shown in Figure 4-1.Figure 4-1: Dependence of refractive index on the annealing rate for several glass types. Reference annealing rate is 7 K/hAn analogous formula applies to the Abbe number.)/log()()(00h h m h h x d d x d ⋅+=ννν (4-2) m νd ? Annealing coefficient for the Abbe number depending on the glass typeThe annealing coefficient m νd can be calculated with sufficient accuracy with the following equation:)/())((0C F nC nF d nd d n n m h m m −⋅−=−νν (4-3)The coefficient m nF-nC has to be determined experimentally.DATE May 2004 PAGE 10/15Figure 4-2 shows that individual glass types vary greatly in their dependence of t he Abbe number on the annealing rate. In general also the Abbe number increases with decreasing annealing rate. High index lead free glass types like N-SF6 show anomalous behavior. Anomalous behaviour means that the Abbe number decreases with decreasing annealing rate.Figure 4-2: Abbe number as a function of the annealing rate for several glass types. Reference annealing rate is 7 K/hValues for Annealing coefficients of some optical glasses are shown in Table 4-1. We will provide the values for the annealing coefficients of our glasses upon request.m nd m nF-nc m νdN-BK7 -0.00087 -0.000005 -0.0682 N-FK51 -0.00054 -0.000002 -0.0644 SF 6 -0.00058 +0.000035 -0.0464 N-SF6 -0.0025 -0.000212 0.0904Table 4-1: Annealing coefficients for several selected glass typesThe annealing rate can be used to adjust the refractive index and Abbe number to the desired tolerance range.In practice the annealing rate influences the refractive index and the Abbe number simultaneously. Figure 4-3 shows a diagram of the Abbe number versus the refractive index for N -BK7. The rectangular boxes indicate the tolerance limits (steps) for the refractive index and the Abbe number. For example the largest box with a dotted frame indicates the tolerance borders for step 3 in refractive index and step 4 in Abbe number. The smallest box indicates step 1 in refractive index and Abbe number. In the center of the frames is the nominal catalog value.DATE May 2004PAGE 11/15 After melting the optical glass is cooled down at a high annealing rate. To control the refractive index during the melting process samples are taken directly from the melt after each casting. These samples are cooled down very fast together with a reference sample of the same glass. The reference sample has a known refractive index at an annealing rate of 2°C/h. By measuring the change in refractive index of the reference sample the refractive index of the sample can be measured with moderate accuracy in the range of ±10-4.The annealing rate dependence of the Abbe number and refractive index of each glass is represented by a line in the diagram having a slope that is characteristic for the glass type. For a given melt the position of the line in the diagram is given by the initial refractive index / Abbe number measurement for a cooling rate of 2°C/h as a fix-point together with the glass typical slope. The refractive index and Abbe number for a given glass part can be adjusted by a fine annealing step along this characteristic line.Glass for cold processing has to be fine annealed to reduce internal stresses. During this fine annealing the annealing rate is in general lower than 2°C/h. The initial refractive index has to be adjusted during melting in such a way that the desired tolerances can be reached during fine annealing. The initial refractive index of N-BK7 for example is in general lower than the target value.Figure 4-3:The influence of the annealing rate on the refractive index and Abbe numberof N-BK7 for different initial refractive indices.DATE May 2004PAGE 12/15 Glass for hot processing i.e reheat pressing is subjected to much more rapid annealing. The heat treatment processes used by the customer in general use annealing rates much higher than 2°C/h. Therefore for N-BK7 pressings for example the initial refractive index needs to be higher than the target value. For a better visualization in figure 4-3 the annealing line for pressings was shifted to higher Abbe numbers. In general it is also possible to achieve step 1/1 for pressings after hot processing. We deliver an annealing schedule for each batch of glass for hot processing purpose. This annealing schedule contains the initial refractive index at 2°C/h and the limit annealing rates to stay within the tolerances.5. TolerancesThe refractive indices, which are listed to 5 decimal places in the data sheets, represent values for a melt with nominal n d-νd position for the glass type in question. The refractive index data are exact to five decimal places (for λ > 2 µm: ± 2·10-5). The accuracy of the data is less in wavelength regions with limited transmission. All data apply to room temperature and normal air pressure (0,10133·10-6 Pa).Defining tolerances for the refractive index of a glass the customer has to distinguish between the refractive index tolerance, the tolerance of refractive index variation within a lot and the refractive index homogeneity (figure 5-1).Figure 5-1:Refractive index variation from within a production sequence.DATE May 2004 PAGE 13/15All deliveries of fine annealed block glass and fabricated glass are made in lots of single batches. The batch may be a single block or some few strip sections. More information on the new lot id system can be found in [3].The refractive index and Abbe number tolerance is the maximum allowed deviation of a single part within the delivery lot from nominal values given in the data sheets of the catalog. The refractive index of the delivery lot given in the standard test certificates is given by the following formulae:2/)(min max n n n lot += (5-1)n max is the maximum and n min the minimum refractive index within the lot.The refractive index variation from part to part within a lot is always smaller than ± 1*10-4. The refractive index homogeneity within a single part is better than ± 2*10-5 in general [4]. A short summary of the refractive index tolerance, variation and homogeneity grades can be found in table 5-1. More information is given in the optical glass catalogue [5].Tolerance Grade Refractive Index [*10-5] Abbe NumberStep 4-- ± 0.8% Step 3 ± 50 ± 0.5% Step 2 ± 30 ± 0.3% AbsoluteStep 1± 20 ± 0.2% SN± 10 -- S0 ± 5 -- Variation S1± 2 -- H1± 2 -- H2 ± 0.5 -- H3 ± 0.2 -- H4 ± 0.1 -- Homogeneity H5 ± 0.05--Table 5-1: Refractive Index Tolerances6. Refractive Index MeasurementFor refractive index measurement two different measurement setups are used: the v -block refractometer (figure 6-2) and the spectral goniometer. Figure 6-1 shows the principle of the v-Block measurement. The samples are shaped in a nearly square shape. One sample is about 20x20x5 mm small. The sample will be placed in a v shaped block prism. The refractive index of this prism is known very precisely. The refraction of an incoming light beam depends on the refractive index difference between the sample and the v-block-prism. The advantage of this method is that up to 10 samples can be glued together into one v -block stack. Therefore many samples can be measured in a very short time. The relative measurement accuracy is very h igh, therefore differences in refractive index within one v -block stack can be measured very accurately.DATE May 2004 PAGE 14/15Figure 6-1: Refractive index variation from within a production sequence .Figure 6-2: V-block refractometer.The spectral goniometric method is based on the measurement of the angle of minimum refraction in a prism shaped sample. This is the most accurate absolute refractive index measurement method. In our laboratory we have standard manual spectral goniometers and automated improved spectral goniometer with higher accuracy and the ability to measure in the infrared and UV region (figure 6-3).Figure 6-3: Manual spectral goniometer (left side), automated spectral goniometer (rightside).sample with lowerrefractive indexsample with higher refractive index samplev-block-prism immersion oillightbeamDATE May 2004PAGE 15/15 Table 6-1 shows a summary of the refractive index measurements available at Schott.Measurement accuracyMeasurementRefractive index DispersionWavelengths MethodV-block standard ± 30*10-6 ± 20*10-6g, F’, F, e, d, C’,CV-block enhanced ± 20*10-6± 10*10-6I, h, g, F’, F, e, d,C’, C, r, tv-blockrefractometerPrecisionspectrometer± 10*10-6± 3*10-6Super precision spectrometer ± 5*10-6± 2*10-6h, g, F’, F, e, d,C’, CspectralgoniometerUV precisionspectrometer± 10-20*10-6± 3*10-6UV super precision spectrometer ± 2-5*10-6± 2*10-6248.3 nm –2325.4 nm(about 30spectral linespossible)automaticspectralgoniometerTable 6-1: Absolute refractive index measurement accuraciesThe temperature coefficient of refractive index is measured using an automated spectral goniometer and a temperature controlled climate chamber with a temperature range from -100°C up to +140°C. The temperature coefficient can be measured with an accuracy of ± 0.5*10-6 K-1.7. Literature[1] The properties of optical glass; H. Bach & N. Neuroth (Editors), Springer Verlag 1998[2] SCHOTT Technical Information No. 19 (available upon request).[3] SCHOTT Technical Note No. 4: Test report for delivery lots[4] SCHOTT Technical Information No. 26: Homogeneity of optical glass[5] SCHOTT Optical Glass Pocket CatalogueFor more information please contact:Optics for DevicesSCHOTT GlasGermanyPhone: + 49 (0)6131/66-3835Fax: + 49 (0)6131/66-1998E-mail: info.optics@/optics_devices。
光学中的光的色散

光学中的光的色散光的色散是光学中一种重要的现象,它描述了光在通过介质时,不同波长的光被折射的角度不同的现象。
光的色散现象可以分为正常色散和反常色散两种。
在本文中,我们将详细探讨光的色散现象,包括其原理、应用以及对光学领域的重要性。
一、光的色散原理光的色散原理是由光的折射率与波长之间的关系导致的。
根据斯涅尔定律,光在介质中传播时会发生折射,而介质的折射率与光的波长有关。
通常来说,折射率对于不同的波长是不同的,因此,当光通过介质时,不同波长的光线会以不同的角度折射出来,从而产生色散现象。
在一般情况下,光在经过介质后,折射角度与入射角度之间的关系可以用斯涅尔定律来描述:n1*sin(θ1) = n2*sin(θ2)其中,n1和n2分别代表了入射介质和折射介质的折射率,θ1和θ2分别为入射角和折射角。
二、正常色散和反常色散根据光的色散特性,我们可以将色散现象分为正常色散和反常色散两种。
1. 正常色散正常色散是指当光从真空进入具有折射率大于1的介质中时,折射角度随着波长的增加而增大的现象。
常见的例子是光经过玻璃体时,不同颜色的光线会以不同的折射角度折射出来,从而形成七彩光谱。
2. 反常色散反常色散则是指当光从真空进入具有折射率小于1的介质中时,折射角度随着波长的增加而减小的现象。
这种现象在一些特殊的介质中发生,例如当光从水进入冰中时,不同颜色的光线会以相反的折射角度折射出来。
三、光的色散应用光的色散现象在科学研究和工程应用中具有广泛的应用价值,下面我们将介绍其中的几个方面。
1. 分光仪分光仪是一种利用光的色散原理来分离混合光的仪器。
它通过将光线经过棱镜或光栅等光学器件,使得不同波长的光线以不同的角度折射出来,从而实现对光谱的分离。
分光仪被广泛应用于化学分析、物质鉴定、天文观测等领域。
2. 光纤通信光纤通信是一种利用光作为信息传输的技术。
在光纤中,光信号会通过不同的波长来传输信息,而不同波长的光信号会以不同的速度传播。
光学器件中的色散特性分析

光学器件中的色散特性分析在光学领域中,色散指的是光波在经过光学器件(例如透镜、棱镜等)时,不同波长的光分离成不同的角度或位置。
光波的色散性质对于许多应用至关重要,例如成像、分光和光通信等。
1. 色散的基本原理色散的基本原理源于光波在透明媒介中不同频率的折射率不同。
根据光传播的速度和频率之间的关系,可以推导出光的折射率随频率变化的规律。
这种频率-折射率关系通常用色散曲线或折射率曲线表示。
2. 色散种类色散可以根据折射率与频率的关系分为正常色散和反常色散两种。
正常色散指的是折射率随频率增加而递增,而反常色散则是折射率随频率增加而递减。
此外,还有角色散和色散的分类。
角色散是指入射光斜入射透镜或棱镜时产生的色散效应,而色散则是垂直入射时的效应。
3. 色散的影响在光学系统中,色散可以造成图像模糊、色彩偏移等问题。
对于光通信系统来说,色散会导致光脉冲的扩散,降低传输速率和距离。
为了解决色散带来的问题,科学家和工程师采用了多种方法来补偿色散。
其中一种常见的方法是使用色散补偿光纤,该光纤具有特殊结构,能够在光信号传输过程中抵消色散带来的影响。
4. 色散的应用色散的特性在许多光学器件中都有重要的应用。
例如,在分光仪中,利用色散的原理可以将不同波长的光分离出来,实现光谱分析。
在摄影领域,色散的特性被用于消除色差,保证图像的准确还原。
此外,色散的应用还涉及光纤通信、光纤传感、光计算等领域。
研究和控制色散的性质对于改善光学器件的性能和创新新的应用具有重要意义。
5. 色散特性分析方法为了分析光学器件中的色散特性,科学家和工程师使用了多种方法和技术。
其中一种常见的方法是使用光谱仪,通过测量不同波长光的位置或角度变化,来确定色散的程度和类型。
此外,还有一种称为径向载波神经网络(Radial basis function neural network)的方法,它可以在没有实际测量数据的情况下,通过建立模型来预测色散效应。
总结:色散作为光学器件中一个重要的特性,对于很多光学应用起着关键的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WANG Yan-hang* ,ZU Cheng-kui,XU Xiao-dian,ZHOU Peng ( Quartz & Special Glass Institute,China Building Materials Academy,Beijing 100024,China)
的比值称为相对部分色散
Pλ1λ2 (
nλ1 nF
- -
nλ2 nC
)
。大部
分光学玻璃的相对部分色散 Pλ1λ2 与阿贝数 νd 近
似直线关 系,这 一 直 线 被 称 为 光 学 玻 璃 的“正 常
线”。各 国 对 正 常 线 位 置 确 定 并 不 统 一,其 中
Schott 公 司 规 定 其 是 由 N-BK7 玻 璃 ( 正 透 镜 材
收稿日期: 2015-09-11; 修订日期: 2015-11-13 基金项目: 中国建材总院重大科研资助项目( No. Yt-94)
Supported by Major Scientific Research Project of China Building Materials Academy( No. Yt-94)
因此,研究光学玻璃的特殊色散机理不仅可以深
入理解光 学 玻 璃 的“组 分-结 构-性 能 ”关 系 规 律,
而且有助于开发特殊色散性能更优异的新型光学
玻璃。
光学玻璃的特殊色散性能最直接的反映就是 色散曲线发生变化[8-10],如图 1 所示。从图 1 可 以看出,在紫外区和红外区偏离了正常色散曲线 时,光学玻璃表现出特殊色散性能。表征光学玻 璃特殊色散性能的主要参数是相对部分色散偏离 值( 如 ΔPg,F) ,它可定量地描述某一牌号光学玻 璃偏离“正 常 玻 璃 ”的 色 散 情 况。 根 据 在 正 常 线 的不同位置,特殊色散玻璃可分为正向色散玻璃 ( ΔPg,F > 0) 和负向色散玻璃( ΔPg,F < 0) 两类,如 图 2 所示。
在本征吸收区两侧,长波一侧的折射率远大于短
波一侧,如图 4 所示。当远离吸收区处,折射率随
波长的变化又表现为正常色散特征。从图 3 还可
以看出,常用的光学玻璃材料在可见光区不存在
本征吸收,因此在可见光区表现出的色散性能只
能称之为“特殊色散”,而不是反常色散。要进一
步揭示在可见光区出现特殊色散现象需要对光学
料) 和 F2 玻璃 ( 负透镜材料) 的光学常数决定。
然而,除了大部分光学玻璃处于正常线上,仍有部
分光学玻璃偏离正常线而处于正常线的下方或上
方位置,这类光学玻璃被称为特殊相对色散玻璃,
简称为特殊色散玻璃。特殊色散玻璃除了具有光
学玻璃的通性外,还拥有较大的相对部分色散偏
离值( 如 ΔPg,F) ,可消除光学系统的二级光谱,是 长焦距、大视场、高精度光学系统的优选材料[5-7]。
Nifi ω20 - ω2
,
( 6)
第1 期
王衍行,等: 光学玻璃的特殊色散机理
125
图 5 光学玻璃的色散和吸收曲线 Fig. 5 Dispersion and absorption curves of optical glass
计需求; ( 2) 高度的光学均匀性,可减少光畸变,
保证成像几何精度; ( 3) 优异的透光性,利于实现
光信号高通量传输; ( 4) 良好的耐候性,可确保光
学元件长期服役要求。随着现代光学系统的不断
拓展,光学玻璃的种类不断增多。目前,光学玻璃
的发展方向主要为特高折射率玻璃、特低色散玻
璃、特殊色散玻璃和低转变温度玻璃等,其中特殊
射率的函数。光学玻璃常用的相对部分色散偏离
值计算公式为:
ΔPC,t = PC,t - 0. 5450 - 0. 004743νd, ( 1) ΔPC,s = PC,s - 0. 4029 - 0. 002331νd, ( 2) ΔPF,e = PF,e - 0. 4884 + 0. 000526νd, ( 3) ΔPg,F = Pg,F - 0. 6438 + 0. 001682νd, ( 4) ΔPi,g = Pi,g - 1. 7241 + 0. 008382νd. ( 5) 根据色散理论,色散可分为正常色散和反常
摘要: 本文对光学玻璃的特殊色散机理进行了深入研究。研究认为,光学玻璃的特殊色散性能表征参数主要是相对部分 色散偏离值 ΔPg,F ,ΔPg,F 绝对值越大,表明光学玻璃的特殊色散越大,越有利于消除光学系统的二级光谱。光学玻璃的 特殊色散机理是由紫外和红外本征吸收引起。色散曲线中本征吸收峰的漂移和强弱将影响可见光区色散曲线斜率,进 而使玻璃的相对部分色散偏离值变化。紫外本征吸收是由电子跃迁引起的; 而红外本征吸收是由分子或分子集团振动 造成的。开展特殊色散机理研究不仅可以深入揭示光学玻璃的“组分-结构-性能”关系规律,而且有助于开发特殊色散 性能更优异的新型光学玻璃。 关 键 词: 光学玻璃; 特殊色散; 本征吸收 中图分类号: TQ171 文献标识码: A doi: 10. 3788 / CO. 20160901. 0122
第1 期
王衍行,等: 光学玻璃的特殊色散机理
123
1引言
2 光学玻璃的特殊色散现象
光学玻璃可用于制作视窗、透镜和棱镜,是构
成光学仪器和装置的核心,已成为现代工农业生
产、国防和科研等领域不可或缺的重要光学材料 之一[1-3]。与其它玻璃相比,光学玻璃具有显著特
征: ( 1) 预先设定的光学常数,可满足不同光学设
需要指出的是,光学玻璃的正向和反向色散 是人为规定的,是为了满足光学系统设计需要,并 不能反映玻璃材料的本征性能。ΔPg,F 绝对值越
124
中国光学
第9 卷
大,表明光学玻璃的特殊色散越大,越有利于消除
光学系统的二级光谱。光学玻璃的相对部分色散
偏离值是由相对部分色散 Pλ1,λ2 和阿贝数 νd 决定 的,但由于相对部分色散 Pλ1,λ2 和阿贝数 νd 均是 折射率的函数,因此,相对部分色散偏离值也是折
很难直接外推到 λ1。λ1 代表了玻璃的紫外本征 吸收波长,主要取决于玻璃中各种化学键的电子
跃迁能量。λ1 值也与玻璃中的阴离子半径有关, 如氟化物玻璃的 λ1 值比氧化物玻璃的小[13]。
泉谷徹郎[12]认为,光学玻璃的色散曲线可用
Drude-Voigt 公式表征,即:
Σ n2 - 1 = e2
πm i
玻璃的特殊色散机理进行深入研究。
Fig. 3
图 3 常用光学玻璃的正常色散曲线 Normal dispersion curves of some familiar optical glasses
图 4 介质的色散和吸收曲线 Fig. 4 Dispersion and absorption curves of optical ma-
色散玻璃因具有较大的相对部分色散偏离值,在 现代光学系统设计中备受关注[4]。
折射率是光学玻璃最重要的光学常数,是计
算光学参数的基本物理量,已成为光学设计的关
键参数。光学玻璃的折射率随波长增大而降低,
即色散现象。任意两个波长折射率之差称为部分
色散( nλ1 - nλ2 ) 。部分色散与中部色散( nF - nC )
terials
3 特殊色散机理
根据洛伦兹经典电子论和麦克斯韦电磁理
论,可较好地理解光学介质中反常色散的产生机
理,由于在本征吸收区存在受迫振动阻力,阻尼系
数 γ≠0,折射率表现为复数形式,导致折射率随
入射光波长的增大而增大,产生反常色散。也就
是说,本征吸收是光学介质存在反常色散的根本
原因。为此,要研究反常色散的机理,首先必须解
* Corresponding author,E-mail: drwangyh@ 126. com
Abstract: Special dispersion mechanism of optical glass is studied deeply in ths paper. The deviation of relative partial dispersion ΔPg,F from normal line is an important parameter to characterize the special dispersion property of optical glass. The optical glass with high absolute value of ΔPg,F can be used to revise secondary spectrum in advanced optical system. The special dispersion phenomenon in visible region is aroused by inherent absorption in the ultraviolet and infrared regions. The shift and strength of inherent absorption peaks have an evident influence on the slope of dispersion curve,which will change the deviation of relative partial dispersion. It is generally thought that the electron transition results in ultraviolet inherent absorption,and libration of molecule or its group leads to infrared inherent absorption. Special dispersion mechanism is studied not only to deeply understand the relationship among composition,microstructure and property of optical glass,but also to develop new optical glasses with more excellent special dispersion property. Key words: optical glass; special dispersion; inherent absorption
