离散数学 函数
合集下载
离散数学 第三章 函数

下面先规定几个标准集合的基数: 1) 空集的基数为0。 2) 设n为一自然数,Nn为从1到n的连贯的自然数集合, Nn={1,2,3,…,n},Nn的基数为n,|Nn|=n 。 3) 设N为自然数的全体,N={1,2,3,…},N的基数为ℵ0(读成 阿列夫零, ℵ是希伯莱文的第一个字母)。 4) 设R为实数的全体,R的基数为ℵ ,|R|= ℵ 。 • • 以上四项规定,对于空集及Nn的基数,实际上就是集 合中元素的个数,关于ℵ0及ℵ,下面将予探讨。 有了标准基数之后,我们可以对各种集合测量其基数。 测量的手段是以双射函数为主体的等价关系一等势。 比如说,一个集合与N等势,那么这个集合的基数为 ℵ0 。
定理6 设A及B为两个可数集,那么A×B为一可数集。 定理 推论1 推论 设A1,A2,A3,…,An为n个可数集,那么 × A是可数集。
i=1 i n
定理7 (0,1)开区间上的实数不是可数集。 定理 定理8 设A为一集Y的函数,若f 是双射函数,则f 的逆关系 f –1是从Y到X的双射函数。 定理2 定理 设f 是从X到Y的函数,g 是从Y到Z的函数,则复合关 系f οg是从 X到Z的函数,将f ο g记为g ο f 。 定理3 定理 设f 是从X到Y的函数,g 是从Y到Z的函数。 1)若f 和g是满射函数,则g ο f 是满射函数; 2)若f 和g是单射函数,则g ο f 是单射函数; 3)若f 和g是双射函数,则g ο f 是双射函数。 定理4 定理 设f 是从X到Y的双射函数, f –1是f 的逆函数,则 1) (f –1) –1 = f 2) f –1 ο f = IX 3) f ο f –1 = IY
定义3 定义 设 |X|=n,P是从X到X的双射函数,称P为X上的置 换,称n为置换的阶。 • 在n个元素的集合中,不同的n阶置换的个数为n!。 • 通常用下面的方法表示置换。 x1 x2 x3 … xn P = p(x ) p(x ) p(x ) … p(x ) 1 2 3 n • 若∀xi∈X 有 p(xi) = xi ,则称P是恒等置换。 • P的逆函数P-1可表示为 p(x1) p(x2) p(x3) … p(xn) P-1 = x1 x2 x3 … xn • 置换的复合与关系的复合相同。 1 2 3 1 2 3 1 2 3 3 2 1 2 1 3 3 1 2
离散数学-----函数
2019/12/13
11
计算机科学学院 刘芳
8.2 函数的性质
解 (1) f : R→R, f(x)= x2+2x1
在x=1取得极大值0. 既不是单射也不是满射的.
(2) f : Z+→R, f(x)=lnx
单调上升, 是单射的. 但不满射, ranf={ln1, ln2, …}.
(3) f : R→Z, f(x)= x
8.1 函数的定义
例3:
设A = {1, 2, 3}, B = {a, b},则A到B共有多少个不
同的函数?分别列出来。
解:
f0={<1,a>,<2,a>,<3,a>} , f2={<1,a>,<2,b>,<3,a>} , f4={<1,b>,<2,a>,<3,a>},
f6={<1,b>,<2,b>,<3,a>} ,
BA={f | f : A→B}
思考:设|A|=m,|B|=n,则|BA|=?
2019/12/13
7
计算机科学学院 刘芳
8.1 函数的定义
解:
设:A={x1, x2, …,xm}, B={y1, y2, …,yn}, 则集合A到B的函数f形如:
f={<x1,□>, {<x2,□>,…… {<xm,□>} 对于每个□所在的 位置都可用B中的任何一个
2019/12/13
19
计算机科学学院 刘芳
8.4 函数的复合和反函数
定理8.1
设f, g是函数, 则f∘g也是函数, 且满足
离散数学 函数部分

一个十分重要的例子。
2020/3/14
计算机科学与技术学院
12
三、函数的合成运算
定义 考虑g:A→B,f:B→C是两个函数,则合成 关系f•g是从A到C的函数,记为 f•g:A→C,
称为函数g与f的合成函数。
显然,对任意x∈A,有 f•g(x)=f(g(x))。
2020/3/14
计算机科学与技术学院
2020/3/14
计算机科学与技术学院
16
例
例1 设f:R→R,满足: 1)f={<x,x2>|x∈R}; 2)f={<x,x+1>|x∈R}。求f-1。
解 1)对任意x∈R,有f(x)=x2与之对应,所以 f不是单射函数,即f非双射函数,因此f的逆函 数不存在。 2)因f是双射函数,所以f-1存在,且有: f-1={<x,x-1>|x∈R}。
计算机科学与技术学院
5
例2
设A={a,b},B={1,2},A×B={<a,1>,<a,2>,<b,1>,<b,2>},
此时从A到B的不同的关系有24=16个。分别如下:
R0=Φ R1={<a,1>} R2={<a,2>} R3={<b,1>};
R4={<b,2>};R5={<a,1>,<b,1>} R6={<a,1>,<b,2>}
2020/3/14
计算机科学与技术学院
10
例2
设An={a1,a2,a3,…,an}是n个元素的有限集, Bn={b1b2b3…bn|bi∈{0,1}},对An的每一个子 集S(即对任意S(An)),令
2020/3/14
计算机科学与技术学院
12
三、函数的合成运算
定义 考虑g:A→B,f:B→C是两个函数,则合成 关系f•g是从A到C的函数,记为 f•g:A→C,
称为函数g与f的合成函数。
显然,对任意x∈A,有 f•g(x)=f(g(x))。
2020/3/14
计算机科学与技术学院
2020/3/14
计算机科学与技术学院
16
例
例1 设f:R→R,满足: 1)f={<x,x2>|x∈R}; 2)f={<x,x+1>|x∈R}。求f-1。
解 1)对任意x∈R,有f(x)=x2与之对应,所以 f不是单射函数,即f非双射函数,因此f的逆函 数不存在。 2)因f是双射函数,所以f-1存在,且有: f-1={<x,x-1>|x∈R}。
计算机科学与技术学院
5
例2
设A={a,b},B={1,2},A×B={<a,1>,<a,2>,<b,1>,<b,2>},
此时从A到B的不同的关系有24=16个。分别如下:
R0=Φ R1={<a,1>} R2={<a,2>} R3={<b,1>};
R4={<b,2>};R5={<a,1>,<b,1>} R6={<a,1>,<b,2>}
2020/3/14
计算机科学与技术学院
10
例2
设An={a1,a2,a3,…,an}是n个元素的有限集, Bn={b1b2b3…bn|bi∈{0,1}},对An的每一个子 集S(即对任意S(An)),令
离散数学第3章 函数
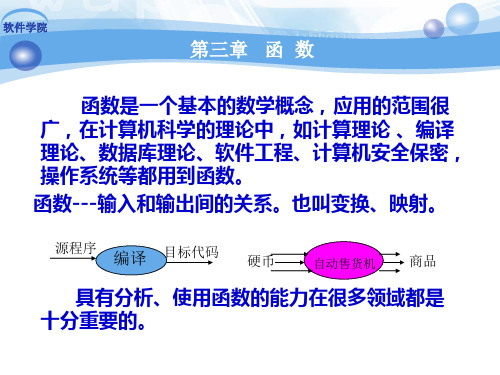
f:X Y 。 a 1。 。 b 2。 。 3。 c fC:Y X 。 1 a。 。 2 b。 。 3 c。
显然fC不是函数。可见如果一个函数不是双射的, 它的逆就不是函数。
软件学院
第三章 函 数 2.自变元与函数值(像源与映像) :
f:XY, 如果<x,y>∈f,称x是自变元(像源),称 y是x 的函数值(x的映像) 。
<x,y>∈f y=f(x) f:XY 3.定义域、值域 :f:XY, f的定义域,记作Df 即
Df ={x|x∈X,y(y∈Y,<x,y>f)} =X
注意:这里把g写在f的左边了.所以叫左复合. g f :XZ,即 g f 是X到Z的函数.这样写是为了
照顾数学习惯: g f(x)=g(f(x))
复合函数的计算方法同复合关系的计算.
软件学院
复合函数
例1 f:XY, g:YZ X={1,2,3} Y={1,2,3,4,} Z={1,2,3,4,5,} f= {<1,2>,<2,4>,<3,1>} g={ <1,3>,<2,5>,<3,2>,<4,1> } g f={ <1,3>,<2,5>,<3,2>,<4,1> } {<1,2>,<2,4>,<3,1>} ={<1,5>,<2,1>,3,3>} g f g 用有向图复合: f X Z X Y X 。 1 。 。 。 1 。 1 1 1 。 2 。 2 。 。 2 。 2。 3 。 2 3 。 。 3。 4 。 4 3。 3 。 。 5 。 5
显然fC不是函数。可见如果一个函数不是双射的, 它的逆就不是函数。
软件学院
第三章 函 数 2.自变元与函数值(像源与映像) :
f:XY, 如果<x,y>∈f,称x是自变元(像源),称 y是x 的函数值(x的映像) 。
<x,y>∈f y=f(x) f:XY 3.定义域、值域 :f:XY, f的定义域,记作Df 即
Df ={x|x∈X,y(y∈Y,<x,y>f)} =X
注意:这里把g写在f的左边了.所以叫左复合. g f :XZ,即 g f 是X到Z的函数.这样写是为了
照顾数学习惯: g f(x)=g(f(x))
复合函数的计算方法同复合关系的计算.
软件学院
复合函数
例1 f:XY, g:YZ X={1,2,3} Y={1,2,3,4,} Z={1,2,3,4,5,} f= {<1,2>,<2,4>,<3,1>} g={ <1,3>,<2,5>,<3,2>,<4,1> } g f={ <1,3>,<2,5>,<3,2>,<4,1> } {<1,2>,<2,4>,<3,1>} ={<1,5>,<2,1>,3,3>} g f g 用有向图复合: f X Z X Y X 。 1 。 。 。 1 。 1 1 1 。 2 。 2 。 。 2 。 2。 3 。 2 3 。 。 3。 4 。 4 3。 3 。 。 5 。 5
离散数学-第八章函数

例8.5 对于以下各题给定的A,B和f,判断是否构成函 数f:A→B。如果是,说明 f:A→B是否为单射,满 射,双射的,并根据要求进行计算。 (1) A={1,2,3,4,5}, B={6,7,8,9,10}, f={<1,8>,<3,9>,<4,10>,<2,6>,<5,9>} 能构成函数f:A→B,但f:A→B既不是单射也不是 满射的。 (2) A,B同(1),f={<1,7>,<2,6>,<4,5>,<1,9>,<5,10>}
令f:A→B,使得f()=f0,f({1})=f1,f({2})=f2,f({3})=f3, f({1,2})=f4,f({1,3})=f5,f({2,3})=f6,f({1,2,3})=f7
(2) A=[0,1],B=[1/4,1/2]
令f:[0,1]→[1/4,1/2],f(x)=(x+1)/4. (3) A=Z,B=N 将Z中元素以下列顺序排列并与N中元素对应:
例8.1 设 F1={<x1,y1>,<x2,y2>,<x3,y2>} F2={<x1,y1>,<x1,y2>} 判断它们是否为函数。 解:F1是函数,F2不是函数。
因为对应于x1存在y1和y2满足x1F2y1和x1F2y2, 与函数定义矛盾。
F 是函数(映射) 对于x1,x2∈A, 如果x1=x2 ,一定有f(x1)=f(x2)。即, 如果对于x1,x2∈A有f(x1) ≠f(x2),则一定有x1≠x2
函数是集合,可以用集合相等来定义函数的相等
定义8.2 设F,G为函数,则 F=G F G∧G F 由以上定义可知,如果两个函数F和G相等,一 定满足下面两个条件: 1.domF=domG 2. x∈domF=domG都有F(x)=G(x)
离散数学第05章 函数

g=f∩(CB)
则称g是f到C的缩小,记为f|c,即g为C到B 的函数:
g:CB
g(x)=f(x)
或
f|c(x)=f(x)
定义5.1.4 设f:CB,g:AB,且CA,
若g|c=f,则称g是f到A的扩大。
下面讨论由集合A和B,构成这样函数 f:AB会有多少呢?或者说,在AB的所有子 集中,是全部还是部分子集可以定义函数?令 BA表示这些函数的集合,即
定理5.3.1 设f:AB和g:BC是函数,通 过复合运算o,可以得到新的从A到C的函数, 记为gof,即对任意aA,有(gof)(x)=g(f(x))。
注意,函数是一种关系,今用斜体“o”表 示函数复合运算,记为gof,这是“左复合”, 它与关系的“右复合”fog次序正好相反,为区 分它们在同一公式中的出现,用粗体符号表示 关系复合fog,故有gof=fog。
BA={f|f:AB}
设 |A|=m , |B|=n , 则 |BA|=nm 。 这 是 因 为 对 每个自变元,它的函数值都有n种取法,故总共 有nm种从A到B的函数。
上面介绍一元函数,下面给出多元函数的 定义。
n 定义5.1.5 设A1,A2,···,An和B为集合,若f:
AiB 为 函 数 , 则 称 f 为 n 元 函 数 。 在
f={<a,a>|xA} 则称f:AA为A上恒等函数,通常记为IA, 因为恒等关系即是恒等函数。 由定义可知,A上恒等函数IA是双射函数。
定义5.2.6 设A和B为集合,且AB,若函 数A:B{0,1}为
{xA(x)=
1 xA
0 否则
则称xA为集合A的特征函数。
特征函数建立了函数与集合的一一对应关 系。于是,可通过特征函数的计算来研究集合 上的命题。
离散数学第五章 函数

f -1({0})={0, 1}, f -1({1})={2, 3}, f -1(Ø)= Ø
像与逆像: 映射的“提升”
设U和V是两个集合, f : U→V 是从U到V的一个函数, ρ(U)是U的幂集,ρ(V)是V的幂集。
像与逆像将从U到V的一个映射 f : U→V “提升” 为从U的幂集 ρ(U) 到V的幂集 ρ(V) 的映射
集合 A 在函数 f 下的 像 f (A)
U
f
V
A
f(A)
集合 B 在函数 f 下的 逆像 f -1(B)
U
f
V
-1
f (B)
B
例5.1.3 设 A={a, b, c, d, e} , B={1, 2, 3, 4} , φ: A→B, φ的定义如图所示。则
φ({a, b, c})={1, 2}
例:设 U={1,2,3,4},V={1,2,…,16},关系 f1={ <1,1>, <2,4>, <3,9>, <4,16> }, f2={ <1,1>, <2,3>, <4,4> }, f3={ <1,1>, <1,2>, <2,15>, <3,16>, <4,1> },
试判断哪些是函数?
解:f1 是,且 f1(a)=a2。 f2 不是,因为f2(3)=? f3 不是,因为两个f3(1)。
n×n×…×n = nm
m
映射:递归定义
例5.1.8 (1) 阶乘 n! f: N→N, f(0)=1, f(n+1)=f(n)(n+1), n∈N。
(但需要检查,是否都有射,是否没有一射多)
像与逆像: 映射的“提升”
设U和V是两个集合, f : U→V 是从U到V的一个函数, ρ(U)是U的幂集,ρ(V)是V的幂集。
像与逆像将从U到V的一个映射 f : U→V “提升” 为从U的幂集 ρ(U) 到V的幂集 ρ(V) 的映射
集合 A 在函数 f 下的 像 f (A)
U
f
V
A
f(A)
集合 B 在函数 f 下的 逆像 f -1(B)
U
f
V
-1
f (B)
B
例5.1.3 设 A={a, b, c, d, e} , B={1, 2, 3, 4} , φ: A→B, φ的定义如图所示。则
φ({a, b, c})={1, 2}
例:设 U={1,2,3,4},V={1,2,…,16},关系 f1={ <1,1>, <2,4>, <3,9>, <4,16> }, f2={ <1,1>, <2,3>, <4,4> }, f3={ <1,1>, <1,2>, <2,15>, <3,16>, <4,1> },
试判断哪些是函数?
解:f1 是,且 f1(a)=a2。 f2 不是,因为f2(3)=? f3 不是,因为两个f3(1)。
n×n×…×n = nm
m
映射:递归定义
例5.1.8 (1) 阶乘 n! f: N→N, f(0)=1, f(n+1)=f(n)(n+1), n∈N。
(但需要检查,是否都有射,是否没有一射多)
离散数学__函数

f3={<x1, y1>,<x3, y2>,<x4, y3>}
解答
f1={<x1, y1>,<x2, y2>,<x2, y3>,<x3, y1>,<x4, y3>}
不是函数。 ∵ x2对应两个不同的像点y2和y3 ∴不满足唯一性。
解答
f2={<x1, y1>,<x2, y1>,<x3, y1>,<x4, y2>}
缩小的举例
X={a1,a2,a3,x4,x5} Y={y1,y2,y3,y4,y5} A={a1,a2,a3} f={<a1,y1>,<a2,y2>,<a3,y5>,
<x4,y4>,<x5,y3>} 求:f/A
解答
f/A={<a1,y1>,<a2,y2>,<a3,y5>}
1、满射函数 2、内射函数 3、单射函数 4、双射函数 5、恒等函数
从左到右 从右到左
定理
函数f: X→Y 函数g: Y→Z g◦f: X→Z是函数 xX (g◦f)(x)=g(f(x))
证明
显然g◦f是从X到Z的关系 (1)任意性: f是函数:对任意的xX 存在yY,使得<x,y>f g是函数:对任意的yY 存在zZ,使得<y,z>g
<x,y>f 由复合关系的定义:
<<0,-1> ,1>,<<0,0> ,0>,<<0,1> ,-1>, <<1,-1> ,2>,<<1,0> ,1>,<<1,1> ,0>}
解答
f1={<x1, y1>,<x2, y2>,<x2, y3>,<x3, y1>,<x4, y3>}
不是函数。 ∵ x2对应两个不同的像点y2和y3 ∴不满足唯一性。
解答
f2={<x1, y1>,<x2, y1>,<x3, y1>,<x4, y2>}
缩小的举例
X={a1,a2,a3,x4,x5} Y={y1,y2,y3,y4,y5} A={a1,a2,a3} f={<a1,y1>,<a2,y2>,<a3,y5>,
<x4,y4>,<x5,y3>} 求:f/A
解答
f/A={<a1,y1>,<a2,y2>,<a3,y5>}
1、满射函数 2、内射函数 3、单射函数 4、双射函数 5、恒等函数
从左到右 从右到左
定理
函数f: X→Y 函数g: Y→Z g◦f: X→Z是函数 xX (g◦f)(x)=g(f(x))
证明
显然g◦f是从X到Z的关系 (1)任意性: f是函数:对任意的xX 存在yY,使得<x,y>f g是函数:对任意的yY 存在zZ,使得<y,z>g
<x,y>f 由复合关系的定义:
<<0,-1> ,1>,<<0,0> ,0>,<<0,1> ,-1>, <<1,-1> ,2>,<<1,0> ,1>,<<1,1> ,0>}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f:X Y 。 a 1。 。 b 2。 。 3。 c fC:Y X 。 1 a。 。 2 b。 。 3 c。
定理1 若f是XY的双射,则fC是YX的函数。
证明:(1)对任意的y∈Y,由f是双射,得f是满 射,所以ran f=Y 故 dom fC=ran f=Y (2)对任意的y∈Y,若存在x1∈X, x2∈X使 <y, x1>∈fC 且 <y, x2>∈fC 则 <x1,y>∈f 且 <x2,y>∈f 由于f是单射,有x1=x2。 由(1)、(2), fC是YX的函数。
⑵ 设f和g是入射的,因g f :XZ,任取x1, x2∈X,
x1≠x2,因f:XY是入射的,f(x1)≠f(x2) , 而 f(x1) ,f(x2)∈Y,因g:YZ是入射的,g(f(x1))≠g(f(x2)) 即g f (x1)≠ g f (x2)
所以g f 也是入射的。
六. 函数的类型
例子:
X 1。 2。
f
。 a 。 b 3。 c 4。 。
Rf=Y
Y
X 1。 2。
g
。 a 。 b 3。 c 4。 。
RgY
Y
X1
1。 2。
。 a 。 b 。 。 3 c 。 d
RhY1 一对一
h
Y1
1。
。 a 。 b 2。 。 c 3。
Rs=Y 一对一
X1
s
Y
函数的类型
1.满射的:f:XY是函数,如果 ran f=Y,则称f 是满射的。 2.入射的:f:XY是函数,如果对于任何x1,x2∈X, 如果 x1≠x2 有f(x1)≠f(x2),(或者若f(x1)=f(x2),则x1=x2), 则称f 是入射的,也称f 是单射的,也称f 是一对一的。 3.双射的:f:XY是函数,如果 f 既是满射的,又是 入射的,则称 f 是双射的,也称f 是一一对应的。 特别地::Y是单射; :是双射。
函数的复合
定义:设
f:XY, g:WZ是函数,若f(X)W,
则 g f ={<x,z>|xXzZy(yY <x,y>f<y,z>g)} 称为g在f的左边
证明:设 f:XY, g:WZ是函数,且f(X)W。 (1)对任意的xX,因为f是函数,故存在唯一 的序偶<x,y>,使得y=f(x)成立,而f(x)f(X)W, 又因为g是函数,故存在唯一的序偶<y,z>,使 得z=g(y)成立,根据复合定义,<x,z>g∘f,即 dom g∘f=X. (2)假设<x,z1>g∘f且<x,z2>g∘f,由复合定 义存在y1Y y2Y,使得 <x,y1>f<y1,z1>g <x,y2>f <y2,z2>g, 由于f、g为函数,所以有,y1=y2,因而z1=z2。 由(1)、(2)得g∘f是X到Z的函数。
用关系图复合:
三.函数复合的性质 4 定理1(满足可结合性)。 f:XY, g:YZ, h:ZW 是函数,则
(h g) f=h (g f)
g f X Y Z 。 。 1 1。 1 。 2 。 。 2 。 2 3 。 。 3 。 4 3 。 。 5
g f X 1。 2。 3。
四. 特殊函数
1. 常值函数:函数f:XY ,如果y0∈Y, 使得对x∈X, 有f(x)=y0 , 即ran f={y0} ,称f是常值函数。 2.恒等函数:恒等关系IX是X到X函数,即IX:XX,称之为 恒等函数。显然对于x∈X,有 IX(x)=x 。
五 .两个函数相等
设有两个函数f:AB g:AB, f=g 当且仅当 对任何x∈A,有f(x)=g(x)。
Z 。 1 。 2 。 3 。 4 。 5
定理2. f:XY, g:YZ是两个函数, 则
⑴如果f和g是 满射的,则 g f 也是满射的;
⑵如果f和g是入射的,则 g f 也是入射的;
⑶如果f和g是双射的,则 g f 也是双射的。 证明:⑴ 设f和g是满射的,因g f :XZ,任取z∈Z, 因 g:YZ是满射的,所以存在y∈Y,使得z=g(y), 又因 f:XY是满射的,所以存在x∈X,使得y=f(x), 于是有 z=g(y)=g(f(x))= g f (x), 所以 g f 是满射的。
二.性质 1.定理1 设f:XY是双射的函数,则(f-1)-1= f 。 2.定理2 设f:XY是双射的函数,则有 f-1 f= IX 且 f f-1 = IY 。 证明:先证明定义域、陪域相等。
因为 f:XY是双射的,f-1:YX也是双射的,所以
f-1 f :XX , IX:XX 可见f-1 f 与IX 具有相同的定义域和陪域。 再证它们的对应规律相同:x∈X,因f:XY,yY, 使得 y=f(x),又f 可逆,故 f-1(y)=x,于是 f-1 f (x)=f-1(f(x))=f-1(y)=x= IX (x) 同理可证 f f-1 = IY 。
思考题:如果 f:XX是入射的函数,则必是满射的,所 以 f 也是双射的。此命题在什么条件下成立吗?
5-2
函数的复合
关系的复合: 设R是从X到Y的关系,S是从Y到Z的关系, 则R和S的复合关系记作R S 。定义为: R S ={<x,z>|xXzZy(yY <x,y>R<y,z>S)}
2.定义域、值域和陪域(共域)
设f:XY, f的定义域(domain),记作dom f,或Df 即 Df =dom f={x|x∈X∧y(y∈Y∧<x,y>f)} =X f的值域(range) :记作ran f, 或Rf 即或f(X) Rf =ran f=f(X)={y| y∈Y∧x(x∈X∧<x,y>f)}
5-1
函数的基本概念
一.概念 定义:X与Y集合,f是从X到Y的关系,如果任何x∈X, 都存在唯一y∈Y,使得<x,y>∈f,则称f是从X到Y的函数, (变换、映射),记作f:X Y, 或X Y. 如果f:XX是函数, 也称f是X上的函数. 下面给出A={1,2,3}上几个关系,哪些是A到A的函数?
1。
X
f
。 3。
2
。 a 。 b 。
c
-1 Y f X
。 1 。 2 。 3
X 1。 2。
IX
X
3。
。 1 。 2 。 3
3.定理3 令 f:XY, g:YX是两个函数, 如果 g f= IX 且 f g = IY ,则 g= f-1 。 证明:⑴证f和g都可逆。因为g f= IX , IX是双射的, 由关系复合性质3得, f是入射的和g是 满射的。 同理由 f g = IY,得g是入射的和f 是 满射的。所 以f和g都可逆。 ⑵显然f-1和g具有相同的定义域和陪域。
f的陪域(codomain):即是Y(称之为f的陪域)。
二. 函数的表示方法
有 枚举法、关系图、关系矩阵、谓词描述法。
三.从X到Y的函数的集合YX:
YX ={f| f:XY} YX :它是由所有的从X到Y函数构成的集合 例 X={1,2,3} Y={a,b} 求所有从X到Y函数. 结论: 若X、Y是有限集合,且|X|=m,|Y|=n,则 |YX|=|Y||X|=nm。从X到Y的关系= |P(X Y)|= 2nm. 规定:从∅到∅的函数只有f=∅。 从∅到Y的函数只有f=∅。 若X≠∅,则从X到∅的函数不存在。
f
1
。
2
1
。
2
1
。
1
。
2
。 。 3
R1
。 。 3
R2
。 。 2。 。 3 3
R3 R4
下面哪些是R到R的函数?
1 f={<x,y>|x,y∈R∧y= __ } x g={<x,y>|x,y∈R∧x2+y2=4 } h={<x,y>|x,y∈R∧y= x2 } r ={<x,y>|x,y∈R∧y=lgx } v ={<x,y>|x,y∈R∧y= √ x }
逆函数的定义
定义:设f是XY的双射函数,则称fC:YX为f的逆函 数,并记f-1。 定理: f-1是YX的双射函数。 证明:由于ran f-1=dom f=X, 所以, f-1是满射。 对任意x∈X,若存在y1, y2 ∈Y,使得 <y1,x> ∈ f-1 且 <y2,x> ∈ f-1 则 <x,y1> ∈f 且 <x, y2> ∈f, 由于f是函数,所以y1= y2,即f-1是单射。 因此, f-1是双射。
c
Y
g
X
。 1 。 2
X 1。 2。
IX
X
。 1 。 2
4.定理4,令 f:XY, g:YX是两个双射函数,则 (g f) -1 =f -1 g-1
定理3 ⑴如果 gf 是满射的,则g是 满射的; ⑵如果gf 是入射的,则 f 是入射的;
⑶如果 gf 是双射的,则f是入射的和g是 满射的。
定理4 f:XY是函数, 则 f IX= f 且 IYf=f 。
5-3
逆函数
R是A到B的关系,其逆关系RC是B到A的 关系。 RC={<y,x>|<x,y>R} f:XY fC:YX, 是否是函数?
⑶证明它们的对应规律相同。 任取yY, f-1(y)= f-1 IY (y) = f-1 (f g) (y) = (f-1 f) g (y) =( IX g) (y) =g(y) 所以f-1 =g 注: f-1 =g 的两个条件必须同时满足,缺一不可。
定理1 若f是XY的双射,则fC是YX的函数。
证明:(1)对任意的y∈Y,由f是双射,得f是满 射,所以ran f=Y 故 dom fC=ran f=Y (2)对任意的y∈Y,若存在x1∈X, x2∈X使 <y, x1>∈fC 且 <y, x2>∈fC 则 <x1,y>∈f 且 <x2,y>∈f 由于f是单射,有x1=x2。 由(1)、(2), fC是YX的函数。
⑵ 设f和g是入射的,因g f :XZ,任取x1, x2∈X,
x1≠x2,因f:XY是入射的,f(x1)≠f(x2) , 而 f(x1) ,f(x2)∈Y,因g:YZ是入射的,g(f(x1))≠g(f(x2)) 即g f (x1)≠ g f (x2)
所以g f 也是入射的。
六. 函数的类型
例子:
X 1。 2。
f
。 a 。 b 3。 c 4。 。
Rf=Y
Y
X 1。 2。
g
。 a 。 b 3。 c 4。 。
RgY
Y
X1
1。 2。
。 a 。 b 。 。 3 c 。 d
RhY1 一对一
h
Y1
1。
。 a 。 b 2。 。 c 3。
Rs=Y 一对一
X1
s
Y
函数的类型
1.满射的:f:XY是函数,如果 ran f=Y,则称f 是满射的。 2.入射的:f:XY是函数,如果对于任何x1,x2∈X, 如果 x1≠x2 有f(x1)≠f(x2),(或者若f(x1)=f(x2),则x1=x2), 则称f 是入射的,也称f 是单射的,也称f 是一对一的。 3.双射的:f:XY是函数,如果 f 既是满射的,又是 入射的,则称 f 是双射的,也称f 是一一对应的。 特别地::Y是单射; :是双射。
函数的复合
定义:设
f:XY, g:WZ是函数,若f(X)W,
则 g f ={<x,z>|xXzZy(yY <x,y>f<y,z>g)} 称为g在f的左边
证明:设 f:XY, g:WZ是函数,且f(X)W。 (1)对任意的xX,因为f是函数,故存在唯一 的序偶<x,y>,使得y=f(x)成立,而f(x)f(X)W, 又因为g是函数,故存在唯一的序偶<y,z>,使 得z=g(y)成立,根据复合定义,<x,z>g∘f,即 dom g∘f=X. (2)假设<x,z1>g∘f且<x,z2>g∘f,由复合定 义存在y1Y y2Y,使得 <x,y1>f<y1,z1>g <x,y2>f <y2,z2>g, 由于f、g为函数,所以有,y1=y2,因而z1=z2。 由(1)、(2)得g∘f是X到Z的函数。
用关系图复合:
三.函数复合的性质 4 定理1(满足可结合性)。 f:XY, g:YZ, h:ZW 是函数,则
(h g) f=h (g f)
g f X Y Z 。 。 1 1。 1 。 2 。 。 2 。 2 3 。 。 3 。 4 3 。 。 5
g f X 1。 2。 3。
四. 特殊函数
1. 常值函数:函数f:XY ,如果y0∈Y, 使得对x∈X, 有f(x)=y0 , 即ran f={y0} ,称f是常值函数。 2.恒等函数:恒等关系IX是X到X函数,即IX:XX,称之为 恒等函数。显然对于x∈X,有 IX(x)=x 。
五 .两个函数相等
设有两个函数f:AB g:AB, f=g 当且仅当 对任何x∈A,有f(x)=g(x)。
Z 。 1 。 2 。 3 。 4 。 5
定理2. f:XY, g:YZ是两个函数, 则
⑴如果f和g是 满射的,则 g f 也是满射的;
⑵如果f和g是入射的,则 g f 也是入射的;
⑶如果f和g是双射的,则 g f 也是双射的。 证明:⑴ 设f和g是满射的,因g f :XZ,任取z∈Z, 因 g:YZ是满射的,所以存在y∈Y,使得z=g(y), 又因 f:XY是满射的,所以存在x∈X,使得y=f(x), 于是有 z=g(y)=g(f(x))= g f (x), 所以 g f 是满射的。
二.性质 1.定理1 设f:XY是双射的函数,则(f-1)-1= f 。 2.定理2 设f:XY是双射的函数,则有 f-1 f= IX 且 f f-1 = IY 。 证明:先证明定义域、陪域相等。
因为 f:XY是双射的,f-1:YX也是双射的,所以
f-1 f :XX , IX:XX 可见f-1 f 与IX 具有相同的定义域和陪域。 再证它们的对应规律相同:x∈X,因f:XY,yY, 使得 y=f(x),又f 可逆,故 f-1(y)=x,于是 f-1 f (x)=f-1(f(x))=f-1(y)=x= IX (x) 同理可证 f f-1 = IY 。
思考题:如果 f:XX是入射的函数,则必是满射的,所 以 f 也是双射的。此命题在什么条件下成立吗?
5-2
函数的复合
关系的复合: 设R是从X到Y的关系,S是从Y到Z的关系, 则R和S的复合关系记作R S 。定义为: R S ={<x,z>|xXzZy(yY <x,y>R<y,z>S)}
2.定义域、值域和陪域(共域)
设f:XY, f的定义域(domain),记作dom f,或Df 即 Df =dom f={x|x∈X∧y(y∈Y∧<x,y>f)} =X f的值域(range) :记作ran f, 或Rf 即或f(X) Rf =ran f=f(X)={y| y∈Y∧x(x∈X∧<x,y>f)}
5-1
函数的基本概念
一.概念 定义:X与Y集合,f是从X到Y的关系,如果任何x∈X, 都存在唯一y∈Y,使得<x,y>∈f,则称f是从X到Y的函数, (变换、映射),记作f:X Y, 或X Y. 如果f:XX是函数, 也称f是X上的函数. 下面给出A={1,2,3}上几个关系,哪些是A到A的函数?
1。
X
f
。 3。
2
。 a 。 b 。
c
-1 Y f X
。 1 。 2 。 3
X 1。 2。
IX
X
3。
。 1 。 2 。 3
3.定理3 令 f:XY, g:YX是两个函数, 如果 g f= IX 且 f g = IY ,则 g= f-1 。 证明:⑴证f和g都可逆。因为g f= IX , IX是双射的, 由关系复合性质3得, f是入射的和g是 满射的。 同理由 f g = IY,得g是入射的和f 是 满射的。所 以f和g都可逆。 ⑵显然f-1和g具有相同的定义域和陪域。
f的陪域(codomain):即是Y(称之为f的陪域)。
二. 函数的表示方法
有 枚举法、关系图、关系矩阵、谓词描述法。
三.从X到Y的函数的集合YX:
YX ={f| f:XY} YX :它是由所有的从X到Y函数构成的集合 例 X={1,2,3} Y={a,b} 求所有从X到Y函数. 结论: 若X、Y是有限集合,且|X|=m,|Y|=n,则 |YX|=|Y||X|=nm。从X到Y的关系= |P(X Y)|= 2nm. 规定:从∅到∅的函数只有f=∅。 从∅到Y的函数只有f=∅。 若X≠∅,则从X到∅的函数不存在。
f
1
。
2
1
。
2
1
。
1
。
2
。 。 3
R1
。 。 3
R2
。 。 2。 。 3 3
R3 R4
下面哪些是R到R的函数?
1 f={<x,y>|x,y∈R∧y= __ } x g={<x,y>|x,y∈R∧x2+y2=4 } h={<x,y>|x,y∈R∧y= x2 } r ={<x,y>|x,y∈R∧y=lgx } v ={<x,y>|x,y∈R∧y= √ x }
逆函数的定义
定义:设f是XY的双射函数,则称fC:YX为f的逆函 数,并记f-1。 定理: f-1是YX的双射函数。 证明:由于ran f-1=dom f=X, 所以, f-1是满射。 对任意x∈X,若存在y1, y2 ∈Y,使得 <y1,x> ∈ f-1 且 <y2,x> ∈ f-1 则 <x,y1> ∈f 且 <x, y2> ∈f, 由于f是函数,所以y1= y2,即f-1是单射。 因此, f-1是双射。
c
Y
g
X
。 1 。 2
X 1。 2。
IX
X
。 1 。 2
4.定理4,令 f:XY, g:YX是两个双射函数,则 (g f) -1 =f -1 g-1
定理3 ⑴如果 gf 是满射的,则g是 满射的; ⑵如果gf 是入射的,则 f 是入射的;
⑶如果 gf 是双射的,则f是入射的和g是 满射的。
定理4 f:XY是函数, 则 f IX= f 且 IYf=f 。
5-3
逆函数
R是A到B的关系,其逆关系RC是B到A的 关系。 RC={<y,x>|<x,y>R} f:XY fC:YX, 是否是函数?
⑶证明它们的对应规律相同。 任取yY, f-1(y)= f-1 IY (y) = f-1 (f g) (y) = (f-1 f) g (y) =( IX g) (y) =g(y) 所以f-1 =g 注: f-1 =g 的两个条件必须同时满足,缺一不可。
