2008研究生固体物理面试答案
研究生复试固体物理
《固体物理》考试大纲一、课程简介固体物理学是研究晶体及其微观属性的基础。
本课程的理想晶体部分，从有关固体最简单的模型，即金属自由电子气体模型出发，逐渐加以丰富完善的体系，系统学习有关固体晶格结构、电子能带论、晶格振动、输运现象、原子间的键合和固体中的缺陷等方面的内容。
兼顾学习近三十年来固体物理的某些新发展，如无序、尺寸、维度和关联等问题，内容包括无序体系中电子的定域化，弱定域化，介观体系的物理、纳米微粒，团簇，库仑阻塞，半导体低维体系，拓扑缺陷，二维体系中的相变，准一维导体，密度泛函理论，强关联初步，高温超导电性和分数量子霍尔效应等。
二、考试内容及要求第一章晶体结构一、考核知识点1．晶体基本知识及结构2．晶体的布喇菲空间点阵3．晶体的周期性基矢的概念4．密堆积配位数5．倒格子空间6．晶体的对称性7．晶格结构的分类8．晶体的布里渊区9．布拉格方程和反射方程、原子散射因子、几何结构因子二、考核要求（一）晶体结构基本知识识记：晶体基本知识及结构（二）晶体的布喇菲空间点阵识记：（1）晶体的布喇菲空间点阵（2）原胞、晶胞、晶列、晶面指数（3）晶体的密勒指数（三）晶体的周期性基矢的概念识记：（1）晶体的周期性（2）基矢的概念（四）密堆积配位数识记：（1）晶体密堆积知识及结构（2）晶体的配位数（五）倒格子空间综合应用：能使用倒格子空间（六）晶体的对称性识记：晶体的对称性（七）晶格结构的分类1．识记：晶格结构的分类2．简单应用：晶格结构的分类的相关知识解决晶体实际问题，完成作业要求。
（八）晶体的布里渊区识记：（1）布里渊区的定义（2）简单正方二维晶格布里渊区的画法（九）X射线衍射布拉格方程和反射方程、原子散射因子、几何结构因子领会：（1）X射线衍射布拉格方程和反射方程（2）原子散射因子的相关知识（3）几何结构因子的相关知识第二章晶体的结合一、考核知识点1．晶体的电负性2．晶体的结合类型3．结合力的一般性质4．分子晶体的结合能5．离子晶体的结合能6．离子半径二、考核要求（一）晶体的电负性识记：晶体的分类和的电负性（二）晶体的结合类型识记：晶体的结合类型（三）结合力的一般性质识记：结合力的一般性质（四）分子晶体的结合能简单应用：非极性分子的结合能计算方法（五）离子晶体的结合能简单应用：离子晶体的结合能和一般计算方法（六）离子半径领会：离子半径的定义和简单求解方法第三章晶体振动及晶体的热学性质一、考核知识点1．原子链的振动2．简正振动声子3．长波近似4．晶格振动的热容理论固体比热容5．非简谐效应二、考核要求（一）原子链的振动识记：一维原子链振动的基本概念和数学模型（二）简正振动、声子识记：（1）声子的概念（2）晶格振动谱的实验测定原理和方法（三）长波近似领会：长波近似概念和模型的数学推导（四）晶格振动的热容理论固体比热容简单应用：（1）晶体比热的爱因斯坦模型基本知识（2）晶体比热的德拜模型基本知识（3）固体比热容公式推导过程和前提条件（五）非简谐效应识记：（1）非简谐效应基本概念（2）晶格的自由能（3）晶体的热力学函数基本知识第四章金属电子论基础一、考核知识点1．自由电子气体模型2．电子比热容的量子理论3．溢出功接触电势差4．外场作用下的金属电子气体5．金属的电导率二、考核要求（一）自由电子气体模型识记：（1）了解自由电子模型（2）布洛赫波函数相关概念（3）布洛赫定理的表述和推导（二）电子比热容的量子理论领会：电子比热容的量子理论基础知识（三）溢出功接触电势差1．领会：晶体溢出功的概念2．简单应用：了解接触电势差原理和应用特点（四）外场作用下的金属电子气体领会：外场作用下的金属电子气体模型的基础和特点（五）金属的电导率识记：掌握金属的电导率的推导过程和方法第五章能带理论基础一、考核知识点1．能带理论的基本假设2．周期场中单电子状态的一般性质3．近自由电子近似4．紧束缚近似5．能带计算的近似方法二、考核要求（一）能带理论的基本假设识记：（1）能带理论的基本假设相关知识（2）理解恒定电场作用下电子的运动规律（3）电子的有效质量（二）周期场中单电子状态的一般性质1．领会：（1）理解周期场中单电子状态的一般性质（2）晶体能态密度基本知识2．综合应用：晶体能态密度的计算（三）近自由电子近似综合应用：（1）近自由电子近似相关知识（2）理解近自由电子近似的应用条件（3）能熟练运用近自由电子近似模型解决实际习题中的问题（四）紧束缚近似近综合应用：能熟练运用紧束缚近似模型解决实际习题中的问题（五）能带计算的近似方法1．识记：能带计算的近似方法中的基本假设相关知识2．综合应用：能熟练运用能带计算的近似方法解决晶体能带计算问题第六章能带结构分析一、考核知识点1．电子运动的半经典模型2．固体导电的能带理论3．磁场作用下的电子运动4．费米面的构造5．费米面的测量6．用光电子谱研究能带结构7．一般金属的能带结构二、考核要求（一）电子运动的半经典模型识记：（1）电子在外加电磁场中的运动（2）漂移速度方程（二）固体导电的能带理论领会：用能带理论解释常见晶体材料的一般性质（三）磁场作用下的电子运动1．识记：（1）磁场作用下的电子能态等概念（2）漂移速度方程2．领会：（1）电子在恒定磁场中的运动规律（2）回旋共振、德·哈斯-范·阿尔芬效应（四）费米面的构造1．识记：费米能级和费米面的概念2．领会：用相关公式计算一般晶体材料的费米能级（五）费米面的测量领会：用相关公式计算一般晶体材料的费米能级（六）用光电子谱研究能带结构识记：（1）光电子谱的产生机制和检测技术（2）能带结构与光电子谱的关系（七）一般金属的能带结构1．识记：金属的能带结构的特点2．综合运用：用金属的能带结构分析晶体的性质。
物理研究所面试问题与答案
物理研究所面试问题与答案中科院物理所面试整理（1）1. 什么是能带？2. 什么是位移电流？是由谁引入的？其物理实质是什么？3. 简述原胞和单胞的区分。
4. 什么是宏观对称素和微观对称素？5. 简述热力学四大定律。
6. 晶体可能有的独立的点对称元素有几种？7. 康普顿散射证明白什么？8. 比热反映了什么，它的微观本质是什么？9. 简述量子力学的进展。
10. 电子单缝试验及其物理内涵？11. 什么是倒格子？引入倒格子的意义是什么？12. 什么事俄歇电子？是怎么产生的？9. 简述量子力学的进展。
经过100多年的进展量子力学已经成为一个日渐完备的体系，它的进展是在19世纪末20世纪初物理晴朗的天空飘来的两朵乌云之一，即在描述黑体辐射试验时适用的瑞利-金斯曲线导致紫外灾难。
1900年Planck提出了一个将能量量子化的公式即Planck公式，这个公式与试验惊人的相符。
该公示认为E，1905年Einstein在解释光电效应试验中提出辐射场是由光子组成的，使得光电效应问题迎刃而解。
1913年波尔在讨论原子光谱时，提出了基于两条假设的原子量子理论，一条是原子具有离散能量的定态假设，即原子中的光子只能在某些特定的经典轨道上运动。
二是电子在轨道上跃迁时会以特定频率放射光子。
并取得了很大胜利，但这仍是一个建立在假设上的理论。
并且也在以后的讨论中消失了许多困难，例如碱金属光谱试验、塞曼效应试验、量子隧穿效应等。
一系列的新理论也开头提出，Pauli不相容原理、Uhlenback和Goudsmit提出了电子自旋假设。
并且Heisenberg提出了矩阵力学也成为量子力学。
这是建立在不确定关系根底上的，其用算符表示力学量胜利的解释了量子力学体系。
后来Schrodinger提出了波动力学也同样有效的解释了量子力学体系。
并且这两个方程由Dirac提出的Dirac 符号所调和。
并且比函数也被Born的概率波所解释。
量子力学进展成为了建立在：波函数公设、算符公设、测量公设（平均值公设）、薛定谔方程公设、全同性原理公设五大公设之上的学科。
固体物理答案
固体物理答案（1）共价键结合的特点？共价结合为什么有“饱和性”和“⽅向性”？饱和性和⽅向性饱和性：由于共价键只能由为配对的电⼦形成，故⼀个原⼦能与其他原⼦形成共价键的数⽬是有限制的。
N<4，有n 个共价键；n>=4，有（8-n ）个共价键。
其中n 为电⼦数⽬。
⽅向性：⼀个院⼦与其他原⼦形成的各个共价键之间有确定的相对取向。
（2）如何理解电负性可⽤电离能加亲和能来表征？电离能：使原⼦失去⼀个电⼦所必须的能量其中A 为第⼀电离能，电离能可表征原⼦对价电⼦束缚的强弱；亲和势能：中性原⼦获得电⼦成为-1价离⼦时放出的能量，其中B 为释放的能量，也可以表明原⼦束缚价电⼦的能⼒，⽽电负性是⽤来表⽰原⼦得失电⼦能⼒的物理量。
故电负性可⽤电离能加亲和势能来表征。
（3）引⼊玻恩-卡门条件的理由是什么？在求解原⼦运动⽅程是，将⼀维单原⼦晶格看做⽆限长来处理的。
这样所有的原⼦的位置都是等价的，每个原⼦的振动形式都是⼀样的。
⽽实际的晶体都是有限的，形成的键不是⽆穷长的，这样的链两头原⼦就不能⽤中间的原⼦的运动⽅程来描述。
波恩—卡门条件解决上述困难。
（4）温度⼀定，⼀个光学波的声⼦数⽬多呢，还是⼀个声学波的声⼦数⽬多？对同⼀振动模式，温度⾼时的声⼦数⽬多呢，还是温度低的声⼦数⽬多？温度⼀定，⼀个声学波的声⼦数⽬多。
对于同⼀个振动模式，温度⾼的声⼦数⽬多。
（5）长声学格波能否导致离⼦晶体的宏观极化？不能。
长声学波代表的是原胞的运动，正负离⼦相对位移为零。
（6）晶格⽐热理论中德拜（Debye ）模型在低温下与实验符合的很好，物理原因是什么？爱因斯坦模型在低温下与实验存在偏差的根源是什么？在甚低温下，不仅光学波得不到激发，⽽且声⼦能量较⼤的短声学波也未被激发，得到激发的只是声⼦能量较⼩的长声学格波。
长声学格波即弹性波。
德拜模型只考虑弹性波对热容德贡献。
因此，在甚低温下，德拜模型与事实相符，⾃然与实验相符。
爱因斯坦模型过于简单，假设晶体中各原⼦都以相同的频率做振动，忽略了各格波对热容贡献的差异，按照爱因斯坦温度的定义可估计出爱因斯坦频率为光学⽀格波。
《固体物理学》测验题
2008级电技专业《固体物理学》测验题一、 （40分）简要回答：1、 什么是晶体？试简要说明晶体的基本性质。
2、 试简要说明CsCl 晶体所属的晶系、布喇菲格子类型和结合键的类型。
3、 试用极射赤平投影图说明3（3次旋转反演轴）的作用效果并给出其等效对称要素。
4、 什么是格波？什么是声子？声子的能量和动量各为多少？5、 试写出自由电子和晶体中电子的波函数。
6、 如需讨论绝缘体中电子的能谱，应采何种模型？其势能函数有何特点？7、 什么是禁带？出现禁带的条件是什么？ 8、 固体中电子的能量和电子波矢间有何关系？ 二、（10分）某晶体具有简立方结构，晶格常数为a 。
试画出该晶体的一个晶胞，并在其中标出下列晶面：（111`），（201），（123）和（110）。
三、（8分）某晶体具有面心立方结构，试求其几何结构因子并讨论x 射线衍射时的消光规律。
四、（12分）试求晶格常数为2a 的一维布喇菲格子晶格振动的色散关系，并由此讨论此一维晶格的比热。
五、（15分）对于六角密积结构晶体，其固体物理原胞的基矢为：kc a ja i a a ja i a a=+-=+=321232232试求（1） 倒格子基矢；（2） 晶面蔟（210）的面间距； （3）试画出以21,a a为基矢的二维晶格的第一、第二和第三布里渊区。
六、（15）已知一维晶体电子的能带可写为：)2cos 81cos 87()(22ka ka mak E +-= 式中a 是晶格常数，试求： （1） 能带的宽度；（2） 电子在波矢k 态时的速度；（3） 能带底部和能带顶部附近电子的有效质量。
《固体物理学》测验参考答案一、（40分）请简要回答下列问题： 1. 实际的晶体结构与空间点阵之间有何关系？ 答：晶体结构=空间点阵+基元。
2. 什么是晶体的对称性？晶体的基本宏观对称要素有哪些？答：晶体的对称性指晶体的结构及性质在不同方向上有规律重复的现象。
描述晶体宏观对称性的基本对称要素有1、2、3、4、6、对称心i 、对称面m 和4次反轴。
固体物理简答题及答案
简答题1、原子联合成晶体时，原子的价电子产生从头散布，进而产生不一样的结协力，剖析离子性、共价性、金属性和范德瓦耳斯性结协力的特色。
答案：离子性联合：正、负离子之间靠库仑吸引力作用而互相凑近，当凑近到必定程度时，因为泡利不相容原理，两个离子的闭合壳层的电子云的交迭会产生强盛的排挤力。
当排挤力和吸引力互相均衡时，形成稳固的离子晶体；共价性联合：靠两个原子各贡献一个电子，形成所谓的共价键；金属性联合：构成晶体时每个原子的最外层电子为全部原子所共有，所以在联合成金属晶体时，失掉了最外层（价）电子的原子实“沉醉”在由价电子构成的“电子云”中。
在这类状况下，电子云和原子实之间存在库仑作用，体积越小电子云密度越高，库仑互相作用的库仑能愈低，表现为原子聚合起来的作用。
范德瓦耳斯性联合：惰性元素最外层的电子为8 个，拥有球对称的稳固关闭构造。
但在某一刹时因为正、负电中心不重合而使原子体现出刹时偶极矩，这就会使其余原子产生感觉极矩。
非极性分子晶体就是依赖这刹时偶极矩的互作用而联合的。
2.什么叫简正振动模式？简正振动数量、格波数量或格波振动模式数量是不是一回事？答案：为了使问题既简化又能抓住主要矛盾，在剖析议论晶格振动时，将原子间互作使劲的泰勒级数中的非线形项忽视掉的近似称为简谐近似 . 在简谐近似下 ,由 N个原子构成的晶体的晶格振动 , 可等效成 3N个独立的谐振子的振动 . 每个谐振子的振动模式称为简正振动模式 , 它对应着全部的原子都以该模式的频次做振动 , 它是晶格振动模式中最简单最基本的振动方式 . 原子的振动 , 或许说格波振动往常是这3N 个简正振动模式的线形迭加 .简正振动数量、格波数量或格波振动模式数量是一回事 , 这个数量等于晶体中全部原子的自由度数之和 , 即等于 3N.3.长光学支格波与长声学支格波实质上有何差异 ?答案：长光学支格波的特色是每个原胞内的不一样原子做相对振动, 振动频次较高 , 它包括了晶格振动频次最高的振动模式 . 长声学支格波的特色是原胞内的不一样原子没有相对位移 , 原胞做整体运动 , 振动频次较低 , 它包括了晶格振动频次最低的振动模式 , 波速是一常数 . 任何晶体都存在声学支格波 , 但简单晶格 ( 非复式格子 ) 晶体不存在光学支格波 .4.长声学格波可否致使离子晶体的宏观极化 ?答案：长光学格波所以能致使离子晶体的宏观极化 , 其本源是长光学格波使得原胞内不一样的原子 ( 正负离子 ) 产生了相对位移 . 长声学格波的特色是 , 原胞内全部的原子没有相对位移 . 所以 , 长声学格波不可以致使离子晶体的宏观极化 .5.何谓极化声子 ? 何谓电磁声子 ?答案：长光学纵波惹起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场 ,称长光学纵波声子为极化声子.由本教科书的式可知 , 长光学横波与电磁场相耦合 , 使得它拥有电磁性质 , 人们称长光学横波声子为电磁声子 .6、什么是声子？答案：晶格振动的能量量子。
考研固体物理和热统面试资料
能带结构可以解释固体中导体、半导体、绝缘体三大类区别的由来。材料的导电性是由“传导带”中含有的电子数量决定。当电子从“价带”获得能量而跳跃至“传导带”时，电子就可以在带间任意移动而导电。
以压强为例，在地球水平线上，大气压强为101.325千帕斯卡，假如在这里煮水，水将于100摄氏度沸腾。但在海拔约8.8公里的珠穆朗玛峰上，大气压强只有若3.2千帕斯卡，假如在这里煮水，水将于69摄氏度沸腾。
以相态为例，液态水的比热容是4200，而冰（水的固态）的比热容则是2060。
固体的比热容随温度升高而增加,在低温时增加较快,在高温时增加较慢。
23.这三年的诺贝尔物理奖都给了什么领域？
2009:在光学通信领域中光的传输的开创性成就;发明了成像半导体电路——电荷藕合器件图像传感器CCD
2010关于二维石墨烯材料的开创性实验
2011通过观测超新星发现宇宙的加速扩张
25.什么是玻色爱因斯坦凝聚？为什么光可以减速原子？
玻色-爱因斯坦冷凝态
理论的详解
。
3.康普顿散射证明了什么？
在原子物理学中，康普顿散射，或称康普顿效应（英语：compton effect），是指当X射线或伽马射线的光子跟物质相互作用，因失去能量而导致波长变长的现象。相应的还存在逆康普顿效应——光子获得能量引起波长变短。这一波长变化的幅度被称为康普顿偏移。这个效应反映出光不仅仅具有波动性。此前汤姆孙散射的经典波动理论并不能解释此处波长偏移的成因，必须引入光的粒子性。这一实验说服了当时很多物理学家相信，光在某种情况下表现出粒子性，光束类似一串粒子流，而该粒子流的能量与光频率成正比。
固体物理问答题习题解答
18、你认为简单晶格存在强烈的红外吸收吗？答：实验已经证实, 离子晶体能强烈吸收远红外光波. 这种现象产生的根源是离子晶体中的长光学横波能与远红外电磁场发生强烈耦合. 简单晶格中不存在光学波, 所以简单晶格不会吸收远红外光波.19、爱因斯坦模型在低温下与实验存在偏差的根源是什么？答：按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.20、在极低温度下，德拜模型为什么与实验相符？答：在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.21、为什么行程一个肖特基缺陷所需能量比一个弗伦克尔缺陷所需能量低？答：形成一个肖特基缺陷时，晶体内留下一个空位，晶体表面多一个原子，因此形成一个肖特基缺陷所需的能量，可以看成晶体表面一个原子与其他原子的相互作用能，和晶体内部一个原子与其他原子的相互作用能的差值，形成一个弗伦克尔缺陷是，晶体内留下一个空位，多一个填隙原子，因此形成一个弗伦克尔缺陷所需的能量，可以看成晶体内部一个填隙原子与其他原子的相互作用能，和晶体内部一个原子与其他原子相互作用能的差值，填隙原子与相邻原子的距离非常小，它与其他原子的排斥力的相互作用能是负值，所以填隙原子与其它原子相互作用能的绝对值，比晶体表面一个原子与其他原子相互作用能的绝对值要小，也就是说形成一个肖特基缺陷所需能量比形成一个弗伦克尔所需能量要低。
22、晶体的结合能，晶体的内能，原子间的相互作用势能有何区别。
答：自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.原子的动能与原子间的相互作用势能之和为晶体的内能.在0K时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K时原子间的相互作用势能的绝对值近似等于晶体的结合能.23、原子间的排斥作用取决于什么原因？答：相邻的原子靠得很近, 以至于它们内层闭合壳层的电子云发生重叠时, 相邻的原子间便产生巨大排斥力. 也就是说, 原子间的排斥作用来自相邻原子内层闭合壳层电子云的重叠.24、原子间的排斥作用与吸引作用有何关系？这两种作用起主导作用的范围是什么起主导的范围是什么？答：在原子由分散无规的中性原子结合成规则排列的晶体过程中, 吸引力起到了主要作用. 在吸引力的作用下, 原子间的距离缩小到一定程度, 原子间才出现排斥力. 当排斥力与吸引力相等时, 晶体达到稳定结合状态. 可见, 晶体要达到稳定结合状态, 吸引力与排斥力缺一不可. 设此时相邻原子间的距离为, 当相邻原子间的距离>时, 吸引力起主导作用; 当相邻原子间的距离<时, 排斥力起主导作用.25、共价结合为什么有饱和性和方向性？答：设N为一个原子的价电子数目, 对于IV A、V A、VI A、VII A族元素，价电子壳层一共有8个量子态, 最多能接纳(8-N)个电子, 形成(8-N)个共价键. 这就是共价结合的“饱和性”.共价键的形成只在特定的方向上, 这些方向是配对电子波函数的对称轴方向, 在这个方向上交迭的电子云密度最大. 这就是共价结合的“方向性”.（同时参考书本第86页）26、共价结合，两原子电子云交迭产生吸引，而原子靠近时，电子云交迭会产生巨大的排斥力，如何解释？答：共价结合, 形成共价键的配对电子, 它们的自旋方向相反, 这两个电子的电子云交迭使得体系的能量降低, 结构稳定. 但当原子靠得很近时, 原子内部满壳层电子的电子云交迭, 量子态相同的电子产生巨大的排斥力, 使得系统的能量急剧增大.27、为什么许多金属为密积结构？答：金属结合中，受到最小能量原理的约束，要求原子实与共有电子电子云间的库伦能要尽可能的低（绝对值尽可能的大）原子实越紧凑，原子实与共有电子电子云靠的就越紧密，库伦能就越低，所以，许多金属的结构为密积结构28、你认为固体的弹性强弱主要排斥作用决定吗，还是吸引作用决定？答：如上图所示, 附近的力曲线越陡, 当施加一定外力, 固体的形变就越小. 附近力曲线的斜率决定了固体的弹性性质. 而附近力曲线的斜率主要取决于排斥力. 因此, 固体的弹性强弱主要由排斥作用决定.29、在布里渊区边界上电子的能带有何特点？答：电子的能带依赖于波矢的方向, 在任一方向上, 在布里渊区边界上, 近自由电子的能带一般会出现禁带. 若电子所处的边界与倒格矢正交, 则禁带的宽度, 是周期势场的付里叶级数的系数.不论何种电子, 在布里渊区边界上, 其等能面在垂直于布里渊区边界的方向上的斜率为零,即电子的等能面与布里渊区边界正交.30、当电子的波矢落在布里渊区边界上时，其有效质量为什么与真实质量有显著区别？答：晶体中的电子除受外场力的作用外, 还和晶格相互作用. 设外场力为F, 晶格对电子的作用力为F l, 电子的加速度为.但F l的具体形式是难以得知的. 要使上式中不显含F l, 又要保持上式左右恒等, 则只有.显然, 晶格对电子的作用越弱, 有效质量m*与真实质量m的差别就越小. 相反, 晶格对电子的作用越强, 有效质量m*与真实质量m的差别就越大. 当电子的波矢落在布里渊区边界上时, 与布里渊区边界平行的晶面族对电子的散射作用最强烈. 在晶面族的反射方向上, 各格点的散射波相位相同, 迭加形成很强的反射波. 正因为在布里渊区边界上的电子与晶格的作用很强, 所以其有效质量与真实质量有显著差别.31、本征半导体的能带与绝缘体的能带有何异同？答：在低温下，本征半导体的能带与绝缘体的能带结构相同，但本征半导体的禁带较窄，禁带宽度通常小于2eV，由于禁带窄，本征半导体禁带下满带项的电子可以借助热激发，跃迁到禁带上面空带的底部，使得满带不满，空带不空，二者都对导电有贡献。
清华大学硕士材料科学基础真题2008年
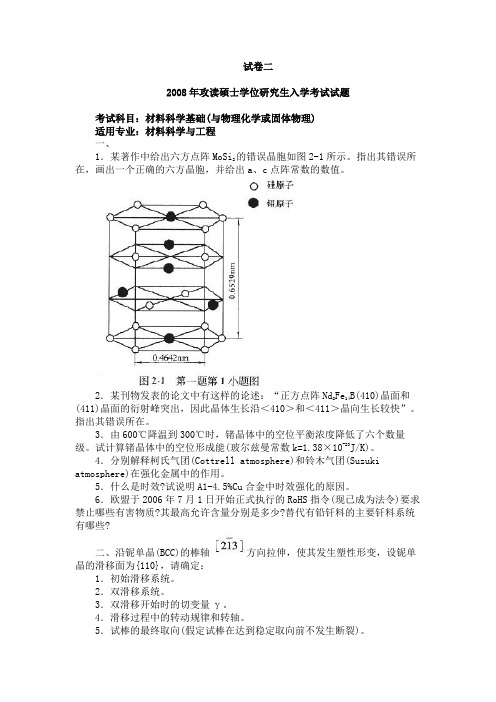
试卷二2008年攻读硕士学位研究生入学考试试题考试科目：材料科学基础(与物理化学或固体物理)适用专业：材料科学与工程一、1．某著作中给出六方点阵MoSi2的错误晶胞如图2-1所示。
指出其错误所在，画出一个正确的六方晶胞，并给出a、c点阵常数的数值。
2．某刊物发表的论文中有这样的论述：“正方点阵Nd2Fe14B(410)晶面和(411)晶面的衍射峰突出，因此晶体生长沿＜410＞和＜411＞晶向生长较快”。
指出其错误所在。
3．由600℃降温到300℃时，锗晶体中的空位平衡浓度降低了六个数量级。
试计算锗晶体中的空位形成能(玻尔兹曼常数k=1.38×10-23J/K)。
4．分别解释柯氏气团(Cottrell atmosphere)和铃木气团(Suzuki atmosphere)在强化金属中的作用。
5．什么是时效?试说明A1-4.5%Cu合金中时效强化的原因。
6．欧盟于2006年7月1日开始正式执行的RoHS指令(现已成为法令)要求禁止哪些有害物质?其最高允许含量分别是多少?替代有铅钎料的主要钎料系统有哪些?二、沿铌单晶(BCC)的棒轴方向拉伸，使其发生塑性形变，设铌单晶的滑移面为{110}，请确定：1．初始滑移系统。
2．双滑移系统。
3．双滑移开始时的切变量γ。
4．滑移过程中的转动规律和转轴。
5．试棒的最终取向(假定试棒在达到稳定取向前不发生断裂)。
三、有如图2-2a所示的位错线ABC及柏氏矢量b，其中AB是极轴位错(不动)，MNPQ为位错BC段的滑移面。
请分析在切应力τ的作用下：1．在图2-2a、b、c、d四种情况下，位错BC、BC'、BC"、BC'"的受力及运动情况。
2．达到动态平衡时，位错线ABC会变成什么形状?3．位错线在扫动时对晶体的塑性变形会产生什么影响?四、欲将一批齿轮进行渗碳，每炉装500件。
在900℃渗10h可以达到规定的深度。
假定在900℃渗碳每炉每小时生产成本为1000元，而在1000℃渗碳为1500元。
2008年
同济大学材料学院材料学专业——2008年真题及解析1，试推导布拉格方程，分析物质产生X衍射的充要条件（必考题）。
2，红外光谱与拉曼光谱的比较。
3，电子束轰击到固体样品表面会产生那些主要物理信号？研究材料的表面形貌一般收集那种物理信号？以及这些信号有那些应用。
4，说明电子探针中波谱的原理和应用，简述波谱和能谱应用方面的异同。
5，简述红外光谱用于分子结构分析的基础，说明其应用。
6，核磁共振中不同质子产生不同化学位移的根本原因是什么？核磁共振光谱在材料分析中的应用。
7，影响红外光谱谱带频率和强度的因素是什么？举例说明其在材料分析中的应用？8，请阐述多晶、非晶、纳米晶体材料在透射电子显微镜选区稍微图像中的区别。
9，采用合适的现代技术表征法分析硅酸盐水泥水化进程，10，请简要叙述布拉格方程在材料微观结构分析和表征领域中的应用。
11，简述X衍射物相分析的过程。
12，试讨论影响差热分析结果的因素，为什么说差热分析只能进行定性或半定量分析，而示差扫描量热分析则可进行定性分析。
13，如何利用差热分析，热重分析，热膨胀分析来区分无机材料中脱水、分解、氧化、多晶转变、烧结等现象。
14，举例说明SEM和TEM在材料分析中的应用。
说明：以上是08年材料研究方法的考研试题，总共有18道。
由于时间间隔太长，只记得14题。
08年试题给我们的感觉是各种研究方法的应用考的很多，几乎每个都考了。
还有一点值得注意的是，在08的试题中，第二章光学显微分析考了一题。
以下是试题的参考答案：1.试推导布拉格方程，分析物质产生X衍射的充要条件。
X-ray作为一电磁波被投射到晶体中时，会受到晶体中原子的散射，而散射波就好像从原子中心出发，每个原子中心发出的散射波就好比一个源球面波。
由于原子在晶体中是按周期排列的，这些散射球波之间存在固定的相位关系，他们之间会在空间产生干涉，结果在某些散射方向上相互加强，某些方向上相互抵消，即衍射。
如图书图3-15所示，1、2、3代表（hkl）的一唯平行网，面网之间间距为d，入射X-rayS0波长为λ，沿与面网成θ角入射，与S1方向散射线满足光学境面反射条件。
物理学面试题及答案
物理学面试题及答案1. 光的干涉现象是如何产生的？答案：光的干涉现象是由两束或多束相干光波在空间中相遇时，由于它们的相位差导致的光强分布出现明暗相间的条纹。
当两束光波的相位差保持恒定时，它们在某些区域相长干涉，光强增强；在另一些区域相消干涉，光强减弱。
这种现象在光学实验中可以通过双缝实验来观察。
2. 简述牛顿第三定律。
答案：牛顿第三定律指出，对于两个相互作用的物体，它们之间的力是相互的，大小相等且方向相反。
这意味着当一个物体对另一个物体施加力时，另一个物体也会对第一个物体施加一个大小相同但方向相反的力。
3. 什么是电磁波谱？答案：电磁波谱是指电磁波按照波长或频率排列的顺序。
它包括从低频的无线电波到高频的伽马射线，中间包括微波、红外线、可见光、紫外线、X射线等。
每种电磁波都有其特定的应用，如无线电波用于通信，可见光使我们能够看到物体，X射线用于医学成像。
4. 描述热力学第一定律。
答案：热力学第一定律，也称为能量守恒定律，指出在一个封闭系统中，能量既不能被创造也不能被消灭，只能从一种形式转换为另一种形式。
在热力学过程中，系统吸收的热量与对外做的功之和等于系统内能的增加。
5. 简述相对论中的时间膨胀效应。
答案：时间膨胀效应是相对论的一个预测，它表明当一个物体以接近光速的速度运动时，相对于静止观察者，该物体上的时间会变慢。
这意味着，如果两个观察者一个静止，另一个以接近光速运动，运动的观察者的时间会流逝得更慢。
6. 什么是量子纠缠？答案：量子纠缠是量子力学中的一个现象，其中两个或多个粒子形成一种特殊的关联，使得一个粒子的状态立即影响另一个粒子的状态，无论它们之间相隔多远。
这种现象在量子计算和量子通信中有重要的应用。
7. 描述波粒二象性。
答案：波粒二象性是指微观粒子如电子、光子等同时表现出波动性和粒子性的特性。
波动性表现为粒子的行为遵循波动方程，如干涉和衍射现象；粒子性则表现为粒子在特定条件下表现出可测量的离散性，如光电效应中的光子能量。
08固体物理试题（五篇）
08固体物理试题（五篇）第一篇：08 固体物理试题2008年春《固体物理》试题（A卷）一、名词解释：1、原胞，魏格纳-赛兹晶胞，第一布里渊区2、密勒指数，倒易点阵，有效质量，能隙，能带，禁带，导带，价带。
3、声子，模式密度，能态密度，长声学波，4、费米面，5、空穴，二、简述题：1、固体的结合形式有哪几种？其键合力的特点是什么？分别决定了固体的什么性质？2、经典理论、爱因斯坦模型、德拜模型是如何解释固体的比热的？电子热容对晶体热容的贡献有多大？3、特鲁德－洛伦兹理论、索墨菲的自由电子理论和布洛赫的能带理论是如何解释金属导电性的？能带理论如何解释导体、半导体和绝缘体的导电性的？为什么碱土金属能导电？三、证明题：1、证明：体心立方晶格的倒格子是面心立方格子。
2、证明：对于一个简单立方晶格，在第一布里渊区顶角上一个自由电子的动能比该区面心上大3倍。
四、计算题1、一维周期势场中电子的波函数应当满足布洛赫定理。
如果晶格常数为a ,电子的波函数为求电子在这些态中的波矢2、设一维晶体的电子能带可以写成式中a为晶格常数。
计算1）能带的宽度；2）电子在波矢k的状态时的速度；3）能带底部和能带顶部电子的有效质量第二篇：物理试题九年级物理上学期状元桥期末抽样检测试卷（二）姓名状元桥级别一、填空题。
1、为了纪念物理学家的杰出贡献，常以他们的名字命名物理量的单位。
如：以安培命名电流的单位，以_________命名_________的单位；以_________命名_________的单位。
2、改变物体内能的方式有两种，但其实质不同，是物体之间内能的转移，而是实现内能与其它形式的能的转变。
3、在1标准大气压下，把3Kg的水从15℃加热到90℃需要吸收的热量；如果让90℃的水再吸收1.5×105J的热量，水的温度又可升高℃。
4、按照我国交通管理的规定，“红灯停、绿灯行、黄灯预备”，有人在科技活动中设计了一个实验电路，用以模拟十字路口的红绿灯，如图1所示。
北京化工大学固体物理期末试题2008答案
北京化工大学2007—2008学年第二学期《固体物理学》期末考试试卷班级：____________ 姓名：______________ 学号：____________ 分数：_________一、简答题（每小题5分，共30分）1．写出体心立方结构的基矢并证明其倒格子为面心立方。
)(21k j i a a ++-= )(22k j i a a +-= )(23k j i a a -+=)(2)(2321k j a a a b +=Ω⨯=ππ 同理 )(22k i ab+=π)(23j i ab+=π所以面心立方结构的倒格子为体心立方2．具有面心立方结构的某元素晶体，给出其多晶样品的X 射线衍射谱中衍射角最小的三个衍射峰相应的面指数。
衍射面指数为（111）（200）（220），面指数为（111）（100）（110）3．晶体的结合类型有哪些？离子性结合，共价结合，金属性结合，范德瓦耳斯结合，氢键结合4．作为能带论基础的三个假设：绝热近似、平均场近似（单电子近似）和周期场近似。
绝热近似：在考虑晶体中电子的运动时，可以认为原子实（原子核）是固定不动的，使一个多粒子问题简化为多电子问题。
平均场近似：用一种平均场来代替价电子之间的相互作用，即假定每个电子的势能均相同，而使多电子问题简化为单电子问题。
周期场近似：单电子薛定谔方程中的势能项具有晶格周期性，因此电子是在一个周期性势场中运动。
5．晶体中位错有几种类型？各有什么特点。
刃型位错，螺型位错。
刃型位错的位错线同滑移方向垂直，螺型位错的位错线同滑移方向平行。
6．说明德哈斯-范阿尔芬效应的物理机制。
处于外磁场中的自由电子其在与磁场垂直的平面内原来连续的能级转变为分离的朗道能级，而且朗道能级的简并度随磁感应强度而变化，致使电子气在磁场中的能量随外磁场的强度而变化。
二、（12分）一维双原子链，晶格常数为2a ，原子质量为分别为M 和m ，线性恢复力系数为β，求该一维双原子链的色散关系。
2008年硕材料物化面试题
2008年硕士研究生物理化学复试题一、选择题（共30分，每小题3分）1. 298K 时，反应2C 6H 6（l ）+15O 2（g ）= 6H 20（l ）+12CO 2（g ）的定压热效应Q P 与定容热效应Q V 之差（Q P - Q V ）约为（1）3.7KJ ⋅mol -1 （2）-3.7KJ ⋅mol -1（3）7.4KJ ⋅mol -1（4）-7.4KJ ⋅mol -12．∆S ＝∆H /T 适合于下列过程中的哪一个？（1）恒压过程 （2）绝热过程 （3）恒温过程（4）可逆相变过程3．d ln p /d T = ∆H /RT 2 适用于下列变化中的哪一种（1）I 2( s ) ↔ I 2( g )（2）C(石墨) ↔ C(金刚石)（3）Hg 2Cl 2( s ) ↔ HgCl( l )4. P Θ 下，C （石墨）+ O 2（g ）= CO 2（g ）的反应热为 ∆r H m Θ，下列说法中错误的是（A ）∆r H m Θ 就是CO 2（g ）的生成焓∆f H m Θ（B ）∆r H m Θ是C （石墨）的燃烧焓（C ）∆r H m Θ = ∆r U m Θ （D ）∆r H m Θ > ∆r U m Θ5．理想溶液形成时，哪些状态函数的变化等于零？（1） ∆H ＝0 （2）∆V ＝0 （3）∆G ＝0 （4）∆S ＝06．纯物质的三相点，其自由度为多少？（1） 4 （2）3 （3） 2 （4）1 （5）07. 在一定温度下，下列平衡体系的组元数，相数及自由度分别为多少？CaCO 3（s ）=CaO （s ）+CO 2（g ）（A ）3，2，3； （B ）3，3，0； （C ）2，2，1；（D ）3，1，2； （E ）2，3，08. 若α，β两相中各含A 和B 两种物质，在相平衡时下列哪些关系式成立？（A ） μA (α)=μA (β) （B ） μA (α)=μB (β) （C ）μA (α)=μB (α)（D ） μB (α)=μB (β)9．1 g-10℃的水凝固成-10℃的冰，其∆S 为多少？（A ） -80/273 +（0.49-1.00）ln263/273; （B ）80/263（C ） 80/273 +（0.49-1.00）ln263/273; （D ）-80/26310. 下列各量中哪些是偏摩尔量，哪些是化学势？（A ）C n p T B n A ,,)/(∂∂（B ）C n S T B n H ,,)/(∂∂（C ）C n V T B n G ,,)/(∂∂（D ）C n V S B n U ,,)/(∂∂（E ）C n p T B B n ,,)/(∂∂μ（F ）Cn p T B p n C ,,)/(∂∂ 二、判断题。
物理研究所面试问题与答案---精品管理资料
中科院物理所面试整理（1）1。
什么是能带？2。
什么是位移电流？是由谁引入的?其物理实质是什么？3. 简述原胞和单胞的区别。
4。
什么是宏观对称素和微观对称素？5. 简述热力学四大定律.6. 晶体可能有的独立的点对称元素有几种？7。
康普顿散射证明了什么？8。
比热反映了什么，它的微观本质是什么？9。
简述量子力学的发展.10. 电子单缝实验及其物理内涵？11。
什么是倒格子?引入倒格子的意义是什么？12。
什么事俄歇电子？是怎么产生的？13。
Maxwell方程组及其各项的物理意义？14. 现在介观物理研究的尺寸范围是多少？15. 分析力学的基本方法？16。
在实验上用什么方法分析晶体的结构？17. 为什么会有半导体,导体,绝缘体?18. 什么是布拉格反射？19。
量子力学中为什么要引入算符？20。
正格子和倒格子之间关系是什么？21。
简述量子力学的基本假设.22. 你认为量子力学的精髓是什么?23。
什么是布里渊区？24。
大致说明一下晶体中电阻率随温度的变化关系。
剩余电阻率都来自哪?25。
什么是得哈斯—范阿尔芬效应?26。
什么是声子？什么是德拜温度？格林－埃森常数代表什么物理意义？27。
Maxwell 方程组的实验基础和假设是什么?28。
矩阵力学最早是由谁引入的？29。
较详细的介绍下你做过的一个近代物理实验？30。
能带论的三个基本假定是什么？简要阐述固体物理中的Born—Oppenheimer 近似。
31。
什么是布洛赫定理？32. 什么是Zeemann效应?介绍下斯特恩－盖拉赫干涉仪?33。
什么是纠缠态？大概介绍下EPR佯谬和薛定谔猫实验。
34。
介绍下你对自旋的认识。
自旋谁发现的，怎样发现的？35。
什么是剩余电阻？36. 介绍下你对狭义相对论的认识。
说说狭义相对论的基本原理。
写出洛伦兹变换的表达式。
37. 什么是霍尔效应?类比电荷霍尔效应,自旋霍尔效应应该怎么定义？38。
什么是Stark效应?39。
什么是超导现象？大概介绍下高温超导。
固体物理习题解答共40页
26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一， 也是成 功的利 器之一 。没有 它，天 才也会 在矛盾 无定的 迷径中 ，徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿．丘吉 尔。 30、我奋斗，所以我快乐。--格林斯 潘。
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
08年中科院近代物理所复试问题
08年中科院近代物理所复试问题08年中科院近代物理所复试问题2011年03月20日1.一群猎人在追杀一头大象，大象向你求助，你怎么解决？把它藏起来2.假如你投篮力气很大，篮球以接近光速飞向篮筐，那么人们看到篮球会成什么样子？椭球，运动方向为短轴3.中微子寿命很短以致很难探测，你能想出什么好的方法延长其寿命么？将中微子加速4.潮汐是怎么产生的？天体（主要是月球）在地球海洋表面及海洋深处的引力势不同，导致海洋表面加速度比海洋深处的大。
5.雷雨时先看到闪电还是先听到雷声？雷声和闪电的共同属性和本质区别是什么？一个机械波一个为电磁波6.解释一下克里奥里力当一个质点相对于惯性系做直线运动时，相对于旋转体系，其轨迹是一条曲线。
立足于旋转体系，可以认为有一个力驱使质点运动轨迹形成曲线，这个力就是科里奥利力。
从物理学的角度考虑，科里奥利力与离心力一样，都不是真实存在的力，而是惯性作用在非惯性系内的体现。
7.宇宙是怎么产生的？你相信这一宇宙起源理论么？为什么？宇宙是由一个致密炽热的奇点于137亿年前一次大爆炸后膨胀形成的。
1929年，埃德温·哈勃发现，即不管你往哪个方向看，远处的星系正急速地远离我们而去。
换言之，宇宙正在不断膨胀。
这意味着，在早先星体相互之间更加靠近。
事实上，似乎在大约100亿至200亿年之前的某一时刻，它们刚好在同一地方，所以哈勃的发现暗示存在一个叫做大爆炸的时刻，当时宇宙无限紧密。
8.虹是怎么产生的？为何大雾的时候为何防雾灯都是红的？天空为啥是蓝的？刚刚下完雨时，空气中浮悬着许多小水珠，在太阳光的照射下，就产生折射和内反射，而太阳的可见光——红、橙、黄、绿、蓝、靛、紫七色的波长都不一样，当它们照射到空中这些小水珠上时，各色光被小水球折射的情况也不同，因此就分解成七色光而形成彩虹。
大雾时防雾灯应该是黄色的，黄光和红光的穿透能力差不多，之所以不用红光是因为人眼的生理反应的问题，比如先看一会红光，就不太容易观察暗区的情况，而黄光要柔和一些。
2008研究生材料物理与化学面试标准答案
2.49 kJ
整个过程的热为：
Q U W 8.31kJ (2.49kJ )
10 .80 kJ
4．用两个银电极电解质量百分数为 0.7422%的 KCl 水溶液。 阳极反应：Ag (s) + Cl- AgCl (s)+e-所产生的 AgCl 沉积于电极上，当有 548.93C（库仑）的电量通过上述电解池 时，实验测出阳极区溶液的质量为 117.51g，其中含 KCl 0.6659g。试求 KCl 溶液中正、 负离子的迁移数。 解：迁移数的计算本质上是电量衡算的问题。电流通过电解池时，伴随着电量的传导， 必然发生相应的物质量的变化，故可通过物料衡算来实现电量的衡算。物料衡算的基准 是假定电解池各区域中的含水量不变。 先计算K+的迁移数： 阳极区含水的质量 m(H2O)=(117.51-0.6659) 10-3kg 电解前阳极区含KCl的质量
11.64 kJ
功或热是过程的变量，与状态的具体途径有关，应分步计算而后求和。
W1 0
W2 P2 (V3 V2 ) nR(T3 T2 )
考生注意：答案写在本试题上无效 第 3 页 共 6 页
4 W3 3 U nCV ,m (T4 T3 )
整个过程的功为
W W2 W3 nR(T3 T2 ) nCV ,m (T4 T3 )
T3 600K 可逆绝热膨胀 P3 P2 3 V3
已知该理想气体的绝热指数： C p,m / CV ,m 1.4 ， C p,m CV ,m R ，此二式结合可 得：
CV ,m R /( 1) 2.5R ； C p,m 3.5R
2008研究生固体物理面试答案
试卷答案选择题1. C2.A3.A4.B5.B6.C7.B简答题1. 晶体可分为哪几大晶系？[解答]七大晶系：三斜，单斜，正交，三角，四方，六角，立方晶系2.晶体的结合能, 晶体的内能, 原子间的相互作用势能有何区别?[解答]自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.原子的动能与原子间的相互作用势能之和为晶体的内能.在0K 时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K 时原子间的相互作用势能的绝对值近似等于晶体的结合能.3. 晶体中包含有N 个原胞，每个原胞中有n 个原子，该晶体晶格振动的格波简正模式总数是多少？其中声学波和光学波各多少？[解答]3nN ，声学波3N ，光学波3(n-1)N4.长光学支格波与长声学支格波本质上有何差别?[解答]长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.5.温度一定，一个光学波的声子数目多呢, 还是声学波的声子数目多? 对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?[解答]频率为ω的格波的(平均) 声子数为11)(/-=T k B e n ωω .因为光学波的频率O ω比声学波的频率A ω高, (1/-T k B O e ω )大于(1/-T k B A e ω ), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.设温度T H >T L , 由于(1/-H B T k e ω )小于(1/-L B Tk eω ), 所以温度高时的声子数目多于温度低时的声子数目.6.爱因斯坦模型在低温下与实验存在偏差的根源是什么? 在甚低温下, 德拜模型为什么与实验相符? [解答]按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为Hz 1013, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.7.在绝对零度时还有格波存在吗? 若存在, 格波间还有能量交换吗?[解答]频率为i ω的格波的振动能为i i i n ωε ⎪⎭⎫ ⎝⎛+=21,其中i i n ω 是由i n 个声子携带的热振动能, (2/i ω )是零点振动能, 声子数11/-=T k i B i e n ω .绝对零度时, i n =0. 频率为i ω的格波的振动能只剩下零点振动能. 格波间交换能量是靠声子的碰撞实现的. 绝对零度时, 声子消失, 格波间不再交换能量.8.一维简单晶格中一个能级包含几个电子?[解答]设晶格是由N 个格点组成, 则一个能带有N 个不同的波矢状态, 能容纳2N 个电子. 由于电子的能带是波矢的偶函数, 所以能级有(N /2)个. 可见一个能级上包含4个电子.9.晶体膨胀时, 费密能级如何变化?[解答]费密能级3/2220)3(2πn m E F =,其中n 是单位体积内的价电子数目. 晶体膨胀时, 体积变大, 电子数目不变, n 变小, 费密能级降低.计算题1.如果基矢,,a b c 构成简单正交系证明晶面族()hkl 的面间距为)d =. 证 简单正交系a b c ⊥⊥ 123,,a ai a bj a ck === 倒格子基矢2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯ 倒格子矢量123G hb kb lb =++222hi k j l k a b c πππ=++ 晶面族()hkl 的面间距2d G π=222()()()h k l a b c=++ 面指数越简单的晶面，其晶面的间距越大晶面上格点的密度越大，这样的晶面越容易解理2. 设晶体中每个振子的零点振动能量具,21γ 试用德拜模型求晶体零点振动能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
试卷答案
选择题
1. C
2.A
3.A
4.B
5.B
6.C
7.B
简答题
1. 晶体可分为哪几大晶系？
[解答]七大晶系：三斜，单斜，正交，三角，四方，六角，立方晶系
2.晶体的结合能, 晶体的内能, 原子间的相互作用势能有何区别?
[解答]自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.
原子的动能与原子间的相互作用势能之和为晶体的内能.
在0K 时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K 时原子间的相互作用势能的绝对值近似等于晶体的结合能.
3. 晶体中包含有N 个原胞，每个原胞中有n 个原子，该晶体晶格振动的格波简正模式总数是多少？其中声学波和光学波各多少？
[解答]3nN ，声学波3N ，光学波3(n-1)N
4.长光学支格波与长声学支格波本质上有何差别?
[解答]长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.
5.温度一定，一个光学波的声子数目多呢, 还是声学波的声子数目多? 对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?
[解答]频率为ω的格波的(平均) 声子数为
11
)(/-=T k B e n ωω .
因为光学波的频率O ω比声学波的频率A ω高, (1/-T k B O e ω )大于(1/-T k B A e ω ), 所以
在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.
设温度T H >T L , 由于(1/-H B T k e ω )小于(1/-L B T
k e
ω ), 所以温度高时的声子数目多于温度低时的声子数目.
6.爱因斯坦模型在低温下与实验存在偏差的根源是什么? 在甚低温下, 德拜模型为什么与实验相符? [解答]按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为Hz 1013
, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.
在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.
7.在绝对零度时还有格波存在吗? 若存在, 格波间还有能量交换吗?
[解答]频率为i ω的格波的振动能为
i i i n ωε ⎪⎭⎫ ⎝⎛+=21,
其中i i n ω 是由i n 个声子携带的热振动能, (2/i ω )是零点振动能, 声子数
11
/-=T k i B i e n ω .
绝对零度时, i n =0. 频率为i ω的格波的振动能只剩下零点振动能. 格波间交换能量是靠声子的碰撞实现的. 绝对零度时, 声子消失, 格波间不再交换能量.
8.一维简单晶格中一个能级包含几个电子?
[解答]设晶格是由N 个格点组成, 则一个能带有N 个不同的波矢状态, 能容纳2N 个电子. 由于电子的能带是波矢的偶函数, 所以能级有(N /2)个. 可见一个能级上包含4个电子.
9.晶体膨胀时, 费密能级如何变化?
[解答]费密能级
3
/2220)3(2πn m E F =,
其中n 是单位体积内的价电子数目. 晶体膨胀时, 体积变大, 电子数目不变, n 变小, 费密能级降低.
计算题
1.如果基矢,,a b c 构成简单正交系证明晶面族()hkl 的面间距为
)d =. 证 简单正交系a b c ⊥⊥ 123,,a ai a bj a ck === 倒格子基矢2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 123123
2a a b a a a π⨯=⋅⨯ 倒格子矢量123G hb kb lb =++222h
i k j l k a b c πππ=++ 晶面族()hkl 的面间距2d G π=222()()()h k l a b c
=++ 面指数越简单的晶面，其晶面的间距越大
晶面上格点的密度越大，这样的晶面越容易解理
2. 设晶体中每个振子的零点振动能量具,2
1γ 试用德拜模型求晶体零点振动能。
解：由德拜模型每频率在ωωωd +→间格波数
又由德拜模型知()129)6(;3312P v v
N N d w p n o m 见教本⎰⋅==ωπωωρ
晶体零点振动能m o m o Nh dv hv Nr E m
γγγ8
921932+⎪⎭⎫ ⎝⎛=⎰
KN
89= 2136()p N k v
γπ= 3. 限制在边长为L 的正方形中的N 个自由电子，电子的能量2
22(,)()2x y x y E k k k k m
=+ 1）求能量E 到E +dE 之间的状态数
2）求此二维系统在绝对零度的费米能量
. 解：（1）采用周期边界条件 由L
n k e y x y L x x x L ik x πψψ21
),(),(1=
∴==+⋅得 每个K 矢在R 空间占体积为2
2
)2(L k k y x π=∆⋅∆ E 到E +dE 间的状态，在k 空间内的体积为,2kdk π在其中的状态数为： 由于dE mL dE m L dz kdk m dE 2
2222222242, πππ=⋅==所以 令22
πmL C = （2）⎰=⋅=⋅⋅=o F
E o o
F CE dE C N dE C E f dN )( 4.设一维晶体的电子能带可以写成2
271()(cos cos 2)88E k ka ka ma =-+ 其中a 为晶格常数，计算
1） 能带的宽度
2） 电子在波矢k 的状态时的速度
3） 能带底部和能带顶部电子的有效质量
解 1) 能带的宽度的计算2
271()(cos cos 2)88E k ka ka ma =-+ 能带底部0k = (0)
0E = 能带顶部k a π= 2
22()E a ma π
= 能带宽度()(0)E E E a π
∆=-2
22ma = 2）电子在波矢k 的状态时的速度
2271()(cos cos 2)88
E k ka ka ma =-+ 电子的速度1()()dE k v k dk =
3) 能带底部和能带顶部电子的有效质量2
271()(cos cos 2)88E k ka ka ma =-+ 电子的有效质量2*22/E m k ∂=∂cos (1/2)cos 2m ka ka =- 能带底部0k = 有效质量*2m m = 能带顶部k a π= 有效质量*23m m =-。