2017-2018学年广东省清远市高一数学上期末教学质量检测试题
2017-2018学年高一上学期期末质量测试数学试题 共享

第一学期期末质量测试高一数学2018.1.12一、填空题(本大题满分36分)本大题共有12题)1.函数的定义域是___________.【答案】【解析】【分析】根据偶次方根被开方数为非负数,列出不等式,解不等式求得函数的定义域.【详解】由于偶次方根被开方数为非负数,故,解得,故函数的定义域为. 【点睛】本小题主要考查函数的定义域的求法.属于基础题.函数的定义域主要由以下方面考虑来求解:一个是分数的分母不能为零,二个是偶次方根的被开方数为非负数,第三是对数的真数要大于零,第四个是零次方的底数不能为零. 对于含有多个以上情况的解析式,要求它们的交集来得到最终的结果.2.不等式的解集为______.【答案】(-2,1)【解析】.点睛:解分式不等式的方法是:移项,通分化不等式为,再转化为整式不等式,然后利用二次不等式或高次不等式的结论求解.3.已知指数函数(且)的图像过点,则实数___________.【答案】【解析】【分析】将点的坐标代入指数函数,解方程求得的值.【详解】将点代入指数函数得,,解得(负根舍去).【点睛】本小题主要考查指数函数的解析式的求法,考查指数的运算,属于基础题.4.设集合、,若,则实数=___________.【答案】【解析】【分析】根据真子集的知识,分别令和,解得的值后利用集合元素的互异性来排除错误的值,由此得出实数的值.【详解】由于集合是集合的子集,令时,或,当时集合中有两个,不符合题意,故舍去.当时,符合题意.令,解得,根据上面的分析,不符合题意.综上所述,故实数.【点睛】本小题主要考查真子集的概念,考查集合元素的互异性,属于基础题.5. 某班共30人,其中有15人喜爱篮球运动,有10人喜爱兵乓球运动,有3人对篮球和兵乓球两种运动都喜爱,则该班对篮球和乒乓球运动都不喜爱的人数有___________.【答案】12【解析】试题分析:设两者都喜欢的人数为x人,则只喜爱篮球的有(15-x)人,只喜爱乒乓球的有(10-x)人,由此可得(15-x)+(10-x)+x+8=30,解得x=3,所以15-x=12,即所求人数为12人,故答案为:12.考点:交、并、补集的混合运算.6.已知,,则___________.【答案】【解析】【分析】分别求得函数和的定义域,取它们的交集,然后将两个函数相乘,化简后求得相应的解析式.【详解】对于函数,由解得;对于函数,同样由解得;故函数的定义域为,且.【点睛】本小题主要考查函数的定义域的求法,考查两个函数相乘后的解析式的求解方法.属于基础题.7.已知二次函数在区间上是增函数,则实数的范围是___________. 【答案】【解析】试题分析:由于二次函数的单调递增区间为,则得. 考点:二次函数的单调性.8.函数的定义域为R,则常数的取值范围是______________。
【真题】2017-2018年广东省清远市高三(上)期末数学试卷(理科)与答案

2017-2018学年广东省清远市高三(上)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)复数Z=1+i+(1+i)6(i为虚数单位)在复平面上对应的点P在()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)函数y=sin(+2x)是()A.最小正周期为π的奇函数B.最小正周期为2π的奇函数C.最小正周期为π的偶函数D.最小正周期为2π的偶函数3.(5分)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1C.D.4.(5分)为了解工厂的1000名工人的生产情况,从中抽取100名工人进行统计,得到如下频率分布直方图,由此可估计该工厂产量在75件以上(含75件)的工人数为()A.50B.100C.150D.2505.(5分)设命题p:若集合A={x∈R|≤0},则∁R A={x∈R|x>0}(其中R为实数集);命题q:∃x∈R,sinx≥1,则()A.p∨(¬q)是假命题B.p∨q是假命题C.p∧q是真命题D.(¬p)∧(¬q)是真命题6.(5分)为了研究某班学生的身高y(单位:厘米)和脚长x(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为.已知=225,=1650,,则的值是()A.750B.75C.80D.8007.(5分)在如图程序框图中,已知:f0(x)=xe x,f i′(x)是f i(x)的导函数,则输出的是()A.2016e x B.2016e x+xe x C.2017e x D.2017e x+xe x 8.(5分)中国古代数学著作《算法统宗》有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378 里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6 天后达到目的地.”则该人最后一天走的路程为()A.4 里B.5 里C.6 里D.8 里9.(5分)已知几何体的三视图如图所示,则该几何体是()A.体积为2的三棱锥B.体积为2的四棱锥C.体积为6的三棱锥D.体积为6的四棱锥10.(5分)已知实数x,y满足,则(x﹣1)2+(y+1)2的取值范围是()A.[,10]B.[,2]C.[,10]D.[,2] 11.(5分)设P是抛物线C1:x2=4y上的动点,M是圆C2:(x﹣5)2+(y+4)2=4上的动点,d是点P到直线y=﹣2的距离,那么d+|PM|的最小值是()A.﹣2B.﹣1C.D.+1 12.(5分)给定两个长度为1的平面向量和,它们的夹角为,如图所示点C在以O为圆心的圆弧上运动,若,其中x,y∈R,则x+y 的取值范围为()A.(1,2]B.[1,2]C.[1,2)D.[﹣2,2]二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知(1+2x)n=a0+a1x+a2x2+a3x3+…+a n x n,若a2=40,则n=.14.(5分)小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是.15.(5分)如图是抛物线形拱桥,当水面在如图所示的n处时,拱顶离水面2米,水面宽4米,水位上升1米后,水面宽米.16.(5分)小明发现,直棱柱的外接球的球心位置一定在上下底面外接圆圆心连线上,现已知三棱柱A1B1C1﹣ABC中,AB=BC=,AC=6,AA1⊥平面ABC,AA1=2,则该三棱柱的外接球表面积为.三、解答题(本大题共5小题,共70分)17.(12分)已知数列{a n}中,a1=1,其前n项和为S n,且满足(n ≥2,n∈N+).(Ⅰ)求证:数列{}是等差数列;(Ⅱ)证明:.18.(12分)朱老师家住H小区,他在C学校工作,从家开车到C学校上班有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;路线L2上有B1,B2两个路口,各路口遇到红灯的概率依次为,.(Ⅰ)若走路线L1,求最多遇到2次红灯的概率;(Ⅱ)若走路线L2,求遇到红灯次数X的数学期望;(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助朱老师分析上述两条路线中,选择哪条路线上班更好些,并说明理由.19.(12分)在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB 是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.(Ⅰ)求证:DE∥平面ABC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.20.(12分)已知双曲线x2﹣=1的左、右顶点分别为A、B,曲线C是以A、B为短轴的两端点且离心率为的椭圆,设点P在第一象限且在双曲线上,直线AP与椭圆相交于另一点T.(Ⅰ)求曲线C的方程;(Ⅱ)设点P、T的横坐标分别为x1、x2,证明:x1x2=1;(Ⅲ)设△TAB与△POB(其中O为坐标原点)的面积分别为S1与S2,且≤10,求的取值范围.21.(12分)已知函数f(x)=﹣x3+2mx﹣m.(Ⅰ)讨论函数f(x)的极大值和极小值;(Ⅱ)证明:当m>,0≤x≤1时,﹣m<f(x)<m﹣.选修4—4:极坐标与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程(θ是参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=.(Ⅰ)求曲线C1的普通方程和直线C2的直角坐标方程;(2)设曲线C1上的点P到直线C2的距离为d,求d的最大值.选修4—5:不等式选讲23.已知f(x)=|2x+2|+|3x﹣3|,g(x)=|x+2m|+|x﹣m|.(Ⅰ)求函数y=的定义域.(Ⅱ)若∀x∈R,∃x0∈R,使得f(x)=g(x0),试求实数m的取值范围.2017-2018学年广东省清远市高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)复数Z=1+i+(1+i)6(i为虚数单位)在复平面上对应的点P在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵Z=1+i+(1+i)6=1+i+[(1+i)2]3=1+i+(2i)3=1﹣7i,∴在复平面上对应的点P的坐标为(1,﹣7),在第四象限.故选:D.2.(5分)函数y=sin(+2x)是()A.最小正周期为π的奇函数B.最小正周期为2π的奇函数C.最小正周期为π的偶函数D.最小正周期为2π的偶函数【解答】解:函数y=sin(+2x)=cos2x,它的周期为=π,且为偶函数,故选:C.3.(5分)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1C.D.【解答】解:由定积分可求得阴影部分的面积S=cosxdx==﹣(﹣)=,所以围成的封闭图形的面积是.故选:D.4.(5分)为了解工厂的1000名工人的生产情况,从中抽取100名工人进行统计,得到如下频率分布直方图,由此可估计该工厂产量在75件以上(含75件)的工人数为()A.50B.100C.150D.250【解答】解:产量在75件以上(含75件)的工人包括第4组和第5组的工人,∵f=f4+f5=0.010×10+0.005×10=0.15.∴该工厂产量在75件以上(含75件)的工人数为:1000×0.15=150.故选:C.5.(5分)设命题p:若集合A={x∈R|≤0},则∁R A={x∈R|x>0}(其中R为实数集);命题q:∃x∈R,sinx≥1,则()A.p∨(¬q)是假命题B.p∨q是假命题C.p∧q是真命题D.(¬p)∧(¬q)是真命题【解答】解:A={x∈R|≤0}={x|x<0},则∁R A={x∈R|x≥0},即命题p是假命题,当sinx=1时,满足sinx≥1,即命题q是真命题,则p∨(¬q)是假命题,故选:A.6.(5分)为了研究某班学生的身高y(单位:厘米)和脚长x(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为.已知=225,=1650,,则的值是()A.750B.75C.80D.800【解答】解:∵=225,=1650,∴=22.5,=165,由165=4×22.5+,解得:=75,故选:B.7.(5分)在如图程序框图中,已知:f0(x)=xe x,f i′(x)是f i(x)的导函数,则输出的是()A.2016e x B.2016e x+xe x C.2017e x D.2017e x+xe x 【解答】解:由程序框图知,f0(x)=xe x,f1(x)=f0′(x)=e x+xe x,∴f2(x)=f1′(x)=e x+e x+xe x=2e x+xe x;…;∴输出f2017(x)=f2016′(x)=2017e x+xe x.故选:D.8.(5分)中国古代数学著作《算法统宗》有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378 里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6 天后达到目的地.”则该人最后一天走的路程为()A.4 里B.5 里C.6 里D.8 里【解答】解:每天走的路形成等比数列{a n},q=,S6=378.∴S6=378=,解得a1=192.∴该人最后一天走的路程=a1q5==6.故选:C.9.(5分)已知几何体的三视图如图所示,则该几何体是()A.体积为2的三棱锥B.体积为2的四棱锥C.体积为6的三棱锥D.体积为6的四棱锥【解答】解:几何体的直观图如图:由题意可得几何体的底面积为:=3,体积为:V=.故选:B.10.(5分)已知实数x,y满足,则(x﹣1)2+(y+1)2的取值范围是()A.[,10]B.[,2]C.[,10]D.[,2]【解答】解:(x﹣1)2+(y+1)2的几何意义是P(1,﹣1)到可行域上的点的距离的平方,d min==,最小值为:;由可得B(2,2),最大值为可行域内的第一象限三角形的顶点到P(1,﹣1)的距离的平方:(2﹣1)2+(2+1)2=10,故选:C.11.(5分)设P是抛物线C1:x2=4y上的动点,M是圆C2:(x﹣5)2+(y+4)2=4上的动点,d是点P到直线y=﹣2的距离,那么d+|PM|的最小值是()A.﹣2B.﹣1C.D.+1【解答】解:圆(x﹣5)2+(y+4)2=4的圆心(5,﹣4),半径为2.抛物线x2=4y的准线方程为:y=﹣1,如图:d为P到y=﹣2的距离,P为抛物线x2=4y上一动点,M为(x﹣5)2+(y+4)2=4上一动点,d+PM最小值就是FC2的连线与抛物线的交点是P,与圆的交点为M,过P作PN垂直直线y=﹣1的交点为N,有抛物线的定义可知:PF=PN,即1+|PF|+|PM|的最小值就是d+PM最小值,∵F(0,1),C2(5,﹣4),∴|FC2|==5,∴d+|PM|≥1+|FC2|﹣2=5﹣1所以d+PM最小值为5﹣1,故选:B.12.(5分)给定两个长度为1的平面向量和,它们的夹角为,如图所示点C在以O为圆心的圆弧上运动,若,其中x,y∈R,则x+y 的取值范围为()A.(1,2]B.[1,2]C.[1,2)D.[﹣2,2]【解答】解:由题意,以O为原点,OA为x轴的正向,建立如图所示的坐标系,设C(cosθ,sinθ),0≤θ≤120°可得A(1,0),B(﹣,),由若=x(1,0)+y(﹣,)得,x﹣y=cosθ,y=sinθ,∴y=sinθ,∴x+y=cosθ+sinθ=2sin(θ+30°),∵0≤θ≤120°,∴30°≤θ+30°≤150°,∴1≤2sin(θ+30°)≤2∴x+y的范围为[1,2],故选:B.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知(1+2x)n=a0+a1x+a2x2+a3x3+…+a n x n,若a2=40,则n=5.【解答】解:∵(1+2x)n=a0+a1x+a2x2+a3x3+…+a n x n,若a2=40,则×4=40,求得n2﹣n﹣20=0,∴n=5,或n=﹣4(舍去),故答案为:5.14.(5分)小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是.【解答】解:小明有4枚完全相同的硬币,他把4枚硬币叠成一摞,基本事件总数n=24=16,所有相邻两枚硬币中至少有一组同一面不相对,包含的基本事件的个数m=24﹣2=14,∴所有相邻两枚硬币中至少有一组同一面不相对的概率:p===.故答案为:.15.(5分)如图是抛物线形拱桥,当水面在如图所示的n处时,拱顶离水面2米,水面宽4米,水位上升1米后,水面宽2米.【解答】解:如图建立直角坐标系,设抛物线方程为x2=my,将A(2,﹣2)代入x2=my,得m=﹣2,∴x2=﹣2y,代入B(x0,﹣1)得x0=,故水面宽为2m.故答案为:2.16.(5分)小明发现,直棱柱的外接球的球心位置一定在上下底面外接圆圆心连线上,现已知三棱柱A1B1C1﹣ABC中,AB=BC=,AC=6,AA1⊥平面ABC,AA1=2,则该三棱柱的外接球表面积为.【解答】解:由题意,圆心到球心的距离为1,∵AB=BC=,AC=6,∴AC的高为,其中一个底角的正弦值为;由正弦定理:2r=;则r=外接球半径R==三棱柱的外接球表面积S=4πR2=故答案为:三、解答题(本大题共5小题,共70分)17.(12分)已知数列{a n}中,a1=1,其前n项和为S n,且满足(n ≥2,n∈N+).(Ⅰ)求证:数列{}是等差数列;(Ⅱ)证明:.【解答】证明:(Ⅰ)数列{a n}中,a1=1,其前n项和为S n,且满足(n ≥2,n∈N+).则:当n≥2时,,整理得:S n﹣S n=2S n﹣1S n,﹣1所以:(常数).所以:数列{}是以为首项,2为公差的等差数列.证明:(Ⅱ)由(Ⅰ)得:,所以:,当n=1时,符合通项.故:,所以:,=,=18.(12分)朱老师家住H小区,他在C学校工作,从家开车到C学校上班有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;路线L2上有B1,B2两个路口,各路口遇到红灯的概率依次为,.(Ⅰ)若走路线L1,求最多遇到2次红灯的概率;(Ⅱ)若走路线L2,求遇到红灯次数X的数学期望;(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助朱老师分析上述两条路线中,选择哪条路线上班更好些,并说明理由.【解答】解:(Ⅰ)【解法一】设“走路线L1,最多遇到2次红灯”为事件A,则P(A)=×+×+××=;∴走L1最多遇到2次红灯的概率为;【解法二】设“走路线L1,最多遇到2次红灯”为事件A,则事件为“走路线L1遇到3次红灯”,∴P(A)=1﹣P()=1﹣×=;∴走L1最多遇到2次红灯的概率为;(Ⅱ)由题意知随机变量X的可能取值为0,1,2;计算P(X=0)=(1﹣)×(1﹣)=,P(X=1)=×(1﹣)+(1﹣)×=,P(X=2)=×=,∴X的数学期望为E(X)=0×+1×+2×=;(Ⅲ)设选择路线L1遇到红灯的次数为Y,随机变量Y服从二项分布,即Y~B(3,),∴E(Y)=3×=,由E(X)<E(Y),∴选择路线L2上班更好些.19.(12分)在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.(Ⅰ)求证:DE∥平面ABC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.【解答】(本小题满分12分)解:(Ⅰ)由题意知,△ABC,△ACD都是边长为2的等边三角形,取AC中点O,连接BO,DO,则BO⊥AC,DO⊥AC,…(2分)又∵平面ACD⊥平面ABC,∴DO⊥平面ABC,作EF⊥平面ABC,那么EF∥DO,根据题意,点F落在BO上,∵BE和平面ABC所成的角为60°,∴∠EBF=60°,∵BE=2,∴,…(4分)∴四边形DEFO是平行四边形,∴DE∥OF,∵DE不包含于平面ABC,OF⊂平面ABC,∴DE∥平面ABC.…(6分)(Ⅱ)解法一:作FG⊥BC,垂足为G,连接EG,∵EF⊥平面ABC,∴EF⊥BC,又EF∩FG=F,∴BC⊥平面EFG,∴EG⊥BC,∴∠EGF就是二面角E﹣BC﹣A的平面角.…(9分)Rt△EFG中,,,.∴.即二面角E﹣BC﹣A的余弦值为.…(12分)解法二:建立如图所示的空间直角坐标系O﹣xyz,B(0,,0),C(﹣1,0,0),E(0,,),∴=(﹣1,﹣,0),=(0,﹣1,),平面ABC的一个法向量为设平面BCE的一个法向量为则,∴,∴.…(9分)所以,又由图知,所求二面角的平面角是锐角,二面角E﹣BC﹣A的余弦值为.…(12分)20.(12分)已知双曲线x2﹣=1的左、右顶点分别为A、B,曲线C是以A、B为短轴的两端点且离心率为的椭圆,设点P在第一象限且在双曲线上,直线AP与椭圆相交于另一点T.(Ⅰ)求曲线C的方程;(Ⅱ)设点P、T的横坐标分别为x1、x2,证明:x1x2=1;(Ⅲ)设△TAB与△POB(其中O为坐标原点)的面积分别为S1与S2,且≤10,求的取值范围.【解答】解:(Ⅰ)设椭圆的方程为+=1,a>b>0,依题意可得A(﹣1,0),B(1,0),所以b=1,因为椭圆的离心率为,所以e2===,即a2=4,∴椭圆方程为+x2=1;(Ⅱ)设点P(x1,y1)、T(x2,y2)(x i>0,y i>0,i=1,2),直线AP的斜率为k(k>0),则直线AP的方程为y=k(x+1),联立方程组,整理,得(4+k2)x2+2k2x+k2﹣4=0,解得x=﹣1或x=.所以x2=.同理可得,x1=.所以x1•x2=1.(Ⅱ)解:设点P(x1,y1)、T(x2,y2)(x i>0,y i>0,i=1,2),则=(﹣1﹣x1,﹣y1),=(﹣1﹣x2,﹣y2),因为•≤10,所以(﹣1﹣x1)(1﹣x1)+y12≤10,即x12+y12≤11,因为点P在双曲线上,则x1﹣=1,所以x12+4x12﹣4≤11,即x12≤3.因为点P是双曲线在第一象限内的一点,所以1<x1≤.因为S1=|AB|•|y2|=|y2|,S2=|OB|•|y1|=|y1|,所以S12﹣S22=y22﹣y12=(4﹣4x22)﹣(x12﹣1)=5﹣x12﹣4x22.由(Ⅱ)知,x1•x2=1,即x2=.设t=x12,则1<t≤3,则S12﹣S22=5﹣t﹣.设f(t)=5﹣t﹣=5﹣(t+)=5﹣4=1,当且仅当t=,即t=2时取等号,所以函数f(t)在(1,2)上单调递增,在(2,3]上单调递减.因为f(3)=5﹣3﹣=,f(1)=0,所以f(1)<f(3)所以S12﹣S22的取值范围为(0,1].21.(12分)已知函数f(x)=﹣x3+2mx﹣m.(Ⅰ)讨论函数f(x)的极大值和极小值;(Ⅱ)证明:当m>,0≤x≤1时,﹣m<f(x)<m﹣.【解答】(I)解:f′(x)=﹣3x2+2m,m≤0时,f′(x)≤0,∴函数f(x)在R上单调递减,无极值.m>0时,f′(x)=﹣3(x+)(x﹣),可得:﹣<x<时,f′(x)>0,此时函数f(x)单调递增;x<﹣,或x>时,f′(x)<0,此时函数f(x)单调递减.∴x=﹣,函数f(x)取得极小值,=﹣﹣m.x=时,函数f(x)取得极大值,f=﹣m.(II)证明:当m>,0≤x≤1时,要证明﹣m<f(x)<m﹣.即证明:f (x)﹣<0.由(I)可得:0<x<时,此时函数f(x)单调递增;x>时,函数f(x)单调递减.①当≥1时,m≥时,f(x)在[0,1]上单调递增,∴f(x)≤f(1).这时f(x)﹣<f(1)﹣|m﹣|=﹣1+2m﹣m﹣(m﹣)=﹣<0.②当<1时,<m<时,f(x)≤f,∴f(x)﹣≤f()﹣|m﹣|=﹣2m+.令=t,则t∈,m=.g(t)=﹣2m+=t3﹣+.∵g′(x)=﹣t=t(t﹣3)<0,∴g(t)在t∈上单调递减,∴g(t)<g()=﹣<0,综上所述:当m>,0≤x≤1时,﹣m<f(x)<m﹣.选修4—4:极坐标与参数方程22.(10分)在直角坐标系xOy中,曲线C1的参数方程(θ是参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=.(Ⅰ)求曲线C1的普通方程和直线C2的直角坐标方程;(2)设曲线C1上的点P到直线C2的距离为d,求d的最大值.【解答】解:(Ⅰ)曲线C1的参数方程(θ是参数),转换为直角坐标方程为:,曲线C2的极坐标方程为ρsin(θ+)=.转换为直角坐标方程为:x+y﹣1=0.(2)设曲线C1上的点P(),则:点P到直线x+y﹣1=0的距离d==.故:d的最大值为.选修4—5:不等式选讲23.已知f(x)=|2x+2|+|3x﹣3|,g(x)=|x+2m|+|x﹣m|.(Ⅰ)求函数y=的定义域.(Ⅱ)若∀x∈R,∃x0∈R,使得f(x)=g(x0),试求实数m的取值范围.【解答】解:(Ⅰ)要使函数有意义,必须f(x)﹣8≥0,当x≤﹣1时,﹣(2x+2)﹣(3x﹣3)﹣8≥0,解得x;当﹣1<x≤1时,(2x+2)﹣(3x﹣3)﹣8≥0,解得x∈∅;当x>1时,(2x+2)+(3x﹣3)﹣8≥0,解得x.综上所述,函数的定义域是(﹣)∪(,+∞).(Ⅱ)∵f(x)=∴f(x)≥f(1)=4又∵g (x )=|x +2m |+|x ﹣m |≥|(x +2m )﹣(x ﹣m )|=3|m | ∴若∀x ∈R ,∃x 0∈R ,使得f (x )=g (x 0),都有3|m |≤4, ∴m 的取值范围为[﹣,].赠送—高中数学知识点二次函数(1)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔xy1x 2x 0>a O∙ab x 2-=0)(>k f k x y1x 2x O∙ab x 2-=k<a 0)(<k f②x 1≤x 2<k ⇔③x 1<k <x 2 ⇔ af (k )<0④k 1<x 1≤x 2<k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔ f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2<k fxy1x 2x O∙<a 1k∙2k 0)(1>k f 0)(2<k f⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ②02b x a->,则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,则()M f q =①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =.x>O-=f(p)f (q)()2bf a-0x x>O-=f(p) f(q) ()2b f a-0xx<O-=f (p) f (q) ()2bf a-x<O-=f (p)f(q)()2b f a-x<O-=f (p)f(q)()2bf a-0xx<O-=f (p)f (q)()2b f a-x<O-=f (p)f (q)()2b f a-0x。
广东清远市2017-2018学年高一第一学期期末教学质量检测数学试题

广东清远市2017-2018学年高一第一学期期末教学质量检测数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 已知集合,,则( ) A.B.C.D.2. 经过点且直线斜率的直线方程是()A.B.C.D.3. 下列图象可作为函数图象的是()A.B.C.D.4. 已知直线,互相垂直,则的值是()A.0 B.1 C.0或-1 D.0或15. 幂函数的图象过点,则函数为()A.奇函数且在上单调递增B.奇函数且在上单调递减C.偶函数且在上单调递增D.偶函数且在上单调递减6. 设,,,则的大小关系为()A.B.C.D.7. 函数的图象如下图,则该函数可能是()A.B.C.D.8. 如图,某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆,则该几何体的体积为()A.4 B.8 C.D.9. 已知圆的半径为4,圆心在轴的负半轴上,直线与圆相切,则圆的方程为()A.B.C.D.10. 若函数是奇函数,其零点为,,…,,且,则关于x的方程的根所在区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)11. 已知两条不同的直线及两个不同的平面,其中,则下面结论正确的是()A.若,则? B.若,则? ? ? ?C.若与相交,则与相交D.若与相交,则与相交12. 已知函数是奇函数,,且当时,是减函数,,则的取值范围是()A.(0,3)B.(1,3)C.( 1,2 ) D.(2,3)二、双空题13. 圆的圆心坐标________,半径________.三、填空题14. 已知、,直线的斜率是直线斜率的倍,则直线的倾斜角为________.15. 在正方体中,到平面的距离为,则正方体棱长是__________.16. 设定义在上的函数,,则当实数满足时,函数的零点个数为__________个.四、解答题17. 已知集合,为实数集,.(I)当时,求及;(II)若,求的取值范围.18. 计算下列各式的值.(I);(II).19. 设函数(I)判断函数的奇偶性并证明;(II)用定义证明函数在上为增函数.20. 如图,正四棱锥中,是正方形,是正方形的中心,底面,是的中点.(I)证明:平面;(II)证明:平面平面;(III)已知:,求点到面的距离.21. 已知圆过点,且与圆()关于轴对称.(I)求圆的方程;(II)若有相互垂直的两条直线,都过点,且被圆所截得弦长分别是,求的值.22. 已知函数,,记(I)判断的奇偶性,并写出的单调区间,均不用证明;(II)对任意,都存在,使得,.若.求实数的值.。
2017-2018高一数学上学期期末考试(带答案)

2017-2018学年上学期期末考试 高中一年级 数学 参考答案一、选择题二、填空题13. 1314. {}6,5,2- 15.55-16. {}1,0,1-三、解答题17.解:{}1A aa=-,,{}2,B b =,.................................2分 (Ⅰ)若2a =,则{}12A =,,A B=∴11b a =-=.若12a -=,则3a =,{}23A =,,∴3b =.综上,b的值为1或3.......................................5分 (Ⅱ)∵{|24}C x x =<<,,A C C A C=∴⊆,.................................7分 ∴24,214a a <<⎧⎨<-<⎩∴34a <<. ∴a的取值范围是(3,4).......................................10分 18.解:(I)直线BC的斜率32141BC k +==+.∴BC边上的高线斜率1-=k,........................... ......3分∴BC边上的高线方程为:()23y x-=-+即:10x y++=,......................... ..............6分(II) )2,1(),3,4(--CB由)2,1(),3,4(--CB得直线BC的方程为:10x y--=........................... ......9分A∴到直线BC的距离d==1152ABC S ∆∴=⨯=........................................12分19.解:根据上表销售单价每增加1元日均销售量就减少40桶,设在进价基础上增加x 元后,日均销售利润为y 元,而在此情况下的日均销售量就为()48040152040x x--=-,.......................3分 由于x >,且520x ->,即0x <<,.......................................6分于是,可得()520y x =-240522,x xx =-+-<<.......................9分 易知,当6.5x =时,y有最大值,所以,只需将销售单价定为11.5元,就可获得最大的利润.......................12分 20.证明(Ⅰ)CDEFABCD 平面平面⊥,CDCDEF ABCD =平面平面 ,在正方形CDEF中,ED DC ⊥∴ABCDED 平面⊥,ED BC∴⊥.................................2分取DC的中点G连接BG,12DG DC =,在四边形ABCD中,//,AB DC 12AB DC =,ABGD四边形∴为平行四边形,所以,点B在以DC为直径的圆上,所以DB BC⊥,............................4分 又ED BD D=,所以BBC 平面⊥,......................................6分 (Ⅱ)如图,取DC的中点G,连接AG,在DC上取点P使13DP DC =,连接NP13D ND P D ED C ==,//PN EC ∴,//PN BCE∴面,................8分连接MP,23DM DP G DC DA DG ∴==为中点,,//MP AG ∴.又//,,AB CG AB CG ABCG=∴为平行四边形,//AG BC∴,//MP BC∴,//MP BCE∴面,.................................10分 又MP NP P=,MNP BCE ∴平面//平面. MNPMN 平面⊂ ,所以MN//平面B........................................12分21.解:(Ⅰ)当3m =时, f(x)为R 上的奇函数。
广东省清远市2017-2018学年高三上学期期末数学试卷(理科) Word版含解析

2017-2018学年广东省清远市高三(上)期末数学试卷(理科)一.选择题(12小题,共60分)1.设集合M={﹣1,0,1},N={a,a2}则使M∩N=N成立的a的值是()A.1 B.0 C.﹣1 D.1或﹣12.若复数z满足iz=1+i,则z的虚部为()A.1 B.i C.﹣1 D.﹣i3.下列函数是偶函数的是()A.B.y=x3C.D.y=x2+14.如图所示程序框图,输出的结果是()A.2 B.3 C.4 D.55.已知数列{a n}的前n项和为,则a3+a17=()A.36 B.35 C.34 D.336.一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于()A.B.2C.3D.47.已知双曲线C:x2+2my2=1的两条渐近线互相垂直,则抛物线E:y=mx2的焦点坐标是()A.(0,1)B.(0,﹣1)C.(0,)D.(0,﹣)8.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币数字一面向上”为事件A,“骰子向上的点数是偶数”为事件B,则事件A,B中至少有一件发生的概率是()A.B.C.D.9.已知实数变量x,y满足,且目标函数z=3x+y的最大值为8,则实数m的值为()A.B.C.2 D.110.下列正确的个数是()A.“在三角形ABC中,若sinA>sinB,则A>B”的逆是真;B.p:x≠2或y≠3,q:x+y≠5则p是q的必要不充分条件;C.“∀x∈R,x3﹣x2+1≤0”的否定是“∀x∈R,x3﹣x2+1>0”;D.“若a>b,则2a>2b﹣1”的否为“若a≤b,则2a≤2b﹣1”.A.1 B.2 C.3 D.411.已知数列{a n}满足:,,若{C n}是单调递减数列,则实数λ的取值范围是()A.λB.λC.λD.λ12.定义:设A,B是非空的数集,a∈A,b∈B,若a是b的函数且b也是a的函数,则称a与b是“和谐关系”.如等式b=a2,a∈[0,+∞)中a与b是“和谐关系”,则下列等中a 与b是“和谐关系”的是()A.B.C.(a﹣2)2+b2=1,a∈[1,2]D.|a|+|b|=1,a∈[﹣1,1]二.填空题13.已知向量在正方形网格中的位置如图所示,则=______14.已知(1﹣x)(1+ax)3的展开式中x2的系数为6,则a=______.15.某人10万元买了1辆车,每年使用的保险费.养路费和油费共1万元,年维修费第一年0.2万元,以后每年递增0.1万元,则这种汽车使用______年时,它的年平均费用最少.16.已知正实数a,b满足=3,则(a+1)(b+2)的最小值是______.三.解答题17.已知函数f(x)=sin2x﹣cos2x﹣(x∈R),设△ABC的内角A,B,C对应边分别为a,b,c,且c=,f(C)=0.(1)求C的值.(2)若向量=(1,sinA)与向量=(2,sinB)共线,求△ABC的面积.18.已知:如图,等腰直角三角形ABC的直角边AC=BC=2,沿其中位线DE将平面ADE 折起,使平面ADE⊥平面BCDE,得到四棱锥A﹣BCDE,设CD、BE、AE、AD的中点分别为M、N、P、Q.(1)求证:M、N、P、Q四点共面;(2)求证:平面ABC⊥平面ACD;(3)求异面直线BE与MQ所成的角.19.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,(1)根据上面的数据判断,y=ax+b与y=+d哪一个适宜作为产品销量y关于单价x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;(计算结果保留两位小数)参考公式其中==.20.如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=﹣2x(x≥0)上运动,且S=4.△AOB (1)求x1•x2;(2)求线段AB的中点M的轨迹方程;(3)判定中点M到两射线的距离积是否是为定值,若是则找出该值并证明;若不是定值说明理由.21.设f(x)=x﹣﹣alnx(a∈R).(1)当a=1时,求曲线y=f(x)在点(, +ln2)处的切线方程;(2)若x=1是函数f(x)的极大值点,求a的取值范围;(3)当a<1时,在[,e]上是否存在一点x0,使f(x0)>e﹣1成立?说明理由.22.如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA 交△ABC的外接圆于点F,连接FB,FC.(1)求证:FB=FC;(2)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6cm,求AD的长.23.在直角坐标系xoy中,曲线C1的参数方程为(α为参数,α≠,k∈z),M是C1上的动点,P点满足=,点P的轨迹为C2.(1)求曲线C1、C2的普通方程.(2)以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐际方程是ρsin(θ﹣)+=0,直线l与曲线C2相交于A、B,求△ABO的面积.24.设f(x)=|x|+|1+|.(1)解不等式f(x)≤1;(2)已知正数a,b,c,当x>0时,f(x)≥++恒成立,求证:a+b+c≥3.2015-2016学年广东省清远市高三(上)期末数学试卷(理科)参考答案与试题解析一.选择题(12小题,共60分)1.设集合M={﹣1,0,1},N={a,a2}则使M∩N=N成立的a的值是()A.1 B.0 C.﹣1 D.1或﹣1【考点】交集及其运算.【分析】由M={﹣1,0,1},N={a,a2},M∩N=N,知,由此能求出a的值.【解答】解:∵M={﹣1,0,1},N={a,a2},M∩N=N,∴,解得a=﹣1.故选C.2.若复数z满足iz=1+i,则z的虚部为()A.1 B.i C.﹣1 D.﹣i【考点】复数的基本概念.【分析】首先由iz=1+i,求出z,根据复数的定义求出虚部.【解答】解:因为iz=1+i,所以z=﹣i+1;所以z的虚部为﹣1;故选C.3.下列函数是偶函数的是()A.B.y=x3C.D.y=x2+1【考点】函数奇偶性的判断.【分析】根据函数奇偶性的定义进行判断即可.【解答】解:A.的定义域为{x|x≠0},则f(﹣x)=﹣﹣x=﹣(+x)=﹣f(x),则函数为奇函数,B.f(﹣x)=﹣x3=﹣f(x),则函数为奇函数.、C.函数的定义域为[0,+∞),函数为非奇非偶函数.D.f(﹣x)=(﹣x)2+1=x2+1=f(x),则函数为偶函数,故选:D.4.如图所示程序框图,输出的结果是()A.2 B.3 C.4 D.5【考点】程序框图.【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量i的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:第一次执行循环体后:S=1,i=2,a=3,不满足退出循环的条件;第一次执行循环体后:S=3,i=3,a=12,满足退出循环的条件;故输出的i的值为3,故选:B5.已知数列{a n}的前n项和为,则a3+a17=()A.36 B.35 C.34 D.33【考点】数列递推式.【分析】前n项和为,当n≥2时,a n=S n﹣S n,代入即可得出.﹣1【解答】解:∵前n项和为,=n2﹣2n﹣[(n﹣1)2﹣2(n﹣1)]=2n﹣3.∴当n≥2时,a n=S n﹣S n﹣1则a3+a17=(2×3﹣3)+(2×17﹣3)=34.故选:C.6.一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于()A.B.2C.3D.4【考点】由三视图求面积、体积.【分析】几何体为四棱锥,棱锥的高为侧视图三角形的高,底面为直角梯形.【解答】解:由三视图可知,几何体为四棱锥,棱锥的高为侧视图中等边三角形的高,棱锥的底面为直角梯形,梯形面积为(1+2)×2=3.∴V==.故选A.7.已知双曲线C:x2+2my2=1的两条渐近线互相垂直,则抛物线E:y=mx2的焦点坐标是()A.(0,1)B.(0,﹣1)C.(0,)D.(0,﹣)【考点】双曲线的简单性质.【分析】求出双曲线的渐近线方程,由两直线垂直的条件,可得m=﹣,再由抛物线方程,注意化为标准方程,可得焦点坐标.【解答】解:双曲线C:x2+2my2=1(m<0),可得渐近线方程为y=±x,由渐近线垂直可得=1,解得m=﹣,即有抛物线E:y=mx2的方程为x2=﹣2y,可得焦点为(0,﹣).故选:D.8.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币数字一面向上”为事件A,“骰子向上的点数是偶数”为事件B,则事件A,B中至少有一件发生的概率是()A.B.C.D.【考点】互斥事件的概率加法公式.【分析】由已知可得P(A)=,P(B)=,则事件A,B中至少有一件发生的概率P=P(A∩B)+P(A∩)+P(∩B),解得答案.【解答】解:投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币数字一面向上”为事件A,“骰子向上的点数是偶数”为事件B,则P(A)=,P(B)=,则事件A,B中至少有一件发生的概率P=P(A∩B)+P(A∩)+P(∩B)=,故选:C9.已知实数变量x,y满足,且目标函数z=3x+y的最大值为8,则实数m 的值为()A.B.C.2 D.1【考点】简单线性规划.【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.【解答】解:作出不等式对应的平面区域如图,由选项知m>0,由z=3x+y,得y=﹣3x+z,平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z,经过点A时,直线y=﹣3x+z的截距最大,此时z最大为8,即3x+y=8由,解得,即A(2,2),同时A也在2mx﹣y﹣2=0上,∴4m﹣2﹣2=0,得m=1,故选:D.10.下列正确的个数是()A.“在三角形ABC中,若sinA>sinB,则A>B”的逆是真;B.p:x≠2或y≠3,q:x+y≠5则p是q的必要不充分条件;C.“∀x∈R,x3﹣x2+1≤0”的否定是“∀x∈R,x3﹣x2+1>0”;D.“若a>b,则2a>2b﹣1”的否为“若a≤b,则2a≤2b﹣1”.A.1 B.2 C.3 D.4【考点】的真假判断与应用.【分析】A项根据正弦定理以及四种之间的关系即可判断;B项根据必要不充分条件的概念即可判断该是否正确;C项根据全称和存在性的否定的判断;D项写出一个的否的关键是正确找出原的条件和结论.【解答】解:对于A项“在△ABC中,若sinA>sinB,则A>B”的逆为“在△ABC中,若A >B,则sinA>sinB”,若A>B,则a>b,根据正弦定理可知sinA>sinB,∴逆是真,∴A正确;对于B项,由x≠2,或y≠3,得不到x+y≠5,比如x=1,y=4,x+y=5,∴p不是q的充分条件;若x+y≠5,则一定有x≠2且y≠3,即能得到x≠2,或y≠3,∴p是q的必要条件;∴p是q的必要不充分条件,所以B正确;对于C项,“∀x∈R,x3﹣x2+1≤0”的否定是“∃x∈R,x3﹣x2+1>0”;所以C不对.对于D项,“若a>b,则2a>2b﹣1”的否为“若a≤b,则2a≤2b﹣1”.所以D正确.故选:C.11.已知数列{a n}满足:,,若{C n}是单调递减数列,则实数λ的取值范围是()A.λB.λC.λD.λ【考点】数列的函数特性.【分析】数列{a n}满足:,两边取倒数可得:=+1,变形为: +1=2,利用等比数列的通项公式可得,代入=2n.由于{C n}是单调递减数列,可得c n<c n,化+1简整理,利用函数的单调性即可得出.【解答】解:∵数列{a n}满足:,∴=+1,变形为: +1=2,∴数列是等比数列,首项为2,公比为2.∴+1=2n,∴=2n,∵{C n}是单调递减数列,∴c n<c n,+1∴2n+1<2n,化为:λ>=,令f(x)=x++3,(x∈[1,+∞)).f′(x)=1﹣=,可知当x≥时,单调递增;而f(1)=6,f(2)=6,∴f(x)的最小值为6,因此的最大值为,∴.故选:B.12.定义:设A,B是非空的数集,a∈A,b∈B,若a是b的函数且b也是a的函数,则称a与b是“和谐关系”.如等式b=a2,a∈[0,+∞)中a与b是“和谐关系”,则下列等中a 与b是“和谐关系”的是()A.B.C.(a﹣2)2+b2=1,a∈[1,2]D.|a|+|b|=1,a∈[﹣1,1]【考点】元素与集合关系的判断.【分析】只要判断所给出的函数单调即可.【解答】解:A.∵,则a>sina,∴b′==>0,因此函数b在上单调递增,正确;B.∵a∈,b′=3a2+5a+2=(3a+2)(a+1),∴a∈(﹣2,﹣1)时单调递增;a ∈(﹣1,﹣)时单调递减,因此不符合题意;C.∵(a﹣2)2+b2=1,a∈[1,2],∴b=±,b不是a的函数,舍去;D.∵|a|+|b|=1,a∈[﹣1,1],∴b=±(1﹣|a|),b不是a的函数,舍去.故选:A.二.填空题13.已知向量在正方形网格中的位置如图所示,则=(2,﹣2)【考点】向量的加法及其几何意义.【分析】根据图形,求出向量、的坐标表示,再求出的坐标表示.【解答】解:根据题意,向量=(4﹣1,3﹣2)=(3,1),=(3﹣4,0﹣3)=(﹣1,﹣3),∴=(3﹣1,1﹣3)=(2,﹣2).故答案为(2,﹣2).14.已知(1﹣x)(1+ax)3的展开式中x2的系数为6,则a=2或﹣1.【考点】二项式系数的性质.【分析】根据题意,列出方程•a2﹣•a=6,求出a的值即可.【解答】解:(1﹣x)(1+ax)3的展开式中x2的系数为•a2﹣•a=6,即a2﹣a﹣6=0,解得a=2或a=﹣1.故答案为:2或﹣1.15.某人10万元买了1辆车,每年使用的保险费.养路费和油费共1万元,年维修费第一年0.2万元,以后每年递增0.1万元,则这种汽车使用10年时,它的年平均费用最少.【考点】基本不等式在最值问题中的应用;函数模型的选择与应用.【分析】通过记第n年维修费用为a n,计算可知a n=0.1n+0.1(万元),进而可知前n年维修费用A n=(万元),化简可知年平均费用S=++,进而利用基本不等式计算即得结论.【解答】解:依题意,记第n年维修费用为a n,则a n=0.2+0.1(n﹣1)=0.1n+0.1(万元),则前n年维修费用A n===(万元),故年平均费用S==++,∵+≥2=,当且仅当=即n=10时取等号,∴这种汽车使用10年时,它的年平均费用最少,故答案为:10.16.已知正实数a,b满足=3,则(a+1)(b+2)的最小值是.【考点】基本不等式.【分析】正实数a,b满足=3,可得,b+2a=3ab.展开(a+1)(b+2)=ab+b+2a+2=4ab+2,即可得出.【解答】解:∵正实数a,b满足=3,∴,化为,当且仅当b=2a=时取等号.b+2a=3ab.∴(a+1)(b+2)=ab+b+2a+2=4ab+2.故答案为:.三.解答题17.已知函数f(x)=sin2x﹣cos2x﹣(x∈R),设△ABC的内角A,B,C对应边分别为a,b,c,且c=,f(C)=0.(1)求C的值.(2)若向量=(1,sinA)与向量=(2,sinB)共线,求△ABC的面积.【考点】三角函数中的恒等变换应用;平面向量数量积的运算;正弦函数的图象.【分析】(1)利用三角函数恒等变换的应用化简可得函数解析式为:f(x)=sin(2x﹣)﹣1,由f(C)=0得sin(2C﹣)=1,结合范围﹣<2C﹣<,即可解得C的值.(2)利用向量共线可得2sinA=sinB,由正弦定理可得b=2a,由余弦定理得a2+b2﹣ab=3,联立解得a,b的值,利用三角形面积公式即可求值得解.【解答】解:(1)∵f(x)=sin2x﹣cos2x﹣,…f(x)=sin(2x﹣)﹣1,…由f(C)=0得sin(2C﹣)=1,…又∵﹣<2C﹣<,…∴2C﹣=,…即C=…(2)∵向量=(1,sinA)与向量=(2,sinB)共线,∴2sinA=sinB,…∴b=2a,①…由余弦定理,得a2+b2﹣ab=3,②…∴由①②得:a=1,b=2…∴△ABC的面积为absinC=.…18.已知:如图,等腰直角三角形ABC的直角边AC=BC=2,沿其中位线DE将平面ADE 折起,使平面ADE⊥平面BCDE,得到四棱锥A﹣BCDE,设CD、BE、AE、AD的中点分别为M、N、P、Q.(1)求证:M、N、P、Q四点共面;(2)求证:平面ABC⊥平面ACD;(3)求异面直线BE与MQ所成的角.【考点】平面与平面垂直的判定;空间图形的公理;异面直线及其所成的角.【分析】(1)要证四点共线,只需找到一个平面,是这四个点在这个平面内,用确定平面的方法,两条平行线确定一个平面,即可证出;(2)要证明两个平面垂直,只需证明其中一个平面经过另一个平面的一条垂线即可,也就是只需证线面垂直即可,而要证线面垂直,只需证明这条直线垂直平面内的两条相交直线,这样,一步步寻找成立的条件.(3)求异面直线所成角,先平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成角就是异面直线所成角或其补角,再放入三角形中计算即可.【解答】(1)证明:由条件有PQ为△ADE的中位线,MN为梯形BCDE的中位线,∴PQ∥DE,MN∥DE,∴PQ∥MN∴M、N、P、Q四点共面.…(2)证明:由等腰直角三角形ABC有AD⊥DE,CD⊥DE,DE∥BC又AD∩CD=D,∴DE⊥面ACD,又DE∥BC∴BC⊥平面ACD,∵BC⊂平面ABC,∴平面ABC⊥平面ACD…(3)解:由条件知AD=1,DC=1,BC=2,延长ED到R,使DR=ED,连结RC …则ER=BC,ER∥BC,故BCRE为平行四边形…∴RC∥EB,又AC∥QM∴∠ACR为异面直线BE与QM所成的角θ(或θ的补角)…∵DA=DC=DR,且三线两两互相垂直,∴由勾股定理得AC=AR=RC=,…∵△ACR为正三角形,∴∠ACR=60°,∴异面直线BE与QM所成的角大小为60°.…19.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,(1)根据上面的数据判断,y=ax+b与y=+d哪一个适宜作为产品销量y关于单价x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;(计算结果保留两位小数)参考公式其中==.【考点】线性回归方程.【分析】(1)观察表格数据可知y与x成反比关系,故选y=;(2)令t=,将回归方程转化为线性回归方程解出.【解答】解:(1)y=更适宜作为产品销量y关于单价x的回归方程.(2)令t=,则y=tc+d,原数据变为:∴=(4+2+1+0.5+0.25)=1.55,=(16+12+5+2+1)=7.2.=64+24+5+1+0.25=94.25,=16+4+1+0.25+0.0625=21.3125.∴c=≈4.13.d=﹣c≈0.8.∴y=0.8+4.13 t.∴y与x的回归方程是y=0.8+20.如图,点A,B分别在射线l1:y=2x(x≥0),l2:y=﹣2x(x≥0)上运动,且S=4.△AOB (1)求x1•x2;(2)求线段AB的中点M的轨迹方程;(3)判定中点M到两射线的距离积是否是为定值,若是则找出该值并证明;若不是定值说明理由.【考点】直线与圆锥曲线的综合问题;轨迹方程.【分析】(1)设M(x,y),A(x1,y1),B(x2,y2),∠AOB=2θ,由y=2x,得tanθ=k=2,=4,能求出x1•x2的值.从而求出sin2θ,由|OA|=,|OB|=,利用S△AOB(2)由M(x,y)是A(x1,y1),B(x2,y2)的中点,得,由此能求出线段AB的中点M的轨迹方程.(3)设中点M到射线OA,OB的距离分别为d1,d2,由此能推导出中点M到两射线的距离积为定值.【解答】解:(1)设M(x,y),A(x1,y1),B(x2,y2),∠AOB=2θ,由y=2x,得tanθ=k=2,∴sin2θ==,∵|OA|=,|OB|=,=|OA|•|OB|•sin2θ==4,∴S△AOB解得x1•x2=2.(2)∵M(x,y)是A(x1,y1),B(x2,y2)的中点,∴x1+x2=2x,y1+y2=2y,且y1=2x1,y2=﹣2x2,联立,得,并代入x1•x2=2,得4x2﹣y2=8,x>0.∴线段AB的中点M的轨迹方程为4x2﹣y2=8,x>0.(3)设中点M到射线OA,OB的距离分别为d1,d2,则,∴d1•d2==.∴中点M到两射线的距离积为定值.…21.设f(x)=x﹣﹣alnx(a∈R).(1)当a=1时,求曲线y=f(x)在点(, +ln2)处的切线方程;(2)若x=1是函数f(x)的极大值点,求a的取值范围;(3)当a<1时,在[,e]上是否存在一点x0,使f(x0)>e﹣1成立?说明理由.【考点】利用导数研究函数的极值;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,计算f′(),代入切线方程即可;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值,得到a的具体范围即可;(3)问题转化为只需证明时,f(x)max>e﹣1即可,根据函数的单调性证明即可.【解答】解:(1)当a=1时,f(x)=x﹣lnx,,所以曲线y=f(x)在点处的切线的斜率为.所求切线方程为,即x+y﹣ln2﹣1=0.(2),令f′(x)=0得,x1=1,x2=a﹣1,综上所述,当a>2时,x=1是函数f(x)的极大值点.即所求取值范围是(2,+∞).(3)假设当a<1时,在存在一点x0,使f(x0)>e﹣1成立,则只需证明时,f(x)max>e﹣1即可.由(2)知,当a<1时,函数f(x)在上递减,在[1,e]上递增,∴.所以只需证明f(e)>e﹣1或即可.∵=由a<1知,∴f(e)﹣(e﹣1)>0即f(e)>e﹣1成立所以假设正确,即当a<1时,在上至少存在一点x0,使f(x0)>e﹣1成立.22.如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA 交△ABC的外接圆于点F,连接FB,FC.(1)求证:FB=FC;(2)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6cm,求AD的长.【考点】与圆有关的比例线段.【分析】(1)由已知得∠EAD=∠DAC,∠DAC=∠FBC,从而∠FBC=∠FCB,由此能证明FB=FC.(2)由已知得∠ACB=90°从而∠ABC=30°,∠DAC=∠EAC=60°,由此能求出AD.【解答】证明:(1)因为AD平分∠EAC,所以∠EAD=∠DAC.…因为四边形AFBC内接于圆,所以∠DAC=∠FBC.…因为∠EAD=∠FAB=∠FCB,…所以∠FBC=∠FCB,…,所以FB=FC.…解:(2)因为AB是圆的直径,所以∠ACB=90°,…又∠EAC=120°,所以∠ABC=30°,…∠DAC=∠EAC=60°,…因为BC=6,所以AC=BCtan∠ABC=2,…所以AD==4(cm).…23.在直角坐标系xoy中,曲线C1的参数方程为(α为参数,α≠,k∈z),M是C1上的动点,P点满足=,点P的轨迹为C2.(1)求曲线C1、C2的普通方程.(2)以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐际方程是ρsin(θ﹣)+=0,直线l与曲线C2相交于A、B,求△ABO的面积.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】(1)曲线C1的参数方程为(α为参数,α≠,k∈z),消去参数α可得普通方程.设P(x,y),M(x0,y0),利用P点满足=,可得x0=2x,y0=2y,代入曲线C1的方程即为点P的轨迹方程.(2)直线l的极坐际方程是ρsin(θ﹣)+=0,展开化为:(ρsinθ﹣ρcosθ)+=0,利用即可化为直角坐标方程.设A(x1,y1),B(x2,y2).与抛物线方程联=d|AB|即可得出.立解得A,B,利用S△AOB【解答】解:(1)曲线C1的参数方程为(α为参数,α≠,k∈z),消去参数α可得普通方程:y2=2x.设P(x,y),M(x0,y0),∵P点满足=,∴x0=2x,y0=2y,代入曲线C1的方程可得:4y2=4x,化为y2=x,即为点P的轨迹方程.(2)直线l的极坐际方程是ρsin(θ﹣)+=0,展开化为:(ρsinθ﹣ρcosθ)+=0,化为直角坐标方程:y﹣x+2=0.设A(x1,y1),B(x2,y2).联立,化为y2﹣y﹣2=0,解得,,∴|AB|==3.原点到直线l的距离d==.=d|AB|=3.∴S△AOB24.设f(x)=|x|+|1+|.(1)解不等式f(x)≤1;(2)已知正数a,b,c,当x>0时,f(x)≥++恒成立,求证:a+b+c≥3.【考点】绝对值不等式的解法;函数恒成立问题.【分析】(1)通过讨论x的范围,求出不等式的解集即可;(2)根据基本不等式的性质证明即可.【解答】解:(1)显然,x≠0,∴当x≤﹣1时,得,…即﹣x2+1≥0,即x=﹣1;…当﹣1<x<0时,得,即(x+1)2≤0,x无解;…当x>0时,得,即x2+1≤0,x无解;…综上,不等式f(x)≤1的解集是{x|x=﹣1}…(2)∵x>0,∴f(x)=|x|+|1+|=x++1≥2+1=3, (6)当且仅当x=1时等号成立…∵当x>0时,f(x)≥++恒成立,∴…∴,∴a+b+c≥3…2016年9月27日。
2017-2018学年高一上学期期末考试数学试题(20201014181259)

现在沿 AE 、 AF 及 EF 把这个正方形折成一个四面体,使 B 、 C 、 D 三点重合,重合后
的点记为 H ,如图②所示,那么,在四面体 A EFH 中必有 ( )
图①
图②
A . AH ⊥△ EFH 所在平面
B. AG ⊥△ EFH 所在平面
C. HF ⊥△ AEF 所在平面
D. HG ⊥△ AEF 所在平面
22 ( 2 3) 2 1 ,即 | m | 1 解得 m
2
2
0或 1 2
2
20.解: ∵ PA⊥平面 ABCD ,CD? 平面 ABCD ∴ PA⊥ CD
∵ CD ⊥AD , AD ∩PA= A∴CD ⊥平面 PAD .[来源:Z#xx#] ∵ PD ? 平面 PAC,∴ CD⊥ PD [来源:Z*xx*]
)
A. a 1或 a 2
B. a 2或 a 1
C. a 1
D. a 2
5.设 l 是直线, , 是两个不同的平面,(
)
A .若 l ∥ , l ∥ ,则 ∥
B.若 l ∥ , l ⊥ ,则 ⊥
C.若 ⊥ , l ⊥ ,则 l ⊥
D.若 ⊥ , l ∥ ,则 l ⊥
6.直线 2 x 3 y 6 0 关于点 (1, 1) 对称的直线方程是 ( )
三、解答题
3x 4y 5 0
17. 解:由
,得 M ( 1, 2)
2x 3y 8 0
22
( 1) x 1 ( 2)设直线方程为 x 2 y C 0 ,则, C 5 ,即 x 2y 5 0
18.解:圆 x2 y2 4 的圆心坐 标为 (0,0) , 半径 r 4
∵ 弦 AB 的长为 2 3 ,
故圆心到直线的距离 d 19.解:
2017-2018学年第一学期期末教学质量监测数学答案
⎺ = y
1 10
∑ yi = 2
10 i = 1
∴
∧
b=
∑ xiyi 10 i = 1
∧
⎺ ⎺ a=y -bx =
∧
∑
i = 1
10
⎺ ⎺ 10 x y = 24 = 0.3 80 ⎺ 2 xi2 - 10x
2 - 0.3×8 = -0.4
∧
故所求回归方程为 y = 0.3
x-0.4
∧
……………… 6 分
(2)试验的全部结束所构成的区域为{(a,b )|0≤a≤3,0≤b ≤2}, 构成事件 A 的区域为{(a,b )|0≤a≤3,0≤b ≤2,a≥b }, 3×2- 1 ×22 2 所以所求的概率为= =2 3×2 3
……………… 10 分 共3页
数学答案第 2 页
⎺ 22.解:(1) x = 1 10
2017-2018 学年第一学期期末教学质量监测
高一数学参考答案
一选择题: 题号 答案 二、填空题: 13. 16 14. 66 15. 4 √ 3 3 16. 101 17. ( -1, 5 ) 4 ……………… 4 分 1 2 3 4 5 6 7 8 9 10 D 11 A 12 B B A C B C D A B A
三、解答题:
18.解:(1)x=6
y= 3 ;
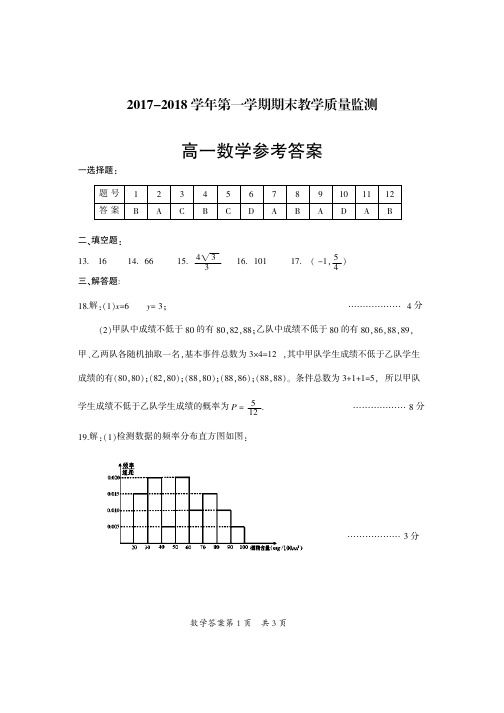
(2)甲队中成绩不低于 80 的有 80,82,88;乙队中成绩不低于 80 的有 80,86,88,89, 甲、乙两队各随机抽取一名,基本事件总数为 3×4=12 ,其中甲队学生成绩不低于乙队学生 成绩的有(80,80);(82,80);(88,80);(88,86);(88,88)。 条件总数为 3+1+1=5, 所以甲队 学生成绩不低于乙队学生成绩的概率为 P = 5 . 12 19.解:(1)检测数据的频率分布直方图如图: ……………… 8 分
清远市 2017—2018 学年度第一学期期末教学质量检测高三文科数学(含详细答案)

成面积相等的两部分,则实数 k 的值为______. 三、解答题(本大题共 7 小题,共 70 分,答题应写出必要的文字说明,推理证明过程或 演算步骤。其中第 17-21 题为必做题,每题 12 分,第 22-23 题为选做题,每题 10 分, 考生只需做其中一道,若多做,只按所做的第一道题得分) 17.(本题满分 12 分) 如图,在△ABC 中, BC = 5 , AB = 7 , BD 是
x
B. 若 m ⊥ n , n ⊥ β , m ⊥α , 则α ⊥ β D. 若 m ⊥ n , n ⊥ β , β ⊥α , 则m ⊥α
11.在如下程序框图中,已知: f 0 ( x) = xe , f i ′( x) 是 f i ( x) 的导函数,则输出的是 开始 输入 f 0 (x )
i=0
x2 y2 13 6.双曲线 C: 2 − 2 = 1( a > 0, b > 0) 的离心率 e = ,则它的渐近线方程 2 a b
3 A. y = ± x 2 2 B. y = ± x 3 9 C. y = ± x 4 4 D. y = ± x 9
7. 在 ∆ABC 中,在线段 AB 上任取一点 P ,恰好满足 A.
⎧log 1 ( x + 1) , 0 ≤ x < 1
2
,则方程
⎪ ⎩1 − x − 3 , x ≥ 1
f ( x) −
A.0
1 = 0 的所有根之和为 2
B. 1 − 2 C.
2
D. 1 + 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东清远市2017—2018学年度第一学期期末教学质量检测高一数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1..已知集合{}3|<=x x M ,{}Z x x N ∈<<=且60,则=⋂N M ( ) A .{}3,2,1 B .{}5,4,3 C .{}2,1 D .{}5,42.经过点()0,3A 且直线斜率1=k 的直线方程是( )A. 03=-+y xB.03=--y xC.03=++y xD.03=+-y x 3.下列图象可作为函数()x f y =图象的是( )4.已知直线()012:1=++-a ay x a l ,02:2=+-a y ax l 互相垂直,则a 的值是( ) A.0 B.1 C.0或-1 D.0或15.幂函数()αx x f =的图象过点⎪⎭⎫ ⎝⎛221,,则函数()x f 为( )A.奇函数且在()∞+,0上单调递增B.奇函数且在()∞+,0上单调递减C.偶函数且在()∞+,0上单调递增D.偶函数且在()∞+,0上单调递减6.设41log 2=a ,311.2=b ,254⎪⎭⎫⎝⎛=c ,则c b a ,,的大小关系为( )A.c b a <<B.b c a <<C.a c b <<D.a b c << 7.函数()x f 的图象如下图,则该函数可能是( )A .()221x x x f -= B .()x x x f 1+= C.()331x x x f += D .()xx x f 1-=8.如图,某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆,则该几何体的体积为( )A .4 B.8 C. π4 D. π6 9.己知圆M 的半径为4,圆心在x 轴的负半轴上,直线0443=++y x 与圆M 相切,则圆M 的方程 为( )A .()16822=++y x B.1631622=+⎪⎭⎫ ⎝⎛-y xC .()16822=+-y xD .1631622=+⎪⎭⎫⎝⎛+y x?10.若函数()x f y =()R x ∈是奇函数,其零点为201721,,,x x x ,且m x x x =+++201721 ,则关于x 的方程m x x =-+22的根所在区间是( )A.(0,1)B. (1,2)C. (2,3)D.(3,4)11.已知两条不同的直线b a ,及两个不同的平面βα,,其中βα⊂⊂b a ,,则下面结论正确的是( ) A .若b a //,则βα//?B .若b a ⊥,则βα⊥? ? ? ?C .若a 与b 相交,则α与β相交D .若α与β相交,则a 与b 相交12.已知函数()x f y =()R x ∈是奇函数,()()x f x x g ∙=,且当()0,∞-∈x 时,()x g 是减函数,()()132g g a <-,则 a 的取值范围是( )A .(0,3)B .(1,3)C . ( 1,2 )D .(2,3)第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.圆()()363122=-++y x 的圆心C 坐标 ,半径=r ________.14.己知()5,3A 、()7,5B ,直线l 的斜率是直线AB 斜率的3倍,则直线l 的倾斜角为 .15.在正方体1111D C B A ABCD -中,1B 到平面11D ABC 的距离为2,则正方体1111D C B A ABCD -棱长是 .16.设定义在R 上的函数()⎪⎩⎪⎨⎧>≤=0,log 0,22x x x x f x,()()a x f x g -=,则当实数a 满足10<<a 时,函数()x g y =的零点个数为 个.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.己知集合{}210|≤-≤=x x A ,R 为实数集,{}321|+<-<=a a x x A . (I)当1=a 时,求B A ⋃及B C A R ⋂; (II)若φ≠⋂B A ,求a 的取值范围. 18.计算下列各式的值.(I)()()1lg 216320184916723-⎪⎭⎫ ⎝⎛⨯-⨯;(II)811log 8log 932log 2log 23333-+-. 19.设函数()2212xx x f -=(I)判断函数()x f 的奇偶性并证明;(II)用定义证明函数()x f 在()∞+,0上为增函数.20. 如图,正四棱锥ABCD P -中,ABCD 是正方形,O 是正方形的中心,⊥PO 底面ABCD ,E 是PC 的中点.(I)证明://PA 平面BDE ; (II)证明:平面⊥PAC 平面BDE ;(III)已知:2==PA AB ,求点C 到面BDE 的距离.21.已知圆M 过点()3,1-P ,且与圆()2222:r y x C =++(0>r )关于y 轴对称.(I)求圆M 的方程;(II)若有相互垂直的两条直线21,l l ,都过点()0,1-A ,且21,l l 被圆C 所截得弦长分别是21,d d ,求2221d d +的值.22.己知函数()x e x f =,()()R b b x x x g ∈++-=22,记()()()x f x f x h 1-= (I)判断()x h 的奇偶性,并写出()x h 的单调区间,均不用证明;(II)对任意[]2,1∈x ,都存在[]2,121∈x x ,xl ,,使得()()1x f x f ≤,()()2x g x g ≤.若()()21x g x f =.求实数b 的值.试卷答案一、选择题1-5:CBADB 6-10: BDDAA 11、12:CC 二、填空题13.()3,1-C ,半径6=r 14.60或填3π15.棱长2 16.3 三、解答题17.解:(Ⅰ){}{}31|210|≤≤=≤-≤=x x x x A 当1=a 时,{}{}62|31211|<<=+⨯<-<=x x x x B{}61|<≤=⋃x x B A{}62|≥≤=x x x B C R 或{}21|≤≤=⋂x x B C A R(Ⅱ)由已知得{}{}331|,31|+<<+=≤≤=a x a x B x x A ⎪⎩⎪⎨⎧+<+>+<+∴≠⋂33113331,a a a a B A φ 解得232<<-a 则a 的取值范围为)2,32(-. 18. 解:(I )原式=0212636)2018(])74[(7)2()3(-⨯-⨯ =17472323-⨯-⨯=103 (Ⅱ)811log 8log 932log 2log 29333-+-=293339log 8log 932log 4log --+- 2)32984(log 3+⨯⨯= 23log 23+=422=+=19.解:(Ⅰ)函数2212)(x x x f -=是偶函数. 证明如下:函数定义域为),0()0,(+∞⋃-∞,定义域关于原点中心对称∵)(12)(1)-(2)-(2222x f xx x x x f =-=--= ∴函数)(x f 为偶函数.(Ⅱ)设21x x 、为),0(+∞上任意两个自变量,且21x x <)12()12()()(2222212121x x x x x f x f ---=-)12)((-)(222212221222122212221x x x x x x x x x x +-=+-=)12)()((212121x x x x x x ++-=∴21,x x 为),0(+∞上任意两个自变量,且21x x < 01200212121>+<->+∴x x x x x x ,, ∴ 0)12)()((22212121<++-x x x x x x )()(0)()(2121x f x f x f x f <<-∴即∴函数)(x f 在),0(+∞上为增函数20.【解析】证明(I )连结EO ,在△BDE 中∵O 是AC 的中点,E 是PC 的中点, ∴OE ∥AP ,又∵OE ⊂平面BDE ,PA ⊄平面BDE , ∴PA ∥平面BDE.(II )∵PO ⊥底面ABCD ,BD ⊂面ABCD, ∴PO ⊥BD ,又∵ABCD 是正方形, ∴AC ⊥BD , 且AC PO=O ∴BD ⊥平面PAC ,而BD ⊂平面BDE ,∴平面PAC ⊥平面BDE. (III )设点C 到面BDE 的距离为h , 由已知得BCD P BCD E BDE C V V V ---==21正四棱锥P-ABCD 中,AB=PA=2 ,由题意得,PO=2,EO=PC 21=1, ∴PO AC BD h OE BD ⋅⋅⋅⋅=⋅⋅⋅212131212131, ∴h =1,即点C 到面BDE 的距离为121. 解:(I )由题意设圆M 的方程222)()(r b y a x =-+- 由题意可知圆C 的圆心为)0,2(-则点)0,2(-关于x 轴对称的点为)0,2(,∴圆M 的方程为222)2(r y x =+- 将点P 代入圆M 的方程得42=r ,∴圆M 的方程4)2(22=+-y x (II )解法一:设12,l l 被圆C 所截得弦得中点分别为F E 、, 根据圆的性质得四边形AECF 为矩形 所以1222==+AC CF CE 即1)2(-4)2(-42221=+d d 化简得282221=+d d 解法二:①当12,l l 一条直线斜率不存在,另一条斜率为0时,222221324)(+=+d d =28 ②当12,l l 一条直线斜率存在,设为)1(1)1(21+-=+=x ky l x k y l :;:将点C 到1l 的距离的平方为22211||k k kk +=+)(,)14(42221k k d +-= 同理点C 到1l 的距离的平方为211k +,)114(4222k d +-= )118(4)114(4)14(4222221k k k k k d d ++-=+-++-=+=28由①②可得282221=+d d22.解(Ⅰ)函数xxee x h 1)(-=, ),(∞+∞∈-x 函数()h x 为奇函数,函数()h x 单调递增为),(+∞-∞(Ⅱ)据题意知,当[]1,2x ∈时,max 1()()f x f x =,max 2()()g x g x = ∵x e x f =)(在区间[]1,2上单调递增, ∴212max )(,)2()(e x f e f x f ===即, 又∵22()2(1)1g x x x b x b =-++=--++∴函数()y g x =的对称轴为1x =∴函数()y g x =在区间[]1,2上单调递减∴max ()(1)1g x g b ==+,即2()1g x b =+由12()()f x g x =,得21e b =+, ∴12-=e b。
