大学物理第10章静电场中的电介质PPT课件
静电场中的电介质

在国际单位制中,ε的单位为法拉每米(F·m–1)。
3.电介质的击穿
如果外电场足够大,电介质分子就会摆脱分子的束缚成为 自由电子,电介质的绝缘性被破坏而成为导体,这个过程称为 电介质的击穿,这个外电场的场强称为击穿场强。下表所示为 几种电介质的相对电容率和击穿场强。
1.3 电介质中的高斯定理
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电 荷的现象。其中,极化电荷又称束缚电荷,是指在外电场中, 均匀介质内部各处仍成电中性,但在介质表面出现的不能离开 电介质到其他带电体,也不能在电介质内部自由移动的电荷。
1.电介质极化的机理
由于组成电介质的分子结构不同,所以在外电场中极化 的微观机理也有所不同。对于无极分子,在外电场E0的作用 下,正、负电荷的中心被电场力拉开,使得正、负电荷中心 产生相对位移(这种极化称为位移极化),形成电偶极子。
由于受到外电场E0的作用,这些电偶极子的电偶极矩P 的方向将转向与外电场E0的方向一致。这样,在垂直E0方向 的介质两端表面就会出现正负电荷,如下图所示。
无外点场时,无极分子 正负电荷中心重合
外电场作用下,正负电荷 中心分离,形成电偶极子
电介质在垂直于外电场的 两端表面出现极化电荷
对于有极分子,无外电场时,虽然每个分子都有一定的电 偶极矩,但由于分子作无规则的热运动,所以各电偶极子的电 偶极矩的取向是杂乱无章的,对外不呈现出电性,如左图所示 但有外电场E0时,每个分子都受到一个力偶矩的作用。在此力 偶矩的作用下,有极分子的电偶极矩方向将转向与外电场基本 一致的方向,这种极化称为转向极化,其结果是电介质的两端 出现等量异号的电荷,如中图和右图所示。
物理学
静电场中的电介质
电介质-PPT课件

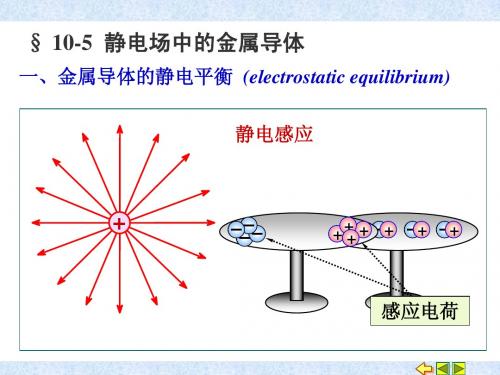
导体的静电感应过程
E0
加外电场---电子在电场力作用下运动
导体的 ' 外场 E 0
导体的静电感应过程
E0
感应 E ' 外场 E 0
导体的静电感应过程
q2
+ q1
q1 + q1
q 1+ q 2
三、静电平衡导体的表面场强
. dS = E s
=
. + S d E 内
0 +
. + S d E 表
E表 S +
. S d E 侧
0
E
1
0
q
i i
1
0
S
σ
E 0
S
有导体时静电场的分析方法
导体放入静电场中:
导体的电荷 重新分布
导体上的电荷分 布影响电场分布
b a
a、b在导体内部:
b
a
U0 E 0
a、b在导体表面:
Ed l 0 即 U 0 E d l
----静电平衡的导体是等势体
静电平衡条件:
用场强来描写: 1、导体内部场强处处为零; 2、表面场强垂直于导体表面。 用电势来描写: 1、导体为一等势体; 2、导体表面是一个等势面。
E0
感应 E ' 外场 E 0
导体的静电感应过程
E0
感应 E ' 外场 E 0
导体的静电感应过程
E0 E ' E E E ' 0 0
第十章静电场中的导体和电介质

第⼗章静电场中的导体和电介质第⼗章静电场中的导体和电介质在上⼀章中,我们讨论了真空中的静电场。
实际上,在静电场中总有导体或电介质存在,⽽且在静电的应⽤中也都要涉及导体和电介质的影响,因此,本章主要讨论静电场中的导体和电介质。
本章所讨论的问题,不仅在理论上有重⼤意义,使我们对静电场的认识更加深⼊,⽽且在应⽤上也有重⼤作⽤。
§10-1 静电场中的导体⼀、静电平衡条件1、导体与电介质的区别:(1)宏观上,它们的电导率数量级相差很⼤(相差10多个数量级,⽽不同导体间电导率数量级最多就相差⼏个数量级)。
(2)微观上导体内部存在⼤量的⾃由电⼦,在外电场下会发⽣定向移动,产⽣宏观上的电流⽽电介质内部的电⼦处于束缚状态,在外场下不会发⽣定向移动(电介质被击穿除外)。
2、导体的静电平衡条件(1)导体内部任何⼀点处的电场强度为零;(2)导体表⾯处的电场强度的⽅向,都与导体表⾯垂直.导体处于静电平衡状态的必要条件:0=i E(当导体处于静电平衡状态时,导体内部不再有⾃由电⼦定向移动,导体内电荷宏观分布不再随时间变化,⾃然其内部电场(指外场与感应电荷产⽣的电场相叠加的总电场)必为0。
⼆、静电平衡时导体上的电荷分布1、导体内部没有净电荷,电荷(包括感应电荷和导体本⾝带的电荷)只分布在导体表⾯。
这个可以由⾼斯定理推得:ii sq E ds ε?=,S 是导体内“紧贴”表⾯的⾼斯⾯,所以0i q =。
2、导体是等势体,导体表⾯是等势⾯。
显然()()0b a b i a V V E dl -=?=?,a,b 为导体内或导体表⾯的任意两点,只需将积分路径取在导体内部即可。
3、导体表⾯以处附近空间的场强为:0E n δε=,δ为邻近场点的导体表⾯⾯元处的电荷密度,?n 为该⾯元的处法向。
简单的证明下:以导体表⾯⾯元为中截⾯作⼀穿过导体的⾼斯柱⾯,柱⾯的处底⾯过场点,下底⾯处于导体内部。
由⾼斯定理可得:12i s s dsE ds E ds δε?+?=,1s ,2s 分别为⾼斯柱⾯的上、下底⾯。
静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
大学物理第10章 电荷和静电场-2
例如 孤立的导体球的电容
Q
Q C V
地球
Q Q 4π 0 R
4π 0 R
6
R
4
RE 6.4 10 m, CE 7 10 F
二 电容器
导体组合,使之不受周 围导体的影响 ——电容器
电容器的电容:
当电容器的两极板分
别带有等值异号电荷Q时 ,电量Q与两极板间相应 的电势差VA-VB的比值。
详细说明如下
二、导体表面的电荷和电场 导体表面电荷的分布与导体本身的形状以及附近 带电体的状况等多种因素有关。
孤立导体的电荷面密度与其表面的曲率有关,曲率越大 电荷面密度越大。 表面突出尖锐部分曲率大, 电荷面密度大;
表面比较平坦部分曲率小, 电荷面密度小; 表面凹进部分曲率为负, 电荷面密度最小。
S
–q'
说明空腔内表面所带总电量与空腔内带电体的电量 相等、符号相反。导体空腔是等势体,腔内场强不 为零,不是等电势区间。
四、导体静电平衡性质的应用
1. 静电屏蔽 (electrostatic shielding)
+q +q +q
-q
-q
利用导体静电平衡的性质,使导体空腔内部空 间不受腔外电荷和电场的影响,或者将导体空腔 接地,使腔外空间免受腔内电荷和电场影响,这 类操作都称为静电屏蔽。无线电技术中有广泛应 用,例如,常把测量仪器或整个实验室用金属壳 或金属网罩起来,使测量免受外部电场的影响。
Cn
VB
等效
VA
C
VB
令 U VA VB
q1 C1U
q2 C2U
•导导体表面外附近的场强 E 0
★ 注意:
E 仅由 S 处电荷产生而与其它电荷无关吗?为什么?
大学物理电磁学ppt课件

i
L Er d
B dS S t
--对导线所围面积积分
28
电磁学复习
自感系数 L I
互感系数 M 12 21
i2
i1
自感磁能
WL
1 2
LI 2
互感磁能 WM = M I1I2
L
L
dI dt
12
M
d i2 dt
普适式(L一定)
长直螺线管: B = nI L = n2V
U
q
40 ( x2
R2 )1 2
8
电磁学复习
第11章 导体和电介质的静电场
11-1 导体的静电平衡 11-2 电容器及其电容 11-3 静电场中的电介质 11-4 有电介质时的高斯定理 11-5 静电场中的能量
9
电磁学复习
知识点:
静电平衡状态下导体上电荷分布、电场强度和电势 电容器的电容及其储能 电介质的极化:求D、E、P 电场能量 典型例题: 例11.1; 例11.3; 例11.5 典型习题: P50 11-1, 6, 8, 10, 14, 17, 19, 20, 21, 22
平行板电容器 C 0S
d
充电介质:
圆柱形电容器 C 20L
ln(R2 R1 )
C rC0
球形电容器电容
C 40
RA RB RB - RA
电容器储能: We
1 CU 2 2
Q2 2C
1 QU 2
12
电磁学复习
3. 电介质极化: 在外场E0中
无极分子 --- 位移极化 有极分子 --- 取向极化
电电负内源源载阻充功功功放率率率电II时I22Rr的功率转充放换电电::充外电电电源路U输I输出入功电率I 源U功II 2率r UI 16
静电场中的电介质

SD dS Q0
选半径为r,长度为L的高斯圆柱 面
r
R2 R1
SD dS l
D2 π rl l D
2πr
E D
ε0εr 2 π ε0εrr
(R1 r R2 )
P
0 E
( r
1) 0 E
r 1 2 πrr
r
R2 R1
(2) E
2π
0
r
r
E1 2 π 0 r R1 (r R1)
q0 有关.
s内
特例: 真空——特别介质
特例: 真空——特别介质
q' 0 , P 0 , D 0E P 0E
回到:
1
E
s
dS
0
(
q0
S内 )
3. 如何求解介质中电场?
本课程只要 求特殊情况
各向同性电介质 q0 ,q' 分布具有某些对称性
(1)各向同性电介质:
P
0E
为常数
D 0E P 0E 0E 0(1 )E
模型 “电子气”
与电场的 相互作用
静电感应
电偶极子
无极分子电介质: 位移极化 有极分子电介质: 转向极化
宏观 效果
静电平衡
导体内 E 导体表面
0, 0 E表面
内部:分子偶极矩矢量
和不为零
pi 0
i
感应电荷 0E 出现束缚电荷(极化电荷)
4.极化现象的描述
1) 从分子偶极矩角度
单位体积内分子偶极矩矢量和——极化强度.
R2的薄导体圆筒组成,其间充
以相对电容率为r的电介质. 设
直导体和圆筒单位长度上的电
荷分别为+和- . 求(1)电介 质中的电场强度、电位移矢量
第章静电场中的导体和电介质PPT课件

q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
EB
1 2 O
2 2 O
3 2 o
4 2 o
0
1
23
4
由电荷守恒:
1S 2 S q1
A
B
3S 4S q2
1
4
q1 q2 2S
2
3
q1 q2 2S
20
1
4
q1 q2 2S
q1
2
3
q1 q2 2S
1
2
上述结果表明:平板相背的两面带电等
R3 R2
R3
RR11
qq1 1
RR33
问题:电势表
达式能直接写
R2 R1
q1
4 or
2
dr
R3
(q q1 )
4 or 2
dr
出来吗?
q1
4 o
1 R1
1 R2
q q1
4 o R3
V1 V2
同理,球壳的电势为:
V2
E dl
R3
R3
(q
4
q1 ) or 2
dr
q q1
2.内屏蔽
+
+
壳外表面上的电荷分布与腔内带电体的位置无关,只 取于导体外表面的形状。
若将空腔接地,则空腔外表面上的感应电荷被大地电荷 中和,腔外电场消失,腔内电荷不会对空腔外产生影响。即 接地空腔对内部电场起到了屏蔽作用,这是静电屏蔽的另外 一种——内屏蔽。
高压设备用金属导体壳接地做保护。 14
五、利用静电平衡条件和性质作定量计算
例1:半径为R和r的球形导体(R>r),用很长的细导线连 接起来,使两球带电Q、q,求两球表面的电荷面密度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cr 1
Pc0E
c称为电介质的电极化率,在各向同性线性电介质中它 是一个纯数。
10-3 有电介质时的高斯定理
一、有电介质时的高斯定理
•设极板上的自由电荷的面密度为0 •电介质表面上极化电荷面密度为′ •高斯面的底面积为S
SE dS10Q0Q
Q0 0S Q S
S
+σ0 -σ'
DE
P
+σ' -σ0
Q=Q01-1r
Q0Q= Q0/r
0rEdSQ0
S
令 D = 0rE E
电位移通量
DdSQ0
S
电位移矢量 只与自由电荷有关
在静电场中,通过任意一个闭合曲面的电位移矢量通量等 于该面所包围的自由电荷的代数和,这就是有介质时的高 斯定理。
二、D 电= 位移0矢rE 量和电场强关于度•电电的位位关移移矢矢系量量是的辅说助明量,电场
三、电极化强度
1 引入
在没有外电场时,电介质未被极化,内部宏观小体积元中各 分子的电偶极矩的矢量和为零;当有外电场时,电介质被极 化,此小体积元中的电偶极矩的矢量和将不为零。外电场越 强,分子的电偶极矩的矢量和越大。
用单位体积中分子的电偶极矩的矢量和来表示电介质的极化 程度
2 电极化强度的定义
3 说明
注意
有介质时求场量的步骤
D E U
解题的一般步骤:
(1)sDdsQ0
求电位移D
(2)D 0rE 求电场强度E
(((53 4)))U P A' B P 0 (A B eE r n d1 l)E 求求极求电化电势电极或荷化电面强势密度差度PU '
例1 一半径为a的导体球, 被围在内半径为b、
+σ0
E0 0/0
E
E0 E′ -σ'
+σ'
E=/0
-σ0
E= E0+ E E=E0E
2 极化电荷与自由电荷的关系
Eσ ε0 0ε σ 0 ε 1 0(σ0σ)E εr 0εσ 0ε 0r
=01-1r
Q=Q01-1r
3
电介质的极化规律
E0 0/0
E=E0/r
P=
=01-1r
P(r1)0E
强度才是基本量;
P(r1)0E
•描述电场性质的物理量是电 场强度和电势;
D= 0E+ P
•在电介质中,环路定理仍然 成立,静电场是保守场。
三、有电介质时的高斯定理的应用
利用电介质的高斯定理可以使计算简化,原因是 只需要考虑自由电荷,一般的步骤为,首先由高斯 定理求出电位移矢量的分布,再由电位移矢量的分 布求出电场强度的分布,这样可以避免求极化电荷 引起的麻烦。
pσΔSl
电极化强度的大小为
P=pσΔS= lσ
ΔV ΔSl
平板电容器中的均匀电介质,其 电极化强度的大小等于极化产生 的极化电荷面密度。
S
l -+ +
r
-+ ++- + P
+-+
+-
+ -+
+- - -+- -+- -+- -+ - +-
' Pn
四、电介质中的电场强度 极化电荷与自由电荷的关系
1 电介质中的电场强度
外半径为c,相对介电系数为 r 的介质同心球
壳内,若导体球带电荷量为Q, 求D(r), E (r)
和导体表面的电势.
解 sDdSq
D4r2 q
0
D
Q
4πr2
0r a ar
Q
a
r
bc
Dε0εrE
0
0ra
Q
4
ε
0
r
2
arb
E Q
UEd
E E0
电介质中的电场强度
r
相对电容率 r 1
电容率 0r
二、电介质的极化
11、电介质的分类
固有电矩:没有外电场 时,分子内部的电荷分 布不对称,表现为具有 电矩。
有极分子:具有固有电矩的分
子,如HCl , H2O 和CO等。在外 电场的作用下,力偶矩的作用
力图使其固
无极分子
无外电场时,分子的正负电荷中心重合;有外电场时,正、负 电荷将被电场力拉开,偏离原来的位置,形成一个电偶极子, 叫作诱导电偶极矩。 极化电荷或束缚电荷:因极化而出现在电介质上的电荷。 自由电荷:可以用传导的方法引走的电荷,例如用摩擦起电 使电介质带上的电荷。
(2)有极分子的极化机理——取向极化 •当没有外电场时,电偶极子的排列是杂乱无章的,因而对 外不显电性。 •当有外电场时,每个电偶极子都将受到一个力矩的作用。 在此力矩的作用下,电介质中的电偶极子将转向外电场的方 向。 •在垂直于电场方向的两个表面上,将产生极化电荷。
与外电场一致的方向上来。
无极分子:没有固有电矩的 分子,如He ,H2 , N2 , O2 和CO2 等。在外电场的作用 下,分子产生与外电场方向 一致的感应电矩(主要是电子 发生位移)。
2 电介质的极化过程
在外电场中,固有电矩的取向或诱导电矩的产生使电介质的 表面(或内部)出现束缚电荷的现象叫做电介质的极化。
第十章
静电场中的电介质
dielectric in electrostatic field
•在静电场中总是存在导体或电介质 •静电场与 静电场中导体或电介质之间有相互作用
主要内容有:
•静电场中的电介质 •电位移 有电介质时的高斯定理 •电容 电容器 •静电场的能量 能量密度
10-1.2.3 静电场中的电介质
在有极分子构成的电介质中,取向极化比位移极化约大一个 数量级;但在高频电场下,只有电子位移极化(电子惯性小)。 在无极分子构成的电介质中,位移极化是唯一的极化机制。
3 电晕现象
在潮湿或阴雨天的日子里,高压输电线附近,常可以见 到有浅蓝色辉光的放电现象,称为电晕现象。 电晕现象可以用水分子的极化和尖端放电来解释。
一、电介质对电场的影响
1 电介质的特点
电中性的分子中,带负电的电子(或负离 子)与带正电的原子核(或正离子)束缚得很 紧,不能自由运动,但其电荷分布会受到外 电场的作用而发生变化。
2 电介质对电场的影响 相对介电常数
U0
Q
+++++++
-------
Q
U
Q
r
+++++++
-------
Q
U
1
r
U0
单位体积中分子的电偶
极矩的矢量和叫作电介
质的电极化强度。
P
p
V
•电极化强度用来表征电介质极化 程度的物理量;
•单位:C.m-2,与电荷面密度的单 位相同;
•若电介质的电极化强度大小和方 向相同,称为均匀极化;否则, 称为非均匀极化。
4 电极化强度和极化电荷面密度的关系
在电介质中取一长为l、面积为 ΔS的柱体,柱体两底面的极化 电荷面密度分别为-σ'和+σ',这 样柱体内所有分子的电偶极矩 的矢量和的大小为
