大学物理II静电场习题
大连理工大学大学物理作业2(静电场二)及答案详解
1．如图所示，把点电荷q +从高斯面外P 移到R 处()OP OR =，O 为S 上一点，则[ ].A 穿过S 的电通量e φ发生改变，O 处E变.B e φ不变，E 变。
.C e φ变，E 不变。
.D e φ不变，E不变。
答案：【B 】[解]闭合面外的电荷对穿过闭合面的电通量无贡献，或者说，闭合面外的电荷产生的电场，穿过闭合面的电通量的代数和为零；移动点电荷，会使电荷重新分布，或者说改变电荷的分布，因此改变了O 点的场强。
2．半径为R 的均匀带电球面上，电荷面密度为σ，在球面上取小面元S ∆，则S ∆上的电荷受到的电场力为[ ]。
.A 0 .B 22Sσε∆ .C2S σε∆ .D2204SRσπε∆答案：【B 】解：应用高斯定理和叠加原理求解。
如图所示。
面元S ∆上的电荷受到的库仑力是其他电荷在面元S ∆处产生的总电场强度1E与面元S ∆上的电荷量S Q ∆=∆σ的乘积：111E S E Q F∆=∆=σ。
面元S ∆处电场强度E是面元S ∆电荷在此产生的电场强度2E 与其他电荷在面元S∆处产生的总电场强度1E 的矢量和，21E E E+=。
首先，由高斯定理求得全部球面分布电荷在面元S ∆处产生的总电场强度 R E ˆ0εσ=其次，面元S ∆上的电荷量S Q ∆=∆σ对于面元S ∆来说，相当于无限大带电平面，因此，面元S ∆上的电荷量S Q ∆=∆σ在面元S ∆处产生的电场强度为R E ˆ202εσ=由叠加原理，其他电荷在面元S ∆处产生的总电场强度为 R E E E ˆ2021εσ=-=面元S ∆上的电荷量S Q ∆=∆σ受到的库仑力为RS R S E S E Q F ˆ2ˆ2020111εσεσσσ∆=∆=∆=∆= 注：本题可以用叠加原理直接进行计算，太麻烦。
3．如图所示，一个带电量为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于[ ]。
.A06q ε .B 012q ε .C24qε .D48q ε答案：【C 】[解] ：如果以A 为中心，再补充上7个相同大小的立方体，则组成一个边长为小立方体边长2倍大立方体，点电荷q 位于大立方体的中心。
2静电场二参考答案
静电场二 参考答案一 . 1.BC 2.D 3.B 4.B 5.D 6.E 7.A 解： 1. 由于0q W U PP =，所以C 正确. 再由电场力做功等于势能增量的负值，B 正确. 2. –q 在空间产生电势，它在A ，B ，C ，D 点产生的电势相等，所以试验电荷0q 在这四点具有相同的电势能U q W 0=， 电场力做功等于势能增量的负值，所以把试验电荷从A 移到B 、C 、D 各点，电场力做功均为0，相等。
3. 电势叠加原理，P 的电势等于q 在P 的电势加上Q 在P 的电势，得B4. 点电荷的电势aQa Q rQ U 0002)2/(44πεπεπε===5. 方法一：可根据场强积分计算⎰⋅=PMP l d E U .方法二：我们知道一点处的电势和电势零点的选取有关，但是两点之间的电势差和电势零点的选取无关. 如果以无穷远处作为电势零点，则aqa q a q U U P M 00084)2(4πεπεπε-=-=-，那么选取P 点为电势零点时（0=P U ），但同样应该aq U U P M 08πε-=-，则得aq U M 08πε-=.6. 场强等于电势的负梯度U E -∇=，分析可得结果.7. 方法一：先计算两带点球面之间的电场强度，再根据场强积分计算电势差 由高斯定理，两带点球面之间一点（距球心为r ）的电场强度为204r q E πε=)11(44020212121Rr qdr r q Edr l d E U U Rr-===⋅=-⎰⎰⎰πεπε 方法二：根据电势叠加原理，先分别计算两球面的电势，再求其差球面1处的电势：R Q r q U 00144πεπε+=球面2处的电势：RQRqU 00244πεπε+=，得21U U -的值二. 1. 106.36-⨯-； 106.36-⨯； 106.36-⨯； 106.36-⨯- 2. 不闭合3. V 0200-.4.垂直（正交）； 电势降落最快5. >6.22028d xR R l q +επ；2204x R q +πε；Rq 04πε；()2/32204x R qx +πε；⎪⎪⎭⎫⎝⎛+-2200114a R Rqq πε解：1. 电场力做功等于势能增量的负值。
大学物理静电场练习题带标准答案
大学物理静电场练习题带答案————————————————————————————————作者：————————————————————————————————日期：大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr)（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
大学物理：静电场练习题
由对称性可知 U p 0
l
l
l
0
12
的均匀电场！
练: 真空中一半径为R的均匀带电球面，总电量为 Q(Q > 0)。今在球面上挖去非常小块的面积
ΔS (连同电荷)， 且假设
不影响原来的电荷分布， 则挖去ΔS后球心处电场
R
O
S
强度的大小E＝ QS /(16 2 0 R 4 )
其方向为 由圆心O点指向S
解：由场强叠加原理，挖去S 后的电场可以看作
和Φ2 ，通过整个球面的电场强度通量为 ΦS ，则
(C) (A) Φ1 Φ2 , ΦS q / 0
S2
q S1 q
O a 2a X
(B)Φ1 Φ2 , ΦS 2q / 0
(C) Φ1 Φ2 , ΦS q / 0
(D) Φ1 Φ2 , ΦS q / 0
解：由高斯定理 ΦS q / 0
(D) 0
解：过P点作如图同轴圆柱形高斯面S，由高斯定理
SE dS 2rlE 0
R1
所以E＝0。
l
2
1 R2O r P
4. 有两个点电荷电量都是 +q， 相距为2a。今以左边的
点电荷所在处为球心，以a为半径作一球形高斯面，
在球面上取两块相等的小面积 S1 和 S2 , 其位置如图 所示。设通过 S1 和 S 2 的电场强度通量分别为 Φ1
2. 上半部带正电，下半部带负电，线密度为
3. 非均匀带电，线密度为 0sin
y
dq
d o
x
R
dE
思路：叠加法
dq dE E
解：1)
dq Rd
dE
dq
4 0 R 2
;沿径向
大学物理2期末复习
(2)假若线圈能以某一条水平边为轴自由摆动,当线圈平衡时,线圈平面与竖直面夹角为多少.
解：1.(1)Pm=IS=Ia2
方向垂直线圈平面.
线圈平面保持竖直,即Pm与B垂直.有
Mm=Pm×B
Mm=PmBsin(/2)=Ia2B
=9.4×10－4mN
(2)平衡即磁力矩与重力矩等值反向
在平面②的上方向左,在平面②的下方向右.
(1)两无限大电流流在平面之间产生的磁感强度方向都向左,故有B=B1+B2=0J
(2)两无限大电流流在平面之外产生的磁感强度方向相反,故有B=B1B2=0
练习九安培力
三、计算题
1.一边长a=10cm的正方形铜导线线圈(铜导线横截面积S=2.00mm2,铜的密度=8.90g/cm3),放在均匀外磁场中.B竖直向上,且B=9.40103T,线圈中电流为I=10A .线圈在重力场中求:
解：1.取窄条面元dS=bdr,
面元上磁场的大小为
B=0I/(2r),面元法线与磁场方向相反.有
1=
2=
1/2=1
2.半径为R的薄圆盘均匀带电，总电量为Q.令此盘绕通过盘心且垂直盘面的轴线作匀速转动，角速度为，求轴线上距盘心x处的磁感强度的大小和旋转圆盘的磁矩.
解;2.在圆盘上取细圆环电荷元dQ=2rdr,
解得1=4=(Q1+Q2)/(2S)=2.66108C/m2
2=3=(Q1Q2)/(2S)=0.89108C/m2
两板间的场强E=2/0=(Q1Q2)/(20S)
V=UA－UB
=Ed=(Q1Q2)d/(20S)=1000V
四、证明题
1.如图6.7所示，置于静电场中的一个导体，在静电平衡后，导体表面出现正、负感应电荷.试用静电场的环路定理证明，图中从导体上的正感应电荷出发，终止于同一导体上的负感应电荷的电场线不能存在.
大学物理II第10章静电场 作业题
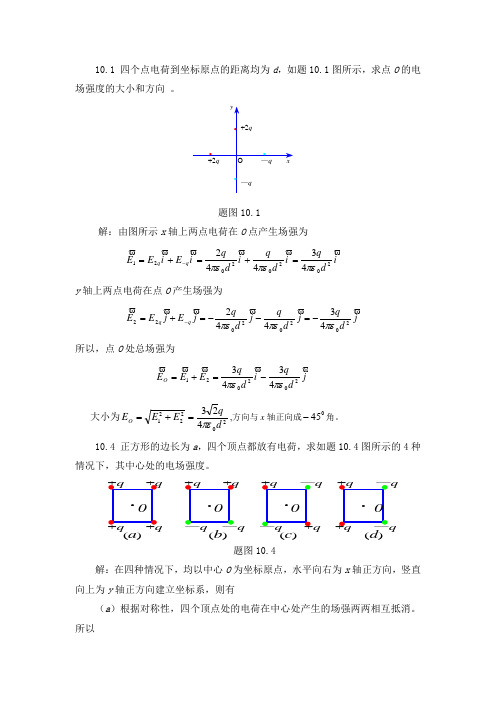
10.1 四个点电荷到坐标原点的距离均为d ，如题10.1图所示，求点O 的电场强度的大小和方向 。
题图10.1解：由图所示x 轴上两点电荷在O 点产生场强为i d q i d q i d q i E i E E q q2020*********πεπεπε=+=+=-y 轴上两点电荷在点O 产生场强为j dq j d q j d q j E j E E q q2020*********πεπεπε-=--=+=- 所以，点O 处总场强为j dq i d q E E E O2020214343πεπε-=+= 大小为202221423dq E E E O πε=+=,方向与x 轴正向成045-角。
10.4 正方形的边长为a ，四个顶点都放有电荷，求如题10.4图所示的4种情况下，其中心处的电场强度。
q qq q (a ) (b ) (c ) (d )题图10.4解：在四种情况下，均以中心O 为坐标原点，水平向右为x 轴正方向，竖直向上为y 轴正方向建立坐标系，则有（a ）根据对称性，四个顶点处的电荷在中心处产生的场强两两相互抵消。
所以0=a E(b ) 根据对称性，电荷在中心处产生的场强在x 轴上抵消，只有y 轴上的分量，所以[]j aq j a a q j E E qy b20220245cos )2/()2/(444πεπε-=+-=-= (c ) 根据对称性，对角线上的电荷在中心处的场强可以相互抵消，所以0=c E(d ) 根据对称性，电荷在中心处产生的场强在y 轴上抵消，只有x 轴上的分量，所以[]i aq i a a q i E E qx d20220245sin )2/()2/(444πεπε=+== 10.5 一半径为R 的半圆细环上均匀地分布电荷+Q ，求环心处的电场强度。
题图10.5解：以环心O 为原心，取如图所示的坐标轴。
在环上取一线元dl ，其所带电量为RQdldq π=，它在环心O 处的电场强度E d 在y 轴上的分量为θππεsin 14120R R Qdl dE y =由于环对y 轴对称，电场强度在x 轴上的分量为零。
大学物理静电场(二)
λdl v0 ∫ 4πε0r2 r L
v dq v0 则 E= ∫ 4π ε0r2 r =
σdS v0 ∫ 4πε0r2 r S
ρdV v0 ∫ 4πε0r2 r V
** 式中 L, S, V, 是 产生电场的源电荷 占据的空间， 占据的空间，由此 来确定上述积分的 变量及上、下限。 变量及上、下限。
dx
dq = dl ⋅ dx ⋅σ
dq ∴ 带电线的线密度 λ = = σ ⋅ dx dl
6
(1).设P点与带电平面（宽度为 ,无限长）在同一平面内 设 点与带电平面 宽度为d,无限长） 点与带电平面（ 设每个细长带电线的线密度为λ
σ
λ dE = 2πε0r
λ =σ ⋅ dx
P o x d dx a
S
∴Φe总 = 0
v v 即 Φe = ∫∫ E ⋅ dS = 0
S
对任何形状的闭合面都成立（面内无电荷） 对任何形状的闭合面都成立（面内无电荷）
19
的圆柱面， 例：匀强电场中有一半径为R的圆柱面，其轴线与电场平 匀强电场中有一半径为 的圆柱面 行，求通过此闭合面的电通量 v v S3 v E S2 v
电通量是标量，有正、 电通量是标量，有正、负
v E v dS
v E
v E
v dS
v dS
0 ≤θ <
π
2
, Φe > 0
π θ = , Φe = 0
2
π
2
< θ ≤ π , Φe < 0
2. 非均匀场中
v n
dS
v v ∴dΦe = E ⋅ dS cosθ = E ⋅ dS
每个小面元视为处在匀强场中
−σ
大学物理学第五版马文蔚高等教育出版社静电场2
(5-13) (5-14)
S
规定： 闭合曲面上任一点的外法线为正向！
{
E 线穿出： </2, d E >0 E 线穿入： >/2, d E < 0
通过闭合曲面的电 场线数目与该曲面 内的电荷间的关系
三．高斯定理
q3
+ -
+ -q
2
q1
S
1. 定理的表述 q4 在任意的静电场中,通过任一闭合曲面的 E 通量,等于该曲面内电荷量的代数和除以0 。 1 E E d S qi (5-16) S
1
2
无限长均匀 带电圆柱
E E r O
+ + + S下 + + +
E
r 2 20 R
E
1 r
R
r
E
r 2 20 R
无限长均匀 带电圆柱面
E
E
E=0 O
1 r
无限长均匀带电圆柱面内 ？ E =0
R
r
用高斯定理求E的要点：
由电荷分布的对称性→电场分布的对称性！ 1．分析电场的对称性。 由此判断出：① 各点 E 的方向 ② 那些点 E 的大小相等。 点电荷，均匀带电球面(体)、球层(套叠)； a.球对称：
o
dE
x
(3) 分解变量
(4) 统一变量
dl d Ex dE sin sin 2 40 R dl d E y dE cos cos 2 40 R d l Rd
参与题：一均 匀带电圆弧， 电荷线密度为 ，圆弧圆心 角为0，求Eo=?
0
方向：沿y轴正向。
湖南大学物理(2)第13章课后习题参考答案
第13章 静电场中的导体和电解质一、选择题1(D)，2(A)，3(C)，4(C)，5(C)，6(B)，7(C)，8(B)，9(C)，10(B)二、填空题(1). 4.55×105 C ；(2). σ (x ，y ，z )/ε0，与导体表面垂直朝外(σ > 0) 或 与导体表面垂直朝里(σ < 0). (3). εr ，1， εr ； (4). 1/εr ，1/εr ；(5). σ ，σ / ( ε 0ε r )； (6).Rq 04επ ；(7). P ，－P ，0； (8) (1- εr )σ / εr ； (9). 452； (10). εr ，εr三、计算题1.如图所示，一内半径为a 、外半径为b 的金属球壳，带有电荷Q ，在球壳空腔内距离球心r 处有一点电荷q ．设无限远处为电势零点，试求： (1) 球壳内外表面上的电荷． (2) 球心O 点处，由球壳内表面上电荷产生的电势． (3) 球心O 点处的总电势．解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q ，外表面上带电荷q +Q ． (2) 不论球壳内表面上的感生电荷是如何分布的，因为任一电荷元离O 点的 距离都是a ，所以由这些电荷在O 点产生的电势为 adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点 产生的电势的代数和 q Q q q O U U U U +-++= r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+2. 一圆柱形电容器，外柱的直径为4 cm ，内柱的直径可以适当选择，若其间充满各向同性的均匀电介质，该介质的击穿电场强度的大小为E 0= 200 KV/cm ．试求该电容器可能承受的最高电压． (自然对数的底e = 2.7183)解：设圆柱形电容器单位长度上带有电荷为λ，则电容器两极板之间的场强分布 为 )2/(r E ελπ= 设电容器内外两极板半径分别为r 0，R ，则极板间电压为⎰⎰⋅π==R rRr r r r E U d 2d ελ 0ln 2r Rελπ=电介质中场强最大处在内柱面上，当这里场强达到E 0时电容器击穿，这时应有002E r ελπ=，000ln r R E r U = 适当选择r 0的值，可使U 有极大值，即令0)/ln(/d d 0000=-=E r R E r U ，得 e R r /0=，显然有22d d r U < 0，故当 e R r /0= 时电容器可承受最高的电压 e RE U /0max = = 147 kV.3. 如图所示，一圆柱形电容器，内筒半径为R 1，外筒半径为R 2 (R 2＜2 R 1)，其间充有相对介电常量分别为εr 1和εr 2＝εr 1 / 2的两层各向同性均匀电介质，其界面半径为R ．若两种介质的击穿电场强度相同，问：(1) 当电压升高时，哪层介质先击穿？(2) 该电容器能承受多高的电压？解：(1) 设内、外筒单位长度带电荷为＋λ和－λ．两筒间电位移的大小为 D ＝λ / (2πr ) 在两层介质中的场强大小分别为E 1 = λ / (2πε0 εr 1r )， E 2 = λ / (2πε0 εr 2r ) 在两层介质中的场强最大处是各层介质的内表面处，即E 1M = λ / (2πε0 εr 1R 1)， E 2M = λ / (2πε0 εr 2R ) 可得 E 1M / E 2M = εr 2R / (εr 1R 1) = R / (2R 1)已知 R 1＜2 R 1， 可见 E 1M ＜E 2M ，因此外层介质先击穿． (2) 当内筒上电量达到λM ，使E 2M ＝E M 时，即被击穿，λM = 2πε0 εr 2RE M 此时．两筒间电压(即最高电压)为：r r r r U R R r M RR r M d 2d 221201012⎰⎰+=επελεπελ⎪⎪⎭⎫ ⎝⎛+=R R R R RE r r M r 22112ln 1ln 1εεε4. 一空气平行板电容器，两极板面积均为S ，板间距离为d (d 远小于极板线度)，在两极板间平行地插入一面积也是S 、厚度为t (<d )的金属片，如图所示. 试求：(1) 电容C 于多少？ (2) 金属片放在两极板间的位置对电容值有无影响？解：设极板上分别带电荷+q 和-q ；金属片与A 板距离为d 1，与B 板距离为d 2；金属片与A 板间场强为 )/(01S q E ε=金属板与B 板间场强为 )/(02S q E ε= 金属片内部场强为 0='E 则两极板间的电势差为2211d E d E U U B A +=- )(210d d S q+=ε)(0t d Sq -=ε 由此得 )/()/(0t d S U U q C B A -=-=ε因C 值仅与d 、t 有关，与d 1、d 2无关，故金属片的安放位置对电容值无影响．O R 1R 2Rεr 2εr 1t S S S d Ad 1t d 2d5. 如图所示，一电容器由两个同轴圆筒组成，内筒半径为a ，外筒半径为b ，筒长都是L ，中间充满相对介电常量为εr 的各向同性均匀电介质．内、外筒分别带有等量异号电荷+Q和-Q ．设 (b - a ) << a ，L >> b ，可以忽略边缘效应，求：(1) 圆柱形电容器的电容；(2) 电容器贮存的能量．解：由题给条件 (a a b <<-)和b L >>，忽略边缘效应, 应用高斯定理可求出两 筒之间的场强为： )2/(0Lr Q E r εεπ= 两筒间的电势差 =π=⎰r drL QU bar εε02a b L Q r ln 20εεπ 电容器的电容 )]//[ln()2(/0a b L U Q C r εεπ== 电容器贮存的能量 221CU W =)/ln()]4/([02a b L Q r εεπ=6. 如图所示，一平板电容器，极板面积为S ，两极板之间距离为d ，其间填有两层厚度相同的各向同性均匀电介质，其介电常量分别为ε1和ε2．当电容器带电荷±Q 时，在维持电荷不变下，将其中介电常量为ε1的介质板抽出，试求外力所作的功．解：可将上下两部分看作两个单独的电容器串联，两电容分别为d S C 112ε=，d SC 222ε= 串联后的等效电容为 ()21212εεεε+=d SC带电荷±Q 时，电容器的电场能量为 ()S d Q C Q W 21212242εεεε+== 将ε1的介质板抽去后，电容器的能量为 ()S d Q W 202024εεεε+='外力作功等于电势能增加，即 ⎪⎪⎭⎫⎝⎛-=-'=∆=102114εεS d Q W W W A7. 如图所示，将两极板间距离为d 的平行板电容器垂直地插入到密度为ρ、相对介电常量为εr 的液体电介质中．如维持两极板之间的电势差U 不变，试求液体上升的高度h ．解：设极板宽度为L ，液体未上升时的电容为 C 0 = ε0HL / d 液体上升到h 高度时的电容为()d hL dL h H C rεεε00+-=()011C H h r ⎥⎦⎤⎢⎣⎡-+=ε 在U 不变下，液体上升后极板上增加的电荷为()d hLU U C CU Q r /100-=-=∆εε电源作功 ()d hLU QU A r /120-==∆εε液体上升后增加的电能20212121U C CU W -=∆()d hLU r /12120-=εε 液体上升后增加的重力势能 2221gdh L W ρ=∆因 A = ∆W 1+∆W 2，可解出 ()2201gdU h r ρεε-=思考题1. 无限大均匀带电平面（面电荷密度为σ）两侧场强为)2/(0εσ=E ，而在静电平衡状态下，导体表面（该处表面面电荷密度为σ）附近场强为0/εσ=E ，为什么前者比后者小一半？参考解答：关键是题目中两个式中的σ不是一回事。
大物考题完整版
2. 把一块两表面电荷密度之和为 0 的无限大导体平板置于均匀电场 中， 与
板面垂直，如图 25-2 所示，则导体左侧面电荷面密度 1=
，右
侧表面外附近的场强 E1=
。
解：设 、 均为正电荷根据电荷守恒得出
静电平衡的时候 得出
左
侧
表
面
外
附
近
的
场
强
4
3. [ 2 ]一金属球壳的内外半径分别为 R1 和 R2,其中心放一点电荷 q，则金属球
C 'C3 C ' C3
1515 15 15
7.5 f
， C ' 与 C3 串联
电容大小相等，所以 C ' 上分到一
般的电压
50V， C1
的储存的电能为We
1 2
C1V
2
1 2
(10106 ) 502
0.0125J
3、[ 3 ] 真空中 A、B 两平行板相距为 d，面积均为 S，分别均匀带电 q 和 q ，不计
D 4 r2 Q
D
Q 4 r2
E
D
Q 40r r 2
R
2
R
(2)U R2 Edr R2 Q dr Q ( 1 1 )
R1
R1 40 r r 2
40r R1 R2
1
(3)C Q 40r R1R2
U
R2 R1
(4)We Q2 Q2 (R2 R1) 2C 80r R1R2
磁场（一） 1、两个载有相等电流 I 的圆线圈，半径均为 R，
（1）导体球壳外附近的场强仍与其表面垂直； （2）导体球壳面上的电荷仍为均匀分布； （3）导体球壳的电势仍保持不变； （4）由于静电屏蔽，球壳外的带电体在球壳内产生的场强处处为零。
《大学物理》习题册题目及答案第10单元静电场(二)
第10单元 静电场（二）第七章 静电场和恒定磁场的性质(二)电势序号 学号 姓名 专业、班级一 选择题[ D ]1．关于静电场中某点电势值的正负，下列说法中正确的是： （A ）电势值的正负取决于置于该点的试验电荷的正负 （B ）电势值的正负取决于电场力对试验电荷作功的正负 （C ）电势值的正负取决于产生电场的电荷的正负 （D ）电势值的正负取决于电势零点的选取[ B ]2. 在边长为a 的正方体中心处放置一电量为Q 的点电荷，设无穷远处为电势零点，则 在一个侧面的中心处的电势为： (A)a Q 04πε (B)a Q 02πε(C)aQ0πε (D)aQ022πε[ C ]3. 静电场中某点电势的数值等于 (A)试验电荷0q 置于该点时具有的电势能。
(B)单位试验电荷置于该点时具有的电势能。
(C)单位正电荷置于该点时具有的电势能。
(D)把单位正电荷从该点移到电势零点外力所作的功。
[ C ]4. 关于电场强度与电势之间的关系，下列说法中，哪一种是正确的 (A)在电场中，场强为零的点，电势必为零。
(B)在电场中，电势为零的点，电场强度必为零。
(C)在电势不变的空间，场强处处为零。
(D)在场强不变的空间，电势处处为零。
[ B ]5．真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示，设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处的电势为 ：（A ）r q 04πε （B ）)(410RQ r q +πε（C ）rQ q 04πε+ （D ）)(410R q Q r q -+πε[ C ]6．在带电量为-Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移到b 点， a 、b 两点距离点电荷A 的距离分别为r 1 和r 2 ，如图所示，则移动过程中电场力做的功为 （A ）)11(4210r r Q --πε （B ）)11(4210r r qQ -πε（C ）)11(4210r r qQ --πε （D ）)(4120r r qQ--πε二 填空题1.静电场中某点的电势，其数值等于_____单位正电荷置于该点的电势能_b)(-Q 2r 1r PROqrQ或__单位正电荷从该点移到电势零点处电场力作的功。
大学物理(第二版)上册课后习题详解第四章-静电场
11
C m-2。求此系统的电场分
布。 解 如题 4.10 图所示， 三个区域的场强由两平行无限大均匀带 电面产生的场强的叠加，其电场强度分别为
E2
E2
4.10 解图
E2
E1
1 ， E2 2 2 0 2 0
设水平向右的方向为场强的正方向，则 左边区域：
EⅠ E1 E2
题 4.8 图
29
电荷为 Q2。求电场分布规律。 解 因电荷呈球对称分布，电场强度也为球对称分布，取半径为 r 的同心球面为高斯面， 由高斯定理得
2 E dS 4r E
q
0
当 r R1 时，该高斯面内无电荷，
q 0 ，故
Q1 (r 3 R13 ) ，故 3 R2 R13
4.2 一根不导电的细塑料杆，被弯成近乎完整的圆，圆的半径为 0.5m，杆的两端有 2cm 的缝隙， 3.12 10 C 的正电荷均匀地分布在杆上，求圆心处电场的大小和方向。 解 运用叠加原理,可以把带电体看成是一个带正电的整圆环和一段长为 2cm 带负电的 圆弧产生的电场的叠加,而圆环在中心产生的电场为零。所以电场就等于长为 2cm 的带负电 的圆弧产生的电场。由于圆弧长度远小于半径,故可看成是一点电荷,所以
q0 必须在两电荷之间才能平衡，设与 2q 之间的距离为 x ，若合力为零，则有
2qq0 qq0 1 2 4 0 x 4 0 (l x) 2 1
由此可得 x 2 4lx 2l 2 0 ，解此方程可得
x (2 2)l 。只能取负号，所以
x (2 2)l ，为稳定平衡状态。
q ， 2l
x
dx
2l
4.11 解图
《大学物理》静电场练习题及答案
《大学物理》静电场练习题及答案一、简答题1、为什么在无电荷的空间里电场线不能相交?答案：由实验和理论知道，静电场中任一给定点上，场强是唯一确定的，即其大小和方向都是确定的．用电场线形象描述静电场的空间分布时，电场线上任一点的切线方向表示该点的场强方向．如果在无电荷的空间里某一点上有几条电场线相交的话，则过此交点对应于每一条电场线都可作出一条切线，这意味着交点处的场强有好几个方向，这与静电场中任一给定点场强具有唯一确定方向相矛盾，故无电荷的空间里电场线不能相交．2、简述静电场中高斯定理的文字内容和数学表达式。
答案：在真空中的静电场内，通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S SqS d E3、写出静电场的环路定理，并分别说明其物理意义。
答案：静电场中，电场强度的环流总是等于零(或0l=⋅⎰l d E)，静电场是保守场。
4、感生电场与静电场有哪些区别和联系?5、在电场中某一点的电场强度定义为0q F E=.若该点没有试验电荷，那么该点的电场强度又如何? 为什么?答案： 电场中某一点的电场强度是由该电场自身性质所决定，与这一点有无试验电荷没有任何关系。
6、在点电荷的电场强度公式中，如果0→r ，则电场强度E 将趋于无限大。
对此，你有什么看法? 答案： 这表明，点电荷只是我们抽象出来的一个物理模型，当带电体较小而作用距离较大时使用点电荷模型较为方便、精确。
但当作用距离r 很小时，点电荷模型的误差会变大，这时我们不能再用点电荷的电场强度公式而要采用更精确的模型。
二、选择题1、如图所示，两个同心均匀带电球面，内球面半径为1R 、带有电荷1Q ，外球面半径为2R 、带有电荷2Q ，则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A 、20214r Q Q επ+B 、()()2202210144R r Q R r Q -π+-πεε C 、()2120214R R Q Q -+επ D 、2024r Q επ2、A 和B 为两个均匀带电球体，A 带电荷q +，B 带电荷q -，作一与A 同心的球面S 为高斯面，如图所示。
大学物理静电场练习题带答案
大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
6、在一点电荷产生的静电场中，一块电介质如图放置，以点电荷所在处为球心作一球形闭合面，则对此球形闭合面： （A ）高斯定理成立，且可用它求出闭合面上各点的场强；（B ）高斯定理成立，但不能用它求出闭合面上各点的场强； （C ）由于电介质不对称分布，高斯定理不成立； （D ）即使电介质对称分布，高斯定理也不成立。
大学物理题库-第5章 静电场习题(含答案解析)
真空中的静电场一 选择题1．两个等量的正电荷相距为2a ，P 点在它们的中垂线上，r 为P 到垂足的距离。
当P 点电场强度大小具有最大值时，r 的大小是：[ ]（A ）42a r =（B ）32a r = （C ）22ar = （D ）a r 2= 2．如图5-1所示，两个点电荷的电量都是q +，相距为a 2，以左边点电荷所在处为球心，以a 为半径作一球形高斯面，在球面上取两块相等的小面积1S 和2S ，设通过1S 和2S 的电通量分别为1Φ和2Φ，通过整个球面的电通量为Φ，则[ ]（A ）021εq=ΦΦ>Φ,（B ）0212,εq=ΦΦ<Φ（C ）021εq=ΦΦ=Φ,（D ）021εq=ΦΦ<Φ,3．在静电场中，高斯定理告诉我们 [ ]（A ）高斯面内不包围电荷，则高斯面上各点E的量值处处相等；（B ）高斯面上各点E只与面内电荷有关，与面外电荷无关；（C ）穿过高斯面的E（D ）穿过高斯面的E 通量为零，则高斯面上各点的E必为零； 4．如图5-2所示，两个“无限长”的同轴圆柱面，半径分别为1R 和2R ，其上均匀带电，沿轴线方向单位长度上的带电量分别为1λ和2λ，则在两圆柱面之间、距轴线为r 的P 点处的场强大小为：[ ]（A ）r 012πελ （B ）r 0212πελλ+ （C ）()r R -2022πελ （D ）()1012R r -πελ5．电荷面密度为+σ和-σ的两块“无限大”均匀带电平行平板，放在与平面垂直的x2-5 图1 - 5 图轴上a +和a -位置，如图5-3所示。
设坐标圆点o 处电势为零，则在a x a +<<-区域的电势分布曲线为： （ ）6．真空中两个平行带电平板A 、B ，面积均为S ，相距为)(S d d <<2，分别带电量q +和q -，则两板间相互作用力的大小为：[ ]（A ）204d q πε （B ）Sq 0ε （C ）Sq 022ε （D ）不能确定7．静电场中，下列说法哪一个是正确的？[ ]（A ）正电荷的电势一定是正值； （B ）等势面上各点的场强一定相等；（C ）场强为零处，电势也一定为零； （D ）场强相等处，电势梯度矢量一定相等。
大学物理电磁学第二章静电场
第二章 有导体时的静电场 练习一、选择题1、［ ］当一个带电导体达到静电平衡时： (A) 表面上电荷密度较大处电势较高． (B) 表面曲率较大处电势较高． (C) 导体内部的电势比导体表面的电势高．(D) 导体内任一点与其表面上任一点的电势差等于零．2、［ ］在一个孤立的导体球壳内，若在偏离球中心处放一个点电荷，则在球壳内、外表面将出现感应电荷，其分布将是：(A) 内表面均匀，外表面也均匀． (B) 内表面不均匀，外表面均匀． (C) 内表面均匀，外表面不均匀． (D) 内表面不均匀，外表面也不均匀． 3、［ ］在一不带电荷的导体球壳的球心处放一点电荷，并测量球壳内外的场强分布．如果将此点电荷从球心移到球壳内其它位置，重新测量球壳内外的场强分布，则将发现： (A) 球壳内、外场强分布均无变化． (B) 球壳内场强分布改变，球壳外不变． (C) 球壳外场强分布改变，球壳内不变． (D) 球壳内、外场强分布均改变．4、［ ］半径为R 的金属球与地连接。
在与球心O 相距d =2R 处有一电荷为q 的点电荷。
如图所示，设地的电势为零，则球上的感生电荷q '为(A) 0. (B)2q . (C) 2q-. (D)q.5、［ ］选无穷远处为电势零点，半径为R 的导体球带电后，其电势为0U ，则球外离球心距离为r 处的电场强度的大小为(A) 203R U r ． (B) 0U R ． (C) 02RU r． (D) 0U r ． 6、［ ］如图所示，一厚度为d 的“无限大”均匀带电导体板，电荷面密度为σ，则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为：(A) 0．(B)2σε．(C)hσε．(D)2hσε．7、［］两个同心薄金属球壳，半径分别为1R和2R(21()R R>，若分别带上电荷1q和2q，则两者的电势分别为1V和2V(选无穷远处为电势零点)．现用导线将两球壳相连接，则它们的电势为:(A)1V. (B)2V. (C)12V V+. (D)121()2V V+.8、［］如图所示，一带负电荷的金属球，外面同心地罩一不带电的金属球壳，则在球壳中一点P处的场强大小与电势(设无穷远处为电势零点)分别为：(A) 0,0E V=>. (B) 0,0E V=<. (C) 0,0E V==；(D) 0,0E V><.9、［］一空气平行板电容器，两极板间距为d，充电后板间电压为U。
大学物理静电场作业(二)习题与解答
1、如图所示, 把单位正电荷从一对等量异号电荷的连线中点, 沿任意路径移到无穷远处时,电场力作功为__0__。
2、在点电荷Q 旁作一高斯面S ，包围Q ，在S 面外再引入另一点电荷q ，则通过S 面的电通量有无变化？__不变化____。
S 面上各处的电场强度有无变化？____有变化_____。
3、电场力作功从该点移动到无穷远处则把试验电荷试验电荷势为以知静电场中某点的电C,103.0100v,-80⨯=-q-3.0×10-6J4、如图所示的电场分布，则A 点的电势比B 点的电势____高__（填高、低、相等）5、两个同心的球面半径分别为R 1和R 2(R 1 < R 2)，带电量分别为q 1和q 2 , 则在小球面内 距球心为 r 1处一点的电势为______________，在两球面之间距球心为 r 2处一点的电势为_______________。
20212201202121014)11(44)11(4R qq R r q R q q R R q πεπεπεπε++-++-6、已知一带电细杆，杆长为l ，其线电荷密度为λ = cx ，其中c 为常数。
试求距杆右端距离为a 的P 点电势。
O+q qA B。
。
Eϖ考虑杆上坐标为x 的一小块d x d x 在P 点产生的电势为x a l xdxc x a l dx dU -+=-+=00441πελπε 求上式的积分,得P 点上的电势为])ln()[(44000l a a l a l c x a l xdx c U l -++=-+=⎰πεπε7、求均匀带电圆环轴线上任一点P 处的电场强度（圆环半径为R ，带电量为Q ）22022223/222001d d d 4 d 01d 44()x x qq E R xE QxE E E R x R x R x πεπεπε⊥=+=∴====+++⎰⎰⎰在圆环上任取电荷元，则，由对称性知，8、在半径为R 1、电荷体密度为ρ的均匀带电球体中挖去一半径为R 2, 的球形空腔, 空腔的中心为O ’ , 球心与空腔的中心的距离OO ’为a , 求空腔内任一点的电场强度E 。
大学物理II练习册答案
大学物理练习八一、选择题：1．有两个点电荷电量都是+q ，相距为2 a 。
今以左边的点电荷所在处为球心，以a 为半径作一球形高斯面。
在球面上取两块相等的小面积S 1和S 2，其位置如图所示。
设通过S 1和S 2的电场强度通量分别为1Φ和2Φ，通过整个球面的电场强度通量为s Φ，则[D ](A)s ΦΦ>Φ,21=0/εq (B)021/2,εq s =ΦΦ<Φ(C)021/,εq s =ΦΦ=Φ(D)021/,εq s =ΦΦ<Φ解∶通过S 1的电场强度通量分别为1Φ,有穿进又有穿出;但通过S 2的电场强度通量分别为2Φ,只有穿出.故,21Φ<Φ据高斯定理通过整个球面的电场强度通量为s Φ只与面内电荷有关。
2．图示为一具有球对称性分布的静电场的E~r 关系曲线。
请指出该静电场是由下列哪种带电体产生的？[](A) 半径为R 的均匀带电球面。
(B) 半径为R 的均匀带电球体。
(C) 半径为R 、电荷体密度Ar =ρ(A 为常数)的非均匀带电球体。
(D) 半径为R 、电荷体密度r A /=ρ(A 为常数)的非均匀带电球体。
解∶（D ）3.关于高斯定理的理解有下面几种说法，其中正确的是：[D ] (A)如果高斯面上E ϖ处处为零，则该面内必无电荷． (B)如果高斯面内无电荷，则高斯面上E ϖ处处为零．(面外有电荷) (C)如果高斯面上E ϖ处处不为零，则高斯面内必有电荷．(D)如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零．4．在磁感应强度为B ϖ的均匀磁场中作一半径为r 的半球面S ，S 边线所在平面的法线方向单位矢量n ϖ与B ϖ的夹角为α，则通过半球面S 的磁通量为[D ](A).2B r π(B)2.2B r π(C)απsin 2B r -.(D)απcos 2B r -.0=∑i q5．如图示，直线MN 长为2 L ，弧OCD 是以点N 为中心，L 为半径的半圆弧，N 点有正电荷+q ，M 点有负电荷-q 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
孤立导体的电容 孤立导体球的电容
C? Q U
C ? 4?? 0R
平行板电容器 同心球形电容器 同轴柱形电容器
C ? ?0?r S
d
C ? 4?? 0?r R1R2 /(R2 ? R1 )
C ? 2??0?r L
ln R2 / R1
17
3.静电场中的电介质
电介质对电场的影响
电位移矢量
D ? ?0E ? P
P
还有电荷守恒定律，它时刻都起作用。
2. 求静电场的方法：
(1)求 E
场强叠加法 高斯定理法 电势梯度法
?
? E
?d
? s
?
q内
?S?
?0
E ? ? grad V
补偿法
8
??场强积分法：Up ?
?
?( P0 ) r
E
(P )
·d
r l
(2)求U ????
（E分段，积分也要分段）
??
??叠加法：U ? ? Ui（零点要同）；
???U ? ???U
? ?
1
4?? 0
1
4?? 0
Q R Q r
(r ? R) (r ? R)
? ??
E
?
?
1
4?? 0
Qr R3
? ??
E
?
1
4?? 0
Q r2
(r ? R) (r ? R)
无限长均匀带电直线： E ? 1 ?
2?? 0 r
14
均匀带电半径为 R的细 圆环轴线上一点：
E? 1
Qx
4?? 0 (x2 ? R2 )3/ 2
U
?
1
4?? 0
( x2
Q ? R2 ): (距电偶极子中心 x)
E? ? 2?0
v E
?
1
4?? 0
v 2p x3
电偶极子中垂线上一点 : (距电偶极子中心距离 y)
v E?
?
1
4?? 0
pv y3
15
i
V ? ?q 4?d?q0r （ U? ? 0）。
9
（3）电势、电势差的计算
1).方法一：场强积分法 (由定义) 步骤： (1) 先算场强 (2)选择合适的路径 L (3)分段积分 (计算)
2).方法二：电势叠加法 步骤：(1)把带电体 ? 分为无限多电荷元 dq (2)由dq ? dU
(3)由dU ? U = ?dU
E? ? 2?0
无限长柱面？
3.电势差： 电场中a、b两点的电势差，在数值上
等于单位正电荷从 a点移到b点时，电
场力做的功。
bv v
? U ab ? U a ? Ub ?
E ?dl
a
4.电势能： 电荷q在电场中某点的电势能，在数 值上等于把电荷 q从该点移到电势零 点时，电场力所做的功。
(0) v v
4?? 0 i?1 ri
? 连续分布电荷的电势： U ? 1 dq
4?? 0 r
电场强度与电势的关系 E ? ?? U
4
注重典型场 注重叠加原理
? E
?
Q
4π?0r 2
r?
U? Q
4 π?0 r
r <R E?0
U
?
Q
4 π? 0 R
r
>R
? E?
Q
4π?0r 2
r?
U? Q
4π?0r
E
?
? 2π?0r
相等。通常在球对称电场中取薄球壳为体积元 dV=4πr2dr；在轴对
称的电场中取薄圆柱壳为体积元 dV=2πrldr。
??? （c）按照电场能公式：We ? V wedV
正确定出积分上下限，计算出结果。
20
1.如图，在一电荷体密度为? 的均匀带电球体中，挖出一个以
O′为球心的球?状小空腔，空腔的球心相对带电球体中心O的
大学物理
——静电学部分
2015.5.18
1
基本概念
1.电场强度： 电场中某点电场强度在数值上等于单
位正电荷在该点受力
vv E ? F /q
点电荷的场强： 电荷组的场强：
v E
?
q
4??0r 2
r er
? v
E?
1
4?? 0
n i?1
qi ri 2
r eri
? 连续分布电荷的场强：
v E
?
1
4?? 0
D的高斯定理
??D ?dS ? ? q0
S
在电场具有某种对称性的情况下 ,可以首先由高斯定 理求解出电位移矢量 D:
思路
???
D ? E ? P ? ? ?? q?
18
4. 能量：
电容器的储能：
We
?
1 2
Q2 C
?
1 C?U2 2
?
1 Q? U 2
静电场的能量密度
we
?
1?E2
2
? 1 DE ? 1 D ?E
3. 几种典型电荷分布的 E 和 V
点电荷（？） 均匀带电球面（？） 均匀带电球体（？） 均匀带电无限长直线（？） 均匀带电无限大平面（？） 均匀带电细圆环轴线上一点（？） 无限长均匀带电圆柱面（？）
11
均匀带电球面：
?0
?
? ??
E
?
1
4?? 0
Q r2
(r ? R) (r ? R)
均匀带电球体：
? 电荷的面密度d, s 面元
3)电荷体分布 .dq ? ? dV
? 电荷的体密度 ,dV 体积元
2.电势： 电场中某点的电势在数值上等于将单位
正电荷由该点移动到电势零点时电场力
所做的功 点电荷的电势：
? U p
?
WP q0
?
(0) v v E ?dl
p
U? q
4??0 r
电荷组的电势：
? U ? 1 n qi
dq r r 2 er
2
场源为点电荷：
E
?
1
4?? 0
q r2
r?
场源为点电荷系 ：
? E ?
n1
i ?1 4?? 0
qi ri 2
e
ri
场源电荷连续分布
：dE
?
dq
4??0r 2
er
? ? E ?
dE ?
dq
4?? 0 r
2
er
1)电荷线分 dq ? ?dx
布.?电荷的线密度, dx线元
2)电荷面分布 . dq ? ? ds
2.导体的静电平衡
静电平衡---导体内部和表面无电荷定向移动
推论：静电平衡时,导体表面场强垂直表面
导体是个等势体，导体表面是个等势面．
有导体存在时静电场的分析与计算
电场
导体上的电荷重新分布
相互影响
利用：
静电场的基本规律 （高斯定理和环路定理）
静电场的叠加原理
电荷守恒定律
导体的静电平衡条件
16
电容： 表征导体和导体组静电性质的一个物理量
? Wa ? a qE ?dl ? qU a
6
基本规律
一、 真空中的静电场
1. 线索
? 库仑定律 ?
? ? ? ?
E ?
? E
? ?
F
?
/?q0 Ei
? ? ?
?
? ?高斯定理： E ?d s ?
?
S
q
?0
???静电场的环路定理：L E ?d l ? 0
? P点电势：U P ?
(
P0
)
r E
?d
r l
2
2
对任意电场都适合
? 静电场的能量 W e ? wedV
19
V
电场能量的计算
（1）带电电容器储存的能量可以按照公式进行计算：
W
?
1
Q2
?
1 CU 2
?
1 QU
2C 2
2
（2）电场能量计算的步骤：
（a）根据电荷分布，计算出电场强度的分布规律，得到电
场能量密度
we
?
1 DE 2
?
1 ?E2
2
（b）取适当的体积元dV，在所取的体积元中各点的电场强度量值