锐角三角形[下学期]--新人教版-
人教版九年级下册数学作业课件 第二十八章 锐角三角函数 第1课时 仰角、俯角与解直角三角形

=
3
3)
=(30
3
+45)米,
3
∴DG=EH=AH-AE=(30 3 +45)-15=(30 3 +30)米,(30 3 +30)÷5=(6 3
+6)秒,∴经过(6 3 +6)秒时,无人机刚好离开了操控者的视线
2.如图,在高为 2 m,倾斜角为 30°的楼梯表面铺地毯,地毯的长度至少需要 (C )
A.[2பைடு நூலகம்( 3 +1)] m B.4 m C.2( 3 +1) m D.2( 3 +3) m
3.(威海中考)小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的 河流宽度.他先在河岸设立 A,B 两个观测点,然后选定对岸河边的一棵树记为点 M.测得 AB=50 米,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的 宽度.(结果精确到 0.1 米,参考数据:sin22°≈38 ,cos22°≈1156 ,tan22°≈25 ,sin67°≈1123 , cos67°≈153 ,tan67°≈152 )
2
∴x = 17 ≈0.82 , ∴OD = 0.82 m , ∴DH = OH - OD = OA - OD = 3.4 - 0.82 =
5
2.58≈2.6(m),答:最大水深约为 2.6 m.
13.(广元中考)如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到 一定高度 D 点处时,无人机测得操控者 A 的俯角为 75°,测得小区楼房 BC 顶端点 C 处的俯角为 45°.已知操控者 A 和小区楼房 BC 之间的距离为 45 米,小区楼房 BC 的高 度为 15 3 米.
解:如图,过点 D 作 DG⊥AE 于点 G,得矩形 GBFD,∴DF=GB,在 Rt△GDE 中,DE=80 cm,∠GED=48°,∴GE=DE·cos 48°≈80×0.67=53.6(cm),∴GB= GE+BE≈53.6+110=163.6≈164(cm).∴DF=GB≈164(cm).答:活动杆端点 D 离地面 的高度 DF 约为 164 cm
人教版九年级下册数学作业课件 第二十八章锐角三角函数 专题:求锐角三角函数常用的3种方法(一题多变)

∴BD=CD=k,AD=2k. ∴tanA=BADD=12.
方法总结:作垂线构造直角三角形时“不破坏”特殊 角(30°,45°,60°),如下展示部分常见构造方 法:
题型二 不含特殊角的非直角三角形 3.(1)[延长+连接线段构造直角三角形]如图,在正 方形网格中,已知△ABC 的三个顶点均在格点上, 则∠ACB 的正切值为( D )
◆类型一 构造直角三角形求解 题型一 含特殊角的非直角三角形 1.如图,在△ABC 中,∠B=45°,∠A=75°, AC=8,求 BC 和 AB 的长. 解:如图,过点 A 作 AD⊥BC,垂足为点 D. ∵在 Rt△ABD 中,∠B=45°, ∴∠BAD=45°,BD=AD,AB= 2AD. ∵∠BAC=75°,
2
2
∴AE=125x.
∴tan∠CAD=EACE=15.
◆类型三 利用等角转化求解【转化思想】 7.如图,CD 是 Rt△ABC 斜边 AB 上的高,AC=8, BC=6,则 cos∠BCD 的值是( D ) A.3 B.3 C.4 D.4
543 5
8.如图,在△ABC 中,AC=BC,过点 C 作 CD⊥AB,
(3)[利用垂径定理构造直角三角形]如图,⊙O 为△ABC
的外接圆,⊙O 的半径为 5,BC=8,则 cosA 的值为
3 5
.
10.如图,在矩形 ABCD 中,AB=2,BC=2 5,E 是 BC 的中点,将△ABE 沿直线 AE 翻折,点 B 落在点 F 处,连接 CF,求 cos∠ECF 的值.
A.2
B.2 5 5
C.
5 5
D.12
(2)如图,△ABC 的三个顶点都在正方形网格线的交 点处,将△ABC 绕着点 A 逆时针旋转得到△AB′C′. 若 A,C,B′三点共线,则 tan∠B′CB= 2 ;
28.1 锐角三角函数 课件 2024-2025学年数学九年级下册人教版

2 A=___4___.
感悟新知
知1-练
例 3 如图28.1-3,在等腰三角形ABC 中,AB=AC,如果 2AB=3BC,求∠B 的三个三角函数值.
解题秘方:紧扣“锐角三角函数的定 义的前提是在直角三角形中”这一特 征,用“构造直角三角形法”求解.
感悟新知
解:过点A作AD⊥BC于点D,如图28.1-3,
学习目标
第二十八章 锐角三角函数
28.1 锐角三角函数
感悟新知
知识点 1 锐角三角函数
1. 正弦、余弦、正切
名称
定义
符号语言
在Rt△ABC中,∠C=
90°,∠A的对边与斜 在Rt△ABC
正弦
边的比叫做∠A 的正 中,∠C=
弦 ,记 作 sin A,即 sin A=∠A斜的边对边
90°,sin =ac
A.
4 3
B.
3 4
C.
3 5
D.
4 5
解题秘方:引入参数,用这个参数表示出三角形的
三边长,再用定义求解.
感悟新知
知1-练
解:由sin A=BACB=45,可设BC=4k(k>0),则AB=5k. 根据勾股定理,得AC=3k, ∴ tan B=ABCC=34kk=34. 答案:B
感悟新知
知1-练
技巧点拨:在直角三角形中,给出某一个锐角的三角 函数值,求另一个锐角的三角函数值时,可以用设辅助 元,即引入“参数”的方法来解决,注意在最后计算时要 约去辅助元.
感悟新知
知1-练
2-1. [期中·盐城射阳县]如图,在Rt△ABC中,∠C=90 °,
sin
A=13,则cos
22 A=___3___,tan
人教版九年级数学下册作业课件 第二十八章 锐角三角函数 第2课时 仰角、俯角与解直角三角形

AF的高度约为9.0米
【素养提升】 11.(18分)(广州中考)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的 高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD, 标杆CD的影子为CE,CD=1.6 m,BC=5CD. (1)求BC的长; (2)从条件①,条件②这两个条件中选择一个作为已知,求旗杆AB的高度. 条件①:CE=1.0 m;条件②:从D处看旗杆顶部A的仰角α为54.46°. 注:如果选择条件①和条件②分别作答,按第一个解答计分. 参考数据:sin 54.46°≈0.81,cos 54.46°≈0.58,tan 54.46°≈1.40.
A.8(3- 3 ) m B.8(3+ 3 ) m C.6(3- 3 ) m D.6(3+ 3 ) m
8.(5分)(广西中考)如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼 顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120 m,则乙楼的高 CD是__4_0__3____m.(结果保留根号)
第二十八章 锐角三角函数
28.2 解直角三角形及其应用 28.2.2 应用举例
第2课时 仰角、俯角与解直角三角形
仰角与俯角问题 1.(5分)(玉林中考)如图,从热气球A看一栋楼底部C的俯角是( ) D A.∠BAD B.∠ACB C.∠BAC D.∠DAC
2.(5分)(教材P78习题T3变式)如图,某地修建高速公路,要从A地向B地修一条隧道 (点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发, 垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为 _____t_a8_n0_0_α__米.
3.(5分)如图,甲,乙两座建筑物相距30 m,从甲顶部点A测得乙顶部点D的仰角为 37°,若甲建筑物AB的高为40 m,则乙建筑物CD的高约为____m6.3 (结果取整数, 参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
第28章 锐角三角函数 2022-2023学年人教版数学九年级下册检测题
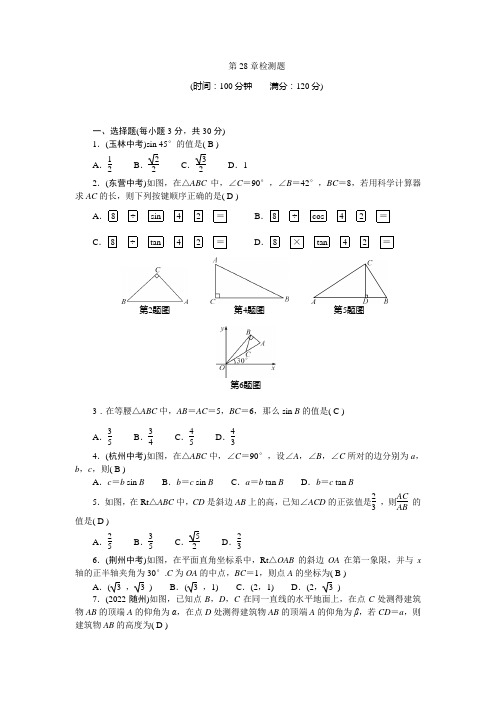
第28章检测题(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分)1.(玉林中考)sin 45°的值是( B ) A .12 B .22 C .32D .1 2.(东营中考)如图,在△ABC 中,∠C =90°,∠B =42°,BC =8,若用科学计算器求AC 的长,则下列按键顺序正确的是( D )A .8 ÷ sin 4 2 =B .8 ÷ cos 4 2 =C .8 ÷ tan 4 2 =D .8 × tan 4 2 =第2题图 第4题图 第5题图第6题图3.在等腰△ABC 中,AB =AC =5,BC =6,那么sin B 的值是( C )A .35B .34C .45D .434.(杭州中考)如图,在△ABC 中,∠C =90°,设∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,则( B )A .c =b sinB B .b =c sin BC .a =b tan BD .b =c tan B5.如图,在Rt △ABC 中,CD 是斜边AB 上的高,已知∠ACD 的正弦值是23 ,则AC AB的值是( D )A .25B .35C .52D .236.(荆州中考)如图,在平面直角坐标系中,Rt △OAB 的斜边OA 在第一象限,并与x 轴的正半轴夹角为30°.C 为OA 的中点,BC =1,则点A 的坐标为( B )A .(3 ,3 )B .(3 ,1)C .(2,1)D .(2,3 )7.(2022·随州)如图,已知点B ,D ,C 在同一直线的水平地面上,在点C 处测得建筑物AB 的顶端A 的仰角为α,在点D 处测得建筑物AB 的顶端A 的仰角为β,若CD =a ,则建筑物AB 的高度为( D )A .a tan α-tan βB .a tan β-tan αC .a tan αtan βtan α-tan βD .a tan αtan βtan β-tan α第7题图 第8题图第9题图8.(温州中考)图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC .若AB =BC =1,∠AOB =α,则OC 2的值为( A )A .1sin 2α +1B .sin 2α+1C .1cos 2α+1 D .cos 2α+1 9.(重庆中考)如图,在建筑物AB 左侧距楼底B 点水平距离150米的C 处有一山坡,斜坡CD 的坡度(或坡比)为i =1∶2.4,坡顶D 到BC 的垂直距离DE =50米(点A ,B ,C ,D ,E 在同一平面内),在点D 处测得建筑物顶A 点的仰角为50°,则建筑物AB 的高度约为(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)(D )A .69.2米B .73.1米C .80.0米D .85.7米10.(绍兴中考)如图,在Rt △ABC 中,∠BAC =90°,cos B =14,点D 是边BC 的中点,以AD 为底边在其右侧作等腰三角形ADE ,使∠ADE =∠B ,连接CE ,则CE AD的值为( D ) A .32 B . 3 C .152D .2 第10题图 第13题图 第14题图第15题图二、填空题(每小题3分,共15分)11.(甘肃中考)在△ABC 中,∠C =90°,tan A =33 ,则cos B =__12 __. 12.(无锡中考)一条上山直道的坡度为1∶7,沿这条直道上山,每前进100米所上升的高度为__102 __米.13.(2022·泰安)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角∠DPC =30°,已知窗户的高度AF =2 m ,窗台的高度CF =1 m ,窗外水平遮阳篷的宽AD =0.8 m ,则CP 的长度为__4.4__m(结果精确到0.1 m).14.(咸宁中考)如图,海上有一灯塔P ,位于小岛A 北偏东60°方向上,一艘轮船从小岛A 出发,由西向东航行24 n mile 到达B 处,这时测得灯塔P 在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P 的正南方,此时轮船与灯塔P 的距离是__20.8__n mile.(结果保留一位小数,3 ≈1.73)15.(深圳中考)如图,在四边形ABCD 中,AC 与BD 相交于点O ,∠ABC =∠DAC =90°,tan ∠ACB =12 ,BO OD =43 ,则S △ABD S △CBD=__332 __. 三、解答题(共75分)16.(8分)计算:(1)3tan30°+cos 245°-2sin60°; (2)tan 260°-2sin45°+cos60°.解:原式=12 解:原式=72-217.(9分)在△ABC 中,∠C =90°.(1)已知c =83 ,∠A =60°,求∠B ,a ,b ;(2)已知a =36 ,∠A =30°,求∠B ,b ,c .解:(1)∠B =30°,a =12,b =43 (2)∠B =60°,b =92 ,c =6618.(9分)(2022·湘潭)湘潭县石鼓油纸伞因古老工艺和文化底蕴,已成为石鼓乡村旅游的一张靓丽名片.某中学八年级数学兴趣小组参观后,进行了设计伞的实践活动.小文依据黄金分割的美学设计理念,设计了中截面如图所示的伞骨结构(其中DH AH≈0.618):伞柄AH 始终平分∠BAC ,AB =AC =20 cm ,当∠BAC =120°时,伞完全打开,此时∠BDC =90°.请问最少需要准备多长的伞柄?(结果保留整数,参考数据:3 ≈1.732)解:作BE ⊥AH 于点E ,∵∠BAC =120°,AH 平分∠BAC ,∴∠BAE =60°,∴AE =AB ·cos60°=20×12 =10(cm),BE =AB ·sin60°=20×32 =103 ≈17.32(cm),∵BD =CD ,∠BDC =90°,∴∠BDE =45°,∴DE =BE =17.32 cm ,∴AD =AE +DE =10+17.32=27.32(cm),∵DH AH =0.618,即AH -27.32AH=0.618,解得AH ≈72,∴最少需要准备72 cm 长的伞柄19.(9分)已知锐角△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,边角总满足关系式:a sin A =b sin B =c sin C. (1)如图①,若a =6,∠B =45°,∠C =75°,求b 的值;(2)某公园准备在园内一个锐角三角形水池ABC 中建一座小型景观桥CD (如图②所示),若CD ⊥AB ,AC =14米,AB =10米,sin ∠ACB =5314,求景观桥CD 的长度.解:(1)∵∠B =45°,∠C =75°,∴∠A =60°,∵a sin A =b sin B =c sin C ,∴6sin 60°=b sin 45°,∴b =26 (2)∵AB sin ∠ACB =AC sin B ,∴105314=14sin B,∴sin B =32 ,∴∠B =60°,∴tan B =CD BD =3 ,∴BD =33 CD ,∵AC 2=CD 2+AD 2,∴196=CD 2+(10-33 CD )2,∴CD =83 或=-33 (舍去),∴CD 的长度为83 米20.(9分)(2022·包头)如图,AB 是底部B 不可到达的一座建筑物,A 为建筑物的最高点,测角仪器的高DH =CG =1.5米.某数学兴趣小组为测量建筑物AB 的高度,先在H 处用测角仪器测得建筑物顶端A 处的仰角∠ADE 为α,再向前走5米到达G 处,又测得建筑物顶端A 处的仰角∠ACE 为45°,已知tan α=79,AB ⊥BH ,H ,G ,B 三点在同一水平线上,求建筑物AB 的高度.解:由题意得:DH =CG =BE =1.5米,CD =GH =5米,DE =BH ,∠AED =90°,设CE =x 米,∴BH =DE =DC +CE =(x +5)米,在Rt △ACE 中,∠ACE =45°,∴AE =CE ·tan45°=x(米),在Rt△ADE中,∠ADE=α,∴tan α=AEDE=xx+5=79,∴x=17.5,经检验:x=17.5是原方程的根,∴AB=AE+BE=17.5+1.5=19(米),∴建筑物AB的高度为19米21.(10分)(2022·怀化)某地修建了一座以“讲好隆平故事,厚植种子情怀”为主题的半径为800米的圆形纪念园,如图,纪念园中心点A位于C村西南方向和B村南偏东60°方向上,C村在B村的正东方向且两村相距2.4 km.有关部门计划在B,C两村之间修一条笔直的公路来连接两村,问该公路是否穿过纪念园?试通过计算加以说明.(参考数据:3≈1.73,2≈1.41)解:过A点作AD⊥BC于D点,由题意知:∠ABC=90°-60°=30°,∠ACD=45°,∴BD=3AD,CD=AD, ∵BC=2.4 km=2400 m,∴3AD+AD=2400,解得AD=1200(3-1)≈876>800,故该公路不穿过纪念园22.(10分)(2022·鄂州)亚洲第一、中国唯一的航空货运枢纽——鄂州花湖机场,于2022年3月19日完成首次全货运试飞,很多市民共同见证了这一历史时刻.如图,市民甲在C 处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,若斜坡CF的坡比=1∶3,铅垂高度DG=30米(点E,G,C,B在同一水平线上).求:(1)两位市民甲、乙之间的距离CD;(2)此时飞机的高度AB.(结果保留根号)解:(1)∵斜坡CF 的坡比=1∶3,DG =30米,∴DG GC =13 ,∴GC =3DG =90(米),在Rt △DGC 中,DC =DG 2+GC 2 =302+902 =3010 (米),∴两位市民甲、乙之间的距离CD 为3010 米(2)过点D 作DH ⊥AB ,垂足为H ,则DG =BH =30米,DH =BG ,设BC =x 米,在Rt △ABC 中,∠ACB =45°,∴AB =BC ·tan45°=x (米),∴AH =AB -BH =(x -30)米,在Rt △ADH 中,∠ADH =30°,∴tan30°=AH DH =x -30x +90 =33,∴x =603 +90.经检验:x =603 +90是原方程的根,∴AB =(603 +90)米,∴此时飞机的高度AB 为(603 +90)米23.(11分)如图,在Rt △ABC 中,∠ACB =90°,CD 平分∠ACB 交AB 于点D ,交⊙O 于点E ,以DB 为直径作⊙O 交BC 于点F ,连接BE ,EF .(1)证明:∠A =∠BEF ;(2)若AC =4,tan ∠BEF =4,求EF 的长.解:(1)连接DF ,∵BD 是⊙O 的直径,∴∠DFB =90°,∵∠ACB =90°,∴∠ACB =∠DFB =90°,∴AC ∥DF ,∴∠A =∠FDB ,∵∠FDB =∠BEF ,∴∠A =∠BEF(2)过点E 作EH ⊥BC ,垂足为H ,∴∠EHF =90°,∵CD 平分∠ACB ,∴∠ACD =∠DCB =12∠ACB =45°,∴∠CDF =90°-∠DCB =45°,∴CF =DF ,设CF =DF =x ,∵∠A =∠BEF ,∴tan A =tan ∠BEF =4,∴BC =AC ·tan A =4×4=16,∴BF =BC -CF =16-x ,∵∠ACF =∠DFB =90°,∴△ACB ∽△DFB ,∴AC DF =BC BF ,∴4x =1616-x,∴x =165 .经检验,x =165 是原方程的根,∴CF =165,∵BD 是⊙O 的直径,∴∠BED =90°,∴∠EBC =90°-∠DCB =45°,∴EC =EB ,∵EH ⊥BC ,∴CH =BH =12 BC =8,∴EH =12BC =8,∴FH =CH -CF =245,∴EF =FH 2+EH 2 =(245)2+82 =85 34 ,∴EF 的长为85 34。
人教版九年级数学下册课件:28.1锐角三角函数--1.2余弦、余切
16
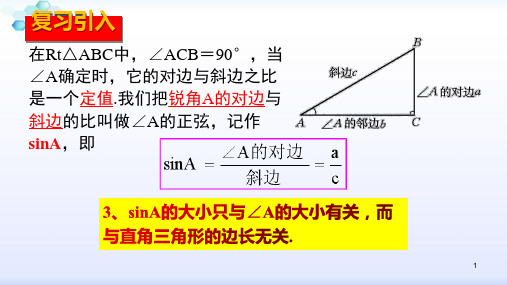
知识点二:正 切
合作探究
如图,若点E为BC的中点,则 tan∠CAE的值是 .
17
知识点二:正 切
学以致用
1.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tan A的值 是( A )
A.
B.
C.
D.
2.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍, 则tan B的值是( D )
的坐标为(4,3),那么cos α的值是( B )
A. B.
C. D.
11
知识点一:余 弦
学以致用
3.如图,在Rt△ABC中,∠B=90°,∠A= 30°,以点A为 圆心,BC长为半径画弧交AB于点D,分别以点A,D为圆心, AB长为半径画弧,两弧交于点E,连接 AE,DE,则∠EAD的余弦值是( B )
28
知识点三:锐角三角函数
归纳总结
(3)sin2A表示sinA·sinA=(sinA)2,不能写成sinA2; (4)由于直角三角形的斜边大于直角边,且各边的边长均 为正数,所以锐角三角函数值都是正实数, 且0<sinA<1,0<cosA<1,tanA>0. (5)正弦、余弦、正切符号后面可以直接写锐角的度数, 如sin28°,cos8°,tan18°等.
A.
B. 3 C.
D.
18
知识点二:正 切
学以致用
3.如图,在△ABC中,∠BAC=90°,AB
=AC,点D 为边AC的中点,DE⊥BC于点
E,连接BD,则tan ∠DBC的值为( A )
A.
B.
C.
D.
4.如图,P(12,a)在反比例函数 y= 图象
Байду номын сангаас
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
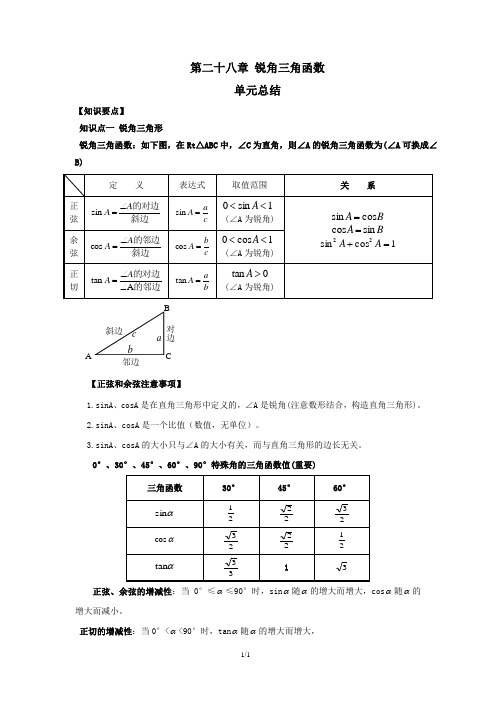
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
精品解析2022年人教版九年级数学下册第二十八章-锐角三角函数难点解析试题(含详细解析)

人教版九年级数学下册第二十八章-锐角三角函数难点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在直角△ABC 中,90C ∠=︒,3AB =,AC =2,则tan A 的值为( )A B C .23 D2、三角形在正方形网格纸中的位置如图所示,则tan α的值是( )A .12B .43C .35D .45 3、某人沿坡度1:2i =的斜坡向上前进了10米,则他上升的高度为( )A .5米B .C .D .4、如图,琪琪一家驾车从A地出发,沿着北偏东60︒的方向行驶,到达B地后沿着南偏东50︒的方向行驶来到C地,且C地恰好位于A地正东方向上,则下列说法正确的是()A.B地在C地的北偏西40︒方向上B.A地在B地的南偏西60︒方向上C.50ACB D.sin BAC∠=°∠=5、在正方形网格中,△ABC在网格中的位置如图,则sin B的值为()A B C D.12∠的顶点位于正方形网格的格6、如图,在44⨯的正方形网格中,每个小正方形的边长均为1,已知α∠是()点上,且cosα=αA.B.C.D.7、如图1所示,△DEF 中,∠DEF =90°,∠D =30°,B 是斜边DF 上一动点,过B 作AB ⊥DF 于B ,交边DE (或边EF )于点A ,设BD =x ,△ABD 的面积为y ,图2是y 与x 之间函数的图象,则△ABD 面积的最大值为( )A .B .C .D .8、如图,E 是正方形ABCD 边AB 的中点,连接CE ,过点B 作BH ⊥CE 于F ,交AC 于G ,交AD 于H ,下列说法:①AH HG AB BG =; ②点F 是GB 的中点;③AG AB =;④S △AHG =16S △ABC .其中正确的结论的序号是( )A .①②③B .①③C .②④D .①③④9、如图,若O 的半径为R ,则它的外切正六边形的边长为( )A B C . D .6R10、将一矩形纸片ABCD 沿CE 折叠,B 点恰好落在AD 边上的F 处,若:4:5AB BC =,则cos AFE ∠的值为( )A.54B.35C.34D.45第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、第6号台风“烟花”于2021年7月25日12时30分前后登陆舟山普陀区,登陆时强度为台风级,中心最大风速38米/秒.此时一艘船以27nmile/h的速度向正北航行,在A处看烟花S在船的北偏东15°方向,航行40分钟后到达B处,在B处看烟花S在船的北偏东45°方向.(1)此时A到B的距离是 _____;(2)该船航行过程中距离烟花S中心的最近距离为 _____.(提示:sin15°=.2、当0≤θ≤α时,将二次函数y=﹣x2(0≤x≤G,绕原点逆时针旋转θ得到图形G均是某个函数的图象,则α的最大值为 _____.3、如图,直线MN过正方形ABCD的顶点A,且∠NAD=30°,AB=,P为直线MN上的动点,连BP,将BP绕B点顺时针旋转60°至BQ,连CQ,CQ的最小值是 ___.4、如图,等边ABC 的边长为2,点O 是ABC 的中心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段,AB BC 于D ,E 两点,连接DE ,给出下列四个结论:①OD OE =;②四边形ODBE 的面积始终等于ODE BDE S S =;④BDE 周长的最小值为3.其中正确的结论是________(填序号).5、矩形ABCD 中,E 为边AB 上一点,将ADE 沿DE 折叠,使点A 的对应点F 恰好落在边BC 上,连接AF 交DE 于点N ,连接BN .若3AD =,13BF BC =.(1)矩形ABCD 的面积为________;(2)sin BNF ∠的值为_________.三、解答题(5小题,每小题10分,共计50分)1、计算:221cot 60cos30tan 60sin 453⋅-+.2、平面直角坐标系中,过点M 的⊙O 交x 轴于A 、B 两点(点A 在点B 的左侧),交y 轴于C 、D 两点,交OM 的反向延长线于点N .(1)求经过A 、N 、B 三点的抛物线的解析式.(2)如图①,点E 为(1)中抛物线的顶点,连接EN ,判断直线EN 与⊙O 的位置关系,并说明理由.(3)如图②,连接MD 、BD ,过点D 的直线l 交抛物线于点P ,且PDB DMN ∠=∠,直接写出直线DP 的解析式.3、如图,在Rt ABC △中,90C ∠=︒,22.5B ∠=︒(1)尺规作图:作AB 的垂直平分线l 交BC 于点D .(保留痕迹,不写作法)(2)在(1)的作图下,试求tan 67.5︒的值(结果保留根号)4、如图,已知抛物线(2)(4)y a x x =+-(a 为常数,且a >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B 的直线34y x b =-+与抛物线的另一交点为D .(1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求a的值;(3)在(1)的条件下,直线BD上是否存在点E,使∠AEC=45°?若存在,请直接写出点E的横坐标;若不存在,请说明理由.5、在⊙O中,AC AD,四边形ABCD是平行四边形.(1)求证:BA是⊙O的切线;(2)若AB=6,①求⊙O的半径;②求图中阴影部分的面积.---------参考答案-----------一、单选题1、B【分析】先利用勾股定理求出BC的长,然后再求tanA的值.【详解】解:∵在Rt△ABC中,AB=3,AC=2,∴BC∴tanA=BCAC故选:B.【点睛】本题考查锐角三角形的三角函数和勾股定理,需要注意求三角函数时,一定要是在直角三角形当中.2、A【分析】根据在直角三角形中,正切值等于对边比上邻边进行求解即可.【详解】解:如图所示,在直角三角形ABC中∠ACB=90°,AC=2,BC=4,∴tanα=αααα=24=12,故选A.【点睛】本题主要考查了求正切值,解题的关键在于能够熟练掌握正切的定义.3、B【分析】由坡度定义可得位置升高的高度即为坡角所对的直角边.根据题意可得BC :AC =1:2,AB =10m ,可解出直角边BC ,即得到位置升高的高度.【详解】解:由题意得,BC :AC =1:2.∴设BC =x ,则AC =2x .∵AB =10, BC 2+ AC 2=AB 2,∴x 2+ (2x )2=102,解得:x =.故选:B .【点睛】本题主要考查了坡度的定义和解直角三角形的应用,注意画出示意图会使问题具体化.4、B【分析】根据题意可知60BAD ∠=︒,50CBP ∠=︒,由此即可得到50BCE CBP ∠∠==︒即可判断A ;由60ABP ∠=︒可以判断B ;由9040ACB BCE ∠∠=︒-=︒可以判断C ;求出30BAC ∠=︒即可判断D .【详解】解:如图所示:由题意可知,60BAD ∠=︒,50CBP ∠=︒,50BCE CBP ∠∠∴==︒,即B 在C 处的北偏西50,故A 不符合题意;60ABP ∠=︒,A ∴地在B 地的南偏西60︒方向上,故B 不符合题意;9040ACB BCE ∠∠=︒-=︒,故C 错误.60BAD ∠=︒,30BAC ∴∠=︒,1sin 2BAC ∠∴=,故D 不符合题意. 故选B .【点睛】本题考查的是解直角三角形和方向角问题,熟练掌握方向角的概念是解题的关键.5、A【分析】利用勾股定理先求出AB 的长度,最后利用正弦值的定义得到sin AD B AB =,进而得到最终答案. 【详解】解:如图所示在Rt ADB ∆中,由勾股定理可得:ABsinAD B AB ∴=== 故选:A . 【点睛】本题主要是考察了勾股定理和锐角三角函数的定义,掌握锐角三角函数的定义是解题的关键. 6、B 【分析】先构造直角三角形,由cos α=邻边斜边求解即可得出答案 【详解】 A.cos α===B.cosα=cosα===cosα===【点睛】本题考查锐角三角函数,掌握在直角三角形中,cos α=邻边斜边是解题的关键. 7、C 【分析】由图得点A 到达点E 时,ABD △面积最大,此时12DB =,由三角函数算出AB ,由三角形面积公式即可求解. 【详解】由图可得:点A 到达点E 时,ABD △面积最大,此时12DB =,tan 3012AB DB =⋅︒==∴1122ABDS=⨯⨯ 故选:C . 【点睛】本题考查二次函数图像问题以及解直角三角形,由题判断点A 运动到哪里能使ABD △面积最大是解题的关键. 8、D 【分析】①先证明△ABH ≌△BCE ,得AH =BE ,则1122AH AD BC ==,即12AH AB =,再根据平行线分线段成比例定理得:12HG BG =即可判断;②设BF =x ,CF =2x ,则BC ,计算FG =23x即可判断;③根据等腰直角三角形得:AC AB ,根据①中得:13AG AC =即可判断; ④根据11,22HG AG BG CG ==,可得同高三角形面积的比,然后判断即可.解:①∵四边形ABCD是正方形,∴AB=BC,∠HAB=∠ABC=90°,∵CE⊥BH,∴∠BFC=∠BCF+∠CBF=∠CBF+∠ABH=90°,∴∠BCF=∠ABH,∴△ABH≌△BCE,∴AH=BE,∵E是正方形ABCD边AB的中点,∴BE=12AB,∴1122AH AD BC==,即12AHAB=∵AH//BC,∴12 AH HG BC BG==∴AH HGAB BG=,故①正确;②1 tan tan2AH BF ABH BCFAB CF ∠=∠===设BF=x,CF=2x,则BC,∴AH x∴52 BH x =∴552263x x xFG BH GH BF x BF=--=--=≠,故②不正确;③∵四边形ABCD 是正方形, ∴AB =BC ,∠ABC =90°, ∴AC, ∵12AG AH CG BC == ∴13AG AC =∴13AG AC AB ==,故③正确; ④∵12GH AGBG CG == ∴11,22AHGABG ABGBCG S S S S ∆∆∆∆== ∴13ABGABCS S∆∆=∴16AHG ABC S S =,故④正确. 故选D . 【点睛】本题属于四边形综合题,主要考查了正方形的性质、全等三角形的判定和性质、勾股定理等知识点,灵活应用相关知识点成为解答本题的关键. 9、B 【分析】如图连结OA ,OB ,OG ,根据六边形ABCDEF 为圆外切正六边形,得出∠AOB =60°△AOB 为等边三角形,根据点G 为切点,可得OG ⊥AB ,可得OG 平分∠AOB ,得出∠AOC =11603022AOB ∠=⨯︒=︒,根据锐角三角函数求解即可. 【详解】解:如图连结OA ,OB ,OG ,∵六边形ABCDEF 为圆外切正六边形,∴∠AOB =360°÷6=60°,△AOB 为等边三角形, ∵点G 为切点, ∴OG ⊥AB , ∴OG 平分∠AOB ,∴∠AOC =11603022AOB ∠=⨯︒=︒,∴cos30°=OGOA,∴cos30OG OA ==︒ 故选择B .【点睛】本题考查圆与外切正六边形性质,等边三角形性质,锐角三角形函数,掌握圆与外切正六边形性质,等边三角形性质,锐角三角形函数是解题关键. 10、D 【分析】由∠AFE +∠CFD =90°得cos sin CD AFE CFD CF∠=∠=,根据折叠的定义可以得到CB =CF ,则CD ABCF BC =,即可求出cos AFE ∠的值,继而可得出答案.【详解】∵∠AFE +∠CFD =90°, ∴cos sin CDAFE CFD CF∠=∠=, 由折叠可知,CB =CF ,矩形ABCD 中,AB =CD ,4cos 5CD AB AFE CF BC ∠===. 故选:D . 【点睛】本题考查了折叠变换的性质及锐角三角函数的定义,解题关键是得到CB =CF . 二、填空题1、 18 nmile 9nmile##993 nmile 【解析】 【分析】如图,过S 作SD AB ⊥于,D 先由路程等于速度乘以时间求解,AB 再利用sin15°=tan1523, 再设,SD m 而,45,SDAB DBS ,18,BD m AD m 再利用tan1523,建立方程,再解方程,从而可得答案. 【详解】解:如图,过S 作SD AB ⊥于,D 由题意可得:40622718,15,45,sin15,604AB BAS DBS62,4DS AS设62,DS k 则4,AS k2284362,AD AS DS k k2tan15=23,62k DSADk设,SD m 而,45,SD AB DBS,18,BD m AD m23,18m m311823,m解得:939,m 经检验符合题意;所以:该船航行过程中距离烟花S 中心的最近距离为:9 nmile.故答案为:18 nmile ,9 nmile. 【点睛】本题考查的是解直角三角形的实际应用,熟练的利用sin15︒的值求解tan15︒是解本题的关键. 2、30 【解析】【分析】根据题意,找到图象G 的切线,进而根据旋转的性质即可求得α的最大值 【详解】解:∵将二次函数y =﹣x 2(0≤x ≤G ,逆时针旋转θ得到图形G 均是某个函数的图象,设过原点的直线y kx =∴当y =﹣x 2,y kx =存在唯一交点时即2x kx -=)20k=解得k =设()P m 为y =上一点,过点P 作PQ y ⊥轴,则,OQ PQ m ==tan POQ ∠=30POQ ∴∠=︒当图象G 旋转30时,与y 轴相切,符合函数图象,故30θ≤︒ 即max =30α︒故答案为:30° 【点睛】本题考查了旋转的的性质,抛物线与直线交点问题,解直角三角形,理解题意求得直线与y 轴的夹角是解题的关键.326【解析】 【分析】如图,连接PQ 交AB 于,F 则,60,BP BQ PBQ 先证明180,APBAQB 把ABP △绕B 顺时针旋转60︒得到,A BQ 证明180,A QBAQB 可得,,A Q A 三点共线,Q 在AA '上运动,过C 作CEAA 于,E 则,Q E 重合时,CQ 最短,再求解26tan 30,3DGAD 2622,3CG DC DG从而可得答案. 【详解】解:如图,连接,,PQ AQ PQ 交AB 于,F 则,60,BP BQ PBQPBQ ∴是等边三角形,60,PQB QBP QPB30,DAN 正方形,ABCD90,22,BAD AB AD DC60,MAB PQB ,AFP BFQ,AFP QFB ∽ ,AFPF QF BF,APF ABQ ,AFQ PFB ,PFB AFQ ∽,PBF AQF60,AQFAPQ ABP ABQ PBQ 360180,APB AQB 把ABP △绕B 顺时针旋转60︒得到,A BQ则,ABP A BQ ≌ ,APBA QB 180,A QB AQB ,,A Q A 三点共线,∴ Q 在AA '上运动,过C作CE AA于,E则,Q E重合时,CQ最短,60,22,ABA AB A BABA是等边三角形,记AA'交DC于,G60,30,BAA DAG60,AGD CGE326tan3022,33DG AD2622,3CG DC DG326sin60226 2.23CE CG所以CQ【点睛】本题考查的是正方形的性质,相似三角形的性质,锐角三角函数的应用,得到Q的运动轨迹是解本题的关键.4、①③④【解析】【分析】如图:连接OB、OC,利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°,再证明∠BOD=∠COE,可证△BOD≌△COE,即BD=CE、OD=OE,则可对①进行判断;利用α△ααα=α△ααα得到四边形ODBE的面积=13α△ααα=√33,则可对③进行判断;再作OH⊥DE,则DH=EH,计算出S△DOE=√34αα2,利用S△DOE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=4+DE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.【详解】解:连接OB 、OC ,如图,∵等边ABC∴∠ABC =∠ACB =60°,∵点O 是△ABC 的中心,∴OB =OC ,OB 、OC 分别平分∠ABC 和∠ACB ,∴∠ABO =∠OBC =∠OCB =30°∵∠BOC =120°,即∠BOE +∠COE =120°,而∠DOE =120°,即∠BOE +∠BOD =120°,∴∠BOD =∠COE ,在△BOD 和△COE 中{∠ααα=∠ααααα=αα∠ααα=∠ααα∴△BOD ≌△COE ,∴BD =CE ,OD =OE ,所以①正确;∴α△ααα=α△ααα∴四边形ODBE 的面积 =α△ααα=13α△ααα=13×√34×22=√33,故②正确;如图:作OH⊥DE,则DH=EH,∵∠DOE=120°,∴∠ODE=_OEH=30°,∴αα=12αα,HE=√3αα=√32αα,∴αα=√3αα,∴α△ααα=12⋅12αα⋅√3αα=√34αα2,即S△DOE随OE的变化而变化,而四边形ODBE的面积为定值,∴α△ααα≠α△ααα;所以③错误;∵BD=CE,∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=2+DE当OE⊥BC时,OE最小,△BDE的周长最小,此时αα=√33,∴△BDE周长的最小值=2+1=3,所以④止确.故填①③④.【点睛】本题考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质等知识点,灵活应用相关知识成为解答本题的关键5、【解析】【分析】(1)矩形ABCD中,由折叠可得DF=AD=3,在Rt CDF中,用勾股定理求得CDABCD的面积;(2)由折叠可得AF DE ⊥,AE EF =,矩形ABCD 中,90ABF ∠=︒,B E N F 、、、四点共圆,故BNF BEF ∠=∠,设AE EF x ==,在Rt BEF △中,由勾股定理得: x =sin BNF ∠的值. 【详解】(1)矩形ABCD 中,3AD =,13BF BC =,∴3BC AD ==,113BF AD ==,2CF BC BF =-=,90C ∠=︒, 由折叠可得DF =AD =3,在Rt CDF 中,CD =∴矩形ABCD 的面积=3AD CD ⋅=故答案为:(2)将ADE 沿DE 折叠,使点A 的对应点F 恰好落在边BC 上,∴AF DE ⊥,AE EF =,矩形ABCD 中,90ABF ∠=︒,B E N F ∴、、、四点共圆,BNF BEF ∴∠=∠,设AE EF x ==,则BE AB AE x =-,在Rt BEF △中,由勾股定理得:222BE BF EF +=,即222)1x x +=,解得x =,∴sin BNF ∠=sin BF BEF EF ∠==【点睛】本题考查了勾股定理、矩形的性质、锐角三角函数等知识,掌握相应的定理是解答此题的关键.三、解答题1、0【解析】【分析】先将特殊角锐角三角锐角三角函数值代入,再合并,即可求解.【详解】解:2213=⨯+原式 11122=-+ =0【点睛】本题主要考查了锐角三角函数的混合运算,熟练掌握特殊角锐角三角锐角三角函数值是解题的关键.2、(1)2y =;(2)直线EN 与⊙O 相切,理由见解析;(3)2y =-或2y =- 【解析】【分析】(1)结合题意,根据圆和勾股定理的性质,计算得圆的半径,从而得()2,0A -,()2,0B ;根据抛物线轴对称的性质,得经过A 、N 、B 三点的抛物线,对称轴为:0x =;通过列二元一次方程组并求解,即可得到答案;(2)根据抛物线的性质,计算得0,E ⎛ ⎝⎭;根据勾股定理的性质,得2NE ,2OE ;根据圆的性质,得ON ;根据勾股定理的逆定理,通过222ON NE OE +=,推导得90ONE ∠=︒,结合圆的切线的定义,即可得到答案;(3)结合(2)的结论,根据特殊角度三角函数的性质,得30NOE ∠=︒,分当点P 纵坐标大于0和小于0两种情况,根据圆周角、圆心角的性质,推导得30QOB NOE ∠=∠=︒;根据含30角直角三角形和勾股定理的性质,计算得点Q 坐标,再通过待定系数法求解一次函数解析式,即可得到答案.【详解】(1)∵⊙O 过点M∴2OM =∵⊙O 交x 轴于A 、B 两点(点A 在点B 的左侧),∴OA OB OM ==∴()2,0A -,()2,0B∴经过A 、N 、B 三点的抛物线,对称轴为:0x =∵⊙O 交OM 的反向延长线于点N∴(1,N - 设经过A 、N 、B 三点的抛物线为:2y ax bx c =++∴经过A 、N 、B 三点的抛物线,对称轴为:0x =∴0b =∴2y ax c =+ ∴40a c a c +=⎧⎪⎨+=⎪⎩∴a c ⎧=⎪⎪⎨⎪=⎪⎩∴经过A 、N 、B三点的抛物线为:2y x =; (2)经过A 、N 、B三点的抛物线为:2y x =,且对称轴为:0x = ∴当0x =时,抛物线取最小值y =0,E ⎛ ⎝⎭∴()222413NE ⎛=-+= ⎝⎭,22163OE ⎛== ⎝⎭∵2ON OM ==∴24ON = ∵416433+= ∴222ON NE OE +=∴90ONE ∠=︒∴直线EN 与⊙O 相切;(3)∵90ONE ∠=︒∴1sin 2NE NOE OE ∠=== ∴30NOE ∠=︒如图,当点P 纵坐标大于0时,直线EP 交⊙O 于点Q ,连接OQ ,过点Q 作QK OB ⊥,交OB 于点K∴2OQ OD OM ===∴()0,2D -∵PDB DMN ∠=∠,2NOE DMN ∠=∠,2QOB PDB ∠=∠ ∴30QOB NOE ∠=∠=︒ ∴112QK OQ ==∴OK ==∴)Q 设直线DP 的解析式为:y kx b =+∴12b b +==-⎪⎩∴2k b ⎧=⎪⎨=-⎪⎩∴2y =-;如图,当点P 纵坐标小于0时,直线EP 交⊙O 于点Q ,连接OQ ,过点Q 作QK OB ⊥,交OB 于点K∴2OQ OD OM === ∵PDB DMN ∠=∠,2NOE DMN ∠=∠,2QOB PDB ∠=∠ ∴30QOB NOE ∠=∠=︒ ∴112QK OQ ==∴OK ==∴)1Q - 设直线DP 的解析式为:y kx b =+∴12b b +=-=-⎪⎩∴2k b ⎧=⎪⎨⎪=-⎩∴2y -; ∴直线DP的解析式为:2y =-或2y =-. 【点睛】本题考查了圆、二次函数、一次函数、勾股定理、直角三角形、轴对称、三角函数的知识;解题的关键是熟练掌握圆的对称性、圆周角、圆心角、二次函数图像、勾股定理及其逆定理、切线、特殊角度三角函数的性质,从而完成求解.3、(1)见解析;(21【解析】【分析】(1)作线段AB 的垂直平分线即可;(2)由垂直平分线的性质求出45ADC DAC ∠=∠=︒,设AC x =,BD AD ==,在三角形ABC 中利用三角函数即可求解.【详解】(1)作图如下,(2)根据垂直平分线的性质知,BD AD =,22.5DBE DAE ∠=∠=︒,在三角形ACD 中,45ADC DAC ∠=∠=︒设AC x =,∴AD =,∴BD AD ==,∴在三角形ABC 中,9022.567.5BAC ∠=︒-︒=︒,∴tan 67.51BC AC ︒===. 【点睛】 本题考查的是作图−基本作图、线段垂直平分线的性质、三角函数,熟知线段垂直平分线的作法是解答此题的关键.4、(1):y =14x 2-12x -2;(2)a (3)在直线BD 上不存在点E ,使∠AEC =45°.理由见解析 【解析】【分析】(1)令y =0可得A 和B 两点的坐标,把点B 的坐标代入直线y =-34x +b 中可得b 的值,根据点D 的横坐标为-5,可得点D 的坐标,将点D 的坐标代入抛物线的解析式中可得答案;(2)因为点P 在第一象限内的抛物线上,所以∠ABP 为钝角.因此若两个三角形相似,只可能是△ABC ∽△APB 或△ABC ∽△PAB .如图1和图2,按照以上两种情况进行分类讨论,分别计算;(3)根据OA =OC =2,∠AOC =90°画圆O ,半径为2,可知若优弧上存在一点E 与A ,C 构建的∠AEC =45°,再证明BD 与⊙O 相离,圆外角小于圆上角,可得结论.【详解】解:(1)抛物线y =a (x +2)(x -4),令y =0,解得x =-2或x =4,∴A (-2,0),B (4,0),把B (4,0)代入直线y =−34x +b 中,b =3,∴直线的解析式为y =-34x +3,当x=-5时,y=-34×(-5)+3=274,∴D(-5,274),∵点D(-5,274)在抛物线y=a(x+2)(x-4)上,∴a(-5+2)(-5-4)=274,∴a=14,∴抛物线的函数表达式为:y=14(x+2)(x-4)=14x2-12x-2;(2)由抛物线解析式,令x=0,得y=-8a,∴C(0,-8a),OC=8a.∵点P在第一象限内的抛物线上,∴∠ABP为钝角.∴若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.过点P作PN⊥x轴于点N,①若△ABC∽△APB,则有∠BAC=∠PAB,如图1所示,设P(x,y),则ON=x,PN=y,tan ∠BAC =tan ∠PAB , ∴OC PN OA AN =,即:822a y x =+, ∴y =4ax +8a ,∴P (x ,4ax +8a ),代入抛物线解析式y =a (x +2)(x -4),得a (x +2)(x -4)=4ax +8a ,整理得:x 2-6x -16=0,解得:x =8或x =-2(与点A 重合,舍去),∴P (8,40a ),∵△ABC ∽△APB ,∴AC ABAB AP =,解得:a ②若△ABC ∽△PAB ,则有∠ABC =∠PAB ,如图2所示,与①同理,可求得:y =2ax +4a ,∴P (x ,2ax +4a ),代入抛物线解析式y =a (x +2)(x -4),得a (x +2)(x -4)=2ax +4a ,整理得:x 2-4x -12=0,解得:x =6或x =-2(与点A 重合,舍去),∴P (6,16a ),∵△ABC ∽△PAB ,∴AB BCAP AB =,解得:a综上所述,a (3)在(1)的条件下,二次函数的解析式为:y =14x 2-12x -2;当x =0时,y =-2,∴C (0,-2),∴OA =OC =2,如图3,以O 为圆心2为半径画圆,在ANC 上取一点E 1,过点O 作OF ⊥BD 于F ,∵∠AOC =90°,∴∠AE 1C =45°,在直线y =-34x +3中,OM =3,OB =4,∴BM =5,∴S △OBM =12×3×4=12×5OF ,∴OF =125>2, ∴直线BD 与⊙O 相离,∴∠AEC <45°,∴在直线BD 上不存在点E ,使∠AEC =45°.【点睛】本题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,解直角三角形,直线和圆的位置关系,圆周角的性质,坐标和图形的性质等知识,解(1)的关键是确定点D 的坐标,解(2)的关键是利用分类讨论的思想;解(3)的关键是作出辅助线,是一道难度比较大的中考常考题.5、(1)证明见解析;(2)①4π-【解析】【分析】(1)连接AO ,由AC AD =,四边形ABCD 是平行四边形,即得推得ACO △为等边三角形,即可得∠BAO =∠BAC +∠CAO =90°,即BA 是⊙O 的切线.(2)①由(1)有A 0=tan 60AB =︒②将阴影面积拆为相等的两部分,其中左侧部分为扇形ACO 面积减去三角形ACO 面积,由扇形面积公式,等边三角形面积公式计算后乘2即可.【详解】(1)证明:连接OA∵四边形ABCD 是平行四边形∴AD//BE∴∠ADC=∠DCO又∵AC AD=∴∠ACD=∠ADC∴∠ACO=∠ACD+∠DCO=2∠ADC又∵2∠ADC=AOC∠∴AOC ACO∠=∠∴AO=AC又∵OC=AO∴ACO△为等边三角形∴∠ACO=∠CAO=60°,∠ACD=∠DCO=30°又∵AB//CD∴∠BAC=∠ACD=30°∴∠BAO=∠BAC+∠CAO=30°+60°=90°∴BA是⊙O的切线.(2)①由(1)可知∠BAO=90°,∠BOA=60°∴tanBA BOAAO ∠=∴AO =6tan tan BA BOA BOA ===∠∠②连接AO ,与CD 交于点M∵AC =OAC =60°∴CM =sin 603AC ⋅︒==∴11322AOC S AO CM =⋅⋅=⨯=△∵AO =AOC =60°∴22360AOCn r S ===︒扇形ππ ∴2AOC AOC S S S =-△阴影扇形()∴224S =-=-阴影(ππ【点睛】本题是一道圆内的综合问题,考察了证明某线是切线、平行四边形性质、等弧的性质、解直角三角形、等边三角形性质、勾股定理、扇形面积公式等,需熟练掌握这些性质及定理,而作出正确的辅助线是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
