五大基本初等函数性质和图像

五个重要的初等函数的图像和性质

五个重要的初等函数的图像和性质：一、羊角线：y=|x-a|（1）图像性质：单调性，对称性，（2）应用：①方程|x-2|=2a-1有两个不等实根，求a 的取值范围；②|x-2|=(1/2)x+a 有两个不等实根，求a 的取值范围；③若y=|x-2a+1|是偶函数，求a 的取值范围；二、槽形线：y=|x-a|+|x-b|（1）图像：值域，单调性，对称性（2）应用：①方程|x-2|+|x-3|=2a-1有2个不等实根，求a 的取值范围；②|x-2|+|x-3|> 2a+1恒成立，求a 的取值范围；③若y=|x-2a|+|x-3a+1|是偶函数，求a 的值；④若|x-2|+|x-3|> 3，求a 的取值范围.三、Z 形线：y=|x-a|-|x-b|（1）图像：值域，单调性，对称性（2）应用：①方程|x-2|+|x-3|=2a-1仅有一个实根，求a 的取值范围；②若|x-2|-|x-3|> 2a+1恒成立，求a 的取值范围；③若y=|x-2a|-|x-3a+1|是奇函数，求a 的值；④若|x+2|-|x-3|> 3，求a 的取值范围.引申：无解问题，有解问题四、最简分式函数：bc)ad 0,(c dcx b ax y ≠≠++= （1）图像：定义域、值域、单调性、对称性、对称中心原式化为：dcx c a d cx b d cx y c ad bc c ad ca ++=++-+=-)(，移项整理则有：)(c d cad bc c ad bc x d cx c a y --=+=---故有： ⅰ⎪⎪⎪⎩⎪⎪⎪⎨⎧≠⎪⎩⎪⎨⎧=-=-≠≠++=;)2(),,()1(),0(的一切实数值域为渐近线为双曲线中心为c a y c a y c d x c a c d bc ad c d cx b ax y ； ⅱ当02>-cad bc 即ad bc >时，函数由反比例函数将对称中心按向量),(c a c d -=ξ平移，再经过横向的伸缩变换（102<-<c ad bc 时横向伸长，21cad bc -<时横向缩短）而得； ⅲ当20cad bc -<即ad bc <时，函数由反比例函数将对称中心按向量),(c a c d -=ξ平移，然后做关于X 轴的对称变换，再经过横向的伸缩变换而得（1||02<-<c ad bc 时横向伸长，||12cad bc -<时横向缩短）而得。

五大基本初等函数①

考点三：五大基本初等函数● 一次函数1、定义：一般地，形如b kx y +=(k ≠0,b 是常数)，那么y 叫做x 的一次函数。

特别地，当b =0时称y 为x 的正比例函数，可表示为kx y =(k ≠0)，这时的常数k 也叫比例系数。

正比例函数图像经过原点。

2、性质：①在正比例函数时，y 与x 的商一定(x ≠0）。

在反比例函数时，y 与x 的积一定； ②一次函数与y 轴交点的坐标总是(0,b )，与x 轴总交于（kb -，0）。

正比例函数的图像都经过原点且为奇函数，定义域、值域均为R ； ③在两个一次函数表达式中，k 相同，b 也相同，则这两个一次函数的图像重合； k 相同，b 不相同，则这两个一次函数的图像平行； k 不相同，b 不相同，则这两个一次函数的图像相交；k 不相同，b 相同，则这两个一次函数图像交于y 轴上的同一点（0,b ）； k 互为负倒数时，则这两个一次函数图像互相垂直； ④图像的性质⑤当k >0时，一次函数在定义域内单调递增；当k <0时，一次函数在定义域内单调递减。

k 、b 的符号 k >0、b >0 k >0、b <0 k <0、b >0 k <0、b <0图像的大致位置 y0 x y0 x y0 x y0 x 经过象限第一、二、三象限第一、三、四象限第一、二、四象限第二、三、四象限性质y 随x 的增大而增大y 随x 的增大而增大y 随x 的增大而减小y 随x 的增大而减小● 二次函数1、定义：一般地，形如c bx ax y ++=2（其中a 、b 、c 是常数，a ≠0，b 、c 可以为0）的函数叫做二次函数，其中a 称为二次项系数，b 为一次项系数，c 为常数项。

2、性质：①二次函数图像是轴对称图形。

对称轴为直线ab x 2-=，对称轴与抛物线唯一的交点为抛物线的顶点P ，顶点坐标P （ab 2-，ab ac 442-）；特别地，当b =0时，抛物线的对称轴是y轴（即直线x =0）。

基本初等函数图像及性质小结

为高等数学小结的——基本初等函数. 幂函数(a为实数)1、图形：要记住最常见的几个幂函数的定义域及图形；2、定义域：随a的不同而不同，但无论a取什么值，x^a在内总有定义。

值域：随a的不同而不同3、主要性质：若a>0,函数在内单调增加；若a<0,函数在内单调减少。

.. 指数函数1、图形：2、定义域：值域：，3、主要性质：图形过（0，1）点暨 a^0=1若a>1 函数单调增加；若0<a<1 函数单调减少直线y=0为函数图形的水平渐近线4、今后用的较多5、. 对数函数1、图形：2、定义域：值域：3、主要性质：与指数函数互为反函数，图形过（1，0）点，a>1时，函数单调增加；0<a<1时，函数单调减少直线x=0为函数图形的铅直渐近线e=2.7182……，无理数经常用到以e为底的对数. 三角函数正弦函数：，[-1,1], 奇函数、有界函数、周期函数；以为周期的周期函数；单调增区间：单调减区间：余弦函数：，[-1,1], 偶函数、有界函数、周期函数周期：；单调增区间：单调减区间：正切函数：，的一切实数，奇函数、周期函数周期定义域：值域单调增区间：单调减区间：函数的铅直渐近线余切函数：，的一切实数，奇函数、周期函数；定义域：值域单调增区间：单调减区间：函数的铅直渐近线，. 反三角函数饭正弦函数：---定义域值域：单调增加；奇函数反余弦函数：---定义域值域：单调减少饭正切函数：---定义域值域：单调增加；奇函数函数图形的水平渐近线：反余切函数---定义域值域：单调减少；函数图形的水平渐近线：以上是五种基本初等函数，关于它们的常用运算公式都应掌握。

注：（1）指数式与对数式的性质由此可知，今后常用关系式，如：（2）常用三角公式积化和差sina*cosb=(sin(a+b)+sin(a-b))/2 cosa*sinb=(sin(a+b)-sin(a-b))/2cosa*cosb=(cos(a+b)+cos(a-b))/2 sina*sinb=-(cos(a+b)-cos(a-b))/2和差化积sinx+siny=2sin((x+y)/2)*cos((x-y)/2) sinx-siny=2cos((x+y)/2)*sin((x-y)/2) cosx+cosy=2cos((x+y)/2)*cos((x-y)/2) cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)。

六大基本初等函数图像及其性质

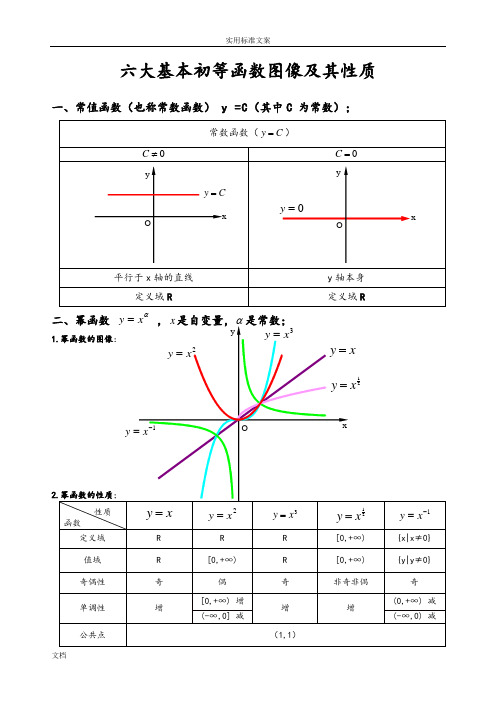
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

(完整版)基本初等函数的图形及性质

初等函数1、基本初等函数及图形基本初等函数为以下五类函数：(1)幂函数y x，是常数；1. 当 u 为正整数时，函数的定义域为区间x ( , )，他们的图形都经过原点，并当u>1 时在原点处与 X 轴相切。

且 u 为奇数时，图形对于原点对称；u 为偶数时图形对于 Y 轴对称；2. 当 u 为负整数时。

函数的定义域为除掉x=0 的全部实数。

3. 当 u 为正有理数 m/n 时， n 为偶数时函数的定义域为（0, + ）， n 为奇数时函数的定义域为（- + ）。

函数的图形均经过原点和（ 1 ,1）.假如 m>n 图形于 x 轴相切 ,假如 m<n,图形于 y 轴相切 ,且 m 为偶数时 ,还跟 y 轴对称 ;m,n 均为奇数时 ,跟原点对称.4.当 u 为负有理数时 ,n 为偶数时除 x=0 之外的一确实数.,函数的定义域为大于零的一确实数;n 为奇数时,定义域为去(2)指数函数y ax(a是常数且a 0，a 1)，x ( , )；1.当 a>1 时函数为单一增 ,当 a<1 时函数为单一减 .2.无论 x 为什么值 ,y 老是正的 ,图形在 x 轴上方 .3.当 x=0 时,y=1, 因此他的图形经过 (0,1)点 .(3)对数函数y logax(a是常数且a 0，a 1)，x (0, )；1.他的图形为于 y 轴的右方 .并经过点 (1,0)2.当 a>1 时在区间 (0,1),y 的值为负 .图形位于 x 的下方 ,在区间(1, + ),y 值为正 ,图形位于 x 轴上方 .在定义域是单一增函数 .a<1 在适用中极少用到 /(4)三角函数正弦函数y sin x ， x ( , ) ， y[ 1,1] ，余弦函数y cos x ，x( , ) ， y[ 1,1] ，x kZ ，y (, ) ，正切函数y tan x ， 2 ，k余切函数y cot x，x k，k Z，y ( , )；(5)反三角函数y arcsin x ，x [ 1,1] y [ , ]反正弦函数， 2 2 ，反余弦函数y arccosx ，x[ 1,1] ， y [0,] ，y arctan x ，x ( , ) y ( , )反正切函数， 2 2 ，反余切函数y arc cot x ，x(, ) ， y (0,) ．函数名称函数的记号函数的图形指数函数对数函数幂函数a 为随意实数这里只画出部分函数图形的一部分。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（此中 C 为常数）；常数函数（ y C ）C 0C0y yy Cx y 0xO O平行于x 轴的直线y 轴自己定义域R定义域R 二、幂函数 y x ，x是自变量，是常数；1y y x1.幂函数的图像：2y x2y xy x3y x1O x2.幂函数的性质；性质y x y x231y x1y x y x2函数定义域R R R[0,+ ∞ ){x|x ≠ 0}值域R[0,+ ∞ )R[0,+ ∞ ){y|y ≠ 0}奇偶性奇偶奇非奇非偶奇单一性增[0,+∞) 增增增(0,+∞ )减(-∞ ,0] 减(-∞ ,0)减公共点（ 1,1）1）当α为正整数时，函数的定义域为区间为x ( , )，他们的图形都经过原点，并当α>1 时在原点处与x 轴相切。

且α为奇数时，图形对于原点对称；α为偶数时图形对于y 轴对称；2）当α为负整数时。

函数的定义域为除掉x=0 的全部实数；3）当α为正有理数m时，n为偶数时函数的定义域为（0, +∞），n为奇数时函数的定义域为（-n∞ ,+∞），函数的图形均经过原点和（ 1 ,1）；4）假如 m>n 图形于 x 轴相切，假如m<n,图形于 y 轴相切，且m 为偶数时，还跟y 轴对称； m， n均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一确实数；n 为奇数时，定义域为去除 x=0 之外的一确实数。

三、指数函数 y a x(x是自变量,a是常数且a0， a1)，定义域是 R ；[ 无界函数 ]1.指数函数的图象：yy a x y a xy(a 1)(0a1)(0,1)y1(0,1)y1 O x O x2.指数函数的性质；性质y a x(a1)y a x(0 a 1)函数定义域R值域(0，+∞)奇偶性非奇非偶公共点过点 (0，1)，即 x0 时，y 1单一性在（，）是增函数在（，）是减函数1 ）当a 1时函数为单调增 , 当0a 1时函数为单调减；2 ）不论x为何值 ,y 总是正的,图形在 x 轴上方；3 ）当x 0时 , y 1, 所以它的图形通过 (0,1) 点。

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+∞) 增增增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

六大大体初等函数图像及其性质

六大大体初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的概念域为区间为),(+∞-∞∈x ，他们的图形都通过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的概念域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的概念域为（0, +∞），n 为奇数时函数的概念域为（-∞,+∞），函数的图形均通过原点和（1 ,1）；4）若是m>n 图形于x 轴相切，若是m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的概念域为大于零的一切实数；n 为奇数时，概念域为去除x=0之外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，概念域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；1(1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 老是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。

.当1>a 时，a 值越大，y 的图像越靠近y 轴；.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。

4.指数的运算法则（公式）；yxf (x xxx g ⎪⎫ ⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，概念域),0(+∞∈x [无界]1.对数的概念：若是a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

五大基本初等函数

五大基本初等函数五大基本初等函数是数学中的重要概念，用于阐明计算机科学中的方程和数学关系。

熟悉了五大基本初等函数，可以更好地理解和分析复杂的数学概念，如几何形状的性质，三角函数的解析和复数的运算和表示等。

以下是五大基本初等函数：1. 指数函数指数函数是指其函数图像呈指数状，是数学上最简单也是最常用的函数，在很多领域都有广泛应用，比如利息计算，复利计算，对数函数中出现概述等。

指数函数是由一个有意义的变量间的关系而构成的，通常用数学表示为y=a^x（其中a为任意正值），其函数图形曲线具有经典的指数曲线特点，曲线的斜率随自变量x的取值变大而变大，变化趋势是上升的。

2. 对数函数对数函数是建立在指数函数基础上的一种反函数，通常用数学表示为y=logaX（a为任意正值），它和指数函数正好相反，而且它是一种以底数为任意正数的单调变换，它的函数图像是一条函数线段，随变量x 的取值变大，函数的值也在增大，但是斜率却有在、趋向-∞的趋势，因此从该函数的性质可以看出它又是一种指数函数的相反函数。

3. 线性函数线性函数是数学中的重要函数，通常用数学表示为y=kax+b（其中a，k为任意实数），比较常见的有一元一次函数和一元二次函数，线性函数的函数图像是一条直线段，它体现了因变量和自变量之间线性的变化特征，线性函数的斜率和截距也是它的重要特征，它可以直观地表示出变量之间的函数关系，但是有些非线性的问题却无法通过线性函数来完美地描述。

4. 幂函数幂函数是类似指数函数的一种特殊函数，通常用数学表示为y= aX^k （其中a，k为任意实数），它具有指数函数强调的指数状特征，但是有所不同，它不仅包括k=1时的指数函数，还包含k>1和k<1时的函数，而函数非线性曲线一般为鹰眼状，斜率具有变大或变小的特点，它有良好的平稳特征，可以用于描述不同数量的衰减或增长的函数关系。

5. 双曲函数双曲函数是一类特殊的曲线函数，具有指数函数和对数函数的结合。

五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。

如，，，都是幂函数。

没有统一的定义域，定义域由值确定。

如,。

但在内总是有定义的，且都经过（1,1）点。

当时，函数在上是单调增加的，当时，函数在内是单调减少的。

下面给出几个常用的幂函数：的图形，如图1-1-2、图1-1-3。

图1-1-2图1-1-32.指数函数函数称为指数函数，定义域，值域；当时函数为单调增加的；当时为单调减少的，曲线过点。

高等数学中常用的指数函数是时，即。

以与为例绘出图形，如图1-1-4。

图1-1-43.对数函数函数称为对数函数，其定义域，值域。

当时单调增加，当时单调减少，曲线过（1，0）点，都在右半平面内。

与互为反函数。

当时的对数函数称为自然对数，当时，称为常用对数。

以为例绘出图形，如图1-1-5。

图1-1-54.三角函数有，它们都是周期函数。

对三角函数作简要的叙述：（１）正弦函数与余弦函数：与定义域都是，值域都是。

它们都是有界函数，周期都是，为奇函数，为偶函数。

图形为图1-1-6、图1-1-7。

图1-1-6 正弦函数图形图1-1-7 余弦函数图形（２）正切函数，定义域，值域为。

周期，在其定义域内单调增加的奇函数，图形为图1-1-8图1-1-8（３）余切函数，定义域，值域为，周期。

在定义域内是单调减少的奇函数，图形如图1-1-9。

图1-1-9（４）正割函数，定义域，值域为，为无界函数，周期的偶函数，图形如图1-1-10。

图1-1-10（５）余割函数，定义域，值域为，为无界函数，周期在定义域为奇函数，图形如图1-1-11。

图1-1-115.反三角函数反正弦函数，定义域，值域，为有界函数，在其定义域内是单调增加的奇函数，图形如图1-1-12；图1-1-12，为有界函数，在其定义域内为单调减少的非奇非偶函数，图形如图1-1-13；图1-1-13反正切函数，定义域，值域为，为有界函数，在定义域内是单调增加的奇函数，图形如图1-1-14；图1-1-14为有界函数，在其定义域内单调减少的非奇非偶函数。

（完整）六大基本初等函数图像及其性质

标准实用文案大全六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点（1,11,1））xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α，他们的图形都经过原点，并当α>1>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm 时，时，n n 为偶数时函数的定义域为（为偶数时函数的定义域为（0, +0, +0, +∞），∞），∞），n n 为奇数时函数的定义域为（为奇数时函数的定义域为（--∞,+,+∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（1 ,11 ,11 ,1）；）；4）如果m>n 图形于x 轴相切，如果m<n,m<n,图形于图形于y 轴相切，且m 为偶数时，还跟y 轴对称；轴对称；m m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，）当α为负有理数时，n n 为偶数时，函数的定义域为大于零的一切实数；为偶数时，函数的定义域为大于零的一切实数；n n 为奇数时，定义域为去除x=0以外的一切实数。

高中数学-函数图像详解

高中数学-函数图像详解基本初等函数的图像1. 一次函数性质：一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减2. 二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac 决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3. 反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图< span>不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的6. 幂函数y=x^a性质：先看第一象限，即x>0时，当a>1时，函数越增越快；当0<a<1时，函数越增越慢；当a<0时，函数单调递减；然后当x<0时，根据函数的定义域与奇偶性判断函数图像即可。

< span>7. 对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

函数图形的变换注意：对于函数图像的变换，有的时候，看到解析式，可能会有两种以上的变换，尤其是针对x轴上的，那么此时，一定要根据上面的规则，判断好顺序，否则顺序错了，可能就没办法经过变换得到了！例如：画出函数y=ln|2-x|的图像通过研究这个函数解析式，我们知道此函数是由基本初等函数y=lnx通过变换而来，那么这个函数经过了几步变换呢？变换的顺序又是如何？下面我们一起来看一看。

通过解析式x上附加的东西，我们会发现，会有对称变换，x前面加了负号，还有翻折变换，x上面还有绝对值，还有平移变换，前面加了一个2，既然有3种变换，那么顺序如何呢？牢记住一点：针对x轴上的变换，那就一定要看x这个符号有啥变化。

基本初等函数及其图像

g( x ) 的值域与 f ( u) 的定义域之交集是空集.
23
y arshx ln( x x 2 1 ).
D : ( , )
奇函数,
y arshx
在 (,) 内单调增加 .
17
反双曲余弦 y archx
y archx ln( x x 2 1 ).
y archx
D : [1, )
在 [1,) 内单调增加.
D {x | x R, x (2n 1) } 2
8

余割函数
1 y csc x sin x
y csc x
D {x | x R, x n }
9
5.反三角函数
反正弦函数 y arcsin x
y arcsin x
y A rc sin x
10
反余弦函数 y arccos x
y f (u) u,
y f ( u) ln u,
u g( x ) x x 2
u g( x ) sin x 1
22
思考题解答
(1) y f [ g( x )] x x2
1 x D { x | 0 x 1}, f ( D ) [0, ] 2 ( 2) 不能． g( x ) sin x 1 0
y arccos x
y A rccos x
11
反正切函数 y arctan x
y arctan x
y A rc tan x
12
反余切函数 y arccot x
y arccot x
y A rc cot x
常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数.

六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m aa a +=⋅(2)nm nmaa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。