定轴转动和转动定律
合集下载
刚体定轴转动转动定律

dv c Fe m dt
c
c
c
8/11/2014 3:31:32 PM 4
4.1 刚体的定轴转动 研究作定轴转动的刚体时,只需选取刚体上任意 一点并确定它的运动状态。由于该点绕固定轴线在垂 直于转轴的平面内作圆周运动,取垂直于转轴的平面 为参考面,刚体的位置由确定。 作定轴转动的刚体 可用角位移、角速度、 角加速度描述。
1
4.1 刚体的定轴转动
一.基本概念 如果我们所研究的物体在运动过程中,它的大 小形状基本不变,我们将其抽象为物体在外力的作 用下,内部任意两点间的距离保持恒定,这种理想 化的物体我们称之为刚体。 刚体的运动可分为平 动和转动。若刚体在运动 过程中,所有点的轨迹完 全相等,或者任意两点的 连线总是平行于它的初始 位置。这种运动称作平动。
17
4.2 刚体的转动定律
例题 求通过匀质细棒中垂线和端点垂线的转动惯量。 解: 棒相对通过质心的转动惯量 J x 2dm l / 2 m dm dx dx l
m l/2 2 J x dx l l / 2 l/2 m x 3 l / 2 3l ml 2 J 12
d d , dt dt
8/11/2014 3:31:32 PM 5
4.1 刚体的定轴转动
平面上刚体的运动可看作是刚体的平动(可以 用质心运动表示)和刚体绕过质心转轴转动(刚体 定轴转动)的叠加。 手榴弹的运动
8/11/2014 3:31:32 PM 6
数理学院
大学物理教学中心
College of Mathematics & Physics
8/11/2014 3:31:32 PM
l/2
y
o
x
dx
c
c
c
8/11/2014 3:31:32 PM 4
4.1 刚体的定轴转动 研究作定轴转动的刚体时,只需选取刚体上任意 一点并确定它的运动状态。由于该点绕固定轴线在垂 直于转轴的平面内作圆周运动,取垂直于转轴的平面 为参考面,刚体的位置由确定。 作定轴转动的刚体 可用角位移、角速度、 角加速度描述。
1
4.1 刚体的定轴转动
一.基本概念 如果我们所研究的物体在运动过程中,它的大 小形状基本不变,我们将其抽象为物体在外力的作 用下,内部任意两点间的距离保持恒定,这种理想 化的物体我们称之为刚体。 刚体的运动可分为平 动和转动。若刚体在运动 过程中,所有点的轨迹完 全相等,或者任意两点的 连线总是平行于它的初始 位置。这种运动称作平动。
17
4.2 刚体的转动定律
例题 求通过匀质细棒中垂线和端点垂线的转动惯量。 解: 棒相对通过质心的转动惯量 J x 2dm l / 2 m dm dx dx l
m l/2 2 J x dx l l / 2 l/2 m x 3 l / 2 3l ml 2 J 12
d d , dt dt
8/11/2014 3:31:32 PM 5
4.1 刚体的定轴转动
平面上刚体的运动可看作是刚体的平动(可以 用质心运动表示)和刚体绕过质心转轴转动(刚体 定轴转动)的叠加。 手榴弹的运动
8/11/2014 3:31:32 PM 6
数理学院
大学物理教学中心
College of Mathematics & Physics
8/11/2014 3:31:32 PM
l/2
y
o
x
dx
一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量

二、刚体定轴转动的转动定律
~利用力矩定义+牛顿第二定律,研究刚体作定 轴转动的动力学规律。 设:oz为定轴, 为 P 刚体中任一质点 i ,其 质量为 ∆ m i。质点 iv ur 受外力 F i ,内力 F i ′ 的作用,均在与 O z 轴 相垂直的同一平面内。 ①牛顿第二定律: ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标:切向、法向;
三、转动惯量 J 1.转动惯量的物理意义: 当以相同的力矩分别作用于两个绕定轴转动的不同 刚体时,它们所获得的角加速度一般是不一样的,转 动惯量大的刚体所获得的角加速度小,即角速度改变 得慢,也就是保持原有转动状态的惯性大;反之,转 动惯量小的刚体所获得的角加速度大,即角速度改变 得快,也就是保持原有转动状态的惯性小。因此,转 动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素:①刚体的质量;②转轴的 位置;③刚体的形状。 实质与转动惯量有关的只有前两个因素。形状即质量 分布,与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的 转动惯量。 B 解:取如图坐标,dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量 解:取离轴线距离相等的点的 集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩 内力矩
③对所有质元的同样的式子求和:
刚体定轴转动定律

角称为角坐标(或角位置)。 角坐标为标量。但可有正负。
o
P
x
2.角位移
描写刚体位置变化的物理量。
角坐标的增量:
称为刚体的角位移
y v2 p v1
P
3.角速度
R
x
描写刚体转动快慢和方向
的物理量。
角速度 lim d
t0 t dt 方向:满足右手定则,沿刚体转动方向右旋大拇指指向。
角速度是矢量,但对于刚体定轴 转动角速度的方向只有两个,在表 示角速度时只用角速度的正负数值 就可表示角速度的方向,不必用矢 量表示。
11mb 2
例4、半径为 R 质量为 M 的 圆环,绕垂直于圆环平面的 质心轴转动,求转动惯量J。
解: J R2dm MR 2
M o R dm
例5、半径为 R 质量为 M 的圆盘,绕垂直于圆盘 平面的质心轴转动,求转动惯量 J。
解:分割圆盘为圆环
dm
M
R2
2
rdr
J r2dm
M
dr
R
0
t 细杆绕一端的转动惯量
J 1 ml 2 3
摩擦阻力
t
例8、质量为 m1 和m2 两个物体, 跨在定滑轮上 m2 放在光滑的桌 面上,滑轮半径为 R,质量为 M,求:m1 下落的加速度,和 绳子的张力 T1、T2。
解:m1 g T1 m1a (1)
T2 m2a
b)作圆周运动的质点的角动量 L= r m v
c)角动量是描述转动状态的物理量;
P L
d)质点的角动量又称为动量矩。
or
dL
d (r mv)
dr
mv
r
d (mv)
r
F
dt
o
P
x
2.角位移
描写刚体位置变化的物理量。
角坐标的增量:
称为刚体的角位移
y v2 p v1
P
3.角速度
R
x
描写刚体转动快慢和方向
的物理量。
角速度 lim d
t0 t dt 方向:满足右手定则,沿刚体转动方向右旋大拇指指向。
角速度是矢量,但对于刚体定轴 转动角速度的方向只有两个,在表 示角速度时只用角速度的正负数值 就可表示角速度的方向,不必用矢 量表示。
11mb 2
例4、半径为 R 质量为 M 的 圆环,绕垂直于圆环平面的 质心轴转动,求转动惯量J。
解: J R2dm MR 2
M o R dm
例5、半径为 R 质量为 M 的圆盘,绕垂直于圆盘 平面的质心轴转动,求转动惯量 J。
解:分割圆盘为圆环
dm
M
R2
2
rdr
J r2dm
M
dr
R
0
t 细杆绕一端的转动惯量
J 1 ml 2 3
摩擦阻力
t
例8、质量为 m1 和m2 两个物体, 跨在定滑轮上 m2 放在光滑的桌 面上,滑轮半径为 R,质量为 M,求:m1 下落的加速度,和 绳子的张力 T1、T2。
解:m1 g T1 m1a (1)
T2 m2a
b)作圆周运动的质点的角动量 L= r m v
c)角动量是描述转动状态的物理量;
P L
d)质点的角动量又称为动量矩。
or
dL
d (r mv)
dr
mv
r
d (mv)
r
F
dt
定轴转动和转动定律

应用场景:定轴转动、 行星运动、弹簧振子 等。
实例分析:单摆运动 中,摆球在摆动过程 中机械能守恒,可以 求出摆球摆动的最大 高度等。
结论:机械能守恒定 律是物理学中一个非 常重要的基本规律, 在许多实际问题中有 广泛的应用。
实例分析
实例名称:单摆
实例分析:根据定轴转动的机械能 守恒定律,单摆的摆动周期与振幅 无关,只与摆长有关。
定轴转动和转动定律
汇报人:XX
定轴转动的定义 转动定律 转动惯量 定轴转动的动能和势能
定轴转动的机械能守恒定律
定轴转动的定义
定义
定轴转动是指刚体 绕某一固定轴线转 动的运动。
定轴转动时,刚体 的角速度矢量与转 动轴线重合。
定轴转动时,刚体 上任意一点绕固定 轴线的速度大小不 变。
定轴转动时,刚体 上任意一点绕固定 轴线的加速度大小 不变。
添加标题
添加标题
添加标题
添加标题
实例描述:单摆在摆动过程中,由 于只有重力做功,所以机械能守恒。
实例结论:通过实例分析,验证了 定轴转动的机械能守恒定律的正确 性。
THANK YOU
汇报人:XX
公式:Iω=M,其中I是转动惯量,ω是角速度,M是外力矩矢量。
意义:定轴转动定律描述了质点系在转动过程中动量矩矢量的变化规律, 是经典力学的基本定律之一。
应用:在工程、物理、天文等领域中,定轴转动定律被广泛应用于分析旋 转运动系统的动力学特性和运动规律。
转动定律的应用
描述定轴转动的 物体在转动过程 中受到的力矩和 角速度的变化关 系。
转动惯量的大小 与质量、转动半 径有关
转动惯量具有方 向性,与转轴的 选取有关
转动惯量是刚体 转动时动量矩的 量度
16定轴转动刚体的角动量转动惯量和定轴转动定律

m
I = I C + md
2
刚体绕质心轴的 转动惯量最小。 转动惯量最小。
12
例5:如图所示刚体对经过棒端且与棒垂直的轴 : 的转动惯量如何计算? 棒长为 棒长为L、圆半径为R) 的转动惯量如何计算?(棒长为 、圆半径为 )
1 2 I L1 = m L L 3 1 I o = mo R 2
1 1 2 I = m LL + moR 3 2
7
.转动惯量的计算 2 .转动惯量的计算
Δm 2 分立质点系 I = ∑( iri ) = ∑ Ii
质量连续分布的刚体
I = ∫ r dm
2
dm为质量元,简称质元。其计算方法如下: 为质量元,简称质元。其计算方法如下:
质量为线分布 质量为面分布
dm = λ dl
dm = σ ds 质量为体分布 dm = ρ dV
Fiτ ri + ∑ f iτ r i = ∑ ∆mi ai ri = ∑ ∆mi ri 2 β ∑
∑ F τ r + ∑ f τ r = ∑ ∆m a r = ∑ ∆m r
i i i
2
⇓ 合外力矩
⇓
i
i i i
i i
β
内力矩之和
刚体定轴 转动定律! 转动定律!
⇓ Iβ
合外力矩) 用M表示∑Fit ri (合外力矩),有: M = Iβ 刚体所受的对于某一固定转动轴的合外力矩等于 刚体所受的对于某一固定转动轴的合外力矩等于 某一固定转动轴 刚体对此转轴的转动惯量与刚体在此合外力矩 对此转轴的转动惯量与刚体在此合外力矩作用 刚体对此转轴的转动惯量与刚体在此合外力矩作用 下所获得的角加速度的乘积。 下所获得的角加速度的乘积。 注意几点: 注意几点: 1. 是矢量式(在定轴转动中力矩只有两个方向)。 是矢量式(在定轴转动中力矩只有两个方向)。 2. M、I、β是对同一轴而言的。 是对同一轴而言的。 3. 具有瞬时性,是力矩的瞬时效应。 具有瞬时性,是力矩的瞬时效应。 4. 转动惯量 是刚体转动惯性大小的量度。 转动惯量I是刚体转动惯性大小的量度 是刚体转动惯性大小的量度。 5.刚体转动定律的地位与牛顿第二定律相当。 刚体转动定律的地位与牛顿第二定律相当。 刚体转动定律的地位与牛顿第二定律相当
力矩 刚体定轴转动的转动定律
dJ R dm
2
第3章 刚体力学基础
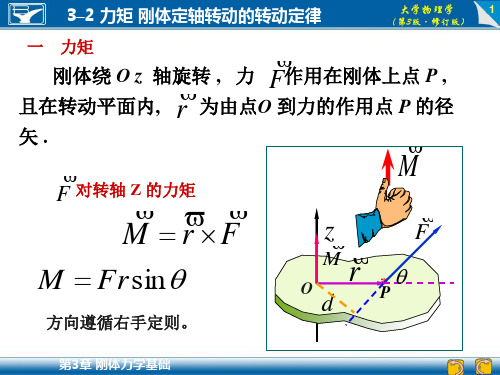
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的 转动惯量为
解 (1) M k 2 ,故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
大学物理Ⅰ刚体定轴转动的转动定律

第五章 刚体的定轴转动
5.1刚体运动的描述
一.刚体
刚体:在外力作用下,形状和大小都不发生变 化的物体 . (任意两质点间距离保持不变的特殊质点 组)
(1)刚体的运动
刚体的运动形式:平动、转动 .
平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线 .
F F11 F
其中F11对转轴的力 矩为零,故 F 对转轴的力矩
M zk r F
z
k F11
F
O r
F
M z rF sin
2)合力矩等于各分 力矩的 矢量和 M M1 M2 M3
第五章 刚体的定轴转动
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
rj
d ri
i
j
Fji Fij
M
rdf
l
grdr
0
1 gl 2
2
1 mgl
2
dm dl
dm ds
dm dV
其中、、分别
为质量的线密度、 面密度和体密度。
线分布
面分布
体分布
第五章 刚体的定轴转动
m 例1 一质量为 、长为 l 的均匀细长棒,求通过棒中
心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质
fi
第五章 刚体的定轴转动
M i外 M i内 miri2
i
i
i
Mi内 0
i
M i外 ( miri2 )
i
i
z
O rj
5.1刚体运动的描述
一.刚体
刚体:在外力作用下,形状和大小都不发生变 化的物体 . (任意两质点间距离保持不变的特殊质点 组)
(1)刚体的运动
刚体的运动形式:平动、转动 .
平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线 .
F F11 F
其中F11对转轴的力 矩为零,故 F 对转轴的力矩
M zk r F
z
k F11
F
O r
F
M z rF sin
2)合力矩等于各分 力矩的 矢量和 M M1 M2 M3
第五章 刚体的定轴转动
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
rj
d ri
i
j
Fji Fij
M
rdf
l
grdr
0
1 gl 2
2
1 mgl
2
dm dl
dm ds
dm dV
其中、、分别
为质量的线密度、 面密度和体密度。
线分布
面分布
体分布
第五章 刚体的定轴转动
m 例1 一质量为 、长为 l 的均匀细长棒,求通过棒中
心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质
fi
第五章 刚体的定轴转动
M i外 M i内 miri2
i
i
i
Mi内 0
i
M i外 ( miri2 )
i
i
z
O rj
刚体的定轴转动和转动定律

受力: F Ft Fn
力矩:M r (Ft Fn )
r Ft rFt k
M F r ma r
z
M
Ft F
O r m
Fn
mr2
at r
即: M mr 2
3 – 2 力矩 转动定律 转动惯量
2、刚体转动定律
质元 m j 受力为:
右手螺旋定则
第三章 刚体的转动
3– 1 刚体的定轴转动
4、角加速度(矢量)
第三章 刚体的转动
大小: d
dt
方向: 若 2 > 1 则 与角速度同向, 若 2 < 1 则 与角速度反向。
3– 1 刚体的定轴转动
第三章 刚体的转动
二、匀变速转动公式
匀变速转动:转动的角加速度为恒量的运动。
J R 2π r3dr π R4 所以 J 1 mR2
0
2
2
3 – 2 力矩 转动定律 转动惯量
第三章 刚体的转动
例3 :质量为m、高为h、半径为r的均匀圆柱体,求其对 圆柱中心的转动轴的转动惯量?
解:dm dV 2 r h dr
其中:
m V
3 – 2 力矩 转动定律 转动惯量
第三章 刚体的转动
三 转动惯量 J mjrj2 , J r 2dm
1、物理意义:
j
描述刚体转动过程中转动惯性大小的物理量.( 转动
惯量的大小取决于刚体的质量、形状及转轴的位置 .)
2、转动惯量的计算方法:
1)质量离散分布刚体的转动惯量:
J mjrj2 m1r12 m2r22
对质量面分布的刚体: dm dS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚体是一种理想模型,其形状和大小始终保持不变。刚体的运动可分为平动和转动,而定轴转动是刚体上所有点绕同一轴线做瞬时圆周运动。在定轴转动中,各质点的角位移、角速度、角加速度相同,并可通过一系列公式来描述其运动状态。力矩是力对转轴的转动效果,它的大小等于力与力臂的乘积,方向由右手法则确定。转动定律指出,刚体绕定轴转动时,其角加速度与所受的合外力矩成正比,与刚体的转动惯量成反比。转动惯量是描述刚体转动惯性大小的物理量,它等于各质点的质量与各质点到转轴距离平方的乘积之和。转动惯量的大小受刚体的总质量、质量的分布以及转轴位置的影响。通过计算转动惯量,可以进一步了解刚体的转动特性。此外的理解和应用。
