一次函数综合应用(讲义及习题)
一次函数应用题(讲义及答案). (1)

一次函数应用题(讲义)➢课前预习1. 一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B 两村相距10 km;②出发1.25 h 后两人相遇;③出发2 h 后甲到达C 村庄;④甲每小时比乙多骑行8km.其中正确的个数是()A.1 个B.2 个C.3 个D.4 个➢知识点睛一次函数应用题的处理思路:1.理解题意,梳理信息结合图象、文字信息理解题意,将实际场景与图象中轴、点、线对应起来理解分析.①看轴,明确横轴和纵轴表示的实际意义.②看点,明确起点、终点、状态转折点表示的具体意义,还原实际情景,提取每个点对应的数据.③看线,观察每段线的变化趋势(增长或下降等),分析每段数据的变化情况.2.辨识类型,建立模型①将所求目标转化为函数元素,借助图象特征,利用表达式进行求解;②将图象中的点坐标还原成实际场景中的数据,借助实际场景中的等量关系列方程求解.3.求解验证,回归实际1➢精讲精练1.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2 400 米,先到终点的人原地休息.已知甲先出发4 分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60 米/分;②甲走完全程用了40 分钟;③乙用16 分钟追上甲;④乙走完全程用了30 分钟;⑤乙到达终点时,甲离终点还有300 米.其中正确的结论是.(填序号)2.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地的过程中y 与x 之间的函数关系,结合图象解答下列问题:(1)求线段AB 所在直线的函数解析式以及甲、乙两地之间的距离;(2)求a 的值;(3)出发多长时间,两车相距140 千米?3.甲、乙两台机器共同加工一批零件,一共用了6 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数y(个)与甲的加工时间x(h)之间的函数图象为折线OA-AB-BC,如图所示,结合图象解答下列问题:(1)这批零件一共有个,甲机器每小时加工个零件,乙机器排除故障后每小时加工个零件;(2)求y 与x 之间的函数关系式;(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?4.在一条笔直的公路上依次有A,C,B 三地,甲、乙两人同时出发,甲从A 地骑自行车去B 地,途经C 地休息1 分钟,继续按原速骑行至B 地,甲到达B 地后,立即按原路原速返回A 地;乙步行从B 地前往A 地.甲、乙两人距A 地的路程y(米)与时间x(分)之间的函数关系如图所示,结合图象解答下列问题:(1)甲的骑行速度为米/分,点M 的坐标为;(2)求甲返回时距A 地的路程y 与时间x 之间的函数关系式(不需要写出自变量的取值范围);(3)甲从A 地出发,经过多长时间在返回途中追上乙?5.某工厂安排甲、乙两个运输队各从仓库调运物资300 吨,两队同时开始工作,甲运输队工作3 天后因故停止,2天后重新开始工作,由于工厂调离了部分工人,甲运输队的工作效率1降低到原来的;乙运输队在整个运输过程中工作效率保持2不变.甲、乙运输队调运物资的数量y(吨)与甲的工作时间x(天)的函数图象如图所示,结合图象解答下列问题:(1)a= ,b= .(2)求甲运输队重新开始工作后,甲运输队调运物资的数量y(吨)与工作时间x(天)的函数关系式;(3)直接写出乙运输队比甲运输队多运50 吨物资时x 的值.6.快、慢两车分别从相距480 千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1 小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图,结合图象解答下列问题:(1)慢车的行驶速度为千米/时,a= ;(2)求快车的速度和B 点坐标;(3)两车出发后几小时相距的路程为200 千米?请直接写出答案.⎨ ⎩【参考答案】➢ 课前预习1. D➢ 精讲精练1. ①②④2. (1)线段 AB 所在直线的函数解析式为 y = -140x + 280 ;甲乙两地之间的距离为 280 千米;(2)a 的值为 210;(3)出发 1 h 或 3 h 时,两车相距 140 千米.3. (1)270,20,40;⎧50x (0 < x ≤1) (2) y = ⎪20x + 30(1 < x ≤3);⎪60x - 90(3 < x ≤ 6) (3)在整个加工过程中,甲加工 1.5 小时或 4.5 小时时, 甲与乙加工的零件个数相等.4. (1)240,(6,1200);(2) y = -240x + 2640 ;(3)甲从 A 地出发,经过 8 分钟在返回途中追上乙;5. (1)5,11;(2) y = 25x + 25 (5 ≤ x ≤11) ;(3)乙运输队比甲运输队多运 50 吨物资时,x 的值为 6 或 9.6. (1)60,360;(2) 快车的速度为 120km/h ,B 点的坐标为(4,0);(3) 两车出发14 h , 34 h 或14 h 时,相距的路程为 2009 9 3千米.。
一次函数的应用(知识点+例题)

1.(2013•鄂州)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:(1)轿车到达乙地后,货车距乙地多少千米?(2)求线段CD对应的函数解析式.(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).一次函数的应用知识点一:一次函数与坐标轴交点和面积问题1:交点问题一次函数b kx y +=的图象是经过(0,b )和(-kb,0)两点。
【典型例题】1.直线y=-x+2与x 轴的交点坐标是 ,与y 轴的交点坐标是 2.直线y=-x -1与x 轴的交点坐标是 ,与y 轴的交点坐标是 3.函数y=x+1与x 轴交点为( )A .(0,-1)B .(1,0)C .(0,1)D .(-1,0)4.直线y=-32x+3与x 轴、y 轴所围成的三角形的面积为( ) A .3 B .6 C .34 D .325.直线y=-2x-4交x 轴、y 轴于点A 、B ,O 为坐标原点,则S △AOB = 。
6.若直线y=3x+b 与两坐标轴所围成的三角形的面积是6个单位,则b 的值是 。
7.如图所示,已知直线y=kx-2经过M 点,求此直线与x 轴交点坐标和直线与两坐标轴围成三角形的面积.2:面积问题面积:一次函数y=kx+b 与x 、y 轴所交的两点与原点组成的三角形的面积为2b k(1):两直线交点坐标必满足两直线解析式,求交点就是联立两直线解析式求方程组的解。
(2):复杂图形“外补内割”即:往外补成规则图形,或分割成规则图形(三角形)。
(3):往往选择坐标轴上的线段作为底,底所对的顶点的坐标确定高。
1. 直线经过(1,2)、(-3,4)两点,求直线与坐标轴围成的图形的面积。
一次函数的综合应用
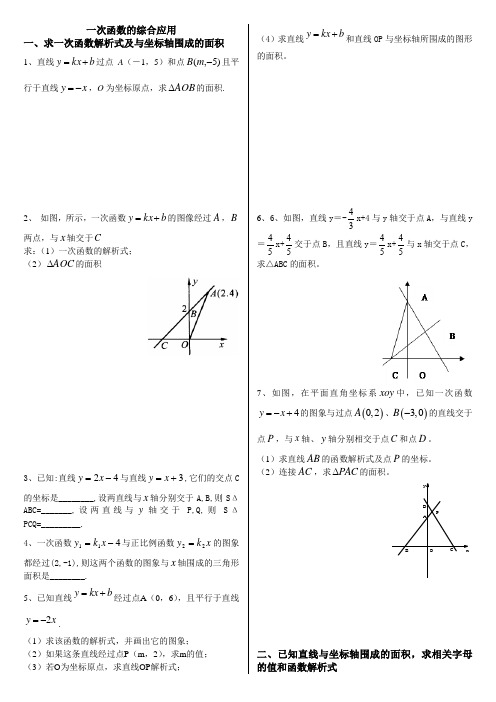
一次函数的综合应用一、求一次函数解析式及与坐标轴围成的面积1、直线b kx y +=过点A (-1,5)和点)5,(-m B 且平行于直线x y -=,O 为坐标原点,求AOB ∆的面积.2、 如图,所示,一次函数b kx y +=的图像经过A ,B 两点,与x 轴交于C 求:(1)一次函数的解析式; (2)AOC ∆的面积3、已知:直线42-=x y 与直线3+=x y ,它们的交点C 的坐标是________,设两直线与x 轴分别交于A,B,则S ΔABC=_______,设两直线与y 轴交于P,Q,则S ΔPCQ=_________.4、一次函数411-=x k y 与正比例函数x k y 22=的图象都经过(2,-1),则这两个函数的图象与x 轴围成的三角形面积是________.5、已知直线y kx b =+经过点A (0,6),且平行于直线2y x =-.(1)求该函数的解析式,并画出它的图象; (2)如果这条直线经过点P (m ,2),求m 的值; (3)若O 为坐标原点,求直线OP 解析式;(4)求直线y kx b =+和直线OP 与坐标轴所围成的图形的面积。
6、6、如图,直线y =-34x+4与y 轴交于点A ,与直线y =54x+54交于点B ,且直线y =54x+54与x 轴交于点C ,求△ABC 的面积。
7、如图,在平面直角坐标系xoy 中,已知一次函数4y x =-+的图象与过点()0,2A 、()3,0B -的直线交于点P ,与x 轴、y 轴分别相交于点C 和点D 。
(1)求直线AB 的函数解析式及点P 的坐标。
(2)连接AC ,求PAC ∆的面积。
OxyPD CBA二、已知直线与坐标轴围成的面积,求相关字母的值和函数解析式8、直线b x y +=2与坐标轴围成的三角形的面积是9,求函数解析式。
9、已知直线y kx b =+经过点5,02⎛⎫ ⎪⎝⎭,且与坐标轴所围成的三角形面积为254,求该直线的解析式。
2024年中考数学复习(全国版)第11讲 一次函数的应用(讲义)(解析版)

目录
一、考情分析
二、知识建构
题型 01 分配问题 题型 02 最大利润问题 题型 03 行程问题 题型 04 几何问题 题型 05 工程问题 题型 06 分段计费问题 题型 07 体积问题 题型 08 调运问题 题型 09 计时问题 题型 10 现实生活相关问题Fra bibliotek考点要求
� = 1400� + 6000 � > 20 (2)解:依题意,把� = 25 代入� = 1600�, 则甲旅行社:� = 1600 × 25 = 40000; 因为 25 > 20 所以把� = 25 代入� = 1400� + 6000 中, 则乙旅行社:� = 1400 × 25 + 6000 = 41000; 因为 41000 > 40000, 所以选择甲旅行社. 【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函 数的性质解答. 【变式 1-2】(2022·陕西西安·统考三模)某校为改善办学条件,计划购进 A、B 两种规格的书架,经市场调 查发现有线下和线上两种购买方式,具体情况如表:
题型 01 分配问题
【例 1】(2023·陕西咸阳·校考一模)某文具商店文具促销给出了两种优惠方案:①买一支钢笔赠送一本笔记 本,多于钢笔数的笔记本按原价收费;②钢笔和笔记本均按定价的八折收费.已知每支钢笔定价为 15 元, 每本笔记本定价为 4 元.某顾客准备购买 x 支钢笔和笔记本 � + 10 本,设选择第一种方案购买所需费用为 �1元,选择第二种方案购买所需费用为�2元. (1)请分别写出�1,�2与 x 之间的关系式: , ; (2)若该顾客准备购买 10 支钢笔,且只能选择其中一种优惠方案,请你通过计算说明选择哪种方案更为优惠. 【答案】(1)�1 = 15� + 40, �2 = 15.2� + 32, (2)选择方案②更为优惠,见解析 【分析】(1)根据两种优惠方案,列出函数关系式即可; (2)将� = 10 代入两个函数解析式,求出函数值,进行比较即可. 【详解】(1)解:由题意,得:�1 = 15� + 4 × � + 10 − � = 15� + 40,�2 = 15� + 4 � + 10 × 80% = 15.2� + 32; (2)当� = 10 时,�1 = 15 × 10 + 40 = 190;�2 = 15.2 × 10 + 32 = 184 ∵ 190 > 184, ∴选择方案②更为优惠. 【点睛】本题考查一次函数的实际应用,读懂题意,正确的列出一次函数的解析式,是解题的关键. 【变式 1-1】(2023·陕西西安·校考一模)李老师计划组织学生暑假去北京研学旅行,经了解,现有甲、乙
一次函数综合应用(习题及解析)精选全文

精选全文完整版(可编辑修改)一次函数综合应用(习题及解析)例题示范例 1:一次函数 y=kx+b 的图象经过点 A(0,3),且与正比例函数y=-x 的图象相交于点 B,点 B 的横坐标为-1,求一次函数的表达式.思路分析:从完整的表达式入手,由正比例函数过点 B,可得 B 点坐标,然后由一次函数 y=kx+b 的图象经过点 A,B,待定系数法求解.解:∵点 B 在正比例函数 y=-x 的图象上,且点 B 的横坐标为-1∴B(-1,1)将 A(0,3),B(-1,1)代入 y=kx+b,得b 3k b 1k 2b 3∴一次函数的表达式为 y=2x+3.巩固练习一次函数 y=2x+a 和 y=-x+b 的图象都经过点 A(-2,0),且与 y 轴分别交于点 B,C,那么△ABC 的面积为.直线 y=kx+b 和直线 y 1 x 3 与 y 轴的交点相同,且经2过点(2,-1),那么这个一次函数的表达式是.一次函数 y=kx-3 经过点 M,那么此直线与 x 轴、y 轴围成的三角形的面积为.在平面直角坐标系中,O 为原点,直线 y=kx+b 交 x 轴于点A(-2,0),交 y 轴于点 B、假设△AOB 的面积为 8,那么 k 的值为直线 y=kx+1,y 随 x 的增大而增大,且与直线 x=1,x=3以及 x 轴围成的四边形的面积为 10,那么 k 的值为.一次函数 y=kx+b 的图象经过点(0,2),且与坐标轴围成的三角形的面积为 2,那么这个一次函数的表达式是如图,在平面直角坐标系中,一次函数 y 1 x 6 的图象与2x 轴、y 轴分别交于点 A,B,与正比例函数 y=x 的图象交于第一象限内的点 C、〔1〕求 A,B,C 三点的坐标;〔2〕S△AOC= .如图,直线 y=2x+3 与直线 y=-2x-1 相交于 C 点,并且与 y 轴分别交于 A,B 两点.〔1〕求两直线与 y 轴交点 A,B 的坐标及交点 C 的坐标;〔2〕求△ABC 的面积.一次函数 y=2x-3 的图象与 y 轴交于点 A,另一个一次函数图象与 y 轴交于点 B,两条直线交于点 C,C 点的纵坐标为 1,且 S△ABC=5,求另一条直线的解析式.一次函数 y=kx+b 的图象经过点(0,10),且与正比例函数y 1 x 的图象相交于点(4,a).2〔1〕求一次函数 y=kx+b 的解析式;〔2〕求这两个函数图象与 y 轴所围成的三角形的面积.如图,直线 y=kx+4 与 x 轴、y 轴分别交于点 A,B,点 A的坐标为(-3,0),点 C 的坐标为(-2,0).〔1〕求 k 的值;〔2〕假设 P 是直线 y=kx+4 上的一个动点,当点 P 运动到什么位置时,△OPC 的面积为 3?请说明理由.【参考答案】巩固练习1.6 2.y=-2x+3 3.9 44.4 或-4 5.2 6. y x 2或y ﹣x 2 7.〔1〕A(12,0),B(0,6),C(4,4) 〔2〕24 8.〔1〕A(0,3) B(0,-1) C(-1,1);〔2〕2 9. y 1 x 2 或 y 9 x 8 2 210. 〔1〕 y 2x 10 〔2〕2011. 〔1〕 k 在这一学年中,不仅在业务能力上,还是在教育教学上都有了一定的提高。
一次函数的应用(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)

专题4.18一次函数的应用(知识梳理与考点分类讲解)【知识点1】确定一次函数的表达式1.正比例函数的表达式为y=kx(k为常数k≠0),只有一个待定系数k,因而只需一个条件就可以求得k的值,从而确定表达式。
2.一次函数一次函数的表达式y=kx+b(k、b为常数k≠0)中,只有确定k,b的值,才能得到表达式,所以利用待定系数法确定一次函数的表达式时需要两个条件,即两个变量的两对对应值才能求出k和b的值,从而确定表达式。
特别提醒:在正比例函数y=kx(k为常数k≠0)中,只有一个待定系数k,只需要一个除(0,0)外的条件即可求出k的值,在一次函数y=kx+b(k、b为常数k≠0)中,有两个待足系数k,b因而需要两个条件才能求出k和b的值.【知识点2】建立一次函数的模型解实际应用题利用一次函数的图象解决实际问题,关键是找到图象中两个变量之间的数量关系,把实际问题抽象、升华为一次函数模型,即建模,再利用一次函数的相关性质解决实际问题,常见类型如下:(1)题目中已知一次函数的关系式,可直接运用一次函数的性质求解;(2)题目中没有给出一次函数的关系式,而是通过语言、表格或图象给出一次函数的情境,这时需要先根据题目给出的信息求出一次函数的关系式,再利用一次函数的性质解决实际问题.特别提醒:实际问题中的函数图象一般是射线或线霈结合题薏理解段,它们的图象是射线或线段的原因,应用一次函数解决实际问题的关键是建立一次函数模型,同时注薏实际问题中目变量的取值范围要使实际问题有薏义【知识点3】一次函数与一元一次方程之间的关系一次函数y=kx+b(k、b为常数k≠0)与一元一次方程kx+b=0(k,b为常数,k≠0)的关系数:函数y=kx+b,函数值y=0时自变量x值是方程kx+b=0的解;形:函数y=kx+b图象与x交点的横坐标是方程kx+b=0的解.特别提醒:实际问题中的函数图象一般是射线或线段,需结合题薏理解它们的图象是射线或线段的原因,应用一次函数解决实际问题的关键是建立一次函数模型,同时注意实际问题中自变量的取值范围要使实际问题有意义。
一次函数综合应用(讲义及解析)

一次函数综合应用(讲义及解析)课前预习如图,直线 l1 的表达式为 y=-3x+3,且 l1 与 x 轴相交于点 D,直线 l 2 经过 A,B 两点,直线 l1,l2 相交于点 C、〔1〕点 D 的坐标为;〔2〕直线 l2 的表达式为;〔3〕点 C 的坐标为.如图,在平面直角坐标系中,点 A(2,0),点 B(0,4).〔1〕△AOB 的面积为;〔2〕点 P 是 y 轴上一点,假设S为.△AOP 1S2△AOB,那么点 P的坐标知识点睛一次函数综合题,往往涉及到多个函数及坐标间的相互转化,梳理信息,理解题意是其关键:理解题意:①确定坐标与表达式间的对应关系;②函数图象不确定时,考虑分类讨论.具体操作:从完整表达式或坐标入手,利用代入或联立的方式进行相互转化.精讲精练直线 l1 与 l2 相交于点 P,直线 l1 的表达式 y=2x+3,点 P 的横坐标为-1,且 l2 交 y 轴于点 A(0,-1).那么直线 l2 的表达式为.函数 y 1 x b 的图象与 x 轴、y 轴分别交与点 A,B,3与函数 y=x 的图象交于点 M,点 M 的横坐标为 3,那么点 A 的坐标为.一次函数 y=kx+b 的图象经过点(-2,5),且与 y 轴相交于点 P,直线与 y 轴相交于点 Q,点 Q 恰与点 P 关于 x 轴对称,那么这个一次函数的表达式为.如图,直线 l1:y=2x+3,直线 l2:y=-x+5,直线 l1,l2 与x 轴分别交于点 B,C,l1,l2 相交于点 A、那么 S△ABC= .如图,直线 y=2x+m〔m>0〕与 x 轴交于点 A(-2,0),直线y=-x+n 〔n>0〕与 x 轴、y 轴分别交于点 B,C 两点,并与直线 y=2x+m〔m>0〕相交于点 D,假设 AB=4.〔1〕求点 D 的坐标;〔2〕求出四边形 AOCD 的面积.直线 y mx 3 中,y 随 x 的增大而减小,且与直线 x=1,x=3 和 x 轴围成的四边形的面积为 8,那么 m=_ .直线 y kx 6 经过第【一】【三】四象限,且与直线 x=-1, x=-3 和 x 轴围成的四边形的面积为 16,那么 k=_ .如图,直线 y=x+2 与 x 轴交于点 A,与 y 轴交于点 B、〔1〕求 A,B 两点的坐标;〔2〕过点 B 作直线 BP,与 x 轴交于点 P,且使 PO=2AO,求直线 B P 的表达式.直线 y=kx+b 经过点(5,0),且与坐标轴所围成的三角形的面积为 2 0,那么该直线的表达式为.假设一次函数 y=kx+3 的图象与坐标轴的两个交点间的距离为5,那么 k 的值为.正比例函数和一次函数的图象都经过点 M(3,4),且正比例函数和一次函数的图象与 y 轴围成的面积为15 ,求此正比2例函数和一次函数的解析式.如图,直线 y=kx+6 与 x 轴、y 轴分别交于点 E,F,点 E的坐标为(8,0),点 A 的坐标为(6,0).〔1〕求 k 的值;〔2〕假设 P 是直线 y=kx+6 上的一个动点,当点 P 运动到什么位置时,△OPA 的面积为 9?请说明理由.如图,在平面直角坐标系中,直线 y x 1与 y 3 x 3相交4于点 A,两直线与 x 轴分别交于点 B 和点 C,D 是直线 AC 上的一个动点.〔1〕求点 A,B,C 的坐标;〔2〕当 BD=CD 时,求点 D 的坐标;〔3〕假设△BDC 的面积是△ABC 面积的 2 倍,求点 D 的坐标.。
一次函数各类题型详解加练习

令 +2=-2 -3,解得 =
(提示:求两个函数之间的交点,令两个解析式相等即可得到交点横坐标)
将 = 带入y₁= +2
得:y₁= +2=
∴点C的坐标为( , )
(2)AB=2-(-3)=5(提示:AB与y轴重合,上y减下y求长度。)
(分析:以AB为底,点C到AB的距离为高,就可以求出△ABC的面积。)
求线段AB、CD的长度。
解:∵AB∥x轴
∴AB=6-(-3)= 9
(右x减左x,即可求得长度)
同理∵CD∥x轴
∴CD=5-2=3
③既不平行于x轴,也不平行于y轴:如:点A(x₁,y₁),点B(x₂,y₂),则使用求线段的通用公式AB=
例:点A的坐标为(3,3),点B的坐标为(-3,-5),
求线段AB的长度。
S△COP=
OC·OP= ×8×(2t-8)=8t-32(t≥4)
(上一问中刚求出)
-8t+32=2×16(0≤t<4)
S△COP=2S△AOB,即或解,得:t=0或者t=8
8t-32=2×16(t≥4)
(4)思路:在△COP和△AOB中:∠COP=∠AOB=90°,OC =OA=8
还差一组条件就能证明两三角形全等了,因为整个题目并未有角度的信息,
解:AB中点的坐标为:( , )整理,得( ,3)
∵直线AB的k₁=2,且k₁·k₂=-1
∴垂直于AB的直线的k₂=
设垂直平分线解析式为:y= +b,将( ,3)代入解析式,
可得AB中垂线的解析式为y= +
把y=0代入解析式可得
点P的坐标为:( ,0)
综上:符合要求的点P共有4个:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数综合应用(讲义)
课前预习
1. 如图,直线l 1的表达式为y =-3x +3,且l 1与x 轴相交于
点D ,直线l 2经过A ,B 两点,直线l 1,l 2相交于点C . (1)点D 的坐标为_____________; (2)直线l 2的表达式为_____________;
(3)点C 的坐标为_____________.
2. 如图,在平面直角坐标系中,点A (2,0),点B (0,4).
(1)△AOB 的面积为_____________;
(2)点P 是y 轴上一点,若1
2AOP AOB
S S =△△,则点P
精讲精练
1. 已知直线l 1与l 2相交于点P ,直线l 1的表达式y =2
x +3,点P 的横坐标为-1,且l 2交y 轴于点
A (0,-1).则直线l 2的表达式为_________________.
2.
已知函数13y x b
=-+的图象与x 轴、y 轴分别交与点A ,B ,与函数y =x 的图象交于点M ,点M
的横坐标为3,则点A 的坐标为___________.
3. 已知一次函数y =kx +b 的图象经过点(-2,5),且与y 轴相交于点P ,直线1
3
2y x =-+与y 轴相交
于点Q ,点Q 恰与点P 关于x 轴对称,则这个一次函数的表达式为
___________.
4. 如图,已知直线l 1:y =2x +3,直线l 2:y =-x +5,直线l 1,l 2与x 轴分别交于点
B ,
C ,l 1,l 2相交于点A .则S △ABC =________.
5. 如图,直线y =2x +m (m >0)与x 轴交于点A (-2,0),直线y =-x +n (n >0)
与x 轴、y 轴分别交于点B ,C 两点,并与直线y =2x +m (m >0)相交于点D ,若AB =4.(1)求点D 的坐标;(2)求出四边形AOCD 的面积.
6. 已知直线3y mx =-中,y 随x 的增大而减小,且与直线x =1,x =3和x 轴围成的四边形的面积为
8,则m =________.
7. 已知直线6y kx =-经过第一、三、四象限,且与直线x =-1,x =-3和x 轴围成的四边形的面积为
16,则k =________.
8. 如图,直线y =x +2与x 轴交于点A ,与y 轴交于点B .
(1)求A ,B 两点的坐标;
(2)过点B 作直线BP ,与x 轴交于点P ,且使PO =2AO ,求直线BP 的表达式.
9. 已知直线y =kx +b 经过点(5,0),且与坐标轴所围成的三角形的面积为20,则该直线的表达式为
____________________.
10. 若一次函数y =kx +3的图象与坐标轴的两个交点间的距离为5,则k 的值为__________.
11. 已知正比例函数和一次函数的图象都经过点M (3,4),且正比例函数和一次函数的图象与y 轴围
成的面积为15
2,求此正比例函数和一次函数的解析式.
12. 如图,直线y =kx +6与x 轴、y 轴分别交于点E ,F ,已知点E 的坐标
为(8,0),点A 的坐标为(6,0).(1)求k 的值;
(2)若P 是直线y =kx +6上的一个动点,当点P 运动到什么位置时,△OPA 的面积为9?请说明理由.
13. 如图,在平面直角坐标系中,直线1y x =+与3
3
4y x =-+相交于点A ,两直线与x 轴分别交于点
B 和点
C ,
D 是直线AC 上的一个动点. (1)求点A ,B ,C 的坐标;
(2)当BD =CD 时,求点D 的坐标;
(3)若△BDC 的面积是△ABC 面积的2倍,求点D 的坐标.
一次函数综合应用(习题)
例题示范
例1:一次函数y=kx+b的图象经过点A(0,3),且与正比例函数y=-x的图象相交于点B,点B的横坐标为-1,求一次函数的表达式.
巩固练习
1.已知一次函数y=2x+a和y=-x+b的图象都经过点A(-2,0),且与y轴分别交于
点B,C,则△ABC的面积为________.
2.已知直线y=kx+b和直线
1
3
2
y x
=-+
与y轴的交点相同,且经过点(2,-1),则这
个一次函数的表达式是____________.
3.已知一次函数y=kx-3经过点M,则此直线与x轴、y轴围成的三角形的面积为________.
4.在平面直角坐标系中,O为原点,直线y=kx+b交x轴于点A(-2,0),交y轴于点B.若△AOB
的面积为8,则k的值为________.
5.已知直线y=kx+1,y随x的增大而增大,且与直线x=1,x=3以及x轴围成的四边形的面积为
10,则k的值为________.
6.已知一次函数y=kx+b的图象经过点(0,2),且与坐标轴围成的三角形的面积为2,则这个一次函
数的表达式是____________.
7.如图,在平面直角坐标系中,一次函数
1
6
2
y x
=-+
的图象与x轴、y轴
分别交于点A,B,与正比例函数y=x的图象交于第一象限内的点C.(1)求A,B,C三点的坐标;
(2)S
△AOC
=________.
8.如图,直线y=2x+3与直线y=-2x-1相交于C点,并且与y轴分别交于
A,B两点.
(1)求两直线与y轴交点A,B的坐标及交点C的坐标;
(2)求△ABC的面积.
9.一次函数y=2x-3的图象与y轴交于点A,另一个一次函数图象与y轴交于点B,两条直线交于点
C,C点的纵坐标为1,且S△ABC=5,求另一条直线的解析式.
10.已知一次函数y=kx+b的图象经过点(0,10),且与正比例函数
1
2
y x
的图象相交于点(4,a).
(1)求一次函数y=kx+b的解析式;
(2)求这两个函数图象与y轴所围成的三角形的面积.
11.如图,直线y=kx+4与x轴、y轴分别交于点A,B,已知点A的坐标为(-3,0),点C的坐标为(-
2,0).
(1)求k的值;
(2)若P是直线y=kx+4上的一个动点,当点P运动到什么位置时,△OPC的面积为3?请说明理由.。
