诱导公式计算题整理
02三角函数诱导公式(含经典例题+答案)
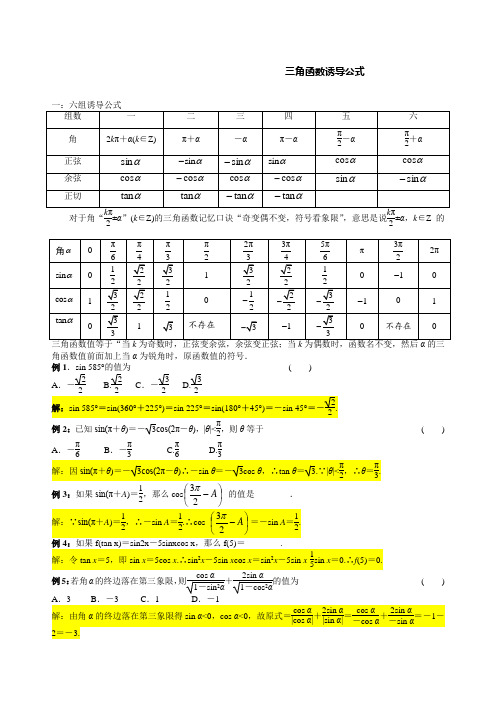
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
诱导公式及典型例题

αα+ 180x yP(x,y)P′(-x ,-y)MM′O(4-5-1)三角函数诱导公式及典型例题【知识梳理】1.公式(一)απαsin )sin(=∙+2kαπαcos )cos(=∙+2kαπαtan )tan(=∙+2k (其中Z ∈k )2.公式(二):αα-sin sin(=-) ααcos cos(=-) ααtan tan(-=-)推导:在单位圆中画出α角与-α角,若没α的终边与单位圆交于点P(x ,y),则角-α的终边与单位圆的交点必为P ´(x ,-y),观察出角的终边关于x 轴对称,结合三角函数定义可得到公式。
3.公式(三)[]απαcos 2(cos -=++1)k []απαsin 2(sin -=++1)k[]απαtan 2(tan =++1)k注:⎩⎨⎧-=+为偶数,为奇数,ααααπαsin sin )sin(n ⎩⎨⎧-=+为偶数,为奇数,ααααπαcos cos )cos(nαπαtan )tan(=+n 【典型例题】例1.下列三角函数值: (1)cos210º; (2)sin 45π例2.求下列各式的值: (1)sin(-34π); (2)cos(-60º)-sin(-210º)例3.化简 )180sin()180cos()1080cos()1440sin(︒--⋅-︒-︒-⋅+︒αααα例4.已知cos(π+α)=- 21,23π<α<2π,则sin(2π-α)的值是( ). (A )23(B) 21 (C)-23 (D)±23求下式的值:2sin(-1110º) -sin960º+)210cos()225cos(2︒-+︒- 2.化简sin(-2)+cos(-2-π)·tan(2-4π)所得的结果是( ) (A )2sin2 (B)0 (C)-2sin2 (D) -1 公式(四)απαsin )2cos(-=+απαcos )2sin(=+ απαsin )2cos(=+- απαcos )2sin(=+-απαcot )2tan(-=+απαtan )2cot(-=+ απαcot )2tan(=+- απαtan )2cot(=+-例5、求证: )2cos()5cos()2sin()4sin()cot()2tan()23cos()2sin(απαπαπαπαπαπαπαπ+-+--=+-+---+k k k例6 的值。
三角函数诱导公式练习题集附答案解析

三角函数诱导公式练习题一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数2、点P(cos2009°,sin2009°)落在()A、第一象限B、第二象限C、第三象限D、第四象限3、已知,则=()A、B、C、D、4、若tan160°=a,则sin2000°等于()A、B、C、D、﹣5、已知cos(+α)=﹣,则sin(﹣α)=()A、﹣B、C、﹣D、6、函数的最小值等于()A、﹣3B、﹣2C、D、﹣17、本式的值是()A、1B、﹣1C、D、8、已知且α是第三象限的角,则cos(2π﹣α)的值是()A、B、C、D、9、已知f(cosx)=cos2x,则f(sin30°)的值等于()A、B、﹣C、0 D、110、已知sin(a+)=,则cos(2a﹣)的值是()A、B、C、﹣D、﹣11、若,,则的值为()A、B、C、D、12、已知,则的值是()A、B、C、 D、13、已知cos(x﹣)=m,则cosx+cos(x﹣)=()A、2mB、±2mC、D、14、设a=sin(sin20080),b=sin(cos20080),c=cos(sin20080),d=cos(cos20080),则a,b,c,d的大小关系是()A、a<b<c<dB、b<a<d<cC、c<d<b<aD、d<c<a<b15、在△ABC中,①sin(A+B)+sinC;②cos(B+C)+cosA;③tan tan;④,其中恒为定值的是()A、②③B、①②C、②④D、③④16、已知tan28°=a,则sin2008°=()A、B、C、D、17、设,则值是()A、﹣1B、1C、D、18、已知f(x)=asin(πx+α)+bcos(πx+β)+4(a,b,α,β为非零实数),f(2007)=5,则f(2008)=()A、3B、5C、1D、不能确定19、给定函数①y=xcos(+x),②y=1+sin2(π+x),③y=cos(cos(+x))中,偶函数的个数是()A、3B、2C、1D、020、设角的值等于()A、B、﹣C、D、﹣21、在程序框图中,输入f0(x)=cosx,则输出的是f4(x)=﹣csx()A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题(共9小题)22、若(﹣4,3)是角终边上一点,则Z的值为.23、△ABC的三个内角为A、B、C,当A为°时,取得最大值,且这个最大值为.24、化简:=25、化简:=.26、已知,则f(1)+f(2)+f(3)+…+f(2009)=.27、已知tanθ=3,则(π﹣θ)=.28、sin(π+)sin(2π+)sin(3π+)…sin(2010π+)的值等于.29、f(x)=,则f(1°)+f(2°)+…+f(58°)+f(59°)=.30、若,且,则cos(2π﹣α)的值是.答案与评分标准一、选择题(共21小题)1、已知函数f(x)=sin,g(x)=tan(π﹣x),则()A、f(x)与g(x)都是奇函数B、f(x)与g(x)都是偶函数C、f(x)是奇函数,g(x)是偶函数D、f(x)是偶函数,g(x)是奇函数考点:函数奇偶性的判断;运用诱导公式化简求值。
5.3-诱导公式 2025年高考数学知识点题型及考项复习

2
2
= ( − 1) + Байду номын сангаас
方法2 (特值法) 因为 为偶函数,所以
π
−
2
−1
2
π
−
2
=
π
2
−1
2
+
π
,得
2
= 2.
π
+ sin +
2
π
π
− =
2
2
,得 = 2.
,即
例12 (2022·浙江节选)若3sin − sin = 10, + =
【解析】
π
,则sin
+ ,
即 = , = .
3sin +2cos
(1)求
的值;
sin −cos
+
【答案】
−
=
+
−
=
+
−
=
×+
∴ cos
11π
2
+ + sin 3π − =
6
11
+
6
11
=
12
..
11
6
,
11
关键能力构建
题型1 利用诱导公式化简
例3 化简:
cos −π
(1)
sin π−
⋅ sin
π
−
2
cos
π
2
+ ;
【解析】原式
=
cos[− π− ]
sin
−cos
诱导公式练习题含答案

诱导公式练习题含答案学校:__________ 班级:__________ 姓名:__________ 考号:__________1. 已知tan(x+π2)=5,则1sin x cos x=()A.265B.−265C.±265D.−5262. cos390∘=( )A.1 2B.√32C.−12D.−√323. cos23π6=()A.1 2B.−12C.√32D.−√324. 已知sin(α2−π4)=√210,则sinα=()A.−1225B.1225C.−2425D.24255. 已知tanα=3,则2sin a+cosα2cos a−3sinα的值是()A.5 3B.1C.−1D.−536. 已知sin(α−π4)=13,则cos(α+π4)的值等于()A.−13B.13C.−2√23D.2√237. 若cosα=−45,且α是第三象限角,则tanα=()A.−34B.34C.43D.−438. 若tanα=√3,且α为第三象限角,则cosα−sinα的值为( )A.−1+√32B.√3−12C.1−√32D.1+√329. 已知f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α).(1)化简f(α);(2)若α是第三象限角,且sin (α−π)=15,求f(α)的值.10. 在△ABC 中,∠A,∠C 均为锐角,且|12−sin A|+(cos C −√22)2=0,求∠B 的度数.11. 已知sin (30∘+α)=35,60∘<α<150∘,求cos α的值.12. 已知f(x)=sin (π2+x)−2cos (π+x)sin (π−x)+cos (−x).(1)求f (π4)的值;(2)若f(α)=2,α是第三象限角,求tan α及sin α的值.13. 已知f (α)=sin (α−π)cos (3π2+α)cos (−α−π)sin (5π+α)sin (α−2π).(1)化简f (α);(2)若sin (α+π2)=−25√6,求f (α+π)的值;(3)若α=2021π3,求f (α)的值.14. 已知f(α)=sin (α−π2)cos (3π2−α)tan (π+α)cos (π2+α)sin (2π−α)tan (−α−π)sin (−α−π).(1)化简f(α);(2)若α是第三象限角,且cos(α−3π2)=15,求f(α)的值.15. 已知sin(x+π3)=13,求sin(4π3+x)+cos2(−x+5π3)的值.16. 已知函数f(x)=2cos x(sin x+cos x)−1.(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在[0, π]上的单调递增区间.参考答案与试题解析诱导公式练习题含答案一、选择题(本题共计 8 小题,每题 5 分,共计40分)1.【答案】B【考点】同角三角函数间的基本关系【解析】本题考查同角三角函数间的基本关系.【解答】解:因为tan(x+π2)=sin(x+π2)cos(x+π2)=cos x−sin x =−1tan x=5,所以tan x=−15,所以1sin x cos x =sin2x+cos2xsin x cos x=tan2x+1tan x =−265.故选B.2.【答案】B【考点】运用诱导公式化简求值【解析】利用诱导公式化简即可得解.【解答】解:cos390∘=cos(360∘+30∘)=cos30∘=√32.故选B.3.【答案】C【考点】运用诱导公式化简求值【解析】由题意,直接利用诱导公式和特殊角的三角函数值进行化简求值即可. 【解答】解:已知cos23π6=cos(23π6−4π)=cos(−π6)=cosπ6=√32.故选C.4.【考点】两角和与差的三角函数【解析】两边同时平方,然后结合二倍角正弦公式即可求解.【解答】∵sin(α2−π4)=√210,∴√22(sin12α−cos12α)=√210,即sin12α−cos12α=15,两边同时平方可得,1+2sin12αcos12α=125,则sinα=−2425.5.【答案】C【考点】运用诱导公式化简求值【解析】此题暂无解析【解答】此题暂无解答6.【答案】A【考点】运用诱导公式化简求值【解析】运用诱导公式即可化简求值.【解答】解:∵sin(α−π4)=13,∴cos(α+π4)=sin[π2−(π4+α)]=sin(π4−α)=−sin(α−π4 )=−13.故选A.7.【考点】同角三角函数间的基本关系 【解析】由cos α的值,及α为第三象限角,利用同角三角函数间的基本关系求出sin α的值,即可确定出tan α的值即可. 【解答】解:∵ cos α=−45,且α是第三象限角, ∴ sin α=−√1−cos 2α=−35, 则tan α=sin αcos α=34. 故选B . 8.【答案】 B【考点】同角三角函数基本关系的运用 运用诱导公式化简求值 【解析】由tan α=2,即sin αcos α=2,sin 2α+cos 2α=1,且α是第三象限角,即可求解sin α,cos α.从而求解cos α−sin α的值. 【解答】解:∵ tan α=√3,α为第三象限角, ∴ sin α=√3cos α,sin α<0,cos α<0, 由sin 2α+cos 2α=1, 则(√3cos α)2+cos 2α=1, 解得cos α=−12,sin α=−√32. 则cos α−sin α=−12−(−√32) =−12+√32=√3−12. 故选B .二、 解答题 (本题共计 8 小题 ,每题 5 分 ,共计40分 ) 9.【答案】f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α) =sin αcos α(−sin α)sin αsin α=−cos α.∵ α是第三象限角,且sin (α−π)=15,∴ sin α=−15,∴ cos α=−√1−sin 2α=−√1−125=−2√65, ∴ f(α)=−cos α=2√65. 【考点】运用诱导公式化简求值 【解析】(1)利用诱导公式化简即可得到结果;(2)由α是第三象限角及sin α的值,利用同角三角函数间的基本关系求出cos α的值,所求式子利用诱导公式化简后,代入计算即可求出值; 【解答】f(α)=sin (π−α)cos (2π−α)cos (3π2−α)cos (π2−α)sin (−π−α)=sin αcos α(−sin α)sin αsin α=−cos α. ∵ α是第三象限角,且sin (α−π)=15,∴ sin α=−15,∴ cos α=−√1−sin 2α=−√1−125=−2√65, ∴ f(α)=−cos α=2√65. 10. 【答案】解:因为|12−sin A|+(cos C −√22)2=0,所以12−sin A =0,cos C −√22=0,所以sin A =12,cos C =√22. 因为∠A,∠C 均为锐角,所以∠A =30∘,∠C =45∘,所以∠B =180∘−30∘−45∘=105∘. 【考点】运用诱导公式化简求值 【解析】 此题暂无解析 【解答】解:因为|12−sin A|+(cos C −√22)2=0,所以12−sin A =0,cos C −√22=0,所以sin A =12,cos C =√22. 因为∠A,∠C 均为锐角,所以∠A =30∘,∠C =45∘,所以∠B =180∘−30∘−45∘=105∘. 11. 【答案】已知sin (30∘+α)=35,60∘<α<150∘, 所以90∘<30∘+α<180∘ 所以cos (30+α)=−45,则:cos α=cos [(30∘+α)−30∘]=cos (30∘+α)cos 30∘+sin (30∘+α)sin 30∘=−45×√32+35×12=3−4√310. 【考点】两角和与差的三角函数 【解析】直接利用三角函数关系式的应用求出结果. 【解答】已知sin (30∘+α)=35,60∘<α<150∘, 所以90∘<30∘+α<180∘ 所以cos (30+α)=−45,则:cos α=cos [(30∘+α)−30∘]=cos (30∘+α)cos 30∘+sin (30∘+α)sin 30∘=−45×√32+35×12=3−4√310. 12. 【答案】 解:(1)∵ f(x)=sin (π2+x)−2cos (π+x)sin (π−x)+cos (−x)=cos x +2cos xsin x +cos x=3tan x+1,∴ f (π4)=3tan π4+1=31+1=32.(2)∵ 已知f(α)=3tan α+1=2, ∴ tan α=sin αcos α=12,又sin2α+cos2α=1,α是第三象限角,∴ 解得:sinα=−√55.【考点】运用诱导公式化简求值同角三角函数间的基本关系【解析】此题暂无解析【解答】解:(1)∵f(x)=sin(π2+x)−2cos(π+x) sin(π−x)+cos(−x)=cos x+2cos x sin x+cos x=3tan x+1,∴f(π4)=3tanπ4+1=31+1=32.(2)∵已知f(α)=3tanα+1=2, ∴tanα=sinαcosα=12,又sin2α+cos2α=1,α是第三象限角,∴ 解得:sinα=−√55.13.【答案】解:(1)f(α)=−sinαsinα(−cosα)−sinαsinα=−cosα(α≠kπ,k∈Z).(2)∵sin(α+π2)=cosα=−2√65,∴ f(α+π)=−cos(α+π)=cosα=−2√65.(3)∵ α=2021π3=674π−π3,∴ f(α)=−cosα=−cos(674π−π3 )=−cosπ3=−12.【考点】运用诱导公式化简求值【解析】(1)由条件利用诱导公式化简所给式子的值,可得f(α)的解析式.(2)由条件利用诱导公式化简可得cosα=−2√65,从而求得f(α)=−cosα的值;(3)α=2021π3=674π−π3,利用诱导公式求得f(α)的值.【解答】解:(1)f(α)=−sinαsinα(−cosα)−sinαsinα=−cosα(α≠kπ,k∈Z).(2)∵sin(α+π2)=cosα=−2√65,∴ f(α+π)=−cos(α+π)=cosα=−2√65.(3)∵ α=2021π3=674π−π3,∴ f(α)=−cosα=−cos(674π−π3 )=−cosπ3=−12.14.【答案】解:(1)由题意知f(α)=−sin(π2−α)(−sinα)tanα(−sinα) sin(−α)(−tanα)[−sin(π+α)]=−cosα(−sinα)tanα(−sinα)−sinα(−tanα)sinα=−cosα.(2)∵cos(α−3π2)=cos(3π2−α)=−sinα=15,∴sinα=−15,又α为第三象限角,∴cosα=−√1−sin2α=−2√65, ∴ f(α)=−cosα=2√65. 【考点】运用诱导公式化简求值【解析】此题暂无解析【解答】解:(1)由题意知f(α)=−sin(π2−α)(−sinα)tanα(−sinα) sin(−α)(−tanα)[−sin(π+α)]=−cosα(−sinα)tanα(−sinα)−sinα(−tanα)sinα=−cosα.(2)∵ cos (α−3π2)=cos (3π2−α)=−sin α=15, ∴ sin α=−15,又α为第三象限角,∴ cos α=−√1−sin 2α=−2√65, ∴ f(α)=−cos α=2√65. 15.【答案】解:∵ sin 2(x +π3)+cos 2(x +π3)=1, 又sin (x +π3)=13,∴ cos 2(x +π3)=1−sin 2(x +π3)=89, ∴ 原式=sin (π+π3+x)+cos 2[2π−(x +π3)]=−sin (π3+x)+cos 2(x +π3) =−13+89=59. 【考点】运用诱导公式化简求值【解析】直接利用诱导公式化简即可.【解答】解:∵ sin 2(x +π3)+cos 2(x +π3)=1, 又sin (x +π3)=13, ∴ cos 2(x +π3)=1−sin 2(x +π3)=89, ∴ 原式=sin (π+π3+x)+cos 2[2π−(x +π3)]=−sin (π3+x)+cos 2(x +π3) =−13+89=59.16.【答案】(Ⅰ)f(x)=2sin x cos x+2cos2x−1=sin2x+cos2x=√2sin(2x+π4).∴f(x)的最小正周期为T=2π2=π;(Ⅱ)由−π2+2kπ≤2x+π4≤π2+2kπ(k∈Z),得−3π8+kπ≤x≤π8+kπ(k∈Z).当x∈[0, π]时,单调递增区间为[0,π8brack和[5π8,πbrack.【考点】运用诱导公式化简求值【解析】(Ⅰ)利用倍角公式降幂,再由辅助角公式化积,由周期公式求周期;(Ⅱ)利用复合函数的单调性求出增区间,进一步得到f(x)在[0, π]上的单调递增区间.【解答】(Ⅰ)f(x)=2sin x cos x+2cos2x−1=sin2x+cos2x=√2sin(2x+π4).∴f(x)的最小正周期为T=2π2=π;(Ⅱ)由−π2+2kπ≤2x+π4≤π2+2kπ(k∈Z),得−3π8+kπ≤x≤π8+kπ(k∈Z).当x∈[0, π]时,单调递增区间为[0,π8brack和[5π8,πbrack.。
诱导公式专项训练

诱导公式专项训练姓名: 班级: 评价:一、单选题1. 下列式子中正确的是( ) A. sin(π-α)=-sin α B. cos(π+α)=cos α C. cos α=sin α D. sin(2π+α)=sin α2. 化简cos(3π-α)=( ) A. cos α B. -cos α C. sin α D. -sin α3. tan 34π-等于( )A. 33-B. 33C. 3-D.34. 已知⎪⎭⎫ ⎝⎛∈ππα,2,若426cos -=⎪⎭⎫ ⎝⎛-απ,则⎪⎭⎫ ⎝⎛+65sin πα的值为( ) A. 42- B. 42 C. 414- D. 4145. tan(5π+α)=m ,则)cos()sin()cos()3sin(απααππα+---+-的值为( )A. 11-+m mB.11+-m mC. -1D. 16. 化简sin 2(π+α)-cos(π+α)·cos(-α)+1的结果为( ) A. 1B. 2sin 2αC. 0D. 27. 设f(α)=)4(cos )2sin(sin 1)cos()2cos()2sin(222απαπαααπαπ--+++--+-,则)623(π-f 的值为( ) A. 33 B. 33- C. 3 D. 3-18. 已知51)25sin(=+απ,那么cos α等于( )A. 52-B. 51-C. 51D. 529. 已知sin(-α)=35,则)2cos(απ+的值为( )A. 32B. 32-C. 35D. 35-10. 若31)23cos(=-θπ,则sin θ的值为( )A. 322-B. 322 C. 31- D. 3111. 已知53)2sin(=-απ,则cos(π+α)的值为( )A. 54B. 54-C. 53D. 53-二、多选题12. 下列化简正确的是( )A. tan(π+1)=tan 1B.αααcos )180tan()sin(=--︒C. ααπαπtan )cos()sin(=+-D.1)2sin()tan()cos(-=----απαπαπ 13. 已知f (x )=sin x ,下列式子中不成立的是( )A. f (x +π)=sin xB. f (2π-x)=sin xC. f (x -π)=-sin xD. f(π-x)=-f (x ) 14. 给出下列四个结论,其中正确的结论是( ) A. sin(π+α)=-sin α成立的条件是角α是锐角B. 若cos(n π-α)=31(n ∈Z ),则cos α=31C. ∈α≠2πk (k∈Z)∈∈ααπtan 1)2tan(-=+D. 若sin α+cos α=1∈则sin n α+cos n α=1 三、填空题15. 将下列三角函数转化为锐角三角函数,并填在题中横线上.(1)sin (1∈π)∈________. (2)cos 210°∈________.(3)tan 617π∈________.16. ∈∈α∈∈∈∈∈∈∈∈∈∈cos(π∈α)∈32∈∈sin(∈π∈α)∈____∈tan(π∈α)∈____.17. ∈∈∈)2tan()sin()3cos(απαπαπ-⋅+-∈________. 18. ∈32)6cos(=-απ∈∈)32sin(πα-∈________. 四、解答题19. ∈∈cos(π∈α)∈21-∈∈α∈∈∈∈∈∈∈∈∈∈(1)sin(π-α); (2)[][])2cos()2sin()12(sin )12(sin παπαπαπαn n n n -++-+++(n ∈Z).20. 已知角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边经过点P (3∈-4).(1)∈sin α∈cos α∈∈∈ (2)∈)sin()2cos()2cos()sin(ααπαπαπ-+++++∈∈∈21. 已知sin θ,cos θ是关于x 的方程x 2-ax +a =0(a ∈R )的两个根.(1)∈)2(sin )2(cos 33θπθπ-+-∈∈∈ (2)∈θθπtan 1)tan(--∈∈∈22. ∈∈32)6cos(=-απ∈∈∈∈∈∈∈∈∈(1))3sin(απ+∈ (2))32sin(πα-.1. 【答案】D【解析】对于选项A∈令α=,得sin(π-α)=sin=1≠-sin,所以A错误;对于选项B∈令α=0∈得cos(π+α)=cos π=-1≠cos 0∈所以B错误;对于选项C∈令α=0∈得cosα=cos 0=1≠sin 0∈所以C错误.2. 【答案】B【解析】cos (3π-α)=cos [2π+(π-α)]=cos (π-α)=-cosα.3. 【答案】C【解析】tan=tan=tan=tan=-tan=-.4. 【答案】C【解析】∵cos=-,∴sin=±=±=±.∵α∈∴-α∈,∴-α∈,∴sin=-,∴sin=sin=sin=-,故选C.5. 【答案】A【解析】因为tan(5π+α)=tanα=m,所以原式=====.6. 【答案】D【解析】原式=sin2α+cos2α+1=1+1=2.7. 【答案】D【解析】f(α)====-,∵tan=tan=tan=,∴f=-.8. 【答案】C【解析】sin=sin=sin=cosα=.9. 【答案】C【解析】因cos=-sinα=sin(-α)=,故应选C.10. 【答案】C【解析】cos=cos=-cos=-sinθ=,∴sinθ=-.11. 【答案】D【解析】因为sin=cosα=,所以cos(π+α)=-cosα=-.故选D.12. 【答案】ABD【解析】对于A∈根据三角函数的诱导公式可知,tan(π+1)=tan 1∈故A正确;对于B∈==cosα,故B正确;对于C∈==-tanα,故C错误;对于D∈==-1∈故D正确.13. 【答案】ABD【解析】f(x+π)=sin(x+π)=-sin x,f(2π-x)=sin(2π-x)=-sin x,f(x-π)=sin(x-π)=-sin(π-x)=-sin x,f(π-x)=sin(π-x)=sin x=f(x).故A∈B∈D不成立.14. 【答案】CD【解析】由诱导公式二,知α∈R时,sin(π+α)=-sinα,所以A错误.当n=2k(k∈Z)时,cos(nπ-α)=cos(-α)=cosα,此时cosα=;当n=2k+1(k∈Z)时,cos(nπ-α)=cos[(2k+1)π-α]=cos(π-α)=-cosα,此时cosα=-,所以B错误.若α≠(k∈Z),则tan===-,所以C正确.将等式sinα+cosα=1两边平方,得sinαcosα=0∈所以sinα=0或cosα=0.若sinα=0∈则cosα=1∈此时sin nα+cos nα=1;若cosα=0∈则sinα=1∈此时sin nα+cos nα=1∈故sin nα+cos nα=1∈所以D正确.15. 【答案】(1)-sin 1(2)-cos 30°(3)-tan【解析】(1)sin(1+π)=-sin 1.(2)cos 210°=cos (180°+30°)=-cos 30°.(3)tan=tan=tan=tan=-tan.16. 【答案】【解析】∵cos(π+α)=,∴cosα=-,又α是三角形的一个内角,∴sinα=1-cos2α=,sin(-π-α)=-sin(π+α)=sinα=,∴tan(π-α)=-tanα=-=. 17. 【答案】-1【解析】原式=·tan(-α)=·(-tanα)=-·tanα=-·=-1.18. 【答案】-【解析】sin=sin=-sin=-cos(-α)=-.19. 【答案】解(1)由cos(π+α)=-可得cosα=,因为α是第四象限角,所以sinα=-1-cos2α=-,故sin(π-α)=sinα=-.(2)==-,而cosα=,所以原式=-4.20. 【答案】解(1)∵角α的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过点P(3∈-4),故x=3∈y=-4∈r=|OP|==5∈∴sinα==-,cosα==.∴sinα-cosα=--=-.(2)===.21. 【答案】解(1)由题意,知对于关于x的方程x2-ax+a=0∈Δ=(-a)2-4a≥0∈所以a≥4或a≤0.又(sinθ+cosθ)2=1+2sinθcosθ,所以a2-2a-1=0∈所以a=1-或a=1+(舍去),所以sinθ+cosθ=sinθcosθ=1-,cos3+sin3=sin3θ+cos3θ=(sinθ+cosθ)·(sin2θ-sinθcosθ+cos2θ)=(1-)[1-(1-)]=-2.(2)tan(π-θ)-=-tanθ-=-=-=-=1+.22. 【答案】解(1)sin=sin=cos=.(2)sin=sin=-sin=-cos=-.。
(完整版)诱导公式练习题

诱导公式练习题一、选择题 1. sin11π6的值是( ) A 。
21 B 。
-21 C 。
23 D.-232.已知的值为( )A.B. C.D.3.已知tan ,是关于x 的方程x 2-kx+k 2—3=0的两个实根,且3π<<,则cos +sin= ( )A.B 。
C 。
-D 。
-4.已知tan =2,,则3sin 2—cos sin +1= ( ) A.3 B.—3 C 。
4 D 。
-45.在△ABC 中,若sinA ,cosA 是关于x 的方程3x 2-2x+m=0的两个根,则△ABC 是 ( ) A.钝角三角形 B 。
直角三角形 C 。
锐角三角形 D 。
不能确定6.若1sin()33πα-=,则5cos()6πα-的值为()A .13 B.13- C.223 D 。
223-7.已知3cos()sin()22()cos()tan()f ππ+α-αα=-π-απ-α,则25()3f -π的值为( )A .12 B .-12C .32D . -328.定义某种运算a S b =⊗,运算原理如上图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .4B .8C .11D .139.若76πα=,则计算21sin(2)sin()2cos ()αππαα+-⋅+--所得的结果为( )A 。
34- B. 14- C. 0 D. 5410.已知sin()0,cos()0θπθπ+<->,则θ是第( )象限角。
A .一 B .二 C .三 D .四11.已知sinx=2cosx ,则sin 2x+1=( ) (A) (B) (C) (D )12.设02x π≤≤sin cos x x =-,则( ) A.0x π≤≤ B.744x ππ≤≤C 。
544x ππ≤≤ D.322x ππ≤≤ 二、填空题13.已知。
角α(0)πα-<<的终边与单位圆交点的横坐标是13,则cos()2πα+的值是___.14.化简:___________)cos()3sin()sin()23cos()3cos()2sin(=---+--+-πααπαπαπαπαπ15.已知32cos =a ,且02<<-a π,求)tan()cos()2sin()tan(a a a a +-+--πππ的值。
整理诱导公式计算题100题

诱导公式计算题100题20 年月日A4打印/ 可编辑三角函数诱导公式检测题1.全国Ⅱ)若sinα<0且tanα>0,则α是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角2.(07·湖北)tan690°的值为()A.- B. C. D.-3.f(sin x)=cos19x,则f(cos x)=()A.sin19x B.cos19x C.-sin19x D.-cos19x4.设f(x)=a sin(πx+α)+b cos(πx+β),其中a,b,α,βⅡR,且ab≠0,α≠kπ(kⅡZ).若f(2009)=5,则f(2010)等于()A.4B.3C.-5D.55.(09·全国Ⅱ文)sin585°的值为()A.- B. C.- D.6.函数y=5sin的最小正周期是()A.πB.πC.D.5π7.(2010·重庆文,6)下列函数中,周期为π,且在[,]上为减函数的是()A.y=sin(2x+) B.y=cos (2x+)C.y=sin(x+) D.y=cos(x+)8.函数y=-2tan的单调递减区间是________.三角函数诱导公式(答案)1.[答案] C2.[答案]A[ 解析]tan690°=tan(-30°+2×360°)=tan(-30°)=-tan30°=-,选A.3.[答案]C[解析]f(cos x)=f(sin(90°-x))=cos19(90°-x)=cos(270°-19x)=-sin19x.4.[答案]C[解析]Ⅱf(2009)=a sin(2009π+α)+b cos(2009π+β)=-a sinα-b cosβ=5,Ⅱa sinα+b cosβ=-5.Ⅱf(2010)=a sinα+b cosβ=-5.5.[答案]A[解析]sin585°=sin(360°+225°)=sin225°=sin(180°+45°)=-sin45°=-.6.[答案]D[解析]T==5π.7.[答案]A[解析]选项A:y=sin(2x+)=cos2x,周期为π,在[,]上为减函数;选项B:y=cos(2x+)=-sin2x,周期为π,在[,]上为增函数;选项C:y=sin(x+)=cos x,周期为2π;选项D:y=cos(x+)=-sin x,周期为2π.故选A.8. [答案](kⅡZ)[解析]求此函数的递减区间,也就是求y=2tan的递增区间,由kπ-<3x+<kπ+,kⅡZ 得:-<x<+,Ⅱ减区间是,kⅡZ.整理丨尼克本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的诱导公式(习题一)
一、选择题
1.如果|cos x |=cos (x +π),则x 的取值集合是( )
A .-
2π+2k π≤x ≤2π+2k π B.-2π+2k π≤x ≤2π3+2k π C . 2π+2k π≤x ≤2
π3+2k π D.(2k +1)π≤x ≤2(k +1)π(以上k ∈Z ) 2.sin (-
6π19)的值是( ) A . 21 B .-21 C .23 D .-2
3 3.下列三角函数:
①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6
π]; ⑤sin [(2n +1)π-
3π](n ∈Z ). 其中函数值与sin
3π的值相同的是( ) A .①② B .①③④ C .②③⑤ D .①③⑤
4.若cos (π+α)=-
510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26 D .2
6 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )
A .cos (A +
B )=cos
C B .sin (A +B )=sin C C .tan (A +B )=tan C
D .sin
2B A +=sin 2C 6.函数f (x )=cos
3πx (x ∈Z )的值域为( ) A .{-1,-
21,0,21,1} B .{-1,-21,21,1} C .{-1,-
23,0,2
3,1} D .{-1,-23,23,1} 二、填空题
7.若α是第三象限角,则)πcos()πsin(21αα---=_________.
8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.
三、解答题
9.求值:sin (-660°)cos420°-tan330°cot(-690°).
10.证明:
1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθ
θθ.
11.已知cos α=31,cos (α+β)=1,求证:cos (2α+β)=31.
12. 化简:︒
+︒︒︒+790cos 250sin 430cos 290sin 21.
13、求证:
)
π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.
14. 求证:(1)sin (
2π3-α)=-cos α; (2)cos (
2
π3+α)=sin α.
三角函数的诱导公式(习题二)
一、选择题:
1.已知sin(4π+α)=23,则sin(4
3π-α)值为( ) A. 21 B. —2
1 C. 23 D. —23 2.cos(π+α)= —21,2
3π<α<π2,sin(π2-α) 值为( ) A. 23 B. 2
1 C. 23± D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )
A.sin2+cos2
B.cos2-sin2
C.sin2-cos2
D.± (cos2-sin2)
4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )
A.sinα=sinβ
B. sin(α-π2) =sinβ
C.cosα=cosβ
D. cos(π2-α) =-cosβ
5.设tanθ=-2, 2
π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 5
1(5-4) 二、填空题:
6.cos(π-x)= 2
3,x ∈(-π,π),则x 的值为 .
7.tanα=m,则=+-+++)
cos(-sin()cos(3sin(απα)απ)απ . 8.|sinα|=sin(-π+α),则α的取值范围是 .
三、解答题:
9.)
cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .
10.已知:sin (x+
6π)=41,求sin ()67x +π+cos 2(65π-x )的值.
11. 求下列三角函数值:
(1)sin
3
π7;(2)cos 4π17;(3)tan (-6π23);
12. 求下列三角函数值:
(1)sin 3π4·cos 6π25·tan 4
π5; (2)sin [(2n +1)π-
3π2].
13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3
π)的值.
三角函数的诱导公式测试(习题三)
一、选择题(本大题共5个小题,每小题6分,共30分. 在每小题给出的四个选择中,只有一项是符合题目要求的.)
1、与-463°终边相同的角可表示为( )
A .k·360°+436°(k ∈Z )
B .k·360°+103°(k ∈Z )
C .k·360°+257°(k ∈Z )
D .k·360°-257°(k ∈Z )
2、下列四个命题中可能成立的一个是( )
A 、2
1cos 21sin ==αα且 B 、1cos 0sin -==αα且
C 、1cos 1tan -==αα且
D 、α是第二象限时,αααcos tan sia -
= 3、)2cos()2sin(21++-ππ等于 ( )
A .sin2-cos2
B .cos2-sin2
C .±(sin2-cos2)
D .sin2+cos2 4、sinαcosα=81,且4π<α<2
π,则cosα-sinα的值为 ( ) A .23 B .23
- C .43
D .43
-
5、若θsin 、θcos 是关于x 的方程0242=++m mx x 的两个实根,则m 值为(
) A 、⎪⎭⎫⎢⎣⎡-∈0,34
m B 、51-=m C 、51±=m D 、5
1+=m 二、填空题(本大题共4个小题,每小题6分,共24分.将答案填在题中横线上)
6、化简=+-+βαβαβα222222cos cos sin sin sin sin .
7、若0cos 3sin =+αα,则ααα
αsin 3cos 2sin 2cos -+的值为 .
8、=-︒)945cos( .
9、=⋅⋅⋅⋅⋅⋅︒︒︒︒89tan 3tan 2tan 1tan .
三、解答题(本大题共3道小题,共46分.解答应写出文字说明,证明过程或演算步骤)
10、求值22sin 120cos180tan 45cos (330)sin(210)︒+︒+︒--︒+-︒(15分)
11、 化简:)(cos )tan()2tan()
cos()(sin 32πααππααππα--⋅+--+⋅+. (15分)
12、已知21
)sin(=+απ,求απααπcos )tan()2sin(⋅-+-的值.(16分)。
