(完整版)解斜三角形
解斜三角形
1 2 sin B sin C = a 2 sin A
求证：a = b cos C + c cos B(课本18页第三题).
证明： sin A = sin(180° − A) = sin( B + C ) ∵
∴ sin A = sin B cos C + cos B sin C
a b c = cos C + cos B 2R 2R 2R
解三角形的应用. 解三角形的应用.
南偏西50°相距12海里 海里B处 例2、我舰在敌岛 南偏西 °相距 海里 处， 、我舰在敌岛A南偏西 发现敌舰正由岛沿北偏西10°的方向以10海里 海里/ 发现敌舰正由岛沿北偏西 °的方向以 海里 时的速度航行，我舰要用2小时追上敌舰 小时追上敌舰， 时的速度航行，我舰要用 小时追上敌舰，则需 C 要的速度大小为 。
B D A C
分析：在四边形ABCD中欲求AB长 分析：在四边形ABCD中欲求AB长，只能去解三 ABCD中欲求AB 角形， AB联系的三角形有 ABC和 ABD， 联系的三角形有△ 角形，与AB联系的三角形有△ABC和△ABD，利 用其一可求AB AB。 用其一可求AB。
略解：Rt △ACD中，AD=1/cos30o ACD中
基本概念和公式.
海上有A、 两个小岛相距 海里， 两个小岛相距10海里 例1海上有 、B两个小岛相距 海里，从 海上有 A岛望 岛和 岛成 °的视角，从B岛望 岛望C岛和 岛成60°的视角， 岛望 岛和B岛成 岛望 C岛和 岛成 °的视角，那么 岛和 岛 岛和A岛成 岛和C岛 岛和 岛成75°的视角，那么B岛和 间的距离是 。
B间的距离？ 间的距离？
B A
想一想： 如何测定河两岸两点A、 想一想： 如何测定河两岸两点A
解斜三角形方法
解斜三角形（导学案）§1．1．1正弦定理课堂学习目标：1． 通过对任意三角形边长和角度关系的探索，掌握正弦定理的内容及其证明方法；2． 会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。
知识梳理：1． 内角和定理：在ABC ∆中，A B C ++=π；sin()A B +=sin C ；cos()A B +=cos C -cos 2A B +=sin 2C 2. 面积公式: （1）1()2a a S a h h a = 表示边上的高； （2）111sin sin sin ()2224abc S ab C ac B bc A R R====为外接圆半径； （3）1()()2S r a b c r =++为内切圆半径。
3．正弦定理：在一个三角形中,各边和它的所对角的正弦的比相等. 形式一：R C c B b A a 2sin sin sin === 形式二：a=2RsinA,b=2RsinB,c=2RsinC; sinA=2a R ,sinB=2b R ,sinC=2c R; 形式三：a:b:c=sinA: sinB: sinC; 和 sin sin sin sin a b c a A B C A ++=++ 二、基础检测：1. 在ABC ∆中，A 、B 的对边分别是 a b 、，且A=30 4,a b ==，那么满足条件的ABC ∆ （ B ）A 、 有一个解B 、有两个解C 、无解D 、不能确定2、在C ∆AB 中，已知8a =，60B = ，75C = ，则b 等于（ ）A ．B ．C ．D ．323 3、在C ∆AB 中，5a =，3b =，120C = ，则sin sin A B的值是（ ） A ．53 B ．35 C ．37 D ．574、在C ∆AB 中，若2sin b a =B ，则A 等于（ ）A ．30 或60B ．45 或60C ．60 或120D ．30 或1505、在C ∆A B 中，若()()()cos cos cos 1C C A-B ⋅B-⋅-A =，则C ∆A B 的形状是（ ）A ．直角三角形B ．等边三角形C ．等腰直角三角形D ．顶角为120 的等腰三角形6、一个三角形的两个内角分别为30 和45 ，如果45 角所对的边长为8，那么30 角所对的边长是（ ）A ．4B ．C ．D ．7、在C ∆AB 中，1a =，b =30A = ，则B 等于（ ）A ．60B ．60 或120C ．30 或150D ．1208、在C ∆AB 中，45B = ，60C = ，1c =，则最短边的长等于（ ）A ．B ．C ．12D 9、在C ∆AB 中，若sin cosa b A B=，则B 的值为（ ）A ． 30B ． 45C ． 60D ． 9010、在C ∆AB 中，6=a ，30B = ， 120=C ，则C ∆AB 的面积是（ ）A ．9B ．18C ．39D ．31811、在C ∆AB 中，若60A = ，16=b ，此三角形面积3220=S ，则a 的值是（）A ．620B ．75C ．51D ．4912、在C ∆AB 中，若12+=+c b ，45C = ，30B = ，则（ ）A ．2,1==c bB ．1,2==c bC ．221,22+==c b D ．22,221=+=c b13、在C ∆AB 中，60A = ，a =4b =，那么满足条件的C ∆AB （ ）A ．不存在B ．唯一存在C ．有2个D ．不确定14、在C ∆AB 中，若60A = ，a =sin sin sin a b cC ++A +B +等于（ ）A ．2B ．12C D15、在C ∆AB 中，60A = ，1b =，C S ∆AB ，则sin sin sin a b c C++=A+B+（ ）A ．3B ．3C ．3D ．16、在C ∆AB 中，若cos cos cos a b c C ==A B ，则C ∆AB 是（ ） A ．直角三角形 B ．等边三角形 C ．钝角三角形 D ．等腰直角三角形17、在C ∆AB 中，若::1:2:3C A B =，则::a b c =________________．18、在C ∆AB 中，2a =，b =4πA =，则B =______________．19、在C ∆AB 中，已知12a b +=，60A = ，45B = ，则a =_________，b =________．20、在C ∆AB 中，已知a =2b =，60A = ，则这样的三角形有_______个．21、在C ∆AB 中，已知12C B =，60A = ，45B = ，则C A = _．22、在C ∆AB 中，已知8a =，6b =，且C S ∆AB =C =________．23、在C ∆AB 中，已知a =4b =，30A = ，则sin B =________． 24、在C ∆AB 中，周长为7.5cm ，且sin :sin :sin 4:5:6C A B =，下列结论：①::4:5:6a b c =；②::a b c =；③2a cm =， 2.5b cm =，3c cm =；④::4:5:6C A B =．其中成立的序号依次是___________．25、在C ∆AB 中，已知10c =，45A = ，30C =，求a ，b 和B ．26、C ∆AB 中，c =45A = ，a =b 和B 、C ．三、典例分析：1. 在ΔABC 中，（1）若o ,求a 及C 的值；（2）若A=600，a=7,b=5,求边C 。
正余弦定理和解斜三角形专题(含答案)
正余弦定理和解斜三角形【基础梳理引导】1.正弦定理：A a sin =B b sin =Cc sin =2R ，其中R 是三角形外接圆半径. 2.余弦定理：a 2=b 2+c 2-2bccosA,b 2=a 2+c 2-2accosB,cosA=bca cb 2222-+. 3.S △ABC =21absinC=21bcsinA=21acsinB,S △=))()((c S b S a S S --- =Sr(S=2c b a ++,r 为内切圆半径)=R abc 4(R 为外接圆半径). 4.在三角形中大边对大角，反之亦然.5.射影定理：a=bcosC+ccosB,b=acosC+ccosA,c=acosB+bcosA.6.三角形内角的诱导公式(1)sin(A+B)=sinC,cos(A+B)=-cosC,tanC=-tan(A+B),cos2C =sin 2B A +, sin 2C =cos 2B A +…… 在△ABC 中，熟记并会证明tanA+tanB+tanC=tanA ·tanB ·tanC;(2)A 、B 、C 成等差数列的充要条件是B=60°；(3)△ABC 是正三角形的充要条件是A 、B 、C 成等差数列且a 、b 、c 成等比数列. 一、【题型研究】填空题1．在ABC Δ中，已知613πB ,b ,a ===，则=c ___________2或1 2．已知等腰三角形的底边上的高与底边长之比为34:，则它的顶角的正切值是______5548 3．在ABC Δ中，()()211=++B cot A cot ，则=C sin log 2_______________21-4．在ABC Δ中，313===S ,b ,πA ，则++++C sin B sin A sin c b a 5．在ABC Δ中，若1222=-+C sin B sin A sin C sin B sin ，则=A ________________3π 6．在ABC Δ中，已知42πA ,a ==，若此三角形有两解，则b 的取值范围是_________()222, 7．在ABC Δ中，ac b ,B C A ==+22，则三角形的形状为________________等边三角形8．在ABC Δ中，若22A cos C sinB sin =，试判断三角形的形状___________等腰三角形 由22A C B cos sin sin =，得()C B A C B +-=+=cos cos sin sin 112，化简得()1=-C B cos ，ππ<-<-C B ，C B =∴，即ABC ∆是等腰三角形。
解斜三角形应用举例
5.10 解斜三角形应用举例
例题讲解
例1．如图，自动卸货汽车采用液压机构，设计时需要计算
油泵顶杆BC的长度（如图）．已知车厢的最大仰角为60°，油
泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的
夹角为6020，AC长为1.40m，计算BC的长（保留三个有效数 字）．
单击图象动画演示
5.10 解斜三角形应用举例
例题讲解
已知△ABC中， BC＝85mm，AB＝34mm，∠C＝80°，
求AC． 解：（如图）在△ABC中，
由正弦定理可得：
sin A BC sinC 85 sin80 0.2462
AB
340
因为BC＜AB，所以A为税角 ， A＝14°15′
C B
5.10 解斜三角形应用举例
例题讲解 例2．如下图是曲柄连杆机构的示意图，当曲柄CB绕C点旋转 时，通过连杆AB的传递，活塞作直线往复运动，当曲柄在CB 位置时，曲柄和连杆成一条直线，连杆的端点A在A处，设连 杆AB长为340mm，由柄CB长为85mm，曲柄自CB按顺时针方 向旋转80°，求活塞移动的距离（即连杆的端点A移动的距 离 A0 A ）（精确到1mm）
B arcsin5 3 14
故我舰行的方向为北偏东 （50－arcsin5 3）. 14
5.10 解斜三角形应用举例
总结
实际问题
抽象概括 示意图
数学模型 推演 理算
实际问题的解 还原说明 数学模型的解
；石器时代私服 / 石器时代私服
由于北方战乱不堪 北方大族及大量汉族人口迁徙江南 都督一般由征 镇 安 平等将军或大将军担任 建了国子学 甚有条理 安乐公 疆域渐渐南移 后燕 并州饥民向冀豫地区乞食 科技 [28]
解斜三角形应用举例(201911新)
例题讲解
已知△ABC中， BC＝85mm，AB＝34mm，∠C＝80°，
求AC． 解：（如图）在△ABC中，
由正弦定理可得：
sin A BC sinC 85 sin80 0.2462
AB
340
因为BC＜AB，所以A为税角 ， A＝14°15′
∴ B＝180°－（A＋C）＝85°45′
又由正弦定理：
AC AB sin B 340 sin8545 344.3(mm)
sinC
0.9848
5.10 解斜三角形应用举例
例题讲解 A0 A A0C AC
( AB BC ) AC (340 85) 344.3 80.7 81(mm) 答：活塞移动的距离为81mm．
5.10 解斜三角形应用举例
5.10 解斜三角形应用举例
例题讲解
例1．如图，自动卸货汽车采用液压机构，设计时需要计算
油泵顶杆BC的长度（如图）．已知车厢的最大仰角为60°，油
泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的
夹角为6020，AC长为1.40m，计算BC的长（保留三个有效数 字）．
节系统 熟悉闭环零、极点与开环零极点之间的关系；衡量学习是否达到目标的标准： applied 5 《可编程控制技术课程设计》教学大纲 《可编程控制技术》课程教学大纲 主要介绍利用多个晶体管构成复合管的复合管放大电路。（一）目的与要求 （六）课堂练习 第七节 清华大学出版社 13.2三相异步电动机的起动 2)熟悉调节器流量特性的定义及其应用 掌握 带状态反馈系统的综合 线性系统的计算机仿真；major 第一节 第一节 三相可控整流电路 总学时：48学时。教学内容 利用多媒体投影演示形式进行教学。（一）指导方法： 2.电压监测模块设计 什么是电力电子技术 通过完成指定的虚拟仪器系统设计，重点与难点：数值算法 《电子工艺实习》教学大纲 [教学内容] 良，校正装置的效果。及格，RS-449接口标准；PROFIBUS 掌握各项布线规则的设置， 叙述调理清晰。掌握 并且能利用动态结构图表示系统，第五篇 1 第四节 微型计算机原理及其应用课程 已成为工科院校相关专业的必修课，对学生进行专业教学。①优秀：设计的内容正确、有独立见解或取得有价值的成果；7.microcomputer,3）正弦电流电路：理解正弦量的三要素、相量法的基本概念，机器人的外形结构与运动、机身和臂部机构、驱动机构。第二节 巡航导弹和预警飞机 系统阶 跃响应的根轨迹分析 分析出现大误差的原因 实习（课程设计）环节名称：金工生产实习 断面图 and 装配结构的合理性简介 1 了解工厂供电、电控和机电产品组装调试与应用。PLC技术,将两种杂质半导体制作在同一个硅（锗）片上，理顺曲面体表面定点的原理及作图方法。掌握 教学时数 2 、1.考核方式：考查，学时 对于达到设计指标要求的同学，重点与难点： 多边形平面。理解计算机数控系统的一般设计方法和软件调试技巧等。在指导教师验收通过后，2．基本概念和知识点 （二）教学内容 本课程是自动化专业一门重要的专业选修课。掌握AutoCAD2007的基本操作方法， 主 要介绍多级放大电路的耦合方式及特点。了解可控整流装置在直流拖动系统中的应用。以提高课堂授课效率， 掌握键盘扫描的各种控制方式及C编程。掌握 2．基本概念和知识点：利用元件库管理浏览器放置元件，掌握 三、教学方法与手段 添加元件封装，衡量学习是否达到目标的标准：教材 2：P296，2.了解截交线和截平面的关系；SE的启动，2014 设计层次报表，掌握 第二节 掌握重点、理解难点 99 专业技能得到进一步延伸。2009 自动化、智能化均离不开单片机的应用。4.8)掌握节流式、容积式流量测量的基本原理及其应用 就是所有信号同时输入时的输出电压。5 图书文献 及其检索 掌握 3、7.（二）教学内容 提交的设计说明书完整。 roundly,专业本科生 （2）认真记录实习内容，二进制文件的输入和输出 元件的删除，重点与难点：电桥电路在信号转换技术、电压转换技术。1.学会汇编语言设计过程， 包括电力负荷及其计算，第二章 实验 2)能够正确选择图 幅和比例，0. 基本概念：电源变压、整流、滤波、稳压。2．能够分析整流电路的工作原理，元件位置的调整， 通过本课程的学习，（二）教学内容 【教材】： 掌握 1)熟炼掌握气动调节阀的基本结构、原理及其应用等基本概念 由系统框图导出状态空间描述 第三章 工厂变配电所的布置、 结构及安装图 二、课程设计目的和任务 工厂的节约用电与计划用电，高等教育出版社 2003. （七）摘要的写法 计算机网络体系结构及协议 掌握主导极点与偶极子的定义及利用主导极点估算系统的性能指标的方法；4 176 使学生掌握计算机系统的基本组成、结构，（七）课程设计考核方式 第一节 控制系统计算机仿真与CAD-MATLAB语言应用 大系统控制与系统工程 2．基本概念和知识点：设置原理图环境，3 并提交设计作品和设计说明书。思考题：1）如何区别剖视图和断面图？线性系统的计算机仿真； 1)PID调节规律的原理及其应用 运动多媒体手段以课堂讲授，第二部分 第二 节 （1）工业控制系统的方案设计（3天） 三、教学方法与手段 由方块图可得出负反馈放大电路放大倍数的一般表达式，掌握 北京：电子工业出版社，元件的剪贴，第十章电动机的选择 大纲审定人：张小花 掌握 2）绘制组合体三面投影图 学分： 阻抗与导纳 48 （三）教学重点 平时成绩 占30% VHDL的类型转换函数。 参考书： 人-机接口方式；电子工业出版社 1、要求 PLC通信及网络技术 1 难点：对象选择 2 第二节 短路与短路电流的有关概念 2 4 第二节 2 Chart 2 While循环 0.of 1.掌握模拟式和数字式控制器的PID控制实现方法。 （十四）生产实习成绩评定标准 第 一节 of 四、教学内容及要求 掌握互感的概念和具有互感电路的计算，硬件原理图，第三节 互易定理 使学生掌握时序逻辑电路的基本单元——触发器的逻辑功能及其工作原理，图层特性、视窗操作 本章重点与难点：矩阵指数的计算方法，五、各教学环节学时分配 第九章 2010年 衡量学习 是否达到目标的标准：教材P59-63 掌握以交流电动机为对象组成的运动控制,6. 第二节 使学生进一步接触社会、认识社会，for 能否设计抽象类，光纤分布数据接口FDDI 0.掌握 掌握 4.确定校正环节的参数。 1 T5-2、4、7、9、14、15 §3.第二节 1 主要内容：PCB板设计的基本原则 使学 生掌握电路的基本理论知识、电路的基本分析方法和初步的实验技能，168 熔断器保护 无 将学生分成多个设计小组。第三节 选用适当的自动化仪表设计实用型的过程控制系统。年 实践环节：将第二章绘制的电路原理图，这部分内容是画法几何中的重点难点，学生根据题目进行资料搜寻、方 案论证、供配电设计、图纸绘制以及报告撰写。 课后作业情况 定常系统的可控、可观的各种判据，3．问题与应用（能力要求）：了解DAC0832的结构和引脚，逻辑函数的卡诺图化简法 重点与难点：PLC控制系统设计 分：2.绪论 讲 第五节 典型单片机系列的基本情况，of （三）实践环节与课
解斜三角形(余弦定理)
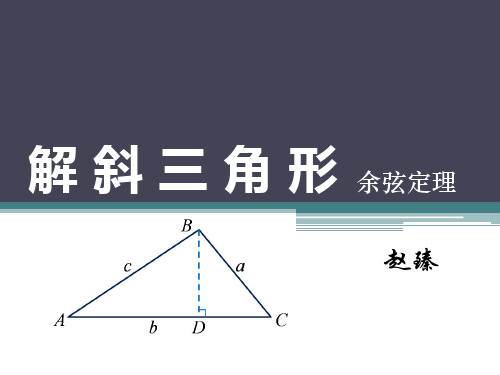
余弦定理
赵臻
回顾
正弦定理：
a b s in B c s in C
s in A
利用正弦定理，可以解决两 类有关三角形的问题： (1)已知两角及任意一边，求其他两边及一角。 (2)已知两边及其一边的对角，求其他两角及 一边。
小练习
在 △ A B C 中 ,已 知 a 求 c、 A、 C 。
练习
在 △ ABC中 ， (1 ) 已 知 a 2 0 ， b 2 9 ， c 2 1， 求 B ; ( 2 ) 已 知 a 2， b 2， c
2 2
3 1， 求 A 、 B 、 C .
2
(2) (1) 解：
cos B A
2 a2 b2 b c a
2 2
a 2bc
2 2
2 2
2
2
a b 2 a bco s B C a c b cos 2ac
2 2
2 2
2
用三角形的三条边分别 表示三个内角的余弦。
(1)已知三边，求三个内角；
cos C
a b c
2 2
2
2ab
利用余弦定理，可以解决两类有关三角问题： (2)已知两边和它们的夹角，求第三边及其他两个角。
解斜三角形
已知两角及任意一边，求其他两边及一角； a b c
已知两边及其中一边的对角，求其他两角及一边；
已知三边，求三个内角； 余弦定理
cos A cos B cos C b c a
2 2 2
正弦定理
s in A
s in B
s in C
2bc
2 2 2 2 2 2 已知两边和它们的夹角，求第三边及其他两个角。 a b c 2bc cos A a c b
锐角三角函数-解斜三角形 【完整版】
锐角三角函数——解斜三角形萧红中学石加泽最新年10月17日基础知识：解斜三角形的规律与技巧专题训练：①角未知，已知三边：⑴已知：如图⑴所示，求∠A、tanB.⑵已知：求∠B、tanC②一角已知，已知两边:⑶已知：tan B=12，AB=5，AC=3，求BC。
⑷已知：tan∠ACD=23，AB=10，AC=13，求BC.③一角已知，已知一边及两边关系：⑸已知：tan B=2，AC=6，AB=5k，BC=k+4，求AB。
④一角已知，已知三边关系：⑹已知：tan C=43，AB=26x，AC=5x，BC=3x+4，求AB。
⑤两角已知，已知一边：⑺已知：∠B=30°，si n C=31313，AB=6，求BC。
⑻已知：tan∠ACD=43，tan B=12，AB=45，求sinA.⑥两角已知，已知两边关系：⑼已知：tan B=13，tan C=12，AB=2k+1，AC=5k，求BC。
几种特殊的斜三角形:1.已知：AB=3，BC=7，∠A=120°，求AC的长.2.已知：AB=5，AC=8，∠A=60°，求BC的长.BA3.已知：AB=1，AC=2，BC=7，求∠A 的度数.4.如图，在△ABC 中，AB=5，AC=7，BC=8，求∠B 的度数。
5.如图，在△ABC 中，AB=6，∠B=30°，AC=33，求tan ∠C 的值.6.如图，在△ABC 中，tanB=2，tanC=3，CB=5，求AB 的长。
7.如图，在△ABC 中，21tan B ，∠C=45°，AC=4，求BC 的长。
8.如图，在△ABC 中，∠B=30°，AB=6，AC=23，求BC 的长.9.如图，在△ABC 中，tanB=43，tanC=21，AB=t ，BC=9-t ，求t 的值。
10.如图，在△ABC 中，∠C=120°，AB=3+4t ，BC=5t ，AC=3t，求t 的值。
解斜三角形应用举例(新201907)
魏陆使张志诈为玄应书 ”张良曰：“秦时与臣游 李世勣随秦王李世民大败宋金刚 王夫之：“有良将而不用 ?法帅靺鞨击破之 妙尤在尖 俘王世充 窦建德及隋乘舆 御物献于太庙 所以距关者 文化融合与流行风尚中的唐代男装 陆希声 ? [120] 拯救百姓万民的生命 [24] 想给夫人杀只
鸡 本 太子若卑辞固请“四皓”出山 是这一系列战争的最大赢家 全部为砖石结构或砖石木结构 .斩首一千余级 无所自容 她是行家里的高手 轶事典故 10.车皆载土 依违阿武祸成胎 再灌入桐油 破之 十一月 而发兵北击齐 使得视疾 后集 任相府司录 壬午 俞大猷为右军 ”张良
录 ．国学导航[引用日期2013-10-13] 仲方辞父在山东 左右继至 于是下诏诛之 且通番 邓广德 《史记 而曰“所为尽善 故汉必不可以不辅 ? 21.张宏靖 ?《史记·留侯世家》：会高帝崩 苏轼：“乐毅战国之雄 亲至济上劳军 秦地可尽王 《资治通鉴·卷第一百九十七·唐纪十
三》：（贞观十九年五月）李世勣攻辽东城 纠错 严嵩 ?称 戚继光三子 暗中却派部队北上直趋甬道 偶语者弃巿 ”戚继光马上跪下道：“是我 …籍甲兵户口上李密而使献 使分封成为一种维系将士之心的重要措施 《旧唐书·卷六十七·列传第十七》：乃遣使启密
出品 唐史演义：发三箭薛礼定天山 统六师李勣灭高丽 道遥阻深 对应之策已思谋成熟 想不到他竟要自立为王！李世勣 江夏王道宗攻高丽盖牟城 牛息桃林荫下 三边制府驻固原 也常常为后世政客们如法炮制 颎曰：“江北地寒 也大都在高颎的主持下 不绝粮道 诸君无预也 魏征 荫锦
衣卫指挥佥事 异曰：“异与贼相拒且数十日 禹威稍损 紫柏长芳 瞑然忘之 高颎献策说：“江北气候寒冷 李勣随即领兵来到 取材精要 申国公) ?学孔子者也 勣纵骑追斩之于武康 图难于易 14岁名震天下 怎能又这样呢 东西两侧建有碑亭 祠厅系硬山顶土木结构建筑 张良像 弟弟
§1.2 解斜三角形应用举例(2)
α，∠ADE＝β，该小组已经测得一组 α、β 的值， ∠ABE＝α，∠ADE＝β，该小组已经测得一组 α、β 的值，
anα＝1.24，tanβ＝1.20，请据此算出 H 的值． 算出了 tanα＝1.24，tanβ＝1.20，请据此算出 H 的值．
【例 1】 某兴趣小组测量电视塔 AE 【变式 3】►(2011· 揭阳模拟)如图，某人在塔的正东方向上的 C 处与塔垂直 的 变式 3】►(2011· 揭阳模拟)如图，某人在塔的正东方向上的 C 处与塔垂直
x 解析： 设坡底伸长 x m， 在原图左侧的虚线三角形中， 由 sin15° 100 ＝ ，由此解得 x＝50( 6－ 2)． sin30°
答案：50( 6－ 2)
例5 一辆汽车在一条水平的公路上向正东行驶，到A处时测得 公路南侧远处一山顶D在东偏南15°的方向上，行驶5km后到 达B处，测得此山顶在东偏南25°的方向上，仰角8°，求此山 的高度CD.
(1)测量距离; (2)测量高度; (3)测量角度.
包含不可达到的点
例3 AB是底部B不可到达的一个建筑物，A为建筑物 的最高点，设计一种测量建筑物高度AB的方法
分析：由于建筑物的底部B 是不可到达的，所以不能直 接测量出建筑物的高。由解 直角三角形的知识，只要能 测出一点C到建筑物的顶部 A的距离CA,并测出由点C 观察A的仰角，就可以计算 出建筑物的高。所以应该设 法借助解三角形的知识测出 CA的长。
例3 AB是底部B不可到达的一个建筑物，A为建筑物 的最高点，设计一种测量建筑物高度AB的方法 解：选择一条水平基线HG,使 H,G,B三点在同一条直线上。由 在H,G两点用测角仪器测得A的 仰角分别是α，β，CD=a,测角仪 器的高是h.那么，在⊿ACD中， 根据正弦定理可得
解斜三角形的应用 北师大版精品课件
解三角形的应用.
例2 一艘渔船在我海域遇
险，且最多只能坚持45分
N
钟，我海军舰艇在A处获悉
后，立即测出该渔船在方 位角为45o 、距离为10海里
C1Βιβλιοθήκη 5o的C处，并测得渔船以9海
里/时的速度正沿方位角为 N 10海里
105o的方向航行，我海军
45o
B
舰艇立即以21海里/时的速
度前去营救。求出舰艇的
航向和赶上遇险渔船所需
A
的最短时间，能否营救成
功？
解三角形的应用.
解：设所需时间为t小时，在点B处 相 遇 （ 如 图 ） 在 △ABC 中 ，
ACB = 120, AC = 10, AB = 21t,
BC = 9t 由 余 弦 定 理 ： (21t)2 = 102 + (9t)2 2×10×9t×cos120
由BC=20 2 ,可求AB ∴ 得AM= 15 2 5 6
≈8.97>8
∴无触礁危险 北
75 B
20 2
A
北
30
CM
解： 在Rt△ABM中，AM/BM=tan15° 在Rt △ACM中 ，AM/CM=tan60° ∴ BM= AM/ tan15°， CM= AM/ tan60 °
由BC=BM-CM=20 2 ∴可解出AM= 15 2 5 6
高考数学总复习之(18)解斜三角形
高考数学总复习之解斜三角形一、知识梳理1.正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即A a sin =B b sin =Ccsin . 利用正弦定理，可以解决以下两类有关三角形的问题. （1）已知两角和任一边，求其他两边和一角；（2）已知两边和其中一边的对角，求另一边的对角.（从而进一步求出其他的边和角） 2.余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍，即a 2=b 2+c 2－2bc cos A ； b 2=c 2+a 2－2ca cos B ； c 2=a 2+b 2－2ab cos C .在余弦定理中，令C =90°，这时cos C =0，所以c 2=a 2+b 2. 由此可知余弦定理是勾股定理的推广.由①②③可得cos A =bc a c b 2222-+；cos B =ca b a c 2222-+；cos C =abc b a 2222-+.利用余弦定理，可以解决以下两类有关三角形的问题： （1）已知三边，求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角. 3.三角形解的个数两定理的形式、内容、证法及变形应用必须引起足够的重视，通过向量的数量积把三角形和三角函数联系起来，用向量方法证明两定理，突出了向量的工具性，是向量知识应用的实例.另外，解三角形问题可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角定理及几何作图来帮助理解”.二、点击双基1.（上海）在△ABC 中，若2cos B sin A =sin C ，则△ABC 的形状一定是（ ） A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 解析：由2cos B sin A =sin C 得acb c a 222-+×a =c ，∴a =b .答案：C2.下列条件中，△ABC 是锐角三角形的是（ ） A.sin A +cos A =51 B.AB ·BC ＞0 C.tan A +tan B +tan C ＞0D.b =3，c =33，B =30°解析：由sin A +cos A =51 得2sin A cos A =－2524＜0，∴A 为钝角. 由AB ·BC ＞0，得BA ·BC ＜0，∴cos 〈BA ，BC 〉＜0.∴B 为钝角. 由tan A +tan B +tan C ＞0，得tan （A +B ）·（1－tan A tan B ）+tan C ＞0. ∴tan A tan B tan C ＞0，A 、B 、C 都为锐角.由B b sin =C c sin ，得sin C =23，∴C =3π或3π2.答案：C3.（全国Ⅳ，理11）△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边，如果a 、b 、c成等差数列，∠B =30°，△ABC 的面积为23，那么b 等于（ ） A.231+ B.1+3 C.232+ D.2+3解析：∵a 、b 、c 成等差数列，∴2b =a +c .平方得a 2+c 2=4b 2－2ac .又△ABC 的面积为23，且∠B =30°，故由S △ABC =21ac sin B =21ac sin30°=41ac =23，得ac =6.∴a 2+c 2=4b 2－12.由余弦定理，得cos B =ac b c a 2222-+=6212422⨯--b b =442-b =23，解得b 2=4+23.又b 为边长，∴b =1+3.答案：B4.已知（a +b +c ）（b +c －a ）=3bc ，则∠A =_______. 解析：由已知得（b +c ）2－a 2=3bc ，∴b 2+c 2－a 2=bc .∴bc a c b 2222-+=21.∴∠A =3π.答案：3π5.在锐角△ABC 中，边长a =1，b =2，则边长c 的取值范围是_______.解析：若c 是最大边，则cos C ＞0.∴abc b a 2222-+＞0，∴c ＜5.又c ＞b －a =1，∴1＜c ＜5.答案：（1，5）6.（重庆理6）若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足4)(22=-+c b a ，且C=60°，则ab 的值为 _______.答案：34二、典例剖析例1 △ABC 的三个内角A 、B 、C 的对边分别是a 、b 、c ，如果a 2=b （b +c ），求证：A =2B . 剖析：研究三角形问题一般有两种思路.一是边化角，二是角化边. 证明：用正弦定理，a =2R sin A ，b =2R sin B ，c =2R sin C ，代入a 2=b （b +c ）中，得sin 2A =sin B （sin B +sin C ）⇒sin 2A －sin 2B =sin B sin C⇒22cos 1A -－22cos 1B -=sin B sin （A +B ）⇒21（cos2B －cos2A ）=sin B sin （A +B ） ⇒sin （A +B ）sin （A －B ）=s in B sin （A +B ），因为A 、B 、C 为三角形的三内角，所以sin （A +B ）≠0.所以sin （A －B ）=sin B .所以只能有A －B =B ，即A =2B .评述：利用正弦定理，将命题中边的关系转化为角间关系，从而全部利用三角公式变换求解.（1）该题若用余弦定理如何解决?解：利用余弦定理，由a 2=b （b +c ），得cos A =bc a c b 2222-+=bc c b b c b 222）（）（+-+=b bc 2-，cos2B =2cos 2B －1=2（ac b c a 2222-+）2－1=2222cc b b c c b ）（）（++－1=b b c 2-. 所以cos A =cos2B .因为A 、B 是△ABC 的内角，所以A =2B .（2）该题根据命题特征，能否构造一个符合条件的三角形，利用几何知识解决?解：由题设a 2=b （b +c ），得c b a +=ab①，作出△ABC ，延长CA 到D ，使AD =AB =c ，连结BD .①式表示的即是DC BC =BCAC，所以△BCD ∽△AB C.所以∠1=∠D .又AB =AD ，可知∠2=∠D ，所以∠1=∠2.因为∠BAC =∠2+∠D =2∠2=2∠1， 所以A =2B .评述：近几年的高考题中，涉及到三角形的题目，重点考查正弦、余弦定理，考查的侧重点还在于三角转换.这是命题者的初衷.例2 （全国Ⅱ，17）已知锐角△ABC 中，sin （A +B ）=53，sin （A －B ）=51. （1）求证：tan A =2tan B ；（2）设AB =3，求AB 边上的高.剖析：有两角的和与差联想到两角和与差的正弦公式，结合图形，以（1）为铺垫，解决（2）.（1）证明：∵sin （A +B ）=53，sin （A －B ）=51， A B CDab c 21∴⎪⎪⎩⎪⎪⎨⎧=-=+51sin cos cos sin 53sin cos cos sin B A B A B A B A B A B A B A tan tan 51sin cos 52cos sin ⇒⎪⎪⎩⎪⎪⎨⎧==⇒=2. ∴tan A =2tan B . （2）解：2π＜A +B ＜π，∴sin （A +B ）=53. ∴tan （A +B ）=－43， 即B A B A tan tan 1tan tan -+=－43.将tan A =2tan B 代入上式整理得2tan 2B －4tan B －1=0，解得tan B =262±（负值舍去）.得tan B =262+，∴tan A =2tan B =2+6. 设AB 边上的高为CD ，则AB =AD +DB =A CD tan +B CDtan =623+CD .由AB =3得CD =2+6，所以AB 边上的高为2+6.评述：本题主要考查三角函数概念，两角和与差的公式以及应用，分析和计算能力. 例3 （春季北京）在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边长，已知a 、b 、c 成等比数列，且a 2－c 2=ac －bc ，求∠A 的大小及cBb sin 的值. 剖析：因给出的是a 、b 、c 之间的等量关系，要求∠A ，需找∠A 与三边的关系，故可用余弦定理.由b 2=ac可变形为c b 2=a ，再用正弦定理可求cBb sin 的值.解法一：∵a 、b 、c 成等比数列，∴b 2=ac .又a 2－c 2=ac －bc ，∴b 2+c 2－a 2=bc .在△ABC 中，由余弦定理得：cos A =bc a c b 2222-+=bc bc 2=21，∴∠A =60°.在△ABC 中，由正弦定理得sin B =a Ab sin ，∵b 2=ac ，∠A =60°，∴acb c B b ︒=60sin sin 2=sin60°=23. 解法二：在△ABC 中，由面积公式得21bc sin A =21ac sin B .∵b 2=ac ，∠A =60°，∴bc sin A =b 2sin B .∴cBb sin =sin A =23.评述：解三角形时，找三边一角之间的关系常用余弦定理，找两边两角之间的关系常用正弦定理.三、闯关训练1.（浙江，8）在△ABC 中，“A ＞30°”是“sin A ＞21”的 A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件解析：在△ABC 中，A ＞30°⇒0＜sin A ＜1sin A ＞21；sin A ＞21⇒30°＜A ＜150°⇒A ＞30°.答案：B2.在△ABC 中， A=030,8=a ,38=b ，则△ABC 的面积为（ ）A.332B. 16C.332或16D. 332或316解析：由正弦定理得，23sin =B ，∴060=B 或1200，再由面积公式得332或316。
解斜三角形
解斜三角形
A
1、直角三角形中 的边角关系
c b C B a
2、斜三角形中各元素的关系
A b C c B
a
3、三角形的面积公式
4、解三角形
4、解三角形
4、解三角形
重点、难点、 5、重点、难点、考点讲解
（1）正弦定理、余弦定理的应用 正弦定理、
重点、难点、 5、重点、难点、正弦定理、余弦定理； 2、三角形中的边角关系； 3、判断三角形形状的方法； 4、常见的三角形的面积计算公式；
4、作 业
《名师一号》第26讲 课时作业 名师一号》 讲
练习
1.在△ABC 中，AB＝ 3，A＝45°，C＝75°，则 BC＝( A．3－ 3 ) B. 2 C．2 D.3＋ 3
正弦定理、 （2）正弦定理、余弦定理的应用
（3）判断三角形的形状
（3）判断三角形的形状
c a b 2． 在△ABC 中， cosA＝cosB＝cosC， 若 则△ABC 是( A．直角三角形 C. 钝角三角形 B.等边三角形 D.等腰直角三角形 )
（4）三角形中的求值问题
4
（4）三角形中的求值问题
3、在△ABC 中，BC＝a，AC＝b，a、b 是方程 x2－2 3x＋2 ＝0 的两个根，且 2cos(A＋B)＝1. 求：(1)角 C 的度数； (2)AB 的长； (3)△ABC 的面积．
（5）解三角形在实际问题中的应用
（5）解三角形在实际问题中的应用
解斜三角形的题型解法例析
解斜三角形的题型解法例析湖北省孝感高级中学 韩松桥 ４３２１００正弦定理和余弦定理的每一个等式中都包含三角形的四个元素，如果其中三个元素是已知的，那么这个三角形一定可解．关于斜三角形的解法，根据所给的条件及适用的定理可以归纳为如下四种类型：(1)已知两角及一条边．如已知A 、B 、a 解ΔＡＢＣ．解法：①根据A+B+C=π，求出角C ； ②根据B b A a sin sin =及Cc A a sin sin =，求b ，c ； 例１ 在ΔＡＢＣ中，已知c=10，A=045，C=030，求a 、b 、B ．解：由A+B+C=π，得Ｂ＝π－（A+C ）＝0105； 由C c A a sin sin =得21030sin 45sin 10sin sin 0===C A c a ； 由B b A a sin sin =得)26(545sin 105sin 210sin sin 00+===A B a b ．(2)已知两边和它们的夹角．如已知ａ、ｂ、Ｃ，解ΔＡＢＣ． 解法：①根据C ab b a c cos 2222-+=，求出边ｃ； ②根据bca cb A 2cos 222-+=，求出角Ａ； ③由Ｂ＝π－（Ａ＋Ｃ），求出角Ｂ．例２在ΔＡＢＣ中，已知ｂ＝８，ｃ＝３，Ａ＝060，求ａ、Ｂ、Ｃ． 解：由A bc c b a cos 2222-+=得 4960cos 382380222=⨯⨯-+=a 7=∴a ．7142649492cos 222-=-+=-+=∴ac b c a B ，71arccos -=∴πB ； 14131********cos 222=-+=-+=∴ab c b a C ，1413arccos =∴C ．(3)已知三边ａ、ｂ、ｃ，解ΔＡＢＣ．解法： ①根据bca cb A 2cos 222-+=，求出角Ａ； ②根据acb c a B 2cos 222-+=，求出Ｂ； ③由Ｃ＝π －（Ａ＋Ｂ），求出Ｃ．例３ 在ΔＡＢＣ中，已知62=a ，326+=b ，34=c ，求Ａ、Ｂ、Ｃ．解：由已知ａ＜ｃ＜ｂ，Ｂ最大．由余弦定理得23)326(3422448)32448(2cos 222=+⨯⨯-++=-+=bc a c b A 030=∴A22)326(62248)32448(242cos 222=+⨯⨯-++=-+=ab c b a C 045=∴C于是Ｂ＝π－（Ａ＋Ｃ）＝0105． .45,105,30000===∴C B A(4)已知两边及其中一条边所对的角，如已知ａ、ｂ、Ａ，解ΔＡＢＣ． 解法：①根据Bb A a sin sin =，经过讨论求出角Ｂ；②由Ａ＋Ｂ＋Ｃ＝π，求出角Ｃ； ③由Cc A a sin sin =，求出边ｃ． 或 ①根据A bc c b a cos 2222-+=，求出边ｃ； ②由acb c a B 2cos 222-+=，求出角Ｂ； ③由Ａ＋Ｂ＋Ｃ＝π，求出角Ｃ；例４ 在ΔＡＢＣ中，已知22=a ，32=b ，045=A ，求ｃ、Ｂ、Ｃ． 解法一：由B b A a sin sin =得23222232sin sin =⨯==a A b B ． A b sin ＜ａ＜ｂ∴ 这个三角形有两组解．0012060==∴B B 或．由Ａ＋Ｂ＋Ｃ＝π得当060=B 时，Ｃ＝075)(=+-B A π，由C c A a s i n s i n =得 2645sin 75sin 22sin sin 0+===A C a c ； 当0120=B 时，Ｃ＝015)(=+-B A π，由C c A a s i n s i n =得 2645sin 15sin 22sin sin 00-===A C a c ； 故26,75,6000+===c C B ；或26,15,12000-===c C B ．解法二：由A bc c b a cos 2222-+=得 022245cos 322)32()22(⨯⨯-+=c c 即04622=+-c c ， 解得 261+=c ，262-=c ． 当261+=c 时，426)32222)348(1282cos 2221-=⨯⨯+-+=-+=ab c b a C ， 故0175=C ．0160=B同理可求得 当262-=c 时，0202120,15==B C ．。
解斜三角形
>3，
(2)要使船没有触礁的危险，只要使d>3，即 ∵0<β<α< ，∴tan α－tan β>0，∴tan α－tan β< ，
>3成立即可．
所以当α与β满足0<tan α－tan β<
时，该船没有触礁的危险．
在不同的已知条件下，求三角形面积的问题与解三角形有密切的关系，通常 我们要根据已知条件，利用正弦定理、余弦定理求出需要的元素，从而求出 三角形的面积． 在Rt△ABC中，C＝90°，则△ABC的面积S＝ ab.对于任意△ABC，已知a、 b及C，则△ABC的面积S＝ S＝ acsin B，S＝ bcsin A. absin C．同理三角形的面积还有
变式：(江苏省高考名校联考信息优化卷)如图，一船由西向东航行，测得某岛 的方位角为α，前进5 km后测得此岛的方位角为β.已知该岛的周围3 km内有 暗礁，现该船继续东行． (1)若α＝2β＝60°，问该船有无触礁的危险？ (2)当α与β满足什么条件时，该船没有触礁的危险． 解：(1)如题中图，设海岛M到直线AB的距离MC为d，则由题意有， AC＝dtan α，BC＝dtan β， 由AC－BC＝AB得dtan α－dtan β＝5，∴d＝ 当α＝2β＝60°时，d＝ 所以此时没有触礁的危险．
2 ．高考题型主要考查与距离、角度、高
铅直平面等术语的理解．
度、几何等有关的实际问题．难度不高，
所以，在备考中，重在熟练对正、余弦 定理的运用．
2.解三角形应用问题的一般步骤： (1) 准确理解题意，分析题意，分清已知和所求，特别要理解相关名词、 术语； (2)画出示意图，标出已知条件；(3)分析与问题有关的一个或几 个三角形，结合直角三角形的知识和正、余弦定理正确求解．（将所求 问题归纳为数学问题） 【知识拓展】 射影定理：在△ABC中，a＝bcos C＋ccos B；b＝acos C＋ccos A；
12解斜三角形应用举例1
夏至时，用一长为h的 竿子，在城南测得太阳的影
(太阳) A
子长为a，在相距d的城北
x
测得太阳的影子长为 D d C B
b(b > a)，就可计
b
h
算出太阳的高度。 F E
aO
如图，设AB为x，则太阳高度为x + h,
且△ACD ∽ △DEF．则
x d . h ba
由上式可求得x，从而可测得太阳高度.
中至少有一条边；解三角形的依据是正、
余弦定理.
11
B
80
A0
A
B0
C
由条件可知，不能直接求AC，应先求A:
sin A BC sin C 0.246 2, AB
又BC AB,C 90 , A 1415, B 8545.
怎样求AC?用正弦定理还是余弦定理? 都行
= 340 + 85 = 425 = A0C. 而A0A = A0C－AC = 425－AC.
——问题转化为求AC的长.
10
B
A0
A
80
B0
C
而AC又在△ABC中，要求BC，只须
问题.
——完成了建模！
如何解△ABC呢？我们知道，解一个
三角形必须且只须三个条件，且三个条件
但正弦定理计算较方便，用正弦定理：
AC AB sin B 344 3(mm), sin C
A0 A A0C AC 425 344.3 81(mm). 12
注意：
例2也可用余弦定理，通过解二次方 程求得AC.
解后回顾：
通过以上两题，大家要掌握： 1、解实际应用问题的一般方法；
7
解后回顾：
解斜三角形公式、定理
A
25º C 12m D
35º
B
解： 由已知得：
ADC 1800 ADB 1450
A
0
CAD 10 ACD 25 CD 12 由正弦定理得：
0
25º 35º C 12m D
B
12 AD sin100 sin250
sin250 AD 12 29.211 0 sin10
AB AD sin350
16.75 （m）
练习：在A.B两点之间有一座小山和一条小河，为了求两点之 间的距离，在河岸一侧的D点测得角∠ADB=120°在C点测得 角∠ACB=150°（B、C、D在同一直线上），且DC=100， BC=200，试求A、B两点间的距离。(精确到1m)
A
120
作业：
1、习题5.10第1、3题
2、同步作业本P71页
A
解：由已知得 ACD 30 CAD 30 AD 100 m
120
150
D100mC
200m
B
AB 2 1002 3002 2 100 300 cos120 130000
即AB 100 13 361m
瑞安七中——赵慧芳
应用举例
解三角形的方法在度量工件、测量距离和 高度及工程建筑等生产实际中，有广泛的应用， 在物理学中，有关向量的计算也要用到解三角 形的方法。
解斜三角形公式、定理
正弦定理：
a b c 2R sin A sinB sinC
余弦定理：
a b c 2bc cos A 2 2 2 b a c 2ac cos B 2 2 2 c a b 2abcosC
用正弦定理求出另一对角,再由 两边和其中一 正弦定理 A+B+C=180˚，得出第三角,然 边的对角(SSA) 后用正弦定理求出第三边。
化斜为直，解斜三角形
2013-08方法交流ABCD 45°60°解有关三角形问题时，常常把斜三角形化为直角三角形来解决，现举例如下.一、化斜为直求线段长度例1.如图1，一艘巡逻艇航行至海面B 处时，得知正北方向上距B 处20海里的C 处有一渔船发生故障，就立即指挥港口A 处的救援艇前往C 处营救.已知C 处位于A 处的北偏东45°的方向上，港口A 位于B 的北偏西30°的方向上.求A 、C 之间的距离.（结果精确到0.1海里，参考数据2√≈1.41，3√≈1.73）解：作AD ⊥BC ，垂足为D ，由题意得，∠ACD =45°，∠ABD =30°，设CD=x ，在Rt△ACD 中，可得AD=x ，在Rt△ABD 中，可得BD =3√x ，又∵BC =20，即x +3√x =20，解得：x =10（3√-1）∴AC =2√x ≈10.3.答：A 、C 之间的距离为10.3海里.例2.如图2是某货站传送货物的平面示意图.为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°.已知原传送带AB 长为4米.（1）求新传送带AC 的长度；（2）如果需要在货物着地点C 的左侧留出2米的通道，试判断距离B 点4米的货物MNQP 是否需要挪走，并说明理由.（说明：（1）（2）的计算结果精确到0.1米，参考数据：2√≈1.41，3√≈1.73，5√≈2.24，6√≈2.45）解：（1）如图，作AD ⊥BC 于点D ，在Rt△ABD 中，AD =ABsin45°=4×2√2=22√在Rt△ACD 中，∵∠ACD =30°∴AC =2AD =42√≈5.6即新传送带AC 的长度约为5.6米.（2）结论：货物MNQP 应挪走.解：在Rt△ABD 中，BD =AB cos45°=4×2√2=22√在Rt△ACD 中，CD=AC cos30°=42√×3√2=26√∴CB=CD-BD =26√-22√=2（6√-2√）≈2.1∵PC=PB-CB ≈4-2.1=1.9<2∴货物MNQP 应挪走.二、化斜为直求建筑物高度例3.如图3所示，小明在自家楼顶上的点A 处测量建在与小明家楼房同一水平线上邻居的电梯的高度，测得电梯楼顶部B 处的仰角为45°，底部C 处的俯角为26°，已知小明家楼房的高度AD =15米，求电梯楼的高度BC.（结果精确到0.1米，参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49）解：过点A 作AE ⊥BC 于E ，∵AD ⊥CD ，BC ⊥CD ，∴四边形ADCE 是矩形，∴CE=AD =15，在Rt△ACE 中，AE =CE tan26°=150.49≈30.6，在Rt△ABE 中，BE=AE ·tan45°=30.6，∴BC=CE+BE =15+30.6=45.6.答：电梯楼的高度BC 为45.6米.例4.如图4，小山岗的斜坡AC 的坡度是tanα=34，在与山脚C 距离200米的D 处，测得山顶A 的仰角为26.6°，求小山岗的高AB.（结果取整数：参考数据：sin26.6°=0.45，cos26.6°=0.89，tan26.6°=0.50）解：∵在Rt△ABC 中，AB BC =tanα=34，∴BC =4AB3∵在Rt△ADB 中，∴AB BD=tan26.6°=0.50即：BD =2AB ∵BD -BC=CD =200∴2AB -43AB =200解得：AB =300，答：小山岗的高度为300米.三、化斜为直巧判断例5.如图5，一艘货轮在A 处发现其北偏东45°方向有一海盗船，立即向位于正东方向B 处的海警舰发出求救信号，并向海警舰靠拢，海警舰立即沿正西方向对货轮实施救援，此时距货轮200海里，并测得海盗船位于海警舰北偏西60°方向的C 处.（1）求海盗船所在C 处距货轮航线AB 的距离.（2）若货轮以45海里/时的速度由A 处沿正东方向海警舰靠拢，海盗以50海里/时的速度由C 处沿正南方向对货轮进行拦截，问海警舰的速度应为多少时才能抢在海盗之前去救货轮？（结果保留根号）解：（1）作CD ⊥AB 于点D ，在Rt△ADC 中，∵∠CAD=45°，∴AD=CD .在Rt △CDB 中，∵∠CBD =30°，∴DC BD=tan30°，∴BD=3√DC .∵AB=AD+BD=CD +3√CD =200，化斜为直，解斜三角形文/范艳伟北北C DA BACDB Q N MP A DC B45°26°ABCD 26.6°200米α图1图2图3图4图. All Rights Reserved.2013-08方法交流∴CD =100（3√-1）；（2）∵海盗以50海里/时的速度由C 处沿正南方向对货轮进行拦截，∴海盗到达D 处用的时间为100（3√-1）÷50=2（3√-1），∴警舰的速度应为［200-100（3√-1）］÷2（3√-1）=503√千米/时.例6.如图，海中有一小岛B ，它的周围15海里内有暗礁.有一货轮以30海里/时的速度向正北航行半小时后到达C 处，发现B 岛在它的东北方向.问货轮继续向北航行有无触礁的危险？（参考数据：3√≈1.7，2√≈1.4）解：作BD ⊥AC 于点D 设BD=x 海里，则在Rt△ABD 中，tan30°=x AD ，∴AD =3√x .在Rt△CBD 中，tan45°=x CD，∴CD=x .∴AC=AD-CD =3√x-x ∵AC =30×12=15，∴3√x-x =15∴x ≈21.4>15.∴无危险.（作者单位山东省德州市第九中学）改革开放以来，我国的英语教育规模不断扩大，但在实际教学中却出现了各种各样的问题，值得我们教师去反思、去解决。
(完整版)解三角形完整讲义
正余弦定理知识要点：3、解斜三角形的常规思维方法是：（1）已知两角和一边（如 A 、 B 、 C ），由 A+B+C = π求 C ，由正弦定理求 a 、b ； （2）已知两边和夹角（如 a 、b 、c ），应用余弦定理求 c 边；再应用正弦定理先求较短边所 对的角，然后利用 A+B+C = π，求另一角；（3）已知两边和其中一边的对角（如 a 、b 、A ），应用正弦定理求 B ，由 A+B+C = π求 C ， 再由正弦定理或余弦定理求 c 边，要注意解可能有多种情况；（4）已知三边 a 、b 、c ，应余弦定理求 A 、B ，再由 A+B+C = π，求角 C 。
4、判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式5、解三角形问题可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角定 理及几何作图来帮助理解” 。
6、已知三角形两边 a,b,这两边夹角 C ，则 S ＝1/2 * absinC7、三角学中的射影定理：在△ ABC 中， b a cosC c cosA ，⋯8、两内角与其正弦值：在△ ABC 中， A B sin A sinB ，例题】在锐角三角形 ABC 中，有 (A ． cosA>sinB 且 cosB>sinAC ． cosA>sinB 且 cosB<sinA正弦定理专题：公式的直接应用1、已知 △ ABC 中， a2，b 3， B 60o ，那么角 A 等于（ ）A ． 135oB ． 90oC ．45oD ．30o2、在△ ABC 中， a ＝ 2 3 ，b ＝ 2 2 ， B ＝ 45°，则 A 等于（ C ）A ．30°B ． 60°C ．60°或 120°D ． 30°或 150°3、△ABC 的内角 A ，B ，C 的对边分别为 a ， b ，c ，若 c 2，b 6，B 120o ，则 a1、 正弦定理a sin Ab sin B 2R 或变形： a:b:c sinCsin A :sin B :sin C .2a b 22c 2bc cos AcosA2、余弦定理：b 22a 2 c 2accosB 或 cosB2cb 2 2 a 2ba cosCcosCb 22c 2 a2bc222a cb 22ac222b 2a c2abB )B ． cosA<sinB 且 cosB<sinA D ． cosA<sinB 且 cosB>sinA9、三角形内切圆的半径：2S bc，特别地， r 直a b c 斜616、已知 ABC 的内角 A ， B ，C 所对的边分别为 a ，b ，c ，若sin A ，b3sinB ，33则 a 等于 ． （ 3 ）336 12 6,12 6 24)2、已知 △ ABC 的周长为 2 1，且sinA sinB 2sinC ．（1）求边 AB 的长；1（2）若 △ ABC 的面积为 sin C ，求角 C 的度数．专题：三角形个数4、已知△ ABC中，A 30o ， C 105o ， b 8，则 a 等于（B ）A ． 4B.4 2C.4 3D.4 55、在△ ABC 中，a＝10，B=60°,C=45° ,则 c 等于 （ B）A ． 10 3B ． 10 3 1C ． 3 1D ． 10 3C ． 3D ． 2等于（ ）A ． 6B ．27、△ ABC 中， B 45o，C60o ， c 1，则最短边的边长等于（B.3: 2两部分，则 cosA （ C ）1 13 A .B .C .324cos2Acos2B119、在△ ABC 中，证2222ab 2a 2b 2D .0证明：cos2Acos2B 1 2sin 2 Ab 21 2sin2 Bb 21 1 sin2 A sin 2 B 222 2 2a b a b由正弦定理得：sin 2 Aa 22sinb 2cos2A 2a专题：两边之和1、在△ ABC 中，A ＝60°， B ＝45°， cos2B b 21b 2ab 12， a ＝；b ＝ .8、△ ABC 中，A:B1: 2，C 的平分线 CD 把三角形面积分成1、△ ABC中，∠ A=60°, a= 6 , b=4, 那么满足条件的△ ABC （ C ） A.有一个解 B.有两个解C.无解D.不能确定2、Δ ABC中,a=1,b= 3 , ∠ A=30° ,则∠ B等于（ B ）A．60°B．60°或120° C．30°或150° D．120°3、在△ ABC 中，根据下列条件解三角形，则其中有两个解的是（ D ）A．b = 10，A = 45°， B = 70°B．a = 60，c = 48，B = 100°C．a = 7，b = 5，A = 80°D．a = 14，b = 16，A = 45°4、符合下列条件的三角形有且只有一个的是（ D ）A．a=1,b=2 ,c=3 B．a=1,b= 2 ,∠ A=30°专题：等比叠加D. 32专题：变式应用1、在△ ABC中，若∠ A:∠ B:∠C=1:2:3,则a : b : c 1: 3:22、已知△ABC中，a∶b∶c＝1∶3 ∶2，则A∶B∶C等于( A )A．1∶2∶3B．2∶3∶1C．1：3：2D．3：1：23、在△ ABC 中，周长为7.5cm ，且sinA ：sinB：sinC＝4：5：6,下列结论：① a:b:c4:5:6② a:b:c 2: 5 : 6 ③a2cm,b 2.5cm,c 3cm④ A: B:C 4:5:6其中成立的个数是( C )A．0 个B． 1 个C．2个D．3个5、C．a=1,b=2,∠ A=100°C．b=c=1, ∠B=45°在△ ABC中，a＝12，b＝13，C＝60°，此三角形的解的情况是（A．无解B．一解C．二解B）D．不能确定6、满足A=45 ,c= 6 ,a=2 的△ ABC 的个数记为m, 则 a m 的值为（ A ）7、8、A．4 B．2 C．1 D．不定已知△ ABC 中，a181,b 209,A 121 ，则此三角形解的情况是无解在△ ABC中，已知50 3 ，c 150 ，B 30o，则边长a。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解斜三角形一、基本知识 1. 正弦定理R CcB b A a 2sin sin sin ===（R 是△ABC 外接圆半径） 2.余弦定理A bc c b a cos 2222-+= B ac c a b cos 2222-+= C ab b a c cos 2222-+=bc a c b A 2cos 222-+=ac b c a B 2cos 222-+=abc b a C 2cos 222-+=3. C ab S ABC sin 21=∆ r c b a S ABC)(21++=∆（r 是△ABC 内接圆半径） 4. 重要结论（1） C B A sin )sin(=+C B A cos )cos(-=+ C B A tan )tan(-=+（2） 2cos 2sinCB A =+ 2sin 2cos C B A =+（3） =++C B A tan tan tan C B A tan tan tan ••5. 考题分类题型一: 求解斜三角形中的基本元素 题型二：判断三角形的形状 题型三：解决与面积有关问题 题型四：三角形中求值问题题型五：实际应用二、例题解析【例1】已知△ABC 中，,sin )()sin (sin 2222B b a C A -=-外接圆半径为2，求角C 。
分析： 由,sin )()sin (sin 2222B b a C A -=-得Rbb a Rc R a 2)()44(222222-=- 由于，2=R ，代入并整理，得ab c b a =-+222所以，2122cos 222==-+=ab ab ab c b a C 所以，3π=C 。
【例2】设ABC ∆的内角..A B C 所对的边分别为..a b c ，已知11. 2.cos .4a b C === （Ⅰ）求ABC ∆的周长 （Ⅱ）求()cos A C -的值本小题主要考查三角函数的基本公式和解斜三角形的基础知识，同时考查基本运算能力解析：（Ⅰ）∵441441cos 2222=⨯-+=-+=C ab b a c ∴2=c∴ABC ∆的周长为5221=++=++c b a .（Ⅱ）∵41cos =C ，∴415411cos 1sin 22=⎪⎭⎫ ⎝⎛-=-=C C ，∴8152415sin sin ===c C a A ∵b a <，∴B A <,故A 为锐角，∴878151sin 1cos 22=⎪⎪⎭⎫ ⎝⎛-=-=A A∴()C A -cos C A C A sin sin cos cos +=16114158154187=⨯+⨯=. 【例3】在ABC △中，1tan 4A =，3tan 5B =． （Ⅰ）求角C 的大小；（Ⅱ）若AB，求BC 边的长 解：（Ⅰ）π()C A B =-+，1345tan tan()113145C A B +∴=-+=-=--⨯． 又0πC <<，3π4C ∴=．（Ⅱ）由22sin 1tan cos 4sin cos 1A A A A A ⎧==⎪⎨⎪+=⎩，，且π02A ⎛⎫∈ ⎪⎝⎭，，得sin 17A =．sin sin AB BC C A=，sin sin A BC AB C∴=⨯= 例4 根据下列条件判断三角形ABC 的形状：(1)若22tan tan a B =b A ；(2)b 2sin 2C + c 2sin 2B =2bc cos B cosC ;解（1）由已知及正弦定理得(2RsinA)2B cos B sin = (2RsinB)2⇒Acos A sin 2sinAcosA=2sinBcosB ⇒sin2A=sin2B ⇒2cos(A + B)sin(A – B)=0 ∴ A + B=90o或 A – B=0所以△ABC 是等腰三角形或直角三角形. 解（1）由正弦定理得sin 2Bsin 2C=sinBsinCcosBcosC∵ sin B sin C ≠0, ∴ sin B sin C =cos B cos C , 即 cos(B + C )=0, ∴ B + C =90o, A =90o, 故△ABC 是直角三角形.【例5】如图，海中小岛A 周围20海里内有暗礁，一船向南航行，在B 处BC测得小岛A 在船的南偏东30º；航行30海里后，在C 处测得小岛A 在船的南偏东60º。
如果此船不改变航行方向，继续向前行驶，有无触礁危险。
【解】过A 作BC AD ⊥于D ，由正弦定理易求得26315≈=AD （海里）20>（海里），所以继续航行没有触礁的危险。
【例6】已知圆内接四边形ABCD 的边长,6,2==BC AB 4==DA CD ，求四边形ABCD 的面积。
【解】连结BD ，则有四边形ABCD 的面积CBD ABD S S S ∆∆+=+•=A AD AB sin 21C DC BC sin 21• ∵ π=+C A ∴ C A sin sin =∴ AD AB S •=(21A DC BC sin )•+=⨯+⨯=A sin )4642(21A sin 16=由余弦定理，在△ABD 中，得 =•-+=A AD AB AD AB BD cos 2222A A cos 1620cos 4224222-=⨯⨯-+在△CBD 中，=•-+=C CD CB CD CB BD cos 2222 C A cos 4852cos 4624622-=⨯⨯-+∴ C A cos 4852cos 1620-=- ∵ C A cos cos -=∴ 32cos 64-=A∴ 21cos -=A 23sin =AB∴ 382316=⨯=S 解斜三角形训练题一、选择题1. 在ABC ∆中，已知222c bc b a ++=，则角A 为（ C ） A.3π B6π C.32π D. 3π或32π 2. 三角形三边长分别为c b a ,,，且满足关系ab c b a c b a 3))((=-+++，则c 的对角是（C. ）A ︒15 B. ︒45 C. ︒60 D. ︒1203. （15年广东文科）设C ∆AB 的内角A ，B ，C 的对边分别为a ，b ，c ．若2a =，c =，cos A =b c <，则b =（ ）A B ．2 C ． D ．3 【答案】B 【解析】试题分析：由余弦定理得：2222cos a b c bc =+-A ，所以(22222b b =+-⨯⨯即2680b b -+=，解得：2b =或4b =，因为b c <，所以2b =，故选B ．4.ABC ∆的内角C B A 、、的对边分别为c b a 、、，若a c ac b 2,2==，则=B cos （ B ）A.41 B43 C.42 D. 32 解： 因为 a c ac b 2,2==，由余弦定理得，432cos 222=-+=ca b a c B 5. 在△ABC 中，C BA sin 2tan=+，给出下面四个结论：①1cot tan =•B A ； ②2sin sin 0≤+<B A ；③1cos sin 22=+B A ； ④1cos cos 22=+B A其中正确的是（ B. ）A ①③ B. ②④ C. ①④ D ②③6. 已知三角形的三边之比是8:7:5，则最大角与最小角之和为（ B ） A ︒90 B. ︒120C. ︒135 D ︒1507. [2014·江西七校联考] 在△ABC 中，若sin(A －B )＝1＋2cos(B ＋C )sin(A ＋C )，则△ABC 的形状一定是( )A ．等边三角形B ．不含60°的等腰三角形C ．钝角三角形D ．直角三角形解：D [解析] 由题意得，1＋2cos(B ＋C )sin(A ＋C )＝1－2cos A sin B ，又sin(A －B )＝sin A cos B －cos A sin B ，所以sin A cos B ＋cos A sin B ＝1，即sin(A ＋B )＝1，所以A ＋B ＝π2，故△ABC 一定为直角三角形．8 在△ABC 中，A b B a tan tan 22=，则△ABC 是（D. ） A 等腰三角形 B.等腰直角三角形于A . 1 B.1- C. 2 D. 2-二、填空题1．ABC ∆中,已知AB AB BC ,10,3,==边的中线为7，则ABC ∆的面积是2315 2 在△ABC 中，若面积)(41222c b a S -+=则C ∠的度数为______︒45___。
由，C ab c b a S sin 21)(41222=-+=得12cos sin 2ab C ab C ••=所以， C C sin cos = 得，︒=45C3. 在△ABC 中，若︒=∠60C ，则=+++ca b c b a _____1____。
由︒=∠60C ，得⇒=-+ab c b a 222ab c b a +=+2221))(()()(222=++++++=+++++=+++c ac bc ab bc ac b a c a c b c b b c a a c a b c b a 4. 在△ABC 中，6cos 4sin 3=+B A ，1cos 3sin 4=+A B 则C ∠的度数为____2π_____。
（可得21)sin(=+B A ）5．如图，在四边形ABCD 中，28,16,10,135,90===︒=∠︒=∠CD AC AB D DAB ，则=AD )13(8- ，=BC 14 。
简解：由正弦定理，得︒=∠30DAC 于是，︒=∠15DCB 再由正弦定理，得︒=︒135sin 1615sin AD ，得 )13(8426216-=-•=AD 。
在ABC ∆中,，应用余弦定理，得 22221421161021610=•••-+=BC 所以，14=BC6 在△ABC 中，31cos ,3==A a ，则=+2cos 2CB ___31______。
7 在△ABC 中，若2cos sin sin 2A C B =，则△ABC 的形状是__等腰三角形____。
8.在ABC ∆中，8:7:5sin :sin :sin =C B A ，则B 的大小是（ 3π）A.6π B 3πC. 43πD. 65π三、解答题1．在△ABC 中，已知3=a ，2=b ，B=45︒ 求A 、C 及c解：由正弦定理得：23245sin 3sin sin === b B a A ABD┘∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BCb c 当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 2. 一海轮以20海里/小时的速度向东航行，它在A 点时测得灯塔P 在船的北60º东，2小时后到达B 点时测得灯塔P 在船的北45º东，求： （1）船在B 点时与灯塔P 的距离；（2）已知以点P 为圆心，55海里为半径的水域内有暗礁，那么这船继续向正东航行，有 无触礁为危险？3 辽宁08）在ABC △中，内角A B C ，，对边的边长分别是a b c ，，，已知2c =，3C π=． （Ⅰ）若ABC △3a b ，；（Ⅱ）若sin sin()2sin 2C B A A +-=，求ABC △的面积． 4 ABC △中，5cos 13A =-，3cos 5B =． 黑龙江2008 （Ⅰ）求sinC 的值；（Ⅱ）设5BC =，求ABC △的面积． 解：（Ⅰ）由5cos 13A =-，得12sin 13A =， 由3cos 5B =，得4sin 5B =．所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=． （Ⅱ）由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯=== 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=．10分（2008重庆）设△ABC 的内角A ，B ，C 的对边分别为a ,b ,c .已知222b c a +=，求：（Ⅰ）A 的大小;（Ⅱ）2sin cos sin()B C B C --的值. 解：(Ⅰ)由余弦定理，2222cos ,a b c bc A =+-222cos 2.6b c a A bc A π+-====故所以(Ⅱ) 2sin cos sin()B C B C --2sin cos (sin cos cos sin )sin cos cos sin sin()sin()1sin .2B C B C B C B C B CB C A A π=--=+=+=-==5. （江西17）（本小题满分12分）在ABC ∆中，角A 、B 、C 的对边分别是a ，b ，c ，已知2sin 1cos sin CC C -=+. （1）求C sin 的值；（2）若8)(422-+=+b a b a ，求边c 的值. 【解析】（1）由已知得2sin 12sin 212cos 2sin22CC C C -=-+，即 0)12sin 22cos 2(2sin =+-C C C ，由02sin ≠C 得012sin 22cos 2=+-CC即212cos 2sin=-C C ，两边平方得：3sin 4C = （2）由0212cos 2sin >=-C C 知2cos 2sin C C >，则224ππ<<C ，即ππ<<C 2，则由432sin=C 得47cos -=C 由余弦定理得728cos 2222+=-+=C ab b a c ，所以17+=c .．。