2015届高三理科数学二轮复习选择、填空题训练10份
2015届高三第二次模拟考试理科数学试题(Word版 含答案)1

2015年高考模拟试题(一)理科数学一、选择题:本大题共10小题,每小题5分。
共50分.在每小题给出的四个选项中。
只有一项是符合题目要求的.1.设i 是虚数单位,若21mii-+为纯虚数,则实数m 的值为 A .2B .2-C .12D .12-2.设集合{}{}22430,log 1,M x x x N x x M N =-+≤=≤⋃=则A .[]1,2B .[)1,2C .[]0,3D .(]0,33.若0a b <<,则下列结论中正确的是 A .22a b <B .2ab b <C .1122ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D .2b aa b+> 4.已知()()F x f x x =-是偶函数,且()()212f f =-=,则 A .4B .2C .3-D .4-5.执行右面的程序框图,若输入7,6x y ==,则输出的有序数对为 A .(11,12)B .(12,13)C .(13,14)D .(13,12)6.已知()xf x e x =-,命题()(),0p x R f x ∀∈>:,则 A .p 是真命题,()00:,0p x R f x ⌝∃∈< B .p 是真命题,()00:,0p x R f x ⌝∃∈≤ C .p 是假命题,()00:,0p x R f x ⌝∃∈< D .p 是假命题,()00:,0p x R f x ⌝∃∈≤7.若()()sin 2f x x θ=+,则“()f x 的图象关于3x π=对称”是“6πθ=-”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件8.已知函数()()()()()()22,log ,ln xf x xg x x xh x x x f a g b h c =+=+=+==,若0=,则 A .c b a <<B .b c a <<C .a b c <<D .a c b <<9.设平面区域D 是由双曲线2214x y -=的两条渐近线和抛物线28y x =-的准线所围成的三角形区域(含边界),若点(),x y D ∈,则211y x x -++的取值范围是A .11,3⎡⎤-⎢⎥⎣⎦B .[]1,1-C .10,3⎡⎤⎢⎥⎣⎦D .40,3⎡⎤⎢⎥⎣⎦10.若对于定义在R 上的函数()f x ,其图象是连续不断的,且存在常数()R λλ∈使得()()0f x f x λλ++=对任意实数x 都成立,则称()f x 是一个“~λ特征函数”.下列结论中正确的个数为 ①()0f x =是常数函数中唯一的“~λ特征函数”;②()21f x x =+不是“~λ特征函数”; ③“13~λ特征函数”至少有一个零点;④()x f x e =是一个“~λ特征函数”. A .1 B .2 C .3 D .4二、填空题:本大题共5小题,每小题5分,共25分.把正确答案填写在答题卡给定的横线上. 11.已知向量与满足()2,a b a b b ==-⊥,则a 与b 的夹角为_________.12.某学校安排甲、乙、丙、丁四位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲、乙不能参加同一学科,则不同的安排方法有______种.13.直线1ax =与圆221x y +=相交于B A ,两点(其中a ,b 是实数),且AOB ∆是直角三角形(O 是坐标原点),则点(),P a b 与点(1,0)之间距离的最小值为_______. 14.已知()()0sin n f n nx dx π=⎰,若对于()()(),1231R f f f n x x ∀∈++⋅⋅⋅+<++-恒成立,则正整数n的最大值为___________.15.已知点D C B A ,,,均在球O的球面上,1,AB BC AC ==,若三棱锥D ABC -体积的最大值是14,则球O 的表面积为_________.三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分) 已知函数()2cos sin 6f x x x π⎛⎫=+⎪⎝⎭. (1)求()f x 的最小正周期;(2)在ABC ∆中,角C B A ,,所对的边分别为(),,1,sin 2sin a b c f C B A ==,若,且ABC ∆的面积为求c 的值.17.(本小题满分12分)某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[]0,100,样本数据分组为[)[)0,20,20,40,[)[)[]40,60,60,80,80,100.(1)求直方图中x 的值;(2)如果年上缴税收不少于60万元的企业可申请政策优惠,若共抽取企业1200个,试估计有多少企业可以申请政策优惠;(3)从企业中任选4个,这4个企业年上缴税收少于20万元的个数记为X ,求X 的分布列和数学期望.(以直方图中的频率作为概率) 18.(本小题满分12分)一个楔子形状几何体的直观图如图所示,其底面ABCD 为一个矩形,其中4,6==AD AB ,顶部线段EF //平面ABCD ,棱FC FB ED EA ====二面角F BC A --.设N M ,分别是BC AD ,的中点.(1)证明:平面EFNM ⊥平面ABCD ;(2)求直线BF 与平面EFCD 所成角的正弦值. 19.(本小题满分12分)已知{}n a 满足()()121n n na n a n N *+=+∈,且13,1,4a a 成等差数列.(1)求数列{}n a 的通项公式;(2)若数列{}n a 满足()sin n n n b a S π=,为数列{}n b 的前n 项和, 求证:对任意,2n n N S π*∈<+. 20.(本小题满分13分) 已知函数()()2ln 1f x ax x =++.(1)当14a =-时,求函数()f x 的极值; (2)当[)0,x ∈+∞时,函数()y f x =图象上的点都在0,x y x ≥⎧⎨-≤⎩所表示的平面区域内,求实数a 的取值范围. 21.(本小题满分14分)已知椭圆C 的中心在原点,焦点在x2x =的焦点. (1)求椭圆C 的方程;(2)直线2x =与椭圆交于Q P ,两点,P 点位于第一象限,B A ,是椭圆上位于直线2x =两侧的动点. (i )若直线AB 的斜率为12,求四边形APBQ 面积的最大值; (ii )当点B A ,运动时,满足APQ BPQ ∠=∠,问直线AB 的斜率是否为定值,请说明理由.。
2015届高考理科数学二轮复习:提能专训5 集合与常用逻辑用语Word版含解析

提能专训(五) 集合与常用逻辑用语A 组一、选择题1.(2014·绵阳第二次诊断)已知集合S ={1,2},集合T ={x |(x -1)(x -3)=0},那么S ∪T =( )A .∅B .{1}C .{1,2}D .{1,2,3}[答案] D[解析] 依题意得,T ={1,3},S ∪T ={1,2,3},故选D.2.(2014·北京西城区期末)设集合A ={x |0<x <2},B ={x ||x |≤1},则集合A ∩B =( )A .(0,1)B .(0,1]C .(1,2)D .[1,2)[答案] B[解析] 由|x |≤1,得-1≤x ≤1,即B ={x |-1≤x ≤1},所以A ∩B ={x |0<x ≤1}.3.(2014·温州十校联考)已知全集U =R ,集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x +2x ≤0,则集合∁U A 等于( )A .{x |x <-2或x >0}B .{x |x ≤-2或x >0}C .{x |x <-2或x ≥0}D .{x |x ≤-2或x ≥0}[答案] C[解析] ∵A =⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x +2x ≤0={x |-2≤x <0}, ∴∁U A ={x |x <-2或x ≥0},故选C.4.(2014·衡水中学二调)已知R 是实数集,M =⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2x <1,N ={y |y =x -1+1},则N ∩(∁R M )=( )A.(1,2) B.[0,2] C.∅D.[1,2] [答案] D[解析]∵2x<1,∴x-2x>0,∴x<0或x>2,∴M={x|x<0或x>2},∴∁R M={x|0≤x≤2}.∵y=x-1+1,∴y≥1,∴N={y|y≥1},∴N∩∁R M=[1,2],故选D.5.(2014·郑州质检一)已知集合A={x|x>2},B={x|x<2m}且A ⊆∁R B,那么m的值可以是()A.1 B.2 C.3 D.4[答案] A[解析]由B={x|x<2m},得∁R B={x|x≥2m},∵A⊆∁R B,∴2m≤2,∴m≤1,故选A.6.(2014·济南模拟)已知集合A={x||x-1|<2},B={x|y=lg(x2+x)},设U=R,则A∩(∁U B)等于()A.[3,+∞) B.(-1,0]C.(3,+∞) D.[-1,0][答案] B[解析]因为x2+x>0,所以x>0或x<-1,所以∁U B=[-1,0],又A=(-1,3),所以A∩(∁U B)=(-1,0].7.(2014·湖北八校联考)设全集U=R,A={x|2x(x-2)<1},B={x|y =ln(1-x)},则图中阴影部分表示的集合为()A.{x|x≥1} B.{x|x≤1}C.{x|0<x≤1} D.{x|1≤x<2}[答案] D[解析] 令x (x -2)<0得0<x <2,即A =(0,2);令1-x >0得x <1,即B =(-∞,1),因此图中阴影部分表示的集合为A ∩(∁U B )=[1,2),故选D.8.(2014·长沙模拟三)已知集合M =(x ,y )⎪⎪⎪ x 29+y 24=1,N ={(x ,y )|y =k (x -b )},若∃k ∈R ,使得M ∩N =∅成立,则实数b 的取值范围是( )A .[-3,3]B .(-∞,-3)∪(3,+∞)C .[-2,2]D .(-∞,-2)∪(2,+∞)[答案] B[解析] 集合M 表示椭圆上的点集,集合N 表示过点(b,0)的直线的点集,∃k ∈R ,使得M ∩N =∅成立,即表示存在过定点(b,0)的直线与椭圆没有交点,即定点(b,0)在椭圆外面,故b 29+0>1,解得b >3或b <-3,故选B.9.(2014·大连一模)给出如下四个叙述:①若“p 且q ”为假命题,则p ,q 均为假命题;②命题“若a >b ,则2a >2b -1”的否命题为“若a ≤b ,则2a ≤2b -1”;③“∀x ∈R ,x 2+1≥1”的否定是“∃x ∈R ,x 2+1≤1”; ④在△ABC 中,“A >B ”是“sin A >sin B ”的充要条件.其中叙述不正确的个数是( )A .4B .3C .2D .1[答案] C[解析] ①错,因为p ,q 只要有一假即可;③错,因为其否定是“∃x∈R,x2+1<1”.故选C.10.(2014·上海十三校调研)集合S={(x,y,z)|x,y,z∈N*,且x<y<z,y<z<x,z<x<y恰有一个成立},若(x,y,z)∈S,且(z,w,x)∈S,则下列选项正确的是()A.(y,z,w)∈S,(x,y,w)∉SB.(y,z,w)∈S,(x,y,w)∈SC.(y,z,w)∉S,(x,y,w)∈SD.(y,z,w)∉S,(x,y,w)∉S[答案] B[解析]因为(x,y,z)∈S,所以x<y<z或y<z<x或z<x<y;又因为(z,w,x)∈S,所以z<w<x或w<x<z或x<z<w;两者结合有w<x<y<z或x<y<z<w或y<z<w<x或z<w<x<y.同理,若(y,z,w)∈S,则有y<z<w或z<w<y或w<y<z;若(x,y,w)∈S,则有x<y<w或y<w<x或w<x<y;两者结合有x<y<z<w 或y<z<w<x或z<w<x<y或w<x<y<z .故选B.二、填空题11.(2014·北京西城区期末)设M={(x,y)|F(x,y)=0}为平面直角坐标系xOy内的点集,若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2<0,则称点集M满足性质P.给出下列三个点集:①R={(x,y)|cos x-y=0};②S={(x,y)|ln x-y=0};③T={(x,y)|x2-y2=1}.其中所有满足性质P的点集的序号是________.[答案]①③[解析]对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2<0,也就是图象上任意一点(x 1,y 1),都会在图象上存在另一点(x 2,y 2),使这两个点与原点形成的夹角大于90°.在y =ln x 的图象上取点(1,0),则不存在另一点使这两个点与原点形成的夹角大于90°,所以②不满足性质P ;画出①③的图象观察可知,①③都满足性质P ,故选①③.12.(2014·济南四校联考)已知集合U ={2,3,a 2+2a -3},A ={|2a -1|,2},∁U A ={5},则实数a 的值为________.[答案] 2[解析] 根据已知得⎩⎪⎨⎪⎧a 2+2a -3=5,|2a -1|=3,解得a =2.13.(2014·上海模拟)如图所示的韦恩图中,A ,B 是非空集合,定义A *B 表示阴影部分集合,若x ,y ∈R ,A ={x |y =2x -x 2},B ={y |y =3x ,x >0},则A *B =________.[答案] [0,1]∪(2,+∞)[解析] ∵A ={x |y =2x -x 2}=[0,2],B ={y |y =3x ,x >0}=(1,+∞),∴A ∪B =[0,+∞),A ∩B =(1,2],∴A *B =[0,1]∪(2,+∞).14.(2014·上海嘉定一模)设集合A ={(x ,y )|(x -4)2+y 2=1},B ={(x ,y )|(x -t )2+(y -at +2)2=1},若存在实数t ,使得A ∩B ≠∅,则实数a 的取值范围是________.[答案] ⎣⎢⎡⎦⎥⎤0,43 [解析] 集合A 表示的是以(4,0)为圆心,以1为半径的圆,集合B 表示的是以(t ,at -2)为圆心,以1为半径的圆.A ∩B ≠∅说明这两个圆至少有一个交点,故(t -4)2+(at -2)2≤1+1=2,即(a 2+1)t 2-4(a +2)t +16≤0,据题意此不等式有实数解,故判别式Δ=16(a +2)2-4(a 2+1)×16≥0,即3a 2-4a ≤0,解得0≤a ≤43.15.(2014·上海徐汇、金山、松江二模)对于集合A ={a 1,a 2,…,a n }(n ∈N *,n ≥3),定义集合S ={x |x =a i +a j,1≤i <j ≤n },记集合S 中的元素个数为S (A ).若a 1,a 2,…,a n 是公差大于零的等差数列,则S (A )=________.[答案] 2n -3[解析] 由题意,集合S 中最小项为a 1+a 2=2a 1+d ,最大项为a n -1+a n =2a 1+(2n -3)d ,对任意的i (1≤i ≤2n -3),如果i ≤n -1,则可取2a 1+id =a 1+(a 1+id )=a 1+a i +1∈S ,若n ≤i ≤2n -3,可取2a 1+id =a 1+(n -1)d +a 1+(i -n +1)d =a n +a i -n +2,显然由于n ≤i ≤2n -3,有2≤i -n +2≤n -1,即2a 1+id ∈S ,所以S (A )=2n -3.16.(2014·北京昌平区期末质量抽测)将含有3n 个正整数的集合M 分成元素个数相等且两两没有公共元素的三个集合A ,B ,C ,其中A ={a 1,a 2,…,a n },B ={b 1,b 2,…,b n },C ={c 1,c 2,…,c n },若A ,B ,C 中的元素满足条件:c 1<c 2<…<c n ,a k +b k =c k (k =1,2,3,…,n ),则称M 为“完并集合”.(1)若M ={1,x,3,4,5,6}为“完并集合”,则x 的一个可能值为________.(写出一个即可)(2)对于“完并集合”M={1,2,3,4,5,6,7,8,9,10,11,12},在所有符合条件的集合C中,其元素乘积最小的集合是________.[答案](1)7(或9或11)(写出一个即可)(2){6,10,11,12}[解析](1)M={1,x,3,4,5,6}共有6个元素,所以3个集合A,B,C中各有2个元素,因为a k+b k=c k,所以集合C中必含有6个元素中最大的一个.当x<6时,由集合元素的互异性可知x=2,此时不能满足a k+b k=c k,故舍去.当x>6时,C={6,x},当1+5=6时,3+4=x,此时x=7.当C={5,x}时,1+4=5,3+6=x,此时x=9.当C={4,x}时,1+3=4,5+6=x,此时x=11.当集合C中另一个元素小于等于3时,不能满足a k+b k=c k,故舍去.所以x的可能取值为7,9,11.(2)M={1,2,3,4,5,6,7,8,9,10,11,12}共含有12个元素,所以集合C中含有元素4个.其中包含最大的元素12.集合C的所有可能有{8,9,10,12},{7,9,11,12},{6,10,11,12}.经计算可知元素乘积最小的集合是{6,10,11,12}.B组一、选择题1.(2014·上海)设a,b∈R,则“a+b>4”是“a>2且b>2”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件[答案] B[解析]若a>2且b>2,则a+b>4,但当a=4,b=1时也有a +b>4,故选B.2.(2014·广州综合检测)命题“对任意x∈R,都有x3>x2”的否定是( )A .存在x 0∈R ,使得x 30>x 20B .不存在x 0∈R ,使得x 30>x 20C .存在x 0∈R ,使得x 30≤x 20D .对任意x ∈R ,都有x 3≤x 2[答案] C[解析] 全称命题的否定是特称命题,易得命题“对任意x ∈R ,都有x 3>x 2”的否定是“存在x 0∈R ,使得x 30≤x 20”,故选C.3.(2014·湖北七市联考)下列说法错误的是( )A .命题“若x 2-5x +6=0,则x =2”的逆否命题是“若x ≠2,则x 2-5x +6≠0”B .已知命题p 和q ,若p ∨q 为假命题,则命题p 与q 中必一真一假C .若x ,y ∈R ,则“x =y ”是“xy ≥⎝ ⎛⎭⎪⎫x +y 22”的充要条件 D .若命题p :∃x 0∈R ,x 20+x 0+1<0,则綈p :∀x ∈R ,x 2+x+1≥0[答案] B[解析] 对于B 选项,若p ∨q 为假命题,则p ,q 均为假命题,所以B 错误,故选B.4.(2014·成都二诊)设命题p :∃α0,β0∈R ,cos(α0+β0)=cos α0+cos β0;命题q :∀x ,y ∈R ,且x ≠π2+k π,y ≠π2+k π,k ∈Z ,若x>y ,则tan x >tan y .则下列命题中真命题是( )A .p ∧qB .p ∧(綈q )C .(綈p )∧qD .(綈p )∧(綈q )[答案] B[解析] 当α0=3π4,β0=-π4时,命题p 成立,所以命题p 为真命题;当x ,y 不在同一个单调区间内时命题q 不成立,命题q 为假命题.故p ∧(綈q )为真命题.5.(2014·北京海淀区统考)在数列{a n }中,“a n =2a n -1,n =2,3,4,…”是“{a n }是公比为2的等比数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 [答案] B[解析] 当a n =0时,也有a n =2a n -1,n =2,3,4,…,但{a n }是等差数列,不是等比数列,因此充分性不成立.当{a n }是公比为2的等比数列时,有a n a n -1=2,n =2,3,4,…,即a n =2a n -1,n =2,3,4,…,所以必要性成立.故选B.6.(2014·石家庄二模)命题p 为:抛物线x 2=4y 的焦点坐标为(0,1);命题q 为:“a =3”是“直线ax +2y =0与直线2x -3y =3垂直”的充要条件.则以下结论正确的是( )A .p 或q 为真命题B .p 且q 为假命题C .p 且綈q 为真命题D .綈p 或q 为假命题[答案] A[解析] p 为真;2a -6=0,a =3,∴q 为真,则p 或q 为真.7.(2014·江西重点中学联考)给出下列命题,其中真命题的个数是( )①存在x 0∈R ,使得sin x 0+cos x 0=2sin 7π24成立;②对于任意的三个平面向量a ,b ,c ,总有(a·b )·c =a·(b·c )成立;③相关系数r (|r |≤1),|r |值越大,变量之间的线性相关程度越高.A .0B .1C .2D .3[答案] B[解析] ∵π4<7π24<π3, ∴2<2sin 7π24< 3.而sin x 0+cos x 0=2sin ⎝ ⎛⎭⎪⎫x 0+π4≤2, ∴①是假命题,向量的数量积不满足结合律,∴②是假命题,③是真命题.8.(2014·衡水中学二调)给定命题p :函数y =ln[(1-x )(1+x )]为偶函数;命题q :函数y =e x -1e x +1为偶函数,下列说法正确的是( ) A .p ∨q 是假命题B .(綈p )∧q 是假命题C .p ∧q 是真命题D .(綈p )∨q 是真命题 [答案] B[解析] 对于命题p :y =f (x )=ln[(1-x )(1+x )],令(1-x )(1+x )>0,得-1<x <1,∴函数f (x )的定义域为(-1,1),关于原点对称,∵f (-x )=ln[(1+x )(1-x )]=f (x ),∴函数f (x )为偶函数,∴命题p 为真命题;对于命题q :y =f (x )=e x -1e x +1,函数f (x )的定义域为R ,关于原点对称,∵f (-x )=e -x -1e -x +1=1e x -11e x +1=1-e x1+e x=-f (x ), ∴函数f (x )为奇函数,∴命题q 为假命题,∴(綈p )∧q 是假命题,故选B.9.(2014·东北三省二模)已知p :x ≥k ,q :3x +1<1,如果p 是q的充分不必要条件,则k 的取值范围是( )A .[2,+∞)B .(2,+∞)C .[1,+∞)D .(-∞,-1] [答案] A[解析] q :3x +1<1⇒3x +1-1<0⇒2-x x +1<0⇒(x -2)·(x +1)>0⇒x <-1或x >2.因为p 是q 的充分不必要条件,所以k ≥2,故选A.10.(2014·南昌二模)下列说法正确的是( )A .命题“存在x 0∈R ,x 20+x 0+2 013>0”的否定是“任意x ∈R ,x 2+x +2 013<0”B .两个三角形全等是这两个三角形面积相等的必要条件C .函数f (x )=1x 在其定义域上是减函数D .给定命题p ,q ,若“p 且q ”是真命题,则綈p 是假命题 [答案] D[解析] 对于A ,特称命题的否定为全称命题,所以命题“存在x 0∈R ,x 20+x 0+2 013>0”的否定是“任意x ∈R ,x 2+x +2 013≤0”,故A 不正确.对于B ,两个三角形全等,则这两个三角形面积相等;反之,不然.即两个三角形全等是这两个三角形面积相等的充分不必要条件,故B 不正确.对于C ,函数f (x )=1x 在(-∞,0),(0,+∞)上分别是减函数,但在定义域(-∞,0)∪(0,+∞)内既不是增函数,也不是减函数,如取x 1=-1,x 2=1,有x 1<x 2,且f (x 1)=-1,f (x 2)=1,则f (x 1)<f (x 2),所以函数f (x )=1x 在其定义域上不是减函数,故C 不正确.对于D ,因为“p 且q ”是真命题,则p ,q 都是真命题,所以綈p 是假命题,故D 正确.二、填空题11.(2014·湖北重点中学统一考试)已知r (x ):sin x +cos x >m ;s (x ):x 2+mx +1>0.如果∀x ∈R ,r (x )与s (x )有且仅有一个是真命题,则实数m 的取值范围是________.[答案] (-∞,-2]∪[-2,2)[解析] 由sin x +cos x =2sin ⎝ ⎛⎭⎪⎫x +π4,故sin x +cos x 的最小值为-2,若∀x ∈R 时,命题r (x )为真命题,则m <- 2.若命题s (x )为真命题,即∀x ∈R ,不等式x 2+mx +1>0恒成立,则Δ=m 2-4<0,解得-2<m <2.若命题r (x )为真命题,命题s (x )为假命题,则m ≤-2;若命题r (x )为假命题,命题s (x )为真命题,则-2≤m <2.综上所述,实数m 的取值范围是(-∞,-2]∪[-2,2). 12.(2014·吉林大学附属中学一模)设a 为实常数,y =f (x )是定义在R 上的奇函数,当x <0时,f (x )=9x +a 2x +7.若“∃x ∈[0,+∞),f (x )<a +1”是假命题,则a 的取值范围为________.[答案] ⎝ ⎛⎦⎥⎤-∞,-87 [解析] y =f (x )是定义在R 上的奇函数,故可求解析式为f (x )=⎩⎪⎨⎪⎧9x +a 2x -7,x >0,0,x =0,9x +a 2x +7,x <0.又“∃x ≥0,f (x )<a +1”是假命题,则∀x ≥0,f (x )≥a +1是真命题.①当x =0时,0≥a +1,解得a ≤-1;②当x >0时,9x +a 2x -7≥a +1,结合基本不等式有6|a |-7≥a +1,解得a ≥85或a ≤-87.①②取交集,得a 的取值范围是a ≤-87. 13.(2014·济南一模)已知下列命题:①设m 为直线,α,β为平面,且m ⊥β,则“m ∥α”是“α⊥β”的充要条件;②⎝ ⎛⎭⎪⎫x 3+1x 5的展开式中含x 3的项的系数为60; ③设随机变量ξ~N (0,1),若P (ξ≥2)=p ,则P (-2<ξ<0)=12-p;④若不等式|x +3|+|x -2|≥2m +1恒成立,则m 的取值范围是(-∞,2).其中真命题的序号是________.(写出所有真命题的序号) [答案] ③[解析] ①因为m ⊥β,m ∥α⇒α⊥β成立,但由α⊥β,m ⊥β,可得到m ∥α或m ⊂α,故该命题为假命题;②⎝ ⎛⎭⎪⎫x 3+1x 5的展开式中第r+1项T r +1=C r 5x 15-4r,令15-4r =3,解得r =3,含x 3的项的系数为10,故该命题是假命题;③由随机变量ξ~N (0,1),若P (ξ≥2)=p ,则P (ξ≤-2)=P (ξ≥2)=p ,所以,P (-2<ξ<2)=1-2p ,P (-2<ξ<0)=P (0<ξ<2)=12-p ,该命题是真命题;④因|x +3|+|x -2|≥|x +3-(x -2)|=5,故2m +1≤5,解得m ≤2,④是假命题.14.(2014·合肥质检二)△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,下列命题正确的是________.(写出所有正确命题的编号)①总存在某内角α,使cos α≥12; ②若A sin B >B sin A ,则B >A ;③存在某钝角△ABC ,有tan A +tan B +tan C >0; ④若2aBC →+bCA →+cAB →=0,则△ABC 的最小角小于π6; ⑤若a <tb (0<t ≤1),则A <tB . [答案] ①④⑤ [解析] ①对;②设f (x )=sin xx ,0<x <π,f ′(x )=x cos x -sin x x 2,故②错; ③tan A +tan B +tan C =tan A ·tan B ·tan C <0,③错; ④2aBC→+bCA →+cAB → =2a (BA→+AC →)+bCA →+cAB → =(2a -b )AC→+(c -2a )AB →=0, ∴⎩⎪⎨⎪⎧2a -b =0,c -2a =0,∴b =c =2a , cos A =78>32,故④对;⑤对. 15.(2014·青岛质检)给出以下命题:①双曲线y 22-x 2=1的渐近线方程为y =±2x ; ②命题p :“∀x ∈R ,sin x +1sin x ≥2”是真命题;③已知线性回归方程为y ^=3+2x ,当变量x 增加2个单位,其预报值平均增加4个单位;④设随机变量ξ服从正态分布N (0,σ2),若P (ξ>1)=0.2,则P (-1<ξ<0)=0.6;⑤已知22-4+66-4=2,55-4+33-4=2,77-4+11-4=2,1010-4+-2-2-4=2,依照以上各式的规律,得到一般性的等式为nn -4+8-n(8-n )-4=2(n ≠4).则正确命题的序号为________.(写出所有正确命题的序号) [答案] ①③⑤[解析] ①正确,注意双曲线焦点在y 轴上;②错误,不符合均值不等式的使用条件;③正确;④错误,因为P (ξ>1)=P (ξ<-1)=0.2,所以P (-1<ξ<0)=1-P (ξ>1)-P (ξ<-1)2=0.62=0.3;⑤正确,由特殊到一般可得等式为n n -4+8-n (8-n )-4=2(n ≠4),综上,可得命题①③⑤为真命题.16.(2014·长沙调研)已知命题p :“∀x ∈[1,2],12x 2-ln x -a ≥0”与命题q :“∃x ∈R ,x 2+2ax -8-6a =0”都是真命题,则实数a 的取值范围是________.[答案] (-∞,-4]∪⎣⎢⎡⎦⎥⎤-2,12 [解析] 命题p :a ≤12x 2-ln x 在x ∈[1,2]上恒成立,令f (x )=12x 2-ln x ,f ′(x )=x -1x =(x -1)(x +1)x ,当1<x <2时,f ′(x )>0, ∴f (x )min =f (1)=12.∴a ≤12.命题q :Δ=4a 2-4(-8-6a )≥0,∴a ≥-2或a ≤-4. 综上,两个命题都是真命题,则有a ∈(-∞,-4]∪ ⎣⎢⎡⎦⎥⎤-2,12.。
2015届高考理科数学二轮复习:提能专训2 数形结合思想Word版含解析
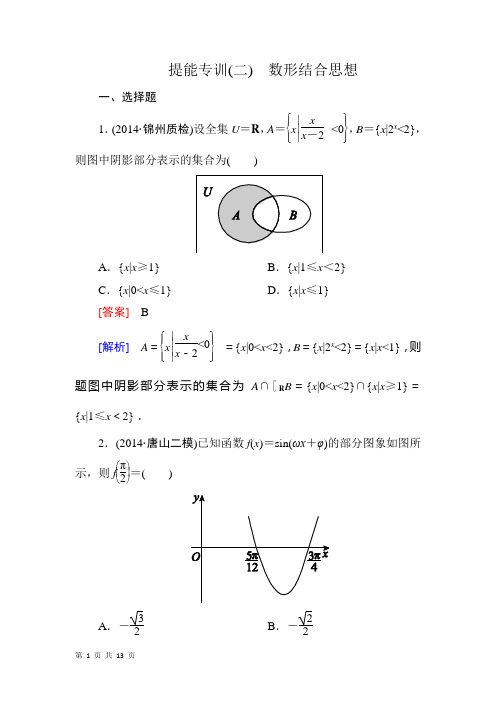
提能专训(二) 数形结合思想一、选择题1.(2014·锦州质检)设全集U =R ,A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x x -2<0,B ={x |2x <2},则图中阴影部分表示的集合为( )A .{x |x ≥1}B .{x |1≤x <2}C .{x |0<x ≤1}D .{x |x ≤1}[答案] B[解析] A =⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x x -2<0={x |0<x <2},B ={x |2x <2}={x |x <1},则题图中阴影部分表示的集合为A ∩∁R B ={x |0<x <2}∩{x |x ≥1}={x |1≤x <2}.2.(2014·唐山二模)已知函数f (x )=sin(ωx +φ)的部分图象如图所示,则f ⎝ ⎛⎭⎪⎫π2=( )A .-32B .-22C.32 D.22[答案] B[解析] 由题图知,T =2⎝⎛⎭⎪⎫3π4-5π12=2π3,∴ω=2πT =3,∴f (x )=sin(3x +φ),代入点⎝⎛⎭⎪⎫5π12,0,得sin ⎝⎛⎭⎪⎫5π4+φ=0,则可取φ=-π4.∴f (x )=sin ⎝ ⎛⎭⎪⎫3x -π4,∴f ⎝ ⎛⎭⎪⎫π2=sin ⎝ ⎛⎭⎪⎫3π2-π4=sin 5π4=-22. 3.(2014·临沂4月质检)当a >0时,函数f (x )=(x 2-ax )e x 的图象大致是()[答案] B[解析] f (x )=(x 2-ax )e x ,∵e x >0,∴当x ∈(0,a )时,f (x )<0;当x ∈(a ,+∞)时,f (x )>0,且增长很快.当x ∈(-∞,0)时,f (x )>0,由于e x 的影响,增长很慢.分析选项知,应选B.4.(2014·郑州质检二)设实数x ,y 满足不等式组⎩⎪⎨⎪⎧x +y ≤2,y -x ≤2,y ≥1,则x 2+y 2的取值范围是( )A .[1,2]B .[1,4]C .[2,2]D .[2,4][答案] B[解析] 如图所示,不等式组表示的平面区域是△ABC 内部(含边界),x 2+y 2表示的是此区域内的点(x ,y )到原点距离的平方.从图中可知最短距离为原点到直线BC 的距离,其值为1;最远的距离为AO ,其值为2,故x 2+y 2的取值范围是[1,4].5.(2014·云南统检)已知圆M 经过双曲线S :x 29-y 216=1的一个顶点和一个焦点,圆心M 在双曲线S 上,则圆心M 到双曲线S 的中心的距离为( )A.134或73B.154或83C.133D.163 [答案] D[解析] 依题意可设圆心M 的坐标为(x 0,y 0).若圆M 经过双曲线同一侧的焦点与顶点,以右焦点F 与右顶点A 为例,由|MA |=|MF |知,x 0=3+52=4,代入双曲线方程可得y 0=±473,故M 到双曲线S 的中心的距离|MO |=x 20+y 20=163.若M 经过双曲线的不同侧的焦点与顶点时,结合图形知不符合.故选D.6.(2014·衡水一模)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x -y -6≤0,x -y +2≥0,x ,y ≥0,若目标函数z =ax +by (a ,b >0)的最大值是12,则a 2+b 2的最小值是( )A.613B.365C.65D.3613 [答案] D[解析] 作出可行域可得,z =ax +by 在x -y +2=0与3x -y -6=0的交点(4,6)处取最大值,即4a +6b =12.化简,得2a +3b =6,又∵(a 2+b 2)(22+32)≥(2a +3b )2,则a 2+b 2≥3613.7.对于图象Γ上的任意点M ,存在点N ,使得OM →·ON →=0,则称图象Γ为“优美图象”.下列函数的图象为“优美图象”的是( )A .y =2x +1B .y =log 3(x -2)C .y =2x D .y =cos x[答案] D[解析] 在y =2x +1图象上取点M (0,2),因为y =2x +1>0,所以在y =2x +1图象上不存在点N ,使OM →·ON →=0,排除A ;在y =log 3(x -2)图象上取点M (3,0),因为x >2,所以在y =log 3(x -2)图象不存在点N ,使OM →·ON →=0,排除B ;在y =2x 图象上取点M (1,2),在y =2x 图象上不存在点N ,使OM →·ON→=0,排除C.故选D. 8.过顶点在原点、焦点在x 轴正半轴上的抛物线C 的焦点F 的直线交抛物线于A ,B 两点,若|BF |=2|AF |=6,则抛物线的方程为( )A .y 2=8xB .y 2=4xC .y 2=2xD .y 2=x [答案] A[解析] 如图,设抛物线C 的方程为y 2=2px (p >0),分别过A ,B 作抛物线的准线的垂线,垂足分别为C ,D ,分别过点A ,F 作AM ⊥BD ,FN ⊥BD ,垂足分别为M ,N ,根据抛物线定义知|AC |=|AF |=3,|BD |=|BF |=6,所以|BM |=3,|BN |=6-p .易知△AMB ∽△FNB ,故|BM ||BN |=|AB ||BF |,即36-p =96,解得p =4,故抛物线C 的方程为y 2=8x ,故选A.9.(2014·唐山期末)f (x )=2sin πx -x +1的零点个数为( ) A .4 B .5 C .6 D .7 [答案] B[解析] 令2sin πx -x +1=0,则2sin πx =x -1,令h (x )=2sin πx ,g (x )=x -1,则f (x )=2sin πx -x +1的零点个数问题转化为两个函数h (x )与g (x )图象的交点个数问题.h (x )=2si n πx 的最小正周期为T =2ππ=2,画出两个函数的图象,如图所示,∵h (1)=g (1),h ⎝ ⎛⎭⎪⎫52>g ⎝ ⎛⎭⎪⎫52,g (4)=3>2,g (-1)=-2,∴两个函数图象的交点一共有5个,∴f (x )=2sinπx -x +1的零点个数为5.10.(2014·安阳调研)设函数f (x )=⎩⎪⎨⎪⎧x -[x ],x ≥0,f (x +1),x <0,其中[x ]表示不超过x 的最大整数,如[-1.1]=-2,[π]=3.若直线y =kx +k (k >0)与函数f (x )的图象恰好有3个不同的交点,则实数k 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,14B.⎣⎢⎡⎭⎪⎫14,13 C.⎝ ⎛⎭⎪⎫13,1 D.⎣⎢⎡⎭⎪⎫14,1 [答案] B[解析] 画出函数f (x )=⎩⎪⎨⎪⎧x -[x ],x ≥0,f (x +1),x <0,g (x )=k (x +1)(k >0)的图象,若直线y =kx +k (k >0)与函数y =f (x )的图象恰有三个不同的交点,结合图象可得:k PB ≤k <k P A ,∵k P A =12-(-1)=13,k PB =13-(-1)=14,∴14≤k <13,故选B.11.(2014·兰州、张掖联合诊断)设f (x )的定义域为D ,若f (x )满足下面两个条件则称f (x )为闭函数:①f (x )是D 上的单调函数;②存在[a ,b ]⊆D ,使f (x )在[a ,b ]上的值域为[a ,b ].现已知f (x )=2x +1+k 为闭函数,则k 的取值范围是( )A.⎝ ⎛⎦⎥⎤-1,-12 B .(-∞,1) C.⎣⎢⎡⎭⎪⎫12,1 D .(-1,+∞)[答案] A[解析] 如图,函数的定义域为x ∈-12,+∞,显然在定义域上函数f (x )单调递增,依题可知,在x ∈⎣⎢⎡⎭⎪⎫-12,+∞上,方程x -k =2x +1有两个不同的解,结合图象易得实数k 的取值范围为-1<k ≤-12.12.(原创题)已知集合A =⎩⎨⎧(x ,y )⎪⎪⎪⎭⎬⎫y =π24-x 2,B ={(x ,y )|y=tan 2x },C =A ∩B ,则集合C 的子集个数为( )A .2B .4C .8D .16 [答案] D[解析] 集合A 表示圆心为(0,0),半径为π2且在x 轴上方的半圆(包括与x 轴的两个交点),因为函数y =tan 2x 的周期为π2,画出函数y =π24-x 2与y =tan 2x 的图象(如图所示),由图知,函数y =π24-x 2与y =tan 2x 的图象有4个交点.因为C =A ∩B ,所以集合C 有四个元素,故集合C 的子集个数为24=16.故选D.二、填空题13.在平面直角坐标系xOy 中,已知圆x 2+y 2=4上有且只有四个点到直线12x -5y +c =0的距离为1,则实数c 的取值范围是________.[答案] (-13,13)[解析] 由题意知,当且仅当圆x 2+y 2=4的圆心到直线12x -5y +c =0的距离小于1时,圆x 2+y 2=4上有且只有四个点到直线12x -5y +c =0的距离为1,此时有d =|c |122+52<1,解得c ∈(-13,13).14.(2014·山西四校联考)已知f (x )=⎩⎪⎨⎪⎧e -x (x ≤0),x (x >0),g (x )=f (x )-x2-b 有且仅有一个零点时,b 的取值范围是________.[答案] (-∞,0]∪⎩⎨⎧⎭⎬⎫12∪[1,+∞)[解析] 要使函数g (x )=f (x )-x2-b 有且仅有一个零点,只需要函数f (x )的图象与函数y =x2+b 的图象有且仅有一个交点,通过在同一坐标系中同时画出两个函数的图象并观察得,要符合题意,须满足b ≥1或b =12或b ≤0.15.(2014·温州十校联考)在△ABC 中,∠ACB 为钝角,AC =BC =1,CO→=xCA →+yCB →且x +y =1,函数f (m )=|CA →-mCB →|的最小值为32,则|CO →|的最小值为________. [答案] 12[解析] 如图,△ABC 中,∠ACB 为钝角,AC =BC =1,记NA →=CA →-mCB →,则当N 在D 处,即AD ⊥BC 时,f (m )取得最小值32,因此|AD →|=32,容易得到∠ACB =120°.∵CO→=xCA →+yCB →且x +y =1,∴O 在边AB 上,∴当CO ⊥AB 时,|C O →|最小,|C O →|min =12.三、解答题16.(2014·浙江抽测)已知抛物线C :y =x 2.过点M (1,2)的直线l 交C 于A ,B 两点.抛物线C 在点A 处的切线与在点B 处的切线交于点P .(1)若直线l 的斜率为1,求|AB |的值; (2)求△P AB 的面积的最小值.解:(1)设点A (x 1,y 1),B (x 2,y 2),由题意知,直线l 的方程为y=x +1,由⎩⎪⎨⎪⎧y =x +1,y =x 2消去y 解得,x 1=1+52,x 2=1-52. 所以|AB |=2⎪⎪⎪⎪⎪⎪1+52-1-52=10. (2)易知直线l 的斜率存在,设直线l 的方程为y =k (x -1)+2,设点A (x 1,y 1),B (x 2,y 2).由⎩⎪⎨⎪⎧y =k (x -1)+2,y =x 2消去y 整理得, x 2-kx +k -2=0,x 1+x 2=k ,x 1x 2=k -2,又y ′=(x 2)′=2x ,所以抛物线y =x 2在点A ,B 处的切线方程分别为y =2x 1x -x 21,y =2x 2x -x 22.得两切线的交点P ⎝ ⎛⎭⎪⎫k 2,k -2.所以点P 到直线l 的距离d =|k 2-4k +8|2k 2+1. 又|AB |=1+k 2(x 1+x 2)2-4x 1x 2=1+k 2·k 2-4k +8.设△P AB 的面积为S ,所以S =12|AB |·d =14((k -2)2+4)3≥2(当k=2时取得等号).所以△P AB 面积的最小值为2.17.(2014·皖南八校二联)已知函数f (x )=ax +1+ln x x ,其中a∈R .(1)若f (x )在定义域上单调递增,求实数a 的取值范围;(2)若函数g (x )=xf (x )有唯一零点,试求实数a 的取值范围.解:(1)f ′(x )=a +1-ln x x 2=ax 2-ln x +1x 2, 又∀x >0,f ′(x )≥0,∴ax 2-ln x +1≥0,∀x >0,∴a ≥ln x -1x 2,令h (x )=ln x -1x 2,则h ′(x )=1x ·x 2-2x (ln x -1)x 4=3-2ln x x 3=0有根:x 0=e 32,x ∈(0,x 0),h ′(x )>0,函数h (x )单调增;x ∈(x 0,+∞),h ′(x )<0,函数h (x )单调减;∴a ≥h (x )max =h (x 0)=12e 3;故实数a 的取值范围是⎣⎢⎡⎭⎪⎫12e 3,+∞. (2)由题g (x )=xf (x )=ax 2+x +ln x =0,即a =-x -ln x x 2有唯一正实数根,令φ(x )=-x -ln x x 2,即函数y =a 与函数y =φ(x )有唯一交点, φ′(x )=⎝⎛⎭⎪⎫-1-1x x 2-(-x -ln x )2x x 4=x -1+2ln x x 3. 再令R (x )=x -1+2ln x ,R ′(x )=1+2x >0,∀x >0,R (x )为增函数,且易得R (1)=0.∴当x ∈(0,1)时,R (x )<0,φ′(x )<0,函数φ(x )单调递减; 当x ∈(1,+∞)时,R (x )>0,φ′(x )>0,函数φ(x )单调递增.即φ(x)≥φ(1)=-1,又当x→0时,φ(x)→+∞,而当x→+∞时,φ(x)→0且φ(x)<0,故满足条件的实数a的取值范围为:{a|a≥0或a=-1}.。
2015届高考理科数学二轮复习总结:提能专训23-导数的简单应用与定积分

提能专训(二十三) 导数的综合应用一、选择题1.(2014·江西八校联考)已知m 是区间[0,4]内任取的一个数,那么函数f (x )=13x 3-2x 2+m 2x +3在x ∈R 上是增函数的概率是( )A.14B.13 C.12 D.23[答案] C[解析] ∵f (x )=13x 3-2x 2+m 2x +3在R 上是增函数,∴f ′(x )=x 2-4x +m 2≥0在R 上恒成立,∴Δ=16-4m 2≤0,解得m ≤-2或m ≥2. 又∵0≤m ≤4,∴2≤m ≤4. 故所求的概率为P =24=12.2.(2014·辽宁五校联考)已知a ,b 是实数,且e<a <b ,其中e 是自然对数的底数,则a b 与b a 的大小关系是( )A .a b >b aB .a b <b aC .a b =b aD .a b 与b a 的大小关系不确定 [答案] A[解析] 构造辅助函数f (x )=ln xx ,因为f ′(x )=1-ln x x 2,所以在(e ,+∞)上,f ′(x )<0,f (x )为减函数,则f (a )>f (b ),即ln a a >ln bb ,b ln a >a lnb ,ln a b >ln b a ,所以a b >b a .3.(2014·忻州联考)定义在⎝ ⎛⎭⎪⎫0,π2上的函数f (x ),f ′(x )是它的导函数,且恒有f (x )<f ′(x )·tan x 成立,则( )A.3f ⎝ ⎛⎭⎪⎫π4>2f ⎝ ⎛⎭⎪⎫π3 B .f (1)<2f ⎝ ⎛⎭⎪⎫π6sin 1C.2f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4D.3f ⎝ ⎛⎭⎪⎫π6<f ⎝ ⎛⎭⎪⎫π3[答案] D[解析] ∵f (x )<f ′(x )·tan x , 即f ′(x )sin x -f (x )cos x >0, ∴⎣⎢⎡⎦⎥⎤f (x )sin x ′=f ′(x )sin x -f (x )cos x sin 2x >0, ∴函数f (x )sin x 在⎝ ⎛⎭⎪⎫0,π2上单调递增,从而f ⎝ ⎛⎭⎪⎫π6sin π6<f ⎝ ⎛⎭⎪⎫π3sin π3,即3f ⎝ ⎛⎭⎪⎫π6<f ⎝ ⎛⎭⎪⎫π3.4.(2014·浙江名校联考)若函数f (x )=x cos x 在(0,+∞)内的全部极值点按从小到大的顺序排列为a 1,a 2,…,a n ,…,则对任意正整数n 必有( )A .π<a n +1-a n <3π2 B.π2<a n +1-a n <π C .0<a n +1-a n <π2D .-π2<a n +1-a n <0[答案] B[解析] f ′(x )=cos x -x sin x ,令f ′(x )=0,得1x =tan x ,函数y =1x 与y =tan x 的图象如图所示,a n 与a n +1就是两个函数图象相邻交点的横坐标.由于函数y =1x 在(0,+∞)上是减函数,故随着n 的增加,a n 越来越接近其所在周期内的零点(y =tan x 的零点),故a n +1-a n <π,又a n 与a n +1在各自周期内零点的右侧,因此a n +1-a n >π2,故选B.5.(2014·陕西卷改编)设函数f (x )=ln(1+x ),g (x )=xf ′(x ),x ≥0,其中f ′(x )是f (x )的导函数.若f (x )≥ag (x )恒成立,则实数a 的取值范围是( )A .(-1,+∞)B .(0,+∞)C .(-∞,0)D .(-∞,1][答案] D[解析] 对f (x )求导,得f ′(x )=11+x ,所以g (x )=xf ′(x )=x 1+x.若f (x )≥ag (x )恒成立,即ln(1+x )≥ax1+x 恒成立.设φ(x )=ln(1+x )-ax 1+x(x ≥0),则φ′(x )=11+x-a (1+x )2=x +1-a(1+x )2. 当a ≤1时,φ′(x )≥0(当且仅当x =0,a =1时等号成立), 所以φ(x )在[0,+∞)上单调递增.又φ(0)=0,即φ(x )≥0在[0,+∞)上恒成立,所以当a ≤1时,ln(1+x )≥ax1+x 恒成立(当且仅当x =0时等号成立).当a >1时,对x ∈(0,a -1),有φ′(x )<0,则φ(x )在(0,a -1]上单调递减,所以φ(a -1)<φ(0)=0,即a >1时,存在x >0,使φ(x )<0, 可知ln(1+x )≥ax1+x不恒成立.综上,实数a 的取值范围是(-∞,1],故选D.6.(2014·鄂尔多斯模拟)已知a ≥0,函数f (x )=(x 2-2ax )e x ,若f (x )在[-1,1]上是单调减函数,则a 的取值范围是( )A .0<a <34B.12<a <34C .a ≥34 D .0<a <12[答案] C[解析] f ′(x )=(2x -2a )e x +(x 2-2ax )e x =[x 2+(2-2a )x -2a ]e x ,由题意当x ∈[-1,1]时,f ′(x )≤0恒成立,即x 2+(2-2a )x -2a ≤0恒成立.令g (x )=x 2+(2-2a )x -2a ,则有⎩⎨⎧g (-1)≤0,g (1)≤0,即⎩⎨⎧(-1)2+(2-2a )·(-1)-2a ≤0,12+2-2a -2a ≤0,解得a ≥34,故选C.7.已知函数f (x )=2x 2-ax +ln x 在其定义域上不单调,则实数a 的取值范围是( )A .(-∞,4]B .(-∞,4)C .(4,+∞)D .[4,+∞)[答案] C[解析] 函数f (x )的定义域为(0,+∞),因为f (x )=2x 2-ax +ln x ,所以f ′(x )=4x -a +1x =1x (4x 2-ax +1).由函数f (x )在区间(0,+∞)上不单调可知f ′(x )=0有两个正解,即4x 2-ax +1=0有两个正解,设为x 1,x 2.故有⎩⎪⎨⎪⎧Δ=(-a )2-4×4×1>0,x 1+x 2=a 4>0,x 1x 2=14>0,解得a >4.所以a 的取值范围为(4,+∞).8.已知三次函数f (x )=ax 3+bx 2+cx +d 的图象如图所示,则f ′(-2)f ′(1)=() A .5 B .-5 C .2 D .-2 [答案] D[解析] 对f (x )求导,得f ′(x )=3ax 2+2bx +c ,结合题中图象知,x =-1,2为导函数的零点,所以f ′(-1)=f ′(2)=0,即⎩⎨⎧3a -2b +c =0,12a +4b +c =0,解得⎩⎪⎨⎪⎧a =-c 6,b =c4.所以f ′(x )=-c 2x 2+c 2x +c =-c 2(x 2-x -2),于是f ′(-2)f ′(1)=4+2-21-1-2=-2.故选D.9.(2014·安庆二模)设1<x <2,则ln x x ,⎝ ⎛⎭⎪⎫ln x x 2,ln x 2x 2的大小关系是( )A.⎝ ⎛⎭⎪⎫ln x x 2<ln x x <ln x2x 2 B.ln x x <⎝ ⎛⎭⎪⎫ln x x 2<ln x 2x 2C.⎝ ⎛⎭⎪⎫ln x x 2<ln x 2x 2<ln xx D.ln x 2x 2<⎝ ⎛⎭⎪⎫ln x x 2<ln x x[答案] A[解析] 令f (x )=x -ln x (1<x <2), 则f ′(x )=1-1x =x -1x >0, ∴函数y =f (x )在(1,2)内为增函数.∴f (x )>f (1)=1>0,∴x >ln x >0⇒0<ln xx <1.∴⎝ ⎛⎭⎪⎫ln x x 2<ln x x .又ln x 2x 2-ln x x =2ln x -x ln x x 2=(2-x )ln xx 2>0, ∴⎝ ⎛⎭⎪⎫ln x x 2<ln x x <ln x2x 2,故选A. 10.(2014·昆明质检)已知函数f (x )=e x -ax -b ,若f (x )≥0恒成立,则ab 的最大值为( )A. e B .e 2 C .e D.e 2[答案] D[解析] 利用导数求解.当a ≤0时,函数f (x )=e x -ax -b 在R 上单调递增,f (x )≥0不恒成立,所以a ≤0舍去.当a >0时,由f ′(x )=e x -a =0解得x =ln a ,且当x <ln a 时,f ′(x )<0,函数f (x )单调递减;当x >ln a 时,f ′(x )>0,函数f (x )单调递增,所以f (x )≥0恒成立,即f (x )min =f (ln a )=a -a ln a -b ≥0,所以b ≤a -a ln a ,ab ≤a 2-a 2ln a ,a >0.令y =x 2-x 2ln x ,x >0,则y ′=2x -2x ln x -x =x (1-2ln x ),x >0,由y ′=0解得x =e ,且x ∈(0,e)时,y ′>0,函数y =x 2-x 2ln x 单调递增;x ∈(e ,+∞)时,y ′<0,函数y =x 2-x 2ln x 单调递减,所以当x =e 时,函数y =x 2-x 2ln x 取得最大值e -12e =12e ,所以ab ≤a 2-a 2ln a ≤12e ,即ab 的最大值是12e ,故选D.11.设直线x =t 与函数f (x )=x 2+1,g (x )=x +ln x 的图象分别交于P ,Q 两点,则|PQ |的最小值是( )A .-12 B.12 C .1 D .-12或1[答案] C[解析] 直线x =t 与函数f (x )=x 2+1,g (x )=x +ln x 的图象分别交于P (t ,f (t )),Q (t ,g (t ))两点,则|PQ |=|f (t )-g (t )|.记h (t )=f (t )-g (t )=t 2+1-(t +ln t ).函数h (t )的定义域为(0,+∞),h ′(t )=2t -1-1t =1t (2t 2-t -1)=1t (2t +1)(t -1).由h ′(t )=0,解得t =1或t =-12(舍去).显然当t ∈(0,1)时,h ′(t )<0,函数h (t )单调递减;当t ∈(1,+∞)时,h ′(t )>0,函数h (t )单调递增.故函数h (t )的最小值为h (1)=12+1-(1+ln 1)=1,故|PQ |的最小值为1.二、填空题12.(2014·南京、盐城二模)表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为________.[答案] 1∶2[解析] 因为12π=2πrh +2πr 2,rh +r 2=6,所以V =πr 2h =πr (6-r 2),0<r < 6.由V ′=π(6-3r 2)=0得r = 2.当0<r <2时,V ′>0,当2<r <6时,V ′<0,所以当r =2时,V 取极大值,也是最大值,此时h =22,r ∶h =1∶2.13.(2014·青岛一模)如果对定义在R 上的函数f (x ),以任意两个不相等的实数x 1,x 2,都有x 1f (x 1)+x 2f (x 2)>x 1f (x 2)+x 2f (x 1),则称函数f (x )为“H 函数”.给出下列函数:①y =-x 3+x +1;②y =3x -2(sinx -cos x );③y =e x+1;④f (x )=⎩⎪⎨⎪⎧ln|x |,x ≠0,0,x =0.以上函数是“H 函数”的所有序号为________.[答案] ②③[解析] 因为x 1f (x 1)+x 2f (x 2)>x 1f (x 2)+x 2f (x 1),即(x 1-x 2)[f (x 1)-f (x 2)]>0,所以函数f (x )在R 上是增函数.由y ′=-3x 2+1>0得-33<x <33,即函数在区间⎝⎛⎭⎪⎫-33,33上是增函数,故①不是“H 函数”;由y ′=3-2(cos x +sin x )=3-22sin ⎝ ⎛⎭⎪⎫x +π4≥3-22>0恒成立,所以②为“H 函数”;由y ′=e x >0恒成立,所以③为“H 函数”;由于④为偶函数,所以不可能在R 上是增函数,所以不是“H 函数”.综上,是“H 函数”的有②③.14.(2014·唐山一模)定义在R 上的函数f (x )满足:f (-x )+f (x )=x 2,当x <0时,f ′(x )<x ,则不等式f (x )+12≥f (1-x )+x 的解集为________.[答案] ⎝⎛⎦⎥⎤-∞,12[解析] ∵f (x )+f (-x )=x 2,∴f ′(x )-f ′(-x )=2x ,∴f ′(-x )=f ′(x )-2x ,当x <0时,f ′(x )<x ,∴f ′(-x )=f ′(x )-2x <x -2x =-x ,∴当x >0时,f ′(x )=f ′(-x )+2x <-x +2x =x ,令g (x )=f (x )+12-f (1-x )-x ,则g ′(x )=f ′(x )+f ′(1-x )-1<x +1-x -1=0,∴g (x )在R 上单调递减,而g ⎝ ⎛⎭⎪⎫12=f ⎝ ⎛⎭⎪⎫12+12-f ⎝ ⎛⎭⎪⎫12-12=0,∴g (x )≥0即g (x )≥g ⎝ ⎛⎭⎪⎫12,故原不等式的解集为⎝ ⎛⎦⎥⎤-∞,12. 三、解答题15.(2014·怀化一模)已知函数f (x )=ax +b ln x +c (a ,b ,c 是常数)在x =e 处的切线方程为(e -1)x +e y -e =0,且f (1)=0.(1)求常数a ,b ,c 的值;(2)若函数g (x )=x 2+mf (x )(m ∈R )在区间(1,3)内不是单调函数,求实数m 的取值范围.解:(1)由题设知,f (x )的定义域为(0,+∞),f ′(x )=a +b x .∵f (x )在x =e 处的切线方程为(e -1)x +e y -e =0,∴f ′(e)=-e -1e ,且f (e)=2-e ,即a +b e =-e -1e ,且a e +b +c =2-e.又f (1)=a +c =0,解得a =-1,b =1,c =1.(2)由(1)知f (x )=-x +ln x +1(x >0),∴g (x )=x 2+mf (x )=x 2-mx +m ln x +m (x >0),∴g ′(x )=2x -m +m x =1x (2x 2-mx +m )(x >0).令d (x )=2x 2-mx +m (x >0).①当函数g (x )在(1,3)内有一个极值时,g ′(x )=0在(1,3)内有且仅有一个根,即d (x )=2x 2-mx +m =0在(1,3)内有且仅有一个根.又∵d (1)=2>0,∴当d (3)=0,即m =9时,d (x )=2x 2-mx +m=0在(1,3)内有且仅有一个根x =32;当d (3)≠0时,应有d (3)<0,即2×32-3m +m <0,解得m >9,∴m ≥9.②当函数g (x )在(1,3)内有两个极值时,g ′(x )=0在(1,3)内有两个根,即二次函数d (x )=2x 2-mx +m =0在(1,3)内有两个不等根,所以⎩⎪⎨⎪⎧ Δ=m 2-4×2×m >0,d (1)=2-m +m >0,d (3)=2×32-3m +m >0,1<m 4<3,解得8<m <9.综上,实数m 的取值范围是(8,+∞).16.(2014·长春调研)已知函数f (x )=x ln x .(1)求f (x )的单调区间和极值;(2)设A (x 1,f (x 1)),B (x 2,f (x 2)),且x 1≠x 2,证明:f (x 2)-f (x 1)x 2-x 1<f ′⎝ ⎛⎭⎪⎫x 1+x 22. 解:(1)f (x )的定义域为(0,+∞),f ′(x )=ln x +x ·1x =1+ln x .令f ′(x )>0,则ln x >-1=ln 1e ,∴x >1e ;令f ′(x )<0,则ln x <-1=ln 1e ,∴0<x <1e ,∴f (x )的单调递增区间是⎝ ⎛⎭⎪⎫1e ,+∞,单调递减区间是⎝ ⎛⎭⎪⎫0,1e , f (x )极小值=f ⎝ ⎛⎭⎪⎫1e =1e ln 1e =-1e ,f (x )无极大值.(2)不防设x 1<x 2,f (x 2)-f (x 1)x 2-x 1<f ′⎝ ⎛⎭⎪⎫x 1+x 22, 即x 2ln x 2-x 1ln x 1x 2-x 1<ln x 1+x 22+1,x 2ln x 2-x 1ln x 1<x 2ln x 1+x 22-x 1ln x 1+x 22+x 2-x 1,∴x 2ln 2x 2x 1+x 2<x 1ln 2x 1x 1+x 2+x 2-x 1, 两边同除以x 1得,x 2x 1ln 2·x 2x 11+x 2x 1<ln 21+x 2x 1+x 2x 1-1, 令x 2x 1=t ,则t >1,即证:t ln 2t 1+t <ln 21+t +t -1. 令g (t )=t ln 2t 1+t -ln 21+t-t +1,则 g ′(t )=ln 2t 1+t +t ·1+t 2t ·2(1+t )2+1+t 2·2(1+t )2-1 =ln 2t 1+t +1-t 1+t=ln ⎝⎛⎭⎪⎫1+t -1t +1-t -1t +1, 令t -1t +1=x (x >0),h (x )=ln(1+x )-x , 则h ′(x )=11+x -1=-x 1+x<0,h (x )在(0,+∞)上单调递减, ∴h (x )<h (0)=0,即ln (1+x )<x ,即g ′(t )=ln ⎝ ⎛⎭⎪⎫1+t -1t +1-t -1t +1<0恒成立,∴g (t )在(1,+∞)上是减函数,∴g (t )<g (1)=0,∴t ln 2t 1+t <ln 21+t+t -1得证, ∴f (x 2)-f (x 1)x 2-x 1<f ′⎝ ⎛⎭⎪⎫x 1+x 22成立. 17.(2014·济南针对性训练)已知函数f (x )=e x -x -1,g (x )=x 2e ax .(1)求f (x )的最小值;(2)求g (x )的单调区间;(3)当a =1时,对于在(0,1)中的任一个常数m ,是否存在正数x 0使得f (x 0)>m 2g (x 0)成立?如果存在,求出符合条件的一个x 0;否则说明理由.解:(1)f (x )的定义域是R ,f ′(x )=e x -1,且在(-∞,0)上f ′(x )<0,在(0,+∞)上f ′(x )>0,所以f (x )min =f (0)=0.(2)g ′(x )=2x e ax +ax 2e ax =(2x +ax 2)e ax .①当a =0时,若x <0,则g ′(x )<0,若x >0,则g ′(x )>0.所以当a =0时,函数g (x )在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数.②当a >0时,由2x +ax 2>0,解得x <-2a 或x >0, 由2x +ax 2<0,解得-2a <x <0.所以当a >0时,函数g (x )在区间⎝⎛⎭⎪⎫-∞,-2a 内为增函数, 在区间⎝ ⎛⎭⎪⎫-2a ,0内为减函数,在区间(0,+∞)内为增函数.③当a <0时,由2x +ax 2>0,解得0<x <-2a , 由2x +ax 2<0,解得x <0或x >-2a . 所以当a <0时,函数g (x )在区间(-∞,0)内为减函数,在区间⎝ ⎛⎭⎪⎫0,-2a 内为增函数,在区间⎝ ⎛⎭⎪⎫-2a ,+∞内为减函数. (3)假设存在这样的x 0满足题意,则f (x 0)>m 2g (x 0),e x 0-x 0-1>m 2x 20e x 0,m 2x 20+x 0+1e x 0-1<0,(*) 要找一个x 0>0,使(*)式成立,只需找到当x >0时,函数h (x )=m 2x 2+x +1e x -1的最小值h (x )min <0即可, h ′(x )=x ⎝ ⎛⎭⎪⎫m -1e x , 令h ′(x )=0得e x=1m ,则x =-ln m ,取x 0=-ln m , 当0<x <x 0时,h ′(x )<0,当x >x 0时,h ′(x )>0,所以h (x )min =h (x 0)=h (-ln m )=m 2(ln m )2-m ln m +m -1.下面只需证明:当0<m <1时,m 2(ln m )2-m ln m +m -1<0成立即可,令p (m )=m 2(ln m )2-m ln m +m -1,m ∈(0,1),则p ′(m )=12(ln m )2≥0,从而p (m )在m ∈(0,1)时为增函数,则p (m )<p (1)=0,从而m 2(ln m )2-m ln m +m -1<0得证.于是h (x )的最小值h (-ln m )<0,因此可找到一个正常数x 0=-lnm (0<m <1),使得f (x 0)>m 2g (x 0)成立.18.(2014·湖北八市联考)定义在R 上的函数g (x )及二次函数h (x )满足:g (x )+2g (-x )=e x+2e x -9,h (-2)=h (0)=1且h (-3)=-2. (1)求g (x )和h (x )的解析式;(2)对于x 1,x 2∈[-1,1],均有h (x 1)+ax 1+5≥g (x 2)-x 2g (x 2)成立,求a 的取值范围;(3)设f (x )=⎩⎪⎨⎪⎧g (x )(x >0),h (x )(x ≤0),在(2)的条件下,讨论方程f [f (x )]=a +5的解的个数情况.解:(1)∵g (x )+2g (-x )=e x+2e x -9,① ∴g (-x )+2g (x )=e -x+2e -x -9,即g (-x )+2g (x )=2e x +1e x -9,② 由①②联立解得,g (x )=e x -3.∵h (x )是二次函数,且h (-2)=h (0)=1,可设h (x )=ax (x +2)+1, 由h (-3)=-2,解得a =-1,∴h (x )=-x (x +2)+1=-x 2-2x +1,∴g (x )=e x -3,h (x )=-x 2-2x +1.(2)设φ(x )=h (x )+ax +5=-x 2+(a -2)x +6,F (x )=g (x )-xg (x )=e x -3-x (e x -3)=(1-x )e x +3x -3,依题意知,当-1≤x ≤1时,φ(x )min ≥F (x )max .∵F ′(x )=-e x +(1-x )e x +3=-x e x +3,在[-1,1]上单调递减, ∴F ′(x )min =F ′(1)=3-e>0,∴F (x )在[-1,1]上单调递增,∴F (x )max =F (1)=0,∴⎩⎪⎨⎪⎧φ(-1)=7-a ≥0,φ(1)=a +3≥0,解得-3≤a ≤7, ∴实数a 的取值范围为[-3,7].(3)设t =a +5,由(2)知,2≤t ≤12.f (x )的图象如图所示:设f (x )=T ,则f (T )=t .当t =2,即a =-3时,T =-1或者T =ln 5,f (x )=-1有2个解,f (x )=ln 5有3个解;当2<t <e 2-3,即-3<a <e 2-8时,T =ln(t +3)且ln 5<T <2,f (x )=T 有3个解;当t =e 2-3,即a =e 2-8时,T =2,f (x )=T 有2个解;当e 2-3<t ≤12,即e 2-8<a ≤7时,T =ln(t +3)>2,f (x )=T 有1个解.综上所述:当a =-3时,方程有5个解;当-3<a <e 2-8时,方程有3个解;当a =e 2-8时,方程有2个解;当e 2-8<a ≤7时,方程有1个解.。
2015年河北省唐山市高考数学二模试卷(理科)

2015年河北省唐山市高考数学二模试卷(理科)参考答案与试题解析一、选择题1.设集合{}1,0,1,2,3,A =-,{}220B x x x =->,则A B = _______. A . {}3 B .{}2,3C .{}1,3-D .{}0,1,2答案:C考点:交集及其运算.专题:集合.分析:求出B 中不等式的解集确定出B ,找出A 与B 的交集即可.解答:解:由B 中不等式变形得:()20x x ->,解得:0x <或2x >,即{}02B x x x <>或,{}1,0,1,2,3A =- ,{}1,3A B ∴=- , 故选:C .点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.在复平面内,复数z 与5i 2-的对应点关于虚轴对称,则z =______ A .2i + B .2i - C .2i -+ D .2i --答案:B考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数代数形式的乘除运算化简得答案. 解答:解:()()()()52i 52i 52i i 22i 2i 5----===------ +, 又复数z 与5i 2-的对应点关于虚轴对称, 则z=2﹣i i 2z =-.故选:B .点评:本题考查了复数的代数表示法及其几何意义,考查了复数代数形式的乘除运算,是基础题.3.在等差数列{a n {}n a 中,78a =,前7项和742S =,则其公差是_______. A . 13- B .13 C .23- D .23 考点:等差数列的通项公式.菁优网版权所有专题:等差数列与等比数列.分析:由通项公式和求和公式可得1a 和d 的方程组,解方程组可得.解答:解:设等差数列{}n a 的公差为d ,78a = ,前7项和742S =,168a d ∴=+,1767422a d ⨯=+, 解得14a =,23d = 故选:D点评:本题考查等差数列的通项公式和求和公式,属基础题.4.执行如图的程序框图,若输入的209a =,76b =,则输出的a 是_______.A .19B .3C .57D .76答案:A考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的a ,b ,c 的值,当0b =时满足条件0b =,退出循环,输出a 的值为19.解答:解:模拟执行程序框图,可得209a =,76b =57c =76a =,57b =,不满足条件0b =,19c =,57a =,19b =不满足条件0b =,0c =,19a =,0b =满足条件0b =,退出循环,输出a 的值为19.故选:A .点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模,本题属于基础知识的考查.5.设3log πa =,πlog 3b =,cos3c =,则______.A .b a c >>B .c b a >>C .a c b >>D .a b c >>答案:C考点:对数值大小的比较.专题:函数的性质及应用.分析:利用对数函数与指数函数、三角函数的单调性即可得出.解答:解:3log π1a => ,π0log 31b <=<,cos30c =<,a b c ∴>>.故选:D .点评:本题考查了对数函数与指数函数、三角函数的单调性,属于基础题.6.函数()()()4sin 0,πy x x ωφωφωφ=><++部分图象如图,其中点2π,03A ⎛⎫ ⎪⎝⎭,8π,03B ⎛⎫ ⎪⎝⎭,则____.A .1=2ω,2π=3φ- B.=1ω,2π=3φ- C .1=2ω,π=3φ- D .=1ω,π=3φ- 答案:C考点:正弦函数的图象.专题:三角函数的图像与性质.分析:结合图象,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式. 解答:解:由函数的图象可得π8π2π233T ω==-,12ω∴=. 再根据五点法作图可得12π023φ⋅=+,求得π3φ=-, 故选:C .点评:本题主要考查由函数()sin y A x ωφ=+的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,属于基础题.7.设实数x ,y 满足约束条件21033020x y x y x y -⎧⎪-⎨⎪-⎩+≥+≥+≤,则1y z x =+的取值范围是_______. A .1,15⎡⎤⎢⎥⎣⎦ B .15,54⎡⎤⎢⎥⎣⎦ C .13,62⎡⎤⎢⎥⎣⎦ D .15,64⎡⎤⎢⎥⎣⎦考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用目标函数的几何意义,结合数形结合进行求解即可. 解答:解:作出不等式组对应的平面区域如图:1y z x =+的几何意义为区域内的点到定点()1,0D -的斜率, 由图象知AD 的斜率最大,BD 的斜率最小,由21020x y x y -=⎧⎨-=⎩++,解得1353x y ⎧=⎪⎪⎨⎪=⎪⎩,即15,33A ⎛⎫ ⎪⎝⎭,此时5531413z ==+, 由33020x y x y -=⎧⎨-=⎩++,解得3212x y ⎧=⎪⎪⎨⎪=⎪⎩,即31,22B ⎛⎫ ⎪⎝⎭,此时1123512z ==+, 故1y z x =+的取值范围是15,54⎡⎤⎢⎥⎣⎦, 故选:B .点评:本题主要考查线性规划的应用,利用目标函数的几何意义以及直线斜率公式是解决本题的关键.8.某几何体的三视图如图所示,则该几何体的体积为______.1111正视图1侧视图俯视图A.43B.52C.73D.53答案:A考点:由三视图求面积、体积.专题:计算题;作图题;空间位置关系与距离.分析:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,该几何体为三棱柱与三棱锥的组合体.解答:解:该几何体为三棱柱与三棱锥的组合体,如右图,三棱柱的底面是等腰直角三角形,其面积11212S=⨯⨯=,高为1;故其体积1111V=⨯=;三棱锥的底面是等腰直角三角形,其面积11212S=⨯⨯=,高为1;故其体积2111133V=⨯⨯=;故该几何体的体积124 3V V V==+;故选:A.C 1B 1A 1CA 点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.9.一种团体竞技比赛的积分规则是:每队胜、平、负分别得2分、1分、0分,已知甲球队已赛4场,积4分,在这4场比赛中,甲球队胜、平、负(包括顺序)的情况共有_____.A .7种B .13种C .18种D .19种答案:D考点:计数原理的应用.专题:应用题;排列组合.分析:由题意4=1120=2200=1111+++++++++,即可得出结论.解答:解:由题意4=1120=2200=1111+++++++++,所以球队胜、平、负(包括顺序)的情况共有122434119C C C =++种,故选:D .点评:本题考查计数原理的运用,考查学生的计算能力,比较基础.10.在ABC △中,2AB BC =,以A ,B 为焦点,经过C 的椭圆和双曲线的离心率分别为1e ,2e ,则___.A .12111e e -=B .12112e e -=C .2212111e e -=D .2212112e e -= 答案:A考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:以AB 所在直线为x 轴,其中点为原点,建立坐标系,再通过椭圆及双曲线的基本概念即可得到答案.解答:解:以AB 所在直线为x 轴,其中点为原点,建立坐标系,则()1,0A -,()1,0B ,()1cos ,sin C θθ+,所以AC =对于椭圆而言,22c=,2a AC BC ==+所以11e a c ==; 对于双曲线而言,22c=,21a AC BC =-,所以21e a c =故12111e e -==, 故选:A .点评:本题考查椭圆、双曲线的概念,建立坐标系是解决本题的关键,属于中档题.11.已知函数()π2f x x =-,()cos sin g x x x x =-,当[]3π,3πx ∈-时,方程()()f x g x =根的个数是___. A .8 B .6C .4D .2 答案:B考点:根的存在性及根的个数判断.专题:计算题;作图题;函数的性质及应用;导数的综合应用.分析:先对两个函数分析可知,函数()f x 与()g x 都是奇函数,且()f x 是反比例函数,()g x 在[]0,π上是减函数,在[]π,2π上是增函数,在[]2π,3π上是减函数,且()00g =,()ππg =-;()2π2πg =;()3π3πg =-;从而作出函数的图象,由图象求方程的根的个数即可. 解答:解:由题意知,函数()π2f x x=-在[]3π,3π-是奇函数且是反比例函数, ()cos sin g x x x x =-在[]3π,3π-是奇函数;()'cos sin cos sin g x x x x x x x =--=-;故()g x 在[]0,π上是减函数,在[]π,2π上是增函数,在[]2π,3π上是减函数,且()00g =,()ππg =-;()2π2πg =;()3π3πg =-;故作函数()f x 与()g x 在[]3π,3π-上的图象如下,结合图象可知,有6个交点;故选:B .点评:本题考查了导数的综合应用及函数的图象的性质应用,同时考查了函数的零点与方程的根的关系应用,属于中档题. 12.已知圆:22C x +y =1,点(),2M t ,若C 上存在两点A ,B 满足MA AB = ,则t t 的取值范围是____.A .[]2,2-B .[]3,3-C .⎡⎣D .[]5,5- 答案:C考点:椭圆的简单性质.专题:平面向量及应用.分析:通过确定A 是MB 的中点,利用圆221x y =+的直径是2,可得2MA ≤,即点M 到原点距离小于等于3,从而可得结论.解答:解:如图,连结OM 交圆于点D . MA AB = ,A ∴是MB 的中点,圆221x y =+的直径是2,2M A AB ∴=≤,又M D M A ≤,1OD =,3OM ∴≤,即点M 到原点距离小于等于3,24t 9∴+≤,t ≤,故选:C .点评:本题考查向量知识的运用,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.二、填空题 13.已知a = 2b = ,若()a b a ⊥ +,则a 与b 的夹角是______. 答案:150︒考点:平面向量数量积的运算.专题:平面向量及应用. 分析:根据已知条件即可得到()0a b a ⋅= +,所以根据a = 2b =进行数量积的运算即可得到3a < +,0b >=,所以求出,cos ,a b = a 与b 的夹角. 解答:解:()0a b a ⊥ +;()23,0a b a a a b a b ∴⋅=⋅== +++;cos ,a b ∴= a ∴ 与b 的夹角为150︒.故答案为:150︒.点评:考查两非零向量垂直的充要条件,以及数量积的计算公式,向量夹角的范围.14.设n S 是数列{}n a 的前n 项和,43n n a S =-,则4S =______. 答案:2027考点:数列递推式.专题:等差数列与等比数列.分析:43n n a S =-,当1n =时,1143a a =-,解得1a .当2n ≥=时,143n n n S S S --=-,化为1313434n n S S -⎛⎫-=-- ⎪⎝⎭,利用等比数列的通项公式即可得出. 解答:解:43n n a S =- ,∴当1n =时,1143a a =-,解得11a =.当2n ≥时,143n n n S S S --=-, 化为1313434n n S S -⎛⎫-=-- ⎪⎝⎭, ∴数列34n S ⎧⎫-⎨⎬⎩⎭是等比数列,首项为14,公比为13-, 33112044327n S ⎛⎫∴-=-= ⎪⎝⎭. 令4n =,则343112044327S ⎛⎫=-= ⎪⎝⎭+. 故答案为:2027. 点评:本题考查了等比数列的通项公式,考查了变形能力,考查了推理能力与计算能力,属于中档题.15.在三棱锥P ABC -中,ABC △与PBC △都是等边三角形,侧面PBC ⊥底面ABC ,AB =该三棱锥的外接球的表面积为_______.答案:20π考点:球的体积和表面积.专题:计算题;空间位置关系与距离.分析:由题意,等边三角形的高为3,设球心到底面的距离为x ,则()22222213r x x ==-++,求出x ,可得r ,即可求出该三棱锥的外接球的表面积.解答:解:由题意,等边三角形的高为3,设球心到底面的距离为x ,则()222222133r x x ==-++,所以1x =,所以该三棱锥的外接球的表面积为24π20πr =.故答案为:20π.点评:本题考查求三棱锥的外接球的表面积,考查学生的计算能力,确定球的半径是关键.161=与两坐标轴所围成图形的面积是_____. 答案:16考点:定积分.专题:导数的概念及应用.分析:首先由题意,画出图象,然后利用定积分表示面积1,即(21y =-即图象与两坐标轴围成的图形如图阴影部分其面积为(()321121200014111236dx x dx x x x ⎛⎫-=-=-= ⎪⎝⎭⎰⎰+; 故答案为:16点评:本题考查了利用定积分求曲边梯形的面积;关键是正确利用定积分表示面积,然后计算.三、解答题17.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,()2222cosB a b a bc -=+. (Ⅰ)求A ;(Ⅱ)D 为边BC 上一点,3BD DC =,π2DAB ∠=,求tan C . 考点:余弦定理;正弦定理.专题:三角函数的求值;解三角形. 分析:(Ⅰ)由余弦定理可得2222cos a B a c b =-+,代入已知等式整理得1cos 2A =-,即可求得A . (Ⅱ)由已知可求π6DAC ∠=,由正弦定理有sin sin AD CD C DAC=∠,又3BD CD =,可得3sin 2sin B C =,由π3B C =-化简即可得解. 解答:解:(Ⅰ)因为2222cos a B a c b =-+,所以()222222a b a c b bc -=-++.… 整理得222a b c bc =++,所以1cos 2A =,即2π3A =.… (Ⅱ)因为π2DAB =△,所以sin AD BD B =⋅,π6DAC ∠=.… 在ACD △中,有sin sin AD CD C DAC=∠,又因为3BD CD =, 所以3sin 2sin B C =,…由π3B C =-3sin 2sin 2C C C -=,…整理得tan C =… 点评:本题主要考查了余弦定理,正弦定理,同角三角函数关系式,三角函数恒等变换的应用,综合性较强,属于基本知识的考查.18.如图,四棱锥P ABCD -的底面ABCD 是平行四边形,侧面PAD 是等边三角形,平面PAD ⊥平面ABCD ,M ,N 分别是棱PC ,AB 的中点,且MN CD ⊥.(Ⅰ)求证:AD CD ⊥;(Ⅱ)若AB CD =,求直线MN 与平面PBD 所成角的正弦值.MD CBA 考点:直线与平面所成的角;空间中直线与直线之间的位置关系.专题:空间位置关系与距离;空间角;空间向量及应用. 分析:(Ⅰ)取PD 边中点E ,连接AE ,EM ,根据MN CD ⊥容易得到CD AE ⊥,而根据已知条件可以说明PO ⊥平面ABCD ,从而得到CD PO ⊥,这样CD 就垂直于平面PAD 内两条相交直线,由线面垂直的判定定理从而得到AD CD ⊥;(Ⅱ)取BC 中点F ,连接OF ,由(Ⅰ)便可知道OA ,OF ,OP 三条直线两两垂直,从而可分别以这三条直线为x ,y ,z 轴,可设2AB =,这样即可求得图形中一些点的坐标.从而求出向量DB ,DP 的坐标,这时候设平面PBD 的法向量为(),,n x y z = ,根据00n DB n DP ⎧⋅=⎪⎨⋅=⎪⎩ 即可求出n 的坐标,若设MN 和平面PBD 所成角为θ,从而根据sin cos ,n MN n MN n MNθ⋅== 即可求得答案. 解答:解:(Ⅰ)证明:如图,取PD 中点E ,连AE ,EM ,则EM AN ∥,且EM AN =;∴四边形ANME 是平行四边形,MN AE ∥;MN CD ⊥ ,AE CD ∴⊥,即CD AE ⊥;取AD 中点O ,连PO ,PAD △是等边三角形,则PO AD ⊥; 又因为平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =; PO ∴⊥平面ABCD ,PO CD ⊥,即CD PO ⊥;故CD ⊥平面PAD ,AD ⊂平面PAD ;CD AD ∴⊥,即AD CD ⊥;(Ⅱ)由AB AD =,AD CD ⊥,得四边形ABCD 是正方形; 取BC 边的中点F ,连接OF ,则分别以OA ,OF ,OP 所在直线为x ,y ,z 轴建立如图所示空间直角坐标系;设2AB =,则()1,0,0A ,()1,2,0B ,()1,0,0D -,(0,0,P,1,0,2E ⎛- ⎝⎭; ()2,2,0DB =,(1,0,DP = ;设平面PBD 的法向量(),,n x y z =,则: 00n DB n DP ⎧⋅=⎪⎨⋅=⎪⎩ ;2x+2y =0=0⎧⎪∴⎨⎪⎩;x y ⎧=⎪∴⎨=⎪⎩,取1z =,()1n ∴= ;3,0,2MN EA ⎛==- ⎝⎭ ; 设直线MN 与平面PBD 所成的角为θ,则:sin cos ,MN n θ=== .点评:考查面面垂直的性质定理,线面垂直的判定定理,以及建立空间直角坐标系,利用向量解决直线和平面所成角的问题,能求空间点的坐标,注意线面角和直线和平面法向量所成角的关系,以及向量夹角余弦的坐标公式.19.某市工业部门计划对所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出12家,然后从这12家中选出9家进行奖励,分别奖励中、小企业每家50万元、10万元,记9家企业所获奖金总数为X 万元,求X 的分布列和期望. 附:()()()()22n ad bc K a b a c b d -=+++考点:独立性检验的应用. 专题:应用题;概率与统计. 分析:(Ⅰ)由题意知根据表中所给的数据,利用公式可求2K 的值,从临界值表中可以知道2 5.024K >,根据临界值表中所给的概率得到与本题所得的数据对应的概率是0.025,得到结论;(Ⅱ)按分层抽样得到的12家中,中小企业分别为3家和9家.X 的可能取值为90,130,170,210,求出相应的概率,即可求出X 的分布列和期望.解答:解:(Ⅰ)()225608020040240 5.657120*********K ⨯-⨯==⨯⨯⨯,因为5.657 5.024>,所以能在犯错概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关.…(Ⅱ)由(Ⅰ)可知“支持”的企业中,中小企业家数之比为1:3,按分层抽样得到的12家中,中小企业分别为3家和9家.设9家获得奖励的企业中,中小企业分别为m 家和n 家,则(),m n 可能为()0,9,()1,8,()2,7,()3,6.与之对应,X 的可能取值为90,130,170,210.…()190220P X -=,()27130220P X ==, ()108170220P X ==,()84210220P X ==,…期望271088490130170210180220220220220EX =⨯⨯⨯⨯=+++.…点评:本题考查独立性检验的应用,考查X 的分布列和期望,考查学生的计算能力,属于中档题. 20.已知抛物线2:4E x y =,m 、n 是过点(),1A a -且倾斜角互补的两条直线,其中m 与E 有唯一公共点B ,n 与E 相交于不同的两点C ,D . (Ⅰ)求m 的斜率k 的取值范围;(Ⅱ)是否存在常数λ,使得2AC AD AB λ⋅=?若存在,求λ的值;若不存在,说明理由. 考点:抛物线的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程. 分析:(Ⅰ)设直线():1m y k x a =-+,():1n y k x a =-+,代入抛物线方程,运用判别式等于0和大于0,解不等式即可得到k 的范围;(Ⅱ)假设存在常数λ,使得2AC AD AB λ⋅=,设()00,B x y ,()11,C x y ,()22,D x y ,代入直线方程,由条件结合二次方程的韦达定理,再由判别式为0,即可判断. 解答:解:(Ⅰ)设直线():1m y k x a =-+,():1n y k x a =-+, 分别代入24x y =,得2440x kx ka -=+(1),24440x kx ka -=++(2), 由1=0△得210k ka --=,由2>0△得210k ka ->+,故有2210k ->,得21k >,即1k <-,或1k >.(Ⅱ)假设存在常数λ,使得2AC AD AB λ⋅=, 设()00,B x y ,()11,C x y ,()22,D x y , 则()()()2120111y y y λ=+++.将()111y k x a =--+,()211y k x a =--+,()001y k x a =-+代入上式,得()()()2120x a x a x a λ--==,即()()2212121x x a x x a x a λ-=-++.由(2)得124x x k =-+,1244x x ka =-+, 由(1)得02x k =,代入上式,得()222444a k ka a λ=-++.又1=0△得210k ka --=,即2444k ka -=, 因此()2244a a λ=++,=1λ.故存在常数=1λ,使得2AC AD AB λ⋅=.点评:本题考查抛物线的方程和性质,主要考查直线和抛物线方程联立,运用判别式和韦达定理,考查运算化简的能力,属于中档题.21.设函数()1ln f x x a x x =++,()11ln g x x x x x x ⎛⎫=- ⎪⎝⎭++,其中a ∈R .(Ⅰ)证明:()1g x g x ⎛⎫= ⎪⎝⎭,并求()g x 的最大值;(Ⅱ)记()f x 的最小值为()h a ,证明:函数()y h a =有两个互为相反数的零点.考点:利用导数求闭区间上函数的最值;函数零点的判定定理;利用导数研究函数的单调性. 专题:函数的性质及应用;导数的综合应用.分析:(Ⅰ)利用已知函数()g x 的解析式,分别计算1g x ⎛⎫⎪⎝⎭,()g x ,可得两者相等;再利用()'g x 求得最大值;(Ⅱ)利用()'f x 可得()f x 的最小值()()11=t ln h a t t g t t t ⎛⎫-= ⎪⎝⎭++,由(Ⅰ)可知210e g ⎛⎫< ⎪⎝⎭,()10g >,利用函数零点的判定定理即得结论.解答:解:(Ⅰ)111111ln ln g x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ++++,()1g x g x ⎛⎫∴= ⎪⎝⎭,则()21'1ln g x x x ⎛⎫=- ⎪⎝⎭+,当()0,1x ∈时,()'0g x >,()g x 单调递增; 当()1,x ∈∞+时,()'0g x <,()g x 单调递减.所以()g x 的最大值为()111021g ==++.(Ⅱ)()1ln f x x a x x= ++,()22211'1a x ax f x x x x -∴=-=++. 令()'0f x =,即210x ax -=+,则2=0a >△+,不妨取0t >,由此得:210t at -=+或写为:1a t t=-. 当()0,x t ∈时,()'0f x <,()f x 单调递减;当(),x t ∈∞+时,()'0f x >,()f x 单调递增.从而()f x 的最小值为()111ln ln f t t a t t t t t t t ⎛⎫==- ⎪⎝⎭++++,即()()11ln h a t t t g t t t ⎛⎫=-= ⎪⎝⎭++(或()h a a =).由(Ⅰ)可知()222213e e 0e e g g ⎛⎫==-< ⎪⎝⎭,()120g =>,分别存在唯一的()0,1c ∈和()1,d ∈∞+,使得()()0g c g d ==,且1cd =,因为()10a t t t =->是t 的减函数,所以()y h a =有两个零点11a d d =-和21a c c =-,又()110c d d c c d d c cd--=-=+++,所以()y h a =有两个零点且互为相反数. 点评:本题考查利用导数判断函数的单调性及零点判定定理,考查转化与化归思想、运算求解能力、数据处理能力和推理论证能力.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分【选修4-1:几何证明选讲】22.如图,AB 为圆O 的直径,PB ,PC 分别与圆O 相切于B ,C 两点,延长BA ,PC 相交于点D . (Ⅰ)证明:AC OP ∥;(Ⅱ)若2CD =,3PB =,求AB .PODCBA考点:与圆有关的比例线段;空间中直线与直线之间的位置关系. 专题:选作题;立体几何. 分析:(Ⅰ)利用切割线定理,可得PB PC =,且PO 平分BPC ∠,可得PO BC ⊥,又AC BC ⊥,可得AC OP ∥;(Ⅱ)由切割线定理得2DC DA DB -⋅,即可求出AB . 解答:(Ⅰ)证明:因PB ,PC 分别与圆O 相切于B ,C 两点, 所以PB PC =,且PO 平分BPC ∠,所以PO BC ⊥,又AC BC ⊥,即AC OP ∥.… (Ⅱ)解:由PB PC =得5PD PB CD ==+, 在Rt PBD △中,可得4BD =.则由切割线定理得2DC DA DB =⋅, 得1DA =,因此3AB =.…点评:本题考查切割线定理,考查学生分析解决问题的能力,正确运用切割线定理是关键. 【选修4-4:极坐标与参数方程】23.在极坐标系中,曲线():2cos 0C a ρθ=>,π31:cos 32ρθ⎛⎫-= ⎪⎝⎭,C 与1有且仅有一个公共点.(Ⅰ)求a ;(Ⅱ)O 为极点,A ,B 为C 上的两点,且π3AOB ∠=,求OA OB +的最大值.考点:简单曲线的极坐标方程. 专题:坐标系和参数方程. 分析:(I )把圆与直线的极坐标方程分别化为直角坐标方程,利用直线与圆相切的性质即可得出a ;(II )不妨设A 的极角为θ,B 的极角为π3θ+,则ππ2cos 2cos 36OA OB θθθ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭++++,利用三角函数的单调性即可得出.解答:解:(Ⅰ)曲线():2cos 0C a a ρθ=>,变形2=2cos a ρρθ,化为222x y ax =+,即()222x a y a -=+.∴曲线C 是以(),0a 为圆心,以a 为半径的圆;由π31:cos 32ρθ⎛⎫-= ⎪⎝⎭,展开为13cos sin 22ρθθ=, 1∴的直角坐标方程为30x -=.由直线l 与圆C 相切可得32a a -=,解得1a =.(Ⅱ)不妨设A 的极角为θ,B 的极角为π3θ+,则ππ2cos 2cos =3cos 36OA OB θθθθθ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭++++,当π=6θ-时,OA OB +取得最大值.点评:本题考查了把圆与直线的极坐标方程分别化为直角坐标方程、直线与圆相切的性质、极坐标方程的应用、三角函数的单调性,考查了推理能力与计算能力,属于中档题. 【选修4-5:不等式选讲】24.设()121f x x x =--+的最大值为m .(Ⅰ)求m ;(Ⅱ)若a ,b ,()0,c ∈∞+,2222a b c m =++,求ab bc +的最大值.考点:绝对值不等式的解法;基本不等式.专题:计算题;分类讨论;不等式的解法及应用. 分析:(Ⅰ)运用零点分区间,讨论x 的范围,去绝对值,由一次函数的单调性可得最大值; (Ⅱ)由()()22222222a b c a b b c =+++++,运用重要不等式,可得最大值. 解答:解:(Ⅰ)当1x -≥时,()32f x x =+≤; 当11x -<<时,()132f x x =--<; 当1x ≥时,()34f x x =---≤. 故当1x =-时,()f x 取得最大值m=2.(Ⅱ)()()()222222222a 2b a b b c ab 2bc ab bc ==++c +++≥++,当且仅当a b c ===时,等号成立. 此时,ab bc +取得最大值π=12.点评:本题考查绝对值不等式的解法和运用,主要考查分类讨论的思想方法和重要不等式的解法,属于中档题.。
2015年普通高考测试(二)数学(理科)附答案
2015年普通高考测试(二)数学(理科)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}231x x M =-<,集合{}13x x N =-<<,则MN =( ).A .MB .NC .{}12x x -<<D .{}3x x <2.已知z 是复数,i 是虚数单位,若i zi +=1,则z =( ).A .i +1B .i -1C .i +-1D .i --13.随机变量ξ服从正态分布)4,3(N ,若)2()32(+>=-<a P a P ξξ,则a 的值为( ).A .37 B .34 C .3 D .44.一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积是( ).A .5πB .6πC .7πD .9π 5.在右图所示的程序框图中,输出的i 和s 的值分别为( ).A .3,21B .3,22C .4,21D .4,226.设)(x f 是定义在R 上的周期为3的周期函数,如图表示该函数在区间]1,2[-上的图像,则)2015()2014(f f +=( ).A .3B .2C .1D .07.若平面向量()1,2a =-与b 的夹角是0180,且53||=b ,则b 的坐标为( ).A .)6,3(-B .)6,3(-C .)3,6(-D .)3,6(- 8.对于任意正整数n ,定义“!!n ”如下:当n 是偶数时,()()!!24642n n n n =⋅-⋅-⋅⋅⋅⋅⋅⋅⋅⋅;当n 是偶数时,()()!!24531n n n n =⋅-⋅-⋅⋅⋅⋅⋅⋅⋅⋅; 且有()()!12321n n n n =⋅-⋅-⋅⋅⋅⋅⋅⋅⋅⋅.则如下四个命题:①()()2015!!2016!!2016!⋅=;②10082016!!21008!=⨯;③2015!!的个位数是5;④2014!!的个位数是0. 其中正确的命题有( ).A .1个B .2个C .3个D .4个 二、填空题(本大题共7小题,考生作答6小题,每小题5分,满分30分.) (一)必做题(9~13题)9.曲线x x y sin +=在点(0,0)处的切线方程是________________.10.双曲线C :221916x y -=的离心率是 . 11.=-⎰dx x |1|20_______________.12.某所学校计划招聘男教师x 名,女教师y 名,x 和y 须满足约束条件⎪⎩⎪⎨⎧<≤-≥-6252x y x y x ,则该校招聘的教师最多是 名.13.已知全集}8,7,6,5,4,3,2,1{=U ,在U 中任取四个元素组成的集合记为},,,{4321a a a a A =,余下的四个元素组成的集合记为},,,{4321b b b b A C U =,43214321b b b b a a a a +++<+++,则集合A 的取法共有____________种.(二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)直线l 的参数方程为31x ty t ⎧=⎪⎨=+⎪⎩(t 为参数),则直线l 的倾斜角是 .15.(几何证明选讲选做题)如图,在梯形CD AB 中,D//C A B ,D 2A =,C 5B =,点E .F 分别在AB .CD 上,且F//DE A ,若34AE =EB ,则F E 的长是 .三.解答题(本大题共6小题,共80分.解答应写出文字说明.证明过程或演算步骤.)16.(本小题满分12分)设函数)(,sin 3cos )(R x x x x f ∈-= (1)求函数)(x f 在区间]2,0[π上的值域(2)记AB C ∆内角C B A ,,的对应边分别为c b a ,,,若1)3(=-πA f ,且b a 23=,求B s i n 的值.17.(本小题满分12分)某中学一名数学教师对全班50名学生某次考试成绩分男生女生进行了统计(满分150分),得到右面频率分布表:其中120分(含120分)以上为优秀. (1)根据以上频率表的数据,完成下面的2⨯2列联表;(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?(3)若从成绩在[130,140]的学生中任取3人,已知取到的第一个人是男生,求取到的另外2人中至少一名女生的概率.18.(本小题满分14分)如图,四棱锥ABCD P -中,045BCD 1AD AB 2CD ,,//AB ABCD =∠===⊥⊥,,且,平面DC AD DC PD . (1)若点M 是PD 的中点,证明:PBC AM//平面;(2)若PBC ∆得面积为2,求二面角D -PC -B 的余弦值.19.(本小题满分14分)数列{}n a 的前n 项和记为n S ,对任意正整数n ,均有()241n n S a =+,且0n a >.()1求1a 及数列{}n a 的通项公式; ()2令114)1(+--=n n n n a a nb ,求数列}{n b 的前n 项和n T .20.(本小题满分14分)已知曲线E 上的任一点到点)3,0(1-F 和点)3,0(F 的距离之和为4. (1)求曲线E 的方程;(2)已知点)0,1(),2,0(C A ,设直线)0(,>=k kx y 与曲线E 交于B .D 两点(B 在第一象限),求四边形ABCD 面积的最大值.21.(本小题满分14分)已知函数b a bx ax x f ,(,1)(2++=为实数,),0R x a ∈≠. (1)若0)1(=-f ,且函数)(x f 的值域为),0[+∞,求)(x f ;(2)设0,0,)()()(<>⎩⎨⎧-=x x x f x f x F ,0,0,0>>+<a n m mn ,且函数)(x f 为偶函数.证明:0)()(>+n F m F ;(3)设)(,1ln )(x g ex x g x+=的导函数是),(x g '当1==b a 时,证明:对任意实数0>x ,21)(]1)([-+<'-e x g x f .。
2015年普通高中高三第二次联合考试理科数学附答案

BA BC 2 ,则 ABC 的面积为 (
A. 2
2
) C. 2 2 D. 4 2
B.
3 2
(10)已知抛物线 y =2px(p>0)与双曲线 2- 2=1(a>0,b>0)有相同的焦点 F,点 A 是两曲线的一个交点,且 AF⊥x 轴,则双曲线的离心率为( ( ) A. 2+2 B. 5+1 C. 3+1
2015 年普通高中高三第二次联合考试理科数学
注意事项: 1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的 姓名、准考证号填写在答题卡上。 2. 回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号框 涂黑。如 需改动,用橡皮擦干净后,再选涂其它答案标号框。写在本试卷上无效。 3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。 4. 考试结束后,将本试卷和答题卡一并交回。
D. 1,1
第Ⅱ卷
本卷包括必考题和选考题两部分。 第 13 题~第 21 题为必考题, 每个试题考生都必须做 答。第 22 题~第 24 题为选考题,考生根据要求做答。 二、填空题:本大题共 4 小题,每小题 5 分。
(13)若复数 z
(a 2 4) (a 2)i 为纯虚数,则
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只 有一项是符合题目要求的。
(1)设集合 A
x y lg(3 2x),集合 B y y
B. (﹣∞,1] C.
)
A. [ 0, )
3 2
(2) 若命题 p 为真命题,命题 q 为假命题,则以下为真命题的是(
A. p q
江西省南昌市2015届高三第二次模拟考试数学理科试题有答案(扫描版)

2015 年 高 三 测 试 卷数学(理科)参考答案及评分标准一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题5分.13.214.13π 15.1316.2212x y -= 三、解答题:解答应写出文字说明,证明过程或演算步骤.17.解:(Ⅰ)由点,C B 的坐标可以得到34AOC π∠=,23AOB π∠=,…………………2分 所以cos cos()COB AOC AOB ∠=∠+∠1()2222=-⨯--4=-;……6分 (Ⅱ)因为c =23AOB π∠=,所以3C π=,所以2sin sin a b A B ===,………8分所以22sin 2sin()3a b A A π+=+-2sin()6A π=+,2(0)3A π<<,……………………11分 所以当3A π=时,a b +最大,最大值是12分18.解:(Ⅰ)该校运动会开幕日共有13种选择,其中运动会期间至少两天空气质量优良的选择有:1日,2日,3日,5日,9日,10日,12日,所以运动会期间至少两天空气质量优良的概率是2713P =.…………………………………6分(Ⅱ)随机变量ξ所有可能取值有:0,1,2,3;………………………………………………7分(0)P ξ==113,(1)P ξ==613,(2)P ξ==613,(3)P ξ==113,……………………9分所以随机变量ξ的分布列是:随机变量ξ的数学期望是1661012313131313E ξ=⨯+⨯+⨯+⨯=2113.……………………12分 19.(Ⅰ)证明:在梯形ABCD 中,因为2AD DC CB ===,4AB =,4212cos 22CBA -∠==,所以60,ABC ∠=︒由余弦定理求得AC=90ACB ∠=︒即BC⊥又因为平面AEFC ⊥平面ABCD ,所以BC ⊥平面所以BC AG ⊥,………………………………………3分 在矩形AEFC 中,tan 1AE AGE EG ∠==,4AGE π∴∠=tan 1CF CGF GF ∠==,4CGF π∠=,所以2CGF AGE π∠+∠=,即AG CG ⊥,所以AG ⊥平面BCG ;……………………………………………………………………………6分(Ⅱ)FC AC ⊥,平面AEFC ⊥平面ABCD ,所以FC ⊥平面ABCD , 以点C 为原点,,,CA CB CF 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系, 则)(0,0,0),(0,2,0),1,0)C A B D-,G ,…………………………8分平面BCG 的法向量(3,0,GA =,设平面GCD 的法向量(,,)n x y z =,则0n CG n CD ⎧⋅=⎪⎨⋅=⎪⎩,从而00x z y +=⎧⎪-=,令1x =则(1,3,1)n =-,…………………………………………………………………………10分 所以cos ,n GA <>==,…………………………………………………11分 而二面角D —GCB 为钝角, 故所求二面角的余弦值为.………………………………………………………………12分 20.解:(Ⅰ)当l 垂直于OD 时||AB 最小,因为||OD =2r ==,…………………………………2分因为圆1C 222:(0)x y r r +=>的一条直径是椭圆2C 的长轴,所以2a =,又点D 在椭圆22222:1(0)x y C a b a b +=>>上,所以291414b b+=⇒=, 所以圆1C 的方程为224x y +=,椭圆2C 的方程为22143x y +=;………………………5分 (Ⅱ)椭圆2C 的右焦点F 的坐标是(1,0),当直线m 垂直于x 轴时,||PQ = ||4MN =,四边形PMQN 的面积S =当直线m 垂直于y 轴时,||4PQ =,||3MN =,四边形PMQN 的面积6S =,…………6分……………………10分当直线m 不垂直于坐标轴时,设n 的方程为(1)y k x =-(0)k ≠,此时直线m 的方程为1(1)y x k=--, 圆心O 到直线m的距离为:d =,所以||PQ ==,…………8分 将直线n 的方程代入椭圆2C 的方程得到:()22224384120k x k x k +-+-=,||MN =所以:四边形PMQN 的面积1||||2S PQ MN =⋅===∈,综上:四边形PMQN的面积的取值范围是.…………………………………………12分21.解:(Ⅰ)21221'()22x ax f x x a x x-+=+-=(0)x >,记2()221g x x ax =-+………1分 (一)当0a ≤时,因为0x >,所以()10g x >>,函数()f x 在(0,)+∞上单调递增;……2分(二)当0a <≤时,因为24(2)0a =-≤△,所以()0g x ≥,函数()f x 在(0,)+∞上单调递增;…………………………………………………………………………………………………3分(三)当a >0()0x g x >⎧⎨>,解得x∈,所以函数()f x 在区间上单调递减,在区间(0,),()2a a +∞上单调递增.…………………………5分(Ⅱ)由(1)知道当(1a ∈时,函数()f x 在区间(0,1]上单调递增, 所以(0,1]x ∈时,函数()f x的最大值是(1)22f a =-,对任意的a ∈,都存在0(0,1]x ∈使得不等式20()ln()f x a m a a +>-成立,等价于对任意的(1a ∈,不等式222ln ()a a m a a -+>-都成立,……………………………………6分即对任意的(1a ∈,不等式2ln (2)20a ma m a +-++>都成立, 记2()ln (2)2h a ama m a =+-++,则(1)0h =,1(21)(1)'()2(2)a ma h a ma m a a --=+-+=,因为(1a ∈,所以210a a->, 当1m ≥时,对任意(1a ∈,10ma ->,所以'()0h a >,即()h a 在区间上单调递增,()(1)0h a h >=成立;…………………………………………………………………………9分 当1m <时,存在0(1a ∈使得当0(1,)a a ∈时,10ma -<,'()0h a <,()h a 单调递减,从而()(1)0h a h <=,所以(1a ∈时,()0h a >不能恒成立.综上:实数m 的取值范围是[1,)+∞.……………………………………………………………12分 22.解:AF 是圆的切线,且18,15AF BC ==,∴由切割线定理得到2218(15)12AF FB FC FB FB FB =⋅⇒=⋅+⇒=,…………………3分 ,AB AD ABD ADB =∴∠=∠,则,//FAB ABD AF BD ∠=∠∴,…………………………………………………………………6分 又//AD FC ,∴四边形ADBF 为平行四边形.12,,18AD FB ACF ADB F ACAF ==∠=∠=∠∴==,//,18AE ADAD FC AE BC∴=-,解得8AE =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇题型专练选择、填空题训练(一)【选题明细表】知识点、方法题号集合与常用逻辑用语1、3平面向量13不等式12、15函数2、7、8、14三角函数与解三角形5、16数列9、11立体几何4、6解析几何10、17一、选择题1.(2014高考新课标全国卷Ⅱ)设集合M={0,1,2},N={x|x2-3x+2≤0},则M∩N等于( D )(A){1} (B){2}(C){0,1} (D){1,2}解析:N={x|x2-3x+2≤0}={x|1≤x≤2},M={0,1,2},∴M∩N={1,2}.故选D.2.下列函数中,在其定义域内,既是奇函数又是减函数的是( C )(A)f(x)= (B)f(x)=(C)f(x)=2-x-2x(D)f(x)=-tan x解析:对于选项A,函数是奇函数,但其单调减区间是(-∞,0)和(0,+∞),在定义域内不是单调函数;对于选项B,其定义域为(-∞,0],其定义域不关于原点对称,是非奇非偶函数;对于选项D,函数在每个区间(kπ-,kπ+)(k∈Z)上是减函数,也不能说在定义域内是减函数.故选C.3.(2014嘉兴二模)已知a,b∈(0,+∞),则“ab>2”是“log2a+log2b>0”的( A )(A)充分不必要条件(B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件解析:若ab>2,则log2a+log2b=log2(ab)>log22=1>0,反之,若log2a+log2b>0,则log2(ab)>0,ab>1.故选A.4.(2014宁波高三十校联考)若直线l,m与平面α、β、γ满足β∩γ=l,l∥α,m ⊂α,m⊥γ,则有( D )(A)m∥β且l⊥m (B)α∥β且α⊥γ(C)α⊥β且m∥γ (D)α⊥γ且l⊥m解析:由m⊂α,m⊥γ知α⊥γ,由m⊥γ,l⊂γ知m⊥l.故选D.5.为了得到函数f(x)=sin 2 x 的图象,只需将函数g(x)=的图象( B )(A)向右平移个单位 (B)向右平移个单位(C)向右平移π个单位 (D)向右平移个单位解析:由于g(x)===cos 2 x=sin 2(x+),因此只需将函数g(x)的图象向右平移个单位即可得到f(x)的图象.6.已知几何体的三视图如图所示,则该几何体的体积为( A )(A)64+4π (B)48+4π(C)64+16π (D)48+16π解析:该几何体上面是一个圆柱,下面是一个正方体,其总体积为V=43+π²12²4=64+4π.7.(2014浙江省“六市六校”联考)已知f(x)=定义f n (x)=f(f n-1(x)),其中f 1(x)=f(x),则f 2014()等于( B )(A) (B) (C) (D)解析:f 1()=f ()=,f 2()=f ()=,f 3()=f ()=,f 4()=,f 5()=,f 6()=,f 7()=f ()=…因此f n ()是以6为周期的周期函数,故又2014=335³6+4,于是f2014()=f4()=.故选B.8.(2013高考山东卷)函数y=xcos x+sin x的图象大致为( D )解析:由y=xcos x+sin x为奇函数,可排除选项B;x=π时y=-π,排除选项A;x=时y=1,可排除选项C.故选D.9.(2014宁波高三十校联考)设a∈R,数列{(n-a)2}(n∈N*)是递增数列,则a的取值范围是( D )(A)a≤0 (B)a<1 (C)a≤1 (D)a<解析:由题知(n+1-a)2-(n-a)2>0对任意n∈N*恒成立,即2a<2n+1恒成立,则a<.故选D.10.(2013厦门模拟)过抛物线x2=-2py(p>0)的焦点F的直线l与抛物线相交于A、B两点,O是坐标原点,则三角形ABO的形状是( C )(A)直角三角形 (B)锐角三角形(C)钝角三角形 (D)不能确定解析:依题意,直线l的斜率存在,设为k,则直线l的方程为y+=kx,由可得x2+2pkx-p2=0,若设A(x1,y1),B(x2,y2),则x1x2=-p2,所以y1y2=,因此²=x1x2+y1y2=-<0,得∠AOB是钝角,故三角形ABO的形状是钝角三角形.二、填空题11.(2013杭州模拟)在等比数列{an }中,an>0(n∈N*),且a6-a4=24,a3a5=64,则{an}的前6项和是.解析:由a3a5==64得a4=8,于是a6=32,设公比为q,则q2==4,得q=2,a1=1,故{an }的前6项和为S6==63.答案:6312.(2013杭州模拟)设x,y满足约束条件:则z=2x-y的最小值为.解析:如图,在直角坐标系中画出约束条件表示的可行域为△ABC及其内部(含边界),其中A(1,),B(1,8),C(4,2),所以当动直线z=2x-y过B(1,8)时,z=2x-y的最小值为-6.答案:-613.(2013泰顺模拟)已知平面向量a,b,c满足|a|=1,|b|=2,|c|=4,且向量a,b,c 两两所成的角相等,则|a+b+c|= .解析:∵a,b,c成等角,∴a,b,c两两成0°或120°,当a,b,c两两成0°时,|a+b+c|=1+2+4=7;当a,b,c两两成120°时,|a+b+c|2=a2+b2+c2+2a²b+2a²c+2b²c=1+4+16-2-4-8=7,|a+b+c|=.答案:7或14.(2012高考新课标全国卷)设函数f(x)=的最大值为M,最小值为m,则M+m= .解析:f(x)===1+,令g(x)=,则g(x)为奇函数,对于一个奇函数来说,其最大值与最小值之和为0,即g(x)max +g(x)min=0,而f(x)max =1+g(x)max,f(x)min =1+g(x)min,所以f(x)max +f(x)min=2.答案:215.(2013浙江省五校联考)已知正实数x,y满足ln x+ln y=0,且k(x+2y)≤x2+4y2恒成立,则k的最大值是.解析:由ln x+ln y=0可得xy=1.又因为k≤==(x+2y)-,由于x+2y≥2=2,令x+2y=t,则g(t)=t-≥2-=.因此当k≤恒成立时,k的取值范围是k≤,故k的最大值为.答案:16.(2013杭州模拟)在△ABC中,角A、B、C所对的边分别为a,b,c.已知a=2,c=2,且1+=,则角C的值为.解析:由正弦定理可知1+²=,即=,又∵sin(A+B)=sin C,∴cos A=,∵0°<A<180°,∴sin A=.由=知sin C=,又c<a,所以C=45°.答案:45°17.(2014温州中学月考)若椭圆+=1的焦点在x轴上,过点P(1,)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是.解析:由题意可设PA垂直于x轴,于是A(1,0),∴c=1,设PB:y-=k(x-1),即kx-y+-k=0,则有=1,∴k=-,∴k=,OB∴B(,),∴直线AB的方程为y=-2x+2,令x=0,得y=2,∴b=2,∴a=,∴椭圆方程为+=1.答案:+=1选择、填空题训练(二)【选题明细表】知识点、方法题号集合与常用逻辑用语1、2平面向量9、14不等式11、16函数4、10、15三角函数与解三角形6、8数列7、13立体几何5、12解析几何3、17一、选择题1.(2013浙江省名校新高考研究联盟第一次联考)设P={x|2x>1},Q={x|logx>1},2则( A )(A)P∪Q=P (B)P∪Q=Q(C)P∩Q Q (D)P∩Q Q解析:P={x|2x>1}={x|x>0},x>1}={x|x>2},Q={x|log2所以Q P,P∪Q=P,P∩Q=Q,故选A.2.(2013浙江省金华十校高三模拟)“a=2”是“直线y=-ax+2与y=x-1垂直”的( A )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件解析:a=2时,直线方程分别为y=-2x+2和y=x-1,此时两直线斜率之积为-1,所以两直线垂直;若直线y=-ax+2与y=x-1垂直,则有-a³=-1,所以a=±2.所以“a=2”是“直线y=-ax+2与y=x-1垂直”的充分不必要条件.故选A.3.已知椭圆+=1(a>b>0),A(4,0)为长轴的一个端点,弦BC过椭圆的中心O,且²=0,|-|=2|-|,则其焦距为( C )(A)(B)(C)(D)解析:由题意,可知||=||=||,且a=4,又|-|=2|-|,所以||=2||.故||=||.又²=0,所以⊥.故△OAC为等腰直角三角形,||=||=2.不妨设点C在第一象限,则点C的坐标为(2,2),代入椭圆方程,得+=1,解得b2=.所以c2=a2-b2=42-=,c=.故其焦距为2c=.故选C.4.(2013浙江省名校新高考研究联盟第一次联考)已知函数f(x)=,若f(a)=,则f(-a)等于( C )(A)(B)-(C)(D)-解析:因为f(x)==1+,所以f(a)=1+=,所以=-,f(-a)=1-=1-(-)=,故选C.5.(2014宁波高三十校联考)设m,n是两条不同的直线,α、β是两个不同的平面,下列命题正确的是( B )(A)m∥α,n∥β,且α∥β,则m∥n(B)m⊥α,n⊥β,且α⊥β,则m⊥n(C)m⊥α,n⊂β,m⊥n,则α⊥β(D)m⊂α,n⊂α,m∥β,n∥β,则α∥β解析:对于选项A,m与n可能平行也可能异面、相交,对于选项C,平面α与β可能平行,也可能相交不垂直,对于选项D,只有m与n是相交直线时才有α∥β,故选B.6.(2013杭州模拟)函数y=sin(x+)+cos(-x)的最大值为( C )(A)(B)(C)(D)解析:因为y=sin(x+)+cos(-x)=cos x+cos x+sin x=cos x+sin x,所以函数的最大值为===.7.(2013淮北市高三二模)已知数列{an }是等差数列,an>0.若2lg a2=lg a1+lg a4,则的值是( B ) (A)(B)1或(C)(D)1或解析:设数列{an }的首项为a1,公差为d.由2lg a2=lg a1+lg a4知=a1a4,即(a1+d)2=a1(a1+3d),解得d=0或d=a1. 当d=0时,=1,当d=a1时,an=na1,于是==.故选B.8.(2013潍坊模拟)在锐角△ABC中,角A、B、C所对的边分别为a、b、c,若b=2,B=,且sin 2A+sin(A-C)=sin B,则△ABC的面积等于( C )(A)2 (B) (C) (D)2解析:∵sin 2A=sin B-sin(A-C),∴2sin Acos A=sin(A+C)-sin(A-C),∴2sin Acos A=2cos Asin C.∵△ABC是锐角三角形,∴cos A≠0,∴sin A=sin C,即A=C=B=,∴S△ABC=³2³2³=.9.△ABC中,∠B=60°,AB=3,∠ABC的角平分线BD交AC于点D,设=x+(x∈R),则||等于( B )(A)(B)2 (C)3 (D)无法确定解析:如图,过点D作DE∥BC,DF∥AB,则四边形DEBF为菱形.且=+,又=x+,所以=.由于==,AB=3,所以AE=1,于是BF=DF=2.△BFD中由余弦定理知|BD|=2.故选B.10.已知R上的增函数f(x)=1+x-+-+…+,设F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,圆x2+y2=b-a的面积的最小值是( A ) (A)π(B)2π (C)3π (D)4π解析:因f(x)为R上的增函数,且f(0)=1>0,f(-1)=(1-1)+(--)+…+(--)<0,∴函数f(x)的唯一零点在[-1,0]内,函数F(x)=f(x+4)的唯一零点在[-5,-4]内.由题意可知,b-a的最小值为1,∴圆x2+y2=b-a的面积的最小值为π.故选A.二、填空题11.(2013豫东、豫北十所名校联考)如果实数x,y满足条件那么目标函数z=2x-y的最小值为.解析:作不等式组所表示的平面区域如图中阴影部分所示,易知当直线z=2x-y经过点A时,z有最小值.由解得A(-2,-1),所以zmin=2³(-2)-(-1)=-3.答案:-312.(2013聊城模拟)若某空间几何体的三视图如图所示,则该几何体的体积是.解析:由三视图可知该几何体是放倒的三棱柱,三棱柱的高为,三角形的两直角边分别为1,,所以三棱柱的体积为³1³³=1.答案:113.(2013海南模拟)已知数列{an }的首项a1=1,其前n项和Sn=n2²an(n∈N*),则a9= .解析:由Sn =n2²an可知,当n≥2时有Sn-1=(n-1)2an-1,两式相减可得an =n2an-(n-1)2an-1,于是=,于是a9=²²…²²a1=³³³³…³³1=.答案:14.(2013温岭中学模拟)在△ABC中,若BC=4,cos B=,则²的最小值为.解析:在△ABC中,设角A、B、C所对的边分别为a、b、c,²=²(+)=c2+4c³(-)=c2-c=(c-)2-≥-,故当c=时,取最小值-.答案:-15.若函数f(x)=a x(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)在[0,+∞)上是增函数,则a= .解析:若a>1,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-为减函数,不合题意.若0<a<1,有a-1=4,a2=m,故a=,m=,检验知符合题意.答案:16.(2013浙江嘉兴模拟)若关于x的不等式x2+ax-2>0在区间[1,5]上有解,则实数a的取值范围为.解析:由x2+ax-2>0可得a>-x,令g(x)=-x,则函数g(x)在[1,5]上单调递减,所以g(x)在[1,5]的最小值g(x)min=g(5)=-,因此当不等式有解时,a的取值范围是a>-.答案:a>-17.(2013抚顺模拟)已知椭圆+=1(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线y2=(a+c)x与椭圆交于B、C两点,若四边形ABFC是菱形,则椭圆的离心率是.解析:由于四边形ABFC是菱形,所以BC与AF垂直,且经过AF的中点(,0),因此B、C两点的横坐标均为,又因为抛物线过B、C两点,可求得B(,b),而B点也在椭圆上,故+=1,整理得4c2-8ac+3a2=0,即4e2-8e+3=0,解得e=,e=(舍去).答案:选择、填空题训练(三)【选题明细表】知识点、方法题号集合与常用逻辑用语1、2平面向量8不等式14函数3、10、17三角函数与解三角形5、11数列7、13立体几何6、12解析几何4、9、15、16一、选择题1.已知集合A={(x,y)|x,y为实数,且x2+y2=1},B={(x,y)|x,y为实数,且y=x},则A∩B的元素个数为( C )(A)0 (B)1 (C)2 (D)3解析:法一A为圆心在原点的单位圆,B为过原点的直线,故直线与圆有2个交点.故选C.法二由可得或故选C.2.(2014温州一模)设a,b∈(0,+∞),则“a-b>1”是“a2-b2>1”的( A )(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件解析:若a-b>1,则(a-b)(a+b)>1,反之若a2-b2>1,则a-b>1不一定成立,如()2-()2>1,而-1<1.所以a-b>1是a2-b2>1的充分不必要条件.故选A.3.若lg a+2a=lg b+3b,则正实数a,b的大小关系是( A )(A)a>b (B)a≥b (C)a<b (D)a≤b解析:因为lg a+2a=lg b+2b+b,由于b>0,所以lg a+2a>lg b+2b,而函数f(x)=lg x+2x在(0,+∞)上单调递增,所以a>b.4.(2014浙江省“六市六校”联考)已知F1,F2分别是椭圆的左,右焦点,现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,若过F1的直线MF1是圆F2的切线,则椭圆的离心率为( A ) (A)-1 (B)2-(C)(D)解析:由题意知MF2⊥MF1,|MF2|=c,|F1F2|=2c,|MF1|=c,由椭圆定义知|MF1|+|MF2|=(+1)c=2a,因此椭圆的离心率为=-1.故选A.5.(2013嘉兴市高三二模)函数y=cos 2x+sin 2x,x ∈R 的值域是( A ) (A)[0,1] (B)[,1] (C)[-1,2] (D)[0,2] 解析:y=cos 2x+sin 2x =cos 2x+=cos 2x+,因为cos 2x ∈[-1,1], 所以y=cos 2x+∈[0,1].故选A.6.(2014温州一模)m 是一条直线,α,β是两个不同的平面,以下命题正确的是( D )(A)若m ∥α,α∥β,则m ∥β (B)若m ∥α,m ∥β,则α∥β (C)若m ∥α,α⊥β,则m ⊥β (D)若m ∥α,m ⊥β,则α⊥β 解析:A 中可能有m ⊂β,不正确; B 中,α,β可能相交; C 中,可能有m ∥β. 故选D.7.(2014温州期末)设等差数列{a n }的前n 项和为S n ,若S 6>S 7>S 5,则满足S n S n+1<0的正整数n 的值为( C ) (A)10 (B)11 (C)12 (D)13解析:由S 6>S 7>S 5得a 6>0,a 7<0,a 6+a 7>0, 所以S 11=³11=11a 6>0,S 12=²12=6(a 6+a 7)>0,S 13=²13=13a 7<0,则S 12²S 13<0,n=12. 故选C.8.(2012浙江温州质检)已知在△ABC 中,AB=AC=4,BC=4,点P 为边BC 所在直线上的一个动点,则关于²(+)的值,下列选项正确的是( B )(A)最大值为16 (B)为定值8(C)最小值为4 (D)与P的位置有关解析:设BC的中点为O,则AO⊥BC且AO2=AB2-(BC)2=4,∴²(+)=2²=2²||²||cos∠PAO=2²||(||cos∠PAO)=2||2=8.故选B.9.(2013日照模拟)在平面直角坐标系xOy中,抛物线C:y2=2px(p>0)的焦点为F,M 是抛物线C上的点,若△OFM的外接圆与抛物线C的准线相切,且该圆面积为9π,则p等于( B )(A)2 (B)4 (C)6 (D)8解析:外接圆的面积为9π,所以外接圆的半径为3,又△OFM的外接圆的圆心一定在线段OF的垂直平分线上,故外接圆圆心的横坐标是,又因为△OFM的外接圆与抛物线C的准线相切,所以外接圆的半径为+==3,解得p=4.10.(2013邯郸市高三一模)已知f(x)=且函数y=f(x)-1恰有3个不同的零点,则实数a的取值范围是( D )(A)(-1,+∞) (B)(-2,0](C)(-2,+∞) (D)(0,1]解析:y=f(x)-1=即y=f(x)-1=作出函数图象如图,可知当x>0时,函数有一个零点x=1;要使函数恰有3个零点,则当x≤0时,函数图象应与x轴有两个交点,则有即解得0<a≤1.故选D.二、填空题11.(2014宁波高三期末)△ABC中,a,b,c分别为角A,B,C的对边,若=+,且2abcos C=c2,则m的值为.解析:由=+得msin Asin Bcos C=sin2C,由正弦定理得mabcos C=c2,所以m=2.答案:212.(2014宁波二模)已知某锥体的三视图(单位:cm )如图所示,则该锥体的体积为.解析:由三视图知几何体为四棱锥,高为2 cm,底面是直角梯形.两底分别为1 cm,2 cm,高为2 cm,于是锥体体积为³2³³(1+2)³2=2 cm3. 答案:2 cm313.(2013宁波市高考适应性考试)已知等比数列{an }的前n项和为Sn,若a 2a8=2a3a6,S5=-62,则a1的值是.解析:设等比数列{an}的公比为q, 则q≠0,由a2a8=2a3a6知a 2a6q2=2a2qa6,∴q=2.由S5==-62,解得a1=-2.答案:-214.(2014温州一模)若不等式组表示的平面区域是三角形,则实数k的取值范围是.解析:x+y-1=0与x-2y-1=0如图.kx+y+1=0为过(0,-1)的直线,当k>0时,若满足题意,则-k>-1,得k<1,当k<0时,若满足题意,则-k<得k>-.又k=0时,满足题意,综上-<k<1.答案:(-,1)15.(2013深圳模拟)已知双曲线的两条渐近线均和圆C:(x-1)2+y2=相切,且双曲线的右焦点为抛物线y2=4x的焦点,则该双曲线的标准方程为.解析:抛物线y2=4x的焦点为(,0),故双曲线焦点在x轴上,设其方程为-=1(a>0,b>0),则c=.一条渐近线方程为y=x,即bx-ay=0,所以=,解得b=1,a2=4,故双曲线的标准方程为-y2=1.答案:-y2=116.(2014嘉兴二模)已知集合A={f(x,y)=0|f(x,y)=(x-a)2+(y-a)2-,a=±1,±2,±3},B={g(x,y)=0|g(x,y)=x+y-b,b=±1,±2,±3},则A中方程的曲线与B中方程的曲线的交点个数是.解析:a=1,2,3时, f(x,y)=0表示圆,C1:(x-1)2+(y-1)2=,C2:(x-2)2+(y-2)2=2,C3:(x-3)2+(y-3)2=,圆C2经过圆C1,圆C3的圆心,b=1,2,3时,g(x,y)=0表示一组平行直线, l1:x+y-1=0,l2:x+y-2=0,l3:x+y-3=0,直线l1,l2,l3分别与圆C1,C2,C3相切,于是直线l1,l2,l3与三个圆C1,C2,C3共有1+3+3=7个交点,由对称性知A中方程的曲线与B中方程的曲线有7³2=14个交点. 答案:1417.(2013浙江五校联盟高三第二次联考)已知正实数x,y满足ln x+ln y=0,且k(x+2y)≤x2+4y2恒成立,则k的取值范围是.解析:法一由ln x+ln y=0可得xy=1,且x>0,y>0,由k(x+2y)≤x2+4y2可得k≤==(x+2y)-,.令m=x+2y,则k≤(m-)min因为m=x+2y≥2=2,且f(m)=m-在[2,+∞)上单调递增,所以m=2时,(m-)=2-=,min所以k≤.法二由ln x+ln y=0,知xy=1,且x>0,y>0,令t=x+2y≥2=2,因此t2-kt-4≥0对t∈[2,+∞)恒成立,记f(t)=t2-kt-4,则f(2)=4-2k≥0⇒k≤.答案:k≤选择、填空题训练(四)【选题明细表】知识点、方法题号集合与常用逻辑用语1、7不等式8、14函数12、16、17三角函数与解三角形6、10、11数列3、13立体几何4、5、15解析几何2、9、14一、选择题1.(2014高考广东卷)已知集合M={-1,0,1},N={0,1,2},则M∪N等于( C )(A){0,1} (B){-1,0,2}(C){-1,0,1,2} (D){-1,0,1}解析:M∪N={-1,0,1,2}.故选C.2.(2013潍坊模拟)已知椭圆方程是+=1,双曲线-=1(a>0,b>0)的焦点是椭圆的顶点,顶点是椭圆的焦点,则双曲线的离心率为 ( C )(A)(B)(C)2 (D)3解析:椭圆的右焦点为(1,0),右顶点为(2,0),即双曲线中a=1,c=2,所以双曲线的离心率为e===2,选C.3.(2014温州二模)已知等比数列{an}的各项均为正数,对k∈N*,ak ak+5=a,ak+10ak+15=b,则ak+15ak+20等于( B )(A)(B)(C)(D)解析:设{an}的公比为q,b=ak+10ak+15=akq10²ak+5q10=aq20,∴q10=,∴ak+15ak+20=akq15²ak+5q15=aq30=a()3=.故选B.4.(2014宁波高三期末)正三棱柱ABC A1B1C1中,AB=2,AA1=,则三棱锥C ABC1的体积为( A )(A)1 (B )3 (C) (D)解析:==S△ABC ²AA1=³³22³=1.故选A.5.(2014浙江建人高复模拟)设b、c表示两条直线,α、β表示两个平面,下列命题中真命题是( C )(A)若b⊂α,c∥α,则b∥c (B)若b⊂α,b∥c,则c∥α(C)若c∥α,c⊥β,则α⊥β(D)若c∥α,α⊥β,则c∥β解析:选项A中b,c可能异面;B中c可能在α内;对于C,由c∥α可知α内存在a ∥c,又由c⊥β得a⊥β,从而α⊥β,即C正确;D中c与β位置关系不确定.故选C.6.(2014高考新课标全国卷Ⅱ)钝角三角形ABC的面积是,AB=1,BC= ,则AC等于( B )(A)5 (B)(C)2 (D)1解析:由S=acsin B得△ABC³³1³sin B=,∴sin B=,cos B=±,∴若cos B=-,由余弦定理得AC===.若cos B=,则AC=1,此时△ABC为直角三角形不合题意.故选B.7.(2013昆明模拟)非零向量a,b使得|a+b|=|a|-|b|成立的一个充分非必要条件是( B )(A)a∥b (B)a+2b=0(C)=(D)a=b解析:要使|a+b|=|a|-|b|,则a,b 共线,且方向相反,且|a|>|b|, 故选B.8.(2013高考新课标全国卷Ⅱ)已知a>0,x,y 满足约束条件若z=2x+y的最小值为1,则a 等于( B ) (A)(B)(C)1(D)2解析:由已知约束条件,作出可行域如图中△ABC 内部及边界部分,由目标函数z=2x+y 的几何意义为直线l:y=-2x+z 在y 轴上的截距,知当直线l 过可行域内的点B(1,-2a)时,目标函数z=2x+y 的最小值为1,则2-2a=1,a=.故选B.9.(2013高考山东卷)抛物线C 1:y=x 2(p>0)的焦点与双曲线C 2:-y 2=1的右焦点的连线交C 1于第一象限的点M.若C 1在点M 处的切线平行于C 2的一条渐近线,则p 等于( D ) (A) (B) (C)(D)解析:如图在同一坐标系中画出C 1、C 2草图,知C 1焦点F(0,),C 2右焦点F 2(2,0).由C 2渐近线方程为y=±x.直线FF 2方程为+=1.联立C1与直线FF2方程得①代入②得2x2+p2x-2p2=0.设M(x0,y),即2+p2x-2p2=0. ③由C1得y′=x,所以x0=,即x=p. ④由③④得p=.故选D.10.(2013西安模拟)在△ABC中,角A、B、C所对的边分别为a、b、c且2b>2a,logsin2b<logsin 2c,b2+c2=a2+bc,若²<0,则cos B+sin C的取值范围是( D )(A)(B)(C)(D)解析:由已知得b>a,b>c.因为b2+c2=a2+bc,cos A===,所以A=,B+C=π-=,因为b>c,所以B>C,即=B+C<B+B=2B,所以B>.因为²<0,所以²=||²||cos (π-B)=-||²||cos B<0,所以cos B>0,所以<B<.又因为cos B+sin C=cos B+sin =cos B+sin B=sin ,因为<B<,所以<B+<,故sin <sin <sin ,即<sin <,所以<sin <.即cos B+sin C的取值范围是.故选D.二、填空题11.(2013浙江高三五校联考)已知α∈[,π],sin α=,则sin 2α= .解析:∵α∈[,π],sin α=,∴cos α=-=-,∴sin 2α=2sin αcos α=2³³(-)=-.答案:-(x+3),则12.(2013嘉兴市高三一模)已知奇函数f(x),当x>0时,f(x)=log2f(-1)= .(1+3)=2.解析:依题意,f(1)=log2又f(x)为奇函数,∴f(-1)=-f(1)=-2.答案:-213.(2013浙江金华十校联考)已知数列{an }是公差为1 的等差数列,Sn是其前n项和,若S8是数列{Sn}中的唯一最小项,则数列{an}的首项a1的取值范围是.解析:依题意应有即解得-8<a1<-7.答案:(-8,-7)14.(2014温州期末)设抛物线y2=4x的焦点为F,过F的直线交该抛物线于A,B两点,则|AF|+9|BF|的最小值为 .解析:设A(x1,y1),B(x2,y2),当AB垂直于x轴时可得|AF|+9|BF|=20, 当AB不垂直于x轴时,设AB方程为y=k(x-1)代入y2=4x整理得k2x2-(2k2+4)x+k2=0,∴x1x2=1,∴|AF|+9|BF|=10+x1+9x2=10++9x2≥16,当且仅当x1=x2时等号成立.答案:1615. (2014杭州二中)已知正四面体的俯视图如图所示,其中四边形ABCD是边长为2的正方形,则这个正四面体的体积为.解析:该四面体为棱长为2的正方体被切去“四个角”(如图)后剩余的部分,其体积V=8-4³³³23=.答案:16.(2014宁波高三十校联考)已知正实数a、b满足2a+b=1,则4a2+b2+的最小值为.解析:4a2+b2+=(2a+b)2-4ab+=1-4ab+,又1=2a+b≥2,1≥8ab,即0<ab≤,而函数y=1-4x+为(0,+∞)上的减函数.于是1-4ab+的最小值为1-+8=.答案:17.(2013温州市高三一模)方程(x-1)sin πx=1在(-1,3)上有四个不同的根x 1,x2,x3,x4,则x1+x2+x3+x4= .解析:显然x-1≠0,∴方程(x-1)²sin πx=1可化为sin πx=,设y1=sin πx,y2=.在同一坐标系内作出y1,y2的大致图象如图所示.可知四交点关于点(1,0)对称,所以x1+x2+x3+x4=4.答案:4选择、填空题训练(五)【选题明细表】知识点、方法题号集合与常用逻辑用语1、3平面向量5、9不等式 4函数10、15、17 三角函数与解三角形2、11、12数列7、16立体几何8、14解析几何6、13一、选择题B等于( A ) 1.(2014嘉兴二模)已知集合A={x|x≤2},B={x|x2<4x},则A∩∁R(A)(-∞,0] (B)(-∞,0)(C)[-1,1] (D)(0,2)B={x|x≤0或x≥4},解析:B={x|0<x<4},∁RB={x|x≤0}.故选A.∴A∩∁R2.(2013济宁模拟)将函数 f(x)=sin的图象向右平移个单位后,所得的图象对应的解析式为( D )(A)y=sin 2x (B)y=cos 2x(C)y=sin(D)y=sin解析:将函数f(x)=sin的图象向右平移个单位得到y=sin=sin,选D.3.(2014宁波期末)“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的( C )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件解析:当m>n>0时,0<<,方程+=1表示焦点在y轴上的椭圆;反之,当方程+=1表示焦点在y轴上的椭圆时,>>0,即m>n>0.故选C.4.(2014高考新课标全国卷Ⅱ)设x,y满足约束条件,则z=2x-y的最大值为( B )(A)10 (B)8 (C)3 (D)2解析:画出可行域如图所示,目标函数z=2x-y斜率为k=2,如图当直线过点A(5,2)时,z最大,=2³5-2=8.∴zmax故选B.5.(2013浙江杭州模拟)如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+等于( C )(A)(B)(C)(D)解析:如图,以OP、OQ为邻边作平行四边形OPMQ,则+=.由图知=,故选C.6.(2013温州市高三一模)已知椭圆+=1的一个焦点与抛物线y2=8x的焦点重合,则该椭圆的离心率为( B )(A)(B)(C)(D)解析:抛物线的焦点为(2,0),依题意,椭圆中c=2.∴a2=b2+c2=12+4=16,∴a=4.∴离心率e==.故选B.}是首项为1的等比数列,若{}是等差7.(2013杭州市高三二模)设数列{an数列,则(+)+(+)+…+(+)的值等于( C )(A)2015 (B)2018 (C)3021 (D)3023}的公比为q,解析:设等比数列{an∵{}是等差数列.∴+=,即+=,∴q2-2q+1=0.解得q=1,=1,∴an∴(+)+(+)+…+(+)==³2014=3021.故选C.8.(2014瑞安调研)已知a,b,c为三条不同的直线,且a⊂平面M,b⊂平面N,M∩N=c.①若a与b是异面直线,则c至少与a、b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有M⊥N.其中正确的命题的个数是( C )(A) 0 (B) 1 (C) 2 (D) 3解析:若c与a,b都不相交,又c与a共面,c与b共面,则c∥a,c∥b,于是a∥b 与a,b异面矛盾,即①正确;②不正确,如b⊥c,a∥c,则a⊥b;③正确,由a∥b可得a∥N,又a⊂M,M∩N=c,所以a∥c;④不正确,当b∥c时,不一定有M⊥N.故选C.9.(2014杭州二中)平面向量a,b,e 满足|e|=1,a ²e=1,b ²e=2,|a-b|=2,则a ²b 的最小值为( B ) (A)1(B)(C)2(D)4解析:由a ²e=1,b ²e=2得(a+b)²e=3,设a+b 与e 的夹角为θ,则|a+b|=,所以a ²b=-=-1=-1≥,当且仅当cos 2θ=1时取等号.故选B.10.(2013烟台模拟)定义域为R 的偶函数f(x)满足对∀x ∈R,有f(x+2)=f(x)-f(1),且当x ∈[2,3] 时,f(x)=-2x 2+12x-18,若函数y=f(x)-log a (|x|+1)在(0,+∞)上至少有三个零点,则a 的取值范围是( B ) (A)(B)(C) (D)解析:令x=-1,由题意知f(-1+2)=f(-1)-f(1), 即2f(1)=f(-1),又f(-1)=f(1),∴f(1)=0.故对任意x ∈R 有f(x+2)=f(x). 设x ∈[1,2],则4-x ∈[2,3],由于x ∈[2,3]时f(x)=-2x 2+12x-18=-2(x 2-6x+9)=-2(x-3)2,因此f(4-x)=-2(x-1)2,∴f(x)=f(-x)=f(4-x)=-2(x-1)2.因此可画出函数y=f(x)的草图如图所示.令y=g(x)=log a (|x|+1),函数y=f(x)-log a (|x|+1)在(0,+∞)上至少有三个零点,即函数f(x)与g(x)的图象在(0,+∞)上至少有三个交点,当x>0时,g(x)=log a (|x|+1)=log a (x+1),过定点(0,0).由图象可知当a>1时,不成立.所以0<a<1.因为f(2)=-2,所以要使两函数图象至少有三个交点,则有g(2)>-2,即g(2)=log a 3>-2=log a a -2,所以3<a -2,即a 2<,所以0<a<,即a 的取值范围是,故选B.二、填空题11.在△ABC中,角A、B、C所对的边分别为a,b,c,已知2a-b=2ccos B,则角C= .解析:由余弦定理及条件知2a-b=2c²,整理得a2+b2-c2=ab,所以cos C=.又C∈(0,π),所以C=.答案:12.(2013嘉兴模拟)在△ABC中,已知a,b,c分别为∠A,∠B,∠C所对的边,S为△ABC的面积.若向量p=(4,a2+b2-c2),q=(1,S)满足p∥q,则∠C= .解析:因为p∥q,所以4S=a2+b2-c2,由三角形的面积公式和余弦定理得4³absinC=2abcos C,所以sin C=cos C,所以∠C=.答案:13.(2013高考辽宁卷)已知F为双曲线C:-=1的左焦点,P,Q为C上的点,若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为. 解析:由题意,双曲线C:-=1的左焦点F(-5,0),所以点A(5,0)是双曲线的右焦点,虚轴长为8.从而|PQ|=16.由双曲线定义及题意知|PF|-|AP|=2a=6 ① |QF|-|QA|=2a=6 ② ①+②得:|PF|+|QF|-|PQ|=12, ∴△PQF 的周长为|PF|+|QF|+|PQ|=12+2|PQ|=44. 答案:4414.(2014乐清模拟)一个空间几何体的三视图如图所示,其中正视图和侧视图都是半径为1的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为 .解析:该几何体为半径为1的球,被从直径出发的两个半平面切去后剩余的部分,表面积S=S 球面+2S 半圆=³4π+π=4π. 答案:4π15.(2013浙江宁波模拟)设函数f(x)=若函数g(x)=f(x)-ax,x ∈[-2,2]为偶函数,则实数a 的值为 . 解析:由已知得g(x)=当-2≤x ≤0时,-x ∈[0,2]. 所以g(-x)=-x-1+ax.由于g(x)是偶函数,因此有-1-ax=-x-1+ax. 解得a=.答案:16.(2013浙江省湖州模拟)已知数列{a n }满足a 1=1,(2n+5)a n+1-(2n+7)a n =4n 2+24n+35(n ∈N *),则数列{a n }的通项公式为 .解析:由已知得-=1,所以{}是公差为1的等差数列,于是=+(n-1),整理得a=.n=(n∈N*)答案:an17.(2013茂名二模)设函数f(x)的定义域为D,若存在非零实数l使得对于任意x ∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上l高调函数.现给出下列命题:①函数f(x)=lo x为(0,+∞)上l高调函数;②函数f(x)=sin x为R上的2π高调函数;③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上m高调函数,那么实数m的取值范围是[2,+∞).其中正确的命题的序号为.解析:①中f(x)为减函数,故不可能是(0,+∞)上l高调函数;②中,f(x+2π)=f(x),故②正确;由f(x)=x2(x≥-1)的图象(图略)可知,要使得f(-1+m)≥f(-1)=1,有m≥2,x≥-1时,恒有f(x+2)≥f(x),故m≥2即可,③正确.答案:②③选择、填空题训练(六)【选题明细表】知识点、方法题号集合与常用逻辑用语1、2、11平面向量17不等式12、16函数5、9、10三角函数与解三角形6、7数列3、14立体几何4、13解析几何8、15一、选择题B等于1.(2014嘉兴一模)已知集合A={x|x2-2x<0},B={x≤-1或x>1},则A∩∁R( C )(A){x|0<x<1} (B){x|1≤x<2}(C){x|0<x≤1} (D){x|1<x<2}解析:A={x|0<x<2},∁RB={x|-1<x≤1},∴A∩∁RB={x|0<x≤1}.故选C.2.(2013浙江名校联盟高三联考)已知a,b为两个非零向量,则“a∥b”是“|a|=|b|”成立的( D )(A)充分不必要条件(B)必要不充分条件(C)充要条件 (D)既不充分又不必要条件解析:非零向量a∥b|a|=|b|,反之|a|=|b|a∥b.因此“a∥b”是“|a|=|b|”成立的既不充分又不必要条件.故选D.3.(2013浙江六校联考)已知数列{an }为等比数列,a4+a7=2,a5²a6=-8,则a1+a10的值为( D )(A)7 (B)-5 (C)5 (D)-7 解析:由于{an}是等比数列,所以a5²a6=a4²a7=-8,又a4+a7=2.因此a4=-2,a7=4或a4=4,a7=-2,设等比数列{an}公比为q, 则q3=-2或q3=-因此有a1=1,a10=-8或a1=-8,a10=1,故a1+a10=-7,故选D.4.(2014嘉兴高三期末)已知α,β是两个不同平面,a,b是两条不同直线,且a∥α,b⊥β,则下列说法正确的是( D )(A)若a⊥b,则α∥β(B)若a⊥b,则α⊥β(C)若α⊥β,则a∥b (D)若α∥β,则a⊥b解析:当a⊥b时, α与β可能平行,也可能相交,因此A、B都不正确;C中a与b 平行、相交、异面都可能;若α∥β,则由b⊥β可得b⊥α,又a∥α,可得a⊥b,即D正确.故选D.5.(2014宁波高三十校联考)已知函数f(x)=则f(2014)的值为( D )(A)(B)2 (C)-(D)-2解析:x>1时,f(x)=-f(x-3),因此x>1时,f(x)是以6为最小正周期的周期函数,f(2014)=f(6³335+4)=f(4)=-f(1)=-2.故选D.6.(2013韶关市高三调研)△ABC中,角A、B、C所对的边为a、b、c, 若a=3,C=120°,△ABC面积S=,则c等于( D )△ABC(A)5 (B)6 (C) (D)7=.∴absin C=,解析:∵S△ABC即³3³b³sin 120°=,∴b=5.在△ABC中,由余弦定理得,c2=a2+b2-2abcos C=32+52-2³3³5³cos 120°=49.∴c=7.故选D.7.(2013烟台模拟)当x=时,函数f(x)=Asin (x+ϕ)(A>0)取得最小值,则函数y=f是( C )(A)奇函数且图象关于点对称(B)偶函数且图象关于点(π,0)对称(C)奇函数且图象关于直线x=对称(D)偶函数且图象关于点对称解析:当x=时,函数f(x)=Asin (x+ϕ)(A>0)取得最小值,即+ϕ=-+2kπ,k∈Z,即ϕ=-+2kπ,k∈Z,所以f(x)=Asin(A>0),所以y=f=Asin=-Asin x(A>0),所以函数为奇函数且图象关于直线x=对称, 故选C.8.点P在双曲线-=1(a>0,b>0)上,F1,F2是双曲线的两个焦点,∠F1PF2=90°,且△F1PF2的三条边长成等差数列,则此双曲线的离心率是( D )(A)(B)(C)2 (D)5解析:不妨设点P在双曲线的右支上,且F1,F2分别为双曲线的左、右焦点,设|PF1|=r1,|PF2|=r2,则由双曲线的定义,可得r1-r2=2a,由已知,可得2r1-r2=2c.解得r1=2c-2a,r2=2c-4a.因为+=4c2,所以将r1=2c-2a,r2=2c-4a代入上式且两边同除以a2,得e2-6e+5=0,解得e=1或e=5. 又e>1,所以e=5. 故选D.9.(2014温州一模)对于函数f(x)=4x-m²2x+1,若存在实数x0,使得f(-x)=-f(x)成立,则实数m的取值范围是( B ) (A)m≤(B)m≥(C)m≤1 (D)m≥1解析:由题意知,存在x满足-m²=-+m²,即m=(+-),令t=+∈[2,+∞),即m=(t-),t∈[2,+∞), 则m∈[,+∞).故选B.10.(2013温州市高三一模)若实数a、b、c满足loga 2<logb2<logc2,则下列关系中不可能成立的是( A ) (A)a<b<c (B)b<a<c (C)c<b<a (D)a<c<b解析:由题意知,a、b、c均为不为1的正数,不等式loga 2<logb2<logc2等价于<<.①若log2a,log2b与log2c均大于0,则a>b>c>1.②若log2a<0,log2b>0,log2c>0,则0<a<1<c<b.③若log2a<0,log2b<0,log2c>0,则0<b<a<1<c.④若log2a<0,log2b<0,log2c<0,则1>a>b>c>0.综上知选项B、C、D均有可能.故选A.二、填空题11.命题p:∃x∈(0,),使得cos x≤x,则命题﹁p为: .解析:命题p是一个特称命题,其否定是一个全称命题.因此﹁p为:∀x∈(0,),使得cos x>x.答案:∀x∈(0,),使得cos x>x12.(2013河南省普通高中新课程高考适应性考试)已知x,y满足则z=x-3y的最大值是.解析:作出不等式组所表示的可行域,如图中阴影部分所示,作出直线y=x-z,可知当直线经过点B 时,z 有最大值.由可解得B(2,1).∴z max =x-3y=2-3³1=-1. 答案:-113.(2014温州中学模拟)在三棱锥D ABC 中,AC=BC=CD=2, CD ⊥平面ABC,∠ACB=90°.若其正视图,俯视图如图所示,则其侧视图的面积为 .解析:由题意可知,其侧视图是两直角边分别为2和的直角三角形,面积S=.答案:14.(2014杭州二中)在等差数列{a n }中,a 1>0,a 10²a 11<0,若此数列的前10项和S 10=36,前18项和S 18=12,则数列{|a n |}的前18项和为 . 解析:由a 1>0,a 10²a 11<0可知n ≤10时,a n >0, 当n ≥11时a n <0,所以|a 1|+|a 2|+…+|a 18|=a 1+a 2+…+a 10-(a 11+a 12+…+a 18) =S 10-(S 18-S 10) =2S 10-S 18 =72-12 =60. 答案:6015.抛物线y 2=8x 的焦点为F,点P(x,y)为该抛物线上的动点,又点A(-2,0),则的最大值是 .解析:由抛物线的定义,可得|PF|=x+2, 又|PA|==,所以===.当x=0时,=1;当x≠0时,=.因为x+≥2=4,当且仅当x=,即x=2时取等号,故x++4≥8,0<≤1,所以∈(1,].综上,∈[1,],所以的最大值是.答案:16.(2013高考天津卷)设a+b=2,b>0,则+的最小值为. 解析:由a+b=2,b>0.则+=+=++,由a≠0,若a>0,则原式=++≥+2=.当且仅当b=2a=时,等号成立.若a<0,则原式=---≥-+2=.当且仅当b=-2a即a=-2,b=4时等号成立.综上得当a=-2,b=4时,+取最小值.答案:17.(2013浙江龙游中学高三期中)已知向量a,b,c,满足|a|=|b|=a²b=2,(a-c)²(b-2c)=0,则|b-c|的最小值为.解析:设a,b夹角为θ,∵|a|=|b|=a²b=2,∴cos θ==.∴θ=,由题意不妨设=a=(2,0),c=(x,y),则=b=(1,).∵(a-c)²(b-2c)=0,∴(2-x,-y)²(1-2x,-2y)=0.∴(2-x)(1-2x)-y(-2y)=0.整理得(x-)2+(y-)2=.而|b-c|=,因此|b-c|的最小值为B(1,)与圆心(,)两点间距离与半径之差,即|b-c|=-min=.答案:选择、填空题训练(七)【选题明细表】知识点、方法题号集合与常用逻辑用语1、2平面向量14、16不等式7、10函数9、11三角函数与解三角形6、13数列5、15立体几何4、17解析几何3、8、12一、选择题1.(2014宁波模拟)设集合M=,N=,则M∩N等于( A )(A)[0,) (B)(-,1](C)[-1,) (D)(-,0]解析:N={x|0≤x≤1},∴M∩N=[0,).故选A.2.(2013浙江五校联考)下列命题是真命题的为( C )(A)若x=y,则= (B)若x2=1,则x=1。
