对角互补+角平分线模型
2022年九年级中考数学冲刺-几何模型讲义

2022年中考几何模型一、角平分线模型知识精讲1. 过角平分线上一点向角的两边作垂线段,利用角平分线上的点到角两边的距离相等的性质来解决问题2. 若题目中已经有了角平分线和角平分线上一点到一边的垂线段(距离),则作另一边的垂线段,例:已知:AD是的平分线,,过点D于点E,则.3. 在角的两边上取相等的线段,结合角平分线构造全等三角形(角边等,造全等),已知:点D是平分线上的一点,在OA、OB上分别取点E、F,且,连接DE、DF4. 过角平分线上一点作角的一边的平行线,构造等腰三角形,例:已知:点D是平分线上的一点,过点D作三角形,即.5. 有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边所在直线于一点,也可构造等腰三角形,例:已知:OC平分,点D是OA上一点,过点D作交OB的反向延长线于点E,则.6. 从角的一边上的一点作角平分线的垂线,使之与角的另一边相交,则可得到一个等腰三角形,例:已知:OE平分∠AOB,点D在OA上,DE⊥OE,则可延长DE交OB于点F,则DE=EF,OD=OF,∠ODF=∠OFD.7. 有角平分线时,可将等角放到直角三角形中,构造相似三角形,也可以另加一对相等的角构造相似三角形,例:4321DA4231EFCB(1)已知:OC 平分,点E 、F 分别在OA 、OB 上,过点E M ,过点F N(2)已知:OC 平分,点E 、F 在OC 上,于点M ,于点N ,则(3)已知:OC 平分,点E 、F 在OC ,8. 利用“在同圆或等圆中,相等的圆周角(圆心角)所对的弦相等”可得相等线段,例:已知:∠BAC 是圆O 的圆周角,∠DOE 是圆O 的圆心角,AF 平分∠BAC ,OG 平分∠DOE ,连接BF 、CF 、DG 、EG ,则BF =CF ,DG =EG .9. 【内内模型】如图,两个内角平分线交于点D ,则.10. 【内外模型】如图,的一个内角平分线和一个外角平分线交于点D ,则.11. 【外外模型】如图,交于点D ,则.二、中点模型知识精讲1. 在等腰三角形中有底边中点或证明底边中点时,可以作底边的中线,利用等腰三角形的“三线合一”性质来解决问题.例:已知:在△ABC中,AB=AC,取BC的中点D,连接AD,则AD平分∠BAC,AD是边BC上的高,AD是BC边上的中线.【说明】应用等腰三角形“三线合一”的性质是证明两条直线垂直的重要方法.2. 在直角三角形中,有斜边中点或有斜边的倍分关系线段时,可以作斜边的中线解决问题,例:(1)如图,在Rt△ABC中,D为斜边AB的中点,连接CD,则CD=AD=BD.(2)如图,在Rt△ABC中,AB=2BC,作斜边AB上的中线CD,则AD=BD=CD=BC,△BCD是等边三角形.【总结】在直角三角形中,若遇到斜边的中点,则连接直角顶点与斜边的中点是解决问题的基本方法,作这条辅助线的目的是得到三条相等的线段及两对相等的角. 3. 将三角形的中线延长一倍,构造全等三角形或平行四边形(倍长中线),例:(1)如图,在△ABC中,AD为△ABC的中线,延长AD至点E,使得DE=AD,连接BE,则△ADC≌△EDB.(2)如图,在△ABC中,AD为△ABC的中线,延长AD至点E,使得DE=AD,连接BE,则四边形ABEC是平行四边形.4. 将三角形中线上的一部分延长一倍,构造全等三角形或平行四边形,例:如图,已知点E是△AD上的一点,延长AD至点F,使得DE=DF,连接BF、CF,则四边形BFCE为平行四边形或△BDF≌△CDE或△BED≌△CFD.【总结】证明两条线段相等常用的方法:①当要证明的两条线段是两个三角形的边时,一般通过证明这两条线段所在的两个三角形全等,通过三角形全等的对应边相等来证明两条线段相等;②当两条线段是同一个三角形的两条边时,一般证明这两条边所对的角相等,利用等角对等边证明两条线段相等.5. 有以线段中点为端点的线段时,可以倍长此线段,构造全等三角形或平行四边形,例:如图,已知点C边AE上一点,O为AB的中点,延长CO至点D,使得,连接AD、BD,四边形ADBC为平行四边形.6. 有三角形中线时,可过中点所在的边的两端点向中线作垂线,构造全等三角形,例:如图,AF为△ABC的中线,作BD⊥AF交AF延长线于点D,作CE⊥AF于点E,则△BDN≌△CEN.7. 在三角形中,有一边的中点时,过中点作三角形一边的平行线或把某条线段构造成中位线,利用已知的条件可求线段长,例:如图,D为AB的中点,过点D作DE∥BC,则DE为△ABC的中位线;过点B作BF∥DC 交AC的延长线于点F,则DC为△ABF的中位线.8. 有两个(或两个以上)中点时,连接任意两个中点可得三角形的中位线,例:如图,D、E、F分别为△ABC三边中点,连接DE、DF、EF,则.9. 有一边中点,并且在已知或求证中涉及线段的倍分关系时,可以取另一边的中点,构造三角形的中位线,例:如图,点E是△ABC边BC的中点,取AC的中点F,连接EF,则EF∥AB,10. 当圆心与弧(或弦)的中点,可以利用垂径定理解决问题,例:(1)如图,,连接AC、OB,则OB⊥AC,OB平分AC.(2)如图,点C为弦AB的中点,连接OC,则OC⊥AB.三、平行模型知识精讲在一些有平行线却没有截线的问题中,通常需要添加辅助线构造“三线八角”,再运用平行线的有关知识解题,常见的辅助线添加方式如下:如果遇到两条平行线之间夹折线,一般应过折点作出与已知平行线平行的直线.1. 如图,已知AB∥CD,点E为AB、CD间的一点,过点E作EF∥AB,则∠A+∠C=∠AEC.2. 如图,已知AB∥CD,则∠A+∠AEC+∠C=360°.3. 如图,AB∥CD,则∠B=∠D+∠E.4. 如图,AB∥CD,则∠BEG+∠D+∠F=180°.5. 如图,AB∥CD,则∠ABE=∠D+∠E.四、垂直模型1. 在三角形中,若题目中已经有一边的高了,常作另一边上的高,然后用同角的余角相等证明角相等.例:如图,在△ABC中,AD⊥BC于点D,过点B作BE⊥AC交AC于点E,交AD于点F,则∠CBE=∠CAD,∠AFE=∠C=∠BFD.除了能得到角度间的关系外,还可以通过构造相似三角形来证明线段成比例或者用于求线段的长度.2. 在四边形中,如果有高线,可以再作垂线,构造特殊的四边形或者直角三角形.例:如图,在四边形ABCD中,AB⊥BC,DC⊥BC,过点D作DE⊥BC,垂足为点E,则四边形BCDE为矩形,△ADE为直角三角形.3. 在直角三角形中,常作斜边上的高,利用同角(等角)的余角相等,可得到相似三角形.例:如图,在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,则∠A=∠DCB,∠B=∠ACD,△ABC∽△CBD∽△ACD.4. 若题中已有直线的垂线时,可再作已知直线的垂线,得到两条平行线.例:如图,在△ABC中,AF⊥BC于点F,过AB上一点D作DE⊥BC于点E,则DE∥AF,∠BDE=∠BAF,∠ADE+∠BAF=180°,△BDE∽△BAF.5. 若存在过一条直线上两点同时向另一条直线作垂线,可以再作一条垂线,构造一组平行线,利用平行线等分线段定理解决问题.6. 当两条互相垂直的弦的交点恰好在圆上,构成90°的圆周角,可构造直径.例:如图,点A在圆O上,∠BAC=90°,连接BC,则BC就是圆O的直径.7. 当圆中有互相垂直的弦时,经常作直径所对的圆周角,可以得到垂直于同一条直线的两条直线,利用平行弦所夹的弧相等来解决问题.例:在圆O中,弦AB⊥CD于点E,连接CO并延长交圆O于点F,连接DF,则FD⊥CD,FD∥AB,.8. 当圆中有和弦垂直的线段时,作直径所对的圆周角,可以得到直角三角形,通过相似三角形来解决问题.例:如图,△ABC内接于圆O,CD⊥AB于点D,连接CO并延长交圆O于点E,连接AE,则△ACE∽△DCB.五、对角互补模型知识精讲1. 全等型—90º如图,已知∠AOB=∠DCE=90º,OC平分∠AOB.则可以得到如下几个结论:①CD=CE,②OD+OE=OC,③2. 如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90º,OC 平分∠AOB.则可得到如下几个结论:①CD=CE,②OE-OD=OC,③.3. 全等型—60º和120º如图,已知∠AOB=2∠DCE=120º,OC平分∠AOB.则可得到如下几个结论:①CD=CE,②OD+OE=OC,③.4. 全等型—和如图,已知∠AOB=,∠DCE=,OC平分∠AOB.则可以得到以下结论:①CD=CE,②OD+OE=2OC·cos,③.5. 相似型—90º如图,已知∠AOB=∠DCE=90º,∠BOC=.结论:CE=CD·.六、半角模型知识精讲1. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则BE+DF=EF.2. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则AE平分∠BEF,AF平分∠DFE.3. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则4. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,过点A作AH⊥EF交EF于点H,则AH=AB.简证:由上述结论可知AE平分∠BEF,又∵AB⊥BC,∴AH=AB.5. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,. 简证:由结论1可得EF=BE+DF,CE+CF+EF=CE+CF+BE+DF=2AB.6. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:如图,将△AND绕点A顺时针旋90º得到△AGB,连接GM.通过证明△AMG≌△AMN得MN=MG,DN=BG,∠GBE=90º,即可证.7. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则△BME△DFN△AMN△BAN△DMA△AFE.简证:通过证明角相等得到三角形相似,要善于使用上述结论.8. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则简证:连接AC,∵∠DAF=∠EAC,∠ADB=∠ACB,∴△ECA△NDA,又∵△AMN△AFE,∴.【补充】通过面积比是相似比的平方比亦可得到9. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:由结论7可得△DAM△BNA,∴,即.10. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:设,在Rt△CEF中,,化简得,.11. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则当BE=DF时,EF.证明:如图,作△AEF的外接圆,点P为EF的中点,连接OA、OE、OF、PC,过点A作AH⊥EF.∵∠EAF=45º,∴∠EOF=90º,设,则,∴当点A、O、P、C四点共线时,即BE=DF,、EF大值.12. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N简证:由结论8可得△△ECA△NDA,同理可得补充:等腰直角三角形与“半角模型”如图所示,在等腰直角三角形ABC中,若∠DCE=45º,则.证明:如图,将△ACD绕着点C顺时针旋转90º得到△,连接.∵旋转,∴△ACD≌△,∴AD=,在△DCE与△中,ED=,∵∠BE=∠BC+∠EBC=∠DAC+∠EBC=90º,∴,.七、倍半角模型知识精讲一、二倍角模型处理方法1. 作二倍角的平分线,构成等腰三角形.例:如图,在△ABC中,∠ABC=2∠C,作∠ABC的平分线交AC于点D,则∠DBC=∠C,DB=DC,即△DBC是等腰三角形.2. 延长二倍角的一边,使其等于二倍角的另一边,构成两个等腰三角形.例:如图,在△ABC中,∠B=2∠C,延长CB到点D,使得BD=AB,连接AD,则△ABD、△ADC都是等腰三角形.二、倍半角综合1. 由“倍”造“半”已知倍角求半角,将倍角所在的直角三角形相应的直角边顺势延长即可.如图,若,则()2. 由“半”造“倍”已知半角求倍角,将半角所在的直角三角形相应的直角边截取线段即可.如图,在Rt△ABC(∠A<45º)的直角边AC上取点D,当BD=AD时,则∠BDC=2∠A,设,则,在Rt△BCD中,由勾股定理可得,解得,故有.三、一些特殊的角度1. 由特殊角30º求tan15º的值如图,先构造一个含有30º角的直角三角形,设BC=1,,AB=2,再延长CA至D,使得AD=AB=2,连接BD,构造等腰△ABD,则∠D=∠BAC=15º,.2. 由特殊角45º求tan22.5º的值由图可得,.3. “345”三角形(1)如图1,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,;(2)如图2,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,;(3)如图3,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,.八、全等模型知识精讲一、几何变换中的全等模型1. 平移全等模型,如下图:2. 对称(翻折)全等模型,如下图:3. 旋转全等模型,如下图:二、一线三等角全等模型4. 三垂直全等模型,如图:5. 一线三直角全等模型,如图:6. 一线三等角与一组对应边相等全等模型,如图:三、手拉手全等模型7. 等腰三角形中的手拉手全等模型如图,△ABC与△ADE均为等腰三角形,且∠BAC=∠DAE,连接BD、CE,则△ABD ≌△ACE.8. 等边三角形中的手拉手全等模型如图,△ABC与△CDE均为等边三角形,点B、C、E三点共线,连接AE、BD,则△BCD≌△ACE.9. 一般三角形中的手拉手全等模型如图,在任意△ABC中,以AB为边作等边△ADB,以AC为边作等边△ACE,连接DC、BE,则△ADC≌△ACE.10. 正方形中的手拉手全等模型如图,在任意△ABC中,以AB为边作正方形ABDE,以AC为边作正方形ACFG,连接EC、BG,则△AEC≌△ABG.九、相似模型知识精讲1. A字型与反A字型相似2. 8字型与反8字型相似3. 蝴蝶型相似4. 共角共边相似模型5. 一线三等角6. 旋转相似模型拓展讲解:1. 射影定理(1)双垂直,如图:结论①△ABD∽△ACB,AB2=AD·AC;②△ADC∽△ACB,AC2=AD·AB;③△CDB∽△ACB,CB2=BD·BA.(2)斜射影相似结论:△ABD∽△ACB,AB2=AD·AC.2. 对角互补相似如图,在Rt△ABC中,∠C=90º,点O是AB的中点,若∠EOF=90º,则.证明:过点O作OD⊥AC于点D,OH⊥BC于点H,如图所示:通过△ODE∽△OHF即可得到3. 三平行相似如图,AB∥EF∥CD,若,则.证明:∵EF∥AB,∴△DEF∽△DAB,∴,即①同理△BEF∽△BCD,∴,即②①+②,得,.4. 内接矩形相似如图,四边形DEFG是△ABC的内接矩形,EF在BC边上,D、G分别在AB、AC边上,则△ADG∽△ABC,△ADN∽△ABM,△AGN∽△ACM,.十、倍长中线模型知识精讲1. 如图,在矩形ABCD中,若BD=BE,DF=EF,则AF⊥CF.2. 如图,四边形ABCD是平行四边形,BC=2AB,M为AD的中点,CE⊥AB于点E,则∠DME=3∠AEM.3. 如图,△ADE与△ABC均为等腰直角三角形,且EF=CF,求证(1)DF=BF;(2)DF⊥BF.4. 如图,△OAB∽△ODC,∠OAB=∠ODC=90º,BE=EC,求证:(1)AE=DE;(2)∠AED=2∠ABO.十一、弦图模型知识精讲1. 证法一以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于2. 证法二以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于3. 证法三以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于4. 证法四如图所示,分别以a、b为直角边,以c为斜边的四个直角三角形全等,图中3个正方形的边长分别为a、b、c,整个图形的面积为S5. 证法五分别以a、b为直角边,以c为斜边的四个直角三角形全等,将它们按如图所示拼成一个多边形,并延长AC交DF于点P.。
中考数学全等三角形的五种模型

结论
①△ABF≌△BCE; ②EC=AB-FC
模型应用
7. (2016·深圳改编)如图,CB=CA,∠ACB= 90°,点D在边BC上(与B,C不重合),四边 形ADEF为正方形,过点F作FG⊥CA,交CA 的延长线于点G,连接FB,交DE于点Q,给 出以下结论:①AC=FG;②S△FAB∶S四边形 CBFG=1∶2;③∠ABC=∠ABF. 其中正确的结论的个数是( )
∵∠1=∠2,AD⊥FG于D,AH⊥EF于H, ∴AD=AH, ∵AD=AB, ∴AH=AB, 又∵AH⊥EF于H,AB⊥BC于B, ∴AE平分∠BEF,故①正确; ∵AE平分∠BEF, ∴∠AEB=∠AEH, ∵∠AEB+∠BAE=90°,
∠AEH+∠HAE=90°, ∴∠BAE=∠HAE,
又∵EH⊥AH于H,EB⊥AB于B, ∴BE=HE, ∵BE=DG, ∴HE=DG, ∵EF=HE+FH,GF=DG+FD,EF=GF, ∴FH=FD,故②正确; ∵△AEF≌△AGF, ∴S△EAF=S△GAF. ∵△ABE≌△ADG,
叠到DF,延长EF交AB于G,连接DG,现在
有如下4个结论:
①△ADG≌△FDG;②GB=2AG;③∠GDE
=45°;④DG=DE.
在以上4个结论中,正确的共有
()
A. 1个
B. 2 个
C. 3 个
D. 4个
3. C 解析:由折叠可知,DF=DC=DA,∠DFE= ∠C=90°, ∴∠DFG=∠A=90°, ∴△ADG≌△FDG,①正确; ∵正方形边长是12, ∴BE=EC=EF=6, 设AG=FG=x,则EG=x+6,BG=12-x, 由勾股定理,得EG2=BE2+BG2, 即(x+6)2=62+(12-x)2,解得x=4, ∴AG=GF=4,BG=8, ∴BG=2AG,②正确;
(完整版)第七讲对角互补模型
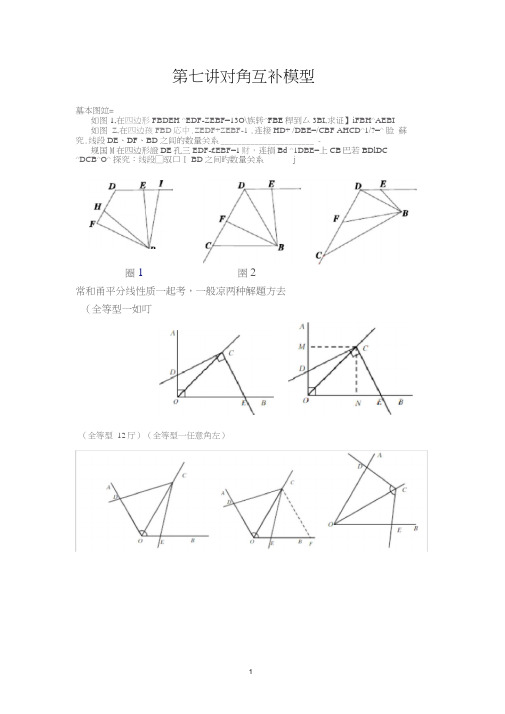
第七讲对角互补模型墓本图竝=如图1,在四边形FBDEH ^EDF-ZEBF=13O\族转^FBE稈到厶3BI,求证】iFBH^AEBI 如图Z,在四边孩FBD応中.ZEDF+ZEBF-1 .连接HD+ /DBE=/CBF AHCD^1/?=^ 脸蘇究.线段DE、DF、BD之闾的数量关系______________________ -规国M在四边形證DE孔三EDF-£EBF=1财,连損Bd ^1DBE=上CB巴若BDlDC^DCB^O^ 探究:线段□驭口I BD之间旳数量关系j圈1 圉2常和甬平分线性质一起考,一般凉两种解題方去(全等型一如叮(全等型_12厅)(全等型一任意角左)破解策略1.全零型之“9TT "如图.EDCE二曲,CT平分厶椒则⑴ CD=C£i(2.)①+偌=Jl OCi证明方^―■如團,11点匸分别作匸站丄函,口丄阳,垂足分别为掘工由角平分线的性假可得口/=口,Zjtv=90a.川而AJ€^A.\C^ (JSJ),故S②品证巴边形一遷吃为正方形”所氏他H-血=亦即舛_迹-2At/LL-切Ct = $正打仲如?方袪二=如图,过&作m■丄处交防于点F. 冨证ZZJCr=ZfiTf=45'・CQ=CF… QXA厶戡F所以△血也ZSQLJ5J)所以S広CD~FF,甬以\uto +比心=片讣=-()( -.【拓展】如图,兰乙DCE的一^与舶的延长线交于点Z?时,则*(1)CD=CE\(2)OE- 0D= 41 OC^如图.证明同上+方迭二 如匡,叹血为一边作ZFCO=^ ,交空于点穴则为等边三角形. 易证△ Dig 鱼ECF (討胡).所以CD=CE ・时库二0F= DC 、SLac+ Ska:*= 5L B = —— OC *4【拓展】如图,当/磁的一边与図的延长线交于点疋时,则;⑴ CD=CE^(2)QD_ 址=g (3)5.^- S— OC :4如图.证明同上"全等型之“任意角"如图,GOB 三2住,^DCE^ 180° -2(y , PC 平分乙迦 贝山Cl ) CD=CE\ (.2)&)+ 便=20C ・心8庄! (3)S^= OC^ sin (7 cos证明:方法一:如图,过点「分别作 少丄加 口丄0吕 垂足分别为M .V易证也]皿鸟疋(4短)■'■ CD= CE, OD^OE=2Qy=2OC- casff■'- ^cr+ IC = 2 Sioc = OC " - sinff cos U方4J-:如图,以£0为一边作ZFC0=Y^ ~2(X ,交 厨于点FZJ/?易证△ DCZ'EC心SDCD= CE t必+ 0E=0F=20C、za二氐临+ S二K=£血=OC " - sin Ct cos a【拓展】如图,当厦处的一边与於的延长线交于点占时,贝!:(1)CD=CE\(戈)0D- QE=20C・cosOr ;(3)— = OC '• sin(7 cos 如图*证明同上—、等边三角形L已知’ 4ABC是奪边三角形,Zl + ^2 = 120°,求证:Zl = Z2 = 60°.2•已知;AABC是等边三角形・4 = 60S求证* Z2 = 60°,3•己知:Zl = Z2 = _BAC = 60°P求证;AABC是等边三角形.4.已知:Zl = Z2 = Z3 = 60°,求证;:A ABC是等边三角形.->等腰直角三角形(对直角型)5.已知=A ABC是等腰直角三角形,ZL1+Z2=90°,求证:Z1 = Z2 = 45°.8•已知t Z1=Z2 = Z3 = 45% 求证,AABC是等腰直角三角形.三、等腰直角三角形(对45。
中考数学几何模型能力 对角互补模型(解析版)

中考数学几何模型 对角互补模型共顶点模型,即四边形或构成的几何图形中,相对的角互补。
主要:含90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。
解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线. 类型一:含90°的对角互补模型(1)如图,∠AOB=∠DCE=90°,OC 平分∠AOB ,则有以下结论:CD CE =①; =2OD OE OC +②;21+=2OCD OCE S S OC V V ③作法1 作法2(2)如图,∠AOB=∠DCE=90°,OC 平分∠AOB ,当∠DCE 的一边与AO 的延长线交于点D 时,则有以下结论:CD CE =①; -=2OE OD OC ②;21-=2OCE OCD S S OC V V ③作法1 作法2类型二:含120°的对角互补模型(1)如图,∠AOB=2∠DCE=120°,OC 平分∠AOB ,则有以下结论:CD CE =①; =OD OE OC +②; 23+=4OCD OCE S S OC V V ③ 作法1 作法2(2)如图,∠AOB=∠DCE=90°,OC 平分∠AOB ,当∠DCE 的一边与AO 的延长线交于点D 时,则有以下结论:CD CE =①; -=2OE OD OC ②;21-=2OCE OCD S S OC V V ③作法1 作法2例题1. 如图,正方形ABCD 与正方形OMNP 的边长均为10,点O 是正方形ABCD 的中心,正方形OMNP 绕O 点旋转,证明:无论正方形OMNP 旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值.变式练习>>>1. 角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.例题2. 四边形ABCD被对角线BD分为等腰直角△ABD和直角△CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.变式练习>>>2. 如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD=_______.例题3. 如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM 交AB于点E,PN交BC于点F,当PE=2PF时,AP=.变式练习>>>3. 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=()A.B.C.D.例题4. 用两个全等且边长为4的等边三角形△ABC和△ACD拼成菱形ABCD.把一个60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合,将三角尺绕点A按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?(直接写出结论,不用证明);(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?说明理由;(3)在上述情况中,△AEC的面积是否会等于?如果能,求BE的长;如果不能,请说明理由.变式练习>>>4. 我们规定:横、纵坐标相等的点叫做“完美点”.(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B 运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.①不管t为何值,E点总是“完美点”;②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.例题5. 已知,点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.(1)利用图1,求证:PA=PB;(2)如图2,若点C是AB与OP的交点,当S△POB=3S△PCB时,求PB与PC的比值;(3)若∠MON=60°,OB=2,射线AP交ON于点D,且满足且∠PBD=∠ABO,请借助图3补全图形,并求OP的长.达标检测领悟提升强化落实1. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连结DE、DF、EF,在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE不可能为正方形;③四边形CDFE的面积保持不变;④DE长度的最小值为4;⑤△CDE面积的最大值为8,其中正确的结论是______________.2. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,求BE的长.3. 如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求:(1)CF的长;(2)OF的长.4. 如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.5. “如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.”这里,根据已学的相似三角形的知识,易证:=.在图1这个基本图形的基础上,继续添加条件“如图2,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F,设=.”(1)探究发现:如图②,若m=n,点E在线段AC上,则=;(2)数学思考:①如图3,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图4的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.6.(2019·贵阳适应性)如图①,已知AC=BC,AC⊥BC,直线MN经过点B,过点A作AD⊥MN,垂足为D,连接CD.(1)动手操作:根据题意,请利用尺规将图①补充完整;(保留作图痕迹,不写作法)(2)探索证明:在补充完成的图①中,猜想CD、BD与AD之间的数量关系,并说明理由;(3)探索拓广:一天小明一家在某公园游玩时走散了,电话联系后得知,三人的位置如图②,爸爸在A处,妈妈在C处,小明在D处,B为公园大门口,若B、D在直线MN上,且AC⊥BC,AD⊥MN,AC=BC,AD=100m,CD=40m,求出小明到公园门口的距离BD的长度.答案例题1. 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O 点旋转,证明:无论正方形OMNP旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值.【解答】解:当OP∥AD或OP经过C点,重叠部分的面积显然为正方形的面积的,即25,当OP在如图位置时,过O分别作CD,BC的垂线垂足分别为E、F,如图在Rt△OEG与Rt△OFH中,∠EOG=∠HOF,OE=OF=5,∴△OEG≌△OFH,∴S四边形OHCG=S四边形OECF=25,即两个正方形重叠部分的面积为25.变式练习>>>1. 角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON.(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.【解答】解:(1)∵四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON;例题2. 四边形ABCD被对角线BD分为等腰直角△ABD和直角△CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.【解答】解:将△ABC绕点A旋转90°,使B与D重合,C到C′点,则有∠CDC′=∠ADC+∠ADC′=∠ADC+∠ABC=180°,所以C、D、C′在同一直线上,则ACDC′是三角形,又因为AC=AC′,所以△ACC′是等腰直角三角形,在△ABC和△ADC′中∴△ABC≌△ADC′(SAS),∴四边形ABCD的面积等于等腰直角三角形ACC′的面积,所以S四边形ABCD=S△ACC′=×2×2=2.变式练习>>>2. 如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD=_______.答案:43例题3. 如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM 交AB于点E,PN交BC于点F,当PE=2PF时,AP= 3 .【解答】解:如图作PQ⊥AB于Q,PR⊥BC于R.∵∠PQB=∠QBR=∠BRP=90°,∴四边形PQBR是矩形,∴∠QPR=90°=∠MPN,∴∠QPE=∠RPF,∴△QPE∽△RPF,∴==2,∴PQ=2PR=2BQ,∵PQ∥BC,∴AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,∴2x+3x=3,∴x=,∴AP=5x=3.故答案为3.变式练习>>>3. 如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=()A.B.C.D.【解答】解:如图,连接BF,取BF的中点O,连接OE,OC.∵四边形ABCD是矩形,EF⊥BE,∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5,∵OB=OF,∴OE=OB=OF=OC,∴B,C,F,E四点共圆,∴∠EBF=∠ECF,∴tan∠EBF=tan∠ACD,∴==,故选:B.【本题两种方法解答,过E作两垂线亦可】例题4. 用两个全等且边长为4的等边三角形△ABC和△ACD拼成菱形ABCD.把一个60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合,将三角尺绕点A按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?(直接写出结论,不用证明);(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?说明理由;(3)在上述情况中,△AEC的面积是否会等于?如果能,求BE的长;如果不能,请说明理由.【解答】解:(1)BE=CF.证明:在△ABE和△ACF中,∵∠BAE+∠EAC=∠CAF+∠EAC=60°,∴∠BAE=∠CAF.∵AB=AC,∠B=∠ACF=60°,∴△ABE≌△ACF(ASA).∴BE=CF;(3)能.△AEC的CE边上的高为等边△ABC的高,为2,∵△AEC的面积等于,∴底边CE=2,∴BE=6或2.变式练习>>>4. 我们规定:横、纵坐标相等的点叫做“完美点”.(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B 运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.①不管t为何值,E点总是“完美点”;②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.【解答】解(1)∵点A(x,y)是“完美点”∴x=y∵x+y=4∴x=2,y=2∴A点坐标(2,2)(2)①∵四边形OABC是正方形,点A坐标为(0,4),∴AO=AB=BC=4∴B(4,4)设直线OB解析式y=kx过B点∴4=4kk=1∴直线OB解析式y=x设点E坐标(x,y)∵点E在直线OB上移动∴x=y∴不管t为何值,E点总是“完美点”.例题5. 已知,点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.(1)利用图1,求证:PA=PB;(2)如图2,若点C是AB与OP的交点,当S△POB=3S△PCB时,求PB与PC的比值;(3)若∠MON=60°,OB=2,射线AP交ON于点D,且满足且∠PBD=∠ABO,请借助图3补全图形,并求OP的长.【解答】解:(1)作PE⊥OM,PF⊥ON,垂足为E、F∵四边形OEPF中,∠OEP=∠OFP=90°,∴∠EPF+∠MON=180°,已知∠APB+∠MON=180°,∴∠EPF=∠APB,即∠EPA+∠APF=∠APF+∠FPB,∴∠EPA=∠FPB,由角平分线的性质,得PE=PF,∴△EPA≌△FPB,即PA=PB;(2)∵S△POB=3S△PCB,∴PO=3PC,由(1)可知△PAB为等腰三角形,则∠PBC=(180°﹣∠APB)=∠MON=∠BOP,又∵∠BPC=∠OPB(公共角),∴△PBC∽△POB,∴=,即PB2=PO•PC=3PC2,∴=达标检测领悟提升强化落实1. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连结DE、DF、EF,在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE不可能为正方形;③四边形CDFE的面积保持不变;④DE长度的最小值为4;⑤△CDE面积的最大值为8,其中正确的结论是______________.答案:①②③2. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,求BE的长.答案:223. 如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求:(1)CF的长;(2)OF的长.【解答】解:(1)如图,在BE上截取BG=CF,连接OG,∵RT△BCE中,CF⊥BE,∴∠EBC=∠ECF,∵∠OBC=∠OCD=45°,∴∠OBG=∠OCF,在△OBG与△OCF中,,∴△OBG≌△OCF(SAS),∴OG=OF,∠BOG=∠COF,∴OG⊥OF,在RT△BCE中,BC=DC=6,DE=2EC,∴EC=2,∴BE===2,∵BC2=BF•BE,则62=BF•2解得:BF=,∴EF=BE﹣BF=,∵CF2=BF•EF,∴CF=;4. 如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是DE+DF=AD;(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=AD,请给出证明;(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.【解答】解:(1)正方形ABCD的对角线AC,BD交于点P,∴PA=PD,∠PAE=∠PDF=45°,∵∠APE+∠EPD=∠DPF+∠EPD=90°,∴∠APE=∠DPF,在△APE和△DPF中∴△APE≌△DPF(ASA),∴AE=DF,∴DE+DF=AD;(2)如图②,取AD的中点M,连接PM,∵四边形ABCD为∠ADC=120°的菱形,∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,∴△MDP是等边三角形,∴PM=PD,∠PME=∠PDF=60°,∵∠PAM=30°,∴∠MPD=60°,∵∠QPN=60°,∴∠MPE=∠FPD,在△MPE和△DPF中,∴△MPE≌△DPF(ASA)∴ME=DF,∴DE+DF=AD;5. “如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.”这里,根据已学的相似三角形的知识,易证:=.在图1这个基本图形的基础上,继续添加条件“如图2,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F,设=.”(1)探究发现:如图②,若m=n,点E在线段AC上,则= 1 ;(2)数学思考:①如图3,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图4的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴=,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴==1,∴=1,故答案为1.(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴=,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴==,∴=,故答案为.(3)由(2)有,△ADE∽△CDF,∵==,∴===,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF===2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,6.(2019·贵阳适应性)如图①,已知AC=BC,AC⊥BC,直线MN经过点B,过点A作AD⊥MN,垂足为D,连接CD.(1)动手操作:根据题意,请利用尺规将图①补充完整;(保留作图痕迹,不写作法)(2)探索证明:在补充完成的图①中,猜想CD、BD与AD之间的数量关系,并说明理由;(3)探索拓广:一天小明一家在某公园游玩时走散了,电话联系后得知,三人的位置如图②,爸爸在A处,妈妈在C处,小明在D处,B为公园大门口,若B、D在直线MN上,且AC⊥BC,AD⊥MN,AC=BC,AD=100m,CD=40m,求出小明到公园门口的距离BD的长度.。
专题13 全等三角形重难点模型(五大模型)(原卷版)

专题13全等三角形重难点模型(五大模型)模型一:一线三等角型模型二:手拉手模型模型三:半角模型模型四:对角互补模型模型五:平行+线段中点构造全等模型【典例分析】【模型一:一线三等角型】如图一,∠D=∠BCA=∠E=90°,BC=AC。
结论:Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二,∠D=∠BCA=∠E,BC=AC。
结论:△BEC≌△CDA图一图二应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).(1)当a=2时,则C点的坐标为;(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.【变式1】点A的坐标为(4,0),点B为y轴负半轴上的一个动点,分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD.(1)如图一,若点B坐标为(0,﹣3),连接AC、OD.①求证:AC=OD;②求D点坐标.(2)如图二,连接CD,与y轴交于点E,试求BE长度.【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.【变式2】已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE =9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD 的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.【模型二:手拉手模型】应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;②作辅助线构造手拉手模型,难度比较大。
全等三角形的对角互补模型解析

全等三角形的对角互补模型解析全等三角形对角互补模型解析1.等腰直角对直角例1:在等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠ADB=45°,证明BD⊥CD。
例2:在等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠ADC=45°,证明∠XXX°。
例3:在等腰直角三角形ABC中,AB=AC,∠ADC=45°,∠ADB=45°,证明XXX。
例4:在直角三角形ABC中,∠BAC=90°,∠ADB=45°,∠ADC=45°,证明AB=AC。
例5:在直角三角形ABC中,AB=AC,∠BAC=90°,∠BDC=90°,证明AD平分∠XXX。
2.等腰直角旁直角例1:在等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠ADB=45°,求∠ADC的度数。
例2:在等腰直角三角形ABC中,AB=AC,∠BAC=90°,∠ADC=135°,证明BD⊥CD。
例3:在等腰直角三角形ABC中,AB=AC,∠ADB=45°,∠ADC=135°,证明∠BAC=90°。
例4:在直角三角形ABC中,∠BAC=90°,∠ADB=45°,BD⊥CD,证明AB=AC。
例5:在直角三角形ABC中,AB=AC,∠BAC=90°,∠XXX°,求∠ADC的度数。
3.等边对120°例1:在等边三角形ABC中,AB=AD,∠BAD=60°,∠ACB=60°,证明∠BCD=120°。
例2:在等边三角形ABC中,AB=AD,∠BAD=60°,∠ACD=60°,证明∠ACB=60°。
例3:在等边三角形ABC中,AB=AD,∠ACB=60°,∠ACD=60°,证明∠BAD=60°。
第3讲对角互补模型(解析版)

第3讲对角互补模型(解析版)中考数学几何模型3:对角互补模型共顶点模型中,四边形或其他几何图形中,相对的角互补。
主要有两种类型:含90°的对角互补和含120°的对角互补,得出的结论会有所不同。
解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线。
类型一:含90°的对角互补模型1)如图,∠AOB=∠DCE=90°,OC平分∠AOB,则有以下结论:①CD=CE;②OD+OE=2OC;③S(OCD)+S(OCE)=OC²。
2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:①CD=CE;②OE-OD=2OC;③S(OCE)-S(OCD)=OC²。
类型二:含120°的对角互补模型1)如图,∠AOB=2∠DCE=120°,OC平分∠AOB,则有以下结论:①CD=CE;②OD+OE=OC;③S(OCD)+S(OCE)=3OC²/4.2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:①CD=CE;②OE-OD=2OC;③S(OCE)-S(OCD)=OC²。
典题探究例题1:如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,证明:无论正方形OMNP旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值。
解答】当OP∥AD或OP经过C点,重叠部分的面积显然为正方形的面积,即25.当OP在如图位置时,过O分别作CD、BC的垂线垂足分别为E、F,在Rt△OEG与Rt△OFH 中,∠EOG=∠HOF,OE=OF=5,所以△OEG≌△OFH,因此S(四边形OHCG)=S(四边形OECF)=25,即两个正方形重叠部分的面积为25.变式练1.角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN。
专题05 全等模型-对角互补模型(原卷版)
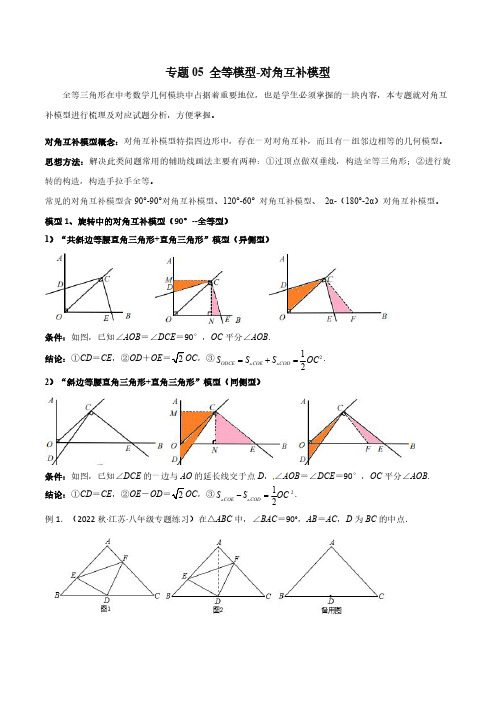
专题05全等模型-对角互补模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就对角互补模型进行梳理及对应试题分析,方便掌握。
对角互补模型概念:对角互补模型特指四边形中,存在一对对角互补,而且有一组邻边相等的几何模型。
思想方法:解决此类问题常用的辅助线画法主要有两种:①过顶点做双垂线,构造全等三角形;②进行旋转的构造,构造手拉手全等。
常见的对角互补模型含90°-90°对角互补模型、120°-60°对角互补模型、2α-(180°-2α)对角互补模型。
模型1、旋转中的对角互补模型(90°--全等型)1)“共斜边等腰直角三角形+直角三角形”模型(异侧型)条件:如图,已知∠AOB =∠DCE =90°,OC 平分∠AOB .结论:①CD =CE ,②OD +OE OC ,③212ODCE COE COD S S S OC =+= .2)“斜边等腰直角三角形+直角三角形”模型(同侧型)条件:如图,已知∠DCE 的一边与AO 的延长线交于点D ,∠AOB =∠DCE =90°,OC 平分∠AOB .结论:①CD =CE ,②OE -OD OC ,③212COE COD S S OC -= .例1.(2022秋·江苏·八年级专题练习)在△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点.(1)如图1,E、F分别是AB、AC上的点,且BE=AF、求证:△DEF是等腰直角三角形例2、在ABC∠=︒,2==,将一块三角板的直角顶点放在斜边AB的中点P处,将此三AC BC∆中,90C角板绕点P旋转,三角板的两直角边分别交射线AC、CB于点D、点E,图①,②,③是旋转得到的三种图形.(1)观察线段PD和PE之间有怎样的大小关系?并以图②为例,并加以证明;(2)观察线段CD、CE和BC之间有怎样的数量关系?并以图③为例,并加以证明;例3.(2022秋·四川绵阳·九年级校联考阶段练习)已知=90ACD ∠︒,AC DC =,MN 是过点A 的直线,过点D 作DB MN ⊥于点B ,连接CB .(1)问题发现:如图(1),过点C 作CE CB ⊥,与MN 交于点E ,BD 、AB 、CB 之间的数量关系是什么?并给予证明.(2)拓展探究:当MN 绕点A 旋转到如图(2)位置时,BD 、AB 、CB 之间满足怎样的数量关系?请写出你的猜想,并给予证明.模型2、旋转中的对角互补模型(60°或120°--全等型)1)“等边三角形对120°模型”(1)条件:如图,已知∠AOB =2∠DCE =120°,OC 平分∠AOB .结论:①CD =CE ,②OD +OE =OC ,③24COD COE S S OC +=.2)“等边三角形对120°模型”(2)条件:如图,已知∠AOB =2∠DCE =120°,OC 平分∠AOB ,∠DCE 的一边与BO 的延长线交于点D ,结论:①CD =CE ,②OD -OE =OC ,③2COD COE S S -= .3)“120°等腰三角形对60°模型”条件:△ABC 是等腰三角形,且∠BAC =120°,∠BPC =60°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对角互补+角平分线模型
已知,四边形ABCD,∠B+∠D=180°,AC平分∠BCD 结论①AB=AD
结论①的证明有三种方法
1 四点共圆
2 双垂法3旋补法
其中双垂法是一种通法,有些变型题,其他俩种方法不好解决,但双垂法百试不爽。
下面,我介绍双垂法和旋补法。
方法一:双垂法
证明:分别过A作CD和CB得垂线AM和AN ∵AC平分∠BCD ∵AM=AN
又∵∠B+∠D=180°
∴∠ABN=∠D
∴△ABN≌△ADM
∴AB=AD
方法二:旋补法
证明:延长CD到E,作等腰△ACE
∴AC=AE,∠AEC=∠ACE=∠ACB
又∵∠B+∠D=180°
∴∠B=∠ADE
∴△ABC≌△ADE
∴AB=AD
其实①∠B+∠D=180°②AC平分∠BCD③AB=AD 只要给出其中任意俩个条件,必定能推出第三个,大家可以自己用双垂法试试。
结论②BC+CD=2ACcosθ
证明:过A作AF⊥CD
由结论①可知:△ACE为等腰三角形,且BC=DE
∴BC+CD=CE=2CF
又∵CF=ACcosθ
∴BC+CD=2CF=2ACcosθ
结论③四边形ABCD的面积=等腰三角形ACE的面积=AC²sinθcosθ
∵黄≌绿,把黄割补到绿的位置
∴四边形ABCD的面积=等腰三角形ACE的面积
∵ACE的面积=AF*CF
(其中AF=ACsinθ,CF=ACcosθ)
∴四边形ABCD的面积=等腰三角形ACE的面积
=AC²sinθcosθ
特别地,当∠BCD=120°时,BC+CD=2ACcos60°=AC 四边形ABCD面积=正三角形ACE面积
特别地,当∠BCD=90°时,BC+CD=2ACcos45°=2AC 四边形ABCD面积=等腰直角三角形ACE面积。
