第13讲 “一线三等角型相似”问题
一线三等角模型相似证明
一线三等角模型相似证明好嘞，今天咱们聊聊一线三等角模型相似证明的事儿。
听起来挺高大上的，但其实说白了就是个有趣的几何故事。
你想啊，几何这个东西，跟生活其实是有很多相似之处的。
就像我们在生活中总是喜欢找到一些规律、一些相似性，这些其实也能帮助我们理解这个世界。
一线三等角模型，其实就是一个很简单的图形构造。
你可以想象一下，就像把三根小棒子拼成一个三角形，哎呀，没事儿，别紧张，这三角形可不复杂。
它的角都是等的，等于是给你一个平等的机会，不管你是哪个角，都是那样的。
这个想法，感觉就像是朋友之间的公平交易，大家都有发言权。
每个角都在发光发热，绝对不是“独角戏”。
再说这相似证明，哈哈，感觉就像是在做一道拼图。
你只要找到那几个对应的边和角，就能搞定。
就像生活中，朋友之间的默契，彼此之间总有些共同点，这种相似感就像是在说：“嘿，我也懂你！”每当你发现这种相似性，心里那个乐啊，真是巴适得很。
想象一下，假如我们把这个模型带到生活中，大家都在一个大舞台上，三角形的三个角分别代表不同的人。
有的人热情似火，有的人冷静如水，还有的人嘛，幽默搞笑，三者相辅相成，缺一不可。
就像在团队中，每个人的特长都能让这个团队更加出彩。
这个时候，你就会发现，只要大家心往一处想，劲往一处使，那绝对能完成一场精彩的表演。
这时候就要提到相似的概念了。
模型里的每个部分都有相同的比例，就像我们生活中那些互相借鉴的经验。
你说我今天遇到的麻烦，你也可能经历过，咱俩一交流，嘿，问题就解决了。
这种相似就像是生活的魔法，能让我们从彼此的经验中获益。
别小看这种分享，生活中的每一份理解都是让人暖心的存在。
咱们再说说那些三等角的性质吧。
这可是个亮点，三角形的内角加起来就是180度，哦，真是太妙了。
这就像是在说，无论你的人生经历如何，最终都要回归到一个平衡的状态。
这种平衡在我们的生活中也很重要。
就像一盘菜，调料、主料、辅料，每样东西都得有适量，才能做出美味佳肴。
否则，光放盐可不行啊，得有个搭配，才能味道更佳。
完整一线三等角型相似初三压轴题
典型例题【例1】如图，等边△ ABC 中，边长为6，D 是BC 上动点，/ EDF=60° (1) 求证：△ BDE CFD (2) 当 BD=1, FC=3 时，求 BE【思路分析】 本题属于典型的三等角型相似，由题意可得/ B= / C=Z EDF=60再用外角可证/ BED= / CDF ，可证△ BDE 与厶CFD 相似排出相似比便可 求得线段BE 的长度解：(1)：公 ABC 是等边三角形，/ EDF=60 °•••/ B= / C=Z EDF =60 ° •••/ EDC=Z EDF + / FDC = / B+ / BED •••/ BED = Z FDC(2)v^ BDECFD• FC CD "BD BE •/ BD=1 , FC=3, CD=5 • BE=53点评：三等角型的相似三角形中的对应边中已知三边可以求第四边。
【例2】如图，等腰△ ABC 中，AB=AC , D 是BC 中点，/ EDF = / B ,求证：△ BDE DFE【思路分析】 比较例1来说区别仅是点 D 成为了 BC 的中点，所以△ BDE 与 △ CFD 相似的结论依然成立，用相似后的对应边成比例，以及 BD=CD 的条件可证得△ BDE 和厶DFE 相似 解:•/ AB=AC ,Z EDF = / B•••/ B= / C=Z EDF•••/ EDC=Z EDF + / FDC = / B+ / BED •••/ BED = Z FDC •••△ BDE CFDBE DE 又••• BD=CDCD DF BE DEBE BD•-即BD DF DE DF•••/ EDF = Z B中考热点5――三等角型相似三角形三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景，一个与等腰三角形的底角等角的顶点在底边上的位置不同得到的相似三角形的结论也不同，当顶点移动到底边的延长线时，形成变 式图形，图形虽然变化但是求证的方法不变。
相似专题：一线三等角模型
由于角顶点位置的改变，或角绕顶点旋转会产生各 种各样的变式，但万变不离其宗： 都是构造相似三角形列比例式解决问题.
常见类型
考题赏析：
考题赏析
应用举例
应用举例.
2、当等角所对的边相等时的两个三角形全等. 如图，当CE=ED时，易得△AEC≌△BDE.
3、“中点型一线三等角”的特殊性质
如图，当∠1=∠2=∠3且D是BC中点时， △BDE∽△CFD∽△DFE.
四、一线三等角的常见构图（以等腰三角形为例）
A与E重合时如图所示
也可以在射线上
点D也可以在线段 BC外面
练习中的问题：
相似专题复习 ：
合肥实验学校 孙红涛
引例
已知相邻两条平行线间距离相等，若等腰直角三角形顶 点分别在三条平行线上，则sinα =
C
a
B
起源
二、“一线三等角”的两种基本类型
1.三等角都在直线的同侧
2.三等角分居直线的两侧
三、“一线三等角”的性质
1.一般情况下，由∠1=∠2=∠3易得△AEC∽△BDE.
中考数学相似三角形重要模型一线三等角模型
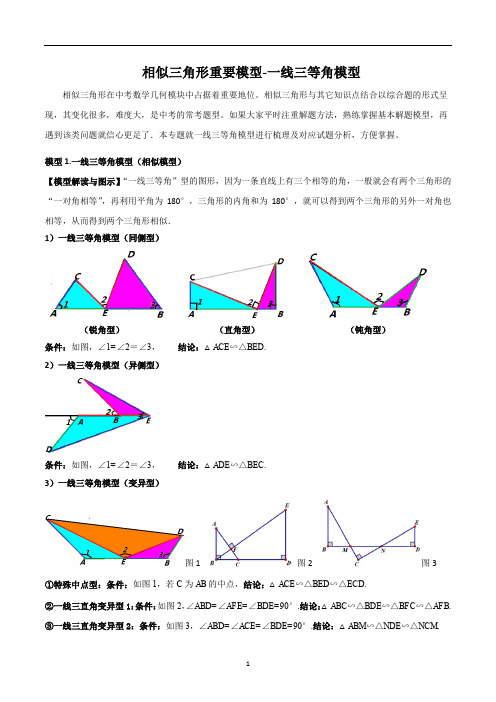
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。
如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就一线三等角模型进行梳理及对应试题分析，方便掌握。
模型1.一线三等角模型（相似模型）【模型解读与图示】“一线三等角”型的图形，因为一条直线上有三个相等的角，一般就会有两个三角形的“一对角相等”，再利用平角为180°，三角形的内角和为180°，就可以得到两个三角形的另外一对角也相等，从而得到两个三角形相似．1）一线三等角模型（同侧型）（锐角型）（直角型）（钝角型）条件：如图，∠1=∠2＝∠3，结论：△ACE∽△BED.2）一线三等角模型（异侧型）条件：如图，∠1=∠2＝∠3，结论：△ADE∽△BEC.3）一线三等角模型（变异型）图1 图2 图3①特殊中点型：条件：如图1，若C为AB的中点，结论：△ACE∽△BED∽△ECD.②一线三直角变异型1：条件：如图2，∠ABD=∠AFE=∠BDE=90°.结论：△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2：条件：如图3，∠ABD=∠ACE=∠BDE=90°.结论：△ABM∽△NDE∽△NCM.例1．（2023·山东东营·统考中考真题）如图，A B C为等边三角形，点D，E分别在边B C，A B上，60A D E∠=︒，若4B D D C=， 2.4D E=，则A D的长为（）A．1.8B．2.4C．3D．3.2例2．（2023·湖南·统考中考真题）如图，,C A ADE D A D⊥⊥，点B是线段A D上的一点，且C B B E⊥．已知8,6,4A B A C D E===．(1)证明：A B C D E B∽△△．(2)求线段B D的长．例3．（2022·河南新乡·九年级期中）某学习小组在探究三角形相似时，发现了下面这种典型的基本图形．（1）如图1，在ABC中，∠BAC＝90°，A BA C＝k，直线l经过点A，BD⊥直线I，CE上直线l，垂足分别为D、E．求证：B DA E＝k．（2）组员小刘想，如果三个角都不是直角，那么结论是否仍然成立呢？如图2，将（1）中的条件做以下修改：在ABC中，A BA C＝k，D、A、E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问（1）中的结论还成立吗？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，在ABC中，沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG，A BA E ＝A CA G＝12，AH是BC边上的高，延长HA交EG于点I．①求证：I是EG的中点．②直接写出线段BC与AI之间的数量关系：．例4．（2022·四川·一模）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：（1）如图1，已知：在△ABC 中，A B A C=，D 、A 、E 三点都在直线m 上，并且有B D AA E CB AC α∠=∠=∠=．试猜想DE 、BD 、CE 有怎样的数量关系，请证明你的结论；（2）老师鼓励学习小组继续探索相似的情形．于是，学习小组又研究以下问题：如图2，△ABC 中，(060)B C αα∠=∠=<<︒．将一把三角尺中30°角顶点P 放在BC 边上，当P 在BC 边上移动时，三角尺中30°角的一条边始终过点A ，另一条边交AC 边于点Q ，P 、Q 不与三角形顶点重合．设C P Qβ∠=．当β在许可范围内变化时，α取何值总有△ABP ∽△PCQ ？当α在许可范围内变化时，β取何值总有△ABP ∽△QCP ？（3）试探索有无可能使△ABP 、△QPC 、△ABC 两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由．例5．（2022·山西晋中·一模）阅读材料：我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①，在A B C中，90A C B ∠=︒，A C B C=，分别过A 、B 向经过点C 直线作垂线，垂足分别为D 、E ，我们很容易发现结论：A D C C E B△≌△．（1）探究问题：如果A CB C≠，其他条件不变，如图②，可得到结论；A D CC E B△∽△．请你说明理由．（2）学以致用：如图③，在平面直角坐标系中，直线12y x=与直线C D 交于点()2,1M ，且两直线夹角为α，且3ta n 2α=，请你求出直线C D 的解析式．（3）拓展应用：如图④，在矩形A B C D 中，3A B=，5B C=，点E为B C 边上—个动点，连接A E ，将线段A E 绕点E 顺时针旋转90︒，点A 落在点P 处，当点P 在矩形A B C D外部时，连接P C ，P D ．若D P C △为直角三角形时，请你探究并直接写出B E 的长．Rt ABD中，上一动点，连接折叠得H E F，延长②B E M H E M≅；③当M2B，则正确的有（九年级校考阶段练习）已知A B C是等边三角形，E F和B D F∠，将B C E沿B则A F=P C D△；九年级校考阶段练习）如图，在A B C中，12．（2022·山东济宁·二模）情境观察:将含45°角的三角板的直角顶点R放在直线l上，分别过两锐角的顶点M，N作l的垂线，垂足分别为P，Q，（1）如图1.观察图1可知：与NQ相等的线段是______________，与N R Q∠相等的角是_____(2)问题探究直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作正方形ACEF 和正方形CDGH，如图2，过E，H分别作BC所在直线的垂线，垂足分别为K，L.试探究EK与HL之间的数量关系，并证明你的结论.(3)拓展延伸：直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作矩形ACEF和矩形CDGH，连接EH交BC所在的直线于点T，如图3.如果A C kC E=，试探究TE与TH=，C D kC H之间的数量关系，并证明你的结论.将．A B P沿着这样的点P，使得点问题解决（3）15．（2023春·四川广安·九年级校考阶段练习）如图1和图2，在平面直角坐标系中，点C的坐标为（0，4），A是x轴上的一个动点，M是线段AC的中点．把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB．过B作x轴的垂线、过点C作y轴的垂线，两直线交于点D，直线DB交x轴于点E．设A点的横坐标为m．（1）求证：△AOC∽△BEA；（2）若m=3，则点B的坐标为；若m=﹣3，则点B的坐标为；（3）若m＞0，△BCD的面积为S，则m为何值时，S=6？（4）是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由．16．（2020·四川雅安·中考真题）如图，已知边长为10的正方形A B C D E、不重，是B C边上一动点（与B C 合），连结A E G，是B C延长线上的点，过点E作A E的垂线交D C G∠的角平分线于点F，若F G B G⊥．（1）求证：A B E E G FE C=，求C E F△△；（2）若2∽△的△的面积；（3）请直接写出E C为何值时，C E F面积最大．的何位置时有B E H B A E∽？B C。
“一线三等角”相似模型
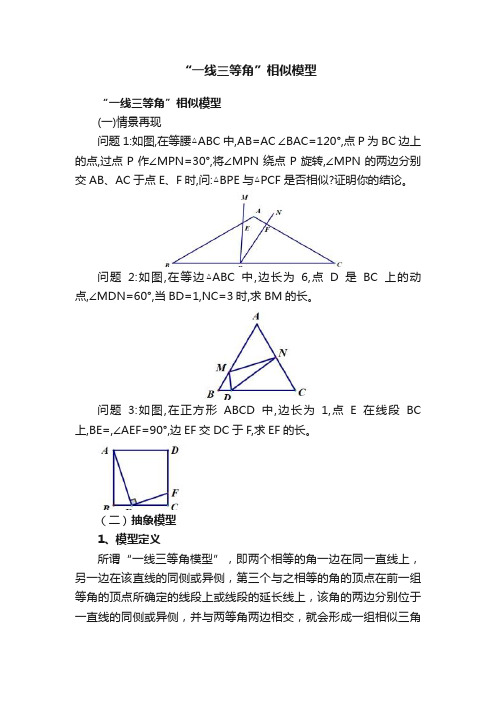
“一线三等角”相似模型“一线三等角”相似模型(一)情景再现问题1:如图,在等腰△ABC中,AB=AC ∠BAC=120°,点P为BC边上的点,过点P作∠MPN=30°,将∠MPN绕点P旋转,∠MPN的两边分别交AB、AC于点E、F时,问:△BPE与△PCF是否相似?证明你的结论。
问题2:如图,在等边△ABC中,边长为6,点D是BC上的动点,∠MDN=60°,当BD=1,NC=3时,求BM的长。
问题3:如图,在正方形ABCD中,边长为1,点E在线段BC 上,BE=,∠AEF=90°,边EF交DC于F,求EF的长。
（二）抽象模型1、模型定义所谓“一线三等角模型”，即两个相等的角一边在同一直线上，另一边在该直线的同侧或异侧，第三个与之相等的角的顶点在前一组等角的顶点所确定的线段上或线段的延长线上，该角的两边分别位于一直线的同侧或异侧，并与两等角两边相交，就会形成一组相似三角形，习惯上把该组相似三角形称为“一线三等角”型相似三角形.(通俗地讲，一条直线上有三个相等的角一般会存在相似三角形)2、基本图形：（1）点P在线段AB上（2）点P在线段AB延长线上三、载体(1)等腰或等边三角形底边上的“一线三等角”模型(2) 矩形或正方形中的“一线三等角”模型(“K”字型)（3）平面直角坐标系中的“一线三等角”模型（三）问题探究问题:如图16,在△ABC中,AB=AC=5,BC=8,点D、E分别在BC、AC上,连接AD、DE,使∠1=∠B 求线段CE的最大值变式1:(2017年无锡中考副卷第28题改编)如图1，在矩形ABCD 中，点P在AD上，AB=2，AP=1，将三角板的直角顶点放于P处，三角板的两直角边分别与AB、BC边相交于点E、F，连接EF。
（1）如图2，当点E与点B重合时，点F恰好与点C重合，求此时PC的长（2）将三角板从图1中点的位置开始，绕点P顺时针旋转，当点E与点A重合时停止，∠PEF的大小是否发生变化?变式2:（1）在平面直角坐标系中，如图，直线l1:y=-2x+4与x 轴、y轴分别交于A、B两点，将△OAB沿l1翻折，求O的对称点P 的坐标（2）直线l2过点P,且与直线l1的夹角是45°,求两直线l1、l2的交点的坐标。
相似三角形专题——一线三等角
相似三角形专题——“一线三等角”图形中的相似教学目标：巩固“一线三等角”图形中的相似判定及分类讨论 结合“一线三等角”图形中相似三角形的特点，确定动点位置 会根据一线两等角图形添加第三个等角构造相似三角形 教学重难点：重点是“一线三等角”图形中判定三角形相似及两类三个三角形两两相似的分类讨论，难点在根据“一线三等角”图形中相似三角形的特点，确定动点位置，构造相似三角形 教学过程：一、巩固“一线三等角”图形中相似的判定及分类讨论 1. 如图，在△ABC 中，AB=AC ，点D 在BC 上，作∠EDF = ∠B ， 点 E 、F 分别落在边AD 、AC 上，求证：△BED ∽△CDF *（A A ）突出“一线三等角，外角证相似” 2. 思考1：练习中，联结EF若点D 是BC 边的中点，求证：△EDF ∽△EBD*注重证明过程，注意BD 与CD 的等量代换及比例的内向交换 3. 思考2：练习中，联结EF 若 BE = CF ，求证：△EDF ∽△DBE*通过比例的转化，更应注意可证明EF 与BC 平行 4.提问：思考3：联结EF若△BDE 与△EDF 相似，应该分析哪些请况*问题直接总结上述两种相似情况，同时为后面分类讨论问题铺垫二、分类讨论，结合“一线三等角”图形中相似三角形的特点，确定动点位置 1. 练习：如图，在△ABC 中，AB = AC ，点D 在BC 上，若 BC = 5， 点E 、点D 是AB 、BC 上的点，且BE=√(6)，作∠EDF = ∠B当△DEF 与△CDF 相似时，求CF 与BD 的长BB2. 如图，在正方形格子中有一个矩形ABCD ， 在AB 上，找出点E ，联结DE 、CE ，使得△DEC 与△DAE 及△EBC 都相似*注意AB 中点不正确的说明3. 思考：如图，在矩形ABCD 中，点M 在AD 上，将△DMC 沿MC 翻折，点D 恰好落在AB 边的E 点位置，若△MEC 与△AME 相似， 求：矩形相邻两边AD 与AB 的比*三个相似三角形带来的特点要注意三、会根据一线两等角图形添加第三个等角构造相似三角形 例题：如图，在Rt △ABC 中，∠C=90°，点D 在AC 上，联结过D 作DE ⊥BD 交AB 边于点E ，若 BC = 4，AC = 8， △BDE ∽△BCD ，求CD*也可以利用角平分线特点，做DG ⊥AB 练习如图，在Rt △ABCD 中，∠C = 90°，AD = 5，AB = 8BC = 9，点E 是BC 边上一点，且∠DEF = 60°， 若△DEF 与△BEF 相似，求BE 长ECB。
相似专题：一线三等角模型
相似专题复习---“一线三等角模型”
一、教学目标
1.学生会运用两组对应角分别相等的两个三角形为相似三角形的判定方法证明两个三角形相似。
2.学生经历观察、比较、归纳的学习过程，归纳出“一线三等角”图形的基本特征，并且能够在不同的背景中认识和把握基本图形。
3.学生在学习过程中感受几何直观图形对几何学习的重要性。
二、教学重点、难点
1、重点：运用判定方法解决“一线三等角”的相关计算与证明
2、难点：在不同背景中识别基本图形
三、教学方法：教师主导与学生合作探究相结合。
四、教学过程
二一线三等角的性质。
《相似三角形之一线三等角》教学课件
《相似三角形之一线三等角》教学ppt课件2023-10-26CATALOGUE目录•引言•相似三角形基本概念•一线三等角定理及其应用•课堂活动与练习•总结与回顾01引言•相似三角形是初中数学的重要内容，而一线三等角是相似三角形的一种重要类型。
通过学习本课，学生能够深入理解相似三角形的性质和判定方法，提高数学思维和解决问题的能力。
课程背景课程目标学会如何利用一线三等角判定两个三角形相似；掌握一线三等角的定义和性质；培养学生的自主学习和合作学习能力。
通过案例分析，培养学生的数学思维和解决问题的能力；教学策略利用PPT课件引导学生逐步深入学习；采用讲解、示范、小组讨论等多种教学方法，帮助学生掌握知识；通过案例分析，让学生了解一线三等角的应用；组织课堂练习和小组讨论，加深学生对知识的理解和应用。
02相似三角形基本概念如果两个三角形三边对应成比例，那么这两个三角形相似。
定义如果$\frac{a}{b} = \frac{c}{d}$，那么$\bigtriangleup ABC\backsim \bigtriangleup DEF$。
数学符号表示相似三角形的定义相似三角形的性质对应角相等相似三角形对应角相等，可以用$\bigtriangleup ABC \backsim \bigtriangleup DEF$推出$\angle A =\angle E$，$\angle B = \angle F$，$\angle C = \angle D$。
对应边成比例相似三角形对应边成比例，可以用$\bigtriangleup ABC \backsim \bigtriangleup DEF$推出$\frac{a}{d} = \frac{b}{e} = \frac{c}{f}$。
定义法根据相似三角形的定义进行判断，即判断两个三角形三边对应成比例。
平行线法通过平行线构造相似三角形，即利用平行线的性质，将两个三角形放在平行线上，通过移动使得对应边成比例，从而证明两个三角形相似。
初三相似三角形之一线三等角专题
相似三角形——“一线三等角型”一、知识梳理：一线三等角：两个等角的一边在同一直线上，另一边在该直线的同侧。
若有第三个与之相等的角、其顶点在该直线上，角的两边（或两边所在直线）分别与两等角的非共线边（或该边所在直线）相交，此时通过证明，一般都可以得到一组相似三角形，该组相似三角形习惯上被称为“一线三等角型”相似三角形．（图1）（图2）（1）如图1，已知三角形ABC中，AB=AC,∠ADE=∠B，那么一定存在的相似三角形有；（2）如图2，已知三角形ABC中，AB=AC,∠DEF=∠B，那么一定存在的相似三角形有 .二、【例题解析】【例1】如图，等边△ABC中，边长为4，D是BC上动点，∠EDF=60°，（1）求证：△BDE∽△CFD；（2）当BD=1，FC=52时，求BE.【变式1】在边长为4的等边ABC∆中，D是BC的中点，点E、F分别在AB、AC上，且保持ABCEDF∠=∠，连接EF.(1) 已知BE=1,DF=2，求DE的值；(2) 求证：∠BED=∠DEF.【变式2】在边长为4的等边ABC ∆中，若BD =1时，当△DEF 与△AEF 相似，求BE 的值.【变式3】如图，已知边长为3的等边ABC ∆，点F 在边BC 上，CF =1，点E 是射线BA 上一动点，以线段EF 为边向右侧作等边EFG ∆，直线EG ，FG 交直线AC 于点M ，N ，（1）写出图中与BEF ∆相似的三角形；（2）证明其中一对三角形相似；（3）设BE =x ，MN =y ，，求y 与x 之间的函数关系式，并写出自变量x 的取值范围.【例2】在ABC ∆中，O BC AC C ,3,4,90===∠o 是AB 上的一点，且52=AB AO ，点P 是AC 上的一个动点，OP PQ ⊥交线段BC 于点Q （不与点B ,C 重合），已知AP =2，求CQ .【变式1】 如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在AC 边上，且C ADE ∠=∠．(1) 求证：△ABD ∽△DCE ；(2) 如果x BD =，y AE =，求y 与x 的函数解析式，并写出自变量x 的定义域；(3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．QC P【变式2】在直角三角形ABC 中，D BC AB C ,,90==∠o是AB 边上的一点，E 是在AC 边上的一个动点（与A ，C 不重合），DF DE DF ,⊥与射线BC 相交于点F .(1) 如图1，当点D 是边AB 的中点时，求证：DF DE =;(2) 如图2，当m DB AD =，求DF DE 的值.图(2)图(1)F CF C A BB A D E D E【例3】已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2，P 为AD 上的一点，满足∠BPC ＝∠A ． ① 求证；△ABP ∽△DPC ； ② 求AP 的长．【变式1】如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；②当CE ＝1时，写出AP 的长．C B AD C B A D【变式2】在梯形ABCD 中，AD ∥BC ，6AB CD BC ===，3AD =．点M 为边BC 的中点，以M 为顶点作EMF B ∠=∠，射线ME 交腰AB 于点E ，射线MF 交腰CD 于点F ，联结EF ．（1）求证：△MEF ∽△BEM ；（2）若△BEM 是以BM 为腰的等腰三角形，求EF 的长；（3）若EF CD ⊥，求BE 的长．【作业】1、如图，在ABC ∆中，90C ∠=︒，6AC =，43=BC AC ，D 是BC 边的中点，E 为AB 边上的一个动点，作90DEF ∠=︒，EF 交射线BC 于点F ．设BE x =，BED ∆的面积为y ．（1）求y 关于x 的函数关系式，并写出自变量x 的取值范围；（2）如果以B 、E 、F 为顶点的三角形与BED ∆相似，求BED ∆的面积.2、如图，已知在△ABC 中， AB =AC =6，BC =5，D 是AB 上一点，BD =2，E 是BC 上一动点，连结DE ，并作DEF B ∠=∠，射线EF 交线段AC 于F ．（1）求证：△DBE ∽△ECF ；（2）当F 是线段AC 中点时，求线段BE 的长；（3）联结DF ，如果△DEF 与△DBE 相似，求FC 的长．3、已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且BC =6，AB =DC =4，点E 是AB 的中点．（1）如图，P 为BC 上的一点，且BP =2．求证：△BEP ∽△CPD ；（2）如果点P 在BC 边上移动（点P 与点B 、C 不重合），且满足∠EPF =∠C ，PF 交直线CD于点F ，同时交直线AD 于点M ，那么:①当点F 在线段CD 的延长线上时，设BP =x ，DF =y ，求y 关于x 的函数解析式，并写出函数的定义域；②当BEP DMF S S ∆∆=49时，求BP 的长.。
一线三等角型的相似三角形问题
D E C B A F D E C B AD FE C B AF ED C B A一线三等角型的相似三角形问题一、问题引入（1）如图1，在△ABC 中，AB=AC ，∠B =∠ADE ，那么一定存在的相似三角形是 。
（2）如图2，在△ABC 中，AB=AC ，∠B =∠EDF ，那么一定存在的相似三角形是 。
二、例题讲解在△ABC 中，AB=AC=6，BC=5，D 是AB 上一点，BD=2，E 是BC 上一动点，联结DE ，并作∠DEF=∠B ，交AC 于点F 。
（1）求证：△DBE ∽△ECF.（2）当F 是AC 的中点时，求线段BE 的长。
（3）联结DF ，如果△DEF 与△DBE 相似，求FC 的长。
三、变式练习1、如图，已知等边△ABC 的边长为6，D 是BC 边上一动点，∠EDF=60°。
（1） 求证：△BDE ∽△CFD ； （2） 当BD=1，CF=3时，求BE 的长。
图1 图2F E D CB A DE C B A 2、如图，在△ABC 中，AB=AC=10，BC=16，∠B =∠ADE ，点D 、E 分别在BC 、AC 上（点D 与B 、C 不重合）.设BD=x ，AE=y ，求y 与x 之间的函数关系式及定义域。
3、已知等边△ABC 的边长为8，点D 、F 、E 分别在AB 、BC 、AC 上，BD=3，E 为AC 的中点，当△BFD 与△CEF 相似时，求BF 的值。
挑战自我： 4、已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．（1）如图，P 为AD 上的一点，满足∠BPC ＝∠A ．①求证；△ABP ∽△DPC②求AP 的长．CCC（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；②当CE ＝1时，写出AP 的长（不必写出解题过程）．四、总结当α为锐角时：BBB 当α为直角时：当α为钝角时：E。
新人教版九年级数学下册《相似专题——“一线三等角”模型》教案_13
《相似专题——“一线三等角”模型》教学设计一、【教材分析】目标知识技能经历观察、比较、归纳的学习过程，归纳出“一线三等角”模型的基本特征，并且能够在不同的背景中认识和把握基本模型。
过程方法1、培养学生观察、分析、想象、归纳和逻辑推理的能力；2、体会由特殊到一般思想、分类讨论思想和化归思想方法。
情感态度敢于面对数学活动中的困难，并能有意识地运用已有知识解决新问题.教学重点归纳“一线三等角”模型的基本特征。
教学难点在不同的背景中识别“一线三等角”模型，以及灵活解决该模型的相关问题。
学情分析该班级学生已完成了中考第一轮基本知识点的复习，对相似的判定以及相似性质的运用较熟练。
为提升综合解决问题的能力，设计了“一线三等角”模型的专题训练。
教学内容分析《相似》一章的教学内容位于人教版九年级下册第二十七章，是中考的重要考点之一,而“一线三等角”模型也曾多次出现在中考的压轴题里面，因此有必要对“一线三等角”模型进行专题训练。
问题设计师生活动设计意图环节一·从特殊到一般【归纳1】“K字型”条件：三个直角学生回忆曾接触过的K字型，教师引导学生回答：K字型题目一般给出什么条件，能得到什么结论。
通过回忆K字型的条件与结论，为归纳“一线三等角”模型的基本特征作铺垫。
结论：△CBE∽△EAD几何画板展示三个直角变为三个相等的锐角或钝角。
【归纳2】“一线三等角”条件：①有三个相等的角；②三等角顶点在同一直线上。
结论：△CBE∽△EAD∠B的对应角为∠C的对应角为∠BEC的对应角为BC的对应边为BE的对应边为CE的对应边为则，学生思考：当三个直角变为三个相等的锐角或钝角的时候，两三角形相似的结论是否还成立？教师引导学生得出证明两三角形相似的过程，并归纳出“一线三等角”模型的基本特征。
学生找准相似三角形的三对对应角，三对对应边，从而得出进一步推论：对应边的比相等。
通过几何画板动态展示，让学生直观感受“一线三等角”模型的几种形态。
相似三角形一线三等角
—线三等角型相似三角形典型例题【例1】如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF =60° （1）求证：△BDE ∽△CFD（2）当BD =1，FC =3时，求BE∙【例3】如图，在△ABC 中，AB =AC =5cm ，BC =8，点P 为BC 边上一动点（不与点B 、C 重合），过点P 作射线PM 交AC 于点M ，使∠APM =∠B ； （1）求证：△ABP ∽△PCM ；（2）设BP =x ，CM =y ．求 y 与x 的函数解析式，并写出函数的定义域． （3）当△APM 为等腰三角形时， 求PB 的长．【例4】（1）在ABC ∆中，5==AC AB ，8=BC ，点P 、Q 分别在射线CB 、AC 上（点P 不与点C 、点B 重合），且保持ABC APQ ∠=∠.①若点P 在线段CB 上（如图10），且6=BP ，求线段CQ 的长；②若x BP =，y CQ =，求y 与x 之间的函数关系式，并写出函数的 定义域；（2）正方形ABCD 的边长为5（如图12），点P 、Q 分别在直线．．CB 、DC 上（点P 不与点C 、点B 重合），且保持︒=∠90APQ .当1=CQ 时，写出线段BP 的长（不需要计算过程，请直接写出结果）.（1）在△ABC 中，AB =A C =5，BC =8，点P 、Q 分别在射线CB 、A C 上（点P 不与点C 、点B 重合），且保持∠A PQ =∠A BC ．①若点P 在线段CB 上（如图），且BP =6，求线段C Q 的长；②若BP =x ，CQ =y ，求y 与x 之间的函数关系式，并写出函数的定义域；（2）正方形ABC D 的边长为5（如图），点P 、Q 分别在直线C B 、DC 上（点P 不与点C 、点B 重合），且保持∠AP Q =90度．当CQ =1时，写出线段BP 的长（不需要计算过程，请A B PC M ABC备用图AB CPQABCD图12直接写出结果）．强化训练：1. 如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在AC 边上，且C ADE ∠=∠． (1) 求证：△ABD ∽△DCE ；(2) 如果x BD =，y AE =，求y 与x 的函数解析式，并写出自变量x 的定义域；(3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．2. 已知：如图，在△ABC 中，5==AC AB ，6=BC ，点D 在边AB 上，AB DE ⊥，点E 在边BC 上．又点F在边AC 上，且B DEF ∠=∠． (1) 求证：△FCE ∽△EBD ；(2) 当点D 在线段AB 上运动时，是否有可能使EBD FCE S S ∆∆=4．如果有可能，那么求出BD 的长．如果不可能请说明理由．3. 如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上一点，且BP =2，将一个大小与∠B 相等的角的顶点放在P 点，然后将这个角绕P 点转动，使角的两边始终分别与AB 、AC 相交，交点为D 、E 。
一线三等角相似模型
在物理学中，可以利用一线三等角 相似模型来研究物理现象和规律， 如光的反射和折射、波的传播等。
04 一线三等角相似模型的证 明方法
直接证明法
定义
直接证明法是通过直接使用已知条件和定理来证明结论的 方法。
步骤
首先，根据已知条件，明确一线三等角的定义和性质；然后， 通过比较两个三角形中的角度和边长，利用相似三角形的性质
03
注意事项
反证法需要熟练掌握反证法的原理和 推理技巧，以及能够灵活运用已知条 件。
综合法与分析法
定义
综合法是从已知条件出发，逐步推导出结论的方法；分析法是从结论出发，逐步推导出已知条件的方法。
步骤
在综合法中，首先明确已知条件和目标结论；然后，根据已知条件逐步推导所需结论；最后，总结推导过程。在分析 法中，首先明确目标结论和已知条件；然后，根据结论逐步推导所需条件；最后，总结推导过程。
，逐步推导出所需的结论。
注意事项
直接证明法需要熟练掌握相似三角形的性质和定理，以及 灵活运用已知条件。
反证法
01
定义
反证法是通过假设结论不成立，然后 推导出矛盾，从而证明结论成立的方 法。
02
步骤
首先，假设结论不成立；然后，根据 已知条件和反证法的原理，推导出与 已知条件相矛盾的结论；最后，根据 矛盾的结论，得出结论成立。
相似变换的性质
相似变换具有一些重要的性质，如保持角度不变、线 段长度比例不变等。
相似变换的应用
相似变换在几何学、物理学、工程学等领域有着广泛 的应用，如建筑设计、机械制造、航天技术等。
相似多边形的性质与应用
1 2
相似多边形的定义
相似多边形是指各对应角相等、各对应边成比例 的多边形。
相似三角形中的 “一线三等角”模型-2023年新九年级数学核心知识点与常见题型(沪教版)(解析版)
重难点专项突破：相似三角形中的“一线三等角”模型【知识梳理】一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。
一般类型：基本类型：同侧“一线三等角”异侧“一线三等角”【考点剖析】例1.如图，直角梯形ABCD 中，AB // CD ，90ABC ∠=︒，点E 在边BC 上，且34AB BE EC CD ==， AD = 10，求AED ∆的面积．【答案】24．【解析】90ABC ∠=，//AB CD ， ∴90DCB ABC ∠=∠=．又34AB BE EC CD ==， ABE ECD ∴∆∆∽．∴AEB EDC ∠=∠． ∴34AE AB ED EC ==．90EDC DEC ∠+∠=，∴90AEB DEC ∠+∠=． ∴90AED ∠=．在Rt AED ∆中，10AD =，68AE ED ∴==，． 24AED S ∆∴=．【总结】本题考查一线三等角模型的相似问题，还有外角知识、平行的判定等．例2.已知：如图，△ABC 是等边三角形，点D 、E 分别在边BC 、AC 上，∠ADE ＝60°．（1）求证：△ABD ∽△DCE ；（2）如果AB ＝3，EC ＝，求DC 的长．【分析】（1）△ABC 是等边三角形，得到∠B ＝∠C ＝60°，AB ＝AC ，推出∠BAD ＝∠CDE ，得到△ABD∽△A B C DEDCE ；（2）由△ABD ∽△DCE ，得到＝，然后代入数值求得结果．【解答】（1）证明：∵△ABC 是等边三角形，∴∠B ＝∠C ＝60°，AB ＝AC ，∵∠B+∠BAD ＝∠ADE+∠CDE ，∠B ＝∠ADE ＝60°，∴∠BAD ＝∠CDE∴△ABD ∽△DCE ；（2）解：由（1）证得△ABD ∽△DCE ，∴＝，设CD ＝x ，则BD ＝3﹣x ，∴＝，∴x ＝1或x ＝2，∴DC ＝1或DC ＝2．【点评】本题考查了等边三角形的性质，相似三角形的判定和性质，注意数形结合和方程思想的应用． 例3.已知，在等腰ABC ∆中，AB = AC = 10，以BC 的中点D 为顶点作EDF B ∠=∠， 分别交AB 、AC 于点E 、F ，AE = 6，AF = 4，求底边BC 的长．【答案】46．【解析】EDC B BED ∠=∠+∠，而EDC EDF FDC ∠=∠+∠，∴B BED EDF FDC ∠+∠=∠+∠． 又EDF B ∠=∠，∴BED FDC ∠=∠．AB C D EFAB AC=，∴B C∠=∠．EDB DCF∴∆∆∽．BE BDDC CF∴=．106104BDDC−∴=−，24DC BD∴=．又12CD DB BC==，BC∴=【总结】本题是对“一线三等角”模型的考查．例4.已知：如图，AB⊥BC，AD // BC， AB = 3，AD = 2．点P在线段AB上，联结PD，过点D作PD的垂线，与BC相交于点C．设线段AP的长为x．（1）当AP = AD时，求线段PC的长；（2）设△PDC的面积为y，求y关于x的函数解析式，并写出函数的定义域；（3）当△APD∽△DPC时，求线段BC的长．满分解答：（1）过点C作CE⊥AD，交AD的延长线于点E．∵AB⊥BC，CE⊥AD，PD⊥CD，AD // BC，∴∠ABC =∠AEC =∠PDC = 90°，CE = AB = 3．∵AD // BC，∴∠A +∠ABC = 180°．即得∠A = 90°．又∵∠ADC =∠DCE +∠DEC，∠ADC =∠ADP +∠PDC，∴∠ADP =∠DCE．又由∠A =∠DEC = 90°，得△APD∽△DCE．∴AD APCE DE=．于是，由AP = AD = 2，得DE = CE = 3．…………………………（2分）在Rt△APD和Rt△DCE中，得PD=，CD=1分）AB CDPAB CD（备用图）于是，在Rt △PDC 中，得 PC = （1分）（2）在Rt △APD 中，由 AD = 2，AP = x ，得 PD 1分）∵ △APD ∽△DCE ，∴AD PD CE CD =．∴ 32CD PD ==1分）在Rt △PCD 中，22113332224PCD S PD CD x ∆=⋅⋅=⨯=+．∴ 所求函数解析式为2334y x =+．…………………………………（2分） 函数的定义域为 0 < x ≤ 3．…………………………………………（1分）（3）当△APD ∽△DPC 时，即得 △APD ∽△DPC ∽△DCE ．…………（1分）根据题意，当△APD ∽△DPC 时，有下列两种情况：（ⅰ）当点P 与点B 不重合时，可知 ∠APD =∠DPC ．由 △APD ∽△DCE ，得 AP PD DE DC =．即得AP DE PD CD =． 由 △APD ∽△DPC ，得AP AD PD DC =． ∴AD DE CD CD =．即得 DE = AD = 2． ∴ AE = 4．易证得四边形ABCE 是矩形，∴ BC = AE = 4．…………………（2分）（ⅱ）当点P 与点B 重合时，可知 ∠ABD =∠DBC ．在Rt △ABD 中，由 AD = 2，AB = 3，得 BD =．由 △ABD ∽△DBC ，得AD BD BD BC =．即得 =． 解得 132BC =．………………………………………………………（2分）∴ △APD ∽△DPC 时，线段BC 的长分别为4或132．方法总结本题重点在于：过点C 作CE ⊥AD ，交AD 的延长线于点E ．(构造一线三角，出现相似三角形，进行求解) 例5.在梯形ABCD 中,AD ∥BC ，︒=∠===90,2,1A BC AB AD .（如图1）(1)试求C ∠的度数；(2)若E 、F 分别为边AD 、CD 上的两个动点(不与端点A 、D 、C 重合),且始终保持︒=∠45EBF ,BD 与EF交于点P .（如图2）①求证:BDE ∆∽BCF ∆；②试判断BEF ∆的形状（从边、角两个方面考虑），并加以说明；③设y DP x AE ==,,试求y 关于x 的函数解析式,并写出定义域.答案：（1）作BC DH ⊥，垂足为H ，在四边形ABHD 中，AD ∥BC ，︒=∠==90,1A AB AD ，则四边形ABHD 为正方形又在CDH ∆中，1,1,90=−====∠︒BH BC CH AB DH DHC ， ∴︒︒=∠−=∠452180DHC C .（2）①∵四边形ABHD 为正方形，∴︒=∠45CBD ,︒=∠45ADB ，又∵︒=∠45EBF ，∴CBF DBE ∠=∠又∵︒=∠=∠45C BDE ,∴BDE ∆∽BCF ∆.②BEF ∆是等腰直角三角形，∵BDE ∆∽BCF ∆， ∴CB FB BD BE =,又∵︒=∠=∠45DBC EBF ,∴EBF ∆∽DBC ∆，又在DBC ∆中，︒=∠=∠45C DBC ,为等腰直角三角形，∴BEF ∆是等腰直角三角形. ③x x x x x x y +−=+−⨯=1221222，（0<x <1）.方法总结 第三问方法提示：过点P 作AD 的垂线于点H ，构造一线三直角相似，进行求解，很简单。
“一线三等角”相似模型专题学习
§专题学习：“一线三等角”相似模型安海中学 谢伟良【教学目标】1、认识“一线三等角”的基本图形并会用模型解决相似中的相关问题2、通过抽象模型，图形变换，变式类比等方法提高综合解题能力 【教学重点】运用“一线三等角”相似模型解题。
【教学难点】“一线三等角”的基本图形的提炼、变式和构造运用 【教学方法】 合作探究、小组讨论 【教具准备】 三角尺，多媒体． 【教学过程】一．类比探究，问题导入：（1）如图，已知∠A=∠BCD=∠E=90°，图中有没有相似三角形？并说明理由。
如图，已知∠A=∠BCD=∠E=60°，图中有没有相似三角形？并说明理由。
（3）如图，已知∠A=∠BCD=∠E=120°，图中有没有相似三角形？并说明理由。
思考：解：△ABC ∽△ECD,理由如下： ∵∠ACD 是△CDE 的一个外角 ∴∠ACD=∠D+∠E=∠D+90°又∵∠ACD=∠ACB+∠BCD=∠ACB+90° ∴∠ACB=∠D ∵∠A=∠E=90° ∴△ABC ∽△ECDEEDCBA观察以上三个图形，同学们能否说说这三个图形的共同特点？1、点A 、C 、E 在同一条直线上2、∠A=∠BCD=∠E= α3、△ABC ∽△ECD我们简单的把这样的图形叫做“一线三等角”BB二、抽象模型，揭示实质如图，已知∠A=∠BCD=∠E=α°，图中有没有相似三角形，并写出证明过程。
特别注意：在写相似三角形时，要找好对应点。
三．运用新知，看图作答四、典例解析综合运用归纳：“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形。
这个等角可以是直角，也可以是锐角或者钝角。
解：△ABC∽△ECD,理由如下：∵∠ACD是△CDE的一个外角∴∠ACD=∠D+∠E=∠D+α°又∵∠ACD=∠ACB+∠BCD=∠ACB+α°∴∠ACB=∠D∵∠A=∠E=α°∴△ABC∽△ECD总结规律：顺口溜：“一线三等角，两头对应好，外角导等角，相似轻易找”E例1：下列每个图形中，∠1=∠2=∠3，请你快速找出“一线三等角”的基本图形所形成的相似三角形(对应顶点写在对应位置）。
《一线三等角——相似三角形知识拓展》
《一线三等角——相似三角形知识拓展》相似三角形，是初中几何学习的重要内容，也是中考考查的重要内容，但是统观近几年的中考考题，单纯考查证明两个三角形相似的知识很少，几乎都是考查它与函数、与圆等知识的综合运用。
而且从各地近几年中考题当中可以发现，一线三等角这一模型是最近几年考试的热门模型，鉴于此，于是我就想在教学中给学生补充这一模型，并且让学生能够快速认识这一模型，并且能够利用这一模型提升解题技能。
根据这一目标，这堂课我主要设计了以下七个环节:（一）整理旧知，提炼模型这一环节，根据学生的认知规律，我设计了如下四个问题：问题1：如图1，等腰直角三角形ABC的顶点B在直线l上，AB=BC，∠ABC=90°，AD⊥直线l于点D，CE⊥直线l于点E．求证：△ADB≌△BEC问题2：如图2，已知点A、C、E在同一条直线上，∠A=∠BCD=∠E=90°，图中三角形相似吗？请说明理由。
问题3：如图3，已知已知点A、C、E在同一条直线上，∠A=∠BCD=∠E=60°，图中三角形相似吗？请说明理由。
问题4：如图4，已知点A、C、E在同一条直线上，∠A=∠BCD=∠E=120°，图中三角形相似吗？请说明理由。
（二）揭示本质，提炼模型第一环节的四个问题，由学生很熟悉的两个三角形全等的图形引入，逐渐弱化条件，从而发现当一条直线上有三个相等角的顶点都在这条直线上，从而所构成的三角形相似。
归纳出这一模型之后，马上强调，以后在做题的过程中，如果碰到一线三等角这一模型的图形，就可联想到有三角形相似，从而可以得出对应边和对应角的关系。
（三）模型运用学生只是认识了这一模型，还不够，于是我又接着设计了这一环节，让学生能快速识别并写出相似的三角形。
于是我设计了一组练习题，如下：下列各图形中，若∠1=∠2=∠3，请你快速找出图中符合“一线三等角”模型的相似三角形。
学生在做完这一组练习之后，帮助学生归纳两个一线三等角模型的相似三角形，对应角的位置之间存在一种交错的对应关系，这一方法，主要便于学生以后碰到一线三等角模型的相似三角形，从而可以快速确定边、角之间的对应关系。
相似三角形汇总3一线三角相似问题(K12教育文档)
相似三角形汇总3一线三角相似问题(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（相似三角形汇总3一线三角相似问题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为相似三角形汇总3一线三角相似问题(word版可编辑修改)的全部内容。
相似三角形汇总第三部分一线三角相似问题重点:“一线三等角”图形中判定三角形相似及两类三个三角形两两相似的分类讨论，难点：在根据“一线三等角”图形中相似三角形的特点，确定动点位置,构造相似三角形.【知识点整理】(一线三等角型）（一线三直角型)【经典例题】1.如图，等边△ABC中，边长为6，D是BC上动点，∠EDF=60°（1）求证：△BDE∽△CFD（2)当BD=1，FC=3时，求BE2. 如图，在正方形格子（正方形小格子的边长为1)中有一个矩形ABCD,在AB 上，找出点E ，联结DE 、CE ，使得△DEC 与△DAE 及△EBC 都相似.3. 如图,在矩形ABCD 中,点M 在AD 上，将△DMC 沿MC 翻折，点D 恰好落在AB 边的E 点位置,若△MEC 与△AME 相似，求:矩形相邻两边AD 与AB 的比。
E AC BDM4. 如图，已知正方形ABCD ，将一块等腰直角三角尺的锐角顶点与A 重合，并将三角尺绕点旋转，当M 点旋转到BC 的垂直平分线PQ 上时，连接ON,若ON=8，求MQ 的长。
5. 在△ABC 中，∠C=90°，AC=3，BC=4，O 是AB 上的一点，且52=AB AO ,点P 是AC 上的一个动点，PQ ⊥OP 交线段BC 于点Q ，（不与点B ，C 重合)，已知AP=2,求CQ.6. 正方形ABCD 的边长为5（如下图），点P 、Q 分别在直线CB 、DC 上(点P 不与点C 、点B 重合），且保持∠APQ=90°.当CQ=1时,求出线段BP 的长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第13讲 “一线三等角相似”问题
二、方法剖析与提炼
例1.如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF ＝60° （1）求证：△BDE ∽△CFD （2）当BD ＝1，FC ＝3时，求BE
【解析】主要考查相似三角形的判定和性质，利用条件得到∠BED=∠FDC 是解题的关键，注意等边三角形性质的应用．
【解答】（1）要证明△BDE 与△CFD 相似，已知条件是∠B ＝∠C ，还缺少一个角或一组对应边成比例；
（2）△ABC 是等边三角形，∠EDF ＝60°∠B ＝∠C ＝∠EDF ＝60°，∠EDC ＝∠EDF ＋∠FDC ＝∠B ＋∠BED ，∠BED ＝∠FDC 。
充分利用三角形的一个外角等于与之不相邻的两个内角之和这一性质；
（3）根据∠BED ＝∠FDC ，∠B ＝∠C ；容易得出△BDE ∽△CFD ； （4）因为△BDE ∽△CFD ，可以得出
BE CD
BD FC
BD ＝1，FC ＝3，CD ＝5 所以BE ＝3
5
【说明】（1）本题属于典型的一线三等角相似，由题意可得∠B ＝∠C ＝∠EDF ＝60°再用外角可证∠BED ＝∠CDF ，可证△BDE 与△CFD 相似，根据相似比便可求得线段BE 的长度
（2）根据一线三等角的相似三角形中的对应边中已知三边可以求第四边。
例2. （2015•泰安）如图，在△ABC 中，AB=AC ，点P 、D 分别是BC 、AC 边上的点，且∠APD=∠B ． （1）求证：AC•CD=CP•BP；
（2）若AB=10，BC=12，当PD ∥AB 时，求BP 的长．
【解析】本题主要考查了相似三角形的判定与性质、等腰三角形的性质、平行线的性质、三角形外角的性质等知识，把证明AC•CD=CP•BP 转化为证明AB•CD=CP•BP 是解决第（1）小题的关键，证到∠BAP=∠C 进而得到△BAP ∽△BCA 是解决第（2）小题的关键．
【解答】（1）根据题意可证得∠B=∠C ，∠BAP=∠DPC ，所以△ABP ∽△PCD 。
由相似三角形的性质可以得出
BP AB
CD CP
=
,有因为AB=AC ，所以AC •CD=CP •BP （2）因为PD ∥AB ，所以∠APD=∠BAP ．又因为∠APD=∠C ，所以∠BAP=∠C ． 根据∠B=∠B ，∠BAP=∠C ，可以得出△BAP ∽△BCA ，所以BA BP
BC BA
=
,把AB=10，BC=12代入就可以求出BP=
253
【说明】（1）易证∠APD=∠B=∠C ，从而可证到△ABP ∽△PCD ，即可得到=，
即AB•CD=CP•BP，由AB=AC 即可得到AC•CD=CP•BP；
（2）由PD ∥AB 可得∠APD=∠BAP ，即可得到∠BAP=∠C ，从而可证到△BAP ∽△BCA ，然后运用相似三角形的性质即可求出BP 的长．
例3.如图，在△ABC 中，AB ＝AC ＝5cm ，BC ＝8，点P 为BC 边上一动点（不与点
B 、
C 重合），过点P 作射线PM 交AC 于点M ，使∠APM ＝∠B ； （1）求证：△ABP ∽△PCM ；
（2）设BP ＝x ，CM ＝y ．求 y 与x 的函数解析式，并写出函数的定义域．
（3）当△APM 为等腰三角形时， 求PB 的长．
【解析】相似三角形的判定及性质定理和等腰三角形的性质，综合运用相似三角形的判定及性质定理解答此题的关键．注重运用分类讨论的思想方法． 【解答】（1）第1小题中，还是有∠APM 等于等腰三角形一个底角（∠B ）这个条件，所以还是符合“一线三等角相似”，所以比较容易证得△ABP ∽△PCM （2）第2小题就是在例2中的已知条件改成未知数x ，y ，把求值改成探究x ，y 的函数关系，提高了思维含量；因为BP ＝x ，CM ＝y ，CP ＝8－x ，根据相似比
MC BP PC AB =
，把值代入比例式就可以得出y x x =-85，x x y 5
8
512+-=)80(<<x
P
A
B
C
P
M A
B
C P
M
（3）当AP ＝PM 时，∵
AB PC
PA PM =
∴PC ＝AB ＝5， ∴BP ＝3 当AP ＝AM
时，∵∠APM ＝∠B ＝∠C ∴∠PAM ＝∠BAC 即点
P 与点B 重合 ∴BP ＝0
当MP ＝AM 时∴∠MAP ＝∠MPA ∴△MAP ∽△ABC ∴85==BC AB AP MP ∴85
==AB PC PA PM
即8558=
-x ∴BP ＝8
39
【说明】（1）第（1）（2）小题都是用常规的一线三等角相似的方法。
对△APM 进行等腰三角形的分类讨论时，可将条件转化成与△ABP ∽△PCM 相关的结论。
（2）等腰三角形分类讨论需要灵活应用，可采用的方法添底边上的高，将等腰的条件进行转化，一线三等角相似这类问题中可将等腰的条件转化至△ABP 和△
PCM 中简化运算。
三、能力训练与拓展
1.如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在AC 边上，且C ADE ∠=∠． (1) 求证：△ABD ∽△DCE ；
(2) 如果x BD =，y AE =，求y 与x 的函数解析式，并写出自变量x 的定义域； (3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．
A
B
C
D
E
2.在△ABC 中，AB=AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD=AE ，∠DAE=∠BAC ，连接CE ． （1）如图1，当点D 在线段BC 上，如果∠BAC=90°，求：∠BCE ．
（2）如图2，当点D 在线段BC 上移动，设∠BAC=α，∠BCE=β．则α，β之间有怎样的数量关系？请说明理由．
3.已知在等腰三角形ABC 中，4,6AB BC AC ===，D 是AC 的中点， E 是BC 上的动点（不与B 、C 重合），连结DE ，过点D 作射线DF ，使EDF A ∠=∠，射线DF 交射线EB 于点F ，交射线AB 于点H . （1）求证：CED ∆∽ADH ∆；
（2）设,EC x BF y ==. ①用含x 的代数式表示BH ；
②求y 关于x 的函数解析式，并写出x 的定义域.
4. （2015•大连）在△ABC 中，点D ，E ，F 分别在AB ，BC ，AC 上，
且∠ADF+∠DEC=180°，∠AFE=∠BDE ．
（1）如图1，当DE=DF 时，图1中是否存在与AB 相等的线段？若存在，请找出，并加以证明；若不存在，说明理由；
（2）如图2，当DE=kDF （其中0＜k ＜1）时，若∠A=90°，AF=m ，求BD 的长（用含k ，m 的式子表示）．
H
A
B
C
D
E
F
四、微课提示与指导
1.方法剖析与提炼例1微视频
2.方法剖析与提炼例3微视频
3.能力训练与拓展题2微视频
4.例题讲解PPT
5.相关链接：易良斌工作室--名师教你学解题
/index.php?r=studio/index&sid=169五、参考答案与解答。