(精品)一线三等角相似模型.ppt
合集下载
精品一线三等角相似模型.ppt课件
• (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
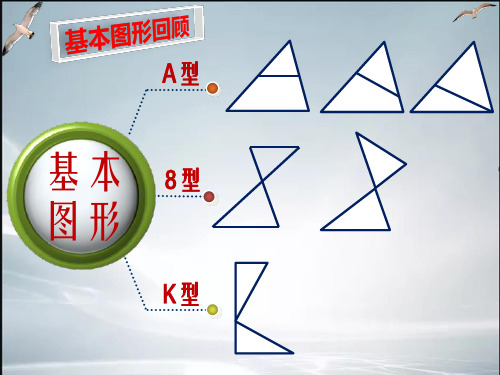
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
CA MBPC5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
CA MBPC5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
相似三角形基本模型一线三等角精品PPT课件

△ABE∽ △ECF ∽ △AEF
A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF
F
((2)1)点点E为E为BBCC上上任任意意一一点点若,∠若B= ∠∠CB==α,∠∠CA=E6F0°= ∠, ∠CA,则EF△=A∠BCE,则与△ EC△FA的B关E与系△还成EC立F吗的?关系还成立吗?
说明理由
B
α
α
B
E
α
C
点拨:要善于运用类比、迁移的数学方法 解决问题。
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E 重合,若AD=10, AB= 8,
则EF=___5___
D
F
C
EE
A
点拨:要善于在复杂图形中寻找基本型。 B
A
E F
B
D
C
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的 中点, 且∠EDF =∠C, (1) 若BE·CF=48,则AB=__8___
(2)在(1)的条件下,若EF=m,
则S△DEF =___3__m__
A EH
F
P
B
D
点拨:联想基本模型,寻找 相关结论。
C
A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF
F
((2)1)点点E为E为BBCC上上任任意意一一点点若,∠若B= ∠∠CB==α,∠∠CA=E6F0°= ∠, ∠CA,则EF△=A∠BCE,则与△ EC△FA的B关E与系△还成EC立F吗的?关系还成立吗?
说明理由
B
α
α
B
E
α
C
点拨:要善于运用类比、迁移的数学方法 解决问题。
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E 重合,若AD=10, AB= 8,
则EF=___5___
D
F
C
EE
A
点拨:要善于在复杂图形中寻找基本型。 B
A
E F
B
D
C
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的 中点, 且∠EDF =∠C, (1) 若BE·CF=48,则AB=__8___
(2)在(1)的条件下,若EF=m,
则S△DEF =___3__m__
A EH
F
P
B
D
点拨:联想基本模型,寻找 相关结论。
C
一线三等角优秀课件

B
D
D
E
AC
E
D
AC
E
思考:以上图形有什么共同点?
一线三等角,两头对应好,互补导等角,相似轻易找
活动三 图形辨析 强化理解
• 下列每个图形中,∠1=∠2=∠3,请你快速找出 “一线三等角”的基本图形所形成的相似三角 形(要求对应的顶点写在对应的位置)
A
2 1 B
D
E
3 C
A E
1 B
2 F
D
G 3
如图,当∠CPD=∠CAB=∠EBD时,两三角形还相似吗?
解: △CPA∽△PDB 理由:∵∠CPD=∠CAB
∠CPA+∠BPD=∠CPA+∠C
∴∠EC=∠BPD
又∵∠CAB=∠EBD ∴1800-∠CAB=1800-∠EBD 即∠PAC=∠PDB ∴△CPA∽△PDB
活动二抽象模型,揭示本质
B
AC B
• (3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E 恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系。
活动五 收获分享
1、通过本节课的学习,你有什么收获? 2、本节课的学习过程,对你今后思考问题有什
么启示?
D 理由:∵∠A=∠BCD=∠E= α°
•
∠ACB+∠DCE=1800-α°
•αα
A• •
C
∠CDE+ ∠DCE=1800-α°
α
∴∠ACB= ∠CDE
E 又∵∠A=∠E
•
∴ △ABC∽△ECD
活动二抽象模型,揭示本质
如图,当∠CPD=∠CAB=∠EBD时,.如图,已知∠A=∠BCD=∠E=120°, △ABC与 △ECD是否相似?并说明由。
一线三等角(公开课)ppt课件

A
D
A
E
E
B1
A 1
E
B
2
F
F
2
G
3C
D 3
G
C
2 1 B
D
A
E
1
2
B
F
3 C
D
3 C 7
典例解析 综合运用
例1:在等边△ABC中,D为BC边上一点,E为AC边上一点, 且∠ADE=60°, BD=3,CE=2,则△ABC的边长为多少?
A
BD
E C
8
典例解析 综合运用
例2、如图,在平面直角坐标系中,o为坐标原点,B点坐标为(5,0) ,梯形OBCD中,CD∥OB,OD=BC=2,DC=3,∠DOB=60°,若点E、F分 别在线段DC、CB上
答:⊿ABE∽ ⊿ECF 理由:∵ ∠B=∠AEF=∠C=90°
A F
∴ ∠A+ ∠1=90°, ∠2+ ∠1=180°- ∠AEF=90 °
∴ ∠A=∠2
1
2
B
E
C
∴ ⊿ABE∽ ⊿ECF
图1
2、如图,已知∠B=∠AEF=∠C=60°,图中有没有相似三角形?并说明理由
。
A
F
3、如图,已知∠B=∠AEF=∠C=120°,图中有没有相B 似
人教版数学九年级下
1
• 学习目标:
1、熟悉“一线三等角”的基本图形,并能解决相似中 的相关问题.
2、通过抽象模型,图形变换,变式类比等方法提高综 合解题能力.
• 学习重点:
运用“一线三等角”相似型的基本图形解题。
2
课前回顾
三角形相似的判定定理有哪些?
3
一线三等角模型复习课Ppt0000050

链接中考
链接中考
挑战自我
在△ABC中,D为BC边的中点,以D为顶点 作∠EDF=∠B. ∠EDF的两边交AC、AB 于E、F。 (1)请问你能找到图中的相似三角形吗?
挑战自我
自我小结
1、一线三等角的证明方法和结论 2、类比思想、从特殊到一般的思想 3、掌握一线三等角的基本图形,并会利用比例关 系解决图形问题 4、。。。。。。
相似三角形基本图形复习
——一线三等角
课前导学
如图,∠C=∠ABE=∠F=90°,AB=BE。 你能得到什么结论?
课前导学
三等角=90°
课前导学
三等角=60°或45°
课前导学
三等角为任意角
方法归纳
类比总结:当某条直线或线段的同一侧有依次排序的 三个相等的角时,首尾两个角所在的三角形相似,我 们把这种特殊的相似称为“一线三等角”。
一线三等角模型ppt课件

一线三等角模型
2019
-
1
通俗地讲,一条直线上有三个相等的角一般就会存在相似的三角形!
什么是一线三等角?
如图,等腰△ABC中,AB=AC,∠EDF=∠B,请问图中 是否有相似三角形?
相似三角形判定 定理一: 两角对应相等, 两三角形相似。
注意:对应边千万不要找错,相同的角 标记同一个符号会比较清晰!
2019 2
“一线三等角”模型 教学目标及重、难点
教学目标: 用“一线三等角”基本模型解决相似三角形中的相 关问题; 重点:掌握“一线三等角”基本模型; 难点: “一线三等角”基本图形的提炼、变式和运用。
特别是“一线三直角”辅助线的构造
2019 3
“一线三等角”模型按照角度的分类
锐角形一线三等角
中点型“一线三等角”模型
中点型: 至少有三 对相似三 角形
β
再次提醒:对应边和对应角千万不要找错!
2019
-
7
一线三直角在直角坐标系中的应用
2012年上海中考24题
1 t 2
4 2
t
2
1 t 2
4
2019
-
8
一线三直角巧求点坐标
尝试用上题中你总结的方法解答下题: 2011年宝山一模18题
方法二:两点 距离公式; 方法三:利用 互相垂直的一 次函数(针对 优等生,且此 法适用于任意 三角形翻折)
PD DH CD CH PD AD CD CH DH AD
3 x
2
3 x 2
2
BC 4
3
13
13 2
PD PC AD PD 13 PC BC 2
15
2019
2019
-
1
通俗地讲,一条直线上有三个相等的角一般就会存在相似的三角形!
什么是一线三等角?
如图,等腰△ABC中,AB=AC,∠EDF=∠B,请问图中 是否有相似三角形?
相似三角形判定 定理一: 两角对应相等, 两三角形相似。
注意:对应边千万不要找错,相同的角 标记同一个符号会比较清晰!
2019 2
“一线三等角”模型 教学目标及重、难点
教学目标: 用“一线三等角”基本模型解决相似三角形中的相 关问题; 重点:掌握“一线三等角”基本模型; 难点: “一线三等角”基本图形的提炼、变式和运用。
特别是“一线三直角”辅助线的构造
2019 3
“一线三等角”模型按照角度的分类
锐角形一线三等角
中点型“一线三等角”模型
中点型: 至少有三 对相似三 角形
β
再次提醒:对应边和对应角千万不要找错!
2019
-
7
一线三直角在直角坐标系中的应用
2012年上海中考24题
1 t 2
4 2
t
2
1 t 2
4
2019
-
8
一线三直角巧求点坐标
尝试用上题中你总结的方法解答下题: 2011年宝山一模18题
方法二:两点 距离公式; 方法三:利用 互相垂直的一 次函数(针对 优等生,且此 法适用于任意 三角形翻折)
PD DH CD CH PD AD CD CH DH AD
3 x
2
3 x 2
2
BC 4
3
13
13 2
PD PC AD PD 13 PC BC 2
15
2019
一线三等角模型ppt(共22张PPT)

(11分)如图,在平面直角坐标系中,直线与抛物线交于A、B两点,点A在x轴上,点B的横坐标为-8.
没边相等证相似.
若不存在,请说明理由.
若存在,请直接写出所有符合条件的点F的坐标;
((21)01如2成图都①),(当本点小Q题在满E线分段10A分C)上,且HAP=AQ时,求证:△BPE≌△CQE; 若(A2)B=根k据A图E,象A写C出= k在A第F,一试象探限究内H,E当与取H何F之值间时F的,数y1量<关y2系?,并说明理由.
FQ之延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为
一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点
H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,
并说明理由. 有边相等证全等;
若存在,请直接写出所有符合条件的点F的坐标;
有边相等证全等;
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图
中所有的相似三角形,并证明你的结论.
已知:在矩形AOBC中,OB=3,OA=2.分别以 OB、OA所在直线为x轴和y轴,建立如图所示的 平面直角坐标系.若点F是边BC上的一个动点( 不与B、C重合),过F点的反比例函数(k>0)的
一个特殊图形的应用——一线三等角模型
考试过程中学生若能遇到自己平时非常熟悉的题型,快 速找到解决问题的突破口,就能减轻思维量,提高做题速 度,缓解考试紧张情绪,取得理想的成绩。因此,平时教 学中模型的渗透就非常重要。
一线三等角解题理念: 有边相等证全等; 没边相等证相似.
建立模型
2013一调13 如图,在平面直角坐标系中,直线y= -2x+2与 x轴、 y轴分别相交于点A、B,四边形ABCD是正方形,曲线在第一象限经 过点D.则________.
初中数学北师大九年级上册图形的相似-相似三角形“一线三等角型”PPT

又ADE C B
△ADE ∽△ABD;
又D为中点
根据三线合一知 ABD为直角三角形
ADE为直角三角形
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(1)证明:AB AC且ADE C ADE B C
DAB ADB 180 B
,求CF的长
证明: ABC 为பைடு நூலகம்边三角形
B C 60
又EDF ABC
EDF B C
在BDE中BED EDB 180 - B
且EDB CDF 180 - EDF
EDB CFD
△BDE ∽△CFD
BD BE CF CD
1 即 1 3
CF 1 CF 1
3
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
ADB CDE 180 ADE
又ADE B
ADB CED △ABD ∽△DCE ;
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(2)解:由(1)可得
y 8
8-y
x
10-x
BD AB CE DC
x 8 8 - y 10 - x
化简得y 1 x2 - 5 x (8 0 x 10) 84
△ADE ∽△ABD;
又D为中点
根据三线合一知 ABD为直角三角形
ADE为直角三角形
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(1)证明:AB AC且ADE C ADE B C
DAB ADB 180 B
,求CF的长
证明: ABC 为பைடு நூலகம்边三角形
B C 60
又EDF ABC
EDF B C
在BDE中BED EDB 180 - B
且EDB CDF 180 - EDF
EDB CFD
△BDE ∽△CFD
BD BE CF CD
1 即 1 3
CF 1 CF 1
3
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
ADB CDE 180 ADE
又ADE B
ADB CED △ABD ∽△DCE ;
【例2】如图,在 ABC中,AC=AB=8,BC=10,D是BC边上的动点,
点
E在AC边上,且 ADE= C
(1)求证:△ABD ∽△DCE
(2)如果BD= x ,AE =y,求y与x的函数关系式,并写出x的取值范围.
(3)当点D是BC的中点时,试说明 ADE是什么三角形,并说明理由
(2)解:由(1)可得
y 8
8-y
x
10-x
BD AB CE DC
x 8 8 - y 10 - x
化简得y 1 x2 - 5 x (8 0 x 10) 84
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
个小正方形EFGH,其中E,F,G分别在AB,BC,FD
上.若BF= 6 ,则小正方形的周长为( ) 2
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
• 解:(1)∵△ABC是等边三角形,∠EDF=60° • ∴∠B=∠C=∠EDF=60° • ∵∠EDC=∠EDF+∠FDC=∠B+∠BED • ∴∠BED=∠FDC • ∴△BDE∽△CFD • (2)∵△BDE∽△CFD
A
E
F
•
∴
FC CD BD BE
BD
C
• ∵BD=1,FC=3,CD=5
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式ቤተ መጻሕፍቲ ባይዱ
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
C
A M
B
P
C
4 4 x x CD CD x2 4x
4
23:33
• 如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点, 当M点在BC上运动时,保持AM和MN垂直.
• (1)证明:Rt△ABM∽Rt△MCN;
• (2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式; 当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大 面积;
• 如图,等边△ABC中,边长为6,D是BC上动点, ∠EDF=60°
• (1)求证:△BDE∽△CFD • (2)当BD=1,FC=3时,求BE
A
E
F
BD
C
• 如图,等边△ABC中,边长为6,D是BC上动点, ∠EDF=60°
• (1)求证:△BDE∽△CFD
• (2)当BD=1,FC=3时,求BE
y 1 x2 8 x (0 x 8) 55
(3)当AP=PM时
∵
PM PC PA AB
∴PC=AB=5
∴BP=3
当AP=AM时
∵∠APM=∠B=∠C
∴∠PAM=∠BAC即点P与点B重合
∴P不与点B、C重合
∴舍去
当MP=AM时
∴∠MAP=∠MPA
∴△MAP∽△ABC
∴ MP AB 5 AP BC 8
• (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
56 A. 8
56 B. 6
C.5 6 D.3 6
2
10
26
6 36
23:33
2
2
26
(2017鄂尔多斯)如图1,正△ABC的边长为4,点P为BC 边上的任意一点,且∠APD=60°,PD交AC于点D,设线 段PB的长度为x,图1中某线段的长度为y,y与x的函数关 系的大致图象如图2,则这条线段可能是图1中的( ) A. 线段AD B. 线段AP C. 线段PD D. 线段CD
围. (3)当△APM为等腰三角形时, 求PB的长.
A
M
B
P
C
解:(1)∵AB=AC,∠APM=∠B∴∠APM=∠B=∠C
∵∠APC=∠APM+∠MPC=∠B+∠BAP ∴∵∠BAP=∠MPC
∴△ABP∽△PCM
(2)∵BP=x,CM=y,CP=8-x
∴ AB BP PC MC
∴
5 x 8x y
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
个小正方形EFGH,其中E,F,G分别在AB,BC,FD
上.若BF= 6 ,则小正方形的周长为( ) 2
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
• 解:(1)∵△ABC是等边三角形,∠EDF=60° • ∴∠B=∠C=∠EDF=60° • ∵∠EDC=∠EDF+∠FDC=∠B+∠BED • ∴∠BED=∠FDC • ∴△BDE∽△CFD • (2)∵△BDE∽△CFD
A
E
F
•
∴
FC CD BD BE
BD
C
• ∵BD=1,FC=3,CD=5
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式ቤተ መጻሕፍቲ ባይዱ
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
C
A M
B
P
C
4 4 x x CD CD x2 4x
4
23:33
• 如图,正方形ABCD边长为8,M、N分别是BC、CD上的两个动点, 当M点在BC上运动时,保持AM和MN垂直.
• (1)证明:Rt△ABM∽Rt△MCN;
• (2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式; 当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大 面积;
• 如图,等边△ABC中,边长为6,D是BC上动点, ∠EDF=60°
• (1)求证:△BDE∽△CFD • (2)当BD=1,FC=3时,求BE
A
E
F
BD
C
• 如图,等边△ABC中,边长为6,D是BC上动点, ∠EDF=60°
• (1)求证:△BDE∽△CFD
• (2)当BD=1,FC=3时,求BE
y 1 x2 8 x (0 x 8) 55
(3)当AP=PM时
∵
PM PC PA AB
∴PC=AB=5
∴BP=3
当AP=AM时
∵∠APM=∠B=∠C
∴∠PAM=∠BAC即点P与点B重合
∴P不与点B、C重合
∴舍去
当MP=AM时
∴∠MAP=∠MPA
∴△MAP∽△ABC
∴ MP AB 5 AP BC 8
• (3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?求此时x的 值.
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
56 A. 8
56 B. 6
C.5 6 D.3 6
2
10
26
6 36
23:33
2
2
26
(2017鄂尔多斯)如图1,正△ABC的边长为4,点P为BC 边上的任意一点,且∠APD=60°,PD交AC于点D,设线 段PB的长度为x,图1中某线段的长度为y,y与x的函数关 系的大致图象如图2,则这条线段可能是图1中的( ) A. 线段AD B. 线段AP C. 线段PD D. 线段CD
围. (3)当△APM为等腰三角形时, 求PB的长.
A
M
B
P
C
解:(1)∵AB=AC,∠APM=∠B∴∠APM=∠B=∠C
∵∠APC=∠APM+∠MPC=∠B+∠BAP ∴∵∠BAP=∠MPC
∴△ABP∽△PCM
(2)∵BP=x,CM=y,CP=8-x
∴ AB BP PC MC
∴
5 x 8x y
