(全国通用)2018版高考数学总复习 考前三个月 解答题滚动练8 理
全国通用2018版高考数学总复习考前三个月解答题滚动练6理.doc

解答题滚动练61.已知函数_f(x)=cos 2^r+2sin2^+2sin x.JI r JI JI (1)将函数广(2x)的图象向右平移;个单位长度得到函数g(x)的图象,若,—,求函0 J.乙乙数g(x)的值域;⑵已知a, b, c分别为△/此'中角』,B,。
的对边,且满足b=2,辰(0,成),f(A)=吏+1,胰a= 2力sin A,求ZX/H。
的面积.解f{x) =cos 2x+2sir?x+2sin x= cos 2x~\~ (1 —cos 2x) +2sin x=l + 2sin x.(1)平移可得g(x) =2sin(2x—耳]+1,r JI JI•12,'JI r JI 2 JI•Q y -- fZZ - -- -----3 6, 3 ,JI当入=正时,g(x)min=0;5 JI当X=~^时,&(才)max = 3 ,..•所求值域为[o, 3].⑵由已^n^3a=2Z?sin 4及正弦定理,得柬sin J=2sin ^sin A,..sin b=^~.JIJI二B=五,由f(W) =yj"^ +1,得sin A— %,由正弦定理,得加从而,=号~,•< _1 ,.厂1 2诉协+忠3+柘••S^ABC—Q abs 1 n C—X X 2 X —.Z L J O 7E O2.在等差数列{&}中,公差必0,勿=1,且切,血,禹成等比数列.(1)求数列{绥}的通项公式;⑵若上=令求数列{〃}的前刀项和Tn.解(1)由切,32, 35成等比数列知,总=3135,即(动+责』'(切+ 44),即d=2axd,又必0, 31 = 1,解得d=2,故&=2刀一1.9n—1 1 Q 4 ?n— 1(2)bn= 2〃,则几=云+瑚+瑚------ 2〃 , ①O O U U O1 / 1 1,3,5, . 2/7—1 —由①式两边><S,有云久=瑚+瑚+卒 ----- 史+i , ②O O O 0由①一②,刀+ 1 化简得1=1一千.3.如图,在四棱锥夕一/时中,底面/助为平行四边形,AP=AB=AC=a, AD=y]2a, PAL 底面ABCD.⑴求证:平面冏平面0G(2)在棱任?上是否存在一点E,使得二面角B-AE-D的平面角的余弦值为一碧?若存在, 求出4=争^值;若不存在,请说明理由.⑴证明在△/6Z?中,AC=a, CD=a, AD=吏a,由勾股定理得CD勾AC,\9PA1_底面0%,:.PAL CD,又也U平面用C,用u平面用乙PAHAC=A,:.CDL平面06:又•.・67XZ平面物,・.・平面皿_L平面PAC.⑵解由(1)知,ABLAC,又用上底面/及刀,・.・以刀为原点,AB, AC, #所在直线分别为x轴,y轴,z轴建立如图所示坐标系,则J(0, 0,0), B(a, 0, 0), C(0, a, 0), D( — a, a, 0), P(0, 0, a),CE 一一假设点E(&,Y E,勿)存在,且=—,则CE=入CP,即 3, Y E~ a., Z E)=人(0, ~a, a),・・ XE= 0, Y E= (1 — 4) a, ZE= 4 a.:.~AB= (a, 0, 0), AE= (0, (1一』)a, 』a), ~AD={~ a, a, 0).设平面冏拓的法向量为Z7i=(xi, yi, zi),平面/Z4E的法向量为4=(*2,巧,勿),则J[必=0,[(1——久)ayi+ az\ = 0,J一翊+a 乃=0,[(1— 4)砂+ 4 必=0..*./71=(0,久,久——1),刀2=(久,久,人——1),! \ Z21 , z?2 2 + ( _ I)2cos s’ m2.^p2+ A2+p_1)22 2— 2 4+1 寸2 J — 2 4+1由题意 | cos〈〃i, ni) I = 土-, o叩.2,「一2』+l 避月3—2 11— 3 '3 (2 2—2 4+1) =2 (3 人之一2 人+1),.•.棱密上存在一点反使得二面角B-AE-D的平面角的余弦值为一*,且此时4.对于函数/V)和g(x),若存在常数#, m,对于任意xER,不等式f(x) N奴+/Ng(x)都成立,则称直线y=kx+m是函数A A-) , g(x)的分界线.已知函数f3 =e'(<3x+l) (e为自然对数的底数,aER为常数).(1)讨论函数f(x)的单调性;⑵设日=1,试探究函数小(入)与函数g(x)=—x’ + 2x+l是否存在“分界线"?若存在,求出分界线方程;若不存在,请说明理由.(0) =0,当解⑴•.•/*(*) =/(宓+1), 「・尸(x) =e'(ax+a+l),.••当a=0时,f' (x) >0, f{x)在R 上单调递增.:・f3单调递减;在[一弓土 +8)上,尸(x)>o, .•.f(x)单调递增.当a<0时,在[—8,一之三]上,f (x)>0,.../■(x)单调递增;在[―弓」’+8)上,f' (x)<0, .♦./■(X )单调递减.(2)假设存在直线 y=kx+m,使不等式 e*(x+l) ^kx+m^~x+ 2x+1, 当 x=0 时,由于 1N 成Nl, m= 1,kx~\~ IN — x + 2x+1 恒成立,x + (k —2) xNO 恒成立.令力=(#—2)2<0,解得 #=2,...只需不等式e\x+l)》2x+1恒成立即可.设力(x) =e"(x+l) —2x —1,则 0 (x) =e 、(x+2) —2,令(H (x))‘ =e'(x+3)=0,得 x= —3,.••当xV —3时,h' (x)单调递减;当x>~3时,h' (x)单调递增,且力' 8时,H (x)—— 2,.••当 xVO 时,h' (x)V0,「.//(x)单调递减;当x>0时,h' (x)>0, .・M(x)单调递增..../(X )min =」(O )=0.h ( JT ) =e 、(x+l) —2x —1N0,.・.不等式e 、(x+l) N2x+1恒成立.综上所述,函数/'(x)与函数g(x)存在分界线,其分界线方程为y=2x+l.。
2018版考前三个月高考数学理科(全国通用)总复习文档:解答题滚动练2

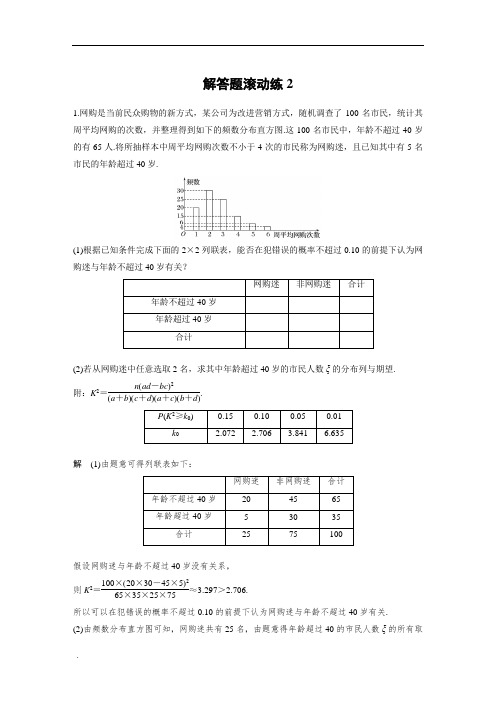
解答题滚动练21.网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人.将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数ξ的分布列与期望.附:K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d).解(1)由题意可得列联表如下:假设网购迷与年龄不超过40岁没有关系,则K 2=100×(20×30-45×5)265×35×25×75≈3.297>2.706.所以可以在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关. (2)由频数分布直方图可知,网购迷共有25名,由题意得年龄超过40的市民人数ξ的所有取值为0,1,2, P (ξ=0)=C 220C 225=1930,P (ξ=1)=C 120C 15C 225=13,P (ξ=2)=C 25C 225=130,所以ξ的分布列为所以E (ξ)=0×1930+1×13+2×130=25.2.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.(1)证明 以D 为原点,射线DA ,DC ,DD 1分别为x 轴,y 轴,z 轴的正半轴建立如图所示空间直角坐标系Dxyz .由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ),N (1,0,2),M (2,1,2),则BC 1=(-2,0,2),FP →=(-1,0,λ),FE →=(1,1,0),NM →=(1,1,0),NP →=(-1,0,λ-2).当λ=1时,FP →=(-1,0,1),因为BC 1=(-2,0,2),所以BC 1=2FP →, 即BC 1∥FP ,又FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ . (2)解 设平面EFPQ 的一个法向量为n =(x ,y ,z ),则 由⎩⎪⎨⎪⎧FE →·n =0,FP →·n =0,得⎩⎪⎨⎪⎧x +y =0,-x +λz =0.于是可取n =(λ,-λ,1). 设平面MNPQ 的一个法向量为m =(x ′,y ′,z ′), 由⎩⎪⎨⎪⎧NM →·m =0,NP →·m =0,得⎩⎪⎨⎪⎧x ′+y ′=0,-x ′+(λ-2)z ′=0, 于是可取m =(λ-2,2-λ,1).若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角,则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22,显然满足0<λ<2.故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角.3.已知数列{a n }中,a 1=1,a 3=9,且a n =a n -1+λn -1(n ≥2). (1)求λ的值及数列{a n }的通项公式;(2)设b n =(-1)n ·(a n +n ),且数列{b n }的前n 项和为S n ,求S 2n . 解 (1)∵a 1=1,a n =a n -1+λn -1,∴a 2=2λ,a 3=5λ-1,由a 3=5λ-1=9,得λ=2,于是a n =a n -1+2n -1,即a n -a n -1=2n -1,a n -1-a n -2=2n -3, a n -2-a n -3=2n -5,…,a 2-a 1=3,n >3. 以上各式累加得a n =1+(n -1)(2n +2)2=n 2,n >3.经验证知,a 1,a 2,a 3也满足a n =n 2,故a n =n 2(n ∈N *).(2)由(1)得b n =(-1)n ·(a n +n )=(-1)n ·n (n +1),故S 2n =-1×2+2×3-3×4+4×5-5×6+6×7-…-(2n -1)·2n +2n ·(2n +1)=2(-1+3)+4(-3+5)+6(-5+7)+…+2n (-2n +1+2n +1)=2(2+4+6+…+2n )=2·n (2n +2)2=2n 2+2n .4.在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个焦点为F 1(-3,0),M (1,y )(y >0)为椭圆上的一点,△MOF 1的面积为34.(1)求椭圆C 的标准方程;(2)若点T 在圆x 2+y 2=1上,是否存在过点A (2,0)的直线l 交椭圆C 于点B ,使OT →=55(OA→+OB →)?若存在,求出直线l 的方程;若不存在,请说明理由. 解 (1)由椭圆的一个焦点为F 1(-3,0)知c =3, 即a 2-b 2=3.①又因为△MOF 1的面积为34,即12×3×y =34,求得y =32,则M ⎝⎛⎭⎫1,32,代入椭圆方程,得1a 2+34b 2=1.②由①②解得a 2=4,b 2=1. 故椭圆C 的标准方程为x 24+y 2=1.(2)假设存在过点A (2,0)的直线l 符合题意,则结合图形易判断知直线l 的斜率必存在, 于是可设直线l 的方程为y =k (x -2),由⎩⎪⎨⎪⎧x 24+y 2=1,y =k (x -2),得(1+4k 2)x 2-16k 2x +16k 2-4=0. (*)解得x B =8k 2-21+4k 2,所以y B =-4k 1+4k 2,即B ⎝ ⎛⎭⎪⎫8k 2-21+4k 2,-4k 1+4k 2.所以OA →+OB →=⎝⎛⎭⎫16k 21+4k 2,-4k 1+4k 2,即OT →=55⎝⎛⎭⎫16k 21+4k2,-4k 1+4k 2. 因为点T 在圆x 2+y 2=1上,所以15⎣⎡⎦⎤⎝⎛⎭⎫16k 21+4k 22+⎝⎛⎭⎫-4k 1+4k 22=1,化简得176k 4-24k 2-5=0,解得k 2=14,所以k =±12.经检验知,此时(*)对应的判别式Δ>0,满足题意. 故存在满足条件的直线l ,其方程为y =±12(x -2).。
考前三个月高考数学理科(全国通用)总复习文档:解答题滚动练2含解析
解答题滚动练21.网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人.将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?网购迷非网购迷合计 年龄不超过40岁 年龄超过40岁合计(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数ξ的分布列与期望. 附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ).P (K 2≥k 0)0.15 0.10 0.05 0.01 k 02.0722.7063.8416.635解 (1)由题意可得列联表如下:网购迷 非网购迷 合计 年龄不超过40岁 20 45 65 年龄超过40岁5 30 35 合计2575100假设网购迷与年龄不超过40岁没有关系, 则K 2=100×(20×30-45×5)265×35×25×75≈3.297>2.706.所以可以在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关. (2)由频数分布直方图可知,网购迷共有25名,由题意得年龄超过40的市民人数ξ的所有取值为0,1,2, P (ξ=0)=C 220C 225=1930,P (ξ=1)=C 120C 15C 225=13,P (ξ=2)=C 25C 225=130,所以ξ的分布列为ξ 0 1 2 P193013130所以E (ξ)=0×1930+1×13+2×130=25.2.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.(1)证明 以D 为原点,射线DA ,DC ,DD 1分别为x 轴,y 轴,z 轴的正半轴建立如图所示空间直角坐标系Dxyz .由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ),N (1,0,2),M (2,1,2),则BC 1=(-2,0,2),FP →=(-1,0,λ),FE →=(1,1,0),NM →=(1,1,0),NP →=(-1,0,λ-2).当λ=1时,FP →=(-1,0,1),因为BC 1=(-2,0,2),所以BC 1=2FP →, 即BC 1∥FP ,又FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ . (2)解 设平面EFPQ 的一个法向量为n =(x ,y ,z ),则 由⎩⎪⎨⎪⎧FE →·n =0,FP →·n =0,得⎩⎪⎨⎪⎧x +y =0,-x +λz =0.于是可取n =(λ,-λ,1). 设平面MNPQ 的一个法向量为m =(x ′,y ′,z ′), 由⎩⎪⎨⎪⎧NM →·m =0,NP →·m =0,得⎩⎪⎨⎪⎧x ′+y ′=0,-x ′+(λ-2)z ′=0,于是可取m =(λ-2,2-λ,1).若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角,则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22,显然满足0<λ<2.故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角.3.已知数列{a n }中,a 1=1,a 3=9,且a n =a n -1+λn -1(n ≥2). (1)求λ的值及数列{a n }的通项公式;(2)设b n =(-1)n ·(a n +n ),且数列{b n }的前n 项和为S n ,求S 2n . 解 (1)∵a 1=1,a n =a n -1+λn -1,∴a 2=2λ,a 3=5λ-1,由a 3=5λ-1=9,得λ=2,于是a n =a n -1+2n -1,即a n -a n -1=2n -1,a n -1-a n -2=2n -3, a n -2-a n -3=2n -5,…,a 2-a 1=3,n >3. 以上各式累加得a n =1+(n -1)(2n +2)2=n 2,n >3.经验证知,a 1,a 2,a 3也满足a n =n 2,故a n =n 2(n ∈N *).(2)由(1)得b n =(-1)n ·(a n +n )=(-1)n ·n (n +1),故S 2n =-1×2+2×3-3×4+4×5-5×6+6×7-…-(2n -1)·2n +2n ·(2n +1)=2(-1+3)+4(-3+5)+6(-5+7)+…+2n (-2n +1+2n +1) =2(2+4+6+…+2n )=2·n (2n +2)2=2n 2+2n .4.在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个焦点为F 1(-3,0),M (1,y )(y >0)为椭圆上的一点,△MOF 1的面积为34.(1)求椭圆C 的标准方程;(2)若点T 在圆x 2+y 2=1上,是否存在过点A (2,0)的直线l 交椭圆C 于点B ,使OT →=55(OA→+OB →)?若存在,求出直线l 的方程;若不存在,请说明理由. 解 (1)由椭圆的一个焦点为F 1(-3,0)知c =3, 即a 2-b 2=3.①又因为△MOF 1的面积为34,即12×3×y =34,求得y =32,则M ⎝⎛⎭⎫1,32,代入椭圆方程,得1a 2+34b 2=1.②由①②解得a 2=4,b 2=1. 故椭圆C 的标准方程为x 24+y 2=1.(2)假设存在过点A (2,0)的直线l 符合题意,则结合图形易判断知直线l 的斜率必存在, 于是可设直线l 的方程为y =k (x -2), 由⎩⎪⎨⎪⎧x 24+y 2=1,y =k (x -2),得(1+4k 2)x 2-16k 2x +16k 2-4=0. (*)解得x B =8k 2-21+4k 2,所以y B =-4k 1+4k 2,即B ⎝ ⎛⎭⎪⎫8k 2-21+4k 2,-4k 1+4k 2. 所以OA →+OB →=⎝⎛⎭⎫16k 21+4k 2,-4k 1+4k 2,即OT →=55⎝⎛⎭⎫16k 21+4k 2,-4k 1+4k 2. 因为点T 在圆x 2+y 2=1上, 所以15⎣⎡⎦⎤⎝⎛⎭⎫16k 21+4k 22+⎝⎛⎭⎫-4k 1+4k 22=1,化简得176k 4-24k 2-5=0,解得k 2=14,所以k =±12.经检验知,此时(*)对应的判别式Δ>0,满足题意.故存在满足条件的直线l ,其方程为y =±12(x -2).合理分配高考数学答题时间找准目标,惜时高效——合理分配高考数学答题时间经过漫长的第一、第二轮复习,对于各知识点的演练同学们已经烂熟于心,我们把这称为战术上的纯熟。
全国通用2018版高考数学总复习考前三个月解答题滚动练7理.doc

的前刀项和(1)由题设可动+ 6d= —5, 2 & + 9(2)求数解答题滚动练71. 盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球,规定取出1个红色 球得1分,取出1个白色球得0分,取出1个黑色球得一1分.现从盒内任取3个球.(1) 求取出的3个球中至少有一个红球的概率;(2) 求取出的3个球得分之和恰好为1分的概率;(3) 设曰为取出的3个球中白色球的个数,求g 的分布列.解(1)由题意知本题是一个古典概型,记事件/为“取出的3个球中至少有一个红球”,则 事件A 的对立事件丁为“取出的3个球中没有红球”,因为试验发生包含的所有事件为从9 个球中任取3个球有C*种结果,满足丁的条件有C ;种结果,所以夕(力=1一夕(丁)=1一§= 712' (2)满足条件取出的3个球得分之和恰好为1分有两种结果,包括取出1个红色球,2个白色 球和取出2个红色球,1个黑色球,记“取出1个红色球,2个白色球”为事件3有种 结果.“取出2个红色球,1个黑色球”为事件C,有CC ;种结果.其中事件3和C 是互斥事件, 则 P(BU 0 =P(0) +尸(。
(3) g 可能的取值为0, 1, 2, 3,则…c 、C1 5 ….CaCe 15R g =0)=另=五,f =1) = Q 3 =2g ,…c 、C3C6 3 …c ; 1R 言―2)—亏―T? R'_3)—覆—商f 的分布列为0 1 2 3 p 521 15 28 3 14 1 842. 已知等差数列{&}的前刀项和为& 且满足&+用=一10, So=—35.(1)求数列{&}的通项公式;解d — —l,所以 7L=2 + 1+^ ^~2^' ■所以尹,=^+2X«+3X§+.由①一②,得 •• +刀・标, =1+云+土+… 1 , 1 1——— 1 2〃 1 1 1 n •刁i= —n •芬 =2—芬所以 S/ =4_日^_刀.法i ,因此 T…=S…~S n '=声.过点。
全国通用2018版高考数学总复习考前三个月解答题滚动练5理.doc

解答题滚动练51.(2017 •北京)如图,在四棱锥尸一』成中,底面』助为正方形,平面0/a平面/砌,点所在线段用上,仞〃平面切G PA=PD=y[6, AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线欢与平面时所成角的正弦值.⑴证明设化BD交于.E,连接必如图.因为愆〃平面切G 平面切CTI平面破=班,所以PD//ME.因为四边形敬力是正方形,所以E为BD的中点,所以M为PB的中点.⑵解取欢的中点。
,连接弟OE.因为PA=PD,所以那_L也,又因为平面平面ABCD,且游u平面PAD,所以必>_L平面ABCD.因为两u平面ABCD,所以OPLOE.因为四边形物⑦是正方形,所以OELAD.如图,建立空间直角坐标系赤*,则尸(0, 0,展),力(2, 0, 0),以一2, 4, 0),航(4, -4, 0),社(2, 0, 一俎). 设平面战£?的法向量n= (x, y, z),n ■BD=g, 则<_0 •应=0, J4x —4y=0, 〔2x —吏 z=0.(3)解 令x=l,则尸1, z=吏.于是n= (1, 1,吏). 平面的法向量为p=(0, 1, 0),n • p 1所以cos 5, p)=扁¥=云由题意知二面角B — PD — A 为锐角,JI所以它的大小为 O设直线必与平面夕班所成的角为a,则sm a = |cos 5,丽 | 笑,\n\\MC\所以直线照与平面妍所成角的正弦值为绊.2. (2017 •安徽太和中学模拟)新一届班委会的7名成员有0, B,。
三人是上一届的成员,现 对7名成员进行如下分工.(1) 若正、副班长两职只能由4 B,。
三人中选两人担任,则有多少种分工方案?(2) 若4 B,「三人不能再担任上一届各自的职务,则有多少种分工方案?解 ⑴先确定正、副班长,有A ;种选法,其余全排列有A?种,共有A 锵= 720(种)分工方案.(2)方法一设B,。
2018考前三个月高考数学理科总复习训练题:——解答题滚动练6 含答案

解答题滚动练61.在△ABC 中,三个内角分别为A ,B ,C ,已知sin ⎝⎛⎭⎪⎫A +π6=2cos A . (1)若cos C =63,求证:2a -3c =0; (2)若B ∈⎝⎛⎭⎪⎫0,π3,且cos(A -B )=45,求sin B . (1)证明 因为sin ⎝⎛⎭⎪⎫A +π6=2cos A ,得32sin A +12cos A =2cos A , 即sin A =3cos A ,因为A ∈(0,π),且cos A ≠0,所以tan A =3,所以A =π3. 因为sin 2C +cos 2C =1,cos C =63,C ∈(0,π), 所以sin C =33, 由正弦定理知a sin A =c sin C ,即a c =sin A sin C =3233=32, 即2a -3c =0.(2)解 因为B ∈⎝ ⎛⎭⎪⎫0,π3,所以A -B =π3-B ∈⎝ ⎛⎭⎪⎫0,π3, 因为sin 2(A -B )+cos 2(A -B )=1, 所以sin(A -B )=35, 所以sin B =sin(A -(A -B ))=sin A cos(A -B )-cos A ·sin(A -B )=43-310. 2.已知函数f (x )=ax 3-2x -ln x ,a ∈R .(1)若曲线y =f (x )在x =1处的切线方程为y =b ,求a +b 的值;(2)在(1)的条件下,求函数f (x )零点的个数.解 (1)f ′(x )=3ax 2-2-1x, 由题意,f ′(1)=0,f (1)=b ,解得,a =1,b =-1,所以a +b =0.(2)由(1)知,f (x )=x 3-2x -ln x ,f ′(x )=3x 2-2-1x =3x 3-2x -1x=(x -1)(3x 2+3x +1)x, 令f ′(x )=0,得x =1,且当0<x <1时,f ′(x )<0;当x >1时,f ′(x )>0,所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增.因为f (1)=-1<0,f ⎝ ⎛⎭⎪⎫1e =1e 3-2e +1>0,f (e)=e 3-2e -1>0,函数f (x )在区间⎣⎢⎡⎦⎥⎤1e ,1和[1,e]上的图象是一条不间断的曲线,由零点存在性定理,知函数f (x )有两个零点.3.已知圆M :x 2+(y -4)2=4,点P 是直线l :x -2y =0上的一动点,过点P 作圆M 的切线PA ,PB ,切点为A ,B .(1)当切线PA 的长度为23时,求点P 的坐标;(2)若△PAM 的外接圆为圆N ,试问:当P 运动时,圆N 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;(3)求线段AB 长度的最小值.解 (1)由题意可知,圆M 的半径r =2,设P (2b ,b ),因为PA 是圆M 的一条切线,A 为切点,所以∠MAP =90°,所以MP =(0-2b )2+(4-b )2=AM 2+AP 2=4,解得b =0或b =85, 所以P (0,0)或P ⎝ ⎛⎭⎪⎫165,85. (2)设P (2b ,b ),因为∠MAP =90°,所以经过A ,P ,M 三点的圆N 以MP 为直径, 其方程为(x -b )2+⎝ ⎛⎭⎪⎫y -b +422=4b 2+(b -4)24, 即(2x +y -4)b -(x 2+y 2-4y )=0.由⎩⎪⎨⎪⎧ 2x +y -4=0,x 2+y 2-4y =0,解得⎩⎨⎧ x =0,y =4,或⎩⎪⎨⎪⎧ x =85,y =45,所以圆过定点(0,4),⎝ ⎛⎭⎪⎫85,45. (3)因为圆N 方程为(x -b )2+⎝ ⎛⎭⎪⎫y -b +422=4b 2+(b -4)24,即x2+y2-2bx-(b+4)y+4b=0.①圆M:x2+(y-4)2=4,即x2+y2-8y+12=0.②②-①得圆M与圆N的相交弦AB所在直线方程为2bx+(b-4)y+12-4b=0,点M到直线AB的距离d=4 5b2-8b+16,相交弦长AB=24-d2=41-45b2-8b+16=41-45⎝⎛⎭⎪⎫b-452+645.当b=45时,AB有最小值11.4.如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽2m(从拐角处,即图中A,B处开始).假定渠内的水面始终保持水平位置(即无高度差).(1)在水平面内,过点A的一条直线与水渠的内壁交于P,Q两点,且与水渠的一边的夹角为θ⎝⎛⎭⎪⎫0<θ<π2,将线段PQ的长度l表示为θ的函数;(2)若从南面漂来一根长为7m的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.解(1)由题意,PA=2sinθ,QA=4cosθ,所以l=PA+QA=2sinθ+4cosθ⎝⎛⎭⎪⎫0<θ<π2. (2)设f(θ)=2sinθ+4cosθ,θ∈⎝⎛⎭⎪⎫0,π2.由f′(θ)=-2cosθsin2θ+4sinθcos2θ=2(22sin3θ-cos3θ)sin2θcos2θ,令f′(θ)=0,得tanθ0=22.且当θ∈(0,θ0),f′(θ)<0;当θ∈⎝⎛⎭⎪⎫θ0,π2,f′(θ)>0,所以f(θ)在(0,θ0)上单调递减,在⎝⎛⎭⎪⎫θ0,π2上单调递增,所以当θ=θ0时,f(θ)取得极小值,即为最小值.当tanθ0=22时,sinθ0=13,cosθ0=23,所以f(θ)的最小值为36,即这根竹竿能通过拐角处的长度的最大值为36m.因为36>7,所以这根竹竿能从拐角处一直漂向东西向的水渠.。
2018版考前三个月高考数学理科全国通用总复习文档:解
解答题滚动练61.已知函数f (x )=cos 2x +2sin 2x +2sin x .(1)将函数f (2x )的图象向右平移π6个单位长度得到函数g (x )的图象,若x ∈⎣⎡⎦⎤π12,π2,求函数g (x )的值域;(2)已知a ,b ,c 分别为△ABC 中角A ,B ,C 的对边,且满足b =2,B ∈⎝⎛⎭⎫0,π2,f (A )=2+1,3a =2b sin A ,求△ABC 的面积.解 f (x )=cos 2x +2sin 2x +2sin x =cos 2x +(1-cos 2x )+2sin x =1+2sin x . (1)平移可得g (x )=2sin ⎝⎛⎭⎫2x -π3+1, ∵x ∈⎣⎡⎦⎤π12,π2, ∴2x -π3∈⎣⎡⎦⎤-π6,2π3, 当x =π12时,g (x )min =0;当x =5π12时,g (x )max =3,∴所求值域为[0,3].(2)由已知3a =2b sin A 及正弦定理,得3sin A =2sin B sin A , ∴sin B =32. ∵0<B <π2,∴B =π3,由f (A )=2+1,得sin A =22, 由正弦定理,得a =263<b ,从而A =π4,∴S △ABC =12ab sin C =12×263×2×6+24=3+33.2.在等差数列{a n }中,公差d ≠0,a 1=1,且a 1,a 2,a 5成等比数列. (1)求数列{a n }的通项公式;(2)若b n =a n3n ,求数列{b n }的前n 项和T n .解 (1)由a 1,a 2,a 5成等比数列知,a 22=a 1a 5,即(a 1+d )2=a 1(a 1+4d ),即d 2=2a 1d , 又d ≠0,a 1=1,解得d =2,故a n =2n -1. (2)b n =2n -13n ,则T n =13+332+533+…+2n -13n ,① 由①式两边×13,有13T n =132+333+534+…+2n -13n 1,②由①-②,得23T n =13+232+233+…+23n -2n -13n +1⇒23T n =13+232⎣⎡⎦⎤1-⎝⎛⎭⎫13n -11-13-2n -13n +1,化简得T n =1-n +13n .3.如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,AP =AB =AC =a ,AD =2a ,P A ⊥底面ABCD.(1)求证:平面PCD ⊥平面P AC ;(2)在棱PC 上是否存在一点E ,使得二面角B -AE -D 的平面角的余弦值为-63?若存在,求出λ=CECP的值;若不存在,请说明理由.(1)证明 在△ACD 中,AC =a ,CD =a ,AD =2a , 由勾股定理得CD ⊥AC , ∵P A ⊥底面ABCD , ∴P A ⊥CD ,又AC ⊂平面P AC ,P A ⊂平面P AC ,P A ∩AC =A , ∴CD ⊥平面P AC . 又∵CD ⊂平面PCD , ∴平面PCD ⊥平面P AC .(2)解 由(1)知,AB ⊥AC ,又P A ⊥底面ABCD ,∴以A 为原点,AB ,AC ,AP 所在直线分别为x 轴,y 轴,z 轴建立如图所示坐标系,则A (0,0,0),B (a ,0,0),C (0,a ,0),D (-a ,a ,0),P (0,0,a ), 假设点E (x E ,y E ,z E )存在,且λ=CE CP ,则CE →=λCP →,即(x E ,y E -a ,z E )=λ(0,-a ,a ), ∴x E =0,y E =(1-λ)a ,z E =λa .∴AB →=(a ,0,0),AE →=(0,(1-λ)a ,λa ),AD →=(-a ,a ,0).设平面BAE 的法向量为n 1=(x 1,y 1,z 1),平面DAE 的法向量为n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧ax 1=0,(1-λ)ay 1+λaz 1=0, ⎩⎪⎨⎪⎧-ax 2+ay 2=0,(1-λ)ay 2+λaz 2=0.∴n 1=(0,λ,λ-1),n 2=(λ,λ,λ-1),cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=λ2+(λ-1)2λ2+(λ-1)2·λ2+λ2+(λ-1)2=2λ2-2λ+12λ2-2λ+1·3λ2-2λ+1=2λ2-2λ+13λ2-2λ+1,由题意|cos 〈n 1,n 2〉|=63, 即2λ2-2λ+13λ2-2λ+1=63,3(2λ2-2λ+1)=2(3λ2-2λ+1), ∴λ=12.∴棱PC 上存在一点E ,使得二面角B -AE -D 的平面角的余弦值为-63,且此时λ=12. 4.对于函数f (x )和g (x ),若存在常数k ,m ,对于任意x ∈R ,不等式f (x )≥kx +m ≥g (x )都成立,则称直线y =kx +m 是函数f (x ),g (x )的分界线.已知函数f (x )=e x (ax +1)(e 为自然对数的底数,a ∈R 为常数).(1)讨论函数f (x )的单调性;(2)设a =1,试探究函数f (x )与函数g (x )=-x 2+2x +1是否存在“分界线”?若存在,求出分界线方程;若不存在,请说明理由. 解 (1)∵f (x )=e x (ax +1), ∴f ′(x )=e x (ax +a +1),∴当a =0时,f ′(x )>0,∴f (x )在R 上单调递增. 当a ≠0时,f ′(x )=a e x ⎣⎡⎦⎤x -⎝⎛⎭⎫-a +1a ,当a >0时,在⎝⎛⎭⎫-∞,-a +1a 上,f ′(x )<0,∴f (x )单调递减;在⎝⎛⎭⎫-a +1a ,+∞上,f ′(x )>0,∴f (x )单调递增.当a <0时,在⎝⎛⎭⎫-∞,-a +1a 上,f ′(x )>0,∴f (x )单调递增;在⎝⎛⎭⎫-a +1a ,+∞上,f ′(x )<0,∴f (x )单调递减.(2)假设存在直线y =kx +m ,使不等式e x (x +1)≥kx +m ≥-x 2+2x +1, 当x =0时,由于1≥m ≥1,∴m =1, ∴kx +1≥-x 2+2x +1恒成立, ∴x 2+(k -2)x ≥0恒成立. 令Δ=(k -2)2≤0,解得k =2,∴只需不等式e x (x +1)≥2x +1恒成立即可. 设h (x )=e x (x +1)-2x -1,则h ′(x )=e x (x +2)-2, 令(h ′(x ))′=e x (x +3)=0,得x =-3,∴当x <-3时,h ′(x )单调递减;当x >-3时,h ′(x )单调递增,且h ′(0)=0,当x →-∞时,h ′(x )→-2,∴当x <0时,h ′(x )<0,∴h (x )单调递减; 当x >0时,h ′(x )>0,∴h (x )单调递增. ∴h (x )min =h (0)=0.∴h (x )=e x (x +1)-2x -1≥0, ∴不等式e x (x +1)≥2x +1恒成立.综上所述,函数f (x )与函数g (x )存在分界线,其分界线方程为y =2x +1.。
全国通用2018版高考数学总复习考前三个月解答题滚动练1理.doc
解答题滚动练11.(2017届长郡中学模拟)四边形如%如图所示,已知AB=BC=CD=2, AD=2^3.(1)求/cos A~cos。
的值;(2)记△姗与△助的面积分别是S与&,求击+&的最大值.解⑴在△刃及?中,BD=A^+A〃—2AB・AD COS,=16一8也COS A,在△冏%中,BB=BO,CB—2BC,CD COS C=8—8COS C,所以漆cos A—cos C=l.(2)依题意强=£朋•应色比勺=12 —12cosW• 6Z^sin七 =4—4cos/所以 5?+&=12 — 12cos粉+4—4COS2C— 16—4(cos C~\~ 1)2—4cos2f =—Scos2^—8cos 61+12 = —8^cos C+^+14,因为2^ —2V刃V4,所以 8—8cos C= BBW (16 —16).解得一IVcos CVy^ —],所以5?+&W14,当cos C=一§时取等号,即§+戎的最大值为14.2.已知等差数列{aj的公差为2,前刀项和为&且S, Si,但成等比数列.(1)求数列{aJ的通项公式;(2)设G+D (a+5),数列{如}的前〃项和为I,求证:T n<-⑴解L.等差数列{&}的公差为2,前”项和为,. 〃(刀一1) 2・・ &=刀31+ 言d-—- n n~\~nai....s, &, S成等比数列,1 - 5 -1 -2 +- 1 - 1 -3 +- 1 - 1 - 4+- 1 - 21 +刀.•.&=&・BP (22—2+2ai )2=ai •(妒—4+4戚,化为(l + ai )2=ai (3 + ai ),解得 ai = l.31+(72— 1) d=l+2 (〃一 1) =2/1— 1.⑵证明由⑴可得&=2刀—1,则勿=(&,+ i )(&+5)(2〃—1 + 1)(2〃—1 + 5厂 〃(〃+2厂 d2刀+3 2 (刀+1)(刀+2)V/?eN*,2刀+3.•.2(〃+1) (〃+2)>°'3 2 刀+3 3 口口 3...「2(〃+1) (〃+2)3 即综上所述,3. 如图,在三棱柱 ABC-A^G 中,侧面 ACQAyL 底面/WG ZA l AC=60° , AC=2AA l = 4, 点D, £分别是WC 的中点.⑴证明:庞〃平面43C ;(2)若AB=2, ZBAC=60° ,求直线庞与平面ABB.A,所成角的正弦值.⑴证明取花的中点凡连接庭7, EF,... 0是死的中点,EF//AB,ABC —AiBC 是三棱柱,AB// AB,:.EF// AB,:.涉'〃平面AW,〃是的中点,1- 1一刀 +0,DF 〃 A 、C,:.班〃平面A^C.又 EFC DF= F,平面奶'〃平面ABC, :.庞〃平面ABC.(2)解 过点4作AO±AC,垂足为0,连接0B,•..侧面ACGA1底面ABC,:.40_L 平面如...AOLOB, AxOLOC.VZAJC=60° , 04 = 2,0A=\, 0A=y[3,':AB=2, ZOAB=60° ,由余弦定理,得0^=0A + Aff-20A • ABcosZBAC=3,:.0B=y[3, ZAOB=90° ,OB LAC,分别以站,OC, <21所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系。
全国通用2018版高考数学总复习考前三个月解答题滚动练8理.doc
⑵根据正弦定理湍丁 b _ c sin B sinC解答题滚动练831 .在及?中,内角瓦B,。
的对边分别为a, b, c,已知cos 2J+-=2cos A (1) 求角K 的大小;(2) 若a=l,求的周长/的取值范围. 解 ⑴根据倍角公式cos 2^=2cos 2^—1, 得 2COS F+;=2COS A, 即 4COS 2T 4—4cos 4+1 = 0, 所以(2cos 力一I)』。
,1JI所以cos A=-,又因为OV/V JI ,所以A=—.得 b=~i=sin B, c=—j=sin C,所以 /=1 +力+c=l+^^(sin B+sin 6), JI2 n 因为刀=耳,所以砰。
=丁,所以 7=l+^^sin B+sin 匕-- j]=l + 2sin(方+~^j, 2 JI因为QVBVp,所以 族(2, 3],o2.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为2万元,贷款期限有6个月、 12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300 元、300元、400元、400元,从2016年享受此项政策的困难户中抽取了 100户进行了调查 统计,其贷款期限的频数如下表:以上表各种贷款期限的频率作为2017年贫困家庭选择各种贷款期限的概率. (1) 某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;(2)设给享受此项政策的某困难户补贴为本元,写出本的分布列,若预计2017年全市有3. 6万户享受此项政策,估计2017年该市共要补贴多少万元.解(1)由已知一困难户选择贷款期限为12个月的概率是0. 4,所以小区2017年准备享受此项政策的3户恰有两户选择贷款期限为12个月的概率是J P I=C3X0. 42 X 0 . 6 = 0 . 28 8.(2) A f =200)=0. 2, A f =300)=0. 6, A f =400)=0. 2,所以f的分布列是200 300 400P0.2 0.6 0.2E( f) =200X0. 2+300X0. 6+400X0. 2=300.所以估计2017年该市共要补贴1 080万元.3.(2017 •北京丰台二模)如图所示的几何体中,四边形/时为等腰梯形,AB//CD, AB=2AD =2, ZDAB=60。
2018考前三个月高考数学理科(江苏专用)总复习训练题:——解答题滚动练8套集合((含答案)35页
2018考前三个月高考数学理科(江苏专用)总复习训练题: ——解答题滚动练8套集合((含答案)解答题滚动练11.(2017·盐城三模)设△ABC 面积的大小为S ,且3AB →·AC →=2S . (1)求sin A 的值;(2)若C =π4,AB →·AC →=16,求AC .解 (1)设△ABC 的内角A ,B ,C 所对边的边长分别为a ,b ,c ,由3AB →·AC →=2S , 得3bc cos A =2×12bc sin A ,得sin A =3cos A .即sin 2A =9cos 2A =9(1-sin 2A ),所以sin 2A =910.又A ∈(0,π),所以sin A >0,故sin A =31010.(2)由sin A =3cos A 和sin A =31010,得cos A =1010,又AB →·AC →=16,所以bc ·cos A =16,得bc =1610① 又C =π4,所以sin B =sin(A +C )=sin A cos C +cos A sin C=31010×22+1010×22=255.在△ABC 中,由正弦定理,得b sin B =csin C ,即b 255=c 22,得c =104b ,②联立①②,解得b =8,即AC =8.2.(2017·江苏泰兴中学质检)如图,在正三棱柱ABC -A 1B 1C 1中,E 是侧面AA 1B 1B 对角线的交点,F 是侧面AA 1C 1C 对角线的交点,D 是棱BC 的中点.求证:(1)EF ∥平面ABC ; (2)平面AEF ⊥平面A 1AD . 证明 (1)连结A 1B 和A 1C .因为E ,F 分别是侧面AA 1B 1B 和侧面AA 1C 1C 的对角线的交点, 所以E ,F 分别是A 1B 和A 1C 的中点,所以EF ∥BC . 又BC ⊂平面ABC ,EF ⊄平面ABC , 故EF ∥平面ABC .(2)因为三棱柱ABC -A 1B 1C 1为正三棱柱, 所以A 1A ⊥平面ABC , 所以BC ⊥A 1A .故由EF ∥BC ,得EF ⊥A 1A .又因为D 是棱BC 的中点,且△ABC 为正三角形,所以BC ⊥AD . 故由EF ∥BC ,得EF ⊥AD .而A 1A ∩AD =A ,A 1A ,AD ⊂平面A 1AD , 所以EF ⊥平面A 1AD .又EF ⊂平面AEF ,故平面AEF ⊥平面A 1AD .3.如图,在平面直角坐标系xOy 中,设椭圆C :x 2a2+y 2=1(a >1).(1)若椭圆C 的焦距为2,求a 的值;(2)求直线y =kx +1被椭圆C 截得的线段长(用a ,k 表示);(3)若以A (0,1)为圆心的圆与椭圆C 总有4个公共点,求椭圆C 的离心率e 的取值范围.解 (1)由椭圆C :x 2a2+y 2=1(a >1)知,焦距为2a 2-1=2,解得a =±2,因为a >1,所以a = 2. (2)设直线y =kx +1被椭圆截得的线段长为AP ,由⎩⎪⎨⎪⎧y =kx +1,x 2a2+y 2=1,得(1+a 2k 2)x 2+2a 2kx =0,解得x 1=0,x 2=-2a 2k 1+a 2k2.因此AP =1+k 2|x 1-x 2|=2a 2|k |1+a 2k2·1+k 2. (3)因为圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有2个不同的公共点为P ,Q ,满足AP =AQ .记直线AP ,AQ 的斜率分别为k 1,k 2,k 1和k 2一正一负,且k 21≠k 22.由(2)知,AP =2a 2|k 1|1+k 211+a 2k 21,AQ =2a 2|k 2|1+k 221+a 2k 22,则2a 2|k 1|1+k 211+a 2k 21=2a 2|k 2|1+k 221+a 2k 22, 所以(k 21-k 22)[1+k 21+k 22+a 2(2-a 2)k 21k 22]=0, 因为k 21≠k 22,所以1+k 21+k 22+a 2(2-a 2)k 21k 22=0,变形得,⎝ ⎛⎭⎪⎫1k 21+1⎝ ⎛⎭⎪⎫1k 22+1=1+a 2(a 2-2),从而1+a 2(a 2-2)>1, 解得a >2,则e =c a=1-1a 2∈⎝ ⎛⎭⎪⎫22,1.4.已知数列{a n }是等差数列,{b n }是等比数列且满足a 1+a 2+a 3=9,b 1b 2b 3=27. (1)若a 4=b 3,b 4-b 3=m .①当m =18时,求数列{a n }和{b n }的通项公式; ②若数列{b n }是唯一的,求m 的值;(2)若a 1+b 1,a 2+b 2,a 3+b 3均为正整数,且成等比数列,求数列{a n }的公差d 的最大值. 解 (1)①由数列{a n }是等差数列及a 1+a 2+a 3=9,得a 2=3, 由数列{b n }是等比数列及b 1b 2b 3=27,得b 2=3. 设数列{a n }的公差为d ,数列{b n }的公比为q ,若m =18,则有⎩⎪⎨⎪⎧3+2d =3q ,3q 2-3q =18,解得⎩⎪⎨⎪⎧d =3,q =3或⎩⎪⎨⎪⎧d =-92,q =-2.所以{a n }和{b n }的通项公式为⎩⎪⎨⎪⎧a n =3n -3,b n =3n -1或⎩⎪⎨⎪⎧a n =-92n +12,b n =3(-2)n -2.②由题设b 4-b 3=m ,得3q 2-3q =m ,即3q 2-3q -m =0,(*) 因为数列{b n }是唯一的,所以若q =0,则m =0,检验知,当m =0时,q =1或0(舍去),满足题意; 若q ≠0,则Δ=(-3)2+12m =0,解得m =-34,代入(*)式,解得q =12,又b 2=3,所以{b n }是唯一的等比数列,符合题意. 所以m =0或-34.(2)依题意,36=(a 1+b 1)(a 3+b 3),设{b n }公比为q ,则有36=⎝ ⎛⎭⎪⎫3-d +3q (3+d +3q ),(**)记s =3-d +3q,t =3+d +3q ,则st =36.将(**)中的q 消去,整理得d 2+(s -t )d +3(s +t )-36=0,d 的大根为t -s +(s -t )2-12(s +t )+1442=t -s +(s +t -6)2-362,而s ,t ∈N *,所以(s ,t )的所有可能取值为:(1,36),(2,18),(3,12),(4,9),(6,6),(9,4),(12,3),(18,2),(36,1). 所以当s =1,t =36时,d 的最大值为35+5372.解答题滚动练21.(2017·南京、盐城二模)如图,在△ABC 中,D 为边BC 上一点,AD =6,BD =3,DC =2. (1)如图1,若AD ⊥BC ,求∠BAC 的大小; (2)如图2,若∠ABC =π4,求△ADC 的面积.解 (1) 由已知,得tan ∠BAD =36=12,tan ∠CAD =26=13,所以tan ∠BAC =tan(∠BAD +∠CAD )=12+131-12×13=1.因为∠BAC ∈(0,π),所以∠BAC =π4.(2) 以B 为原点,BC 所在直线为x 轴建立平面直角坐标系,则B (0,0),D (3,0),C (5,0). 因为∠ABC =π4,所以设A (a ,a ),其中a >0.由AD =6,BD =3,得(a -3)2+a 2=62,即2a 2-6a -27=0,解得a =32(1+7).所以S △ADC =12DC ·a =32(1+7).2.如图,ABCD 是一块边长为100米的正方形地皮,其中ATPS 是一半径为90米的底面为扇形小山(P 为圆弧TS 上的点),其余部分为平地.今有开发商想在平地上建一个两边落在BC 及CD 上的长方形停车场PQCR.(1)设∠PAB =θ,试将矩形PQCR 面积表示为θ的函数; (2)求停车场PQCR 面积的最大值及最小值.解 (1)S PQCR =f (θ)=(100-90cos θ)(100-90sin θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000 , θ∈⎣⎢⎡⎦⎥⎤0,π2.(2)由(1)知S PQCR =f (θ)=8100sin θcos θ-9000(sin θ+cos θ)+10000,θ∈⎣⎢⎡⎦⎥⎤0,π2.令sin θ+cos θ=t ,则t =2sin ⎝ ⎛⎭⎪⎫θ+π4∈[1,2].∴S PQCR =81002t 2-9000t +10000-81002,当t =109时,S PQCR 取得最小值950(m 2),当t =2时,S PQCR 取得最大值14050-90002(m 2).答 停车场面积的最大值和最小值分别为14050-90002(m 2)和950(m 2).3.如图,点A (1,3)为椭圆x 22+y 2n=1上一定点,过点A 引两直线与椭圆分别交于B ,C 两点.(1)求椭圆方程;(2)若直线AB ,AC 与x 轴围成的是以点A 为顶点的等腰三角形. ①求直线BC 的斜率;②求△ABC 的面积的最大值,并求出此时直线BC 的方程.解 (1)把点A (1,3)代入x 22+y 2n =1得n =6,故椭圆方程为x 22+y 26=1.(2)①显然题中等腰三角形腰所在的直线不可能与x 轴垂直. 因此其斜率必存在,设两腰的斜率分别为k 1,k 2,由⎩⎪⎨⎪⎧y -3=k 1(x -1),x 22+y 26=1,消去y ,得(3+k 21)x 2+2k 1(3-k 1)x +(3-k 1)2-6=0,∴点B 的横坐标为x =1-6+23k 1k 21+3(x =1为点A 的横坐标),∴点B 的纵坐标为y =3-23k 21+6k 1k 21+3,即B ⎝ ⎛⎭⎪⎫1-6+23k 1k 21+3,3-23k 21+6k 1k 21+3.∵k 1+k 2=0,∴直线BC 的斜率为k BC = 3.②设B (x 1,y 1),C (x 2,y 2),直线BC 的方程为y =3x +m ,代入方程x 22+y 26=1得6x 2+23mx+m 2-6=0,∴x 1+x 2=-33m ,x 1x 2=m 2-66,∴BC =1+(3)2·|x 1-x 2| =2·(x 1+x 2)2-4x 1x 2 =23312-m 2,又点A 到直线BC 的距离为d =|m |2,∴S △ABC =12BC ·d =36m 2(12-m 2)=36-(m 2-6)2+36, ∴当m 2=6,即m =6或m =-6时,△ABC 面积取得最大值 3. 此时,直线BC 的方程为y =3x ± 6.4.已知函数f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R ).(1)若函数f (x )为奇函数,且图象过点(-1,2),求f (x )的解析式; (2)若x =1和x =2是函数f (x )的两个极值点. ①求a ,b 的值;②求函数f (x )在区间[0,3]上的零点个数. 解 (1)因为函数f (x )为奇函数,所以f (-x )=-f (x ),即2(-x )3+a (-x )2+b (-x )+c =-2x 3-ax 2-bx -c , 整理得,ax 2+c =0,所以a =c =0,从而f (x )=2x 3+bx , 又函数f (x )图象过点(-1,2),所以b =-4. 从而f (x )=2x 3-4x .(2)①f (x )=2x 3+ax 2+bx +c (a ,b ,c ∈R )的导函数f ′(x )=6x 2+2ax +b . 因为f (x )在x =1和x =2处取得极值, 所以f ′(1)=0,f ′(2)=0,即⎩⎪⎨⎪⎧6+2a +b =0,24+4a +b =0,解得a =-9,b =12.②由①得f(x)=2x3-9x2+12x+c(c∈R),f′(x)=6(x-1)(x-2).列表:显然,函数f(x)在[0,3]上的图象是一条不间断的曲线.由表知,函数f(x)在[0,3]上的最小值为f(0)=c,最大值为f(3)=9+c.所以当c>0或9+c<0(即c<-9)时,函数f(x)在区间[0,3]上的零点个数为0.当-5<c<0时,因为f(0)f(1)=c(5+c)<0,且函数f(x)在(0,1)上是单调增函数,所以函数f(x)在(0,1)上有1个零点.当-5<c<-4时,因为f(1)f(2)=(5+c)(4+c)<0,且f(x)在(1,2)上是单调减函数,所以函数f(x)在(1,2)上有1个零点.当-9<c<-4时,因为f(2)f(3)=(4+c)(9+c)<0,且f(x)在(2,3)上是单调增函数,所以函数f(x)在(2,3)上有1个零点.综上,当c>0或c<-9时,函数f(x)在区间[0,3]上的零点个数为0;当-9≤c<-5或-4<c≤0时,零点个数为1;当c=-4或c=-5时,零点个数为2;当-5<c<-4时,零点个数3.解答题滚动练31.(2017·镇江期末)已知向量m =(cos α,-1),n =(2,sin α),其中α∈⎝⎛⎭⎪⎫0,π2,且m ⊥n .(1)求cos2α的值; (2)若sin(α-β)=1010,且β∈⎝⎛⎭⎪⎫0,π2,求角β的大小.解 方法一 (1)由m ⊥n ,得2cos α-sin α=0,所以sin α=2cos α,代入cos 2α+sin 2α=1,得5cos 2α=1,且α∈⎝⎛⎭⎪⎫0,π2,则cos α=55,sin α=255, 则cos2α=2cos 2α-1=2×⎝⎛⎭⎪⎫552-1=-35. (2)由α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,得α-β∈⎝ ⎛⎭⎪⎫-π2,π2.又sin(α-β)=1010,则cos(α-β)=31010. 则sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=255×31010-55×1010=22. 因为β∈⎝⎛⎭⎪⎫0,π2,所以β=π4.方法二 (1)由m ⊥n ,得2cos α-sin α=0,tan α=2,故cos2α=cos 2α-sin 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α=1-41+4=-35. (2)由(1)知,2cos α-sin α=0,且cos 2α+sin 2α=1,α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝⎛⎭⎪⎫0,π2,则sin α=255,cos α=55,以下同方法一(2).2.如图,在四棱锥P -ABCD 中,AB ⊥平面PAD ,DC ∥AB ,DC =2AB ,E 为棱PA 上一点. (1)设O 为AC 与BD 的交点,若PE =2AE ,求证:OE ∥平面PBC ; (2)若DE ⊥AP ,求证:PB ⊥DE .证明 (1)在△AOB 与△COD 中, 因为DC ∥AB ,DC =2AB ,所以AO CO =AB CD =12, 又因为PE =2AE ,所以在△APC 中,有AO CO =AE PE =12,则OE ∥PC . 又因为OE ⊄平面PBC ,PC ⊂平面PBC ,所以OE ∥平面PBC . (2)因为AB ⊥平面PAD ,DE ⊂平面PAD , 所以AB ⊥DE .又因为AP ⊥DE ,AB ⊂平面PAB ,AP ⊂平面PAB ,AP ∩AB =A , 所以DE ⊥平面PAB ,又PB ⊂平面PAB ,所以DE ⊥PB .3.已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为1.8元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下:7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(1)当9天购买一次配料时,求该厂用于配料的保管费用P 是多少元?(2)设该厂x 天购买一次配料,求该厂在这x 天中用于配料的总费用y (元)关于x 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?解 (1)当9天购买一次时,该厂用于配料的保管费用P =70+0.03×200×(1+2)=88(元). (2)①当0<x ≤7时,y =360x +10x +236=370x +236, ②当x >7时,y =360x +236+70+6[(x -7)+(x -8)+…+2+1]=3x 2+321x +432∴y =⎩⎪⎨⎪⎧370x +236,0<x ≤7,3x 2+321x +432,x >7.∴设该厂x 天购买一次配料平均每天支付的费用为f (x )元. f (x )=⎩⎪⎨⎪⎧370x +236x ,0<x ≤7,3x 2+321x +432x,x >7.当0<x ≤7时,f (x )=370+236x ,当且仅当x =7时f (x )有最小值28267≈404(元),当x >7时,f (x )=3x 2+321x +432x=3⎝ ⎛⎭⎪⎫x +144x +321≥393,当且仅当x =12时取等号.∵393<404,∴当x =12时f (x )有最小值393元.4.已知函数f (x )=2ln x -x 2+ax (a ∈R ).(1)当a =2时,求f (x )的图象在x =1处的切线方程;(2)若函数g (x )=f (x )-ax +m 在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点,求实数m 的取值范围;(3)若函数f (x )的图象与x 轴有两个不同的交点A (x 1,0),B (x 2,0),且0<x 1<x 2,求证:f ′⎝ ⎛⎭⎪⎫x 1+x 22<0(其中f ′(x )是f (x )的导函数). (1)解 当a =2时,f (x )=2ln x -x 2+2x ,f ′(x )=2x-2x +2,切点坐标为(1,1),切线的斜率k =f ′(1)=2,则切线方程为y -1=2(x -1),即y =2x -1. (2)解 g (x )=2ln x -x 2+m ,则g ′(x )=2x -2x =-2(x +1)(x -1)x,∵x ∈⎣⎢⎡⎦⎥⎤1e ,e ,故g ′(x )=0时,x =1.当1e <x <1时,g ′(x )>0;当1<x <e 时,g ′(x )<0.故g (x )在x =1处取得极大值g (1)=m -1.又g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2,g (e)=m +2-e 2,g (e)-g ⎝ ⎛⎭⎪⎫1e =4-e 2+1e 2<0,则g (e)<g ⎝ ⎛⎭⎪⎫1e ,所以g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值为g (e). g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点的条件是⎩⎪⎨⎪⎧g (1)=m -1>0,g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2≤0,解得1<m ≤2+1e 2,所以实数m 的取值范围是⎝⎛⎦⎥⎤1,2+1e 2.(3)证明 因为f (x )的图象与x 轴交于两个不同的点A (x 1,0),B (x 2,0),所以方程2ln x -x 2+ax =0的两个根为x 1,x 2,则⎩⎪⎨⎪⎧2ln x 1-x 21+ax 1=0,2ln x 2-x 22+ax 2=0,两式相减得a =(x 1+x 2)-2(ln x 1-ln x 2)x 1-x 2,又f (x )=2ln x -x 2+ax ,f ′(x )=2x -2x +a ,则f ′⎝ ⎛⎭⎪⎫x 1+x 22=4x 1+x 2-(x 1+x 2)+a =4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2.下证4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即证明2(x 2-x 1)x 1+x 2+ln x 1x 2<0,令t =x 1x 2. 因为0<x 1<x 2,所以0<t <1,即证明u (t )=2(1-t )t +1+ln t <0在0<t <1上恒成立.因为u ′(t )=-2(t +1)-2(1-t )(t +1)2+1t =1t -4(t +1)2=(t -1)2t (t +1)2,又0<t <1,所以u ′(t )>0, 所以u (t )在(0,1)上是增函数,则u (t )<u (1)=0,从而知2(x 2-x 1)x 1+x 2+ln x 1x 2<0,故4x 1+x 2-2(ln x 1-ln x 2)x 1-x 2<0,即f ′⎝ ⎛⎭⎪⎫x 1+x 22<0成立.解答题滚动练41.如图,在四棱锥P -ABCD 中,已知底面ABCD 为矩形,且AB =2,BC =1,E ,F 分别是AB ,PC 的中点,PA ⊥DE .(1)求证:EF ∥平面PAD ; (2)求证:平面PAC ⊥平面PDE .证明 (1)方法一 取线段PD 的中点M ,连结FM ,AM . 因为F 为PC 的中点,所以FM ∥CD ,且FM =12CD .因为四边形ABCD 为矩形,E 为AB 的中点, 所以EA ∥CD ,且EA =12CD .所以FM ∥EA ,且FM =EA .所以四边形AEFM 为平行四边形,所以EF ∥AM . 又AM ⊂平面PAD ,EF ⊄平面PAD , 所以EF ∥平面PAD .方法二 连结CE 并延长交DA 的延长线于N ,连结PN .因为四边形ABCD 为矩形,所以AD ∥BC , 所以∠BCE =∠ANE ,∠CBE =∠NAE . 又AE =EB ,所以△CEB ≌△NEA . 所以CE =NE .又F 为PC 的中点,所以EF ∥NP . 又NP ⊂平面PAD ,EF ⊄平面PAD , 所以EF ∥平面PAD .方法三 取CD 的中点Q ,连结FQ ,EQ .在矩形ABCD 中,E 为AB 的中点, 所以AE =DQ ,且AE ∥DQ . 所以四边形AEQD 为平行四边形, 所以EQ ∥AD .又AD ⊂平面PAD ,EQ ⊄平面PAD , 所以EQ ∥平面PAD .因为Q ,F 分别为CD ,CP 的中点, 所以FQ ∥PD .又PD ⊂平面PAD ,FQ ⊄平面PAD , 所以FQ ∥平面PAD .又FQ ,EQ ⊂平面EQF ,FQ ∩EQ =Q ,所以平面EQF ∥平面PAD . 因为EF ⊂平面EQF ,所以EF ∥平面PAD .(2)设AC ,DE 相交于G . 在矩形ABCD 中, 因为AB =2BC ,E 为AB 的中点,所以DA AE =CDDA= 2.又∠DAE =∠CDA ,所以△DAE ∽△CDA , 所以∠ADE =∠DCA .又∠ADE +∠CDE =∠ADC =90°, 所以∠DCA +∠CDE =90°.由△DGC 的内角和为180°,得∠DGC =90°. 即DE ⊥AC . 又PA ⊥DE ,PA ∩AC =A ,PA ,AC ⊂平面PAC ,所以DE ⊥平面PAC ,又DE ⊂平面PDE ,所以平面PAC ⊥平面PDE .2.如图所示,A ,B 是两个垃圾中转站,B 在A 的正东方向16km 处,AB 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在AB 的北面建一个垃圾发电厂P .垃圾发电厂P 的选址拟满足以下两个要求(A ,B ,P 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点P 到直线AB 的距离要尽可能大).现估测得A ,B 两个中转站每天集中的生活垃圾量分别约为30吨和50吨,问垃圾发电厂该如何选址才能同时满足上述要求?解 方法一 由条件①,得PA PB =5030=53. 设PA =5x ,PB =3x ,则cos ∠PAB =(5x )2+162-(3x )22×16×5x =x 10+85x ,所以点P 到直线AB 的距离h =PA sin ∠PAB =5x1-⎝ ⎛⎭⎪⎫x 10+85x 2=-14x 4+17x 2-64 =-14(x 2-34)2+225, 所以当x 2=34,即x =34时,h 取得最大值15km. 即选址应满足PA =534km ,PB =334km.方法二 以AB 所在直线为x 轴,线段AB 的中垂线为y 轴,建立如图所示的平面直角坐标系, 则A (-8,0),B (8,0).由条件①,得PA PB =5030=53.设P (x ,y )(y >0),则3(x +8)2+y 2=5(x -8)2+y 2, 化简得(x -17)2+y 2=152(y >0),即点P 的轨迹是以点(17,0)为圆心、15为半径的圆位于x 轴上方的部分. 则当x =17时,点P 到直线AB 的距离最大,最大值为15km. 所以点P 的选址应满足在上述坐标系中坐标为(17,15)即可.方法三 由条件①,得PA PB =5030=53.过点P 作PD 垂直于AB ,设PD =h ,AD =x ,则DB =|16-x |, 3x 2+h 2=5h 2+(16-x )2,h 2=-(x -25)2+225.所以当x =25时,h 取得最大值15. 答 选址应满足PA =534km ,PB =334km. 3.已知数列{a n }满足a n +a n +1=2n -3,n ∈N *. (1)若数列{a n }为等差数列,求a 1;(2)设a 1=a (a >0),∀n ∈N *,n ≥2,不等式a 2n +a 2n +1a n +a n +1≥3成立,求实数a 的最小值.解 (1)设数列{a n }公差为d ,则2n -3=a n +a n +1=a 1+(n -1)d +a 1+nd =2dn +(2a 1-d )对∀n ∈N *成立,所以⎩⎪⎨⎪⎧2d =2,2a 1-d =-3,故d =1,a 1=-1.(2)由a n +a n +1=2n -3,知{a n -(n -2)}为等比数列,公比q =-1, 所以a n -(n -2)=(a +1)(-1)n -1,故a n =(n -2)+(a +1)(-1)n -1.①当n 为不小于3的奇数时,由a 2n +a 2n +1a n +a n +1≥3,得(n -1+a )2+(n -2-a )22n -3≥3,化简得a 2+a ≥-(n -3)2+2恒成立,所以a 2+a ≥2,解得a ≥1. ②n 为不小于2的偶数时,同理有a 2+3a ≥-(n -3)2恒成立,因为a >0,显然恒成立.所以a >0.由①②得a ≥1,故a 的最小值为1.4.已知椭圆C 的方程为x 2a 2+y 2b2=1(a >b >0),点A ,B 分别为其左、右顶点,点F 1,F 2分别为其左、右焦点,以点A 为圆心、AF 1为半径作圆A ,以点B 为圆心、OB 为半径作圆B .若直线l :y =-33x 被圆A 和圆B 截得的弦长之比为15∶6. (1)求椭圆C 的离心率;(2)已知a =7,问在x 轴上是否存在点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4,若存在,请求出所有点P 的坐标;若不存在,请说明理由.解 (1)分别过点A ,B 作直线l 的垂线,垂足为A 1,B 1, 由题意得AA 1=BB 1,由点到直线距离公式得AA 1=BB 1=a2,因为圆A 以AF 1为半径,所以半径为a -c ,被直线l 截得的弦长为2(a -c )2-⎝ ⎛⎭⎪⎫a 22,因为圆B 以OB 为半径,所以半径为a ,被直线l 截得的弦长为2a 2-⎝ ⎛⎭⎪⎫a 22. 因为直线l :y =-33x 被圆A 和圆B 截得的弦长之比为15∶6,化简得7a 2-32ac +16c 2=0,两边同时除以a 2,得16e 2-32e +7=0, 解得e =14或e =74(舍去).所以所求的离心率为14.(2)存在点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4, 设点P (x 0,0),由题意可得直线方程为y =k (x -x 0), 则直线截圆A 所得的弦长为2(a -c )2-⎝⎛⎭⎪⎫|k (-7-x 0)|1+k 22, 直线截圆B 所得的弦长为2a 2-⎝⎛⎭⎪⎫|k (7-x 0)|1+k 22,2(a -c )2-⎝ ⎛⎭⎪⎫k (7+x 0)1+k 222a 2-⎝ ⎛⎭⎪⎫k (7-x 0)1+k 22=34, 即有16⎣⎢⎡⎦⎥⎤(a -c )2-⎝ ⎛⎭⎪⎫7k +kx 01+k 22=9⎣⎢⎡⎦⎥⎤a 2-⎝ ⎛⎭⎪⎫7k -kx 01+k 22,其中a =7,c =74,a -c =214,上式整理得,16(7k +kx 0)21+k 2=9(7k -kx 0)21+k 2,关于k 的方程有无穷多解, 故有7x 20+350x 0+343=0, 解得x 0=-1或x 0=-49,故存在2个点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为3∶4,P 点坐标为(-1,0)或(-49,0).解答题滚动练51.已知α∈(0,π),且sin ⎝ ⎛⎭⎪⎫α+π3=6-24. (1)求sin ⎝ ⎛⎭⎪⎫α-π4的值;(2)求cos ⎝⎛⎭⎪⎫2α-π3的值. 解 方法一 联立⎩⎪⎨⎪⎧sin ⎝⎛⎭⎪⎫α+π3=6-24,sin 2α+cos 2α=1.⇒4sin 2α-(6-2)sin α-(1+3)=0, 解得sin α=6+24或sin α=-22, 因为α∈(0,π),所以sin α=6+24, 所以cos α=2-64. (1)sin ⎝ ⎛⎭⎪⎫α-π4=sin αcos π4-cos αsin π4=6+24×22-2-64×22=62×22=32. (2)sin2α=2sin αcos α=2×6+24×2-64=-12,cos2α=1-2sin 2α=-32. cos ⎝⎛⎭⎪⎫2α-π3=cos2αcos π3+sin2αsin π3=-32.方法二 因为α∈(0,π),sin ⎝ ⎛⎭⎪⎫α+π3=6-24<12,所以5π6<α+π3<4π3,sin 11π12=sin ⎝ ⎛⎭⎪⎫π4-π6=sin π4cos π6-cos π4sin π6=6-24,所以α+π3=11π12,所以α=7π12.(1)sin ⎝ ⎛⎭⎪⎫α-π4=sin ⎝ ⎛⎭⎪⎫7π12-π4=sin π3=32.(2)cos ⎝ ⎛⎭⎪⎫2α-π3=cos ⎝⎛⎭⎪⎫2×7π12-π3=cos 5π6=-32.2.如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.(1)求证:AD⊥平面PAB;(2)求证:CN∥平面PAB.证明(1)因为BD垂直平分AC,所以BA=BC,在△ABC中,因为∠ABC=120°,所以∠BAC=30°.因为△ACD是正三角形,所以∠DAC=60°,所以∠BAD=90°,即AD⊥AB.因为AB=1,∠ABC=120°,所以AD=AC=3,又因为PA=1,PD=2,由PA2+AD2=PD2,知∠PAD=90°,即AD⊥AP.因为AB,AP⊂平面PAB,AB∩AP=A,所以AD⊥平面PAB.(2)方法一取AD的中点H,连结CH,NH.因为N为PD的中点,所以HN∥PA,因为PA⊂平面PAB,HN⊄平面PAB,所以HN∥平面PAB.由△ACD是正三角形,H为AD的中点,所以CH⊥AD.由(1)知,BA⊥AD,所以CH∥BA,因为BA⊂平面PAB,CH⊄平面PAB,所以CH∥平面PAB.因为CH,HN⊂平面CNH,CH∩HN=H,所以平面CNH∥平面PAB.因为CN⊂平面CNH,所以CN∥平面PAB.方法二取PA的中点S,过C作CT∥AD交AB的延长线于T,连结ST,SN.因为N 为PD 的中点,所以SN ∥AD ,且SN =12AD ,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB ⊥AD ,所以CT ⊥AT , 在Rt △CBT 中,BC =1,∠CBT =60°, 得CT =32. 由(1)知,AD =3,所以CT =12AD ,所以CT =SN .所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .3.已知圆O :x 2+y 2=4,两个定点A (a,2),B (m,1),其中a ∈R ,m >0.P 为圆O 上任意一点,且PA PB=k (k 为常数). (1)求常数k 的值;(2)过点E (a ,t )作直线l 与圆C :x 2+y 2=m 交于M ,N 两点,若M 点恰好是线段NE 的中点,求实数t 的取值范围.解 (1)设点P (x ,y ),x 2+y 2=4,PA =(x -a )2+(y -2)2,PB =(x -m )2+(y -1)2,因为PAPB=k ,所以(x -a )2+(y -2)2=k 2[(x -m )2+(y -1)2], 又x 2+y 2=4,化简得2ax +4y -a 2-8=k 2(2mx +2y -m 2-5), 因为P 为圆O 上任意一点,所以⎩⎪⎨⎪⎧2a =2mk 2,4=2k 2,a 2+8=k 2(m 2+5),又m >0,k >0,解得⎩⎨⎧k =2,a =2,m =1,所以常数k = 2.(2)方法一 设M (x 0,y 0),M 是线段NE 的中点,N (2x 0-2,2y 0-t ),又点M ,N 在圆C 上,即关于x ,y 的方程组⎩⎪⎨⎪⎧x 20+y 20=1,(2x 0-2)2+(2y 0-t )2=1有解,化简得⎩⎪⎨⎪⎧x 20+y 20=1,8x 0+4ty 0-t 2-7=0有解,即直线n :8x +4ty -t 2-7=0与圆C :x 2+y 2=1有交点, 则点(0,0)到直线n 的距离d =|t 2+7|64+16t2≤1,化简得,t 4-2t 2-15≤0, 解得t ∈[-5,5].方法二 设过E 的切线与圆C 切于切点F ,EF 2=EM ·EN , 又M 是线段NE 的中点,所以EN =2MN ,EM =MN ,所以EF 2=2MN 2, 又EF 2=EC 2-CF 2=22+t 2-1=t 2+3,MN ≤2, 所以t 2+3≤8, 所以t ∈[-5,5].4.已知函数f (x )=-x 2-(2a +1)x +ln x ,且该函数在x =1处取得极值. (1)求实数a 的值,并求出函数的单调区间; (2)若函数g (x )=f (x )-b +5x2在区间(0,2018)上只有一个零点,求实数b 的值. 解 (1)由已知,得f ′(x )=-2x -2a -1+1x,据题意,f ′(1)=0,得到a =-1, 所以f (x )=-x 2+x +ln x ,f ′(x )=-2x +1+1x=(2x +1)(-x +1)x.由x >0,令f ′(x )>0,得0<x <1,令f ′(x )<0,得x >1,所以函数f (x )在x =1处取得极值,所以a =-1,f (x )的单调增区间为(0,1),f (x )的单调减区间为(1,+∞).(2)g (x )=f (x )-b +5x 2=-x 2+7x 2+ln x -b ,x ∈(0,2018).则g ′(x )=-2x +72+1x,令g ′(x )=0, 得x =2,负值舍去.当0<x <2时,g ′(x )>0,g (x )的单调增区间为(0,2), 当2<x <2018时,g ′(x )<0,g (x )的单调减区间为(2,2018). 所以函数g (x )=f (x )-b +5x2在区间(0,2018)上只有一个零点,等价于g (2)=0, 解得b =ln2+3.解答题滚动练61.在△ABC 中,三个内角分别为A ,B ,C ,已知sin ⎝⎛⎭⎪⎫A +π6=2cos A .(1)若cos C =63,求证:2a -3c =0; (2)若B ∈⎝⎛⎭⎪⎫0,π3,且cos(A -B )=45,求sin B .(1)证明 因为sin ⎝ ⎛⎭⎪⎫A +π6=2cos A ,得32sin A +12cos A =2cos A ,即sin A =3cos A ,因为A ∈(0,π),且cos A ≠0, 所以tan A =3,所以A =π3.因为sin 2C +cos 2C =1,cos C =63,C ∈(0,π), 所以sin C =33, 由正弦定理知a sin A =c sin C ,即a c =sin A sin C =3233=32,即2a -3c =0.(2)解 因为B ∈⎝ ⎛⎭⎪⎫0,π3,所以A -B =π3-B ∈⎝ ⎛⎭⎪⎫0,π3,因为sin 2(A -B )+cos 2(A -B )=1, 所以sin(A -B )=35,所以sin B =sin(A -(A -B ))=sin A cos(A -B )-cos A ·sin(A -B )=43-310.2.已知函数f (x )=ax 3-2x -ln x ,a ∈R .(1)若曲线y =f (x )在x =1处的切线方程为y =b ,求a +b 的值; (2)在(1)的条件下,求函数f (x )零点的个数. 解 (1)f ′(x )=3ax 2-2-1x,由题意,f ′(1)=0,f (1)=b ,解得,a =1,b =-1, 所以a +b =0.(2)由(1)知,f (x )=x 3-2x -ln x ,f ′(x )=3x 2-2-1x=3x 3-2x -1x=(x -1)(3x 2+3x +1)x,令f ′(x )=0,得x =1,且当0<x <1时,f ′(x )<0;当x >1时,f ′(x )>0, 所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增.因为f (1)=-1<0,f ⎝ ⎛⎭⎪⎫1e =1e -2e +1>0,f (e)=e 3-2e -1>0,函数f (x )在区间⎣⎢⎡⎦⎥⎤1e ,1和[1,e]上的图象是一条不间断的曲线,由零点存在性定理,知函数f (x )有两个零点. 3.已知圆M :x 2+(y -4)2=4,点P 是直线l :x -2y =0上的一动点,过点P 作圆M 的切线PA ,PB ,切点为A ,B .(1)当切线PA 的长度为23时,求点P 的坐标;(2)若△PAM 的外接圆为圆N ,试问:当P 运动时,圆N 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由; (3)求线段AB 长度的最小值.解 (1)由题意可知,圆M 的半径r =2,设P (2b ,b ), 因为PA 是圆M 的一条切线,A 为切点, 所以∠MAP =90°,所以MP =(0-2b )2+(4-b )2=AM 2+AP 2=4, 解得b =0或b =85,所以P (0,0)或P ⎝⎛⎭⎪⎫165,85.(2)设P (2b ,b ),因为∠MAP =90°,所以经过A ,P ,M 三点的圆N 以MP 为直径,其方程为(x -b )2+⎝⎛⎭⎪⎫y -b +422=4b 2+(b -4)24,即(2x +y -4)b -(x 2+y 2-4y )=0.由⎩⎪⎨⎪⎧2x +y -4=0,x 2+y 2-4y =0,解得⎩⎨⎧x =0,y =4,或⎩⎪⎨⎪⎧x =85,y =45,所以圆过定点(0,4),⎝ ⎛⎭⎪⎫85,45.(3)因为圆N 方程为(x -b )2+⎝ ⎛⎭⎪⎫y -b +422=4b 2+(b -4)24,即x 2+y 2-2bx -(b +4)y +4b =0.①圆M :x 2+(y -4)2=4,即x 2+y 2-8y +12=0.② ②-①得圆M 与圆N 的相交弦AB 所在直线方程为 2bx +(b -4)y +12-4b =0, 点M 到直线AB 的距离d =45b 2-8b +16, 相交弦长AB =24-d 2=41-45b 2-8b +16 =41-45⎝ ⎛⎭⎪⎫b -452+645.当b =45时,AB 有最小值11.4.如图是一“T ”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m ,东西向渠宽2m(从拐角处,即图中A ,B 处开始).假定渠内的水面始终保持水平位置(即无高度差).(1)在水平面内,过点A 的一条直线与水渠的内壁交于P ,Q 两点,且与水渠的一边的夹角为θ⎝⎛⎭⎪⎫0<θ<π2,将线段PQ的长度l 表示为θ的函数;(2)若从南面漂来一根长为7m 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.解 (1)由题意,PA =2sin θ,QA =4cos θ,所以l =PA +QA =2sin θ+4cos θ⎝ ⎛⎭⎪⎫0<θ<π2. (2)设f (θ)=2sin θ+4cos θ,θ∈⎝⎛⎭⎪⎫0,π2.由f ′(θ)=-2cos θsin 2θ+4sin θcos 2θ=2(22sin 3θ-cos 3θ)sin 2θcos 2θ, 令f ′(θ)=0,得tan θ0=22. 且当θ∈(0,θ0),f ′(θ)<0;当θ∈⎝ ⎛⎭⎪⎫θ0,π2,f ′(θ)>0,所以f (θ)在(0,θ0)上单调递减,在⎝⎛⎭⎪⎫θ0,π2上单调递增,所以当θ=θ0时,f (θ)取得极小值,即为最小值.即这根竹竿能通过拐角处的长度的最大值为36m.因为36>7,所以这根竹竿能从拐角处一直漂向东西向的水渠.解答题滚动练71.如图,在三棱柱ABC -A 1B 1C 1中,所有棱长都相等,且∠ABB 1=60°,D 为AC 的中点,求证:(1)B 1C ∥平面A 1BD ; (2)AB ⊥B 1C .证明 (1)连结AB 1交A 1B 于点E ,连结DE .因为D ,E 分别为AC ,AB 1的中点,所以DE ∥B 1C . 因为DE ⊂平面A 1BD ,B 1C ⊄平面A 1BD , 所以B 1C ∥平面A 1BD .(2)取AB 的中点O ,连结OC ,OB 1.因为BA =BB 1,且∠ABB 1=60°,所以△ABB 1为正三角形,而O 为AB 的中点,所以OB 1⊥AB . 在正三角形ABC 中,O 为AB 中点,所以OC ⊥AB . 因为OB 1∩OC =O ,且OB 1⊂平面OB 1C ,OC ⊂平面OB 1C , 所以AB ⊥平面OB 1C .又因为B 1C ⊂平面OB 1C ,所以AB ⊥B 1C .2.已知数列{a n }的前n 项和S n 满足:S n =t (S n -a n +1)(t 为常数,且t ≠0,t ≠1). (1)证明:{a n }成等比数列;(2)设b n =a 2n +S n ·a n ,若数列{b n }为等比数列,求t 的值. (1)证明 当n =1时,S 1=t (S 1-a 1+1),得a 1=t ,当n ≥2时,S n =t (S n -a n +1),即(1-t )S n =-ta n +t ,(1-t )S n -1=-ta n -1+t , 所以a n =ta n -1,故{a n }成等比数列.(2)解 由(1)知{a n }成等比数列且公比是t ,∴a n =t n,故b n =(t n )2+t (1-t n )1-t ·t n ,即b n =t 2n +t n +1-2t 2n +11-t.若数列{b n }是等比数列,则有b 22=b 1·b 3,而b 1=2t 2,b 2=t 3(2t +1),b 3=t 4(2t 2+t +1), 故[t 3(2t +1)]2=(2t 2)·t 4(2t 2+t +1),解得t =12,再将t =12代入b n 得b n =⎝ ⎛⎭⎪⎫12n ,由b n +1b n =12知{b n }为等比数列,所以t =12. 3.图1是一段半圆柱形水渠的直观图,其横断面如图2所示,其中C 为半圆弧ACB 的中点,渠宽AB 为2m.(1)当渠中水深CD 为0.4m 时,求水面的宽度;(2)若把这条水渠改挖(不准填土)成横断面为等腰梯形的水渠,且使渠的底面与地面平行,则当改挖后的水渠底宽为多少时,所挖出的土量最少?解 (1) 如图,以AB 所在直线为x 轴,AB 的垂直平分线为y 轴,以1m 为单位长度,建立平面直角坐标系xOy .半圆弧ACB 的方程为x 2+y 2=1(y ≤0),A (-1,0),B (1,0),C (0,-1),D (0,-0.6).直线y =-0.6与半圆弧的交点为(±0.8,-0.6). 答 所求的水面宽度为1.6 m.(2)要使得所挖出的土量最少,则等腰梯形的两腰及下底与半圆弧ACB 相切.设等腰梯形的右腰与半圆弧ACB 相切于点T (cos θ,sin θ)⎝ ⎛⎭⎪⎫-π2<θ<0,则切线EF 的方程为x cos θ+y sin θ=1. 令y =0,得E ⎝⎛⎭⎪⎫1cos θ,0,令y =-1,得F ⎝⎛⎭⎪⎫1+sin θcos θ,-1,设梯形OCFE 的面积为S ,则S =12(CF +OE )·OC=12⎝ ⎛⎭⎪⎫1cos θ+1+sin θcos θ×1=2+sin θ2cos θ, S ′=2cos 2θ-(2+sin θ)·(-2sin θ)4cos 2θ=1+2sin θ2cos 2θ, 令S ′=0,得θ=-π6.当θ=-π6时,S 取得最小值,最小值为32,此时CF =1+sin ⎝ ⎛⎭⎪⎫-π6cos ⎝ ⎛⎭⎪⎫-π6=33.答 当改挖后的水渠底宽为233m 时,所挖出的土量最少. 4.函数f (x )=1+ln x -k (x -2)x,其中k 为常数. (1)若k =0,求曲线y =f (x )在点(1,f (1))处的切线方程; (2)若k =5,求证:f (x )有且仅有两个零点;(3)若k 为整数,且当x >2时,f (x )>0恒成立,求k 的最大值. (1)解 当k =0时,f (x )=1+ln x . 因为f ′(x )=1x,从而f ′(1)=1.又f (1)=1,所以曲线y =f (x )在点(1,f (1))处的切线方程为y -1=x -1, 即x -y =0.(2)证明 当k =5时,f (x )=ln x +10x-4.因为f ′(x )=x -10x 2,从而当x ∈(0,10)时,f ′(x )<0,f (x )单调递减;当x ∈(10,+∞)时,f ′(x )>0,f (x )单调递增. 所以当x =10时,f (x )有极小值. 因为f (10)=ln10-3<0,f (1)=6>0, 所以f (x )在(1,10)之间有一个零点. 因为f (e 4)=4+10e4-4>0,所以f (x )在(10,e 4)之间有一个零点. 从而f (x )有两个不同的零点. (3)解 方法一 由题意知,1+ln x -k (x -2)x>0在(2,+∞)上恒成立, 即k <x +x ln xx -2在(2,+∞)上恒成立. 令h (x )=x +x ln x x -2,则h ′(x )=x -2ln x -4(x -2)2. 设ν(x )=x -2ln x -4,则ν′(x )=x -2x. 当x ∈(2,+∞)时,ν′(x )>0,所以ν(x )在(2,+∞)上为增函数.因为ν(8)=8-2ln8-4=4-2ln8<0,ν(9)=5-2ln9>0, 所以存在x 0∈(8,9),ν(x 0)=0,即x 0-2ln x 0-4=0.当x ∈(2,x 0)时,h ′(x )<0,h (x )单调递减,当x ∈(x 0,+∞)时,h ′(x )>0,h (x )单调递增.所以当x =x 0时,h (x )的最小值为h (x 0)=x 0+x 0ln x 0x 0-2.因为ln x 0=x 0-42,所以h (x 0)=x 02∈(4,4.5). 故所求的整数k 的最大值为4. 方法二 由题意知,1+ln x -k (x -2)x>0在(2,+∞)上恒成立. f (x )=1+ln x -k (x -2)x ,f ′(x )=x -2kx2.①当2k ≤2,即k ≤1时,f ′(x )>0在(2,+∞)上恒成立, 所以f (x )在(2,+∞)上单调递增. 而f (2)=1+ln2>0成立,所以满足要求. ②当2k >2,即k >1时,当x ∈(2,2k )时,f ′(x )<0,f (x )单调递减,当x ∈(2k ,+∞)时,f ′(x )>0,f (x )单调递增.所以当x =2k 时,f (x )有最小值f (2k )=2+ln2k -k . 从而f (x )>0在(2,+∞)上恒成立等价于2+ln2k -k >0.令g (k )=2+ln2k -k ,则g ′(k )=1-kk<0,从而g (k )在(1,+∞)为减函数.因为g (4)=ln8-2>0,g (5)=ln10-3<0, 所以使2+ln2k -k >0成立的最大正整数k =4. 综合①②,知所求的整数k 的最大值为4.解答题滚动练81.(2017·江苏溧阳中学模拟)在三棱锥S -ABC 中,SA ⊥平面ABC ,SA =AB =AC =33BC ,点D 是BC 边的中点,点E 是线段AD 上一点,且AE =4DE ,点M 是线段SD 上一点.(1)求证:BC ⊥AM ;(2)若AM ⊥平面SBC ,求证:EM ∥平面ABS . 证明 (1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC , ∵SA ⊥平面ABC ,BC ⊂平面ABC , ∴SA ⊥BC ,又AD ∩SA =A ,AD ,SA ⊂平面SAD , ∴BC ⊥平面SAD ,又AM ⊂平面SAD ,∴BC ⊥AM .(2)∵AM ⊥平面SBC ,SD ⊂平面SBC ,∴AM ⊥SD .设SA =1,则AD =12,SD =52,AM =55,SM =255,MD =510.∴SM =4MD . 又AE =4DE , ∴ME ∥SA ,又ME ⊄平面ABS ,SA ⊂平面ABS , ∴EM ∥平面ABS .2.(2017·江苏郑集高级中学质检)在△ABC 中,已知(sin A +sin B +sin C )(sin B +sin C -sin A )=3sin B sin C . (1)求角A 的值;(2)求3sin B -cos C 的最大值.解 (1)因为(sin A +sin B +sin C )(sin B +sin C -sin A )=3sin B sin C , 由正弦定理,得(a +b +c )(b +c -a )=3bc ,所以b 2+c 2-a 2=bc ,所以cos A =b 2+c 2-a 22bc =12,因为A ∈(0,π),所以A =π3. (2)由A =π3,得B +C =2π3,所以3sin B -cos C =3sin B -cos ⎝ ⎛⎭⎪⎫2π3-B=3sin B -⎝ ⎛⎭⎪⎫-12cos B +32sin B =sin ⎝ ⎛⎭⎪⎫B +π6,因为0<B <2π3,所以π6<B +π6<5π6,当B +π6=π2,即B =π3时,3sin B -cos C 取最大值1.3.(2017·南通、扬州、淮安、宿迁、泰州、徐州六市二调)一缉私艇巡航至距领海边界线l (一条南北方向的直线)3.8海里的A 处,发现在其北偏东30°方向相距4海里的B 处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°=36,33≈5.7446); (2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.解 (1)如图甲,设缉私艇在点C 处拦截到走私船. 在△ABC 中,B =120°,AB =4,设BC =a ,AC =3a . 由正弦定理,得sin A a =sin120°3a ,所以sin A =36.因为B =120°,所以A 为锐角,从而A =17°. 由余弦定理,得(3a )2=42+a 2-2×4a cos120°, 即2a 2-a -4=0,解得a =1+334≈1.7. 点B 到l 的距离为3.8-2=1.8,而a <1.8,所以点C 在领海内. 答 缉私艇的追击方向应为北偏东47°.(2)如图乙,以A 为原点,正北方向为y 轴正方向,1海里为1个单位长度,建立平面直角坐标系xAy ,则A (0,0),B (2,23),直线l 的方程为x =3.8. 设缉私艇在点P (x ,y )处拦截到走私船.由AP =3BP ,得x 2+y 2=9[(x -2)2+(y -23)2].整理,得⎝ ⎛⎭⎪⎫x -942+⎝ ⎛⎭⎪⎫y -9342=94.点P 的轨迹是以M ⎝ ⎛⎭⎪⎫94,934为圆心,半径r =32的圆.圆心M 到直线l 的距离d =3.8-94=1.55>r ,所以直线l 与圆M 外离,即点P 总在领海内.答 无论走私船沿何方向逃跑,缉私艇总能在领海内成功拦截.4.如图,在平面直角坐标系xOy 中,已知圆O :x 2+y 2=4,椭圆C :x 24+y 2=1,A 为椭圆右顶点.过原点O 且异于坐标轴的直线与椭圆C 交于B ,C 两点,直线AB 与圆O 的另一交点为P ,直线PD 与圆O 的另一交点为Q ,其中D ⎝ ⎛⎭⎪⎫-65,0.设直线AB ,AC 的斜率分别为k 1,k 2.(1)求k 1k 2的值;(2)记直线PQ ,BC 的斜率分别为k PQ ,k BC ,是否存在常数λ,使得k PQ =λk BC ?若存在,求λ值;若不存在,说明理由; (3)求证:直线AC 必过点Q .(1)解 设B (x 0,y 0),则C (-x 0,-y 0),x 204+y 20=1,所以k 1k 2=y 0x 0-2·y 0x 0+2=y 20x 20-4=1-14x 20x 20-4=-14.(2)解 由题意得直线AP 的方程为y =k 1(x -2),联立⎩⎪⎨⎪⎧y =k 1(x -2),x 2+y 2=4,得(1+k 21)x 2-4k 21x+4(k 21-1)=0, 设P (x p ,y p ),解得x p =2(k 21-1)1+k 21,y p =k 1(x p -2)=-4k 11+k 21,联立⎩⎪⎨⎪⎧y =k 1(x -2),x 24+y 2=1,得(1+4k 21)x 2-16k 21x +4(4k 21-1)=0,设B (x B ,y B ),解得x B =2(4k 21-1)1+4k 21,y B =k 1(x B -2)=-4k 11+4k 21,所以k BC =y B x B =-2k 14k 21-1,k PQ =y p x p +65=-4k 11+k 212(k 21-1)1+k 21+65=-5k 14k 21-1,所以k PQ =52k BC ,故存在常数λ=52,使得k PQ =52k BC ,(3)证明 当直线PQ 与x 轴垂直时,Q ⎝ ⎛⎭⎪⎫-65,-85,则k AQ =852+65=12=k 2,所以直线AC 必过点Q .当直线PQ 与x 轴不垂直时,直线PQ 方程为y =-5k 14k 21-1⎝ ⎛⎭⎪⎫x +65, 联立⎩⎪⎨⎪⎧y =-5k 14k 21-1⎝ ⎛⎭⎪⎫x +65x 2+y 2=4,,解得x Q =-2(16k 21-1)16k 21+1,y Q =16k 116k 21+1, 所以k AQ =16k 116k 21+1-2(16k 21-1)16k 21+1-2=-14k 1=k 2, 故直线AC 必过点Q .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答题滚动练8
1.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知cos 2A +3
2=2cos A .
(1)求角A 的大小;
(2)若a =1,求△ABC 的周长l 的取值范围. 解 (1)根据倍角公式cos 2x =2cos 2
x -1, 得2cos 2
A +12=2cos A ,
即4cos 2
A -4cos A +1=0, 所以(2cos A -1)2
=0,
所以cos A =12,又因为0<A <π,所以A =π
3.
(2)根据正弦定理a sin A =b sin B =c
sin C ,
得b =
2
3sin B ,c =2
3
sin C , 所以l =1+b +c =1+
23
(sin B +sin C ),
因为A =π3,所以B +C =2π
3
,
所以l =1+23⎣⎢⎡⎦⎥⎤sin B +sin ⎝ ⎛⎭⎪⎫2π3-B =1+2sin ⎝ ⎛⎭⎪⎫B +π6,
因为0<B <2π
3
,所以l ∈(2,3].
2.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查统计,其贷款期限的频数如下表:
以上表各种贷款期限的频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共要补贴多少万元. 解 (1)由已知一困难户选择贷款期限为12个月的概率是0.4,
所以小区2017年准备享受此项政策的3户恰有两户选择贷款期限为12个月的概率是
P 1=C 23×0.42×0.6=0.288.
(2)P (ξ=200)=0.2,P (ξ=300)=0.6,P (ξ=400)=0.2, 所以ξ的分布列是
E (ξ)=200×0.2+300×0.6+400×0.2=300.
所以估计2017年该市共要补贴1 080万元.
3.(2017·北京丰台二模)如图所示的几何体中,四边形ABCD 为等腰梯形,AB ∥CD ,AB =2AD =2,∠DAB =60°,四边形CDEF 为正方形,平面CDEF ⊥平面ABCD .
(1)若点G 是棱AB 的中点,求证:EG ∥平面BDF ; (2)求直线AE 与平面BDF 所成角的正弦值;
(3)在线段FC 上是否存在点H ,使平面BDF ⊥平面HAD ?若存在,求FH
HC
的值;若不存在,请说明理由.
(1)证明 由已知得EF ∥CD ,且EF =CD . 因为四边形ABCD 为等腰梯形,所以有BG ∥CD . 因为G 是棱AB 的中点,所以BG =CD . 所以EF ∥BG ,且EF =BG ,
故四边形EFBG 为平行四边形,所以EG ∥FB . 因为FB ⊂平面BDF ,EG ⊄平面BDF , 所以EG ∥平面BDF .
(2)解 因为四边形CDEF 为正方形,所以ED ⊥DC . 因为平面CDEF ⊥平面ABCD , 平面CDEF ∩平面ABCD =DC ,
DE ⊂平面CDEF ,所以ED ⊥平面ABCD .
在△ABD 中,因为∠DAB =60°,AB =2AD =2, 所以由余弦定理,得BD =3,所以AD ⊥BD . 在等腰梯形ABCD 中,可得DC =CB =1.
如图,以D 为原点,以DA ,DB ,DE 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则D (0,0,0),A (1,0,0),E (0,0,1),B (0,3,0),F ⎝ ⎛⎭
⎪⎫-1
2,32,1,
所以AE →=(-1,0,1),DF →=⎝ ⎛⎭⎪⎫-1
2,32,1,DB →=(0,3,0).
设平面BDF 的法向量为n =(x ,y ,z ), 由⎩⎪⎨
⎪⎧
n ·DB →=0,
n ·DF →=0,
得⎩⎪⎨⎪⎧
3y =0,
-12
x +3
2y +z =0,
取z =1,则x =2,y =0, 得n =(2,0,1).
设直线AE 与平面BDF 所成的角为θ,则sin θ=|cos 〈AE →
,n 〉|=|AE →
·n ||AE →|| n |=1010,
所以AE 与平面BDF 所成的角的正弦值为
1010
. (3)解 线段FC 上不存在点H ,使平面BDF ⊥平面HAD .理由如下: 假设线段FC 上存在点H ,设H ⎝ ⎛⎭⎪⎫-1
2,32,t (0≤t ≤1),
则DH →=⎝ ⎛⎭
⎪⎫-1
2,32,t ,
设平面HAD 的法向量为m =(a ,b ,c ), 由⎩⎪⎨
⎪⎧
m ·DA →=0,m ·DH →=0,
得⎩⎪⎨⎪
⎧
a =0,-12
a +3
2b +tc =0,
取c =1,则a =0,b =-
2
3
t ,得m =⎝ ⎛⎭⎪⎫
0,-23 t ,1.
要使平面BDF ⊥平面HAD ,只需m ·n =0,
即2×0-
23
t ×0+1×1=0,此方程无解.
所以线段FC 上不存在点H ,使平面BDF ⊥平面HAD .
4.已知函数f (x )=a ln x +b (a ,b ∈R ),曲线f (x )在x =1处的切线方程为x -y -1=0. (1)求a ,b 的值; (2)证明:f (x )+1
x
≥1;
(3)已知满足x ln x =1的常数为k .令函数g (x )=m e x
+f (x )(其中e 是自然对数的底数,e =2.718 28…),若x =x 0是g (x )的极值点,且g (x )≤0恒成立,求实数m 的取值范围. (1)解 f (x )的导函数f ′(x )=a x
,
由曲线f (x )在x =1处的切线方程为x -y -1=0,知f ′(1)=1,f (1)=0,所以a =1,b =0.
(2)证明 令u (x )=f (x )+1x -1=ln x +1
x
-1,
则u ′(x )=1x -1x 2=x -1
x
2,
当0<x <1时,u ′(x )<0,u (x )单调递减;当x >1时,
u ′(x )>0,u (x )单调递增,所以当x =1时,u (x )取得极小值,也即最小值,该最小值为u (1)
=0,
所以u (x )≥0,即不等式f (x )+1
x
≥1成立.
(3)解 函数g (x )=m e x
+ln x (x >0), 则g ′(x )=m e x
+1x
,
当m ≥0时,g ′(x )>0,函数g (x )在(0,+∞)上单调递增,g (x )无极值,不符合题意; 当m <0时,由g ′(x )=m e x +1x =0,得e x
=-1mx
,
结合y =e x ,y =-1mx 在(0,+∞)上的图象可知,关于x 的方程m e x
+1x
=0一定有解,其解为
x 0(x 0>0),且当0<x <x 0时,g ′(x )>0,g (x )在(0,x 0)内单调递增;
当x >x 0时,g ′(x )<0,g (x )在(x 0,+∞)内单调递减. 则x =x 0是函数g (x )的唯一极值点,也是它的唯一最大值点,
x =x 0也是g ′(x )=0在(0,+∞)上的唯一零点,
即m 0e x
=-1x 0
,则m =-10e x x 0
.
所以g (x )max =g (x 0)=m 0e x
+ln x 0=-1x 0
+ln x 0.
由于g (x )≤0恒成立,则g (x )max ≤0, 即-1
x 0
+ln x 0≤0,
(*)
考查函数h (x )=ln x -1x ,则h ′(x )=1x +1
x
2>0,
所以h (x )为(0,+∞)上的增函数,且h ⎝ ⎛⎭⎪⎫1e =-1-e <0,h (e)=1-1e >0, 又常数k 满足k ln k =1,即-1
k
+ln k =0,
所以k 是方程-1
x 0
+ln x 0=0的唯一根,
于是不等式(*)的解为x 0≤k ,
又函数t (x )=-1e x x (x >0)为增函数,故m =-10e x x 0≤-1
e k k ,
所以m 的取值范围是⎝
⎛
⎦
⎥⎤-∞,-1e k
k .。
