2020年高考复习数学算法初步
2020高考文科数学(人教A版)总复习课件:第十章 算法初步、统计与统计案例10.1

考点1
第十章
考点2
考点3
10.1 算法初步
必备知识·预案自诊
关关键键能能力力··学学案案突突破破
-22-
解析: (1)由程序框图可知,
程序的作用是计算分段函数 y=
������-1 ������
,������
≤
������, 的函数值,
������-1 ������
,������
>
������
因为(log√22√2)☆
(2)条件结构的出口有两个,但在执行时,只有一个出口是有效的.
( √)
(3)输入框只能紧接开始框,输出框只能紧接结束框. ( × )
(4)输入语句可以同时给多个变量赋值. ( √ )
(5)在算法语句中,x=x+1是错误的. ( × )
第十章
10.1 算法初步
必必备备知知识识··预预案案自自诊诊 关键能力·学案突破
②WHILE 语句
第十章
知识梳理 考点自诊
10.1 算法初步
必必备备知知识识··预预案案自自诊诊 关键能力·学案突破
-10-
5.中国古代数学中的算法案例 (1)求两个正整数(奇数)最大公约数的算法
①更相减损术:用两数中较大的数减较小的数,把得到的差,与较
小的数再构成一对新的数;再用这对数中较大的数减较小的数,以 同样的操作一直做下去,直到产生一对相等的数,这个数就是最大 公约数.
T=12
+
14,
i=5…最后输出
S=N-T=1-12
+
1 3
−
14+…+919
−
1010,一次处理1������
与 ������+11两项,故 i=i+2.
2020版高考数学一轮复习第十六单元算法初步、复数、推理与证明学案文
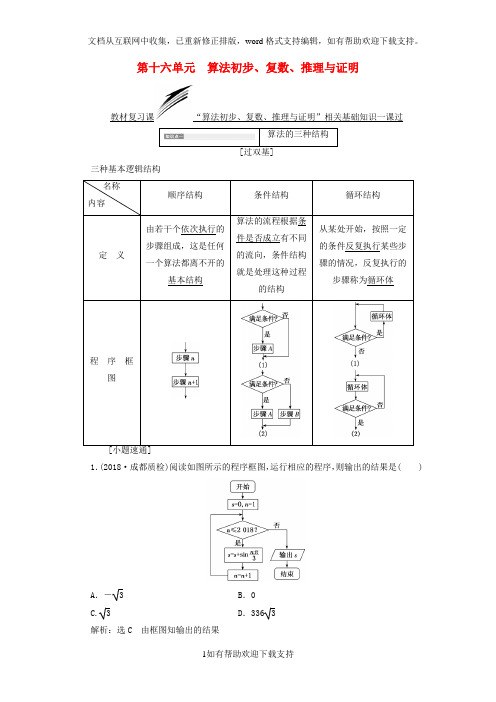
第十六单元算法初步、复数、推理与证明教材复习课“算法初步、复数、推理与证明”相关基础知识一课过算法的三种结构[过双基]三种基本逻辑结构名称内容顺序结构条件结构循环结构定义由若干个依次执行的步骤组成,这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向,条件结构就是处理这种过程的结构从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体程序框图1.(2018·成都质检)阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )A.- 3 B.0C. 3 D.336 3解析:选C 由框图知输出的结果s =sin π3+sin2π3+…+sin 2 018π3, 因为函数y =sin π3x 的周期是6,所以s =336⎝ ⎛⎭⎪⎫sin π3+sin 2π3+…+sin 6π3+sin π3+sin 2π3=336×0+32+32= 3.2.执行如图所示的程序框图.若输出y =-3,则输入的角θ=( )A.π6 B .-π6C.π3D .-π3解析:选D 由输出y =-3<0,排除A 、C ,又当θ=-π3时,输出y =-3,故选D.3.执行如图所示的程序框图,已知输出的s ∈[0,4],若输入的t ∈[m ,n ],则实数n -m 的最大值为( )A .1B .2C .3D .4解析:选D 由程序框图得s =⎩⎪⎨⎪⎧3t ,t <1,4t -t 2,t ≥1,作出s 的图象如图所示.若输入的t ∈[m ,n ],输出的s ∈[0,4],则由图象得n -m 的最大值为4.4.某程序框图如图所示,若输出的p 值为31,则判断框内应填入的条件是( )A .n >2?B .n >3?C .n >4?D .n >5?解析:选B 运行程序:p =1,n =0;n =1,p =2;n =2,p =6;n =3,p =15;n =4,p =31,根据题意,此时满足条件,输出p =31,即n =3时不满足条件,n =4时满足条件,故选B.[清易错]1.易混淆处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.2.易忽视循环结构中必有选择结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.某程序框图如图所示,若该程序运行后输出的值是74,则a =________.解析:由已知可得该程序的功能是计算并输出S =1+11×2+12×3+…+1aa +1=1+1-12+12-13+…+1a -1a +1=2-1a +1. 若该程序运行后输出的值是74,则2-1a +1=74, 解得a =3. 答案:3复数的基本运算 [过双基]1.复数的有关概念 名称 内容备注复数的概念 形如a +b i(a ∈R ,b ∈R)的数叫复数,其中实部为a ,虚部为b若b =0,则a +b i 为实数;若a =0且b ≠0,则a +b i 为纯虚数 复数相等 a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R)共轭复数a +b i 与c +d i 共轭⇔a =c 且b =-d (a ,b ,c ,d ∈R)复平面建立平面直角坐标系来表示复数的平面叫做复平面,x 轴叫实轴,y 轴叫虚轴 实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,各象限内的点都表示虚数复数的模设OZ ―→对应的复数为z =a +b i ,则向量OZ ―→的长度叫做复数z =a +b i 的模|z |=|a +b i|=a 2+b 22.复数的几何意义复数集C 和复平面内所有的点组成的集合是一一对应的,复数集C 与复平面内所有以原点O 为起点的向量组成的集合也是一一对应的,即(1)复数z =a +b i 一一对应复平面内的点Z (a ,b )(a ,b ∈R). (2)复数z =a +b i(a ,b ∈R)一一对应平面向量OZ ―→. 3.复数的运算设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R),则①加法:z 1+z 2=(a +b i)+(c +d i)=(a +c )+(b +d )i ; ②减法:z 1-z 2=(a +b i)-(c +d i)=(a -c )+(b -d )i ; ③乘法:z 1·z 2=(a +b i)·(c +d i)=(ac -bd )+(ad +bc )i ; ④除法:z 1z 2=a +b ic +d i =a +b ic -d ic +d i c -d i=ac +bd +bc -ad ic 2+d 2(c +d i≠0).[小题速通]1.(2016·全国卷Ⅲ)若z =4+3i ,则z|z |=( )A .1B .-1C.45+35iD.45-35i 解析:选D ∵z =4+3i ,∴z =4-3i ,|z |=42+32=5, ∴z|z |=4-3i 5=45-35i. 2.若复数z 满足(1+i)z =|3+i|,则在复平面内,z 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析:选A 由题意,得z =32+121+i =21-i1+i 1-i=1-i ,所以z =1+i ,其在复平面内对应的点为(1,1),位于第一象限.3.复数2i1+i (i 为虚数单位)实部与虚部的和为( )A .2B .1C .0D .-2解析:选A 因为2i1+i =2i 1-i 1+i 1-i =1+i ,所以复数2i1+i(i 为虚数单位)实部与虚部的和为2.4.已知(1+2i)z =4+3i ,则z =________. 解析:∵z =4+3i 1+2i =4+3i 1-2i 1+2i 1-2i =10-5i5=2-i ,∴z =2+i. 答案:2+i[清易错]1.利用复数相等a +b i =c +d i 列方程时,注意a ,b ,c ,d ∈R 的前提条件. 2.注意不能把实数集中的所有运算法则和运算性质照搬到复数集中来.例如,若z 1,z 2∈C ,z 21+z 22=0,就不能推出z 1=z 2=0;z 2<0在复数范围内有可能成立.1.已知4+m i1+2i ∈R ,且m ∈R ,则|m +6i|=( )A .6B .8C .8 3D .10解析:选D4+m i 1+2i =4+m i1-2i 1+2i1-2i =4+2m +m -8i5,因为复数4+m i1+2i ∈R ,故m =8,所以|m +6i|=|8+6i|=10.2.已知5i2-i =a +b i(a ,b ∈R ,i 为虚数单位),则a +b =______.解析:5i 2-i =5i 2+i 2-i 2+i=-1+2i , 由5i2-i=a +b i ,得-1+2i =a +b i ,∴a =-1,b =2, ∴a +b =1. 答案:1合情推理与演绎推理1.合情推理类型定义特点归纳 推理由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理由部分到整体、由个别到一般 类比 推理 由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理由特殊到特殊 (1)定义:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.简言之,演绎推理是由一般到特殊的推理.(2)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的一般原理; ②小前提——所研究的特殊情况;③结论——根据一般原理,对特殊情况作出的判断. [小题速通]1.已知2和3都是无理数,试证:2+3也是无理数,某同学运用演绎推理证明如下:依题设2和3都是无理数,而无理数与无理数之和是无理数,所以2+3必是无理数.这个同学证明是错误的,错误原因是( )A .大前提错误B .小前提错误C .推理形式错误D .以上都可能解析:选A 大前提:无理数与无理数之和是无理数,错误; 小前提:2和3都是无理数,正确; 结论:2+3也是无理数,正确, 故只有大前提错误.2.我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线x 2a 2-y 2b2=1(a >0,b >0)与x 轴,直线y =h (h >0)及渐近线y =bax 所围成的阴影部分(如图)绕y 轴旋转一周所得的几何体的体积为________.解析:由题意可知,该几何体的横截面是一个圆环,设圆环的外半径与内半径分别为R ,r ,其面积S =π(R 2-r 2).∵x 2a 2-y 2b 2=1⇒R 2=a 2+a 2b 2y 2, 同理:r 2=a 2b2y 2,∴R 2-r 2=a 2,由祖暅原理知,此旋转体的体积等价于一个半径为a ,高为h 的柱体的体积,为πa 2h .答案:πa 2h 3.有如下等式: 2+4=6;8+10+12=14+16;18+20+22+24=26+28+30;……以此类推,则2 018出现在第________个等式中. 解析:①2+4=6; ②8+10+12=14+16;③18+20+22+24=26+28+30, ……其规律为:各等式首项分别为2×1,2×(1+3),2×(1+3+5),…, 所以第n 个等式的首项为2[1+3+…+(2n -1)]=2×n 1+2n -12=2n 2,当n =31时,等式的首项为2×312=1 922, 当n =32时,等式的首项为2×322=2 048, 所以2 018在第31个等式中. 答案:31证明方法1.直接证明 内容综合法分析法定义利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止实质由因导果执果索因框图表示P ⇒Q 1→Q 1⇒Q 2→…→Q n ⇒QQ ⇐P 1→P 1⇐P 2→…→得到一个明显成立的条件文字语言 因为……,所以…… 或由……,得……要证……,只需证……,即证……间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法. (1)反证法的定义:假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立的证明方法.(2)用反证法证明的一般步骤: ①反设——假设命题的结论不成立;②归谬——根据假设进行推理,直到推出矛盾为止; ③结论——断言假设不成立,从而肯定原命题的结论成立. [小题速通]1.(2018·成都一模)要证a 2+b 2-1-a 2b 2≤0,只需证明( ) A .2ab -1-a 2b 2≤0 B .a 2+b 2-1-a 4+b 42≤0C.a +b22-1-a 2b 2≤0D .(a 2-1)(b 2-1)≥0解析:选D a 2+b 2-1-a 2b 2≤0⇔(a 2-1)(b 2-1)≥0.2.观察(x 2)′=2x ,(x 4)′=4x 3,(cos x )′=-sin x ,由归纳推理可得:若定义在R 上的函数f (x )满足f (-x )=f (x ),记g (x )为f (x )的导函数,则g (-x )=( )A .f (x )B .-f (x )C .g (x )D .-g (x )解析:选D 由所给函数及其导数知,偶函数的导函数为奇函数,因此当f (x )是偶函数时,其导函数应为奇函数,故g (-x )=-g (x ).3.下列命题适合用反证法证明的是________.(填序号) ①已知函数f (x )=a x+x -2x +1(a >1),证明:方程f (x )=0没有负实数根; ②若x ,y ∈R ,x >0,y >0,且x +y >2, 求证:1+x y 和1+y x中至少有一个小于2;③关于x 的方程ax =b (a ≠0)的解是唯一的;④同一平面内,分别与两条相交直线垂直的两条直线必相交.解析:①是“否定”型命题,②是“至少”型命题,③是“唯一”型命题,且命题中条件较少,④中条件较少,不足以直接证明,因此四个命题都适合用反证法证明.答案:①②③④一、选择题1.若z =i(3-2i)(其中i 为复数单位),则z =( ) A .3-2i B .3+2i C .2+3iD .2-3i解析:选D 由z =i(3-2i)=2+3i ,得z =2-3i. 2.已知i 为虚数单位,a 为实数,复数z =a -3i1-i在复平面上对应的点在y 轴上,则a为( )A .-3B .-13C.13D .3解析:选A ∵z =a -3i1-i=a -3i1+i 1-i 1+i =a +3-3-a i2,又复数z =a -3i1-i在复平面上对应的点在y 轴上,∴⎩⎪⎨⎪⎧a +3=0,3-a ≠0,解得a =-3.3.分析法又称执果索因法,若用分析法证明“设a >b >c ,且a +b +c =0,求证:b 2-ac <3a ”索的因应是( )A .a -b >0B .a -c >0C .(a -b )(a -c )>0D .(a -b )(a -c )<0解析:选Cb 2-ac <3a ⇔b 2-ac <3a 2⇔(a +c )2-ac <3a 2⇔a 2+2ac +c 2-ac -3a 2<0⇔-2a 2+ac +c 2<0⇔2a 2-ac -c 2>0⇔(a -c )(2a +c )>0⇔(a -c )(a -b )>0.4.[n ]表示不超过 n 的最大整数. 若S 1=[ 1 ]+[ 2 ]+[ 3 ]=3,S 2=[ 4 ]+[ 5 ]+[ 6 ]+[7 ]+[8 ]=10,S 3=[9 ]+[10 ]+[11 ]+[12 ]+[13 ]+[14 ]+[15 ]=21,…… 则S n =( ) A .n (n +2)B .n (n +3)C .(n +1)2-1D .n (2n +1)解析:选D 观察得到:S n 是从n 2开始到n +12(不含)之前共2n +1个n 的和,所以S n 为n (2n +1).即[n 2]+[n 2+1]+[n 2+2]+…+[n +12-1]=n (2n +1).5.(2017·北京高考)执行如图所示的程序框图,输出的s 值为( )A .2 B.32 C.53D.85解析:选C 运行该程序,k =0,s =1,k <3;k =0+1=1,s =1+11=2,k <3; k =1+1=2,s =2+12=32,k <3; k =1+2=3,s =32+132=53,此时不满足循环条件,输出s ,故输出的s 值为53.6.若数列{a n }是等差数列,b n =a 1+a 2+…+a nn,则数列{b n }也为等差数列.类比这一性质可知,若正项数列{c n }是等比数列,且{d n }也是等比数列,则d n 的表达式应为( )A .d n =c 1+c 2+…+c nnB .d n =c 1·c 2·…·c nnC .d n = n c n 1+c n 2+…+c n nnD .d n =nc 1·c 2·…·c n解析:选D 因为数列{a n }是等差数列,所以b n =a 1+a 2+…+a n n =a 1+(n -1)·d2(d 为等差数列{a n }的公差),{b n }也为等差数列,因为正项数列{c n }是等比数列,设公比为q ,则d n =n c 1·c 2·…·c n =nc 1·c 1q ·…·c 1qn -1=c 1qn -12,所以{d n }也是等比数列.7.执行如图所示的程序框图,若输出的结果是99199,则判断框内应填的内容是( )A .n <98?B .n <99?C .n <100?D .n <101?解析:选B 由14n 2-1=12n -12n +1=1212n -1-12n +1, 可知程序框图的功能是计算并输出S =12⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1=12⎝ ⎛⎭⎪⎫1-12n +1=n 2n +1的值. 由题意令n 2n +1=99199,解得n =99,即当n <99时,执行循环体,若不满足此条件,则退出循环,输出S 的值.8.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )A .(7,5)B .(5,7)C .(2,10)D .(10,1)解:选B 依题意,把“整数对”的和相同的分为一组,不难得知第n 组中每个“整数对”的和均为n +1,且第n 组共有n 个“整数对”,这样的前n 组一共有n n +12个“整数对”,注意到10×10+12<60<11×11+12,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).二、填空题 9.M =1210+1210+1+1210+2+…+1211-1与1的大小关系为__________. 解析:因为M =1210+1210+1+1210+2+…+1211-1=1210+1210+1+1210+2+…+1210+210-1<1210+1210+1210+…+1210=1, 所以M <1. 答案:M <1 10.若复数z =a +ii(其中i 为虚数单位)的实部与虚部相等,则实数a =________.解析:因为复数z =a +i i =a i +i 2i2=1-a i ,所以-a =1,即a =-1. 答案:-111.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =________.解析:a =14,b =18.第一次循环:14≠18且14<18,b =18-14=4; 第二次循环:14≠4且14>4,a =14-4=10; 第三次循环:10≠4且10>4,a =10-4=6; 第四次循环:6≠4且6>4,a =6-4=2; 第五次循环:2≠4且2<4,b =4-2=2; 第六次循环:a =b =2,跳出循环,输出a =2. 答案:212.设n 为正整数,f (n )=1+12+13+…+1n ,计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,观察上述结果,可推测一般的结论为________.解析:∵f (21)=32,f (22)>2=42,f (23)>52,f (24)>62,∴归纳得f (2n)≥n +22(n ∈N *).答案:f (2n)≥n +22(n ∈N *)三、解答题13.若a >b >c >d >0且a +d =b +c , 求证:d +a <b +c . 证明:要证d +a <b +c , 只需证(d +a )2<(b +c )2, 即证a +d +2ad <b +c +2bc ,因为a +d =b +c ,所以只需证ad <bc ,即证ad <bc ,设a +d =b +c =t ,则ad -bc =(t -d )d -(t -c )c =(c -d )(c +d -t )<0, 故ad <bc 成立,从而d +a <b +c 成立.14.等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+3 2. (1)求数列{a n }的通项a n 与前n 项和S n ;(2)设b n =S n n(n ∈N *),求证:数列{b n }中任意不同的三项都不可能成为等比数列.解:(1)由已知得⎩⎨⎧a 1=1+2,3a 1+3d =9+32,所以d =2,故a n =2n -1+2,S n =n (n +2).(2)证明:由(1),得b n =S n n=n + 2.假设数列{b n }中存在三项b p ,b q ,b r (p ,q ,r 互不相等)成等比数列,则b 2q =b p b r ,即(q +2)2=(p +2)(r +2), 所以(q 2-pr )+2(2q -p -r )=0.因为p ,q ,r ∈N *,所以⎩⎪⎨⎪⎧q 2-pr =0,2q -p -r =0,所以⎝⎛⎭⎪⎫p +r 22=pr ,(p -r )2=0.所以p =r ,这与p ≠r 矛盾,所以数列{b n }中任意不同的三项都不可能成为等比数列. 高考研究课(一)算法与程序框图考查2类型——推结果、填条件 [全国卷5年命题分析]考点 考查频度 考查角度循环结构 5年10考 循环结构程序框图的输出功能及应用程序框图补条件 5年1考补全满足框图的条件程序框图的推结果问题[典例] a =-1,则输出的S =( )A.2 B.3C.4 D.5(2)(2017·山东高考)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )A.0,0 B.1,1C.0,1 D.1,0[解析] (1)运行程序框图,a=-1,S=0,K=1,K≤6成立;S=0+(-1)×1=-1,a=1,K=2,K≤6成立;S=-1+1×2=1,a=-1,K=3,K≤6成立;S=1+(-1)×3=-2,a=1,K=4,K≤6成立;S=-2+1×4=2,a=-1,K=5,K≤6成立;S=2+(-1)×5=-3,a=1,K=6,K≤6成立;S=-3+1×6=3,a=-1,K=7,K≤6不成立,输出S=3.(2)当输入x=7时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x成立,故a=1,输出a的值为1.当输入x=9时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x不成立且x 能被b 整除,故a =0,输出a 的值为0.[答案] (1)B (2)D [方法技巧]解决程序框图推结果问题要注意几个常用变量(1)计数变量:用来记录某个事件发生的次数,如i =i +1. (2)累加变量:用来计算数据之和,如S =S +i . (3)累乘变量:用来计算数据之积,如p =p ×i . [即时演练]1.(2016·全国卷Ⅰ)执行如图所示的程序框图,如果输入的x =0,y =1,n =1,则输出x ,y 的值满足( )A .y =2xB .y =3xC .y =4xD .y =5x解析:选C 输入x =0,y =1,n =1, 运行第一次,x =0,y =1,不满足x 2+y 2≥36; 运行第二次,x =12,y =2,不满足x 2+y 2≥36;运行第三次,x =32,y =6,满足x 2+y 2≥36,输出x =32,y =6.由于点⎝ ⎛⎭⎪⎫32,6在直线y =4x 上,故选C. 2.执行如图所示的程序框图,输出的s 是________.解析:第一次循环:i=1,s=1;第二次循环:i=2,s=-1;第三次循环:i=3,s =2;第四次循环:i=4,s=-2,此时i=5,执行s=3×(-2)=-6,故输出s=-6.答案:-6程序框图的补全及逆向求解问题[典例] (1)《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )A.4 B.5C.7 D.11(2)一个算法的程序框图如图所示,该程序输出的结果为3655,则空白处应填入的条件为( )A.i≤9? B.i≤6?C.i≥9? D.i≤8?[解析] (1)起始阶段有m=2a-3,i=1,第一次循环:m=2×(2a-3)-3=4a-9,i=2,第二次循环:m=2×(4a-9)-3=8a-21,i=3,第三次循环:m=2×(8a-21)-3=16a-45,i=4,第四次循环:m =2×(16a -45)-3=32a -93, 跳出循环,输出m =32a -93=35,解得a =4. (2)由1i i +2=12⎝ ⎛⎭⎪⎫1i -1i +2及题意知,该程序框图的功能是计算S =121-13+12-14+…+1i -1-1i +1+1i -1i +2=34-121i +1+1i +2的值,由S =3655,得i =9. 故空白处应填入的条件为:i ≤9. [答案] (1)A (2)A [方法技巧]程序框图的补全及逆向求解问题(1)先假设参数的判断条件满足或不满足;(2)运行循环结构,一直到运行结果与题目要求的输出结果相同为止; (3)根据此时各个变量的值,补全程序框图. [即时演练]1.执行如图所示的程序框图,若输出k 的值为16,则判断框内可填入的条件是( )A .S <1510?B .S >85?C .S >1510?D .S <85?解析:选D 运行程序:k =10,S =1;S =1110,k =11;S =1210,k =12;S =1310,k =13;S =1410,k =14;S =1510,k =15;S =1610=85,k =16,此时不满足条件,循环结束,输出k =16,所以判断框内可填入条件是S <85?.2.运行如图所示的程序框图,若输出的y 值的范围是[0,10],则输入的x 值的范围是________.解析:该程序的功能是计算分段函数的值, y =⎩⎪⎨⎪⎧3-x ,x <-1,x 2,-1≤x ≤1,x +1,x >1.当x <-1时,由0≤3-x ≤10,可得-7≤x <-1; 当-1≤x ≤1时,0≤x 2≤10成立;当x >1时,由0≤x +1≤10,可得1<x ≤9, 综上,输入的x 值的范围是[-7,9]. 答案:[-7,9]1.(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n ,那么在◇和▭两个空白框中,可以分别填入( )A .A >1 000和n =n +1B .A >1 000和n =n +2C .A ≤1 000和n =n +1D .A ≤1 000和n =n +2解析:选D 程序框图中A =3n-2n,且判断框内的条件不满足时输出n ,所以判断框中应填入A ≤1 000,由于初始值n =0,要求满足A =3n-2n>1 000的最小偶数,故执行框中应填入n =n +2.2.(2017·全国卷Ⅲ)执行如图所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5 B.4C.3 D.2解析:选D 执行程序框图,S=0+100=100,M=-10,t=2;S=100-10=90,M=1,t=3,S<91,输出S,此时,t=3不满足t≤N,所以输入的正整数N的最小值为2.3.(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )A.7 B.12C.17 D.34解析:选C 第一次运算:s=0×2+2=2,k=1;第二次运算:s=2×2+2=6,k=2;第三次运算:s=6×2+5=17,k=3>2,结束循环,s=17.4.(2016·全国卷Ⅲ)执行如图所示的程序框图,如果输入的a=4,b=6,那么输出的n =( )A.3 B.4C.5 D.6解析:选B 程序运行如下:开始a=4,b=6,n=0,s=0.第1次循环:a=2,b=4,a=6,s=6,n=1;第2次循环:a=-2,b=6,a=4,s=10,n=2;第3次循环:a=2,b=4,a=6,s=16,n=3;第4次循环:a=-2,b=6,a=4,s=20,n=4.此时,满足条件s>16,退出循环,输出n=4.故选B.5.(2015·全国卷Ⅰ)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )A .5B .6C .7D .8解析:选C 运行第一次:S =1-12=12=0.5,m =0.25,n =1,S >0.01;运行第二次:S =0.5-0.25=0.25,m =0.125,n =2,S >0.01; 运行第三次:S =0.25-0.125=0.125,m =0.062 5,n =3,S >0.01; 运行第四次:S =0.125-0.062 5=0.062 5,m =0.031 25,n =4,S >0.01; 运行第五次:S =0.031 25,m =0.015 625,n =5,S >0.01; 运行第六次:S =0.015 625,m =0.007 812 5,n =6,S >0.01; 运行第七次:S =0.007 812 5,m =0.003 906 25,n =7,S <0.01. 输出n =7.故选C.6.(2014·全国卷Ⅰ)执行如图所示程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M =( )A.203B.165C.72D.158解析:选D 第一次循环:M =32,a =2,b =32,n =2;第二次循环:M =83,a =32,b =83,n =3;第三次循环:M =158,a =83,b =158,n =4.则输出M =158.7.(2014·全国卷Ⅱ)执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A.4 B.5C.6 D.7解析:选D 执行循环体,第一次循环,M=2,S=5,k=2;第二次循环,M=2,S=7,k=3.故输出的S=7.一、选择题1.(2017·山东高考)执行如图所示的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )A.x>3 B.x>4C.x≤4 D.x≤5解析:选B 当x=4时,若执行“是”,则y=4+2=6,与题意矛盾;若执行“否”,则y=log24=2,满足题意,故应执行“否”.故判断框中的条件可能为x>4.2.执行如图所示的程序框图,若输入的a的值为2,则输出的b的值为( )A .-2B .1C .2D .4解析:选A 第一次循环,a =12,b =1,i =2;第二次循环,a =-1,b =-2,i =3;第三次循环,a =2,b =4,i =4;第四次循环,a =12,b =1,i =5;……;由此可知b 的值以3为周期出现,且当i =2 019时退出循环,此时共循环2 018次,又2 018=3×672+2,所以输出的b 的值为-2.3.某班有50名学生,在一次数学考试中,a n 表示学号为n 的学生的成绩,则执行如图所示的程序框图,下列结论正确的是( )A .P 表示成绩不高于60分的人数B .Q 表示成绩低于80分的人数C .R 表示成绩高于80分的人数D .Q 表示成绩不低于60分,且低于80分的人数解析:选D P 表示成绩低于60分的人数,Q 表示成绩低于80分且不低于60分的人数,R 表示成绩不低于80分的人数.4.(2017·天津高考)阅读如图所示的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为( )A .0B .1C .2D .3解析:选C 第一次循环,24能被3整除,N =243=8>3;第二次循环,8不能被3整除,N =8-1=7>3; 第三次循环,7不能被3整除,N =7-1=6>3; 第四次循环,6能被3整除,N =63=2<3,结束循环,故输出N 的值为2.5.执行如图所示的程序框图,则输出S 的值为( )A .3B .-6C .10D .-15解析:选D 第一次执行程序,得到S =0-12=-1,i =2; 第二次执行程序,得到S =-1+22=3,i =3; 第三次执行程序,得到S =3-32=-6,i =4; 第四次执行程序,得到S =-6+42=10,i =5; 第五次执行程序,得到S =10-52=-15,i =6, 结束循环,输出的S =-15.6.某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:组别(i)睡眠时间组中值(Z i)频数频率(P i)1[4.5,5.5)520.042[5.5,6.5)660.123[6.5,7.5)7200.404[7.5,8.5)8180.365[8.5,9.5)930.066[9.5,10.5)1010.02 现根据如下程序框图用计算机统计平均睡眠时间,则判断框①中应填入的条件是( )A.i>4? B.i>5?C.i>6? D.i>7?解析:选B 根据题目中程序框图,用计算机统计平均睡眠时间,总共执行6次循环,则判断框①中应填入的条件是i>5(或i≥6?).7.下图为某一函数的求值程序框图,根据框图,如果输出y的值为3,那么应输入x=( )A.1 B.2C.3 D.6解析:选B 该程序的作用是计算分段函数y =⎩⎪⎨⎪⎧x -3,x >66,2<x ≤6,5-x ,x ≤2的函数值,由题意,若x >6,则当y =3时,x -3=3,解得x =6,舍去; 若x ≤2,则当y =3时,5-x =3,解得x =2, 故输入的x 值为2.8.给出30个数:1,2,4,7,…,其规律是:第1个数是1;第2个数比第1个数大1;第3个数比第2个数大2;第4个数比第3个数大3,…,以此类推,要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框①处和执行框②处应分别填入( )A .i ≤30?;p =p +i -1B .i ≤29?;p =p +i +1C .i ≤31?;p =p +iD .i ≤30?;p =p +i解析:选D 由于要计算30个数的和,故循环要执行30次,由于循环变量的初值为1,步长为1,故①中应填写“i ≤30?”.又由第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,故②中应填p =p +i .二、填空题9.(2017·江苏高考)如图是一个算法流程图.若输入x 的值为116,则输出y 的值是________.解析:由流程图可知其功能是运算分段函数y =⎩⎪⎨⎪⎧2x,x ≥1,2+log 2x ,0<x <1,所以当输入的x的值为116时,y =2+log 2116=2-4=-2.答案:-210.按下列程序框图来计算:如果输入的x =5,则应该运算________次才停止. 解析:由题意,该程序按如下步骤运行:经过第一次循环得到x =3×5-2=13,不满足x >200,进入下一步循环; 经过第二次循环得到x =3×13-2=37,不满足x >200,进入下一步循环; 经过第三次循环得到x =3×37-2=109,不满足x >200,进入下一步循环; 经过第四次循环得到x =3×109-2=325,因为325>200,结束循环并输出x 的值 因此,运算进行了4次后,输出x 值而程序停止.故答案为4. 答案:411.中国古代有计算多项式值的秦九韶算法,该算法的程序框图如图所示. 执行该程序框图,若输入的x =3,n =3,输入的a 依次为由小到大顺序排列的质数(从最小质数开始),直到结束为止,则输出的s =________.解析:运行程序:x =3,n =3,k =0,s =0;a =2,s =2,k =1;a =3,s =9,k =2;a =5,s =32,k =3;a =7,s =103,k =4,此时满足条件,循环结束,输出s =103.答案:10312.阅读如图所示的程序框图,运行相应的程序,输出的结果是a =________.解析:运行程序,可得a=10,i=1,不满足i≥5,不满足a是奇数,a=5,i=2,不满足i≥5,满足a是奇数,a=16,i=3,不满足i≥5,不满足a是奇数,a=8,i=4,不满足i≥5,不满足a是奇数,a=4,i=5,满足i≥5,退出循环,输出a的值为4.答案:413.已知某程序框图如图所示,则程序运行结束时输出的结果为________.解析:第一次循环结束时,n=2,x=3,y=1;第二次循环结束时,n=4,x=9,y=3;第三次循环结束时,n=6,x=27,y=3.此时满足n>4,结束循环,输出log y x=log327=3.答案:314.(2018·黄山调研)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=________.解析:第一次循环,得S =2;第二次循环,得n =2,a =12,A =2,S =92;第三次循环,得n =3,a =14,A =4,S =354;第四次循环,得n =4,a =18,A =8,S =1358>10,结束循环,输出的n =4.答案:41.图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A 1,A 2,…,A 16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )图1图2A .6B .7C .10D .16解析:选C 由程序框图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知,数学成绩大于等于90的人数为10,因此输出结果为10.2.如果执行程序框图,如果输出的S=2 550,则判断框内应填入的条件是( )A.k≤50? B.k≥51?C.k<50? D.k>51?解析:选A 根据题中的程序框图,可得该程序经过第一次循环得到S=2,k=2;经过第二次循环得到S=2+4,k=3;经过第三次循环得到S=2+4+6,k=4;……设经过第n次循环得到2+4+6+…+2n=n2+n=2 550,解得n=50,由此说明,当n>50时不满足判断框中的条件,则正好输出S=2 550,∴判断框应填入的条件是k≤50?.高考研究课(二)数系的扩充与复数的引入的命题3角度——概念、运算、意义[全国卷5年命题分析]考点考查频度考查角度复数的有关概念5年4考虚部、模等有关概念与运算结合考查复数的几何意义5年2考与运算结合考查几何意义复数的运算5年6考考查乘法、除法、幂的运算复数的有关概念(a∈R)是纯虚数,则a的值为( ) [典例] (1)设i是虚数单位.若复数a-3-iA.-3 B.-1C.1 D.3(2)已知复数z 满足z1+i =|2-i|,则z 的共轭复数对应的点位于复平面内的( )A .第一象限B .第二象限C .第三象限D .第四象限(3)若复数 z 满足z (1+i)=2i(i 为虚数单位),则|z |=( ) A .1 B .2C. 2D. 3[解析] (1)∵复数a -103-i =a -103+i10=(a -3)-i 为纯虚数,∴a -3=0,∴a =3.(2)∵z1+i=|2-i|=5,∴z =5+5i ,则z 的共轭复数5-5i 对应的点(5,-5)位于复平面内的第四象限.(3)法一:设z =a +b i(a ,b ∈R),则由z (1+i)=2i ,得(a +b i)·(1+i)=2i ,所以(a-b )+(a +b )i =2i ,由复数相等的条件得⎩⎪⎨⎪⎧a -b =0,a +b =2,解得a =b =1,所以z =1+i ,故|z |=12+12= 2.法二:由z (1+i)=2i ,得z =2i 1+i =2i1-i 2=i -i 2=1+i ,所以|z |=12+12= 2. [答案] (1)D (2)D (3)C [方法技巧]求解与复数概念相关问题的技巧复数的分类、复数的相等、复数的模,共轭复数的概念都与复数的实部与虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即a +b i(a ,b ∈R)的形式,再根据题意求解.[即时演练]1.(2017·山东高考)已知a ∈R ,i 是虚数单位.若z =a + 3 i ,z ·z =4,则a =( ) A .1或-1 B.7或-7 C .- 3 D. 3解析:选A 法一:由题意可知z =a -3i ,∴z ·z =(a +3i)(a -3i)=a 2+3=4,故a =1或-1. 法二:z ·z =|z |2=a 2+3=4,故a =1或-1.2.若复数2+a i1-i (a ∈R)是纯虚数(i 是虚数单位),则复数z =a +(a -3)i 在复平面内对应的点位于第________象限.解析:∵2+a i1-i =2+a i1+i 1-i1+i =2-a +2+a i 2=2-a 2+2+a2i 是纯虚数,∴⎩⎪⎨⎪⎧2-a 2=0,2+a 2≠0,解得a =2.∴z =2-i ,在复平面内对应的点(2,-1)位于第四象限. 答案:四3.(2017·浙江高考)已知a ,b ∈R ,(a +b i)2=3+4i(i 是虚数单位),则a 2+b 2=________,ab =________.解析:∵(a +b i)2=a 2-b 2+2ab i =3+4i ,∴⎩⎪⎨⎪⎧a 2-b 2=3,2ab =4,∴⎩⎪⎨⎪⎧a =2,b =1或⎩⎪⎨⎪⎧a =-2,b =-1,∴a 2+b 2=5,ab =2. 答案:5 2复数的代数运算[典例] (1)i 为虚数单位,则⎝ ⎛⎭⎪⎫1+i 2 018=( )A .-iB .-1C .iD .1(2)(2017·全国卷Ⅱ)3+i1+i =( )A .1+2iB .1-2iC .2+iD .2-i(3)(2017·全国卷Ⅱ)(1+i)(2+i)=( ) A .1-i B .1+3i C .3+iD .3+3i[解析] (1)∵1-i 1+i =1-i 21+i 1-i =1-2i -12=-i ,∴⎝⎛⎭⎪⎫1-i 1+i 2 018=(-i)2 018=(-i)2 016·(-i)2=-1.(2)3+i 1+i=3+i 1-i 1+i1-i =4-2i2=2-i. (3)(1+i)(2+i)=2+i 2+3i =1+3i. [答案] (1)B (2)D (3)B [方法技巧]复数代数形式运算问题的解题策略(1)复数的乘法复数的乘法类似于多项式的四则运算,可将含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可.(2)复数的除法除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式. [提醒] 在进行复数的代数运算时,记住以下结论,可提高计算速度. (1)(1±i)2=±2i;1+i 1-i =i ;1-i 1+i =-i ;(2)-b +a i =i(a +b i); (3)i 4n=1,i 4n +1=i ,i4n +2=-1,i4n +3=-i ,i 4n+i4n +1+i4n +2+i 4n +3=0,n ∈N *.[即时演练]1.设复数z =1+i(i 是虚数单位),则2z+z 2=( )A .1+iB .1-iC .-1-iD .-1+i解析:选A 2z +z 2=21+i +(1+i)2=1-i +2i =1+i.2.已知复数z =3+i 1-3i 2,z 是z 的共轭复数,则z ·z =________.解析:∵z =3+i 1-3i 2=3+i-2-23i=3+i -21+3i =3+i1-3i -21+3i1-3i=23-2i -8=-34+14i , 故z =-34-14i ,∴z ·z =⎝ ⎛⎭⎪⎫-34+14i ⎝ ⎛⎭⎪⎫-34-14i =316+116=14. 答案:143.已知i 是虚数单位,⎝ ⎛⎭⎪⎫21-i 2 018+⎝ ⎛⎭⎪⎫1+i 1-i 6=________.解析:原式=⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫21-i 2 1 009+⎝ ⎛⎭⎪⎫1+i 1-i 6=⎝ ⎛⎭⎪⎫2-2i 1 009+i 6=i 1 009+i 6=i4×252+1+i 4+2=i +i 2=-1+i.答案:-1+i复数的几何意义[典例] (1)已知复数z =a +i(a ∈R).若|z |<2,则z +i 2在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限(2)(2017·北京高考)若复数(1-i)(a +i)在复平面内对应的点在第二象限,则实数a 的取值范围是( )A .(-∞,1)B .(-∞,-1)C .(1,+∞)D .(-1,+∞)[解析] (1)因为复数z =a +i(a ∈R).若|z |<2,则a 2+1<2,解得-1<a <1,所以z +i 2=a -1+i 在复平面内对应的点(a -1,1)位于第二象限.(2)复数(1-i)(a +i)=a +1+(1-a )i , 其在复平面内对应的点(a +1,1-a )在第二象限,故⎩⎪⎨⎪⎧a +1<0,1-a >0,解得a <-1.[答案] (1)B (2)B [方法技巧](1)复数z 、复平面上的点Z 及向量OZ ―→相互联系,即z =a +b i(a ,b ∈R)⇔Z (a ,b )⇔OZ ―→. (2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.[即时演练]1.如图,若向量OZ ―→对应的复数为z ,则z +4z表示的复数为( )A .1+3iB .-3-iC .3-iD .3+i解析:选 D 由图可得Z (1,-1),即z =1-i ,所以z +4z =1-i +41-i =1-i +41+i 1-i 1+i =1-i +4+4i2=1-i +2+2i =3+i.2.若z =(a -2)+(a +1)i 在复平面内对应的点在第二象限,则实数a 的取值范围是________.解析:∵z =(a -2)+(a +1)i 在复平面内对应的点在第二象限,∴⎩⎪⎨⎪⎧a -2<0,a +1>0,解得-1<a <2.即实数a 的取值范围是(-1,2). 答案:(-1,2)1.(2017·全国卷Ⅰ)设有下面四个命题:p 1:若复数z 满足1z ∈R ,则z ∈R ;p 2:若复数z 满足z 2∈R ,则z ∈R ; p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=z 2; p 4:若复数z ∈R ,则z ∈R.其中的真命题为( ) A .p 1,p 3 B .p 1,p 4 C .p 2,p 3D .p 2,p 4解析:选B 设复数z =a +b i(a ,b ∈R),对于p 1,∵1z =1a +b i =a -b ia 2+b 2∈R ,∴b =0,∴z ∈R ,∴p 1是真命题;对于p 2,∵z 2=(a +b i)2=a 2-b 2+2ab i ∈R ,∴ab =0,∴a =0或b =0,∴p 2不是真命题; 对于p 3,设z 1=x +y i(x ,y ∈R),z 2=c +d i(c ,d ∈R),则z 1z 2=(x +y i)(c +d i)=cx。
2020版高考数学理科一轮复习课件(北师大版):算法初步

个算法都离不开
同的流向,条件结构就是 况,反复执行的步骤称
的 基本结构
处理这种过程的结构 为 循环体
程序 框图
课前双基巩固
4.基本算法语句 (1)输入语句、输出语句 用来实现算法的 输入信息 功能的语句叫作输入语句.输入语句要求输入的值只 能是 具体的常数 ,不能是函数、 变量 或表达式. 用来实现算法的 输出结果 功能的语句叫作输出语句.输出语句可以输出常量、 变量、表达式的值以及字符等,如输出3+6,输出a,输出“student”等,一个语句可以输 出多个表达式,不同的表达式之间用“,”分隔.
第66讲 UNIT 10
算法初步
课前双基巩固│课堂考点探究│教师备用例题
考试说明
1.了解算法的含义、算法的思想. 2.理解程序框图的三种基本逻辑结构:顺序结构、选择结构、循环结构. 3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环 语句的含义.
课前双基巩固 知识聚焦
1.算法 (1)算法通常是指按照 一定规则 解决某一类问题的 明确 和 有限 (2)应用:算法通常可以编成计算机 程序 ,让计算机执行并解决问题.
课前双基巩固
2.[教材改编] 运行如图 10-66-6 所示的程序后输出的
结果是 3,则输入的 x 值是
.
[答案] 3 或-3
[解析] 该程序是求函数 y=|x|的函
数值,∵y=3,∴x=±3.
图 1 常错题
◆索引:注意循环结构中控制循环的条件;注意区分程序框图是选择结构还是循环结构.
>
2,输出的结
果为
1,即
������ ≤ 2, -2������-3 =
1或
������ > 2, log3(������2
2020年高考数学(文科)一轮复习 第55讲算法初步

听课手册第55讲算法初步1.算法与程序框图(1)算法:①算法通常是指按照解决某一类问题的和的步骤.②算法通常可以编成计算机,让计算机执行并解决问题.(2)程序框图程序框图又称流程图,是一种用、流程线及来表示算法的图形.2.三种基本逻辑结构名称内容顺序结构条件结构循环结构定义由若干个的步骤组成,这是任何一个算法都离不开的算法的流程根据有不同的流向,条件结构就是处理这种过程的结构从某处开始,按照一定的条件某些步骤的情况,反复执行的步骤称为程序框图3.基本算法语句(1)输入语句、输出语句和赋值语句的格式与功能:语句一般格式功能输入语句INPUT“提示内容”;变量输出语句PRINT“提示内容”;输出常量、变量的值和系统信息赋值语句变量=表达式将表达式所代表的值赋给(2)条件语句的格式及框图:①IF-THEN格式:图10-55-1②IF-THEN-ELSE格式:图10-55-2(3)循环语句的格式及框图:①UNTIL语句:图10-55-3②WHILE语句:图10-55-4题组一常识题1.[教材改编]如图10-55-5所示的程序框图中含有顺序结构和结构,执行此程序框图,则输出S的值为.图10-55-5图10-55-62.[教材改编]执行如图10-55-6所示的程序框图,则输出s的值为.图10-55-73.[教材改编]如图10-55-7为计算y=|x|的函数值的程序框图,则此程序框图中的判断框内应填.题组二常错题◆索引:分不清程序框图是条件结构还是循环结构致错;把握不好循环结构中控制循环的条件致错.4.执行如图10-55-8所示的程序框图,它的功能是.若输出的y值的范围是[0,10],则输入的x值的范围是.图10-55-8图10-55-95.秦九韶是我国南宋时期著名的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图10-55-9所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入整数n的值为.6.执行如图10-55-10所示的程序框图,若输入k的值为3,则输出S的值为.图10-55-10图10-55-117.执行如图10-55-11所示的程序框图,输出的s值为.探究点一算法的基本结构例1(1)[2017·全国卷Ⅱ]执行如图10-55-12所示的程序框图,如果输入的a=-1,则输出的S=()A.2B.3C.4D.5,则输出y的值是.(2)[2017·江苏卷]图10-55-13是一个算法流程图.若输入x的值为116图10-55-12图10-55-13[总结反思]高考对算法初步的考查主要是对程序框图含义的理解与运用,重点应放在读懂框图上,尤其是条件结构、循环结构.特别要注意条件结构中条件的判断,对于循环结构要搞清进入或退出循环的条件、循环的次数,这是解题的关键.按流程线依次执行各框,是解题的基本思路.变式题(1)[2018·甘肃西北师大附中诊断]某程序框图如图10-55-14所示,若输出的s=57,则判断框内可以填()A.k>4?B.k>5?C.k>6?D.k>7?图10-55-14图10-55-15(2)执行如图10-55-15所示的程序框图,则输出x的值为()A. 12B. 10C. 9D. 8探究点二算法的交汇性问题例2(1)[2018·广西钦州质检]执行如图10-55-16所示的程序框图,输入正整数n(n≥2)和数据a1,a2,…,a n,如果输出的s是数据a1,a2,…,a n的平均数,则程序框图的处理框★处应填写的是()A.s=is+a ii B.s=(i-1)s+a iiC.s=(i-1)s+a ii-1D.s=is+a ii-1图10-55-16图10-55-17(2)执行如图10-55-17所示的程序框图,若输入n的值为3,则输出的S的值为.[总结反思]与其他知识交汇的程序框图问题,主要涉及数列求和、三角函数的计算、函数、统计等问题,注意观察是否能利用数列的求和公式、三角函数的周期性等知识解决问题.变式题(1)[2018·河南安阳二模]若执行如图10-55-18所示的程序框图,其中rand[0,1]表示区间[0,1]上任意一个实数,则输出数对(x,y)的概率为()A.12B.π6C.π4D.√32图10-55-18图10-55-19(2)执行如图10-55-19所示的程序框图,若输入的x值的取值范围是[-1,4],则输出y值的取值范围是()A. [-1,2]B. [-1,15]C. [0,2]D. [2,15]探究点三基本算法语句例3运行如图10-55-20所示的程序,若输出y的值为1,则输入x的值为()INPUT xIF x>=0THENy=2∧xELSEy=ABS(x)END IFPRINT yEND图10-55-20A. 0B. 0或-1C. ±1D. 1[总结反思]算法语句应用的四个关注点:(1)输入、输出语句:在输入、输出语句中加提示信息时,要加引号,变量之间用逗号隔开.(2)赋值语句:左、右两边不能对换,赋值号左边只能是变量.(3)条件语句:要分清条件语句的内外条件结构,保证结构的完整性.(4)循环语句:分清“UNTIL”语句和“WHILE”语句的格式与特征,不能混用.变式题(1)如图10-55-21为一个求20个数的平均数的程序,则横线上应填充的语句为()S=0i=1DOINPUT xS=S+xi=i+1LOOP UNTILa=S/20PRINT aEND图10-55-21A. i>20B. i<20C. i>=20D. i<=20(2)[2018·河北保定模拟]根据如图10-55-22所示的程序,可知输出的结果为S= .S=1i=1WHILE i<8S=S+2i=i+3WENDPRINT SEND图10-55-22完成课时作业(五十五)。
2020版高考数学总复习第一章集合常用逻辑用语、算法初步及框图第2讲命题及其关系充分条件与必要条件课件

若pq,则p是q的___充__分___条件,q p成立的对象的集合为A,
是p的__必__要____条件
q成立的对象的集合为B
p是q的_充__分__不__必___要 条件
p q且q p
A是B的_真__子__集___ 集
p是q的_必__要__不__充__分__ 条件
p q且q p
【解析】根据命题的四种形式可知,命题“若 p, 则 q”的否命题是“若綈 p,则綈 q”.该题中,p 为
a2>b2,q 为 a>b,故綈 p 为 a2≤b2,綈 q 为 a≤b.所以 原命题的否命题为:若 a2≤b2,则 a≤b.
【答案】B
(2)命题“若 x2-3x-4=0,则 x=4”的逆否命题 及其真假性为( )
【解析】①是能判断出真假的陈述句,故①是命题; ②不能判断出真假,故②不是命题; ③是疑问句,故③不是命题; ④不能判断出真假,故④不是命题.故选 A.
【答案】A
2.下列命题是真命题的为( ) A.若1x=1y,则 x=y B.若 x2=1,则 x=1 C.若 x=y,则 x= y D.若 x<y,则 x2<y2
【解析】因为 fx=ln x 为增函数,故有 a>b 时,ln a>ln b,同时,若 ln a>ln b 必有 a>b,故 a>b 是 ln a>ln b 的充要条件,故选 D.
【答案】D
4.已知条件 p:log21-x<0,条件 q:x>a,若 p 是 q 的充分不必要条件,则实数 a 的取值范围是______.
【解析】“若 x+y=0,则 x,y 互为相反数”的逆 命题为“若 x,y 互为相反数,则 x+y=0”,其为真命 题,①正确;“全等三角形的面积相等”的否命题为“不 全等三角形的面积不相等”,显然是假命题,②错误; 对于③,若 q≤1,则 4-4q≥0,即 Δ=4-4q≥0,所以 x2+2x+q=0 有实根.又原命题与逆否命题同真假, 故③正确;“不等边三角形的三个内角相等”的逆命 题为“三个内角相等的三角形为不等边三角形”,显 然是假命题,④错误,选 C.
2020版高考数学(福建专用)一轮复习课件:10.1 算法初步

-31-
考点1
考点2
考点3
考点4
-32-
考点1
考点2
考点3
考点4
关闭
A.i=i+1 B.i=i+2 C.i=i+3 D.i=i+4 思考程序框图的补全问题的解题方法是什么?
关闭
解析 答案
-33-
考点1
考点2
考点3
考点4
解题心得补全程序框图的条件或内容时,应结合初始条件和输出 结果,分析控制循环的变量应满足的条件,或累乘、累加的变量的 表达式,明确进入循环体时变量的情况、累加或累乘变量的变化. 具体解题方法有以下两种:一是先假定空白处填写的条件,再正面 执行程序,来检验填写的条件是否正确;二是根据结果进行回溯,直 至确定填写的条件是什么.
环结构.( )
(2)条件结构的出口有两个,但在执行时,只有一个出口是有效的.
( ) (3)输入框只能紧接开始框,输出框只能紧接结束框.( ) (4)输入语句可以同时给多个变量赋值.( ) (5)在算法语句中,x=x+1是错误的.( )
(1)√ (2)√ (3)× (4)√ (5)×
关闭
答案
知识梳理
-13-
知识梳理 双基自测
12345
2.阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输
出N的值为( )
A.0 B.1 C.2 D.3
运行程序,当输入N的值为24时,24能被3整除,所以N=8. 因为8≤3不成立,且8不能被3整除,所以N=7. 因为7≤3不成立,且7不能被3整除,所以N=6. 因为6≤3不成立,且6能被3整除,所以N=2. 因为2≤3,所以输出N=2.故选C. C
2020版高考理科数学(人教版)一轮复习课件:第十一章 第一节 算法初步

END IF
IF 条件 THEN 语句体 1
ELSE 语句体 2
END IF
名称
直到 刑循 循 环结 环构 结 构 当型 循环 结构
示意图
相应语句
DO 循环体
LOOP UNTIL条件
WHILE 条件 循环体Wຫໍສະໝຸດ ND考点——在细解中明规律
题目千变总有根,梳干理枝究其本
看 个 性
找 共 性
(单击进入电子文档)
目录
基础——在批注中理解透
单纯识记无意义,深刻理解提能力
课时跟踪检测
考点——在细解中明规律
题目千变总有根,梳干理枝究其本
基础——在批注中理解透
单纯识记无意义,深刻理解提能力
名称
顺序 结构
条 件 结 构
示意图
相应语句
①输入语句:INPUT “提示内容”; 变量 ②输出语句:PRINT “提示内容”; 表达式 ③赋值语句:变量=表达式
2020高三数学一轮复习(人教版文):算法初步

第九章算法初步、统计、统计案例第一节算法初步2019考纲考题考情「基础微械理一知识必备哂椒基JICHUWE1SHUL.I1. 三种基本逻辑结构\^称内补y顺序结构条件结构循环结构定义由若F个依次执行的步骤组成的,这是任何一个算法都离不开的基本结构算法的流程根据条件是否成从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体宴有不同的流向裏条件结构就是处理这种过程的结构考纲要求考鈕举创考向标諾L i■昴H辻约比亶」■辭篦适的黠轮二用钳輕1?杠闪的三呻临宮時詰为r吨序蒂枸*殆件塔耐.漪炜帖恂XTM几种甚杰舞祂谄旬一ffiAifitj.iffi J:识<r, Kffi m 4i梟”谍冒圖评1,",旬的201 fi・全個淮||・[;〔判IM第悴}201 i •无坤届唐* T,C^;hiA)::1 ■- g満号* 1 •亦;閘1如林•愛国曲1・T屮如押川书*件>JO1?・全国軽U・T显输川犁累〉20)7・全M$nj・1?崔竹战蜡果)曲販币度「1.法的苓事箱钳瓷挥屹怖主忙性闻■ 轉心H岸;抽亍盘損敦材I“I扣垄础白別2•算法的特征概括性、逻辑性、有穷性、不唯一性、普遍性。
语句一般格式功能输人语句INPUT"提示内容J变量输入信息输出语句PRINT提示内容S表达式输出常量、变量的值和系统信息赋值语句变量=表达式将表达式的值赋给变量4•条件语句(1) 算法中的条件结构与条件语句相对应。
(2) 条件语句的格式及框图。
①IF —THEN格式:5.循环语句(1)算法中的循环结构与循环语句相对应。
⑵循环语句的格式及框图。
①UNTIL语句:IX)循环体UN I IL 条件②WHILE语句:1.赋值号左边只能是变量(不能是表达式),在一个赋值语句中只能给一个变量赋值。
2. 直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相题纠徴谢身-TIZl WEIRESHEN一、走进教材1.(必修3P25例5改编)如图为计算y= |x|函数值的程序框图,则此程序框图中的判断框内应填___________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.2.程序框图程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.3.三种基本逻辑结构突破点一 程序框图的输入、输出问题例1 1、执行如图所示的程序框图,输出的s 值为_____56___.2、执行如图所示的程序框图,则输出S 的值为( D )A .-32 B.32 C .-12 D.123、执行如图所示的程序框图,则输出的S =____940____.4、执行如图所示的程序框图,如果输出的k 的值为3,则输入的a 的值可以是( A )A.20 B.21 C.22 D.235、我国古代数学著作《骨髀算经》有如下问题:“今有器中米,不知其数.前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k的值为(B)A.4.5 B.6 C.7.5 D.9突破点二程序框图的补全问题例2 1、执行如图所示的程序框图,若输出S的值为-20,则条件框内可填写(D)A .i >3?B .i <4?C .i >4?D .i <5?解析:选D 初始值:i =1,S =10; 第一次循环:S =10-21=8,i =2; 第二次循环:S =8-22=4,i =3; 第三次循环:S =4-23=-4,i =4;第四次循环:S =-4-24=-20,i =5. 因为输出S 的值为-20,所以条件框内可填“i <5?”. 2、执行如图所示的程序框图,若输出的值为21,则判断框内可填( )A .n ≥5?B .n >6?C .n >5?D .n <6?解析:选B 初始值:n =0,S =0; 第一次循环:n =1,S =1; 第二次循环:n =2,S =1+2=3; 第三次循环:n =3,S =3+3=6; 第四次循环:n =4,S =6+4=10;第五次循环:n =5,S =10+5=15; 第六次循环:n =6,S =15+6=21; 第七次循环:n =7. 因为输出的值为21,所以结合选项可知判断框内可填“n >6?”,故选B.3、执行如图所示的程序框图,若输入m =1,n =3,输出的x =1.75,则空白判断框内应填的条件为( B )A .|m -n |<1?B .|m -n |<0.5?C .|m -n |<0.2?D .|m -n |<0.1?解析::输入m =1,n =3. 第一次执行,x =2,22-3>0,n =2,返回;第二次执行,x =32,⎝⎛⎭⎫322-3<0,m =32,返回; 第三次执行,x =3+44=74,⎝⎛⎭⎫742-3>0,n =74.输出x =1.75,故第三次执行后应满足判断框,此时m -n =32-74=-14,故选B.4、(2018·全国卷Ⅱ)为计算S =1-12+13-14+…+199-1100,设计了如图所示的程序框图,则在空白框中应填入( B )A .i =i +1B .i =i +2C .i =i +3D .i =i +4[解析] (1)由题意可将S 变形为S =⎝⎛⎭⎫1+13+…+199-⎝⎛⎭⎫12+14+…+1100,则由S =N -T ,得N =1+13+…+199,T =12+14+…+1100.据此,结合N =N +1i ,T =T +1i +1易知在空白框中应填入i =i +2.故选B. 突破点二 辨析程序框图的功能例3如图所示的程序框图,该算法的功能是( C )A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值D.计算[1+2+3+…+(n-1)]2+(20+21+22+…+2n)的值1、(2016·全国卷Ⅰ)执行如图的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足(C)A.y=2x B.y=3x C.y=4x D.y=5x2、(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入(D)A.A>1 000?和n=n+1 B.A>1 000?和n=n+2C.A≤1 000?和n=n+1 D.A≤1 000?和n=n+23、(2017·全国卷Ⅱ)执行如图所示的程序框图,如果输入的a=-1,则输出的S=(B)A.2 B.3 C.4 D.5解析:B[当K=1时,S=0+(-1)×1=-1,a=1,执行K=K+1后,K=2;当K=2时,S=-1+1×2=1,a=-1,执行K=K+1后,K=3;当K=3时,S=1+(-1)×3=-2,a=1,执行K=K+1后,K=4;当K=4时,S=-2+1×4=2,a=-1,执行K=K+1后,K=5;当K=5时,S=2+(-1)×5=-3,a=1,执行K=K+1后,K=6;当K=6时,S=-3+1×6=3,执行K=K+1后,K=7>6,输出S=3.结束循环.故选B.]4、(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如是图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=(C)A.7 B.12 C.17 D.34解析:C[输入x=2,n=2.第一次,a=2,s=2,k=1,不满足k>n;第二次,a=2,s=2×2+2=6,k =2,不满足k>n;第三次,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17.]5、如图所示的程序框图,其作用是输入x 的值,输出相应的y 值,若x =y ,则这样的x 的值有( C )A .1个B .2个C .3个D .4个解析:C [当x ≤2时,令y =x 2=x ⇒x (x -1)=0,解得x =0或x =1;当2<x ≤5时,令y =2x -4=x ⇒x =4;当x >5时,令y =1x=x ,无解.综上可得,这样的x 的值有3个.]6、如图是计算1+13+15+…+131的值的程序框图,则图中①②处应填写的语句分别是( A )A .n =n +2,i >16?B .n =n +2,i ≥16?C .n =n +1,i >16?D .n =n +1,i ≥16?7、“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前.如图所示的程序框图的算法思路就是来源于“欧几里得算法”,执行该程序框图(图中“a MOD b ”表示a 除以b 的余数),若输入的a ,b 分别为675,125,则输出的a =( )A .0B .25C .50D .75解析:选B初始值a=675,b=125.第一次循环c=50,a=125,b=50;第二次循环c=25,a=50,b=25;第三次循环c=0,a=25,b=0,此时不满足循环条件,退出循环,输出a的值为25,故选B.8、执行如图所示的程序框图,若输入的t=4,则输出的i=()A.7 B.10 C.13 D.16解析:选D输入t=4,i=1,S=0,S<4,i=1不是质数,S=0-1=-1,i=4,S<4;i=4不是质数,S=-1-4=-5,i=7,S<4;i=7是质数,S=-5+7=2,i=10,S<4;i=10不是质数,S=2-10=-8,i=13,S<4;i=13是质数,S=-8+13=5,i=16,S>4,退出循环,故输出的i=16.故选D.9、某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图中记录了每天的销售量(单位:台),把这些数据经过如图所示的程序框图处理后,输出的S=()A.28 B.29 C.196 D.203解析:选B由程序框图可知,该程序框图输出的是销售量的平均值,结合茎叶图可知,输出的S=20+22+26+33+33+34+357=29,故选B.10、执行如图所示的程序框图,若输出的s=25,则判断框中可填入的条件是()A.i≤4? B.i≥4? C.i≤5? D.i≥5?解析:选C执行程序框图,i=1,s=100-5=95;i=2,s=95-10=85;i=3,s=85-15=70;i =4,s=70-20=50;i=5,s=50-25=25;i=6,退出循环.此时输出的s=25.结合选项知,选C.11、我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:“今有出门望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?”现在我们用如图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是()A.S>10 000? B.S<10 000?C.n≥5? D.n≤6?解析:选B根据题意,利用程序框图求禽的数目,输出结果应为S=9×9×9×9×9=59 049.循环共执行了5次,所以判断框中应填入的条件是“S<10000?”或“n≤5?”或“n<6?”.故选B.12、图(1)是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( D )A.7 B.8 C.9 D.10解析:D[从算法流程图可知,该图是统计成绩大于或等于90分的考试次数.从茎叶图可知输出的结果为10.] 13、如图,如图算法框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1 000,输出的结果为788,则运用此方法估计的π的近似值为________(保留四位有效数字).解析:根据算法框图知,如果点在圆x2+y2=1内,m就增加1;现输入N=1 000,m起始值为0,输出结果为788,说明m增加了788次,也就是说有788个点在圆x2+y2=1内.设圆的面积为S1,正方形的面积为S2,则概率p=7881 000≈S1S2=π4,∴π≈4p=4×0.788=3.152.答案:3.152。
