大学物理 第四章统计物理学基础
大学物理知识点总结

大学物理知识点总结大学物理涵盖了广泛的知识领域,包括经典力学、电磁学、热力学、光学、量子力学等。
以下是一些常见的大学物理知识点总结:1.经典力学:经典力学是物理学的基础,研究物体的运动规律。
主要包括牛顿三定律、动量定理、动能定理、万有引力定律等。
其中牛顿三定律指出物体在无外力作用下保持静止或匀速直线运动;动量定理描述了力对物体运动状态的改变;动能定理解释了物体的动能和力的关系;万有引力定律用于解释天体运动等。
2.电磁学:电磁学研究电荷和电磁场的相互作用,涉及电场、磁场、电磁感应等内容。
其中库仑定律描述了电荷之间的相互作用力;高斯定律解释了电场的分布规律;安培定律和法拉第电磁感应定律描述了电流和磁场之间的相互作用;麦克斯韦方程组总结了电磁场的基本规律。
3.热力学:热力学是研究热量转化和能量守恒的学科。
主要包括温度、热量、功、熵等概念。
热力学第一定律描述了能量守恒的原理;热力学第二定律描述了熵增原理和热传导的不可逆性;卡诺循环是理想热机的最高效率循环。
4.光学:光学研究光的传播和相互作用现象。
主要包括光的波动理论和光的几何理论。
干涉和衍射是光的波动性质的重要现象;折射和反射是光的几何性质的基本原理。
5.量子力学:量子力学是描述微观粒子行为的物理学理论。
主要包括波粒二象性、不确定性原理、波函数和薛定谔方程等。
波粒二象性描述了微观粒子既具有波动性又具有粒子性;不确定性原理阐述了无法同时准确测量粒子的位置和动量;波函数和薛定谔方程描述了粒子在量子力学中的运动和演化。
6.相对论:相对论是描述高速物体运动的理论。
狭义相对论主要包括以光速为上界的物体运动规律,如时间膨胀、长度收缩、质能等效等;广义相对论涉及引力和时空弯曲等现象。
7.统计物理学:统计物理学基于统计学原理,研究了宏观系统的微观基础。
热力学统计学描述了大量微观粒子构成的系统的性质和行为,如分子速度分布、热平衡等;量子统计学描述了费米子和玻色子的统计行为。
大学物理热力学与统计物理

大学物理热力学与统计物理热力学与统计物理是大学物理中重要的分支,它研究了物质的热学性质以及微观粒子的统计规律。
本文将简要介绍热力学与统计物理的基本概念、原理和应用。
一、热力学基本概念热力学研究的是能量的转化与守恒,包括传热、传能和能量转换等方面的内容。
热力学基本定律包括能量守恒定律、熵增加原理等。
能量守恒定律指出能量在封闭系统中不会凭空产生或消失,只能通过各种形式的转化转移到其他物体或形式。
熵增加原理则是指随着时间的推移,封闭系统中的熵(系统无序程度)总是增加的。
二、热力学基本原理热力学基本原理包括热平衡、热力学第一定律和热力学第二定律。
热平衡是指系统内各部分之间的温度是相等的状态,这是热力学的基础概念。
热力学第一定律是能量守恒的表示,它表明系统的内能变化等于吸收的热量与对外做功的代数和。
热力学第二定律则是热力学的核心内容,它描述了自然界的不可逆性和熵增加的趋势。
三、统计物理基本原理统计物理是热力学的基础,它从微观角度研究了物质中微观粒子的统计规律。
统计物理主要利用统计学方法描述了大量微观粒子的行为,并推导出宏观热力学定律。
基于统计物理,我们可以计算系统的平均能量、熵以及其他宏观状态量。
四、热力学与统计物理的应用热力学和统计物理在各个领域具有广泛的应用,包括能源开发、材料科学、天体物理等。
在工程领域,热力学可以用来设计高效的能源转换系统,提高能源利用效率。
在材料科学领域,热力学对材料的相变、热膨胀等性质有着重要的解释和研究价值。
而在天体物理学中,热力学与统计物理的应用可以帮助我们理解星际物质的形成和演化过程。
总结:本文简要介绍了大学物理中的热力学与统计物理。
热力学是研究能量转化与守恒的学科,其基本定律包括能量守恒定律和熵增加原理。
统计物理是基于热力学的微观解释,通过统计学方法研究大量微观粒子的行为,推导出宏观热力学规律。
热力学与统计物理在能源、材料和天体等领域有着广泛的应用。
通过深入研究热力学与统计物理,我们能够更好地理解和解释自然界中的物质与能量转化过程。
大学物理课程总结

大学物理课程总结大学物理课程总结大学物理课程总结在大二上学期,我们学习了大学物理这门课程,物理学是一切自然科学的基础,处于诸多自然科学学科的核心地位,物理学研究的粒子和原子构成了蛋白质、基因、器官、生物体,构成了一切天然的和人造的物质以及广袤的陆地、海洋、大气,甚至整个宇宙,因此,物理学是化学、生物、材料科学、地球物理和天体物理等学科的基础。
今天,物理学和这些学科之间的边缘领域中又形成了一系列分支学科和交叉学科,如粒子物理、核物理、凝聚态物理、原子分子物理、电子物理、生物物理等等。
这些学科都取得了引人瞩目的成就。
在该学期的学习中,我们主要学习了以下几个章节的内容:第4章机械振动第5章机械波第6章气体动理论基础第7章热力学基础第12章光的干涉第13章光的衍射第14章光的偏振在对以上几个章节进行学习了之后,我们大致了解了有关振动、热力学、光学几个方面的知识。
下面,我对以上几个章节的内容进行详细的介绍。
第四章主要介绍了机械振动,例如:任何一个具有质量和弹性的系统在其运动状态发生突变时都会发生振动。
任何一个物理量在某一量值附近随时间做周期性变化都可以叫做振动。
本章主要讨论简谐振动和振动的合成,并简要介绍阻尼振动、受迫振动和共振现象以及非线性振动。
在第五章机械波的学习中,我们知道了什么是“波”。
如果在空间某处发生的振动,以有限的速度向四周传播,则这种传播着的振动称为波。
机械振动在连续介质内的传播叫做机械波;电磁振动在真空或介质中的传播叫做电磁波;近代物理指出,微观粒子以至任何物体都具有波动性,这种波叫做物质波。
不同性质的波动虽然机制各不相同,但它们在空间的传播规律却具有共性。
本章一机械波为例,讨论了波动运动规律。
从第六章开始,我们开始学习气体动理论和热力学篇,其中,气体动理论是统计物理最简单、最基本的内容。
本章介绍热学中的系统、平衡态、温度等概念,从物质的微观结构出发,阐明平衡状态下的宏观参量压强和温度的微观本质,并导出理想气体的内能公式,最后讨论理想气体分子在平衡状态下的几个统计规律。
《大学物理》课程教学大纲
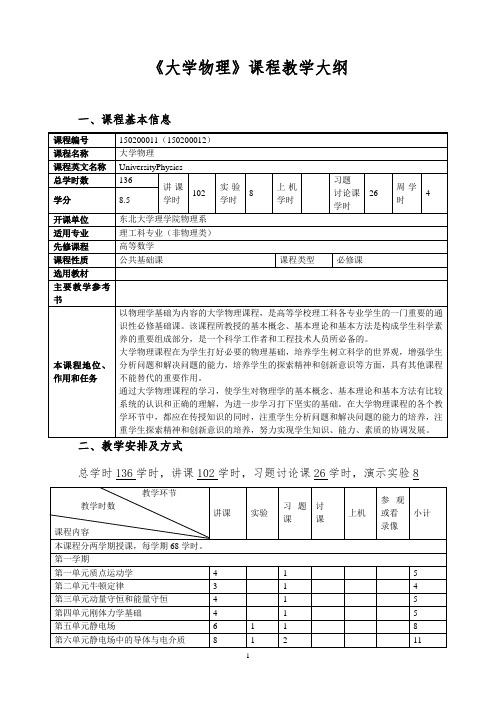
《大学物理》课程教学大纲一、课程基本信息总学时136学时,讲课102学时,习题讨论课26学时,演示实验8三、课程教学的有关说明1、本课程课内外学时比例:1:2;平均周学时:4。
2、本课程是公共基础课,分连续两个学期完成。
3、在教学中注意把传统教学手段和现代化教学手段相结合,充分利用现代化教学手段进行教学。
四、对于能力培养的基本要求通过大学物理课程教学,应注意培养学生以下能力:1.独立获取知识的能力——逐步掌握科学的学习方法,阅读并理解相当于大学物理水平的物理类教材、参考书和科技文献,不断地扩展知识面,增强独立思考的能力,更新知识结构;能够写出条理清晰的读书笔记、小结或小论文。
2.科学观察和思维的能力——运用物理学的基本理论和基本观点,通过观察、分析、综合、演绎、归纳、科学抽象、类比联想、实验等方法培养学生发现问题和提出问题的能力,并对所涉问题有一定深度的理解,判断研究结果的合理性。
3.分析问题和解决问题的能力——根据物理问题的特征、性质以及实际情况,抓住主要矛盾,进行合理的简化,建立相应的物理模型,并用物理语言和基本数学方法进行描述,运用所学的物理理论和研究方法进行分析、研究。
五、对于素质培养的基本要求通过大学物理课程教学,应注重培养学生以下素质:1.求实精神——通过大学物理课程教学,培养学生追求真理的勇气、严谨求实的科学态度和刻苦钻研的作风。
2.创新意识——通过学习物理学的研究方法、物理学的发展历史以及物理学家的成长经历等,引导学生树立科学的世界观,激发学生的求知热情、探索精神、创新欲望,以及敢于向旧观念挑战的精神。
3.科学美感——引导学生认识物理学所具有的明快简洁、均衡对称、奇异相对、和谐统一等美学特征,培养学生的科学审美观,使学生学会用美学的观点欣赏和发掘科学的内在规律,逐步增强认识和掌握自然科学规律的自主能力。
六、教学内容及基本要求模块1力学:第一单元质点运动学第一讲质点运动的描述,第二讲圆周运动与一般平面曲线运动,第三讲相对运动基本要求:1、质点运动的描述(1)掌握:位矢、位移、速度、加速度等物理量的定义及表达式,能够从已知的运动方程求导得到速度、加速度;同时能够从已知的速度或加速度积分得出运动方程。
《大学物理》教学全套课件

物质的电磁性质
物质的导电性
阐述金属、半导体和绝缘体的导电机制及特点。
物质的介电性
介绍电介质的极化现象,以及介电常数和介电 损耗的概念。
物质的磁性
分析物质的抗磁性、顺磁性和铁磁性的产生机理及特点,并讨论磁性材料的应 用。
05
光学基础
几何光学基础
光的直线传播 光在同种均匀介质中沿直线传播,形 成影和像。
02
力学基础
质点运动学
质点的基本概念
定义、特点、适用条件
速度与加速度
定义、物理意义、计算方法及关系
位置矢量与位移
定义、物理意义、计算方法
运动学方程
建立方法、求解及应用
牛顿运动定律
牛顿第一定律
内容、意义及应用
牛顿第二定律
内容、表达式、意义及应用
牛顿第三定律
内容、表达式、意义及应用
牛顿运动定律的应用
重力势能、弹性势能等的计算方法
03
热学基础
温度与热量
1 2
温度的定义和测量 温度是物体热度的量度,通常使用温度计进行测 量。温度的SI单位是开尔文(K)。
热量的定义和性质 热量是物体之间由于温度差异而进行的能量转移。 热量总是从高温物体流向低温物体。
3
热力学第零定律 如果两个系统分别与第三个系统达到热平衡,那 么这两个系统之间也将达到热平衡。
课程内容
本课程涵盖力学、热学、电磁学、 光学和近代物理等多个领域,通 过系统的理论学习和实验训练, 使学生掌握物理学的基本知识和 实验技能。
课程地位
《大学物理》为后续专业课程的 学习打下坚实的物理基础,对于 提高学生的科学素质和创新能力 具有重要意义。
教学目标与要求
知识目标
物理学的发展

第四章物理学的发展物理学是研究物质基本结构和物质运动的最一般规律的科学,是其它科学和技术的基础和发源地。
一方面,它推动着人们的认识观念与思维方式的变革与发展,另一方面,又通过技术转化为直接生产力,为社会和经济服务。
同时,物理学也是一门不断发展的科学,向着物质世界的深度和广度不断前进。
原始的自然观和物理学的起源与发展在第二章中已经谈到一些,本章叙述的主要是经典物理学至现代物理学的发展和相关内容。
经典物理学是指19世纪末以前的物理学部分,包括经典力学、热力学、统计物理学、经典电磁学等;现代物理学是指20世纪初发展起来的物理学部分,包括量子力学、相对论、原子核物理、粒子物理学等内容。
4.1 经典物理学的诞生与发展从16世纪到18世纪,大约有300年的时间,是近代自然科学形成和发展时期。
这一时期,在资产阶级民主革命和资本主义生产发展的推动下,自然科学摆脱了宗教神学的束缚和坚持对自然界进行精密的观察和实验的研究,以前所未有的速度发展起来。
第谷、开普勒、伽利略、笛卡尔、牛顿等科学家都为新时代科学思想的建立作出了贡献。
其中最杰出的成就是牛顿创立了经典力学体系,实现了以力学为中心的科学知识的第一次大综合。
4.1.1 经典力学体系的建立丹麦天文学家第谷·布拉赫(T.Brahe, 1546~1601年)以毕生精力进行观测,获得了大量数据资料,为开普勒(J.Kepler,1571~1630年)行星运动三定律的108研究作了充分准备。
与此同时,以伽利略(G.Galileo,1564~1642年)为代表的物理学家对力学开展了广泛研究,得到了自由落体定律。
伽利略的两部著作《关于托勒密和哥白尼两大世界体系的对话》和《关于力学和局部运动的两门新科学的对话和数学证明》(通常简称为《两门新科学》,所谓两门新科学是指材料力学和运动力学),为力学的发展奠定了思想基础。
随后,牛顿(I.Newton,1642~1727年)在总结伽利略和开普勒等人研究成果的基础上,进行分析综合,建立了牛顿力学三定律和万有引力定律。
西南大学《统计物理基础》复习思考题及答案

(0132)《统计物理基础》复习思考题一、解释如下概念⑴热力学平衡态;⑵可逆过程;⑶准静态过程;⑷焦耳-汤姆逊效应;⑸μ空间;⑹Γ空间;⑺特性函数;⑻系综;⑼混合系综;⑽非简并性条件;⑾玻色——爱因斯坦凝聚;二回答问题⒈写出热力学第一定律的文字叙述、数学表示、简述该定律的重要性、适用范围。
⒉写出热力学第二定律的文字叙述、数学表示、适用条件,在热力学中的重要性。
⒊写出热力学第三定律的文字叙述、重要性并给予微观解释。
⒋写出熵增加原理的文字叙述、数学表示、适用范围及其微观解释⒌写出等概率原理,举例说明为什么它是平衡态统计物理的基本原理?⒍写出玻尔兹曼关系表达式,简述公式的物理意义和重要性,并用此公式对热力学的熵增加原理给以解释。
⒎写出弛豫时间近似下的玻尔兹曼方程,简述方程的物理意义、适用条件三. 填空题1 气体普适常数R=-------------------,玻尔兹蔓常数K=--------------------,1mol范氏气体物态方程为---------------------------。
⒉照能量均分定理,刚性双原子分子理想气体的内能U=-5NKT/2------------------,摩尔定容热容量C=-------------------,光子气体的化学vμ-----------------------------。
势为=μ______________; 工作于温度为500C与⒊理想气体的焦耳—汤姆孙系数=10000C的两热源之间的热机或致冷机热机效率的最大值。
⒋对等温等容系统平衡态时,U、S、F、G、H、中______________最小;而对等温等压系统,U、S、F、G、H中________________最小玻耳兹曼统计中分布公为_______ ___________ _______________,适用条件为。
5. 1moI单原子理想气体在温度为T、体积为v的状态等温膨胀到体积为2v的状∆u________________;吸收热量△Q = 态、则此过程中,内能改变=____________;对外作功△W = _____________________;熵的改变△S= ________________________。
西南大学《统计物理基础》网上作业及参考答案

1:[判断题]参考答案:错误2:[判断题]参考答案:错误3:[判断题]参考答案:错误4:[判断题]参考答案:错误5:[判断题]参考答案:正确6:[判断题]参考答案:错误7:[判断题]参考答案:正确8:[判断题]参考答案:错误9:[判断题]参考答案:错误10:[判断题]参考答案:错误1:[判断题]参考答案:错误2:[判断题]宏观物理量是相应微观物理量的统计平均值参考答案:正确3:[判断题]孤立系统处于稳定平衡的充要条件是dS=0参考答案:错误4:[判断题]利用气体节流过程不能使气体降温参考答案:错误5:[判断题]理想气体等温膨胀过程中吸收的热量等于对外做功参考答案:正确6:[判断题]理想气体的内能与体积有关参考答案:错误7:[判断题]热力学第一定律就是能量守衡定律参考答案:正确8:[判断题]化学元素相同的物质构成一个相参考答案:错误9:[判断题]所有工作于两个一定温度之间的热机的效率相等参考答案:错误10:[判断题]由两个等温过程和两个等压过程组成的循环叫卡诺循环。
参考答案:错误1:[论述题]被吸附在平面上的单原子理想气体分子总分子数N,温度T,面积A。
求:(1)用玻尔兹曼统计公式求系统的内能、定容热容量、状态方程、熵参考答案:)波尔兹曼统计方法粒子自由度,,,(内能2:[论述题]写出等概率原理,举例说明为什么它是平衡态统计物理的基本原理参考答案:等概率原理讲的是:处于平衡态的孤立系统,系统各种可能的微观状态出现的概率相同。
该原理适用条件:平衡态、孤立系统,大量粒子组成的宏观系统。
它是统计物理的一个最基本的原理,其原因是:①它是实验观察的总结;而不能由其它定理或原理来推证。
②各种统计规律的建立均以它为基础。
例如:(1)推导玻尔兹曼统计、玻色统计、费米统计时找出最可几分布,正是等概率原理,才可由确定微观状态数最多的分布来确定;(2)微正则系综概率分布的建立也是以等概率原理为基础。
1:[论述题]参考答案:①热力学第二定律文字叙述有两种:克氏说法:热传导不可逆开氏说法:功变热不可逆②数学表示:(等号对应可逆,不等号对应不可逆)③适用范围:大量微观粒子构成的宏观系统,且在时间和空间上有限,不适用宇宙。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l1
x t 2l / vix
单位时间内i分子对A1面的碰撞次数 Z 1 / t vix / 2l1
单位时间内i分子对A1面的冲量 2mv ix vix / 2l1
i分子对A1面的平均冲力 Fix 2mvix vix / 2l1
所有分子对A1面的平均作用力
压强
Fx
N i 1
Fix
m l1
第四章 统计物理学基础
4-1 统计物理的基本概念
一、物质的微观模型 热力学系统(热力学研究的对象): 大量微观粒子(分子、原子等)组成的宏观体系。 外界:热力学系统以外的物体。 微观粒子体系的基本特征(1)分子(或原子)非常小。 (2)热力学系统所包含的微观粒子数非常巨大. (3)分子之间存在相互作用力--分子力. (4)分子或原子都以不同的速率不停地运动。
铁钉
隔板
统计规律和方法
伽尔顿板
再投入小球: 经一定段时间后 , 大量小 球落入狭槽。
分布情况:中间多,两边少。
重复几次 ,结果相似。
单个小球运动是随机的 , 大量小球运动分布是确定的。
大量偶然事件整体所遵 循的规律 —— 统计规律。
小球数按空间 位置 分布曲线
统计规律特点:
(1)只对大量偶然的事件才有意义. (2)它是不同于个体规律的整体规律(量变到质变).
R 普适气体常量
o
8.31J / mol
I ( p1,V1,T1)
•
•
II ( p2,V2,T2 )
V
三、分子热运动的无序性和统计规律性 什么是统计规律性(statistical regularity) 大量偶然性从整体上所体现出来的必然性。
例. 扔硬币
统计规律和方法
伽尔顿板 从入口投入小球 与钉碰撞 落入狭槽 ( 偶然 ) 为清楚起见 , 从正面来观察。
例如:粒子数
假想把箱子分成两相同体积的部 分,达到平衡时,两侧粒子有的 穿越界线,但两侧粒子数相同。
•平衡态是一种理想状态
状态方程 当系统处于平衡态时,三个状态参量存在一定的
函数关系: f ( p,V ,T ) 0 物态方程
(状态方程)
理想气体 pV M RT p
M mol
M 气体质量
Mmol 气体的摩尔质量
表示方式
1
P1
2
P2
S
PS
S
Pi 0(i 1,2, S ) 有 Pi 1 i 1
2. 连续型随机变量 取值无限、连续
随机变量X的概率密度
( x) dP( x)
dx
变量取值在x—x+dx间 隔内的概率
概率密度等于随机变量取值在单位间隔内的概率。
( X )又称为概率分布函数(简称分布函数)。
温度改变,内能改变量为 E M i RT
Mmol 2
例 就质量而言,空气是由76%的N2,23%的O2和 1%的Ar三种气体组成,它们的分子量分别为28、32、
40。空气的摩尔质量为28.910-3kg,试计算1mol空气
在标准状态下的内能。
解: 在1摩尔空气中
N2质量 M1 28.9103 76% 22.1103 kg
“涨落”现 象 ------测量值与统计值之间总有偏离
处在平衡态的系统的宏观量,如压强P,不随 时间改变, 但不能保证任何时刻大量分子撞击器 壁的情况完全一样, 分子数越多,涨落就越小。
布朗运动是可观测的涨落现象之一。
例:氧气瓶的压强降到106Pa即应重新充气,以免混入 其他气体而需洗瓶。今有一瓶氧气,容积为32L,压
4-2 理想气体的压强 温度和内能 一、理想气体的微观模型和统计假设
1 . 理想气体微观模型 分子本身的大小比起它们之间的平均距离
可忽略不计。
除碰撞外,分子之间的作用可忽略不计。 分子间的碰撞是完全弹性的。
分子所受重力忽略不计 理想气体的分子模型是弹性的自由运动的质点。
2 . 统计假设 ① 分子数密度处处相等;
2 如果某种气体的分子有个 t 个平动自由度, r 个转 动自由度, s 个振动自由度.则分子具有:
平均平动动能
t kT 2
平均转动动能
r kT 2
平均振动动能
s kT 2
注意:对应分子的一个振动自由度,除有一份 振动的动能外,还有一份平均势能。
结论:分子的平均总能量
1 (t 2
r
s)kT
1 2
skT
( x)dx 1
3. 统计平均值
对于离散型
随机变量
算术平均值为
iNi
Ni
iNi N
统计平均值为
lim N
iNi N
i
lim (
N
N
i
N)
i Pi
随机变量的统计平均值等于一切可能状态
的概率与其相应的取值 i 乘积的总和。
对于连续型随机变量
统计平均值为 x x( x)dx
平衡态下,理想气体分子速度分布是有规律 的,这个规律叫麦克斯韦速度分布律。若不考虑 分子速度的方向,则叫麦克斯韦速率分布律。
测定分子速率分布的实验装置
真空室 B
•••
A••• •••
S
P
G
P
分子源 狭缝 圆筒
G 弯曲玻璃板,可沉积 射到上面的各种速率分子
圆筒不转,分子束的 分子都射在P处
z
C(x, y, z)
y x
单原子分子
平动自由度t=3
i tr 3
z
C(x, y, z)
y
x 双原子分子
平动自由度t=3 转动自由度r=2
i tr5
z
三原子或三
C(x, y, z)
原子以上 的分子
y 平动自由度t=3 i t r
x
转动自由度r=3 6
实际气体不能看成刚性分子,因原子之间还有振动
设一容器,用隔板将其隔开当 隔板右移时,分子向右边扩散 在这过程中,各点密度、温度等均不相同,这就是 非平衡态。但随着时间的推移,各处的密度、压强 等都达到了均匀,无外界影响,状态保持不变,就 是平衡态。
说明: •平衡态是一种热动平衡 处在平衡态的大量分子仍在作热运动,而且因
为碰撞, 每个分子的速度经常在变,但是系统的宏 观量不随时间 改变。
d
二、系统状态的描写
宏观量——状态参量 描写热力学系统宏观状态的参量。
如 压强 p、体积 V、温度 T 等。
微观量 描述系统内个别微观粒子特征和运动状态的物理
量。 如分子的质量、 直径、速度、动量、能量 等。
微观量与宏观量有一定的内在联系。
平衡态: 在无外界的影响下,系统的宏观性质不随 时间改变的稳定状态。
(3)分子之间存在相互作用力--分子力。
r r r0 为斥力且 增加时f急剧增加
r r0 为平衡态,f=0
r f r r0 为吸引力且 增加时f先增再减少
r0 rm
d
注意 d 可视为分子力程;
r
数量级在10-10--10-8m数
量级,可看为分子直径
(有效直径)。
分子力是电性力,远大于万有引力。
强为1.3107Pa,若每天用105Pa的氧气400L,问此瓶 氧气可供多少天使用?设使用时温度不变。
解: 根据题意,可确定研究对象为原来气体、用去气 体和剩余气体,设这三部分气体的状态参量分别为
p1 V1 M1 p2 V2 M2 p3 V3 M3 使用时的温度为T
设可供 x 天使用
原有 x 每天用量 剩余
气体分子的方均根速率
w 1 mv2 3 kT
2
2
v2
大量分子速率的平方平均值的平方根
v2 3kT 3RT
m
M mol
v2 T v2 1 / Mmol
气体分子的方均根速率与气体的热力学温度的平
方根成正比,与气体的摩尔质量的平方根成反比。
四、能量按自由度均分定理
1. 自由度 确定一个物体的空间位置所需要的独立坐标数目。 以刚性分子(分子内原子间距离保持不变)为例
p1 V1 M1 T
p2 V2 M2 T
p3 V3 M3 T
分别对它们列出状态方程,有
p1 V1
M1 M mol
RT
p2 V2
M2 M mol
RT
p3 V3
M3 M mol
RT
V1 V3 M1 M3 xM2
x M1 M3 ( p1 p3 )V1
M2
p2V2
(130 10 ) 32 9.6天 1 400
二、能量均分定理
w 1 mv2 3 kT
2
2
vx2
vy2
vz2
1 3
v2
1 2
mvx2
1 2
mv y 2
1 2
mvz2
1 2
kT
气体分子沿 x,y,z 三个方向运动的平均平动
动能完全相等,可以认为分子的平均平动动 能 3 kT 均匀分配在每个平动自由度上。
2
能量按自由度均分定理
平衡态下,不论何种运动,相应于每一个可 能自由度的平均动能都是 1 kT
(3) 大数量现象在一定宏观条件下的稳定性。
四、 统计的基本概念
1. 概率 如果N次试验中出现A事件的次数为NA,当 N时,比值NA/N称为出现A事件的概率。
lim P( A)
NA
N N
概率的性质:
(1) 概率取值域为 0 P( A) 1
(2) 各种可能发生的事件的概率总和等于1.
N Ai
E
i1 2
n1 RT
i2 2
n2 RT
i3 2
n3 RT
1 2 ( i1n1 i2n2 i3n3 )RT
