2017年山东科技大学研究生入学考试805弹性力学考研真题
山东科技大学微积分2013--2015,2017年考研专业课真题

4、 lim
x 0
x
0
arctan tdt x2
二、 (本题包括 2 个小题,第 1 小题 15 分,第 2 小题 7 分,共 22 分)
1 2 2 , ( x, y ) (0,0) ( x y ) sin 2 1、设 f ( x, y ) ,试问在点 处(注: (0,0) x y2 0 , ( x, y ) (0,0)
1 n f ( xi ) 。 n i 1
2、设 f ( x) 在 0, 1 上连续,在 0, 1 内可导,且 f (1) 0 。证明: 0, 1 , 使 f ( )
f ( )
。
一、 (本题包括 4 个小题,每小题 7 分,共 28 分)求以下函数极限:
2 2
dy dy xy 。 dx dx
2、求微分方程 y 2 y 3 y 1 的通解。 七、 (本题包括 2 个小题,每小题 8 分,共 16 分) 1、 证明: 若 f ( x) 在 a, b上连续,a x1 x2 xn b , 则 x1 , xn , 使 f ( )
1 x2 1 tan 1、 lim x x 1 x
x 1 2、 lim x x 1
x
3、 lim
1 1 x x 0 x e 1
x 2 t 0 e dt 4、 lim x 0
2
te
0
x
2t 2
dt
二、 (本题包括 3 个小题,第 1、3 小题各 8 分,第 2 小题 12 分,共 28 分) 1、求函数 f ( x) xe 的带有皮亚诺型余项的 n 阶麦克劳林展开式。
山东科技大学 2013 年招收硕士学位研究生入学考试
山东科技大学结构力学2004--2020年考研初试真题

D.常变体系。
图1图2、如图2所示结构,杆1的轴力FF P; B.-2F P;F P/2; D.-1.12F P。
、如图3所示结构,当其高度h增加时,水平支座反力F Ax()A.增大;B.减少;C.不变;D.不确定。
图3图44、如图4所示结构,在给定荷载作用下,BA为()A.F P l;B.F P l/2;C.F P l/4;D.F P l/8。
5、机动法作静定梁影响线应用的原理为()A.变形条件;B.平衡条件;C.虚功原理;D.叠加原理。
共4页第1页C.0.05rad;D.0.06rad。
图5图66所示结构,可视为多余约束的三根链杆是()、6、7; B.3、6、8;6、7; D.5、6、7。
7所示结构,梁式杆EI=常数,桁架杆常数,杆AB的轴力为()拉力; B.压力;零; D.无法确定。
图7图8、如图8所示结构,截面C的剪力影响线在处的竖标y E的绝对值为()A.1;B.l;0.5; D.0.5l。
二、填空题(共20分,每题4分)、如图9所示体系的计算自由度W=①。
、用力法计算图10所示结构时,取A、B支座反力为基本未知量:X1,X2。
当EI1增大时,力法方程中∆1P②。
(填不变、增大或减小)共4页第2页共4页第3页图9图103、如图11所示结构,已知I 1/I 2=K ,则|M AB |/|M DC |=③。
4、如图12所示结构,已知力偶矩M =16kN·m ,则杆端弯矩M DA =④。
(顺时针为正)图11图125、如图13所示结构,各杆EI =常数,忽略杆件轴向变形,M CA =⑤。
图13图14三、计算题(共100分,每题20分)1、如图14所示刚架,忽略杆件轴向变形。
绘制刚架的剪力图,并求C 点的竖向位移ΔC V 。
2、如图15所示桁架,计算指定杆件1、2、3的轴力。
3、用力法计算图16所示刚架,并作出刚架的弯矩图。
已知I /A =10。
共4页第4页图15图164、用位移法计算图17所示刚架,并作出刚架的弯矩图。
山东科技大学805弹性力学18-19年真题

一、简述题(60分)1、简述弹性力学基本假定,以及它们在建立弹性力学基本方程中的作用?(12分)2、什么是弹性体内一点的应力状态,如何表示一点的应力状态?(5分)3、满足平衡微分方程和应力边界条件的应力是否是实际存在的应力?为什么?(10分)4、什么情况下需要应用圣维南局部性原理?应用圣维南原理时应注意哪些问题。
(10分)5、简述弹性力学平面应力问题和平面应变问题的简化条件?(8分)6、何为最小势能原理?基于最小势能原理的近似计算方法有哪两种?(5分)7、满足什么条件的应力是静力可能的应力?要使ij ij sij δσσσ+=(其中,ij σ为真实应力)成为静力可能的应力,虚应力ij δσ应满足什么条件?(10分)二、(15分)如图1所示为一三角形水坝,已求得应力分量为:x σ=Ax +By ,y σ=Cx +Dy ,Z σ=0,zy zx τ=τ=0,gx xy τ=-Dx -Ay -ρ,其中ρ,1ρ分别表示坝体和液体密度。
试根据应力边界条件确定常数A、B、C、D。
图1三、试验证下两组应变状态能否存在(B A K ,,为常量)(10分)1、222(),,x y xy K xy Ky Kxyεεγ=+==2、0,,22===xy y x y Bx Axy γεε四、(15分)己知受力弹性体内某点的主应力为:1σ、2σ、3σ,试求与这3个主应力成相同角度的面上的正应力和剪应力。
五、(10分)如图2所示,一楔形体,顶部受集中力偶作用,假设单位厚度上力偶为M ,试采用量纲分析法,给出该问题极坐标系下应力函数的表示形式。
(注:只给出应力函数的构造形式即可,不需要给出具体解答)。
2017年山东科技大学研究生入学考试830普通化学考研真题

一、选择题(共36分,每小题1.5分)(请选择以下各题中的正确答案,并将答案务必写在答题纸上。
注意:只选一个答案,多选不得分)1、用来描述气体状态的四个物理量分别是(用符号表示)()(A) n, V, p, T(B) n, R,V, p(C) n, V, R, T(D) n, R, p, T2、下列各分子中,是极性分子的为()(A)BeCl2(B) BF3(C) NF3(D) C6H63、在一个原子中最多可以有几个电子处于量子数为n = 3,l = 1的亚层中()(A) 2 (B) 6 (C) 10 (D) 144、下列各物质中只需克服色散力就能使之气化的是()(A) HCl (B)H2O (C)N2(D) MgCO35、下列分子或离子中键长最短的是()(A) O4+(B) O2(C) O2-(D) O22-6、下列原子轨道重叠时,能形成π键的是()(A)只有p y与p y(B)只有p z与p z(C)只有d xy与p y(D) 上述都可能7、H2O中O的杂化方式()(A) sp2(B) sp 3(C) d2 sp 3(D) sp8、下列过程中,任意温度下均不能自发的为()(A) △r H m>0,△r S m>0 (B) △r H m>0,△r S m<0(C) △r H m<0,△r S m>0 (D) △r H m<0,△r S m<09、已知反应:2HgO(s)—2Hg(l)+O2(g),△r H m =181.4 KJ.mol-1,则△f H m(HgO,s)为()(A) 181.4 kJ.mol-1(B) -90.7 kJ.mol-1 (C) 90.7 (D) –181.4 kJ.mol-110、反应C(s) + H2O(g) = CO(g) + H2(g), △r H m =133.9 kJ.mol-1, 则()(A)平衡时系统压力为100 kPa (B)增大压力不影响此反应的平衡移动(C)此反应的定容热Q v=133.9 kJ.mol-1(D)升高温度将提高碳的转化率11、没有其它已知条件,下列何种物理量增加一倍时,已知平衡的反应3A(g)+2B(g) == 2C(g)+D(g) 的平衡移动方向无法确定()(A)温度(B)总压力(C)物质A的分压(D)物质D的分压12、某温度时,反应 H 2(g)+Br 2(g) ===2HBr(g) 的标准平衡常数 K= 4×10-2,则反应21H 2(g) +21Br 2(g)=== HBr(g) 的标准平衡常数 K=( ) (A)21041-⨯ (B)21041-⨯ (C)4×10-2(D) 0.213、在体积不变的密闭容器中进行的反应 2SO 2+O 2==2SO 3,达到平衡时,若向其中充入氮气,则平衡移动的方向为( )(A)向正方向移动 (B)向逆方向移动 (C)不移动 (D)无法确定 14、欲配制pH 为3左右的缓冲溶液,应选下列( )种酸及共轭碱(括号内为p K a)。
山东科技大学材料力学2004--2006 2008,2013--2014,2016--2019年考研真题
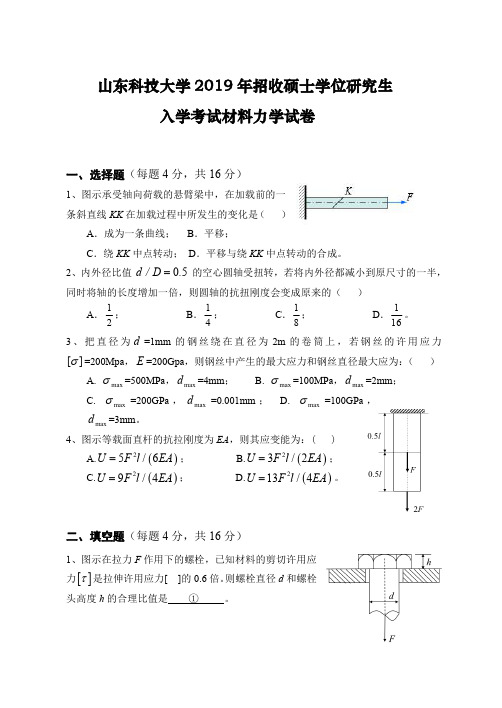
山东科技大学2019年招收硕士学位研究生入学考试材料力学试卷一、选择题(每题4分,共16分)1、图示承受轴向荷载的悬臂梁中,在加载前的一条斜直线KK 在加载过程中所发生的变化是()A .成为一条曲线;B .平移;C .绕KK 中点转动;D .平移与绕KK 中点转动的合成。
2、内外径比值05d /D .=的空心圆轴受扭转,若将内外径都减小到原尺寸的一半,同时将轴的长度增加一倍,则圆轴的抗扭刚度会变成原来的()A .21;B .41;C .81;D .161。
3、把直径为d =1mm 的钢丝绕在直径为2m 的卷筒上,若钢丝的许用应力][σ=200Mpa ,E =200Gpa ,则钢丝中产生的最大应力和钢丝直径最大应为:()A.max σ=500MPa ,max d =4mm ; B.max σ=100MPa ,max d =2mm ;C.max σ=200GPa ,max d =0.001mm ;D.max σ=100GPa ,max d =3mm 。
4、图示等载面直杆的抗拉刚度为EA ,则其应变能为:()A.()25/6U F l EA =; B.()23/2U F l EA =;C.()29/4U F l EA =;D.()213/4U F l EA =。
二、填空题(每题4分,共16分)1、图示在拉力F 作用下的螺栓,已知材料的剪切许用应力[]τ是拉伸许用应力[]的0.6倍。
则螺栓直径d 和螺栓头高度h 的合理比值是①。
2、螺栓受轴向的最大拉力F max =6kN ,最小拉力F min =5kN 作用;螺栓直径d =12mm ,则其交变应力的循环特征r =②,应力幅值a σ=③MPa ,平均应力m σ=④MPa 。
3、已知图(a )所示梁C 截面的转角()2/8c Fl EI θ=,则图(b )所示梁B 截面的挠度为⑤。
4、图示梁的A、B、C、D 四点中,单向应力状态的点是⑥,纯剪应力状态的点是⑦,在任何截面上应力均为零的点是⑧。
山东科技大学结构力学考研真题2017—2019年

图 12
3、(20 分)用力法计算图 13 所示刚架,并作出弯矩图和剪力图。已知A=1.5I/l2。
FP
B
EI
C
l
EI
EA
A
D
l
图 13
共5页 第 4 页
4、(20 分)用位移法计算图 14 所示刚架,并作出弯矩图。已知各杆 EI=常数。
20kN/m
A
C
60kN
20kN/m
D
G
E
6m
B
F
6m
3m 3m
A. 有变形,有内力;
B. 有变形,无内力;
C. 无变形,有内力;
D. 无变形,无内力。
8、计算超静定结构在荷载作用下的内力和位移时,各杆的刚度( )
A. 都只需用相对比值;
B. 都必须用实际数值;
C. 内力计算须用实际数值,位移计算可用相对比值;
D. 内力计算可用相对比值,位移计算须用实际数值。
9、如图 7 所示静定梁的 MC 的影响线,当全梁承受均布荷载时,MC( )
2、三铰拱的合理拱轴线的形状与
(2)
有关。
体系。
3、位移法的典型方程中,系数kij=kji(i≠j),该结论可根据
4、机动法作影响线是以 (4)
原理为依据的。
5、如图 9 所示结构,用位移法求解时,基本未知量的数目为
(3) (5)
定理得出。 。
6、如图 10 所示结构,已知其在荷载作用下的M图,则对于同一结构,由于支座A的转角θ引 起的C点的竖向位移Δ= (6) 。
FPl/8 A
C FP
l/2
l/2
FPl/8
B (a)
A
C
θ
山东科技大学结构力学考研真题2017—2019年

l图图11 所示桁架的杆1、的轴力。
a /3a /3a /3图12分)用力法计算图所示刚架,并作出弯矩图和剪力图。
已知A =1.5ABCllEIEIF PEAD图13图15D.常变体系。
图1图2、如图2所示结构,杆1的轴力FF P; B.-2F P;F P/2; D.-1.12F P。
、如图3所示结构,当其高度h增加时,水平支座反力F Ax()A.增大;B.减少;C.不变;D.不确定。
图3图44、如图4所示结构,在给定荷载作用下,BA为()A.F P l;B.F P l/2;C.F P l/4;D.F P l/8。
5、机动法作静定梁影响线应用的原理为()A.变形条件;B.平衡条件;C.虚功原理;D.叠加原理。
C.0.05rad;D.0.06rad。
图5图66所示结构,可视为多余约束的三根链杆是()、6、7; B.3、6、8;6、7; D.5、6、7。
7所示结构,梁式杆EI=常数,桁架杆常数,杆AB的轴力为()拉力; B.压力;零; D.无法确定。
图7图8、如图8所示结构,截面C的剪力影响线在处的竖标y E的绝对值为()A.1;B.l;0.5; D.0.5l。
二、填空题(共20分,每题4分)、如图9所示体系的计算自由度W=①。
、用力法计算图10所示结构时,取A、B支座反力为基本未知量:X1,X2。
当EI1增大时,力法方程中∆1P②。
(填不变、增大或减小)图9图103、如图11所示结构,已知I1/I2=K,则|M AB|/|M DC|=③。
4、如图12所示结构,已知力偶矩M=16kN·m,则杆端弯矩M DA=④。
(顺时针为正)图11图125、如图13所示结构,各杆EI=常数,忽略杆件轴向变形,M CA=⑤。
图13图14三、计算题(共100分,每题20分)1、如图14所示刚架,忽略杆件轴向变形。
绘制刚架的剪力图,并求C点的竖向位移ΔC V。
2、如图15所示桁架,计算指定杆件1、2、3的轴力。
2015年山东科技大学考研真题804弹性力学硕士研究生专业课考试试题

一、填空题(共30分,每空2分)
1、弹性力学是研究弹性体在外力、温度变化等外界因素作用下所产生的 ① 、 ② 和 ③ 的一门学科。
2、物体内同一点各微分面上的应力情况称为一点的 ① 。
3、弹性力学求解过程中的逆解法和半逆解法的理论依据是: ① 。
4、在通过同一点的所有微分面中,最大正应力所在的平面一定是 ① 。
5、针对平面应力问题,=z σ ① ,=z ε ② ;在平面应变问题中,=z σ ③ ,
=z ε ④ 。
6、当体力为常量时,按应力求解弹性力学平面问题,归结为在给定的边界条件下求解 ① 方程。
7、已知一平面应变问题内某一点的正应力分量为:MPa 35x =σ、MPa 25y =σ、 泊松比3.0=ν,则=z σ ① MPa 。
8、如果函数能够作为应力函数,则系数a 、b 、c 需满足的关系是4224,cy y bx ax y x U ++=)( ① 。
9、最小势能原理可表述为:在所有几何可能的位移中, ① 使总势能取得极小值。
10、瑞利-里兹法的求解思路是:首先选择一组带有待定系数的、满足 ① 的位移分量,由位移求出应变、应力,得到弹性体的总势能,再对总势能取极值。
山东科技大学2015年招生硕士学位研究生入学考试试卷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、简述题(每题10分,共60分)
1、简述弹性力学的基本假定及意义。
2、简述弹性力学基本方程的组成及各自所表达的关系。
3、简要说明按位移法求解弹性力学问题的基本方法。
4、什么是弹性力学的逆解法?其理论依据是什么?
5、简要说明平面应变问题与平面应力问题的区别与联系。
6、简述弹性力学中变分法的本质以及最小势能原理。
二、写出下列各图的应力边界条件(固定端不必写)
(每题8分,共40分)
1、在直角坐标系下写出图1的边界条件。
图1
2、在直角坐标系下写出图2的边界条件。
图2
3、在极坐标系下写出图3的边界条件。
图3
4、在极坐标系下写出图4的边界条件。
图4
5、在极坐标系下写出图5的边界条件,内半径为a,外半径为b。
图5
三、已知受力物体内某点的应力分量为:σx = 0,σy = 2MPa,σz = 1MPa,τxy = 1MPa,τyz = 0,τxz = 2MPa。
试求经过此点的平面x+3y+z=1上的沿坐标轴方向的应力分量以及该平面上的正应力和切应力。
(15分)
四、若假设函数U=a(x4-y4),试检查它能否作为应力函数?若能,试写出应力分量(不计体力),并求出图6所示矩形薄板边界上的面力。
(15
分)
图6
五、如图7所示简支梁()受线性分布载荷作用,体力不计。
取应力函数为,求应力分量。
(20分)
h l >>2Bxy +5
3
Fxy Ex Dxy y Cx y Ax U ++++=3
3
3
3
图7。
