静定结构的内力计算..
合集下载
建筑力学第三章静定结构内力计算
01
02
03
04
排架是由两个单层刚架组成的 结构，其内力可以通过整体法
和分离法进行计算。
整体法是将两个单层刚架作为 一个整体进行分析，从而求得
整个排架的内力。
分离法是将排架拆分成两个单 层刚架进行分析，然后分别求
得每个单层刚架的内力。
在计算过程中，需要考虑到排 架的自重、外力以及支座反力
的影响。
组合结构的内力计算实例
03 静定结构的内力计算方法
截面法
总结词
通过在指定截面上截取隔离体，然后对隔离体进行受力分析，计算出内力的方法。
详细描述
截面法是静定结构内力计算的基本方法之一。在截面法中，我们首先在结构中选择一个或多个截面， 然后将这些截面处的杆件暂时断开，并分析这些杆件的内力。通过这种方法，我们可以确定每个杆件 的内力大小和方向。
组合结构是由两种或多种结构组成的 结构，其内力可以通过叠加法进行计 算。
在计算过程中，需要考虑到组合结构 是将每种结构的内力分别计算 出来，然后根据结构的特点进行叠加， 从而求得整个组合结构的内力。
05 静定结构内力计算的注意 事项
材料强度的考虑
材料强度
在计算静定结构内力时，必须考虑材 料的强度。不同的材料有不同的抗拉 、抗压、抗剪强度，应确保结构中的 应力不超过材料的容许应力。
节点法
总结词
通过分析节点处的平衡状态，计算出节点所受内力的方法。
详细描述
节点法是一种基于力的平衡原理的计算方法。在节点法中，我们首先确定节点 的位置和数量，然后分析每个节点处的平衡状态。通过这种方法，我们可以计 算出每个节点所受的内力大小和方向。
弯矩图法
总结词
通过绘制弯矩图，直观地表示出结构的弯矩 分布情况，进而计算出结构的内力。
静定结构的内力计算图文
30 30
4m
4m
4m
4m
12kN
12kN 12kN
M 图（kN·m）
9kN
9kN
2kN/m
7kN
5kN
9kN
4.5kN
7.5kN
39
第40页/共76页
作业
习题3-5、3-6、3-9 习题3-10、3-12
40
第41页/共76页
§3-3 三铰拱
41
第42页/共76页
一、 概述
1、定义：
通常杆轴线为曲线，在竖向荷载作用下，支座产生水平反力的结构。
AC段受力图：
q
MC
t
C
FNC
FQC
n
x
FAY
FAYSinα
（2）求内力方程：
MC = 0 Ft = 0 Fn= 0
M = 1 qlx 1 qx2 (0 x l) 22
FN
=
q(1 l 2
x) sin
(0 x l)
FQ
=
q(1 2
l
x) cos
(0 x l)
FAYcosα
FAY
M中 =162 / 8 6.23/ 2 =1.385kN.m(下拉)
弯矩图见下图。
1kN/m
6.23 D
C 1.385
6.23 E
1.385kN A
4.5kN
M 图(kN.m)
B 1.385kN
1. 5kN
38
第39页/共76页
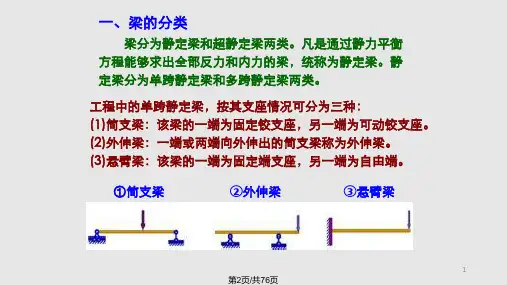
例：主从刚架弯矩图。
12kN
2kN/m
36 36
6m
12 42 30
F
F
曲梁
拱
f / l : 高跨比（1～1/10）
第13章静定结构的内力计算
由此可知，两者的受力状态完全相同，故两者的弯矩图也是相 等的。可得出结论：结构中绘制任意区段梁的弯矩图的问题可 把单个荷载作用下的简支梁的弯矩图利用叠加原理竖向叠加， 就可以得到相应的简支梁在荷载共同作用下的弯矩图，这就是 所谓的分段叠加法。 分段叠加法绘制任意直杆件的弯矩图，可归纳为如下几个步骤： （１）选取杆上外荷载变化（不连续处）的位置（如集中力、 力偶作用点、分布荷载的起点和终点等）作为控制截面，计算 出该截面上的弯矩值。 （２）根据各控制截面之间有无均布荷载狇绘制弯矩图。当控 制截面间无均布荷载作用（狇＝０）时，可用直线依次连接各 控制截面的弯矩值绘制出该区段内弯矩图；当控制截面有均布 •荷载作用（狇≠０）时，先用直线依次连接各控制截面的弯矩 值，然后再叠加上该区段上相应简支梁的弯矩图
若将此多跨静定梁的弯矩犕图与相应多跨简支梁的弯矩图犕
是后者的最大弯矩值的６８．８％。这说明由于在多跨静定梁 中布置了伸臂梁的缘故，一方面，减少了附属部分的跨度，另 一方面，又使伸臂梁上的荷载对基本部分产生负弯矩，从而部 分抵消了跨中外荷载所产生的正弯矩。因此，多跨静定梁比相 应多跨简支梁在材料用量上较节省，但在构造上较之复杂一些。 静定平面刚架
利用上述关系式，可以借助简支梁的支座反力和内力的计算结 果来求三铰拱的支座反力。只受竖向荷载作用的三铰拱，两固 定铰支座的竖向反力与相应简支梁的相同，水平反力等于相应 简支梁截面犆处的弯矩与拱高的比值。由于拱轴线为曲线，三 铰拱的内力计算较为复杂，但也可以借助相应的简直梁的内力 计算结果，来求拱上任意截面的内力。
静定平面桁架 桁架概述 所示。桁架结构中，依杆件所在位置不同，可分为弦杆和腹 杆两类。上下缘的杆件分别称为上弦杆和下弦杆，上下弦杆 间的杆件称为腹杆，腹杆包括斜杆和竖杆。两个相邻弦杆间 的水平距离称为结点长度，桁架两个支座间的水平距离称为 跨度。支座连线至桁架最高点的距离犺称为桁高。
第三章 静定结构的内力计算
FAy
1 3a 4 FP a M q 3a 3a 2 5
第三章
静定结构的内力计算
M
B
0
3a 4 FAy 3a M q 3a FP a 0 2 5 1 3a 4 FAy FP a M q 3a 3a 2 5
第三章
无荷载 平行轴线
Q图
静定结构的内力计算
均布荷载
集中力 发生突变
P
集中力偶
无变化 发生突变
m
斜直线
M图
二次抛物线 凸向即q指向
出现尖点
两直线平行 备 注
Q=0区段M图 Q=0处，M 平行于轴线 达到极值
集中力作用截 集中力偶作用 面剪力无定义 面弯矩无定义
在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩 等于零，有集中力偶作用，截面弯矩等于集中力偶的值。
第三章 静定结构的内力计算
第三章
静定结构的内力计算
§3-1单跨静定梁
一、静定结构概述 1．概念：是没有多余约束的几何不变体系。 2．特点：在任意荷载作用下，所有约束反力和内力都 可由静力平衡方程唯一确定。 平衡方程数目 = 未知量数目 3．常见的静定结构 常见的静定结构有：单跨静定梁、多跨静定梁、静 定平面刚架、三铰拱、静定平面桁架、静定组合结构等 (如下图）。
0 FYA FYA 0 FYB FYB
A
x
C
L
斜梁的反力与相应简支 梁的反力相同。
第三章
（2）内力
静定结构的内力计算
求斜梁的任意截面C的内力，取隔离体AC： a FP1 A
FYA x Fp1 FYA
0
MC
结构力学二3-静定结构的内力计算
以例说明如下
例 绘制刚架的弯矩图。 解：
E 5kN
由刚架整体平衡条件 ∑X=0 得 HB=5kN← 此时不需再求竖向反力便可 绘出弯矩图。 有：
30
20 20 75 45
40
0
MA=0 , MEC=0 MCE=20kN· m（外） MCD=20kN· m（外） MB=0 MDB=30kN· m（外） MDC=40kN· m（外）
有突变
铰或 作用处 自由端 (无m）
m
Q图
M图
水平线
⊕
⊖㊀
Q=0 处 突变值为P 如变号 无变化
有极值 尖角指向同P 有极值 有突变 M=0 有尖角
斜直线
→
↑
利用上述关系可迅速正确地绘制梁的内力图（简易法）
简易法绘制内力图的一般步骤：
（1）求支反力。 （2）分段：凡外力不连续处均应作为分段点， 如集中力和集中力偶作用处，均布荷载两端点等。 （3）定点：据各梁段的内力图形状，选定控制 截面。如集中力和集中力偶作用点两侧的截面、均 布荷载起迄点等。用截面法求出这些截面的内力值， 按比例绘出相应的内力竖标，便定出了内力图的各 控制点。
说明：
（a）M图画在杆件受拉的一侧。 （b）Q、N的正负号规定同梁。Q、N图可画在杆的 任意一侧，但必须注明正负号。 （c）汇交于一点的各杆端截 面的内力用两个下标表示，例如： MAB表示AB杆A端的弯矩。 MAB
例 作图示刚架的内力图
RB↑
←HA
VA→
CB杆：
由∑ X=0 可得： M = CD RB=42kN↑ HA=48kN←， H （左） A=6×8=48kN← 由∑M144 VA=22kN↓ 48 A=0 可得： MEB=MEC=42×3 ↑ （2）逐杆绘M图 R=126kN = 126 · m （下） B 192 MDC=0 CD杆： M =42 × 6-20 × 3 由 ∑Y=0 可得： CB MCD=48kN·m（左） =192kN· m（下） VA=42-20=22kN↓
第三章 静定结构的内力计算(组合结构)
A A A A 0 0 0 0
0 0 0 0
8 8 8 8
HC
3、求梁式杆内力 处理结点A处力
结构力学
第3章静定结构的内力计算
静定结构特性
结构力学
第3章静定结构的内力计算
静定结构特性 静定结构特性 一、结构基本部分和附属部分受力影响
A
F1
B
C
F2
D
E
F3
F
如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； Ⅰ Ⅱ Ⅲ 如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； 如只有 F1 作用。则Ⅱ、Ⅲ无内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F3 作用。则Ⅰ、Ⅱ均有内力和反力； 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 特性一、静定结构基本部分承受荷载作用，只在基本部分上产 如只有 F2 作用。则Ⅲ无内力和反力，但Ⅰ有内力和反力。 生反力和内力；附属部分上承受荷载作用，在附属部分和基本 部分上均产生反力和内力。
第3章静定结构的内力计算
q = 1 kN/m A FR Ax FR Ay FNDA F C FNFD VC
8 8 8 8
M M图 图 （ m M图 （kN· kN· m） ） M 图 （kN· m） （kN· m） F 图 FQ 图 Q （ ） FkN 图 （ kN Q ） FkN 图 （ Q ） （kN） F 图 FN N图 （ ） FkN （ kN ） N图 FkN N图 （ ） （kN）
结构力学
第3章静定结构的内力计算
二、平衡荷载的影响
F C B D
A B q C
【土木建筑】第16章：静定结构的内力计算
= M0x
单跨静定梁小结
要求： １）理解内力、内力图的概念； ２）了解梁的主要受力、变形特点； ３）理解并掌握截面法计算内力的方法； ４）熟练掌握用叠加法做直杆段的弯矩图。
本节难点及重点： １）内力正、负号的判断； ２）叠加法做弯矩图。
§16-2 多跨静定梁
多跨静定梁由相互在端部铰接、水平放置的若干直 杆件与大地一起构成的结构。
绕曲线杆端切线
q
XA A
B XB
C
E
D B
A
• 一、静定刚架支座反力的计算：平衡方 程
二、绘制内力图：用截面法求解刚架任意 指定截面的内力，应用与梁相同的内力符 号正负规定原则即相同的绘制规律与绘图 方法作内力图（M图、Q图、N图）
40kN
(+) (-)
40kN
q=20kN/m
B
C
P=40kN D
例16-2-2 分析图示多跨静定梁可分解成单跨梁分 别计算的条件，并作梁的FQ、M图。
分析：（１）图示梁的荷载以及约束的方向，是竖 向平行力系。一个平面平行力系只能列两个独立的 平衡方程，解两个未知数。 （２）杆ＣＥ有两个与大地相连的竖向支座链杆， 当仅在竖向荷载作用下时，可维持这个平行力系的 平衡。所以，杆ＣＥ在仅有竖向荷载的作用下，可 视为与杆ＡＢ同等的基本部分。
２）求C截面的内力 切开过C点的横截面，将梁分成两部分。取左侧
部分考虑，其暴露的截面上按规定的内力的正方向 将内力示出，建立静力平衡方程。
说明：计算内力要点： １）所取的隔离体（包括结构的整体、截面法截取 的局部），其隔离体周围的所有约束必须全部切断 并代以约束力、内力。 ２）对未知外力（如支座反力），可先假定其方向， 由计算后所得结果的正负判断所求力的实际方向， 并要求在计算结果后的圆括号内用箭线表示实际方 向。 ３）计算截面的内力时，截面两侧的隔离体可任取 其一，一般按其上外力最简原则选择。截面内力均 按规定的正方向画出。
单跨静定梁小结
要求： １）理解内力、内力图的概念； ２）了解梁的主要受力、变形特点； ３）理解并掌握截面法计算内力的方法； ４）熟练掌握用叠加法做直杆段的弯矩图。
本节难点及重点： １）内力正、负号的判断； ２）叠加法做弯矩图。
§16-2 多跨静定梁
多跨静定梁由相互在端部铰接、水平放置的若干直 杆件与大地一起构成的结构。
绕曲线杆端切线
q
XA A
B XB
C
E
D B
A
• 一、静定刚架支座反力的计算：平衡方 程
二、绘制内力图：用截面法求解刚架任意 指定截面的内力，应用与梁相同的内力符 号正负规定原则即相同的绘制规律与绘图 方法作内力图（M图、Q图、N图）
40kN
(+) (-)
40kN
q=20kN/m
B
C
P=40kN D
例16-2-2 分析图示多跨静定梁可分解成单跨梁分 别计算的条件，并作梁的FQ、M图。
分析：（１）图示梁的荷载以及约束的方向，是竖 向平行力系。一个平面平行力系只能列两个独立的 平衡方程，解两个未知数。 （２）杆ＣＥ有两个与大地相连的竖向支座链杆， 当仅在竖向荷载作用下时，可维持这个平行力系的 平衡。所以，杆ＣＥ在仅有竖向荷载的作用下，可 视为与杆ＡＢ同等的基本部分。
２）求C截面的内力 切开过C点的横截面，将梁分成两部分。取左侧
部分考虑，其暴露的截面上按规定的内力的正方向 将内力示出，建立静力平衡方程。
说明：计算内力要点： １）所取的隔离体（包括结构的整体、截面法截取 的局部），其隔离体周围的所有约束必须全部切断 并代以约束力、内力。 ２）对未知外力（如支座反力），可先假定其方向， 由计算后所得结果的正负判断所求力的实际方向， 并要求在计算结果后的圆括号内用箭线表示实际方 向。 ３）计算截面的内力时，截面两侧的隔离体可任取 其一，一般按其上外力最简原则选择。截面内力均 按规定的正方向画出。
静定结构内力计算全解[详细]
![静定结构内力计算全解[详细]](https://img.taocdn.com/s3/m/290a22ba7cd184254b3535d4.png)
➢ 杆件结构的组成和分析是两个相关的过程，应当 把受力分析与组成分析联系起来，根据结构的组 成特点确定受力分析的合理途径。
从组成的观点，静定结构的型式： ✓悬臂式、简支式（两刚片法则） ✓三铰式（三刚片法则） ✓组合式（两种方式的结合）
悬臂式 三铰式
简支式 组合式
组合式结构中:
✓基本部分：结构中先组成的部分，能独立承载； ✓附属部分：后组成的以基本部分为支承的部分，不能独立 承载。
三铰拱作业：
y
100kN
1
A O
2m
20kN/m
4m 8m
2
B x
Hale Waihona Puke 2m求图示抛物线拱的1、2截面的内力。
三、三铰拱的合理拱轴线
使拱在给定荷载下只
M M 0 FH y 0 产生轴力的拱轴线，被
y M0
称为与该荷载对应的合 理拱轴
FH
三铰拱的合理拱轴线 的纵坐标与相应简支梁弯 矩图的竖标成正比。
Mik
i
FQik
Mik
i
Fiy
q Mki
k
FQki q
Mki
k
Fky
叠加法作弯矩图： 叠加法作弯矩图：
+
要点：先求出杆两端 截面弯矩值，然后在 两端弯矩纵距连线的 基础上叠加以同跨度、 同荷载简支梁的弯矩 图。
§3 静定多跨梁与静定平面刚架
一、静定多跨梁 多根梁用铰连接组成的静定体系。
AB、CD梁为基本部分 BC梁为附属部分。
2、求支座反力和内部约束力
根据组成和受力情况，取整个结构或部分结构为隔离 体，应用平衡方程求出。
B
B
F
F
FBy
A FC
FAx A FAy
从组成的观点，静定结构的型式： ✓悬臂式、简支式（两刚片法则） ✓三铰式（三刚片法则） ✓组合式（两种方式的结合）
悬臂式 三铰式
简支式 组合式
组合式结构中:
✓基本部分：结构中先组成的部分，能独立承载； ✓附属部分：后组成的以基本部分为支承的部分，不能独立 承载。
三铰拱作业：
y
100kN
1
A O
2m
20kN/m
4m 8m
2
B x
Hale Waihona Puke 2m求图示抛物线拱的1、2截面的内力。
三、三铰拱的合理拱轴线
使拱在给定荷载下只
M M 0 FH y 0 产生轴力的拱轴线，被
y M0
称为与该荷载对应的合 理拱轴
FH
三铰拱的合理拱轴线 的纵坐标与相应简支梁弯 矩图的竖标成正比。
Mik
i
FQik
Mik
i
Fiy
q Mki
k
FQki q
Mki
k
Fky
叠加法作弯矩图： 叠加法作弯矩图：
+
要点：先求出杆两端 截面弯矩值，然后在 两端弯矩纵距连线的 基础上叠加以同跨度、 同荷载简支梁的弯矩 图。
§3 静定多跨梁与静定平面刚架
一、静定多跨梁 多根梁用铰连接组成的静定体系。
AB、CD梁为基本部分 BC梁为附属部分。
2、求支座反力和内部约束力
根据组成和受力情况，取整个结构或部分结构为隔离 体，应用平衡方程求出。
B
B
F
F
FBy
A FC
FAx A FAy
《工程力学》课题十二：静定结构的内力计算
只需求出与杆轴线垂直的反力。
1.悬臂刚架
可以不求反力，由自由端开始直接 求作内力图。
L
q ½qL²↓↓↓↓↓↓↓↓↓
L
qL² qL²
2.简支刚架弯矩图
简支型刚架绘制弯矩图时，往往
只须求出一个与杆件垂直的支座
反力，然后由支座作起。
q
l
D
qa2/2
C
l/2
l/2
q
↓↓↓↓↓↓↓↓↓↓↓↓
ql2/2
qL2/2
（3）绘制内力图(弯矩图 剪力图 轴力图）
由已求得各杆端力，分别按各杆件作内力图。
弯矩图可由已知杆端弯矩，按直杆段的区段叠加法作杆
件的弯矩图。
连接两个杆端的刚结点,若 结点上无外力偶作用,则两 个杆端的弯矩值相等,方向 相反.
M图（KN·m）
拆成单个杆,求出杆两端的所 有内力,按与单跨梁相同的方法 画内力图.
铰拱的合理拱轴线的纵
只限于三铰平拱受 竖向荷载作用
坐标与相应简支梁弯矩 图的竖标成正比。
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线。
MC0=ql2/8 H=ql2/8f M0(x)=qlx/2-qx2 /2 =qx(l-x)/2
y=4fx(l-x)/l2
抛物线
拱的合理拱轴线的形状与相应的简支梁的弯矩 图相似。
三铰拱在竖向集中荷载作用下的的无荷载区段上， 合理拱轴是一条直线，并在集中荷载作用点出现转折； 在均布荷载作用区段上，合理拱轴是一条抛物线。
（２）计算杆端力 取AB杆B截面以下部分， 计算该杆Ｂ端杆端力：
MBA = 160kN·m (右侧受拉) 同理：取BD杆B截面以右部 分，计算该杆B端杆端力： MBD = 160kN·m (下侧受拉)
第七章静定结构的内力计算
C
B
q a
qa 2
qa
A
a
qa
2
1．求支反力 2．分段 3．截面法求各段杆端内力值 4．用直线或曲线连接各段 5．标出数据、正负、图名
M CB
qa2 2
(下拉)
M CA
qa2 2
(右拉)
qa 2
C2
B
qa 2
2
qa 2
8
A
M
内力图的作法——剪力图
C
B
qa 2
qa
FQAC qa
FQCA 0
3m 1m
5kN
A
C
D
B
5kN 4kN
5m
4kN
5kN
FQDA
M DA
FDA
截面法计算D截面杆端内力
5kN
A
C
D
FNDC
M DC
FDC
4kN
3m 1m
B
5kN 4kN
5m
4kN
截面法计算D截面杆端内力
3m 1m
5kN
A
C
D
B
5kN 4kN
5m
4kN
FNDB
M DB
FQDB
5kN
4kN
内力图的作法——弯矩图
超静定结构
对于具有多余约束的几何不变体系，却不 能由静力平衡方程求得其全部反力和内力，这 类结构称为超静定结构
杆件类型
杆件
内力：轴力、剪力、弯矩 梁式杆
类型：梁、刚架、拱
链杆
内力：轴力 类型：桁架
梁
概念：是一种受弯构件，其轴线为直线， 有单跨和 多跨之分
单跨静定梁
《结构力学》静定结构内力计算
只承受竖向荷载和弯矩
FP1 A
FP2
B
C
基本部分：能独立承受外载。 附属部分：不能独立承受外载。
FP
A
B
C
■作用在两部分交接处的集 中力，由基本部分来承担。
FP1
FP2
A B
■基本部分上的荷载不影响附 属部分受力。
■附属部分上的荷载影响基本 部分受力。
先算附属部分， 后算基本部分。
例 确定x值，使支座B处弯矩与AB跨中弯矩相等，画弯矩图
ql ql/2
FQ图 ql
7ql/4 ql
5ql/4 ql/2
3ql/4
ql/2
练习
10kNm 20kN 10kN
10kN/m
1m 1m 1m 1m
1m 1m 10kN/m
10kNm
20kN 10kN 0
0
30kN
10kNm
20kN 10kNm
10kNm
10kNm
20kN 10kN 0
0
30kN
2m 2m
解 （1）求支反力
q=20kN/m FP=40kN
70kN
50kN
（2）取隔离体，求截面内力
MC C FQC
FP=40kN
B 50kN
（2）叠加法作弯矩图
120kNm
+
40kNm
40kNm
=
120kNm
40kNm
40kNm M图
例 试绘制梁的弯矩图。
40kNm
FP=40kN q=20kN/m
26
26
8 FQ图(kN)
6
12
M图(kNm)
24 12
例
解 （1）求支反力
建筑力学第11章静定结构的内力计算
2）联合桁架 由几个简单桁架按几何不变规律 联合组成的桁架（图 11.28（c）所示）。 3）复杂桁架 不按上述两种方式组成的其他形 式的桁架（图 11.28（d）所示）。 46
11.4.2 静定平面桁架的内力计算 （1）结点法 结点法是以桁架的结点为研究对象，适用于计 算简单桁架。当截取桁架中某一结点为隔离体后， 得到一平面汇交力系，根据平面汇交力系的平衡条 件可求得各杆内力。又因为根据平面汇交力系的平 衡条件，对于每一结点只能列出两个平衡方程，因 此每次所选研究对象（结点）上未知力的个数不应 多于两个。
13
图 11.9
14
图 11.10
15
图 11.11 静定多跨梁与简支梁的受力比较
16
11.2 静定平面刚架 11.2.1 刚架的特征 刚架是由若干根梁和柱主要用刚结点组成的结 构。当刚架各杆轴线和外力作用线都处于同一平面 内时称为平面刚架，如图 11.12（b）所示。 在刚架中，它的几何不变性主要依靠结点 刚性来维持，无需斜向支撑联系，因而可使结构内 部具有较大的净空便于使用。如图 11.12（a）所 示桁架是一几何不变体系，如果把 C 结点改为刚 结点，并去掉斜杆，则该结构即为静定平面刚架， 如图 11.12（ b）所示。
6
图 11.3
7
图 11.4
8
（3）斜梁的内力图 在建筑工程中，常会遇到杆轴倾斜的斜梁，如 图11.5所示的楼梯梁等。 当斜梁承受竖向均布荷载时，按荷载分布情况 的不同，可有两种表示方式。一种如图 11.6 所示 ，斜梁上的均布荷载 q按照沿水平方向分布的方式 表示，如楼梯受到的人群荷载的情况就是这样。另 一种如图 11.7所示，斜梁上的均布荷载 q′按照沿 杆轴线方向分布的方式表示，如楼梯梁的自重就是 这种情况。
11.4.2 静定平面桁架的内力计算 （1）结点法 结点法是以桁架的结点为研究对象，适用于计 算简单桁架。当截取桁架中某一结点为隔离体后， 得到一平面汇交力系，根据平面汇交力系的平衡条 件可求得各杆内力。又因为根据平面汇交力系的平 衡条件，对于每一结点只能列出两个平衡方程，因 此每次所选研究对象（结点）上未知力的个数不应 多于两个。
13
图 11.9
14
图 11.10
15
图 11.11 静定多跨梁与简支梁的受力比较
16
11.2 静定平面刚架 11.2.1 刚架的特征 刚架是由若干根梁和柱主要用刚结点组成的结 构。当刚架各杆轴线和外力作用线都处于同一平面 内时称为平面刚架，如图 11.12（b）所示。 在刚架中，它的几何不变性主要依靠结点 刚性来维持，无需斜向支撑联系，因而可使结构内 部具有较大的净空便于使用。如图 11.12（a）所 示桁架是一几何不变体系，如果把 C 结点改为刚 结点，并去掉斜杆，则该结构即为静定平面刚架， 如图 11.12（ b）所示。
6
图 11.3
7
图 11.4
8
（3）斜梁的内力图 在建筑工程中，常会遇到杆轴倾斜的斜梁，如 图11.5所示的楼梯梁等。 当斜梁承受竖向均布荷载时，按荷载分布情况 的不同，可有两种表示方式。一种如图 11.6 所示 ，斜梁上的均布荷载 q按照沿水平方向分布的方式 表示，如楼梯受到的人群荷载的情况就是这样。另 一种如图 11.7所示，斜梁上的均布荷载 q′按照沿 杆轴线方向分布的方式表示，如楼梯梁的自重就是 这种情况。
静定结构的内力分析
40
第 三 章80 静定结构的内力计算
D
FNDE FNED
E
30
30
FNDC
FNEB
FQ
40 kN
FN 30 kN
80 kN
练习：
第三章
静定结构的内力计算
解： (1) 求支座反力。
F=qa
C
D
由 X 0
E
FxA q 2a 0
q
a B
得 FAx 2qa
a
由 M A 0
FxA
A
FyB
2qa a F a FyB 2a 0
首先进行定性分析。
由内力图的外观校核。杆上无分布荷载FS图为水 平直线；M图为斜直线。杆上有分布荷载FS图为斜直 线；M图为二次抛物线。 FS图为零的截面M为极值。 杆上集中荷载作用的截面, FS图上有突变；M图上有折 弯。根据这些特征来检查，本题的M图、FS图均无误。
第 三 章 静定结构的内力计算
6
FA=58 kN 26
10
18 FB=12 kN
q ME
FQE
MF
FS 图 ( kN )
FQF
第 三 章 静定结构的内力计算
二、 多跨静定梁 (multi-span statically determinate beam)
附属部分--依赖基本
基本部分--不依赖其它
部分的存在才维持几
部分而能独立地维持其
据
3.外力与杆轴关系(平行,垂直,重合) 4.特殊部分(悬臂部分,简支部分)
5.区段叠加法作弯矩图
第 三 章 静定结构的内力计算
结点平衡条件的应用：
一、铰结点： （集中力偶只能作用于杆端处）
M
第三章静定结构的内力计算(精)
第三章静定结构的内力计算学习目的和要求不少静定结构直接用于工程实际，另外，它还是静定结构位移计算及超静定结构的计算基础。
所以静定结构的内力计算是十分重要的，是结构力学的重点内容之一。
通过本章学习要求达到：1、练掌握截面内力计算和内力图的形状特征。
2、练掌握截绘制弯矩图的叠加法。
3、熟练掌握截面法求解静定梁、刚架及其内力图的绘制和多跨静定梁及刚架的几何组成特点和受力特点。
4、了解桁架的受力特点及按几何组成分类。
熟练运用结点法和截面法及其联合应用，会计算简单桁架、联合桁架既复杂桁架。
5、掌握对称条件的利用；掌握组合结构的计算。
6、熟练掌握截三铰拱的反力和内力计算。
了解三铰拱的内力图绘制的步骤。
掌握三铰拱合理拱轴的形状及其特征学习内容梁的反力计算和截面内力计算的截面法和直接内力算式法；内力图的形状特征；叠加法绘制内力图；多跨静定梁的几何组成特点和受力特点。
静定梁的弯矩图和剪力图绘制。
桁架的特点及分类，结点法、截面法及其联合应用，对称性的利用，几种梁式桁架的受力特点，组合结构的计算。
三铰拱的组成特点及其优缺点；三铰拱的反力和内力计算及内力图的绘制；三铰拱的合理拱轴线。
§3.1梁的内力计算回顾一、截面法1、平面杆件的截面内力分量及正负规定：轴力N (normal force) 截面上应力沿轴线切向的合力以拉力为正。
剪力Q (shearing force)截面上应力沿轴线法向的合力以绕隔离体顺时针转为正。
弯矩M (bending moment) 截面上应力对截面中性轴的力矩。
不规定正负，但弯矩图画在拉侧。
2、截面内力计算的基本方法：截面法：截开、代替、平衡。
内力的直接算式：直接由截面一边的外力求出内力。
1、轴力=截面一边的所有外力沿轴切向投影代数和。
2、剪力=截面一边的所有外力沿轴法向投影代数和，如外力绕截面形心顺时针转动，投影取正否则取负。
3、弯矩=截面一边的所有外力对截面形心的外力矩之和。
弯矩及外力矩产生相同的受拉边。
《结构力学》第三章 静定结构内力计算(1)
技巧：“求谁不管谁”：不考虑待求未知力，而考虑其
它未知力有什么特点，具体分为下面两种情况：
（a）其余未知力平行，在其垂直方向投影。
（b）其余未知力汇交于一点，对该点取矩。
X 0,X A 0;
1
1
MB
0,YA
l ql
l 2
0,YA
ql 2
Y
0,YA
YB
ql
0,YB
1 2
ql
step2：求指定截面内力 （1）取脱离体：从指定c截面截开梁，取左半脱离体为 研究对象，受力如图所示：
轴力、剪力 符号规定
梁、拱的弯 矩符号通常 假定使下侧 受拉为正
2、杆件任一截面上内力的计算---截面法
沿计算截面用一假想截面将构件切开，任取一侧 脱离体为研究对象，利用脱离体的静力平衡条 件，可建立三个平衡方程：
X 0,Y 0,M 0
由此就可求得杆件任一截面上的内力。
注意：
• 脱离体要与周围的约束全部断开，并用相应的约束力 代替。例如，去掉辊轴支座、铰支座、固定支座时应 分别添加一个、二个以及三个支座反力，等等。
（二）简支结构
通过一铰、一链杆或三根链杆与基础相连的结构。
（三）三铰结构
若结构体系（不含基础）有两个刚片，其与基础 的连接满足三刚片法则，则称该体系为三铰结 构。
（四）组合结构
多次运用几何不变体系的简单组成规则构成的结 构。
2、静定结构内力分析（即绘制内力图） 方法
有三种常用的绘制内力图的方法。
（2）熟记几种常见单跨梁的弯矩图，如悬臂梁、简
支梁等。特别记住简支梁在均布荷载、集中力以及集 中力偶作用下的弯矩图。
（1）
（2） （3）
梁长均为L
静定结构内力计算
4、受力特点：
荷载作用在基本部分时，附属部分不受力
荷载作用在附属部分时，基本部分和附属部分都受力
4
2:46:01 PM
Chap3 静定结构内力计算
练习 A
一、静定多跨梁
D B
C 3qa/4
2qa
qa2
9qa/4
qa/2
D
A
qa
B M图
C qa/2
qa2/2
qa
5
+
A
qa/4 B
2:46:01 PM
⑥根据荷载与内力之间的微分关系和增量关系，判断内力 图的形状特征；
⑦注意结点的平衡条件：结点的力矩平衡条件；
⑧对称性的利用。
20
2:46:01 PM Chap3 静定结构内力计算
二、静定平面刚架
对称性的利用
对称结构：结构构成对称于某一几何轴线（对折后完全重合） 对称（反对称）荷载：绕对称轴折叠，荷载作用点、大小相 同、方向相同（相反）。
1、定义：由若干直杆组成；
所有杆件两端均用铰结，几何不变； 杆件主要承受轴力。
桁架工程实例
24
2:46:01 PM
Chap3 静定结构内力计算
三、静定平面桁架
2、桁架结构的优点
杆截面应力均匀分布，材料效用充分发挥，用材经济， 自重较轻，适用于大跨度结构。
3、理想桁架的三项基本假定
a.各杆在两端用理想铰（光滑而无摩擦）相互联结； b.各杆的轴线均为直线，并通过铰的几何中心； c.荷载和支座反力均作用在结点上。
-
C
7qa/4
+
qa/2
-
D
Q图
Chap3 静定结构内力计算
一、静定多跨梁
荷载作用在基本部分时，附属部分不受力
荷载作用在附属部分时，基本部分和附属部分都受力
4
2:46:01 PM
Chap3 静定结构内力计算
练习 A
一、静定多跨梁
D B
C 3qa/4
2qa
qa2
9qa/4
qa/2
D
A
qa
B M图
C qa/2
qa2/2
qa
5
+
A
qa/4 B
2:46:01 PM
⑥根据荷载与内力之间的微分关系和增量关系，判断内力 图的形状特征；
⑦注意结点的平衡条件：结点的力矩平衡条件；
⑧对称性的利用。
20
2:46:01 PM Chap3 静定结构内力计算
二、静定平面刚架
对称性的利用
对称结构：结构构成对称于某一几何轴线（对折后完全重合） 对称（反对称）荷载：绕对称轴折叠，荷载作用点、大小相 同、方向相同（相反）。
1、定义：由若干直杆组成；
所有杆件两端均用铰结，几何不变； 杆件主要承受轴力。
桁架工程实例
24
2:46:01 PM
Chap3 静定结构内力计算
三、静定平面桁架
2、桁架结构的优点
杆截面应力均匀分布，材料效用充分发挥，用材经济， 自重较轻，适用于大跨度结构。
3、理想桁架的三项基本假定
a.各杆在两端用理想铰（光滑而无摩擦）相互联结； b.各杆的轴线均为直线，并通过铰的几何中心； c.荷载和支座反力均作用在结点上。
-
C
7qa/4
+
qa/2
-
D
Q图
Chap3 静定结构内力计算
一、静定多跨梁
第七章静定结构的内力计算
在檩条梁中，AB梁是基本部分，而BC梁、CD 梁则是附属部分。
为清晰起见，可将它们的支承关系分别用图表 示，这样的图形称为层次图。
7.1.2 多跨静定梁的内力计算
通过层次图可以看出力的传递过程。因为基本 部分直接与基础相联结，所以当荷载作用于基本部 分时，仅基本部分受力，附属部分不受力；当荷载 作用于附属部分时，由于附属部分与基本部分相联 结，故基本部分也受力。
系列简支梁 的弯矩图
多跨静定 梁的弯矩 图
7.2 静定平面刚架
7.2.1 概述 1. 刚架的特点
刚架是由直杆组成的具有刚性结点的结构。
在刚架中的刚结点处，刚结在一起的各杆不 能发生相对移动和转动，变形前后各杆的夹角保 持不变，故刚结点可以承受和传递弯矩。
由于存在刚结点，使刚架中的杆件较少，内 部空间较大，比较容易制作，所以在工程中得到 广泛应用。
【例7.1】绘制图（a）所示多跨静定梁的内力图。
【解】 1) 绘制层次图。
梁ABC固定在基础上，是基本部分；梁CDE固 定在梁ABC上，是第一级附属部分；梁EF固定在梁 CDE上，是第二级附属部分。
根据上述分析，多跨静定梁由三个层次构成。
2) 求约束反力。 在计算时，先计算EF梁，再计算CDE梁，最 后计算ABC梁。
FAx
MA
FAy
2) 绘制内力图。 由区段叠加法绘制弯矩图。在CD段，将控制 截面上的弯矩值竖标按比例标出并用虚线连接， 以此虚线为基线，叠加上相应简支梁在均布荷载 作用下的弯矩图。在AC段，以连接控制截面上的 弯矩值竖标的虚线为基线，叠加上相应简支梁在 跨中点受集中荷载作用下的弯矩图。
240
240
【解】 悬臂刚架可不计算支座反力，直接计算内力。 1) 求各控制截面上的内力。 取每个杆件的两端为控制截面，从自由端开始，根
《建筑力学》 李前程 第六章 静定结构的内力计算
F sB Lqa, M B Lmqa22
BC 段
qa2 F sB RqaF3qa, M B R2 F sC LF sC=3qa
M Cqa2qa1.5a2qaa2.5qa2
M图 qa2
F= 2qa q
B
C
a
a
qa 3qa
2.5qa 2
0.5qa2
23
第二节 内力方程·内力图
2qa2
[例题 7] 用简便法绘制梁的剪力图和弯矩图。
Ax
B D
x
x q2x
2m
M (x) qx
(0x2 m )
22
AD段
6
F s ( x ) F A q 1 x .5 4 3 x ( 2 m x 6 m )
M (x ) F A x q x 2 x 1.5 x 4 q 2 2x (2 m x 6 m )
-
4m
2m
M(kN.m)图
DB段 F s(x ) F B 3 .5(0 x 2 m )
《建筑力学》 李前程 第六章 静定 结构的内力计算
第六章 静定结构的内力计算
第一节 杆件的内力·截面法 第二节 内力方程·内力图 第三节 用叠加法作剪力图和弯矩图 第四节 静定平面刚架 第五节 静定多跨梁 第六节 三拱桥 第七节 静定平面桁架 第八节 各种结构形式及悬索的受力特点
2
第六章 静定结构的内力计算
+
4
M (x ) F B x(0 x 2 m )
6.04
7
x=4.83m
18
第二节 内力方程·内力图
四、作梁内力图的简便方法
不列剪力和弯矩方程，简便法画出剪力图和弯矩图的基本步骤： 1.正确计算出约束力，将梁分段； 2.按照梁段上外力情况,判断各段内力图的大致形状； 3.计算剪力、弯矩在各段的极值(控制截面)； 4.用光滑曲线连接，标注大小,正负。
BC 段
qa2 F sB RqaF3qa, M B R2 F sC LF sC=3qa
M Cqa2qa1.5a2qaa2.5qa2
M图 qa2
F= 2qa q
B
C
a
a
qa 3qa
2.5qa 2
0.5qa2
23
第二节 内力方程·内力图
2qa2
[例题 7] 用简便法绘制梁的剪力图和弯矩图。
Ax
B D
x
x q2x
2m
M (x) qx
(0x2 m )
22
AD段
6
F s ( x ) F A q 1 x .5 4 3 x ( 2 m x 6 m )
M (x ) F A x q x 2 x 1.5 x 4 q 2 2x (2 m x 6 m )
-
4m
2m
M(kN.m)图
DB段 F s(x ) F B 3 .5(0 x 2 m )
《建筑力学》 李前程 第六章 静定 结构的内力计算
第六章 静定结构的内力计算
第一节 杆件的内力·截面法 第二节 内力方程·内力图 第三节 用叠加法作剪力图和弯矩图 第四节 静定平面刚架 第五节 静定多跨梁 第六节 三拱桥 第七节 静定平面桁架 第八节 各种结构形式及悬索的受力特点
2
第六章 静定结构的内力计算
+
4
M (x ) F B x(0 x 2 m )
6.04
7
x=4.83m
18
第二节 内力方程·内力图
四、作梁内力图的简便方法
不列剪力和弯矩方程，简便法画出剪力图和弯矩图的基本步骤： 1.正确计算出约束力，将梁分段； 2.按照梁段上外力情况,判断各段内力图的大致形状； 3.计算剪力、弯矩在各段的极值(控制截面)； 4.用光滑曲线连接，标注大小,正负。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a、在拱结构中，由于水平推力的存在，其各截面的弯 矩要比相应简支梁或曲梁小得多，因此它的截面就 可做得小一些，能节省材料、减小自重、加大跨度。 b、在拱结构中，主要内力是轴压力，因此可以用 抗 拉性能比较差而抗压性能比较好的材料来做。 c、由于拱结构会对下部支撑结构产生水平的推力，因 此它需要更坚固的基础或下部结构。同时它的外形 复杂，导致施工比较困难，模板费用也比较大 。
6 三铰拱
一、 概述
拱式结构：指的是在竖向荷载作用下，会产生水 平推力的结构。通常情况下它的杆轴线是曲线的。
如下所示结构在竖向 荷载作用下，水平反力 等于零，因此它不是拱 结构，而是曲梁结构。
下面所示结构在竖向荷 载作用下，会产生水平反 力，因此它是拱结构。
FP FP
曲梁
三铰拱
6 三铰拱
拱结构的应用：主要用于屋架结构、桥梁结构。 拱结构的优缺点：
在研究它的反力、 内力计算时，为了便于 理解，始终与相应的简 支梁作对比。
B
B
三铰拱
a1
a3 a2 FP2 FP1 k yk
0 FYA
L L b1 C f
b3 b2 FP3
1）支座反力的计算
MB 0
FYA
L MA 0
F
Pi i
b
A
xk L1 L2 L FP1 k FP2 C FP3
6 三铰拱
2）弯矩计算 求拱轴线上任意点k的弯矩， 为此取Ak为隔离体：
FP1 k H FYA MK FQk FNk
η
Mk FYA xk FP1 xk a1 Hyk F 3）剪力计算 k M 求拱轴线上任意点k的剪力， F F 同样以Ak为隔离体： 0 FQk FYACosk HSink FP1Cosk
P1 YA Qk
M
k
0
k
FQk F Cosk HSink
0 Qk
FYA FP1 Cosk HSink
相应简支 梁的剪力
6 三铰拱
4）轴力计算 求拱轴线上任意点k的剪力， 同样取Ak为隔离体： H 0
FNk FYASink HCosk FP1Sink
FNC FQC
左
左
求弯矩：
67.5kN m
0 MD MD HyD 105 3 82.5 3
H FYA
6 三铰拱
求剪力： 由于D点处有集中力作用，简支梁的剪力有突变， 因此三铰拱在此处的剪力和轴力都有突变。
MC C H FYA
左 0左 FQD Cos D HSin D FNC FQD 105 0.832 82.5 0.555 41.6kN FQC
FYA FP1 Sink HCosk
0 FNk FQk Sin k HCos k
FP1 k
MK FQk
FNk
η
FYA FP1 k FYA FQk Mk
三铰拱内力计算公式： 0 F F k Qk Qk Cos k HSin 0 M k M k Hyk 0 FNk FQk Sin k HCos k
6 三铰拱
b、求D点的内力 先求计算参数： 4 4 xD 3m yD 2 (12 3) 3 3m 12 dy 4 f 4 4 tg D 2 ( L 2 x) 2 (12 2 3) 0.667
dx L 12
MC C
D 3342'
Cos D 0.832 Sin D 0.555
6 三铰拱
拱各部分的名称：
拱顶
f 拱高
起拱线
拱趾
L
L—跨度（拱趾之间的水平距离）
f—矢高或拱高（两拱趾间的连线到拱顶的竖向距离）
f/L——高跨比（拱的主要性能与它有关，工程中这 个值控制在1—1/10 ）
6 三铰拱
常见的拱式结构有：
三铰拱
带拉杆三铰拱
两铰拱
无铰拱
6 三铰拱
二、三铰拱的内力计算
a1 FP1 k yk A xk L1 L FP1 k A FP2 C FP3 L2 a3 a2 FP2 L L b1 C f FP3 b3 b2
左 左
左 0左 FND FQD Sin D HCos D
105 0.555 82.5 0.832 127kN
6 三铰拱
100kN MC FNC C FQC
右 右
H FYA
右 0右 FQD FQD Cos D HSin D
(105 100) 0.832 82.5 0.555 41.6kN
6 三铰拱
4 f 例1：图示三铰拱的拱轴线方程为：y ( L x) x 2 L 请求出其D点处的内力。
解：a、求反力
100kN C y D 4m B x 3m 3m 6m
20kN/m
M
B
ቤተ መጻሕፍቲ ባይዱ0
FYA (20 6 3 100 9) /12
Y 0
105kN
A
FYB 100 20 6 105 115kN 105 6 100 3 H 82.5kN 4
只有轴力，该拱轴线称为合理拱轴线。
0 M M 已知： k k Hyk
令： M k M k0 Hyk 0
0 y M 有： k k /H
6 三铰拱
例：求图示对三铰拱在均布荷载作用下的合理拱轴线。
B
L 取左半跨为隔离体：
FYB
F
Pi i
a
0 FYB
M
0 A 0 FYA L1 FP1 L1 a1 FP 2 L1 a2 M C H f f
C
B
6 三铰拱
由前面计算可见： 三铰拱的竖向反力与相应简支梁的相同，水平 反力等于相应简支梁C点的弯矩除以拱高f。H与f 成反比，f越小，H越大，f越大，H越小。也就是 说：f越小，拱的特性就越突出。
F
右 ND
F
0右 QD
Sin D HCos D
(105 100) 0.555 82.5 0.832 71.4kN
6 三铰拱
三、三铰拱的合理拱轴 为了充分利用材料的潜力，应设法减小拱截面上 的弯矩，以使其处于均匀受压状态。 最理想的情况是使拱轴上所有截面弯矩均为零，
6 三铰拱
一、 概述
拱式结构：指的是在竖向荷载作用下，会产生水 平推力的结构。通常情况下它的杆轴线是曲线的。
如下所示结构在竖向 荷载作用下，水平反力 等于零，因此它不是拱 结构，而是曲梁结构。
下面所示结构在竖向荷 载作用下，会产生水平反 力，因此它是拱结构。
FP FP
曲梁
三铰拱
6 三铰拱
拱结构的应用：主要用于屋架结构、桥梁结构。 拱结构的优缺点：
在研究它的反力、 内力计算时，为了便于 理解，始终与相应的简 支梁作对比。
B
B
三铰拱
a1
a3 a2 FP2 FP1 k yk
0 FYA
L L b1 C f
b3 b2 FP3
1）支座反力的计算
MB 0
FYA
L MA 0
F
Pi i
b
A
xk L1 L2 L FP1 k FP2 C FP3
6 三铰拱
2）弯矩计算 求拱轴线上任意点k的弯矩， 为此取Ak为隔离体：
FP1 k H FYA MK FQk FNk
η
Mk FYA xk FP1 xk a1 Hyk F 3）剪力计算 k M 求拱轴线上任意点k的剪力， F F 同样以Ak为隔离体： 0 FQk FYACosk HSink FP1Cosk
P1 YA Qk
M
k
0
k
FQk F Cosk HSink
0 Qk
FYA FP1 Cosk HSink
相应简支 梁的剪力
6 三铰拱
4）轴力计算 求拱轴线上任意点k的剪力， 同样取Ak为隔离体： H 0
FNk FYASink HCosk FP1Sink
FNC FQC
左
左
求弯矩：
67.5kN m
0 MD MD HyD 105 3 82.5 3
H FYA
6 三铰拱
求剪力： 由于D点处有集中力作用，简支梁的剪力有突变， 因此三铰拱在此处的剪力和轴力都有突变。
MC C H FYA
左 0左 FQD Cos D HSin D FNC FQD 105 0.832 82.5 0.555 41.6kN FQC
FYA FP1 Sink HCosk
0 FNk FQk Sin k HCos k
FP1 k
MK FQk
FNk
η
FYA FP1 k FYA FQk Mk
三铰拱内力计算公式： 0 F F k Qk Qk Cos k HSin 0 M k M k Hyk 0 FNk FQk Sin k HCos k
6 三铰拱
b、求D点的内力 先求计算参数： 4 4 xD 3m yD 2 (12 3) 3 3m 12 dy 4 f 4 4 tg D 2 ( L 2 x) 2 (12 2 3) 0.667
dx L 12
MC C
D 3342'
Cos D 0.832 Sin D 0.555
6 三铰拱
拱各部分的名称：
拱顶
f 拱高
起拱线
拱趾
L
L—跨度（拱趾之间的水平距离）
f—矢高或拱高（两拱趾间的连线到拱顶的竖向距离）
f/L——高跨比（拱的主要性能与它有关，工程中这 个值控制在1—1/10 ）
6 三铰拱
常见的拱式结构有：
三铰拱
带拉杆三铰拱
两铰拱
无铰拱
6 三铰拱
二、三铰拱的内力计算
a1 FP1 k yk A xk L1 L FP1 k A FP2 C FP3 L2 a3 a2 FP2 L L b1 C f FP3 b3 b2
左 左
左 0左 FND FQD Sin D HCos D
105 0.555 82.5 0.832 127kN
6 三铰拱
100kN MC FNC C FQC
右 右
H FYA
右 0右 FQD FQD Cos D HSin D
(105 100) 0.832 82.5 0.555 41.6kN
6 三铰拱
4 f 例1：图示三铰拱的拱轴线方程为：y ( L x) x 2 L 请求出其D点处的内力。
解：a、求反力
100kN C y D 4m B x 3m 3m 6m
20kN/m
M
B
ቤተ መጻሕፍቲ ባይዱ0
FYA (20 6 3 100 9) /12
Y 0
105kN
A
FYB 100 20 6 105 115kN 105 6 100 3 H 82.5kN 4
只有轴力，该拱轴线称为合理拱轴线。
0 M M 已知： k k Hyk
令： M k M k0 Hyk 0
0 y M 有： k k /H
6 三铰拱
例：求图示对三铰拱在均布荷载作用下的合理拱轴线。
B
L 取左半跨为隔离体：
FYB
F
Pi i
a
0 FYB
M
0 A 0 FYA L1 FP1 L1 a1 FP 2 L1 a2 M C H f f
C
B
6 三铰拱
由前面计算可见： 三铰拱的竖向反力与相应简支梁的相同，水平 反力等于相应简支梁C点的弯矩除以拱高f。H与f 成反比，f越小，H越大，f越大，H越小。也就是 说：f越小，拱的特性就越突出。
F
右 ND
F
0右 QD
Sin D HCos D
(105 100) 0.555 82.5 0.832 71.4kN
6 三铰拱
三、三铰拱的合理拱轴 为了充分利用材料的潜力，应设法减小拱截面上 的弯矩，以使其处于均匀受压状态。 最理想的情况是使拱轴上所有截面弯矩均为零，