20180121二次函数压轴题专题一 面积问题
【中考压轴】二次函数背景下的面积问题,一道题全讲明白,你能拿下吗?

【中考压轴】二次函数背景下的面积问题,一道题全讲明白,
你能拿下吗?
中考压轴题难,欢迎入群
压轴题拿不到满分?那是你没掌握方法
解题没有思路?那是没有经历学习
海量精品学习资料下载,尽在会员群
视频+文档资料更新不断,永久有效.
二次函数压轴之面积问题
面积问题涵盖的题型
1.面积最值问题
2.面积倍分关系问题
3.面积比例及最值问题
经典题解析与方法分析
抛物线y=x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y 轴交于点C,直线y=kx-3,经过点B,C.
(1)求抛物线的解析式
(2)点P是直线BC下方抛物线上一动点,求PBC面积最大时点P 的坐标;
分析:坐标系背景下的面积问题,主要涉及的方法是面积的求解方法,一般是铅垂法、割补法、平移法,一般铅垂法是通用方法,在解决一些复杂问题时非常实用.
方法简介:铅垂法,一般是求解三角形面积时,找到水平宽和与之对应的铅垂高,其乘积的一增即为三角形的面积.
方法一:铅垂法
点评:设点,再分别求水平宽和铅垂高的表达式,从而得到三角形面积的表达式,通过二次函数的性质求得取最值时的P点坐标方法二:平移法
点评:通过平移至临界位置,面积即可求最值,思路与前面比较新颖,且解决方法比较快捷;
方法三:割补法
点评:割补法思考起来难度不大,但是计算需要一定的耐心,对同学们的计算能力有一定的要求;。
专题01 二次函数压轴题-线段周长面积最大值(专项训练)(解析版)

专题01 线段周长面积最大值(专项训练)1.(2022春•丰城市校级期末)如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.求线段PM的最大值;【解答】解:(1)将A,B,C代入函数解析式得,,解得,∴这个二次函数的表达式y=x2﹣2x﹣3;(2)①设BC的解析式为y=kx+b,将B,C的坐标代入函数解析式得,,解得,∴BC的解析式为y=x﹣3,设M(n,n﹣3),P(n,n2﹣2n﹣3),PM=(n﹣3)﹣(n2﹣2n﹣3)=﹣n2+3n=﹣(n﹣)2+,当n=时,PM最大=,∴线段PM的最大值;2.(2022•玉州区一模)如图,抛物线y=﹣x2x+4交x轴于A,B两点(点B在A的右边),与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P 的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.(1)求A、B两点坐标;(2)过点P作PN上BC,垂足为点N,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?【解答】解:(1)当y=0,﹣x2+x+4=0,解得x1=﹣3,x2=4,∴A(﹣3,0),B(4,0),(2)设点P(m,﹣m2+m+4),则点Q(m,﹣m+4),∵OB=OC,∴∠ABC=∠OCB=45°=∠PQN,P~N=PQ•sin∠PQN=(﹣m2+m+4+m﹣4)=﹣(m﹣2)2+,∵﹣<0,∴PN有最大值,当m=2时,PN的最大值为.3.(2022•怀化)如图一所示,在平面直角坐标中,抛物线y=ax2+2x+c经过点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为点D.在线段CB上方的抛物线上有一动点P,过点P作PE⊥BC于点E,作PF∥AB交BC于点F.(1)求抛物线和直线BC的函数表达式.(2)当△PEF的周长为最大值时,求点P的坐标和△PEF的周长.【解答】解:(1)∵抛物线y=ax2+2x+c经过点A(﹣1,0)、B(3,0),∴,解得,∴抛物线的解析式为y=﹣x2+2x+3,令x=0,可得y=3,∴C(0,3),设直线BC的解析式为y=kx+b,则,∴,∴直线BC的解析式为y=﹣x+3;(2)如图一中,连接PC,OP,PB.设P(m,﹣m2+2m+3),∵B(3,0),C(0,3),∴OB=OC=3,∴∠OBC=45°,∵PF∥AB,∴∠PFE=∠OBC=45°,∵PE⊥BC,∴△PEF是等腰直角三角形,∴PE的值最大时,△PEF的周长最大,∵S△PBC=S△POB+S△POC﹣S△OBC=×3×(﹣m2+2m+3)+×3×m﹣×3×3=﹣m2+m=﹣(m﹣)2+,∵﹣<0,∴m=时,△PBC的面积最大,面积的最大值为,此时PE的值最大,∵×3×PE=,∴PE=,∴△PEF的周长的最大值=++=+,此时P(,);4.(2022•黄冈模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交点为A(﹣4,0)、B(1,0),与y轴交于点C,P为抛物线上一点,过点P作PD⊥AC于D.(1)求抛物线的解析式;(2)如图1,若P在直线AC上方,PE⊥x轴于E,交AC于F.①求sin∠PFD的值;②求线段PD的最大值.【解答】解:(1)∵抛物线y=ax2+bx+2与x轴交点为A(﹣4,0)、B(1,0),与y 轴交于点C,令x=0,则c=2,∴C(0.2),设抛物线的解析式为y=a(x+4)(x﹣1),将点(0,2)代入得,2=﹣4a,解得:a=﹣,∴y=﹣(x+4)(x﹣1)=﹣x2﹣x+2,∴抛物线的解析式为y=﹣x2﹣x+2;(2)①∵PE⊥x轴,∴∠AFE=∠ACO,又∵∠PFD=∠AFE,∴∠PFD=∠ACO,∴sin∠PFD=sin∠ACO=,∵A(﹣4,0),C(0,2),∴AO=4,OC=2,∴AC==2.∴sin∠PFD=sin∠ACO===;②设过A(﹣4,0)C(0,2)的直线解析式为y=kx+b,则,解得:,∴直线AC解析式为y=x+2,设P(m,﹣m2﹣m+2),则F(m,m+2),∴PF=﹣﹣m+2﹣m﹣2=﹣m2﹣2m=﹣(m+2)2+2,∴当m=﹣2时,PF有最大值2,∵PD=PF•sin∠PFD,∴PF取最大值时,PD取最大值,∴PD最大值为×2=;5.(2022•齐齐哈尔模拟)综合与探究如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,对称轴与x轴交于点D,点P是直线BC上方抛物线上一点.(1)求抛物线的解析式;(2)在直线BC上方的抛物线上找一点P,作PG⊥BC,求线段PG的最大值;【解答】解:(1)将点A(﹣1,0),B(3,0)代入y=ax2+bx+3,∴,解得,∴y=﹣x2+2x+3;(2)如图1,过P点作PH∥y轴交BC于点H,令x=0,则y=3,∴C(0,3),设直线BC的解析式为y=kx+b,∴,解得,∴y=﹣x+3,设P(t,﹣t2+2t+3),则H(t,﹣t+3),∴PH=﹣t2+3t,∵C(0,3),B(3,0),∴BC=3,∴S△PBC=×BC×PG=×BO×PH,∴PG×3=3(﹣t2+3t),∴PG=﹣(t﹣)+,∵点P是直线BC上方抛物线上,∴0<t<3,∴当t=时,PG有最大值;6.(2022•习水县模拟)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,C 两点(点A在点C的左侧),与y轴交于点B,且C(1,0),OA=OB=3.(1)求二次函数的解析式;(2)若点P是抛物线位于第二象限上的点,过点P作PQ∥y轴,交直线AB于点Q,交x轴于点H,过点P作PD⊥AB于点D.求线段PD的最大值;【解答】解:(1)∵OA=OB=3,∴A(﹣3,0),B(0,3),∵C(1,0),∴,∴,∴二次函数的解析式为y=﹣x2﹣2x+3;(2)①∵OA=OB,∠AOB=90°,∴∠ABO=∠BAO=45°,∵PQ∥y轴,∴PH⊥OA,∴∠QHA=90°,∴∠PQD=∠AQH=45°,∴△PQD是等腰直角三角形,∴PD=PQ,∴当PQ取得最大值时,PD的值最大,设AB的解析式为y=kx+n,∴,∴,∴y=x+3,设P(m,﹣m2﹣2m+3),∵PQ∥y轴,∴Q(m,m+3),∴PQ=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+,∴m=﹣时,PQ最长为,∴线段PD的最大值为7.(2022•覃塘区三模)如图,已知抛物线y=x2+bx+c经过点A(0,﹣1)和点B(5,4),P是直线AB下方抛物线上的一个动点,PC∥y轴与AB交于点C,PD⊥AB于点D,连接P A.(1)求抛物线的表达式;(2)当△PCD的周长取得最大值时,求点P的坐标和△PCD周长的最大值;【解答】解:(1)由题意得:,解得:,则抛物线的表达式为:y=x2﹣4x﹣1;(2)设直线AB的表达式为:y=kx+a(k≠0),∵A(0,﹣1),B(5,4),∴,解得:,∴直线AB的表达式为:y=x﹣1,设直线AB交x轴于点M,当y=0时,x=1,∵OA=OM=1,∵∠AOM=90°,∴∠OAB=45°,∵CP∥y轴,∴∠DCP=∠OAB=45°,∵PD⊥AB,∴△PCD是等腰直角三角形,即CD=PD,∴PC==CD,即CD=PD=PC,∴△PCD的周长为:PC+PD+CD=(+1)PC,设点P的坐标为(x,x2﹣4x﹣1),则点C的坐标为(x,x﹣1),∴(+1)PC=(+1)[(x﹣1)﹣(x2﹣4x﹣1)]=﹣(+1)[(x﹣)2﹣],∵﹣(+1)<0,∴当x=时,△PCD周长取得最大值,最大值为(+1),此时点P的坐标为(,﹣);8.(2022•大同三模)综合与实践如图,二次函数y=x2﹣x﹣3的图象与x轴交于点A和B,点A在点B的左侧,与y轴交于点C.(1)求直线BC的函数解析式;(2)如图2,点D在直线BC下方的抛物线上运动,过点D作DM∥y轴交BC于点M,作DN⊥BC于点N,当△DMN的周长最大时,求点D的坐标及△DMN周长的最大值;【解答】解:(1)由抛物线y=x2﹣x﹣3,x=0时,y=﹣3,∴C(0,﹣3),y=0时,x2﹣x﹣3=0,解得x1=﹣3,x2=4,∴A(﹣3,0),B(4,0),设直线BC的解析式为y=kx+b(k≠0),将B(4,0),C(0,﹣3)代入,,解得,∴直线BC的解析式为y=x﹣3;(2)∵DM∥y轴,∴∠OCB=∠CMD,∵B(4,0),C(0,﹣3),∴BC=,∵sin∠OCB=,cos∠OCB=,DN⊥BC,∴sin∠DMN=,cos∠DMN=,∴DN=,MN=,设△DMN的周长为L,∴L=DM+DN+MN=,设D(x,x2﹣x﹣3),则M(x,),∴DM==,∴L=,即L=﹣,∵开口向下,∴顶点(2,)最高,∴x=2时,,∴,∴D(2,﹣),∴△DMN的周长最大时,D点的坐标(2,﹣),△DMN的周长最大值为;9.(2022春•浦江县期末)如图,已知二次函数图象的顶点坐标为A(1,9),与坐标轴交于B、C、D三点,且B点的坐标为(﹣2,0).(1)求二次函数的解析式;(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;【解答】解:(1)设抛物线的解析式为y=a(x﹣1)2+9,将点B(﹣2,0)代入,∴9a+9=0,∴a=﹣1,∴y=﹣(x﹣1)2+9=﹣x2+2x+8;(2)设M(m,﹣m2+2m+8),则N(2﹣m,﹣m2+2m+8),∴MN=2m﹣2,MG=﹣m2+2m+8,∴矩形MNHG的周长=2(MN+MG)=2(﹣m2+4m+6)=﹣2(m﹣2)2+20,∴当m=2时,矩形MNHG的周长有最大值20;10.(娄底)如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.【答案】(1):y=x2﹣2x﹣3 (2)①﹣m2+m+3②【解答】解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设点P(m,m2﹣2m﹣3),①当点P在第三象限时,设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S△POD=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,②当点P在第四象限时,设PD交y轴于点M,同理可得:S△POD=×OM(x D﹣x P)=﹣m2+m+3,综上,S△POD=﹣m2+m+3,∵﹣1<0,故S△POD有最大值,当m=时,其最大值为;11.(2022春•青秀区校级期末)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y 轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),抛物线的对称轴与AB 交于点M.(1)求二次函数的解析式;(2)若点P是直线AB上方抛物线上的一动点,连接PB,PM,求△PMB面积的最大值;【解答】解:(1)∵点A(0,5),B(5,0)在抛物线y=﹣x2+bx+c上,∴,∴,∴二次函数的解析式为y=﹣x2+4x+5;(2)如图,∵A(0,5),B(5,0),∴直线AB的解析式为y=﹣x+5,∵点M是抛物线的对称轴与直线AB的交点,∴M(2,3),由(1)知,二次函数的解析式为y=﹣x2+4x+5,过点P作PH∥y轴交AB于H,设P(m,﹣m2+4m+5)(0<m<5),∴H(m,﹣m+5),∴PH=﹣m2+4m+5﹣(﹣m+5)=﹣m2+5m,∴S△PMB=PH(x B﹣x M)=(﹣m2+5m)(5﹣2)=﹣(x﹣)2+,∴当x=时,S△PMB最大=,即△PMB面积的最大值为;12.直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,与抛物线y=ax2﹣2ax+a+4(a <0)交于点B,如图所示.(1)求该抛物线的解析式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,四边形OAMB的面积为S,求S与m的函数表达式,并求出S的最大值;【解答】解:(1)∵直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,∴A(1,0)、B(0,3);∵抛物线y=ax2﹣2ax+a+4(a<0)经过点B,∴a+4=3,∴a=﹣1,∴该抛物线的解析式为y=﹣x2+2x+3;(2)过点M作MH⊥x轴于点H,如图所示:设点M(m,﹣m2+2m+3),则S=S梯形BOHM﹣S△AMH=(3﹣m2+2m+3)×m﹣(m﹣1)×(﹣m2+2m+3)=﹣m2+m+,∵﹣<0,∴S有最大值,当m=时,S的最大值是.∴S与m的函数表达式为S=﹣m2+m+,S的最大值是;。
中考数学压轴题:二次函数中的面积问题(含答案)

学生/课程年级日期学科时段课型数学授课教师核心内容二次函数中求面积最值,图形平移或折叠面积问题1.会利用函数的图象性质来研究几何图形的面积最值问题;教学目标重、难点2.掌握几种求图形面积的常见解题方法与技巧,如:割补法、平行等积变换法等。
3.掌握图形平移或折叠变换过程中找等量关系列函数解析式求图形面积问题的一般方法.割补法求三角形面积,动态问题一般解题思路。
了解学生的学习情况S△ = a h或S△ = a d (d表示已知点到直线的距离)以动点作垂直(平行)x轴的直线,即铅垂高,再分别过点A,C作PF的高,即和为水平宽。
S△ = ×水平宽×铅垂高如下图:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.如图,AD∥BC中,AC与BD交点O,则S△ABC = S△DBC,S△AOB = S△COD2如图,在平面直角坐标系中,抛物线y=mx -8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x ,10),C(x ,0),且x -x =4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线,直线AD2 2 1的交点分别为P,Q.(1)求抛物线的解析式;(2)当0<t≤8时,求△APC面积的最大值.图形面积的求法常见有三种,分别是:(1)_______________________________(2)_______________________________(3)_______________________________[学有所获答案] (1)直接公式求法 割补法 平行线等积变换法(2)(3) 2 如图,已知抛物线y =x +bx +c 与 轴交于A ,B 两点(点A 在点B 的左侧)与 轴交于点C (0,-3),对称轴是直线x=1,直线BC 与抛物线的对称轴交于点D ,点E 为y 轴上一动点,CE 的垂直平分线交抛物线于P ,Q 两点(点P 在第三象限)(1)求抛物线的函数表达式和直线BC 的函数表达式;(2)当△CDE 是直角三角形,且∠CDE =90°时,求出点P 的坐标;(3)当△PBC 的面积为 时,求点E 的坐标.2 如图,已知抛物线y = x +ax +4a 与x 轴交于点A ,B ,与y 轴负半轴交于点C 且OB =OC ,点P 为抛物线上的一个动点,且点P 位于x 轴下方,点P 与点C 不重合.(1)求该抛物线的解析式;(2)若△PAC 的面积为 ,求点P 的坐标;(3)若以A ,B ,C ,P 为顶点的四边形面积记作S ,则S 取何值时,对应的点P 有且只有2个?将()的图像如何平移到的图像。
中考压轴复习:二次函数中的面积问题

二次函数中的面积问题一、运用∣y ∣.1. 已知二次函数y=-x 2+2x+3的图像分别交x 轴、y 轴于A 、B 、C 三点.(1)若D 为抛物线上的一动点(点D 与点C 不重合),且S △ABD =S △ABC ;求点D 的坐标.(2)点N 为直线BC 上方的二次函数图象上的一个动点(点N 与B 、C 不重合),过点N 作y 轴的平行线交BC 于点F.若点N 的横坐标为m ,请你表示出△NBC面积,并求出△NBC 面积的最大值.二、运用s=21(水平宽⨯铅垂高) 2. 如图,抛物线213222y x x =--的图象与x 轴交于A 、B 两点,与y 轴交于C 点.若点M 是线段BC 下方的抛物线上一点,求△MBC 的面积的最大值,并求出此时M 点的坐标.三、运用相似3.(广东)如图,抛物线213y=x x 922--与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC 、AC .(1)求AB 和OC 的长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作直线l 平行BC ,交AC 于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围;(3)在(2)的条件下,连接CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π).四、运用分割方法1.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C 其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.2.将直角边长为6的等腰Rt △AOC 放在如图所示的平面直角坐标系中,点O 为坐标原点,点C 、A 分别在x 、y 轴的正半轴上,一条抛物线经过点A 、C 及点B (–3,0).(1)求该抛物线的解析式;(2)若点P 是线段BC 上一动点,过点P 作AB 的平行线交AC 于点E ,连接AP ,当△APE 的面积最大时,求点P 的坐标;(3)在第一象限内的该抛物线上是否存在点G ,使△AGC 的面积与(2)中△APE 的最大面积相等?若存在,请求出点G 的坐标;若不存在,请说明理由.3.如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .x(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.4.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C 其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.五、运用等积变形 4.(湖北十堰)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . A Cx y B OA B O P Mx y3 -3 2 -2 (1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.5.如图,在平面直角坐标系中,抛物线y =x 2+mx +n 经过点A (3,0)、B (0,-3),点P 是直线AB上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t .(1)分别求出直线AB 和这条抛物线的解析式. (2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.6. (浙江义乌市) 如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.7.【恩施】如图,已知抛物线y=﹣x2+bx+c 与一直线相交于A (﹣1,0),C (2,3)两点,与y 轴交于点N .其顶点为D .(1)抛物线及直线AC 的函数关系式;(2)设点M (3,m ),求使MN+MD 的值最小时m 的值; A(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.8.(宁波)如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E,(1)求点E的坐标(2)求抛物线的函数解析式(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连结ON、BN,当点F在线段OB上运动时,求⊿BON面积的最大值,并求出此时点N的坐标(4)连结AN,当⊿BON面积最大时,在坐标平面内求使得⊿BOP与⊿OAN相似(点B、O、P分别与点O、A、N对应)的点P的坐标。
二次函数中的面积问题
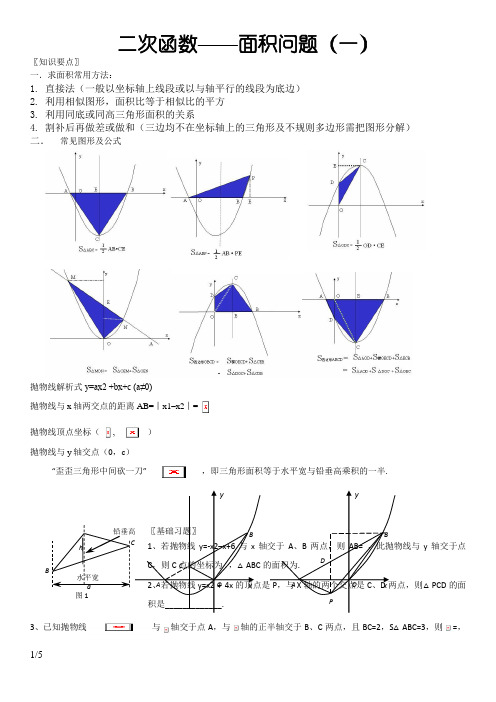
二次函数——面积问题(一)〖知识要点〗一.求面积常用方法:1. 直接法(一般以坐标轴上线段或以与轴平行的线段为底边)2. 利用相似图形,面积比等于相似比的平方3. 利用同底或同高三角形面积的关系4. 割补后再做差或做和(三边均不在坐标轴上的三角形及不规则多边形需把图形分解) 二. 常见图形及公式抛物线解析式y=ax2 +bx+c (a≠0)抛物线与x 轴两交点的距离AB=︱x1–x2︱=抛物线顶点坐标(-, ) 抛物线与y 轴交点(0,c )“歪歪三角形中间砍一刀”,即三角形面积等于水平宽与铅垂高乘积的一半. 〖基础习题〗 1、若抛物线y=-x2–x+6与x 轴交于A 、B 两点,则AB= ,此抛物线与y 轴交于点C ,则C 点的坐标为 ,△ABC 的面积为.2、若抛物线y=x2 + 4x 的顶点是P ,与X 轴的两个交点是C 、D 两点,则△PCD 的面积是_____________.3、已知抛物线与轴交于点A ,与轴的正半轴交于B 、C 两点,且BC=2,S △ABC=3,则=,B C 铅垂高水平宽ha图1 C BA O y x DB A O y x P=.〖典型例题〗● 面积最大问题1、二次函数的图像与轴交于点A (-1,0)、B (3,0),与轴交于点C ,∠ACB=90°.(1)求二次函数的解析式;(2)P 为抛物线X 轴上方一点,若使得△PAB 面积最大,求P 坐标(3)P 为抛物线X 轴上方一点,若使得四边形PABC 面积最大,求P 坐标(4) P 为抛物线上一点,若使得,求P 点坐标。
● 同高情况下,面积比=底边之比2.已知:如图,直线y=﹣x+3与x 轴、y 轴分别交于B 、C ,抛物线y=﹣x2+bx+c 经过点B 、C ,点A 是抛物线与x 轴的另一个交点.(1)求B 、C 两点的坐标和抛物线的解析式;(2)若点P 在直线BC 上,且,求点P 的坐标.3.已知:m 、n 是方程x2﹣6x+5=0的两个实数根,且m <n ,抛物线y=﹣x2+bx+c 的图象经过点A (m ,0)、B (0,n ).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x 轴的另一交点为C ,抛物线的顶点为D ,试求出点C 、D 的坐标和△BCD 的面积;(注:抛物线y=ax2+bx+c (a≠0)的顶点坐标为(3)P 是线段OC 上的一点,过点P 作PH ⊥x 轴,与抛物线交于H 点,若直线BC 把△PCH 分成面积之比为2:3的两部分,请求出P 点的坐标. yx B A C O三角形面积等于水平宽与铅垂高乘积的一半4.阅读材料:如图,过△ABC的三个顶点分别作出水平垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可以得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图,抛物线顶点坐标为点C(1,4)交x轴于点A,交y轴于点B(0,3)(1)求抛物线解析式和线段AB的长度;(2)点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;(3)在第一象限内抛物线上求一点P,使S△PAB=S△CAB.法一:同底情况下,面积相等转化成平行线法二:同底情况下,面积相等转化成铅垂高相等变式一:如图2,点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.变式二:抛物线上是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明点动+面积5.如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC.(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.形动+面积6.如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.(1)试求抛物线的解析式;(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?。
2018年二次函数压轴题复习专题1:线段、面积最值问题 含简单答案、解题思路与详细解答

1.二次函数压轴题专题1:线段、面积最值问题一种用坐标表示三角形面积的重要方法:铅锤法三角形的面积=1/2*垂线上两点纵坐标之差*斜线上两点横坐标之差(*表示相乘)例1:如图2,A是抛物线y=﹣x2﹣2x+3与X轴的左交点,D是此抛物线的顶点。
F是此抛物线上A、D之间的一动点,其横坐标为x,如何用x的代数式表示△ADF的面积为S?例2:如图3,B、C分别是抛物线y=﹣x2﹣2x+3与X轴的右交点、与Y轴的交点。
F是此抛物线上对称轴左侧的一动点,其横坐标为x,如何用x的代数式表示△FBC的面积为S?E斜线:过两定点(如左图中的点A和点D;右图中的点B和点C)作斜线铅垂线:过抛物线上一动点(如点F)作X轴的垂线,与斜线(或其延长线)相交(左图交于E、右图交于Q)优先考虑作斜线:过两已知点作斜线,这样容易求出斜线的解析式△AFD(或右图中△BFC)的面积=1/2*铅垂线上两点纵坐标之差)*斜线上两点横坐标之差垂线上的两点:第1点就是作垂线时的起点(往往是抛物线上的一动点,如左、右图中的点F)第2点是垂线与斜线(或其延长线)的交点(如左图中的点E,右图中的点Q)左图:S△FAD=S△FAE +S△FDE 右图:S△BFC=S△FBQ -S△FCQ=FE•(左边△的高+右边△的高)=FQ•(△FBQ的高-△FCQ的高)=FE•(D的横坐标-A的横坐标) =FQ•(B的横坐标-C的横坐标)1.周长最小,面积最大例1如图1,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值及点P的坐标。
;(3)如图(2),若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.E例1(拓展).(2015•深圳)如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D 为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.例3已知某二次函数的图象与x 轴分别相交于点()30A -,和点()10B ,,与y 轴相交于点()()030C m m ->,,顶点为点D 。
中考数学压轴题专题汇编01 二次函数中因动点产生的三角形面积问题 (解析版)
1 x 1 与抛物线 y=ax2+bx-3 交于 A、B 两点,点 A 在 x 2
轴上,点 B 的纵坐标为 3.点 P 是直线 AB 下方的抛物线上的一动点(不与点 A、B 重合) ,过点 P 作 x 轴 的垂线交直线 AB 于点 C,作 PD⊥AB 于点 D. (1)求 a、b 及 sin∠ACP 的值; (2)设点 P 的横坐标为 m. ①用含 m 的代数式表示线段 PD 的长,并求出线段 PD 长的最大值;
的左侧) ,与 y 轴的负半轴交于点 C,点 A 的坐标为(-1,0). (1)b=___பைடு நூலகம்__,点 B 的横坐标为_______(上述结果均用含 c 的代数式表示) ; (2)连结 BC,过点 A 作直线 AE//BC,与抛物线交于点 E.点 D 是 x 轴上一点,坐标为(2,0),当 C、 D、E 三点在同一直线上时,求抛物线的解析式; (3)在(2)的条件下,点 P 是 x 轴下方的抛物线上的一动点,连结 PB、PC.设△PBC 的面积为 S. ①求 S 的取值范围; ②若△PBC 的面积 S 为正整数,则这样的△PBC 共有_____个.
顶点坐标为 ( , ) .
3 25 2 8
考点伸展
第(2)题 S△MFQ∶S△MEB=1∶3,何需点 M 一定要在抛物线上? 从上面的解题过程可以看到,△MFQ 与△MEB 的高的比
FQ m 与 n 无关,两条底边的比 = MN 4 m
MQ m 也与 n 无关. = ME 3 2m
如图 3,因此只要点 E 与点 M 关于直线 x=
思路点拨
1.用 c 表示 b 以后,把抛物线的一般式改写为两点式,会发现 OB=2OC. 2.当 C、D、E 三点共线时,△EHA∽△COB,△EHD∽△COD. 3.求△PBC 面积的取值范围,要分两种情况计算,P 在 BC 上方或下方.
二次函数专题一:面积问题-含答案
专题一:二次函数中的面积问题(一)利用割补:将图形割(补)成三角形或梯形面积的和差,其中需使三角形的底边在坐标轴上或平行于坐标轴;(例如以下4、5两图中,连结BD 解法不简便。
)例1:如图抛物线与轴交于两点,与轴交于点, (1)k=___-3_____,点的坐标为___(-1,0)___,点的坐标为____(3,0)____; (2)设抛物线的顶点为,求的面积;(3)在轴下方的抛物线上是否存在一点,使四边形的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由;解:(2)M (1,-4);(3)设,,当m =52时,四边形ABDC 面积最大,为52。
练习1、如图,抛物线与轴交于A 、B 两点,与轴交于点C ,抛物线的对称轴交轴于点D ,已知A (﹣1,0),C (0,2). (1)求抛物线的表达式;(2)点E 是线段BC 上的一个动点,过点E 作轴的垂线与抛物线相交于点F ,当点E 运动到什么位置时,四边形CDBF 的面积最大?求出四边形CDBF 的最大面积及此时E 点的坐标.解:(1)y =-12x 2+32x +2(2)对称轴x =-b 2a =32,\D (32,0), 令-12x 2+32x +2=0,x 1=-1,x 2=4,\B (4,0) ,设F (a ,-12a 2+32a +2),y =x 2-2x +k x A ,B y C (0,-3)A B M D BCM x D ABDC S D BCM =S D OCM +S D BOM -S D BOC =12´3´1+12´3´4-12´3´3=3D (m ,m 2-2m -3) S 四边形ABDC =S D AOC +S D BOD +S D COD=12´1´3+12´|m 2-2m -3|´3+12´m ´3=-12m 2+52m +3-b 2a =-522´(-12)=52,0<m <3y =-12x 2+mx +n x y xxS四边形CDBF =SD COF+SD BOF-SD COD=12´2´a+12´4´(-12a2+32a+2)-12´2´32=-a2+4a+52∵-42´(-1)=2,0<a<4,-1<0,\当a=2时,S四边形CDBF最大,为132此时,直线BC解析式可求得y=-12x+2,\E(2,1)练习2:已知:抛物线的顶点坐标为C(1,4),抛物线交x轴于点A,交y轴于点B(0,3).点P是在第一象限内的抛物线上的一个动点,过点P作y轴的平行线,交AB于点D.是否存在点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.解:设抛物线解析式为y=a(x-1)2+4,将B(0,3)代入得a=-1\y=-(x-1)2+4=-x2+2x+3,令y=0得x1=-1,x2=3,\A(3,0)连结OC,SD ABC =SD CBO+SD ACO-SD ABO=3,\SD PAB=54×SD ABC=54´3=154设P(m,-m2+2m+3),连结OP、BP,SD PAB =SD BPO+SD APO-SD AOB=12´3´m+12´3´(-m2+2m+3)-12´3´3=-32m2+92m-32m2+92m=154,整理得2m2-6m+0,D=(-6)2-4´2´5=-4<0,所以不存在这样的点P。
2018-2019中考数学专题训练:面积问题(15道).docx
题库:二次函数压轴题- 面积问题1.已知:二次函数 y=- x2-2x+M 的图象与 x 轴交于点 A(1,0)、B,与 y 轴交于点 C.(1)求 M 的值;(2)求点 B 的坐标;(3)若该二次函数图象上有一点 P(不与点 C 重合 ),满足 S△ABP= S△ABC,求点 P 的坐标.第 1 题图2 解: (1)将点 A(1,0)代入 y=- x -2x+M 中,得- 1-2+M=0,(2)由(1)知 y=- x2-2x+3,令 y=0,则- x2-2x+ 3=0,解得 x1=1,x2=- 3,∵A(1,0),∴B(-3,0);(3)①当点 P 在 x 轴上方时,∵S△ABP=S△ABC,且点 P 不与点 C 重合,∴点 C 和点 P 关于二次函数图象的对称轴对称,由二次函数的解析式可知,对称轴为直线 x=- 1,∵C(0,3),∴P(-2,3);②当点 P 在 x 轴下方时,∵△ ABP 与△ABC 的底边均为 AB,∴△ ABP 的边 AB 上的高应等于 OC,即此时点 P 的纵坐标 y=- 3,即- 3=- x2-2x+3,2整理得 x +2x-6=0,∴点 P 的坐标为 (-1+7,- 3)或(-1-7,- 3).综上,当 S△ABP=S△ABC时,点 P 的坐标为 (-2,3)或(-1+7,-3)或(-1-7,- 3).2.如图,抛物线 y=Ax2+2x+C 经过点 A(0,3),B(-1,0).(1)求抛物线的表达式;(2)抛物线的顶点为D,对称轴与x 轴交于点 E,连接 BD,求 BD 的长;(3)在抛物线的对称轴上是否存在点 M,使得△MBC 的面积是 4,若存在,请求出点 M 的坐标;若不存在,请说明理由.第 2 题图解: (1)∵抛物线 y=Ax2+2x+ C 经过点 A(0,3),B(-1,0),a-2+c=0∴,c=3a=- 1解得,c=3∴抛物线的表达式为y=- x2+2x+3;(2)∵抛物线的顶点为D,对称轴与 x 轴交于点 E,y=- x2+2x+3=- (x-1)2+4,B(-1,0),∴点 D 的坐标是 (1,4),点 E 的坐标是 (1,0),∴D E=4,BE=2,∴B D= DE2+BE2= 42+22= 20=2 5,∴B D 的长是 2 5;(3)在抛物线的对称轴上存在点 M ,使得 △MBC 的面积是 4. 设点 M 的坐标为 (1,M),2令- x +2x +3=0 得 x =- 1 或 3,∴ B C =3- (-1)=4,∵△ MBC 的面积是 4,BC ×|m|4×|m|∴S △ BCM =2=2=4,解得 M =±2,∴点 M 的坐标为 (1,2)或(1,-2).3.如图,抛物线 y =21x 2-32x -2 与 x 轴交于 A ,B 两点,与 y 轴交于点 C ,点 D 与点 C 关于 x 轴对称.(1)求点 A 、B 、C 的坐标;(2)求直线 BD 的解析式;(3)在直线 BD 下方的抛物线上是否存在一点P ,使△PBD 的面积最大?若存在,求出点 P 的坐标;若不存在,请说明理由.第 3 题图1 23解: (1)令 y=0,则2x -2x-2=0,解得 x1=- 1,x2=4,∴A(-1,0),B(4,0),令x=0,得 y=- 2,∴C(0,- 2);(2)∵C,D 两点关于 x 轴对称,∴D(0,2),设直线 BD 的解析式为 y=kx+b(k≠ 0),4k b=0将 B、D 坐标代入可得,b=2解得 k=-12 ,b=21∴直线 BD 的解析式为 y=-2x+2;(3)存在这样的点 P,使得△PBD 的面积最大.23设P(m,2m -2m-2),1如解图,过点 P 作 PE⊥x 轴于点 F,与 BD 交于点 E,第 3 题解图1则 E 点坐标为 (m,-2m+2),∴PE=(-112312+m+4,2m+2)-(2m -2m-2)=-2m∴S△ PBD=S△ PDE+S△PEB11=2PE·OF+2PE·BF1=2PE·OB112×4=2×(-2m +m+4)=- m2+2m+8=- (m-1)2+9,当 m=1 时, S△PBD取得最大值,最大值为9,1 23此时2m -2m-2=- 3,∴P(1,- 3).4. 如图,在平面直角坐标系xOy 中,已知二次函数y=Ax2+2Ax+C 的图象与 y 轴交于点 C(0, 3),与 x 轴交于 A、B 两点,点 B 的坐标为 (-3,0).(1)求二次函数的解析式及顶点 D 的坐标;(2)点 M 是第二象限内抛物线上的一动点,若直线OM 把四边形ACDB 分成面积为 1∶2 的两部分,求出此时点M 的坐标;(3)点 P 是第二象限内抛物线上的一动点,当点P 在何处时△ CPB 的面积最大?求出最大面积?并求出此时点P 的坐标.第 4 题图解: (1)根据题意将 B(-3,0),C(0,3)代入抛物线解析式,得c=3,解得a=- 1,9a-6a+c=0c= 3∴二次函数的解析式为 y=- x2-2x+3,将其化为顶点式为 y=- (x+1)2+4,∴顶点 D 的坐标为 (-1,4);(2)如解图①,连接 OD 、AD、AD 与 y 轴交于点 F,第 4 题解图①111 S△OBD=2×3×4=6,S 四边形ACDB=S△ABD+S△CDF+S△ACF=2×4×4+2 11×1×1+2×1×1+2×1×1=9,因此直线 OM 必过线段 BD,由B(-3,0),D(-1,4)得线段 BD 的解析式为 y=2x+6,设直线 OM 与线段 BD 交于点 E,则△ OBE 的面积可以为 3 或 6.1①当 S△OBE=3 时,2×3×y E=3,解得 y E=2,将 y=2 代入 y=2x+6中,得 x=- 2,∴E点坐标 (-2,2).则直线 OE 的解析式为 y=- x.设M 点坐标为 (x,- x),联立抛物线的解析式可得- x=- x2-2x +3,解得 x1=-1- 13-1+ 132,x2=2(舍去 ).∴点 M( -1- 13 1+ 13); 2 ,21②当 S △ OBE =6 时,2×3×y E =6,解得 y E =4,将 y =4 代入 y =2x +6 中得 x =- 1,此时点 E 、M 、D 三点重合.∴点 M 坐标为 (-1,4);- 1- 13 -1+ 13综上所述,点 M 的坐标为 (2 , 2 ),(-1,4).(3)如解图 ②,连接 OP ,设 P 点的坐标为 (M ,- M 2-2M + 3),第 4 题解图 ②∵点 P 在抛物线上,∴S △CPB= △ CPO + △ - △S S OPB S COB 1 11 = OC ·(-M)+ OB ·(-M2-2M +3)- OC ·OB222=-3M +3(-M 2-2M +3)- 9 2 2 2 =-3(M 2+3M) 23 3 2 27 =- 2(M +2) + 8 .∵- 3<M < 0,3 21527∴当 M =-时, -M-2M+ =,△CPB的面积有最大值 .2 (3)483 15∴当点 P 的坐标为 (-,4 )时, △CPB 的面积有最大值,且最大227值为 8 .1 25. 如图,在平面直角坐标系中, 二次函数 y =- 4x +Bx +C 的图象与坐标轴交于 A 、B 、C 三点,其中点 A 的坐标为 (0,8),点 B 的坐标为 (-4,0).(1)求该二次函数的表达式及点 C 的坐标;(2)点 D 的坐标为 (0,4),点 F 为该二次函数在第一象限内图象上的动点,连接 CD 、CF ,以 CD 、CF 为邻边作平行四边形 CDEF ,设平行四边形 CDEF 的面积为 S.①求 S 的最大值;②在点 F 的运动过程中,当点E 落在该二次函数图象上时,请直接写出此时 S 的值.第 5 题图1 2解: (1)∵二次函数 y =-4x +Bx +C 过 A(0,8)、B(-4,0)两点,1)2- 4b + = b =1∴ 44c 0,解得,c =8c =8∴二次函数的解析式为 y =- 14x 2+x +8,当 y =0 时,解得 x 1=- 4,x 2=8, ∴C 点坐标为 (8,0);(2)①如解图,连接 DF ,OF ,设 F(M ,- 14M 2+M +8),第 5 题解图∵S 四边形 OCFD =S △ CDF +S △ OCD =S △ ODF +S △OCF ,∴S △ CDF =S △ ODF +S △OCF -S △OCD ,= 1×4×M +1×8×(-1M 2+ M + -1×8×42 2 48) 2=2M -M 2+4M +32-16=- M2+6M +16=- (M-3)2+25,当M=3 时,△CDF 的面积有最大值,最大值为 25,∵四边形 CDEF 为平行四边形,∴S 四边形CDEF=2S△CDF=50,∴S 的最大值为 50;②S=18.【解法提示】∵四边形 CDEF 为平行四边形,∴CD∥ EF,CD= EF,∵点 C 向左平移 8 个单位,再向上平移 4 个单位得到点 D,∴点 F 向左平移 8 个单位,再向上平移 4 个单位得到点 E,即 E(M-8,-14M2+M+12),∵E(M -8,-14M2+M+ 12)在抛物线上,∴-14(M-8)2+(M-8)+8=-14M2+M+12,解得 M=7,当M=7 时, S△CDF=- (7- 3)2+25=9,∴此时 S=2S△CDF=18.6. 如图,抛物线 y=Ax2+Bx-3 与 x 轴交于点 A(1,0)和点 B,与y 轴交于点 C,且其对称轴 L 为直线 x=- 1,点 P 是抛物线上 B,C 之间的一个动点 (点 P 不与点 B,C 重合 ).第 6 题图(1)直接写出抛物线的解析式;(2)小唐探究点 P 的位置时发现:当动点 N 在对称轴 L 上时,存在PB⊥NB,且 PB=NB 的关系,请求出此时点 P 的坐标;(3)是否存在点P 使得四边形 PBAC 的面积最大?若存在,请求出四边形 PBAC 面积的最大值,若不存在,请说明理由.解: (1)y=x2+2x-3;【解法提示】∵A(1,0),对称轴 L 为直线 x=- 1,∴B(-3,0),将 AB 两点坐标代入得,∴a+b-3=0a=1,解得,9a-3b-3=0b=2∴抛物线的解析式为y=x2+2x-3.(2)如解图①,过点 P 作 PM⊥x 轴于点 M,连接 BP,过点 B作 BN⊥PB交直线 L 于点 N,设抛物线的对称轴与x 轴交于点 Q,第6 题解图①∵P B⊥NB,∴∠ PBN=90°,∴∠ PBM+∠NBQ=90°.∵∠ PMB=90°,∴∠ PBM+∠BPM=90°.∴∠ BPM=∠NBQ.又∵ PB=NB,∴△ BPM≌△ NBQ.∴P M=BQ.由(1)得 y=x2+2x-3,∴Q(-1,0),B(-3,0)∴B Q=2,∴P M=BQ=2.∵点 P 是抛物线 y= x2+2x-3 上 B、C 之间的一个动点,且点P 的纵坐标为- 2,将 y=- 2 代入 y=x2+ 2x-3,得- 2=x2+2x-3,解得 x1=- 1-2, x2=- 1+2(不合题意,舍去 ),∴点 P 的坐标为 (-1-2,- 2);(3)存在.如解图②,连接 AC,BC,CP,PB,过点 P 作 PD∥y 轴交 BC 于点 D,第6 题解图②∵A(1,0), B(-3,0),C(0,- 3),1∴S△ABC=2×3×4=6,直线 BC 的解析式为 y=- x-3.设P(T,T2+2T-3),则 D(T,- T-3),∴S△BPC =1× ×---T2-2T+=-3 2-9,2 3 ( T33)2T2T329∴S 四边形PBAC=- T -T+6223 3 2 75=-2(T+2) +8,375当 T=-2时, S 四边形PBAC存在最大值,最大值为8 .315此时点 P 的坐标为 (-2,-4 ).12 37.如图,抛物线 y=-2x +2x+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C,且 A 点坐标为 (-3,0),连接 BC、AC.(1)求抛物线的解析式;(2)点 E 从点 B 出发,沿 x 轴向点 A 运动 (点 E 与点 A、B 不重合 ),过点 E 作直线 L 平行于 AC,交 BC 于点 D,设 BE 的长为 M,△BDE的面积为 S,求 S 关于 M 的函数关系式,并写出自变量 M 的取值范围;(3)在(2)的条件下,连接CE,求△CDE 面积的最大值.第 7 题图1 23解: (1)∵抛物线 y=-2x +2x+c 过 A 点,且 A(-3,0),13∴0=-2×9-2×3+c,解得 c=9,∴抛物线的解析式为 y=-12x2+32x+9;1 23(2)∵抛物线的解析式为y=-2x +2x+9,∴C点坐标为 (0,9),∴O C=9,23令y=0 可得-2x +2x+9=0,解得x=-3 或x=6,∴B 点坐标为 (6,0),∴AB=6-(-3)=9;设直线 AC 的解析式为 y=kx+b,1把 A、 C 两点坐标代入可得-3k+b=0,b=9k=3解得,b=9∴直线 AC 的解析式为 y=3x+9,∵直线 ED∥AC,∴可设直线 ED 的解析式为 y=3x+m,∵O B=6,BE=m,∴OE=6-m,∴E 点的坐标为 (6-m,0),代入直线 ED 的解析式可得 0=3(6-m)+n,解得 n=3(m-6),∴直线 ED 的解析式为 y=3x+3m-18,设直线 BC 的解析式为 y=rx+s,把 B 、 C 两点坐标代入可得6r +s =0,s =9r =- 32解得 ,s =93∴直线 BC 的解析式为 y =- 2x +9,y =3x +3m -18x =6-2m 联立,解得 3 , y =-23x +9y =m2∴D 点坐标为 (6-3m ,m), ∴D 到 BE 的距离为 m ,∴S =S △ BDE =112· =2m,2m m又∵ E 在线段 AB 上,且不与点 A 、B 重合,∴0<BE<AB ,∴m 的取值范围为 0<m<9;(3)∵OC =9,BE =m ,∴S △ BEC = 1· = 1 × ×= 9 ,2BE OC2m92m∴S △CDE= △BEC- △BDE=9 -1 2=-1 -92+81,SS2m 2m 2(m 2)8981 ∴当 m =时, △CDE 的面积有最大值,最大值为8 .28.已知抛物线 y=x2+4x+3 交 x 轴于 A、B 两点 (点 A 在点 B 的左侧),交 y 轴于点 C,抛物线的对称轴 l 交 x 轴于点 E.(1)求抛物线的对称轴及点 A 的坐标;(2)点 P 为坐标系内一点,且以点A、B、C、P 为顶点的四边形为平行四边形,求出所有满足条件的P 点的坐标.(3)连接 CA 与 L 交于点 D,M 为抛物线上一点,是否存在点 M,使经过点 C、M 的直线恰好将四边形 DEOC 的面积平分?若存在,请求出直线 CM 的解析式;若不存在,请说明理由.第 8 题图4解: (1)对称轴为直线 x=-2=- 2,当y=0 时,有x2+4x+3=0,解得x1=-1,x2=-3,∴点 A 的坐标为 (-3,0);(2)由 y=x2+4x+3 可知 A(-3,0),B(-1,0),C(0,3),①当 AC 是平行四边形的对角线时,将点 C 向左平移两个单位长度即是 P 点,即 P(-2,3);②当 BC 是平行四边形的对角线时,将点 C 向右平移两个单位长度即是 P 点,即 P(2, 3);③当 AB 是平行四边形的对角线时,将点 A 向下平移三个单位长度再向左平移 1 个单位长度即是 P 点,即 P(-4,- 3);满足条件的点 P 有 3 个,分别为 (-2,3),(2,3),(-4,- 3);(3)存在;∵点 C 的坐标为 (0,3),又DE∥y 轴, AO=3,EO=2, AE=1,CO=3,∴△ AED∽△ AOC,AE DE1DE∴AO=CO,即3=3,∴D E=1,1∴S 四边形DEOC=2×(1+3) ×2=4,4在 OE 上找点 F,使 OF=3,1 4此时 S△COF=× ×3=2,2 3直线 CF 把四边形 DEOC 分成面积相等的两部分,交抛物线于点 M ,4设直线 CM 的解析式为 y=kx+3,它经过点 F(-3,0),49则-3k+3=0,解得 k=4,9∴直线 CM 的解析式为 y=4x+3.1 29. 如图,已知抛物线y=-2x +bx+c 与 x 轴交于点 B,E 两点,与 y 轴交于点 A,OB=8,tan∠ABD=1,动点 C 从原点 O 开始沿 OA 方向以每秒 1 个单位长度移动,动点 D 从点 B 开始沿 BO 方向以每秒 1 个单位长 x 度移动,动点 C,D 同时出发,当动点 D 到达原点 O 时,点 C,D 停止运动.(1)求抛物线的解析式;(2)求△CED 的面积 S 与 D 点运动时间 t 的函数解析式;当 t 为何值时,△CED 的面积最大?最大面积是多少?(3)当△CED 的面积最大时,在抛物线上是否存在点P(点 E 除外 ),使△ PCD 的面积等于△CED 的最大面积,若存在,直接写出P 点的坐标;若不存在,请说明理由.第 9 题图解: (1)∵OB =8,tan ∠ABD =1,∴ O A =OB =8,∴ A (0,8), B(8,0).1 2+bx +c ,把点 A(0,8),B(8,0)代入 y =- 2x c =8b =3得1 2,解得 ,×8c =8-2 +8b +c =0∴抛物线解析式为 y =- 1 2++ ;2x3x 812(2)令 y =0 时,有- 2x +3x +8=0, 解得 x 1=- 2,x 2=8,∴ E (-2,0),∴ B E =10,1∵S △ CED =2DE ·OC ,∴S =1- =-122 21 21225∴S 与 T 的函数解析式为 S =- 2t +5t =-2(t -5) + 2 (0 ≤t ≤ 8),∴当 t =5 时, △CED 的面积最大,最大面积为252 ;4 100 34 200 (3)存在, P 点坐标为 (8,0)或(3, 9 )或( 3 ,-9 ).【解法提示】 当△CED 的面积最大时, t =5,即 BD =DE =5,此时要使 S △PCD =S △CED ,CD 为公共边,只需求出过点 B 、或点 E 且平行于 CD 的直线即可,如下:设直线 CD 的解析式为 y =kx +B ,由 (2)可知 OC =5,OD =3,∴C(0,5), D(3,0),把 C(0,5)、D(3,0)代入,5得b =5,解得k =-3,3k +b =0b =55∴直线 CD 的解析式为 y =- 3x +5,∵DE = DB =5,5∴过点 B 且平行于 CD 的直线为 y =- 3(x -5)+5,5过点 E 且平行于 CD 的直线为 y =- 3(x +5)+ 5,与抛物线解析式联立得1 25方程 ①:- 2x +3x +8=- 3(x -5)+5,4解得 x 1=8,x 2=3,方程 ②:- 12x 2+3x +8=- 53(x +5)+5,34解得 x3=3,x4=- 2,100200分别将 x 的值代入抛物线的解析式,得 y1=0,y2=9,y3=-9,y4=0,又∵ P 点不与 E 点重合,∴满足题意的 P 点坐标有 3 个,分别是 P,,4100,(34,93,1(8 0) P2(3) P3 200-9 ).第 9 题解图10.如图①,在平面直角坐标系中,已知抛物线y=ax2+-与xbx 5轴交于 A(-1,0),B(5,0)两点,与 y 轴交于点 C.(1)求抛物线的函数表达式;(2)若点 D 是 y 轴上的一点,且以B,C,D 为顶点的三角形与△ ABC 相似,求点 D 的坐标;(3)如图②,CE∥x 轴与抛物线相交于点E,点 H 是直线 CE 下方抛物线上的动点,过点 H 且与 y 轴平行的直线与 BC,CE 分别相交于点 F,G,试探究当点 H 运动到何处时,四边形 CHEF 的面积最大,求点 H 的坐标及最大面积.第10 题图解: (1)∵抛物线过点 A(-1,0)和点 B(5,0),∴a-b-5 0 a=1 ,解得, 25a 5b5=0 b= 4∴抛物线的函数表达式为y=x2-4x-5;(2)∵OB=OC=5,∴∠ ABC=∠OCB=45°,∴以 B、C、D 三点为顶点的三角形要与△ABC相似,必须要有一个角等于 45 °.(ⅰ)当点 D 在点 C 的下方时,∠BCD=180°-45°=135°,∴不会出现 45°角,∴此种情况不存在;(ⅱ)当点 D 在点 C 的上方时,∠BCD=45°,易得 BC=2OB=5 2,AB =OA +OB =1+5=6,存在两种情况:BC CD①当△BCD ∽△ ABC 时, AB =BC ,5 2CD即=,65225∴CD = 3 ,2510OD =CD -OC = 3 -5= 3 ,10∴D(0, 3 );DC CB②当△DCB ∽△ ABC 时, AB =BC ,CD 5 2 即6=5 2,∴CD =6,OD =CD -OC =6-5=1,∴点 D(0,1),10∴综上所述,点 D 的坐标为 (0,1)或(0, 3 )时,以 B ,C ,D 为顶点的三角形与 △ABC 相似;(3)令 y =- 5 得 x 2-4x -5=- 5,解得 x 1=0,x 2=4,∴E(4,- 5),∴C E=4,设 H(a,a2-4a-5),点 H 是在直线 CE 下方抛物线上的动点,∴0<a<4.设直线 BC 的表达式为 y=kx+b,把点 B(5,0)、C(0,- 5)代入得5k b=0 ,解得k =1,b= 5b=5∴直线 BC 的表达式为 y=x-5,则点 F(a,a-5),∴F H=a-5-(a2-4a-5)=-a2+5a,∵CE⊥FH,∴S 四边形1× =-2a25225222∵0<a<4,525,∴当 a=2时,四边形 CHEF 面积有最大值,最大值是 2535此时 H(2,-4 ).11.如图,在平面直角坐标系 xOy 中,已知抛物线 y=x2+Bx+C 经过 A(0,3),B(1,0)两点,顶点为 M.(1)求 B、C 的值;(2)将△OAB 绕点 B 顺时针旋转 90°后,点 A 落到点 C 的位置,该抛物线沿 y 轴上下平移后经过点 C,求平移后所得抛物线的表达式;(3)设(2)中平移所得的抛物线与y 轴的交点为 A1,顶点为 M1,若点P 在平移后的抛物线上,且满足△PMM1的面积是△PAA1面积的3倍,求点 P 的坐标.第11 题图解:(1)∵抛物线 y=x2+Bx+C 经过 A(0,3),B(1,0)两点,∴c=3,解得b=-4;1+b+c=0c=3(2)由(1)知,抛物线的表达式为y=x2-4x+3.∵A(0,3), B(1,0)∴O A=3,OB=1,∴C点坐标为 (4,1),当x=4 时,由 y=x2- 4x+3 得 y=3,则抛物线 y=x2-4x+3 经过点 (4,3),∴将原抛物线沿y 轴向下平移 2 个单位后过点 C,∴平移后的抛物线的表达式为y=x2-4x+1;(3)∵点 P 在 y=x2-4x+1 上,可设 P 点的坐标为 (x0,x20-4x0+1),将y=x2-4x+1 配方得 y=(x-2)2-3,∴抛物线的对称轴为直线 x=2,1∵S△PMM 1=2|x0-2| MM·1,1S△PAA1=2|x0| ·AA1,S△PMM 1=3S△PAA1,MM1=AA1=2,∴x0<2,|x0-2|=3|x0|.分情况讨论:①当 0<x0<2 时,则有 2-x0=3x0,13解得 x0=2,则 x20-4x0+1=-4,1 3∴点 P 的坐标为 (2,-4);②当 x0<0 时,则有 2-x0=- 3x0,解得 x0=- 1,则 x20-4x0+1=6,∴点 P 的坐标为 (-1,6).1故满足△ PMM1的面积是△ PAA1面积的 3 倍时,点 P 的坐标为 (2,3-4)或(-1,6).12.如图,在平面直角坐标系中有一 RT△AOB,O 为坐标原点,OA=1,TAN∠BAO=3,将此三角形绕原点O 逆时针旋转90°,得到△DOC,抛物线 y=- x2+Bx+C 经过 A、B 两点.(1)求抛物线的解析式及顶点 G 的坐标;(2)连接 CG、DG ,求△GCD 的面积;(3)在第二象限内,抛物线上存在异于点 G 的一点 P,使△PCD 与△CDG 的面积相等,请直接写出点 P 的坐标.解: (1)∵OA=1,∴A(1,0),OB又∵ tan∠BAO=OA=3,∴O B=3,∴B(0,3),将 A(1,0)、B(0,3)代入抛物线的解析式,-12+b+c=0b=- 2得,解得c=3,c=3∴抛物线的解析式为 y=- x2-+3.2x∵y=- x2-2x+3=- (x+1)2+4,∴抛物线的顶点 G 的坐标为 (-1,4);(2)如解图①,过点 G 作 GE⊥y 轴于点 E.第 12 题解图①∵G(-1,4),∴G E=1,OE=4,∴S 梯形1+· =1× +×=,GEOC=2(GE OC) OE 2 (13) 4 8∵由旋转的性质可知OD=OA=1,∴D E=3,∴S△1· =1× × =3OCD=2OC OD2 3 12,113S△GED=2EG·ED=2×1×3=2,3 3∴S△CDG=S 梯形GEOC-S△OCD-S△GED=8-2-2=5;435(3)点 P 的坐标为 (-3,9 ).【解法提示】如解图②,过点 G 作 PG∥CD,交抛物线于点P.第 12 题解图②∵PG∥CD,∴S△PCD=S△GCD,∵OD=OA=1,∴D(0,1),设直线 CD 的解析式为 y=Kx+B.将点 C(-3,0)、D(0,1)代入得1-3k+b=0k=3,,解得b=1b=11∴直线 CD 的解析式为 y=3x+1,∵PG∥CD,1 ,将点 G 的坐标代入得- 1+b 1=4,∴设 PG 的解析式为 y = x +b 13313解得 b 1= 3 ,1 13∴直线 PG 的解析式为 y =3x + 3 ,1 13联立得 y =3x +3 ,=-x 2-2x +3y4x 1=-3x 2=- 1解得或 ,=35y 2=4y 19∴点 P 不与点 G 重合,4 35∴点 P 坐标为 (-3, 9 ).13. 如图,四边形 OABC 是矩形, OA =4,OC =8,将矩形 OABC沿直线 AC 折叠,使点 B 落在点 D 处, AD 交 OC 于点 E.(1)求 OE 的长;(2)求过 O ,D ,C 三点的抛物线的解析式;(3)若 F 为过 O ,D ,C 三点的抛物线的顶点, 一动点 P 从点 A 出发,沿射线 AB 以每秒 1 个单位长度的速度匀速运动, 当运动时间 T(秒)为何值时,直线 PF 把△FAC 分成面积之比为 1∶3 的两部分.第 13 题图解: (1)∵四边形 OABC 是矩形,∴∠ CDE =∠ AOE =90°,OA =BC =CD.又∵∠ CED =∠OEA ,∴△ CDE ≌△ AOE ,∴ O E =DE ,∴ OE 2+OA 2=(AD -DE)2,即 OE 2+42=(8-OE)2,解得 OE =3;(2)∵EC =8-3=5,如解图,过 D 作 DG ⊥EC 于 G ,易得 △DGE ∽△ CDE ,DE DG EG∴CE =CD ,ED ,129∴DG = 5 ,EG =5,9 24∴ OG =3+5= 5 .24 12∴ D( 5 , 5 ),∵O 点为坐标原点,故可设过 O ,C ,D 三点的抛物线的解析式为y =Ax 2+Bx ,将 C(8,24120)与 D( 5 , 5 )代入 y =ax 2+bx ,得,564a +8b =0a =-3224 24 12,解得,( 5 )2a + 5b = 5b =54∴所求抛物线的解析式为y =-5x 2+5x ; 32 4第 13 题解图5 2 5 5 25 (3)∵y =- 32x +4x =- 32(x -4) +2,5∴F(4,2).设直线 AC 的解析式为 y =Kx +B(K ≠ 0),将 A(0,- 4)与 C(8,0)代入 y =Kx +B ,得1b=- 4k=2,,解得8k+b=0b=- 41∴直线 AC 的解析式为 y=2x-4.1如解图,设直线 FP 交直线 AC 于 H(M ,2M-4),过 H 作 HM ⊥OA 于点 M,∴△ AMH∽△ AOC,∴M H∶OC= AH∶AC.∵S△FAH∶S△FHC=1∶3 或 3∶1,∴A H∶ HC=1∶3 或 3∶1,∴M H∶OC= AH∶AC=1∶4 或 3∶4,∴H M=2 或 6,即M=2 或 6,∴H1(2,- 3),H2(6,- 1),1117∴直线 FH1的解析式为 y=4 x-2,18令y=- 4,x=11;719直线 FH2的解析式为 y=-4x+2,54令 y=- 4,x=7,18 54∴当 T=11或7时,直线 PF 把△FAC 分成面积之比为1∶3 的两部分.2514. 如图,抛物线y=ax +bx+2过点 A(-1,0)、B(5,0),直线 y= x+1 交抛物线的对称轴于点M,交抛物线于点A,C.(1)求抛物线的解析式;(2)点 P 为线段 AM 上一动点,过点 P 作 PQ∥y 轴交抛物线于点Q,2设点 P 的横坐标为 M .当 M 为何值时, PQ=4 AC;(3)在(2)的条件下,过点 P 作 PN∥QM 交抛物线的对称轴于点 N,当四边形PQMN 是正方形时,直线y=x+1 上是否存在一点D,使△DPQ 的面积与正方形 PQMN 的面积相等?若存在,请求出点 D 的坐标;若不存在,请说明理由.解: (1)把 A(-1,0),B(5,0)代入 y=ax25+bx+2中,510=a -b +2a =-2,得= + + ,解得b =20 5 25a 5b 2125 ∴抛物线的解析式为 y =-+ ;22x2(2)根据题意,令- 1 25,x ++ = +2 2x2x 1解得 x 1=- 1,x 2=3,即点 C 的坐标为 (3,4).∴ A C = 42+42=4 2, ∵点 P 的横坐标为 m ,∴ 点 P 的坐标为 (m ,m +1)且- 1≤m ≤2, ∵PQ ∥ y 轴, ∴点 Q 的横坐标为 M ,∴点 Q 的坐标为 (m ,- 12m 2+2m +52),125∴PQ =(-2m +2m +2)-(m +1)1 2 3=-2m+m +2=- 1(m -1)2+2,2根据题意,得- 12(m -1)2+2= 42×4 2,解得 m 1=m 2=1,2∴当 m =1 时, PQ = 4 AC ;(3)存在.根据题意可得,抛物线的对称轴为直线 x=2,将 x =2 代入 y=x+1,可得 y=3,即 M(2,3),由(2)可得∠AMN=∠ BAM=45 °,∵PQ∥y 轴,MN 是对称轴,∴PQ∥MN,又∵ PN∥QM,∴四边形 PQMN 是平行四边形,当 QM⊥MN 时,四边形 PQMN 是矩形,又∵∠ BAM=45 °,∴四边形 PQMN 是正方形,∴Q 点的纵坐标是 3,125,即- m ++=22m23解得 m1=2-3,m2=2+ 3(不合题意,舍去 ).∴M的值是 2- 3.∴P Q=QM=2-(2- 3)= 3.∵△ DPQ 的面积与正方形PQMN 的面积相等,∴点 D 到 PQ 的距离为 2 3.设点 D 的横坐标为 n.当点 D 在 PQ 的左侧时,可得 2-3- n=2 3,解得 n=2-3 3,∴点 D 的坐标为 (2-3 3,3-3 3);当点 D 在 PQ 的右侧时,可得 n-(2- 3)=2 3,解得 n=2+ 3,∴点D 的坐标为 (2+ 3,3+ 3).综上所述,存在满足条件的点D,点 D 的坐标为 (2-3 3,3-3 3)或 (2+3,3+3).1 215.如图①,抛物线 y=3x +bx+c 经过 A(- 2 3,0)、B(0,- 2)两点,点C 在y 方向以每秒 2 0),过点 D 作轴上,△ABC 为等边三角形,点 D 从点 A 出发,沿 AB 个单位长度的速度向终点 B 运动,设运动时间为t 秒(t>DE⊥AC 于点 E,以 DE 为边作矩形 DEGF ,使点 F 在 x轴上,点 G 在 AC 或 AC 的延长线上.(1)求抛物线的解析式;(2)将矩形 DEGF 沿 GF 所在直线翻折,得矩形 D′E′GF,当点 D 的对称点 D′落在抛物线上时,求此时点 D′的坐标;(3)如图②,在 x 轴上有一点 M(2 3,0),连接 BM、CM,在点 D 的运动过程中,设矩形DEGF 与四边形ABMC 重叠部分的面积为S,写出S 与 t 之间的函数关系式,并写出自变量 t 的取值范围.第15 题图1 2解: (1)把 A(-2 3,0),B(0,- 2)代入抛物线 y=3x +bx+c 中,得=-c=- 2c21,解得=3,×12-2 3b+c=03b313∴抛物线的解析式为y=3x2+3 x-2;(2)∵A(-2 3, 0),B(0,- 2),∴OA=2 3,OB=2,∵A D=2t, ∠DEA=90°,∠ BAC=60°,∴A E=t,ED= 3 t,∵△ ABC 为等边三角形,∴∠BAC=60°,∵A O⊥ BC,∴∠ CAO=∠ BAO=30°,∵四边形 DEGF 为矩形,∴D F∥ AC,GF=DE= 3t,∴∠ DFA=∠CAO=30°,∴A F=2GF=2 3t;∴∠ DFA=∠BAO=30°,∴ D F =AD =2t ,由翻折得 D ′F =DF =2t ,如解图 ①,过点 D ′作 D ′H ⊥x 轴于点 H ,第 15 题解图 ①∵∠ D ′FH =∠AFD =30°,1∴D ′H =2D ′F =t ,FH = 3D ′H = 3t ,∴AH =AF +FH =3 3 t,∴OH =AH -AO =3 3t -2 3,∴D ′(33 t -23, t),1 2 3把 D ′ (33 t -2 3,t)代入 y =3x + 3 x -2 中,1 3∴t =3(3 3t -2 3)2+ 3 (3 3t -2 3)-2,整理得 9t 2-10t =0,解得 t 1=104109 ,t 2=0(舍去),∴ D ′(3,9 ).3(3)由( 2)可知: DE= 3t ,DF= 2t.4 当 AE+EG ≤AC 时,即 t+2t ≤4,解得 t ≤,34如解图②,当 0<t≤时,3第 15 题解图②S=S 矩形DEGF,∴S=2t·3t=2 3t2;4如解图③,当3<t≤2时,第15 题解图③∵CG=AG-AC=3t-4,GH=3CG=3(3t-4),∴S=S 矩形DEGF-S△CGH,∴S=2 3t2-12(3t-4) ·3(3t-4)=-523t2+12 3t-8 3.综上所述, S与 t 的函数关系式为S=错误!。
中考复习之二次函数压轴之面积问题,含详细参考答案
二次函数压轴之面积问题问题简介:1.抛物线y=x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,直线y=kx-3,经过点B,C.(1)求抛物线的解析式(2)点P是直线BC下方抛物线上一动点,求 PBC面积最大时点P的坐标;2.如图,在平面直角坐标系中,已知抛物线y=x2﹣2x﹣3与x轴交于点A和点B,点A在点B的左侧,与y轴交于点C.(1)求A点、C点的坐标;(2)点P是第四象限内的抛物线上一点,连接AC,CP,BP,若四边形ACPB面积为63 8请求出此时点P的坐标;3.如图,抛物线y =24832999x x -++与x 轴交于A ,B 两点(点A 在点B 的左侧),顶点为D .点P 为对称轴右侧抛物线上的一个动点,其横坐标为m ,直线AD 交y 轴于点C ,过点P 作PF ∥AD ,交x 轴于点F ,PE ∥x 轴,交直线AD 于点E ,交直线DF 于点M . (1)求直线AD 的表达式及点C 的坐标;(2)当四边形AFPE 的面积与△ADF 的面积相等时,求m 的值;4.如图,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B . (1)求抛物线和直线AB 的解析式;(2)设点Q 是抛物线上的一个动点,是否存在一点Q ,使S △QAB =S △CAB ,若存在,直接写出Q 点的坐标;若不存在,请说明理由.5.如图1,抛物线y =12x 2+b x +c 与x 轴、y 轴分别交于点B (6,0)和点C (0,﹣3). (1)求抛物线的解析式;(2)点P 是直线BC 下方抛物线上一动点,其横坐标为m ,连接PB 、PC ,当△PBC 的面积为152时,求m 值;6.已知抛物线y =12x 2﹣3x +52与x 轴交于A ,B 两点(点A 在点B 的左边).(1)求A ,B 两点的坐标;(2)如图1,若点P 是抛物线上在第四象限的点,PBC S 13PAB S ∆∆=时.求点P 的坐标;7.已知二次函数y=ax2+bx+2(a≠0)交x轴于点A,B(点A在点B左侧),AB=3,交y轴于点C,设抛物线的对称轴为直线x=m,且m≥0.(1)用含m的代数式表示出点A、点B的坐标;(2)若抛物线上存在点P使得S△ABP=S△ABC=3(点P与点C不重合),且这样的点P 恰好存在两个,求此时抛物线的解析式;8.如图,在平面直角坐标系中,一抛物线的对称轴为直线x=﹣1,与y轴负半轴交于点C,与x轴交于A,B两点,其中点A的坐标为(﹣3,0),且OA=OC,D为抛物线的顶点.(1)求抛物线的解析式;(2)若M(﹣2,y)是抛物线上一点,P是抛物线上另一点(点P与点D不重合),当S△BDM=S△BPM时,求出此时点P的坐标;9.如图,抛物线y=﹣x2+bx+c过点A(﹣1,0)和点B(3,0),与y轴交于点C在x轴上有一动点E(m,0)(其中m为实数,0<m<3),过动点E作直线l⊥x轴,交抛物线于点M.(1)求抛物线解析式及点C的坐标;(3)连接BM并延长交y轴于点N,连接AM,OM若△AEM的面积等于△MON面积的2倍,求m的值.10.如图1,抛物线y=ax2﹣2ax+b(a<0)与x轴交于A、B两点(A点在B点的左边),与y轴的正半轴交于点C,顶点为D,OB=OC=3OA.(1)求抛物线解析式;(2)如图2,点E的坐标为(0,7),若过点E作一条直线与抛物线在对称轴右侧有且只有一个交点H,直线y=kx﹣2k﹣5(k≠0)与抛物线交于F、G两点,求当k为何值时,△FGH面积最小,并求出面积的最小值;参考答案1. 解:方法一:过点P 作PD||y 轴交BC 于点D ,设P(m ,m 2-2m -3),易知BC 的解析式为y =x -3,则D(m ,m -3)铅垂高PD=m -3-(m 2-2m -3)=-m 2+3m 水平宽x B -x C =3,S △PBC =32(-m 2+3m),当m =32时,△PBC 的面积取最大值,此时P(32,154-) 方法二:将BC 向下平移,当它与抛物线相切时,此时△PBC 的面积最大设平移后的直线l解析式为y=x+m 与抛物线y =x 2-2x -3联立得x 2-3x -(m+3)=0,此时△=0,即有9+4(m +3)=0,m =214-此时方程的根为x 1=x 2=32,P 点的坐标为(32,154-) 方法三:过点P 作EF||x 轴,过点B 作BF△EF 于点F ,设P(m,m 2-2m -3)S △PBC =S 四EFBO -S △BOC -S △PCE -S △PBF =32(-(m 2-2m -3)-12(3-m)(m 2-2m -3)-12m(-(m 2-2m -3-3)=32(-m 2+3m),当m =32时,△PBC 的面积取最大值,此时P(32,154-)2. 解:(1)A(-1,0),C(0,-3)(2)易知AB=4,OC=3,故S △ABC =6,而S 四ACBP =S △ABC +S △BCP ,故S △BCP =158设P(m ,m 2-2m -3),直线BC 的解析式为y=x -3,过点P 作PD||y 轴交BC 于点D ,则D(m ,m -3),PD=m -3-(m 2-2m -3)=-m 2+3m ,S △BCP =32(-m 2+3m)=158得m 1=12,m 2=52,此时P 点的坐标为(12,154-)或(52,74-)3. 解:(1)y =43x +83,C(0,83) (2) 作DG 、PH 垂直于x 轴于点G 、H ,P(m ,24832999m m -++),PH=|24832999m m -++|S AFPE =AF∙PH ,S △ADF =12AF∙DG ,即有|24832999m m -++|=2,解得m 1=1+2,m 2=1-2(舍去)m 3=1+2,m 4=1-2(舍去),故m 的值为1+2或1+24. 解:(1)y =-x 2+2x +3(2)作CD||y 交AB 于点D ,易知直线AB 的解析式为y =-x +3,故D(1,2),S ABC =3, 方法一:设Q(m ,-m2+2m+3)则E(m,-m+3),则QE=|-m 2+2m+3-(-m+3)|=|-m 2+3m|S ABQ =32|-m2+3m|=3,解得m 1=1,m 2=2,m 3=32,m 4=32,故Q 点的坐标为(1,4)或(2,3)或(32+,12-)或(32,12-+)5. 解:(1)y=12x 2-52x -3 (3) 易知直线BC 的解析式为y =12x -3设P(m,12m 2-52m -3),E(m ,12m -3),PE=12m -3-(12m2-52m -3)=-12m2+3m,S PBC =12∙6∙(-12m 2+3m)=152,解得m 1=1,m 2=56. 解:(1)A(1,0),B(5,0)y =12x2﹣3x+52 (2)易知直线BC 的解析式为y=-12x+52,设P(m,12m2﹣3m+52),则E(m,-12m+52),PE=-12m+52-(12m2﹣3m+52)=-12m2+52m ,S PBC =52(-12m2+52m),而S PAB =2(12m2﹣3m+52),PBC S 13PAB S ∆∆=得22152(3)1225153()222m m m m -+=+7. 解:(1)A(m -1.5,0)B(m+1.5,0)(2)1.a <0时,x 轴下方恰好存在两个纵坐标为-2的点,而x 轴上方有且仅有一点C ,则C 为最高点时,满足题意,故b =0,对称轴为直线x=0,m =0,得a =-89,抛物线的解析式为y=-89x 2+22. a >0时,x 轴上方有一个纵坐标为2的点,x 轴下方有一个纵坐标为-2的点,故(m ,-2)为其顶点,设y=a (x -m )2-2,点B(m+1.5,0)和(0,2)代入得a =89,m=2,故抛物线的解析式为y =89(x-2)2-28. 解:(1)y=x 2+2x -3(2) 易知M(-2,-3)故直线BM 的解析式为y =35x -95,D(-1,-4)过点D 、P 分别作DE 、PF 平行于y 轴,E(-1,-125),故DE=85,S △BDM =12∙385=125,设P(m ,m 2+2m -3)则F(m ,35m -95) PF=|35m -95-(m 2+2m -3)|=|-m 2+135m+65|,故S △BMP =12∙3|-m 2+135m+65|=125,解得m 1=0,m 2=-3(舍),m 3=12-,m 4=12-+,故点P 的坐标为(0,-3)或(12-,12)或(12-+,12)9. 解:(1)y=-x 2+2x+3(3) E(m ,0),M(m ,-m 2+2m+3),直线BM 的表达式为y=(-m -1)x+3m+3,x=0时,y=3m+3, 故N(0,3m+3),S AEM =21(1)(23)2m m m +-++,2S MON =(3m+3)m,即21(1)(23)2m m m +-++=(3m+3)m ,解得m=-2或-1(舍去负值),故-210. 解:(1)y=-x 2+2x+3(2) 设直线EH 的解析式为y =mx +7,与抛物线y=-x 2+2x +3联立得x 2+(m -2)x +4=0,∆=0,即有(m -2)2=16,得m=-2或6(舍),y =-2x +7,H(2,3)而M(2,-5),HM=8;联立y =kx -2k -5抛物线y =-x 2+2x +3得x 2+(k -2)x -2k -8=0,x F +x G =2-k ,x F ∙x G =-2k -8, x G -x FS FGH k =-2时,面积最小,最小值为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数压轴题专题一 面积问题
【例1】如图,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .
(1)求抛物线和直线AB 的解析式;
(2)求△CAB 的铅垂高CD 及S △CAB ;
(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.
【变式练习】
1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .
(1)求点B 的坐标;
(2)求经过A 、O 、B 三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.
(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB 的最大面积;若没有,请说明理由.
2.如图,抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .
(1)求抛物线的函数解析式,并写出顶点D 的坐标;
(2)在直线EF 上求一点H ,使△CDH
(3)若点K 在x 轴上方的抛物线上运动,当K 运动到什么位置时,
△EFK 的面积最大?并求出最大面积.
3.如图,已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y=ax 2+bx+c 经过A 、
B 、
C (1,0)三点.
(1)求抛物线的解析式;
(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;
(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.
4、如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
5、如图,抛物线y=x2﹣x﹣3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
6、如图,已知抛物线212
y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).
(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);
(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S .
①求S 的取值范围;
②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.。
