Matlab分析RLC电路的电压调制系统
基于Matlab的电力系统电压调整仿真实验教学平台设计

第43卷 第1期2021年2月电气电子教学学报JOURNALOFEEEVol.43 No.1Feb.2021收稿日期:2019 06 14;修回日期:2020 09 30基金项目:福建省中青年教师教育科研项目(JT180797),漳州市自然科学基金项目(ZZ2019J28)第一作者:杨家豪(1990 ),男,讲师,硕士,主要从事电力系统优化运行的教学和研究,E mail:yangjiahao1990@foxmail.com基于Matlab的电力系统电压调整仿真实验教学平台设计杨家豪,何 畅,叶子薇(厦门大学嘉庚学院普瑞特先进打印技术创新实验室,福建漳州363105)摘要:电压调整是“电力系统分析”课程中一个重要内容。
传统教学大多依靠理论分析,抽象且不易理解,配套实验存在局限性。
本文基于Matlab图形用户界面设计并开发了一种电力系统电压调整仿真实验教学平台,师生通过计算机以交互方式进行电压调整仿真实验,界面友好、操作简捷、教学便利,帮助学生加深对电力系统电压调整的理解,有助于开放式实验教学、培养学生实践能力。
关键词:电力系统;电压调整;仿真实验中图分类号:G64 文献标识码:A 文章编号:1008 0686(2021)01 0145 06DesignofVoltageAdjustmentSimulationExperimentTeachingPlatformforPowerSystemBasedonMatlabYANGJia hao,HECHang,YEZi wei(ThePRTAdvancedPrintingTechnologicalInnovationLab,TanKahKeeCollege,XiamenUniversity,Zhangzhou363105,China)Abstract:VoltageadjustmentisanimportantpartofPowerSystemAnalysiscourse.Traditionalteachingmostlyre liesontheoreticalanalysis,whichisabstractanddifficulttounderstand.Thesupportingexperimentshavelimita tions.ThispaperdesignsanddevelopsvoltageadjustmentsimulationexperimentteachingplatformforpowersystembasedonMatlabgraphicaluserinterface.Teachersandstudentscanconductvoltageadjustmentexperimentsthroughcomputerinaninteractivewaywithfriendlyinterfaceandconvenientoperation,whichisconvenientforun dergraduateteaching.Itcanhelpstudentsdeepentheirunderstandingofpowersystemvoltageadjustmentanditisusefultoopenexperimentalteachinganddevelopstudents'practicalability.Keywords:powersystem;voltageadjustment;simulationexperiment0 引言“电力系统分析”是电气工程及其自动化专业本科阶段的专业必修课,由于课程本身理论性强、难度较大,教学过程中仅对模型、公式进行理论分析常使学生不易理解,且形式较为枯燥,无法取得较好的教学效果[1]。
交流电机调压调速系统matlab正文

1 设计任务1、了解并熟悉双闭环三相异步电机调压调速原理及组成。
2、学习 SIMULINK,熟悉相关的模块功能。
3、进一步理解交流调压系统中电流环和转速环的作用。
2 设计要求1、利用SIMULINK建立闭环调速系统仿真模型。
2、调试完成调压模块仿真、开环系统仿真、闭环系统仿真。
3 设计设备1、计算机一台2、MATLAB仿真软件4 设计原理调压调速即通过调节通入异步电动机的三相交流电压大小来调节转子转速的方法。
理论依据来自异步电动机的机械特性方程式:其中,p为电机的极对数;为定子电源角速度;w1为定子电源相电压;U1R’为折算到定子侧的每相转子电阻;2为每相定子电阻;R1L为每相定子漏感;11为折算到定子侧的每相转子漏感;L12S为转差率。
图1 异步电动机在不同电压的机械特性由电机原理可知,当转差率s 基本保持不变时,电动机的电磁转矩与定子电压的平方成正比。
因此,改变定子电压就可以得到不同的人为机械特性,从而达到调节电动机转速的目的。
4.1 调压电路改变加在定子上的电压是通过交流调压器实现的。
目前广泛采用的交流调压器由晶闸管等器件组成。
它是将三个双向晶闸管分别接到三相交流电源与三相定子绕组之间通过调整晶闸管导通角的大小来调节加到定子绕组两端的端电压。
这里采用三相全波星型联接的调压电路。
图2 调压电路原理图4.2 开环调压调速开环系统的主电路由触发电路、调压电路、电机组成。
原理图如下:图3 开环调压系统原理图AT为触发装置,用于调节控制角的大小来控制晶闸管的导通角,控制晶闸管输出电压来调节加在定子绕组上的电压大小。
4.3 闭环调压调速速度负反馈闭环调压调速系统的工作原理:将速度给定值与速度反馈值进行比较,比较后经速度调节器得到控制电压,再将此控制电压输入到触发装置,由触发装置输出来控制晶闸管的导通角,以控制晶闸管输出电压的高低,从而调节了加在定子绕组上的电压的大小。
因此,改变了速度给定值就改变了电动机的转速。
基于matlab的三相交流调压电路仿真与研究

基于matlab的三相交流调压电路仿真与研究一、引言随着电力电子技术和控制理论的不断发展,交流调压技术在许多领域得到了广泛应用。
三相交流调压电路由于其能够实现对三相交流电的独立调节,因此在电机控制、电力质量改善以及无功补偿等方面具有重要作用。
本文旨在通过Matlab仿真研究三相交流调压电路的工作原理和性能。
二、三相交流调压电路工作原理三相交流调压电路通常采用相位控制方式,通过调节开关的导通和关断时间来改变输出电压的大小。
在三相系统中,每一相都有一个独立的调压电路,通过对每一相的独立调节,可以实现三相输出电压的平衡控制。
三、Matlab仿真环境设置Matlab是一款强大的数学计算软件,可用于电力电子系统仿真。
在Matlab中,我们首先需要设置仿真参数,包括仿真时间、采样时间、仿真算法等。
然后,我们需要构建三相交流调压电路的数学模型,并转化为Simulink模型。
四、电路模型的建立与参数设置在Simulink中,我们需要根据三相交流调压电路的工作原理,建立相应的电路模型。
这个模型应该包括电源、开关、二极管、电感和电容等元件。
然后,我们需要为这些元件设置合适的参数,以模拟实际的电路行为。
五、仿真结果分析通过运行仿真,我们可以得到输出电压的波形。
通过对这些波形的分析,我们可以了解调压电路的性能。
例如,我们可以观察输出电压的幅值、相位和频率等参数的变化情况。
六、实验验证与结果对比为了验证仿真结果的准确性,我们需要进行实验验证。
在实验中,我们需要搭建实际的三相交流调压电路,并使用示波器等设备记录输出电压的波形。
然后,我们将实验结果与仿真结果进行对比,以评估仿真的准确性。
七、结论通过以上分析和对比,我们可以得出结论:基于Matlab的三相交流调压电路仿真能够准确反映实际电路的工作情况。
这为进一步研究三相交流调压电路的性能提供了有力支持。
同时,通过仿真和实验的结合,我们可以更好地理解电路的工作原理,优化电路设计,提高系统的稳定性和可靠性。
RLC电路matlab仿真

R
iL (t)Leabharlann EC uc (t)
三、要求
1) 利用替换法、跟匹配法建立图1电路的离散数需模型; 2) 建立计算机仿真模型; 3) 选择一组离散时间间隔值,进行仿真试验; 4) 分析仿真结果,从仿真模型实现的难易性、模型的稳定性、模型的精度及
离散时间间隔等方面,对两种方法构造的离散系统模型进行对比分析,并 给出分析结论。 5) 分析仿真结果,从仿真模型实现的难易性、模型的稳定性、模型的精度及 离散时间间隔等方面,对比分析根匹配法和替换法(简单替换法和双线性 替换法)构造的离散系统模型的优缺点。
108T 2
差分方程
仿真结果
2、双线性替换法
系统数学模型: 传递函数
G(z)
z2 2*z 1
[LC4( 1 )2 RC2( 1 ) 1]* z2 [2 8LC( 1 )2 ]* z [LC4( 1 )2 RC2( 1 ) 1]
T
T
T
T
T
系统仿真模型
y(n 2)
1
((8 2108T 2 ) y(n 1)
108T 2 103 2T 4
(108T 2 103 2T 4) y(n) 4108T 2 )
仿真结果
实验结论 结果分析
对于简单线性替换法和双线性替换法,从仿真模型实现的难易性、模型的 稳定性、模型的精度及离散时间间隔等方面,对两种方法构造的离散系统模型进 行对比分析,可以看出对于给定的函数 G(s),设法找到 S 域到 Z 域的某种映射 关系,它将域的变量 S 映射到 Z 平面上,由此得到与连续系统传递函数相对应 的离散函数 G(Z)。进而根据 G(Z)由 Z 反变换求得系统的时域离散模型—差分方 程,据此便可以进行快速求解,且具有较高的精度,但离散时间间隔得取得较小 才合适。而在本实验中采样周期取得是 T=e-6 和 T=e-7。
使用Matlab研究RLC电路

使用Matlab 研究RLC 电路电子信息和电气工程学院 F0703024 5070309663 曹龙飞Email:mathsniper@摘要:此论文主要是结合Matlab功能分析RLC电路特性。
关键字:Matlab,RLC。
1 使用Matlab 分析使用Matlab 分析Parallel RLC 电路的目的在於测试不同的电阻R 值对电路各变量值的影响情况。
设有如下图:圖表 1-1得出齐次二阶微分方程:22()1()1()0d v t dv t v t dt RC dt LC++= (1.1) 因应R 值不同,得出的解也会相应不同,分别有过阻尼(overdamped),临界阻尼(critically damped),欠阻尼(underdamped)和无阻尼(non-damped)四种情况。
为了分析方便,以欠阻尼的情况分析:假设电感和电容值分别为L=0.1H 和C=1mF ,初始值为v(0)=10V 和i_L(0)=-0.6A , 而当电路参数满足R >(1.2) 即电路是欠阻尼的情况。
计算上式预设值,有1/2*sqrt(L/C)=5(Ohms)。
由此可知,当电阻值大於5Ohms 时,为欠阻尼,当等於5 Ohms 时,为临界阻尼。
以下会在给定不同的电阻R 值而得出v(t)-t 图。
由基本的二阶Parallel RLC 电路有指数因子12RCα=(1.3) 和响应角频率ω= (1.4)并记阻尼响应角频率ω=跟据以上给定值和因子,分别对R=5, 20, 50, 100(Ohms)用Matlab画出对应的v(t)-t图。
以下为跟据需求的M file(For Matlab using)。
2RLC_simple.m file%--------------------------------------------------------------% Set component values%--------------------------------------------------------------L=0.1;C=0.001;R=5;%--------------------------------------------------------------% Solve for the damping coefficient, natural frequency, and% damped resonance frequency%--------------------------------------------------------------a=1/(2*R*C);w0=1/sqrt(L*C);w=sqrt(w0*w0 - a*a);%--------------------------------------------------------------% Set coefficients based on initial conditions%--------------------------------------------------------------B1=10;B2=(a/w)*B1 - 10/(w*R*C) + 0.6/(w*C);%--------------------------------------------------------------% Create a time base and calculate the response at those times%--------------------------------------------------------------t=0:0.001:0.12;v=B1*exp(-a*t).*cos(w*t) + B2*exp(-a*t).*sin(w*t);hold offplot(1000*t,v,'b+-')hold on%--------------------------------------------------------------% R=20, 50, 100(Ohms)%--------------------------------------------------------------R=20;a=1/(2*R*C);w=sqrt(w0*w0 - a*a);B2=(a/w)*B1 - 10/(w*R*C) + 0.6/(w*C);v=B1*exp(-a*t).*cos(w*t) + B2*exp(-a*t).*sin(w*t);plot(1000*t,v,'mo-');R=50;a=1/(2*R*C);w=sqrt(w0*w0 - a*a);B2=(a/w)*B1 - 10/(w*R*C) + 0.6/(w*C);v=B1*exp(-a*t).*cos(w*t) + B2*exp(-a*t).*sin(w*t);plot(1000*t,v,'kx-');R=100;a=1/(2*R*C);w=sqrt(w0*w0 - a*a);B2=(a/w)*B1 - 10/(w*R*C) + 0.6/(w*C);v=B1*exp(-a*t).*cos(w*t) + B2*exp(-a*t).*sin(w*t);plot(1000*t,v,'rd-');%--------------------------------------------------------------% Finally, add some information to the graph to make it% clearer and explain the axes%--------------------------------------------------------------legend('R=25/3','R=20','R=50','R=100')ylabel('v_n(t), V');xlabel('t, ms');title('Natural Response of an Underdamped Parallel RLC Circuit');3 运行结果圖表 3-14 代码分析第一部分,是设定电容,电感的初始值,并第一个电阻值取为5。
使用Matlab进行信号调制和解调技术

使用Matlab进行信号调制和解调技术信号调制和解调是通信系统中非常重要的环节,它们能够将原始信号转换为适合传输的调制信号,并在接收端将其恢复为原始信号。
Matlab是一种功能强大的工具,提供了丰富的信号处理函数和算法,可以方便地进行信号调制和解调的研究与实现。
本文将介绍如何使用Matlab进行信号调制和解调技术,并通过实例展示其在通信系统中的应用和效果。
一、调制技术概述调制技术是将需要传输的信息信号转换为载波信号的过程。
常见的调制技术包括幅度调制(AM)、频率调制(FM)和相位调制(PM)。
调制的目的是将低频信号转换为高频信号,使得信号能够在较长距离传输,并能够通过信道传输到接收端。
在Matlab中,可以使用内置函数如ammod、fmmod和pmmod来实现不同的调制技术。
以幅度调制为例,可以使用ammod函数来实现。
下面给出一个简单的幅度调制实例。
```matlabfs = 1000; % 采样频率t = 0:1/fs:1-1/fs; % 时间序列fc = 100; % 载波频率Ac = 1; % 载波幅度ym = sin(2*pi*10*t); % 原始信号ym_mod = ammod(ym, fc, fs, Ac); % 幅度调制```上述代码中,首先定义了采样频率fs、时间序列t、载波频率fc和载波幅度Ac。
然后,生成了一个原始信号ym,其中使用了sin函数生成了一个频率为10Hz的正弦波。
最后使用ammod函数对原始信号进行幅度调制,得到了调制后的信号ym_mod。
二、解调技术概述解调技术是将调制后的信号恢复为原始信号的过程。
解调技术主要包括幅度解调(AM)、频率解调(FM)和相位解调(PM)。
解调的目的是从调制信号中提取出原始信号,以实现信息的传输。
在Matlab中,可以使用内置函数如amdemod、fmdemod和pmdemod来实现不同的解调技术。
以幅度解调为例,可以使用amdemod函数来实现。
matlab电力电子 自动控制 电力系统仿真
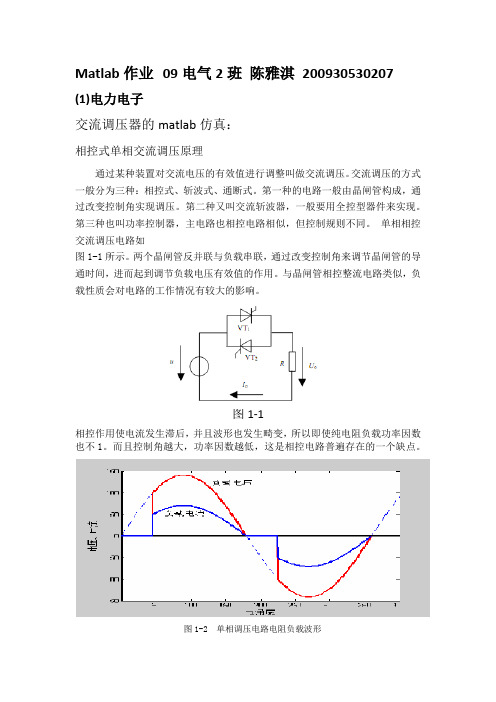
Matlab作业09电气2班陈雅淇200930530207 (1)电力电子交流调压器的matlab仿真:相控式单相交流调压原理通过某种装置对交流电压的有效值进行调整叫做交流调压。
交流调压的方式一般分为三种:相控式、斩波式、通断式。
第一种的电路一般由晶闸管构成,通过改变控制角实现调压。
第二种又叫交流斩波器,一般要用全控型器件来实现。
第三种也叫功率控制器,主电路也相控电路相似,但控制规则不同。
单相相控交流调压电路如图1-1所示。
两个晶闸管反并联与负载串联,通过改变控制角来调节晶闸管的导通时间,进而起到调节负载电压有效值的作用。
与晶闸管相控整流电路类似,负载性质会对电路的工作情况有较大的影响。
图1-1相控作用使电流发生滞后,并且波形也发生畸变,所以即使纯电阻负载功率因数也不1。
而且控制角越大,功率因数越低,这是相控电路普遍存在的一个缺点。
图1-2 单相调压电路电阻负载波形图1-3 带感性负载的交流调压电路图1-4 感性负载的电压和电流波形仿真如下:图 1-5 单相交流调压仿真图图1-8 输入脉冲信号设置仿真参数,仿真时间设置0.04s,仿真算法ode15s;启动仿真,结果如图1-9和图1-10。
图1-9 α=90°电流电压波形图1-10 α=10°电流电压波形(2)电力系统matlab仿真为了保证问题研究具有普遍性,我们选择了典型的电力系统——单机一无穷大系统如图1所示.vi 是机端电压、xi是变压器的电抗、x 1 和x 2 是线路电抗、Vs是无穷大电源电压.直接利用PSB中的以下模块来组成我们要研究的传统励磁控制系统。
仿真之前必须合理的设置算法和精度.算法和精度选择的不适合,将使仿真结果偏离理论与实际,出现仿真图象不连续或者发散的情况,很可能令仿真难以进行,甚至被系统自动中断.MATLAB针对不同的系统提供给用户两大仿真算法——定步长和变步长,可以通过Simulation中的Solver 进行设置.定步长求解器使用固定的步长对系统进行求解,有Discrete,ode5,ode4,ode3,ode2,ode1;变步长求解器则能够根据用户指定的积分误差自动调整仿真步长,有Discrete,ode45,ode23,ode13,ode15 s,ode23 s,ode23 t,ode23 tb.仿真算法的选择很重要,算法的合理与否将影响到仿真的结果和仿真速度.MATLAB 针对刚性系统(系统的特征值相差很大,既有快变特性又有慢变特性的系统)提供了ode15 s,ode23 s,ode23 t与ode23 tb 等算法.电力系统模型由于含有发电机这类刚性系统应采用ode15 s,ode15 s是刚性系统的变阶次多步解法,因此仿真结果较准确.MATLAB 使用户方便地控制仿真精度,用户可以对积分绝对误差和相对误差进行合理的设置.减小积分误差限可提高系统仿真结果的精度,但系统仿真速度将变慢;使用较大的积分误差限或者定步长求解器可以加快系统的仿真速度,但会使仿真结果的精度降低.具体应用时应综合考虑系统仿真精度与仿真效率,来决定仿真模型的Relative tolerance 和Absolute tolerance: 的选项.综上,将求解器设置(Solver options)如下:Type: Varible step. Ode15 (s) (stiff/NDF) Max step size: auto Relative tolerance:1e-2Min step size: auto Absolute tolerance:1e-16Initial step size: auto Maximum order 5小扰动试验t= 5 s时在系统的励磁调节器机端电压参考输入端(vref)加上阶跃扰动(5%),进行小扰动试验,记录下该扰动下电功率Pe的时域响应如图3所示短路试验在t = 5.1 s时系统出现三相短路故障,在=5.2 s排除故障将线路重新闭合,得到系统电功率短路故障的时域响应如图4 所示.(3)自动控制matlab仿真三阶系统单位反馈传递函数F(s)=3(s^2+4s+3)/(2s^3+s^2+4s+2)Matlab参数如下:num=3*[1 4 3];den=[2 1 4 2];sys=tf(num,den);p=roots(den)t=0:0.01:3;figure(1)impulse(sys,t);gridxlabel('t');ylabel('c(t)');title('impulse response'); figure(2)step(sys,t);gridxlabel('t');ylabel('c(t)');title('step response'); figure(3)u=t;lsim(sys,u,t,0);gridxlabel('t');ylabel('c(t)');title('ramp response');单位脉冲响应单位阶跃响应单位斜坡响应。
电路原理的MATLAB模拟研究

电路原理的MATLAB模拟研究引言电路原理是电子信息类专业中必修的一门课程,它是电子领域的基础。
电路原理的学习过程中,需要通过理论学习、实验操作及仿真模拟等方式进行深入了解。
其中,MATLAB模拟技术是一种常用的电路仿真方法,其可以在计算机上进行电路分析和测试,是电路设计和优化的重要工具。
本文将对电路原理的MATLAB模拟研究进行探讨。
一、电路原理的基本知识电路是指由电子元件及其组成的系统。
它可以分为直流电路和交流电路两种,其中直流电路是指电流方向不变的电路,如电池供电的电路。
而交流电路则是指电流方向会反复变化的电路,如交流电源供电的电路。
电路中的主要元件包括电源、电阻、电容和电感等。
电路中,电源提供电流,电阻限制电流,电容和电感则分别充当电荷和磁场的存储器。
电路中的电压、电流、功率及其他参数都是通过电路的分析和测试来测量和计算的,因此电路分析和测试是电路原理课程学习的重要内容。
二、MATLAB电路模拟技术MATLAB电路模拟是一种常用的电路仿真技术,它使用MATLAB软件来模拟电路的行为和性能。
因为MATLAB具有可视化的优势,所以该技术可以帮助电子工程师和设计师更好地理解电路的各个部分,并在设计和优化电路时进行分析。
1. MATLAB电路仿真原理MATLAB电路仿真的基本原理是将电路模型转换为MATLAB语言,然后使用MATLAB电路仿真工具箱中的相关函数和命令来模拟电路的行为和性能。
MATLAB电路仿真工具箱通常可以包括电路仿真软件、工具箱和用于可视化信号处理的MATLAB脚本。
【注】MATLAB是一款数学计算软件,它提供了各种工具箱、函数库和模型库,可以进行高级数学计算、数据分析、信号处理等各种数学操作。
2. MATLAB电路仿真步骤MATLAB电路仿真的步骤主要包括电路建模、仿真参数配置、仿真模拟和结果输出等。
电路建模是指利用MATLAB语言将电路模型转换为MATLAB的仿真模型。
在该过程中,需要创建电路模型、电路参数、传输关系和基本元件等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Southwest university of science and technology Matlab分析RLC电路的电压调制系统姓名:李海浪学号:20085054班级:自动0802姓名:文静学号:20085100班级:自动0804姓名:冯艺学号:20085105班级:自动0804姓名:于志民学号:20085106班级:自动0804姓名:李智豪学号:20085125班级:自动0804姓名:李春华学号:20085126班级:自动0804Matlab分析RLC电路的电压调制系统串联电路如图所示:其中R、L、C均为常数,输出端开路(或者负载很大,可以忽略),建立输入输出间的数学模型,并用Matlab仿真调试,修改电路。
遵照建立微分方程的步骤,可有:(1)确定输入量为U r(t),输出量U c(t),中间量为i(t)。
(2)该电路由一个电感L,一个电阻R和一个电容C组成,由霍尔夫电压定律可得:L didt+Ri+u c=u r(t)(1-1)(3)列写出中间变量i和输出量uc的关系式:i=C du cdt(1-2)(4)为消去中间变量i,可对式(1-2)微分,得:di dt =C d2u cdu2 (1-3)(5)将式(1-2)和式子(1-3)代入式子(1-1),可得:LC d2u cdt2+RC du cdt+u c=u r (1-4)将R=1000Ω,L=500H,C=500uF带入(1-4)既可以得出:d 2u c dt 2+2du cdt+4u c =4u r 下面借助于MATLAB 来进一步分析:有微分方程,可以得到其传递函数,由其传递函数在来分析其系统的其他因素 在MATLAB 下输入: num=[4]; den=[1 2 4]; G=tf(num,den) 得到:Transfer function: 4 -------------- s^2 + 2 s + 44)2(4)()(++=S S S R S C由传递函数可以知道其零、极点分布图 在MATLAB 下输入: >>num=[0 4];>>den=conv([0 1],conv([0 1],[1 2 4])); >>pzmap(num,den); >>grid;>>title('Pole-Zero Map 4/(s^2+2s+4)');由零、极点分布可以知道此系统为欠阻尼系统。
系统最终趋向于稳定的…… 由MATLAB 得出系统根轨迹…… >>num=[0 0 4]; >>den=[1 2 4]; >>rlocus(num,den) >> v=[-3 0 -10 10]; >>axis(v) >>grid>>title('Rott Locus Plot of G(S)=4/(S^2+2*S+4)')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.1P ole-Zero M ap 4/(s 2+2s+4)Real AxisI m a g i n a r y A x i s稳定性:由根轨迹图可见,无论开环增益K 取何值,系统的根轨迹曲线和相应大的系统极点分布在S 的左半平面内,故该闭环系统总是稳定的。
关于系统的稳定,也可以用劳斯表判定。
观察响应曲线 在MATLAB 输入: >>num=[0 0 4]; >>den=[1 2 4]; >>step(num,den); >>grid;>>title('response of 4/(s^2+2s+4)');-3-2.5-2-1.5-1-0.5-10-8-6-4-2246810Rott Locus P lot of G(S)=4/(S 2+2*S+4)Real AxisI m a g i n a r y A x i s动态性能指标可如下求得: 建立m 文件 num=[0 0 4]; den=[1 2 4];[y,x,t]=step(num,den); [peak,k]=max(y); overshoot=(peak-1)*100 tp=t(k) n=1;while y(n)<1 n=n+1; end tr=y(n) m=length(t)while(y(m)>0.98)&(y(m)<1.02)12345600.20.40.60.811.21.4response of 4/(s 2+2s+4)Tim e (sec)A m p l i t u d em=m-1; end ts=t(m)后在debug 下save and runovershoot = 16.3011 tp = 1.8221 tr = 1.0033 m = 109 ts = 4.0307上升时间:t r =1.0033S 峰值时间:t p =1.8221S 调节时间:ts =4.0307S 超调量:б%=16.3011%静态性能:静态速度误差常数:2S 1- 静态加速度误差常数:0以上性能指标可以通过超前、滞后和滞后超前装置改变来适应工程的要求。
现就基于根轨迹法的超前校正: 开环传递函数为:G(S)=)2(s 4s系统闭环传递函数为4)2(4)()(++=S S S R S C =))((3j 1314-+++S j S闭环极点位于 S=-1±j 3闭环系统的阻尼比为0.5,无阻尼自然振荡频率为2rad/S ,静态速度误差常数为2S 1-。
现在要求改变闭环极点,使无阻尼自然振荡频率为n ω=4rad/S ,同时又不改变阻尼比的值,即保持5.0=ξ。
阻尼比0.5要求复数极点位于一条通过原点且与负实轴成±60°夹角的直线上。
因为阻尼比确定了共轭复数闭环极点的角坐标,极点与原点之间的距离取决与无阻尼自然振荡频率n ω,所以确定期望闭环极点的位置是:S=-2±j23G(s)在希望的闭环极点上的幅角为:∠︒-=++-=210)2(4322j s s s为了使根轨迹通过希望的闭环极点,超前校正装置必须在该点上产生︒=30φ的幅角。
据此确定超前校正装置的极点和零点,有两个未知数α和T ,下面介绍求α的最大可能值的步骤,见图1(比较大的α值将产生比较大的v K 值,比较大的v K 值代表比较好的系统性能。
)图1首先,通过期望主导闭环极点的位置P 值,画一条水平线A P 和一条连接P 点与原点的直线P O 。
将A P 与P O 之间的夹角等分得PB ,然后画PC 和PD 两条直线,它们与等分线PB 构成夹角2/φ±。
PC 和PD 与负实轴的交点,给出了超前网络极点和零点的值。
这样设计出来的校正装置,将使P 点落在校正系统的根轨迹上。
利用幅值条件,可以确定开环增益。
可以确定超前校正装置的零点和极点,如图2所示。
它们是零点位于s=-2.9,极点位于s=-5.4或345.09.21==T ,T α=185.04.51= 因此537.0=α。
则校正后系统的开环传递函数:()()()))(()()(4.5s 2s s 9.2s 2s s 44.5s 9.2s s 1s 1s s s cc c +++K =+•++K =•T+T +K =G G G α式中c 4K =K ,已校正系统的根轨迹如图所示。
图2增益K 可以根据幅值条件计算如下: 参考图2,增益K 为:()()()14.529.2s 322=+++K +-=j s s s s即7.18=K 由此得到()()()()()4.529.27.18+++=s s s s s G s G s 超前校正装置的常数68.447.18==K c 因此,51.2=K αc 。
于是超前校正装置的传递函数为 ()4.59.268.41185.01345.051.2++=++=s s s s s G c采用运算放大器的电子线路用作设计出来的超前校正装置,则该超前校正装置的参数值由下式确定:()()1185/01345.051.21122311142o ++⨯=++=E E s s s C R R R s C R R R s s i 如图3所示。
我们可以任意选择()F C C u 1021==和()Ω=k 103R 静态速度误差常数v K 由下式求出:v K =()()()()()()100s 02.54.529.27.18lim lim -→→=+++=s s s s s s s G s sG s c 设计出的系统的第三个闭环极点,可以通过用已知因式除特征方程式求得如下: ()()()()()()4.33223229.27.184.52+-+++=++++s j s j s s s s s图3上述校正方法使我们能够将闭环主导极点配置到复平面内希望的位置上。
第三个极点s=-3.4靠近增加的零点s=-2.9。
因此,该极点对瞬间响应的影响相当小。
因为对非主导极点未做任何限制,对于静态速度误差系数的值也未做任何规定,所以我们断定,上述设计是令人满意的。
下面用MATLAB 研究校正前后系统的单位阶跃响应特性。
校正系统的闭环传递函数为()()()()()()9.27.184.529.27.18s +++++=s s s s s s R C =23.545.294.723.547.1823++++s s s s 因此对未校正和校正后的阶跃响应图绘制如下:建立m 文件:numc=[0 0 18.7 54.23]denc=[1 7.4 29.5 54.23]num=[0 0 4]den=[1 2 4]t=0:0.05:5;[c1,x1,t]=step(numc,denc,t);[c2,x2,t]=step(num,den,t);plot(t,c1,t,c1,'o',t,c2,t,c2,'x')gridtitle ('Unit-step Response of Compensated and Uncompensated Systems') xlable('t Sec')ylable('Output c1 and c2')text(0.6,1.32,'Compensated system')text(1.3,0.68,'Uncompensated system')保存并运行Unit-step Response of Compensated and Uncompensated Systems00.51 1.52 2.53 3.54 4.55已校正系统的最大过调量显得略大一些,已校正系统的调整时间是未校正系统的一半。
