大学物理《力学》课后思考题题解
《力学》杜婵英 漆安慎课后习题答案大全集

h(10)=99.0005 米;显然,x=-10 亦是极小值点,h(-10)=h(10).
3.求下列不定积分
⑴ ∫ (x3 − 3x + 1)dx
∫ ⑵ (2 x + x 2 )dx
第 1 章物理学力学数学 微积分初步习题解答
∫ ⑶
(
3 x
+
2e x
−
1 )dx
xx
∫ ⑸
dx x2
1+ x2
∫ ⑺ e−2x dx
⑼ ∫ sin 2 x cos xdx
⑷ ∫ (sin x − cos x)dx
⑹ ∫ sin(ax + b)dx
∫ ⑻
dx
ax+b
∫ ⑽ xe−x2 dx
(11) ∫ cos2 xdx
∫ (12)
ln x x
dx
解:
∫ ∫ ∫ ∫ ⑴ (x3 − 3x +1)dx =
x3dx − 3 xdx +
dx
=
1 4
x4
−
3 2
x2
+
x
+
c
∫ ∫ ∫ ⑵
(2 x + x 2 )dx =
2x dx +
x 2dx
=
2x ln 2
+
1 3
x3
+
c
∫ ∫ ∫ ∫ ⑶
(
3 x
+
2e x
−
1 )dx
xx
=
3
dx x
+
2
e x dx −
x −3 / 2 dx
= 3ln x + 2e x + 2 + c x
《理论力学》思考题及习题

《理论力学》思考题及习题宁夏大学机械工程学院技术基础部使用教材:理论力学(Ⅰ).哈尔滨工业大学理论力学教研室,第六版.北京:高等教育出版社.说明:以下各章的思考题及习题的页码和题号均以“哈工大”第六版《理论力学》教材为准。
静力学第一章静力学公理和物体的受力分析思考题:1.合矢与合力概念相同吗?2.几何法求合矢时,分矢与合矢怎样区别?3.力沿任意两个轴分解时的两个分力与力向该二轴的投影大小是否相同?4.二力平衡与作用力、反作用力的概念有什么不同?5.二力杆或二力构件的受力特点是什么?6.不计重力但作用有力偶的杆是二力杆吗?7.三力平衡汇交时怎样确定第三个力的作用线方向?8.画受力图的一般步骤是什么?在画物系中各个分离体的受力图时需要注意什么?9.P18思考题。
习题:P20-21:1-1 (a) (c) (d) (e) (g) (i) (j) (k); 1-2 (a) (d) (f)(i)(m) (o) 第二章平面汇交力系与平面力偶系思考题:1.汇交力系的几何法与解析法在应用上各有什么特点?2.解平衡问题时的一般步骤与注意事项?3.解物系问题时的注意事项?4.P33思考题。
5.力偶的特点与等效条件是什么?6.解力偶系平衡问题时的一般步骤与注意事项?习题:P36-40:2-1;2-3; 2-9; 2--12 (a) (c);2—14;2—17第三章平面任意力系思考题:1.力线平移定理的含义?2.用二矩式、三矩式求解问题时,附加什么条件才能保证物系平衡?3.求解平衡问题时,有哪些技巧可以使计算方便?4.P61思考题。
5.物系问题的解题思路?怎样选取研究对象?怎样列方程?6.销钉既受力又连接两个以上物体时的受力分析需掌握什么原则?7.怎样能做到一个方程求解一个未知数?8.节点法的本质是什么?9.截面法的本质是什么?10.怎样判断零杆?习题:P63-71:3-1;3-4;3-6;3-12(a);3-13;3-22;3-34第四章空间力系思考题:1.空间力系化简结果与平面力系化简结果的关系?2.什么力系有六个平衡方程?什么力系有三个平衡方程?什么力系有两个平衡方程?什么力系只有一个平衡方程?3.计算重心的常用方法。
大学物理-量子力学基础习题思考题及答案

习题22-1.计算下列客体具有MeV 10动能时的物质波波长,(1)电子;(2)质子。
解:(1) 电子高速运动,设电子的总能量可写为:20K E E m c =+ 用相对论公式,222240E c p m c=+ 可得p ===h p λ==834-=131.210m -=⨯(2)对于质子,利用德布罗意波的计算公式即可得出:3415h 9.110m p λ--====⨯22-2.计算在彩色电 视显像管的加速电压作用下电子的物质波波长,已知加速电压为kV 0.25,(1)用非相对论公式;(2)用相对论公式。
解:(1)用非相对论公式:mmeU h mE h 123193134108.71025106.1101.921063.622p h ----⨯=⨯⨯⨯⨯⨯⨯⨯====λ(2)用相对论公式:420222c m c p +=EeU E E k ==-20c mm eU eU c m hmE h 12220107.722p h -⨯=+===)(λ22-3.一中子束通过晶体发生衍射。
已知晶面间距nm 1032.72-⨯=d ,中子的动能eV 20.4k =E ,求对此晶面簇反射方向发生一级极大的中子束的掠射角.解:先利用德布罗意波的计算公式即可得出波长:3411h 1.410m λ--====⨯再利用晶体衍射的公式,可得出:2sin d k ϕλ= 0,1,2k =…11111.410sin 0.095k λϕ--⨯=== , 5.48ϕ= 22-4.以速度m/s 1063⨯=v 运动的电子射入场强为5V/cm =E 的匀强电场中加速,为使电子波长A 1=λ,电子在此场中应该飞行多长的距离?解:3410h 110p m λ--====⨯ 可得:U=150.9V ,所以 U=Ed ,得出d=30.2cm 。
22-5.设电子的位置不确定度为A 1.0,计算它的动量的不确定度;若电子的能量约为keV 1,计算电子能量的不确定度。
大学物理课后习题全解及辅导
列平衡方程:
(2)研究AB(二力杆),受力如图:
可知:
(3)研究O1B杆,受力分析,画受力图:
列平衡方程:
第三章
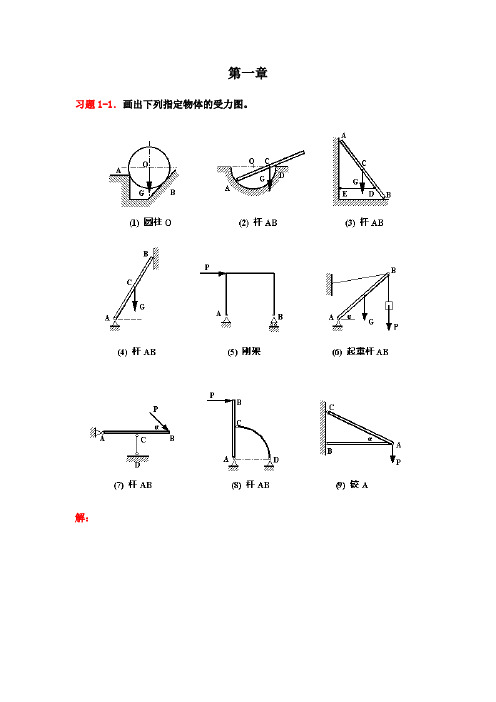
习题3-1.求图示平面力系的合成结果,长度单位为m。
解:(1)取O点为简化中心,求平面力系的主矢:
求平面力系对O点的主矩:
(2)合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
由图知:
(2)研究铰C,受力分析,画力三角形:
由图知:
习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
解:(1)研究滑块A,受力分析,画力三角形:
由图知:
研究AB杆(二力杆)和滑块B,受力分析,画力三角形:
(2)由力三角形得:
(3)列平衡方程:
由(2)、(3)得:
(4)求摩擦系数:
习题5-3.尖劈顶重装置如图所示,尖劈A的顶角为α,在B块上受重物Q的作用,A、B块间的摩擦系数为f(其他有滚珠处表示光滑);求:(1)顶起重物所需力P之值;(2)取支力P后能保证自锁的顶角α之值。
解:属平面汇交力系;
合力大小和方向:
习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:
画力三角形:
相似关系:
几何关系:
约束反力:
(2)研究AB,受力分析:
画力三角形:
相似关系:
几何关系:
约束反力:
习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。求撑杆BC所受的力。
大学物理课后习题-答案详解

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线 (2)质点的位置 : 22(48)r ti t j =+- 由d /d v r t =则速度: 28v i tj =+ 由d /d a v t =则加速度: 8a j =则当t=1s 时,有 24,28,8r i j v i j a j =-=+= 当t=2s 时,有 48,216,8ri j v i j a j =+=+=2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式. 解:=a d v /d t 4=t d v 4=t d t⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的d d r t ,d d v t ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t = 而落地所用时间 gh2t = 所以0d -2g h d r v i j t =d d v g j t =- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
大学物理学基础教程力学部分习题详解

第一章 力学引论本章主要阐述了力学的研究内容(即物体的机械运动),以及矢量分析和量纲分析的方法。
习 题1-1 什么叫质点?太阳、地球是质点吗?分子、原子是质点吗?试举例说明。
分析:本题说明参考系选择的重要性。
对于相同的物体,如果参考系的选择不同,结果将完全不同。
选择某一参考系,可以看成质点;选择另一参考系,就不可以看成质点。
答:在某些问题中,物体的形状和大小并不重要,可以忽略,可看成一个只有质量、没有大小和形状的理想的点,这样的物体就称为质点。
关于太阳、地球、分子、原子是否是质点,要视具体研究的问题而定。
例如,如果我们考察银河系或者整个宇宙的运动,那么太阳和地球的大小可以忽略,而且我们没有必要去考察他们的转动,此时它们可以被看作质点。
但是,如果我们要研究人造卫星、空间站的话,太阳和地球的大小和形状以及其自转就不能被忽略,那么它们就不能被看作质点。
1-2 西部民歌:“阿拉木汗住在哪里,吐鲁番西三百六。
”从位矢定义分析之。
分析:本题是关于参考系和坐标系选择的问题。
遇到一个问题,首先要搞清楚研究对象,然后选择一个合适的参考系,在此参考系中选择一个点作为坐标原点,建立坐标系,然后才可以定量的分析问题。
本题中心意思是选择则吐鲁番作为参照点,来定义阿拉木汗所住的位置。
答:选择地面参照系,以吐鲁番作为原点,正东方向为x 轴正方向,正北方向为y 轴正向,在地面上建立直角坐标系。
那么阿拉木汗住址的位矢为:i ˆ360r −=v1-3 判断下列矢量表达式的正误:分析:本题考察矢量的运算问题。
矢量既有大小,又有方向,所以在进行矢量运算时,既要考虑矢量的大小,又要考虑矢量的方向。
(1)B A B A v v v v +=+答:× 矢量按平行四边形法则相加,而不是简单的数量相加(2)A B B A v v v v ×=×答:× 矢量相乘按右手定则,上式方程两边的矢量大小相同,方向相反。
大学物理学课后习题答案

习题及解答(全)习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r -=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆt r t d d d d d d r rr += 式中t rd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a trv ==其二,可能是将22d d d d t r tr 与误作速度与加速度的模。
大学物理 力学部分习题解答

第1章 质点运动与牛顿定律1-9 一人自坐标原点出发,经20(s)向东走了25(m),又用15(s)向北走了20(m),再经过10(s)向西南方向走了15(m),求:(1)全过程的位移和路程;(2)整个过程的平均速度和平均速率。
分析:从位移的概念出发,先用分量之差表示出每段位移,再通过矢量求和而求出全过程的位移,进而由路程、平均速度和平均速率的概念求出路程、平均速度和平均速率。
解: (1)以人为研究对象,建立如图所示的直角坐标系, 全过程的位移为:r r r r OC OA AB BC Δ=Δ+Δ+Δ()()()()A O B A C B C B =x x +y y +x x +y y ----i j i j =25+2015451545i j i j 00cos sin --j i 4.94.14+=其大小为:2222Δ=(Δ)+(Δ)=(14.4)+(9.4)=17.2()OC r x y m全过程位移的方向为:01.334.144.9==∆∆=arctg x y arctg θ 即方向向东偏北01.33 (2)平均速度 OCr tυ∆=∆ 其大小为:()117.20.3845OC r m s t υ-∆===⋅∆ 平均速度的方向沿东偏北01.33 平均速率 25201545s t υ∆++==∆()133.1-⋅=s m 1-10 一质点P 沿半径 3.00m R =的圆周作匀速率运动,运动一周所需时间为20.0s ,设0t =时,质点位于O 点。
按如图所示的坐标系oxy ,求:(1)质点P 在任意时刻的位矢;(2)5s 时的速度和加速度。
分析:只要找出在任意时刻质点P 点的坐标x 、y ,(通过辅助坐标系'''o x y 而找出)就能表示出质点P 在任意时刻的位矢x y =+r i j ,进而由r 对时间求导求出速度υ和加速度a 。
解:如图所示,在'''o x y 坐标系中,因t Tπθ2=,则质点P 的参数方程为: 22`,`x Rsin t y Rcos t T Tππ==- 图1-30 习题1-10图解习题1-9图解坐标变换后,在oxy 坐标系中有: 2`x x Rsint T π==,02`y y y Rcos t R Tπ=+=-+ 则质点P 的位矢方程为: 22ππ=Rsint +Rcos t +R T T ⎛⎫ ⎪⎝⎭-r i j ()()=30.1310.1i j sin t cos t ππ+⎡⎤⎣⎦- 5s 时的速度和加速度分别为 :22220.3r i j j υd R cos t R sin t dt T T T Tπππππ==+=2222222=()+()(0.03)22d =R sin t R cos t =dt T T T Tπππππ--r a i j j1-11 已知一质点的运动方程为2362x t t =-(单位为SI 制),求:(1)第2秒内的平均速度;(2)第3秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考题参考答案1.1 国际单位制中的基本单位是哪些? 答: m (米)、kg (千克,公斤)、s (秒)、A (安培)、K (开尔文)、mol (摩尔)和cd (坎德拉).1.2 中学所学匀变速直线运动公式为2021at t v s +=,各量单位为时间:s (秒),长度:m (米). (1)若改为以h (小时)和km (公里)作为时间和长度的单位,上述公式如何?(2)若仅时间单位改为h,如何?(3)若仅0v 单位改为km/h,又如何?答: (1)因为加速度的单位是m/s 2,所以需将时间t 乘上系数3600化成秒,再与a相乘后单位变成了m,最后再乘上系数10001从而将单位化成km,故2202110003600at t v s ⋅+=(2) 220213600at t v s ⋅+=(3) 202136001000at t v s +=1.3 设汽车行驶时所受阻力F 与汽车的横截面S 成正比且和速率v 之平方成正比.若采用国际单位制,试写出F 、S 和2v 的关系式;比例系数的单位如何?其物理意义是什么? 答: 2kSvF = k 的单位为:()()322222m kg s mm s m kg s mm N=⨯⋅=⨯ 物理意义:汽车行驶时所受的空气阻力与空气的密度成正比.1.4 某科研成果得出⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=--1321312910110m m m m m m p α 其中m 、1m 、2m 和Pm 表示某些物体的质量,310-、2910-、α和1为纯数即量纲为1.你能否初步根据量纲判断此成果有误否?答: 等式两边的量纲相等,均为1,所以,此成果无误.2.1 质点位置矢量方向不变,质点是否一定作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?答: 位置矢量:由参考点引向质点所在位置的矢量.(1)当位置矢量方向不变时有21t t r k r=(t 1、t 2为任意两个时刻,k 为常数),说明质点各个时刻必处于1t r所在方向的直线上,所以质点做直线运动.(2)当质点沿直线运动时,其位置矢量的方向改变与否可分以下三种情况进行讨论.○1若所选的参考点O 在质点运动轨迹的延长线上,那么其位置矢量的方向不变.○2若所选的参考点O 在质点运动轨迹上,那么其位置矢量的方向会发生改变.○3若所选的参考点O 在质点运动所在直线之外,那么其位置矢量的方向会发生改变.2.2 若质点的速度矢量的方向不变仅大小改变,质点作何种运动?速度矢量的大小不变而方向改变,作何种运动?答:(1)若质点的速度矢量的方向不变仅大小改变,质点将作变速直线运动; (2)若质点的速度矢量的大小不变而方向改变,质点将作匀速率曲线运动(比如匀速圆周运动)2.3 “瞬时速度就是很短时间内的平均速度”,这一说法是否正确?如何正确表述瞬时速度的定义?我们是否能按照瞬时速度的定义通过实验测量瞬时速度? 答: 不正确. 质点在t 时刻的瞬时速度等于t 至t+△t 时间内平均速度△r /△t当△t →0时的极限.即trv v t t ∆∆==→∆→∆lim lim 00.按照瞬时速度的定义,瞬时速度不O能通过实验测量.2.4 试就质点直线运动论证:加速度与速度同符号时,质点作加速运动;加速度与速度反号时作减速运动.是否可能存在这样的直线运动,质点速度逐渐增加但其加速度却逐渐减小?答:(1)设质点做直线运动的初速度0v 的方向为正,由加速度定义dtdva =得⎰⎰=tt v v adt dv t,()00t t a v v t -=-则○1当加速度与初速度同符号时,即0>a ,有()00>-t t a ,所以0v v t>即质点作加速运动;○2当加速度与初速度反号时,即0<a ,有()00<-t t a ,所以0v v t<即质点作减速运动。
(2)经过(1)中讨论得知,在直线运动中,不论加速度的大小如何变化,只要加速度与初速度同符号,质点就作加速运动,即速度逐渐增加。
所以质点速度逐渐增加但其加速度却逐渐减小的直线运动是存在的。
2.5 设质点直线运动时瞬时加速度a x =常量,试证明在任意相等的时间间隔内的平均加速度相等.2.6 在参考系一定的条件下,质点运动的初始条件的具体形式是否与计时起点和坐标系的选择有关?答:质点运动的初始条件的具体形式与计时起点和坐标系的选择有关。
在平面直角坐标系中()()()()00000000t v v t v v t y y t x x y y x x ====在自然坐标系中 ()00t s s = 在极坐标系中 ()()0000t t r r θθ==2.7 中学时曾学过at v v t +=0,2021at t v s +=,as v v t 222=-这几个匀变速直线运动的公式,你能否指出在怎样的条件下,可得出这几个公式.答:(1)由dt dva =得⎰⎰=t t v v adt dv t 00,()00t t a v v t -=-则要得到at v v t +=0必须有初始条件00=t 。
(2)匀变速直线运动的位移()()()200000021t t a t t v s t t v s s -+-+=-+=则要得到2021at t v s +=必须有初始条件0,000==s t 。
(3)由at v v t +=0,2021at t v s +=两式消去t 可得到as v v t 222=-,所以得到as v v t 2202=-的初始条件是0,000==s t 。
2.8 试画出匀变速直线运动公式(2.3.8)和(2.3.9)的t v x -图和t a x -图.2.9 对于抛体运动,就发射角为2;0;0πααπα±==->>这几种情况说明它们各代表何种运动.答:(1)πα->>0且2πα-≠时为斜向下抛;(2)0=α时为平抛;(3)2,2παπα-==时分别为竖直上抛和竖直下抛。
2.10A 、B 、C 、D 、E 各点图2.102.11 质点作上斜抛运动时,在何处的速率最大,在何处速率最小? 答:如图2.10,质点作上斜抛运动,其在水平方向上的分运动为匀速直线运动,在竖直方向上的分运动为初速度为y v0,加速度为g 的匀变速直线运动。
故在抛出点A 及落地点E 处的速率最大,在最高点C 处的速率最小。
2.12 试画出斜抛运动的速率-时间曲线.答:斜抛运动可分解为在水平方向上的匀速直线运动,在竖直方向的匀变速直线运动。
故有:gt v v v v y y x x -==00,所以在A C 阶段:()220222gt v v v v v oy x y x -+=+=,v 是关于t 的二次函数,所以可根据数学知识作图在C E 阶段:()222202220oy ox oy x y x v gt v gv t g v v v v -+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++=+=仍为二次2.13 在利用自然坐标研究曲线运动时,v v v t、、三个符号的含义有什么不同? 答:t t t t e dtds e t s t r v=∆∆=∆∆=→∆→∆00lim lim 这是自然坐标中质点做曲线运动的速度dtdsv t = 这是速度v 在切向单位矢量方向的投影,有t t e v v =。
v 是速率,由于质点任何时刻的速度总沿轨迹切线,速度v只有切向投影t v ,不存在速度法向分量,t v 不同于v ,t v 的正负反映运动的方向,因此有t v v =。
2.14 如图所示质点沿圆周运动,自A 点起,从静止开始作加速运动,经B 点到C 点;从C 点开始作匀速圆周运动,经D 点直到E 点;自E 点以后作减速运动,经F 点又到A 点时,速度变成零.用矢量表示出质点在A 、B 、C 、D 、E 、F 各点的法向加速度和切向加速度的方向.答:由t t n t t n n e dtdv e R v e a e a a+=+=2得到下图2.15 什么是伽利略变换?它所包含的时空观有何特点?3.1 试表述质量的操作型定义.答:通过实验发现在气垫平台上两滑块1和2以某速度运动并相互碰撞,它们各自的速度改变1v ∆和2v ∆总有这样的关系:12v v ∆-=∆α或12/v v∆∆=α,其中α为常量。
取不同的滑块反复实验多次仍得到上式,只是α取值不同而已,所以α与两滑块有关。
那么令标准物体(质量kg m 10=)与某物体(质量为m )相互作用,并用v v∆∆、0分别表示标准物体与某物体速度的改变量,将与二物体有关的α记作0/m m ,则有:kg v v v v m m∆∆=∆∆=//000。
这便是某物体“质量的操作型定义”。
3.2 如何从动量守恒得出牛顿第二、第三定律.何种情况下,牛顿第三定律不成立? 答:(1)在经典力学中,质点质量保持恒定则:()a m dtv d m dtv m d F i===∑ 即牛顿第二定律 (2)两个质点组成的系统动量守恒则有:()()dtv m d dt v m d v m v m 22112211-=⇒∆-=∆又因为()()dt v m d F dt v m d F 22121121 ==、 所以得 1221F F-= 即牛顿第三定律(3)在经典的电磁理论中,粒子和场均有动量,带电质点间的相互作用以电磁场为媒介,将动量守恒定律应用于含两带电质点和场组成的体系中,质点和场的动量均需计算在内。
如在某过程中,该体系动量守恒,而场的动量发生了变化,两带电质点的动量和也将改变。
于是,两质点各自动量变化率将不再等值反向,牛顿第三定律不再成立。
3.3 在磅秤上称物体重量,磅称计数给出物体的“视重”或“表观重量”.现在电梯中测视重,何时视重小于重量(称作失重)?何时视重大于重量(称作超重)?在电梯中,视重可能等于零吗?能否指出另一种情况使视重等于零? 答:(1)磅秤称物体重量的原理是利用牛顿第三定律,磅秤对物体的支持力N 和物体对磅秤的压力是一对作用力与反作用力。
对物体进行受力分析如图所示: 选取竖直向上为正方向,那么○1当电梯向上加速或向下减速运行时 0>=-ma G N ,所以G N >即超重;○2当电梯向下加速或向上减速运行时 0<-=-ma G N ,所以G N <即失重。
(2)当电梯向下加速或向上减速的加速度大小g a =时有:mg G N -=-,从而有0=N 视重为零。
(3)用弹簧称吊一个物体一起做自由落体运动,弹簧称的读数将为零,即此时物体的视重等于零。
3.4 一物体静止于固定斜面上.(1)可将物体所受重力分解为沿斜面的下滑力和作用于斜面的正压力. (2)因物体静止,故下滑力αsin mg 与静摩擦力N F 0μ相等,α表示斜面倾角,N F 为作用于斜面的正压力,0μ为静摩擦系数。
