热力学基本公式的导出关系概念图
热力学函数的基本关系式

麦克斯韦关系式 S p V T T V
14
思考:定容或定压下S 随T 的变化率各等于什么?
S(T,p) S(T,V)
由定义式出发
1)由定义式出发
dS Qr C dT
定压
S Cp T p T
H p
T
T
V T
p
V
热力学状态方程,将U(或H)与p,V,T联系起来了。
—— 对实际气体,已知pVT状态方程式,代入,积分 可求ΔU、ΔH。
13
典型证明题:
证明: H T p V p V T T V V T
证:由热力学基本方程 dH = TdS + Vdp 定温下等式两边同除以dV,得
除了定义式外, 还可以导出四种类型的重要关系式
2
1. 热力学基本方程
封闭系统中, 微小可逆过程:dU=δQr+δWr
δWr ′=0时,
dS δ Qr T
δWr=-pdV,
dU=TdS-pdV
H=U+pV
dH=dU+pdV+Vdp
A=U-TS dA=dU-TdS-SdT
dH=TdS+Vdp
dA= - SdT - pdV
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V HS p源自H p SdA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
物理化学(第五版) 演示文稿2.10 热力学函数基本关系式

吉布斯函数的性质 及其应用
12
(1) 求U随V的变化关系
由基本方程 dU=TdS -pdV
等温下, dUT=TdST - pdVT
等式两边除以dVT ,即
dUT T dST p
dVT
dVT
写成 U T S p V T V T
由麦克斯韦方程 S p V T T V
于是 U T p p
S p
T
V T
p
可得
H p
T
T V T
p
V
15
(3) 求S与ቤተ መጻሕፍቲ ባይዱp的变化关系
1)由 dH=Qp,r= CpdT =TdS,可得
S Cp T p T
2)由热力学基本方程:dH = TdS+Vdp
等压(dp=0)下,等式两边同除以dT,则
H S T T p T p
V T T V
13
U T p p V T T V
对理想气体,由 pV=nRT
得
p
T V
nR V
代入上式,得 U 0 V T
证明了前面理想气体的特点:U=f(T)
14
(2) 求H随p的变化关系 由 dH=TdS+Vdp 出发,有
H p
T
T
S p
T
V
用麦克斯韦方程
答:-p ; -S。
G T p
2. 麦克斯韦关系式不涉及“熵与温度”的偏微商。
问题 S T p
S T V
答: Cp/T ; CV/T。
10
3.对于只做膨胀功的封闭系统,
A T
V
的值(
)
(A) 大于零; (B) 小于零; (C) 等于零。
4. 从热力学四个基本方程可导出 U ( )
2.11热力学函数间的关系

dc = 0 d ( cv ) = cdv d ( u ± v ) = du ± dv d ( uv ) = vdu + udv
u vdu − udv d = 2 v v
c为常数; u、v 为变量 为常数; 为常数
不定积分公式
∫ du = u + C
u m +1 u m du = +C ∫ m +1 du ∫ u = ln u + C
一、热力学基本关系式
(2) 因为
dH = TdS + Vdp
H = U + pV
d H = d U + p d V + Vd p
dU = TdS − pdV dH = TdS + Vdp
所以
一、热力学基本关系式
(3)
dF = − SdT − pdV
F = U − TS dF = dU − TdS − SdT
式中:m为常数(指数); C为积分常数。
二、对应系数关系式
U = f ( S ,V )
可逆过程) (W’=0;可逆过程) 可逆过程
F = f (T , V )
dU = (
∂U ∂U )V dS + ( ) S dV ∂S ∂V ∂U p = −( )S ∂V
dU = T dS − pdV
∂F ∂F )V dT + ( )T d V ∂T ∂V dF = − SdT − pdV dF = ( S = −( ∂F )V ∂T p = −( ∂F θ )T ∂V
第十一节 热力学函数间的关系
H
H = U + pV pV
U
U = H − pV
TS TS
课件热力学定律与能量守恒定律图文

2023课件热力学定律与能量守恒定律图文•热力学第一定律•热力学第二定律•能量的转化与守恒定律•热力学定律与能量守恒的相互关系目•实例分析•总结录01热力学第一定律1定义与内容23热力学第一定律的定义是能量守恒定律在热现象中的表现。
它表明,在封闭系统中,能量不能创造也不能消失,只能从一种形式转换成另一种形式。
热力学第一定律的内容是能量平衡方程,即Q=ΔU。
热力学第一定律的数学表达式是Q=ΔU+W,其中Q为传热热量,ΔU为系统内能的增量,W为系统对外做的功。
Q表示热力学系统吸收的热量,ΔU表示系统的内能增量,W 表示系统对外做的功。
数学表达式与符号热力学第一定律适用于封闭系统中涉及热现象的各种物理过程,如传热、相变、化学反应等。
对于开放系统,如气体膨胀对外做功或液体蒸发等过程,需要引入其他形式的能量转化,如电磁能、化学能等。
适用范围02热力学第二定律热力学第二定律的定义热力学第二定律是关于热现象的宏观自然过程具有方向性的原理,也就是说,热现象不可能自发地使物质的全部或一部分从低温状态向高温状态转化。
热力学第二定律的内容热力学第二定律规定了热力学过程中熵增加的方向,即熵增加原理。
在任何自然过程中,一个孤立系统的总熵不会减少,即系统的熵增加原理。
定义与内容热力学第二定律可以用数学公式表示为 dS≥0,其中S为熵,dS为微分符号,表示微分运算。
数学表达式热力学第二定律的符号为“≥”,表示在孤立系统中,系统的熵增加的方向是朝着熵增加的方向进行的。
符号数学表达式与符号适用范围01热力学第二定律适用于封闭系统,即系统与外界没有物质交换和能量交换。
02热力学第二定律适用于宏观自然过程,而不是微观粒子运动。
03热力学第二定律适用于孤立系统,即系统与外界没有相互作用。
03能量的转化与守恒定律定义能量守恒定律是指,在孤立系统中,能量既不会创生也不会消失,而只会从一种形式转变为另一种形式,从一个物体传递给另一个物体,能量的总玳保持不变。
热力学一般关系式思维导图-高清简单脑图模板-知犀思维导图
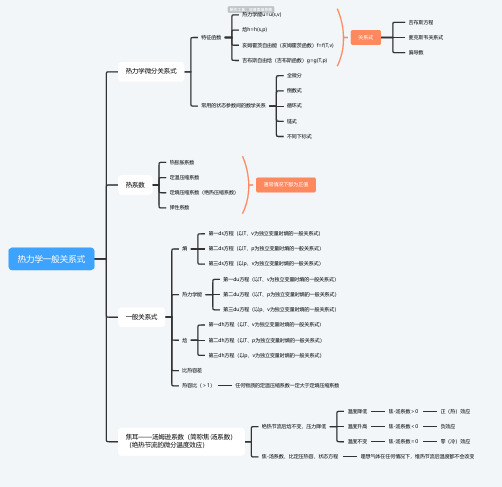
热力学一般关系式热力学微分关系式
特征函数
热力学能u=u(s,v)
焓h=h(s,p)
亥姆霍茨自由能(亥姆霍茨函数)f=f(T,v)
吉布斯自由焓(吉布斯函数)g=g(T,p)
关系式
吉布斯方程
麦克斯韦关系式
偏导数
常用的状态参数间的数学关系
全微分
倒数式
循环式
链式
不同下标式
热系数
热膨胀系数
定温压缩系数
定熵压缩系数(绝热压缩系数)
弹性系数
通常情况下都为正值
一般关系式
熵
第一ds方程(以T、v为独立变量时熵的一般关系式)
第二ds方程(以T、p为独立变量时熵的一般关系式)
第三ds方程(以p、v为独立变量时熵的一般关系式)
热力学能
第一du方程(以T、v为独立变量时熵的一般关系式)
第二du方程(以T、p为独立变量时熵的一般关系式)
第三du方程(以p、v为独立变量时熵的一般关系式)
焓
第一dh方程(以T、v为独立变量时熵的一般关系式)
第二dh方程(以T、p为独立变量时熵的一般关系式)
第三dh方程(以p、v为独立变量时熵的一般关系式)
比热容差
热容比(>1)任何物质的定温压缩系数一定大于定熵压缩系数
焦耳——汤姆逊系数(简称焦·汤系数)
(绝热节流的微分温度效应)
绝热节流后焓不变,压力降低
温度降低焦-汤系数>0正(热)效应
温度升高焦-汤系数<0负效应
温度不变焦-汤系数=0零(冷)效应
焦-汤系数、比定压热容、状态方程理想气体在任何情况下,维热节流后温度都不会改变。
2.5热力学第二定律公式的导出

代表着某个性质的改变量。我们把这种状态性质称为熵,
用S表示,其改变量S
S
SB
SA
B A
Qr
T
;
dS
Qr
T
熵是全微分
二、热力学第二定律
Q ir
(QT1 QT 2 QT 2
) ir
T2 T1 T2
;
QT 1 T1
QT 2 T2
ir
0
即
第五节 热力学第二定律 公式的导出
p
V
一、熵的引出
根据热力学第一定律和卡诺循环
dU 0 W ( Q1 Q2 )
-W Q2 Q1 T2 T1
Q2
Q2
T2
即 Q1 = - T1
Q2
T2
定义: Q 热温商
T
Q1 + Q2 = 0 T1 T2
结论:卡诺循环中,过程的热温商之和等于零。
方法:将与系统密切相关的环境包括在一起, 构成一个孤立系统。
S孤立= S系统S环境 0
“>” 号为自发过程 “=” 号为可逆过程 “<” 号为不可能发生的过程
S孤立 0
等号表示可逆过程,不等号表示不可逆过程。 孤立系统排除了环境对系统以任何方式的干扰,因此,孤立系 统中的不可逆过程必然是自发过程。
熵增加原理可表述为:孤立系统中自发过程的方向总是朝 着熵值增大的方向进行,直到在该条件下系统熵值达到最 大为止,此时孤立系统达平衡态。
三、熵增加原理
应用:熵增加原理用于孤立系统,可判别过程的方 向和限度。
T
结合 dS Qr 可逆过程
1.6 热力学函数的基本关系式

∂ H ∂ V ∂ p = −T ∂ T +V p T
11
δWr ′=0时, = 时
δ Qr dS = T
δWr=- =-pdV, ,
H=U+pV dH=dU+pdV+Vdp
dU=TdS-pdV
A=U-TS dA=dU-TdS-SdT
dH=TdS+Vdp
G=H-TS dG=dH-TdS-SdT
3
dA= - SdT - pdV
dG= - SdT+Vdp
dU = TdS- pdV - dH = TdS + Vdp dA = -SdT- pdV - dG = -SdT + Vdp 应用条件是 应用条件是: (1) 封闭系统;(2) 无非体积功;(3) 可逆过程。 封闭系统; 无非体积功; 可逆过程。 另外,下面的情况相当于具有可逆过程的条件: 另外 下面的情况相当于具有可逆过程的条件: 下面的情况相当于具有可逆过程的条件 (i) 定量纯物质单相系统 定量纯物质单相系统 单相系统; (ii) 定量,定组成的单相系统 定量,定组成的单相系统 单相系统; (iii) 保持相平衡及化学平衡的系统 保持相平衡 化学平衡的系统 相平衡及 的系统.
麦克斯韦关系式 :表示的是系统在同一状态的两种变化 率数值相等。因此应用于某种场合等式左右可以代换。 率数值相等。因此应用于某种场合等式左右可以代换。 等式左右可以代换
9
2. 热力学状态方程
由 dU=TdS-pdV = -
∂ U ∂ S = T −p ∂ V T ∂ V T
∂G ∂T P
[ ]
∂G ∂P T
=V
5
吉布斯2. 吉布斯-亥姆霍茨方程
第三章热力学第二定律13共50页PPT资料

M (y)x
2z, xy
N (x)y
2z xy
所以
M ( y )x
(
N x
)
y
Maxwell 关系式
将
dzM dxNdy
(
M y
)x
N ( x )y
应用于基本方程
四 (1) dUTdSpdV (V T)S (Sp)V 麦
个
基 (2) dHTdSVdp
本
方 (3) dASdTpdV
程
(Tp)S
(V S
用得多
( 4 ) ( d U ) S ,V 0 (5) (dH )S,p 0 (6) (dS )H ,p 0
用得少
五、Maxwell 关系式
全微分的性质
设函数 z 的独立变量为x,y 且z具有全微分性质
z z(x, y)
dz(xz)ydx(yz)xdy MdxNdy
M 和N也是 x,y 的函数
)p
克 斯
( S V
)T
(Tp)V
威 系 式
(4) dG SdTV dp
S (p)T
(V T
)p
Maxwell 关系式
Mexwell关系式
(T V
)S
(p S
)V
(T p
)S
(V S
)p
( S V
)T
( p T
)V
( S p
)T
(V T
)p
记忆规律: T-S,V-P对角。 带有(∂T-∂V)项有负号
§3.13 几个热力学函数间的关系
几个热力学函数之间的关系 热力学基本方程 从基本方程导出的关系式 特性函数 Maxwell 关系式 Maxwell 关系式的及其应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1
助学体系材料之五
运用概念图制作技术,掌握热力学函数关系
丽水学院化学化工系 张启伟
材料简介:运用概念图制作技术,构建了热力学函数关系概念图,包括了:四个热力学基本公式的导出关系概念图,八个派生公式及四个麦克斯韦(Maxwell)关系式,便于记忆。
一、热力学基本公式的导出关系概念图:
从热力学第一定律开始,根据各热力学函数的定义式,依次建立四个热力学基本公式的导出关系概念图(见图)。
热力学基本方程的适用条件:于封闭的热力学平衡系统所进行的一切可逆过程。
说的更详细些,它们不仅适用于一定量的单相纯物质,或组成恒定的多组分系统发生单纯p , V, T 变化的过程。
也可适用于相平衡或化学平衡的系统,由一平衡
状态变为另一平衡态的过程。
二、导出派生公式的二种方法
根据上面的四个热力学基本公式,每个热力学基本公式可派生出二个派生公式,共8个派生公式。
分别可以按二种方法得到派生公式,见图。
图2
图3
派生公式汇总表如下:
2
d H = T d S + V d p
等 压
(∂H /∂S )p =T 等 熵 (∂H /∂p )S =V 3
d A =-S d T - p d V
等 容
(∂A /∂T )V =-S 等 温 (∂A /∂V )T =-p 4
d G =-S d T + V d p
等 压
(∂G /∂T )p =-S 等 温
(∂G /∂p )T =V
注:同色偏微分的相同关系。
归纳为四组: T = (∂U /∂S )V = (∂H /∂S )p ;
p =-(∂U /∂V )S =-(∂A /∂V )T V = (∂H /∂p )S =
(∂G /∂p )T S =-(∂A /∂T )V =-(∂G /∂T )p
在学习过程中,一是要注意不同偏微分的相互替代关系;二是要注意难测或难得的偏微分可用一个简单的状态函数取代的关系。
三、麦克斯韦(Maxwell)关系式导出关系概念图
同样以四个热力学基本公式为基础,每个基本公式可导出一个Maxwell 关系式。
导出的数学模式概念图如下(见图):
按此求Maxwell 关系通式概念图,可分别写出四个热力学基本公式的Maxwell 关系式。
如:由热力学基本公式(1),写出该式的Maxwell 关系式。
图
2 求Maxwell 关系通式概念图
在学习过程中,重点掌握Maxwell关系的应用。
