发电机组的优化配置问题数学建模论文
数学建模论文

论文 2电力市场的输电阻塞管理奖奖等级:全国二等奖指导教师:参赛队员:、、摘要:本文根据电力市场的交易规则,就目前我国电力系统中各个发电机组的出力分配预案和各线路的有功潮流问题进行了深入分析,并对产生输电阻塞的分配预案进行了调整,得到了较好的出力分配方案。
1.根据各机组出力和各线路潮流的关系建立了一个多元线性回归模型(见模型一),利用所给实验数据采用最小二乘法回归,得到每条线路上的潮流值关于各发电机组出力的的近似表达式,并对每一个表达式进行了误差分析,得出各表达式的复相关系数,可以看出我们的回归效果显着,说明我们的模型是可靠、合理的。
2.我们采用pool 模式下的输电阻塞费用计算方法,公平对待序内序外两种情况,设计出了一种简明、合理的阻塞费用计算规则:第一、采用序外多发电量按照发电报价计算;第二、序内少发电量按清算价与发电报价之差价结算。
并建立了一个合理的计算阻塞费用模型。
3.在下一时段预报负荷需求为的条件下,根据市场规则,以最小购电费用为目标、以机组的段容量,爬坡速率作为约束条件,采用动态规划算法建立了一个单目标规划模型,通过数学软件MATLAB 编程给出各机组的出力分配预案,各台机组的出力分别为(MW ):150、79、180、、125、140、95、。
总费用为:总C =元。
清算价为:303=Q 元/MWh4.通过对预案分析计算可得,第一、五、六线路出现输电阻塞现象,根据安全且经济的原则,利用排序算法进行了调整,得到了消除输电阻塞的分配方案,分别是:,,,,,,,。
其清算价格Q =303元/MWh阻塞费用:=C 元;总费用为:总C =元5.同理对下一时段预报负荷需求为的条件下,重复步骤3、4的工作,得到分配预案为(MW):,,,,,,,.总费用为:总C =元。
清算价为:356=Q 元/MWh;通过调整预案不能消除阻塞,然后采用输电阻塞管理原则第二条,得到新的方案:,,,,,,,。
阻塞费用为:8.1255=C 元;总费用为:总C =元.最后,对所得结果进行了详细的分析、评价和推广。
优化调度的数学模型

1)目标函数假设系统可运行的机组数为n,总负荷为d P,以电厂内所有机组的总煤耗量最小为目标,建立如下的数学模型:其中:——机组序号;——第i台机组的煤耗量;——n 台机组的总煤耗;——第i台机组的负荷;——第i台机组的煤耗量与负荷的函数关系。
2)约束条件约束条件包括功率平衡约束和机组出力约束。
(1)功率平衡约束:(2)机组出力约束:其中:——n台机组的总负荷;——第i台机组的负荷下限和负荷上限。
假设系统可运行的机组数为,总负荷为,以调度周期为一昼夜来考虑,分为h个时段。
1)目标函数机组优化组合的目标函数如下:式中——机组序号;——n 台机组的总煤耗;——机组i运行状态的变量,仅取0、1 两个值,表示停机,表示运行。
——第i台机组在t时刻的负荷;——第i台机组在t时刻的煤耗量与负荷的函数关系;——机组的启动耗量。
2)约束条件考虑机组运行的实际情况,本文确定的机组约束条件包括功率平衡约束、机组出力约束、最小停机时间约束、最小运行时间约束以及功率响应速度约束。
(1)功率平衡约束:式中——机组序号;——第i台机组在t时刻的负荷;——n台机组的总负荷。
(2)机组出力约束:式中——机组的启停状态,0 表示停机,1 表示运行。
——第i台机组的负荷下限和负荷上限。
(3)最小停机时间约束:式中——机组i的最小停机时间。
(4)最小运行时间约束:式中——机组i的最小运行时间。
(5)功率响应速度约束:式中——机组i每分钟输出功率的允许最大下降速率和最大上升速率。
由于是在火电厂内部进行优化组合,可不考虑网损和系统的旋转热备用约束(这两项通常是电网调度中需要考虑的)。
因此,机组优化组合从数学角度上讲就是在(5)~(9)的约束条件下求式(4)的最小值。
3)机组启停耗量能耗Si 的确定通常情况下,对Si的处理采用如下的方法:机组的启动耗量包括汽机和锅炉两部分,由于汽机的热容量很小,其启动耗量一般可近似当作一个与停机时间长短无关的常数;对于锅炉,由于热容量很大,其启动过程中的燃料耗量与启动前锅炉的冷却程度有很大的关系。
《2024年风光互补发电系统的建模与仿真研究》范文

《风光互补发电系统的建模与仿真研究》篇一摘要:随着对可再生能源需求的增长和对环境可持续发展的追求,风光互补发电系统因其在地理和能源来源上的优势受到了广泛的关注。
本文着重介绍了风光互补发电系统的建模、仿真以及相关的研究成果,通过对系统结构、运行机制及模拟方法的深入研究,旨在为进一步推动可再生能源领域的技术创新和优化提供理论支持。
一、引言风光互补发电系统,即利用风能和太阳能进行发电的系统,具有无污染、可持续、分布广泛等优点。
随着全球能源结构的转变,风光互补发电系统已成为未来能源发展的重要方向。
因此,对其建模与仿真研究具有重要的理论和实践意义。
二、风光互补发电系统的建模1. 系统结构模型风光互补发电系统的结构模型主要包括风力发电机组、太阳能光伏板、储能装置(如电池组)以及控制系统等部分。
通过建立各部分的数学模型,可以描述系统的运行特性和能量转换过程。
2. 能量转换模型能量转换模型主要描述风力和太阳能如何被转换成电能的过程。
风力发电机组和太阳能光伏板的工作原理和性能参数是建模的关键。
此外,还需要考虑环境因素如风速、光照强度等对能量转换效率的影响。
三、仿真方法及工具1. 仿真方法仿真方法主要采用物理建模和数学建模相结合的方式。
通过建立系统的物理模型,可以更直观地了解系统的运行机制;而数学建模则可以通过数学方程描述系统的行为,为后续的仿真分析提供基础。
2. 仿真工具仿真工具的选择对于提高仿真效率和准确性具有重要意义。
常用的仿真软件如MATLAB/Simulink等,具有强大的建模和仿真功能,可以有效地用于风光互补发电系统的建模与仿真。
四、仿真结果与分析通过仿真,我们可以得到以下结果:1. 系统输出特性仿真结果可以清晰地展示风光互补发电系统的输出特性,包括在不同风速和光照强度下的发电量,以及系统的日、月、年发电量等。
2. 系统性能评价通过对比不同配置和参数下的系统性能,可以评价系统的稳定性和经济性等指标,为实际工程提供参考依据。
基于matlab的同步发电机组建模与仿真

基于matlab的同步发电机组建模与仿真基于matlab的同步发电机组建模与仿真I 基于MATLAB 的同步发电机组建模与仿真摘要随着电网的规模越来越大,电力系统的运行也随之越来越复杂。
同步发电机及其控制系统作为电源是电力系统中的重要组成部分,其性能对电力系统有着极大的影响,直接关系到系统的稳定运行。
为了使电力系统安全而经济地运行,我们必须对同步发电机组特性进行深入的研究。
而同步发电机组运行是一个相当复杂的过程,其动态特性随着机组的运行状态而不断变化,所以建立机组的模型并进行仿真研究是掌握发电机动态特性,评价其各个控制系统性能的有效手段,并且对工作人员的培训和研究将起到很大的作用。
同步发电机组模型的建立将涉及到机组的机理分析,有利于从理论建模中引出新的设计方法,为优化设计提供理论依据。
本文将对同步发电机及其励磁系统、调速系统的数学模型进行研究,利用MATLAB/Simulink 搭建同步发电机组的仿真模型,建立单机无穷大系统,最后对模型进行仿真,并分析仿真结果。
关键词:电力系统;单机无穷大系统;MATLAB/Simulink;仿真;同步发电机组华北电力大学本科毕业设计(论文)摘要II SYNCHRONOUS GENERATOR UNIT MODELING AND SIMULATION BASED ON MATLAB Abstract With the enlargement of the power grid scale, the operation of the power system is becoming more and more complex. As supply unit of the system, synchronous generator and its control system plays an important part in the power system. Their performance also imposes great influence to the power system and has a direct connection with the power system stability. In order to ensure the safe and economic operation of the power system, we shall do a profound research on the synchronous generator unit characteristics. However, the operation of the synchronous generator unit is a extremely complex process. Its dynamic characteristics are subject to the changing states of the unit operation. Therefore, it is efficient to build a unit model and do simulations research to acquire the dynamic characteristics of the unit, and evaluate the performance of each control system. This will also play a great role in the staff training and researches. The building of the synchronous generator unit model will involve the mechanic analysis of the unit, do favor to deduce new designing methods from theoretical model buildingand provide theoretical basis to the optimization design. In this paper the mathematical model of the synchronous generator and its excitation system, speed regulating system will be researched; the simulation model of synchronous generator unit will be built based on MATLAB/Simulink; a single-unit infinite system will be established; finally simulate the model and verify the accuracy of the model. Key Words: Power System; Single-unit Infinite System; MATLAB/Simulink; Simulation; Synchronous Generator Unit 华北电力大学本科毕业设计(论文)目录i 目录摘要∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙IAbstract∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙II 1 绪论∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 1.1 课题背景和意义∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 1.2 电力系统仿真发展现状∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 1.3 本课题所完成的主要工作∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 2 同步发电机组数学模型∙∙∙∙∙∙4 2.1 同步发电机数学模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 2.1.1 同步发电机数学建模概述∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 2.1.2 同步发电机基本方程∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 2.1.3 同步发电机三阶模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 2.1.4 单机无穷大系统∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 2.2 励磁系统数学模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 2.2.1 同步发电机励磁自动控制系统概述∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 2.2.2 同步发电机励磁自动控制系统数学模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 2.3 调速系统数学模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 2.3.1 同步发电机组调速控制系统概述∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 2.3.2 同步发电机调速系统数学模型于MATLAB 同步发电机组仿真∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 3.1 MATLAB 介绍∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 3.1.1 MATLAB/Simulink∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 3.1.2 常用Simulink 库模块∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13 3.2 同步发电机组仿真的初值计算∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙14 3.3 同步发电机组仿真模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙15 3.3.1 同步发电机模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙16 3.3.2 同步发电机励磁自动控制系统仿真模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙17 3.3.3 同步发电机调速系统仿真模型∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙18 3.4 系统仿真及结果分析∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙18 3.4.1 稳定运行∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙19 3.4.2 系统电压突增或突降∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙20 3.4.3 增加励磁系统给定电压∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 1 3.4.4 增加调速系统给定功率∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 3 华北电力大学本科毕业设计(论文)目录ii 3.4.5 三相突然短路∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙24 4 结论与展望∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙26 参考文献∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙27 致谢∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙28 华北电力大学本科毕业设计(论文)1 1 绪论1.1 课题背景和意义随着现代电力系统网络规模的不断扩大和电网电压等级的不断升高,电力系统规划、运行和控制的复杂性亦日益增加。
基于CFD的风力发电机组优化设计

基于CFD的风力发电机组优化设计一、引言随着可再生能源的快速发展,风力发电作为一种清洁、可再生的能源形式,受到了广泛关注和重视。
风力发电机组作为风能利用的主要设备,其性能对发电效率和经济效益具有重要影响。
为了提高风力发电机组的效率和可靠性,基于计算流体力学(CFD)的优化设计成为了一个重要的研究方向。
二、CFD在风力发电机组设计中的应用CFD是一种利用计算机模拟流动过程中的物理现象和数学方程的方法。
它可以预测流动的速度、压力分布等参数,为风力发电机组的设计和优化提供了重要的工具。
1. 空气流动模拟在风力发电机组中,空气流动是影响叶片受力和发电效率的关键因素。
通过CFD技术,可以模拟风力发电机组叶片和气流之间的相互作用,预测叶片受力和振动情况,进而优化叶片形状和材料,提高发电效率和可靠性。
2. 流场优化CFD技术可以模拟风力发电机组周围的流场分布,预测气流速度、压力等参数。
通过优化风力发电机组的布局和方向,可以降低气流的扰动,提高发电效率。
三、CFD模拟风力发电机组优化设计的方法基于CFD的风力发电机组优化设计通常包括以下几个步骤:1. 几何建模首先,需要对风力发电机组的几何形状进行建模。
通过CAD软件或者其他建模工具,将发电机组的外形、叶片、塔筒等部件建立为三维模型。
2. 网格划分在CFD模拟中,需要将风力发电机组的模型划分为网格。
网格划分的好坏会直接影响模拟结果的准确性和计算效率。
通过合理划分网格,可以提高模拟的精度,同时控制计算资源的消耗。
3. 定义边界条件和物理模型在进行模拟之前,需要通过定义边界条件和选择适当的物理模型来规定模拟参数。
边界条件包括风速、气温、湍流强度等;物理模型则包括流体运动的方程、湍流模型等。
4. 求解流动场在CFD模拟中,通过求解Navier-Stokes方程组来计算流动场的速度、压力分布等参数。
根据模拟结果,可以获得叶片受力、振动情况等重要信息。
5. 优化设计基于CFD模拟结果,可以通过修改风力发电机组的几何形状、布局等进行优化设计。
火电机组优化运行关键技术分析论文[大全5篇]
![火电机组优化运行关键技术分析论文[大全5篇]](https://img.taocdn.com/s3/m/595519b96aec0975f46527d3240c844769eaa015.png)
火电机组优化运行关键技术分析论文[大全5篇]第一篇:火电机组优化运行关键技术分析论文摘要:火电厂作为我国电厂的主要组成部分,为社会发展提供电能支持,推进社会现代化建设。
但火电厂运行中需要消耗大量能源,同时还会造成严重的环境污染,不符合可持续发展战略,火电厂实行节能减排已成为必然。
有鉴于此,文章中以火电厂火电机组为切入点,分析火电机组节能降耗的原理,并给出火电机组优化运行的主要技术,分析节能运行的方法,以供参考。
关键词:火电机组;节能降耗;运行措施近些年我国社会经济快速发展,市场对电能的需求量持续增加,火电厂的规模与数量也在快速增加,做好节能减排工作已成为火电厂工作的主要内容。
火电厂运行中发电机组作为主要设备,其能耗直接决定火电厂的能耗。
通过优化火电机组运行模式,可以提高机组运行效率并降低能耗,增加火电厂经济效益,提高市场竞争力,本研究就此展开论述。
1火电机组优化运行分析能源供应日趋紧张化的背景下,火电厂更应该提高节能意识,强化能源管理工作,在保证正常运行的基础上降低能源消耗,提高火电厂的经济效益。
如何有效运行火电机组,达成节能降耗目的已成为火电厂行业研究的重要课题。
火电厂优化运行,指的是不增加新投入的基础上,通过调整运行参数并改变运行方式的方法,提高能源利用率。
火电厂的优化分成两类,即单设备优化与全厂优化。
前者通过优化单机的热经济性指标,后者则对全厂机组设备进行优化[1]。
火电机组运行优化及节能研究,有助于降低火电厂运行成本。
火电机组优化运行试验内容,主要包括:调整锅炉、调整汽轮机组与辅机、优化热控系统等。
此外,大型火电机组的热力系统构成较为复杂,很多因素都会对机组性能产生影响,单纯的理论研究需要附加较多的假设条件,还需要进行简化处理,难以获得准确的经济化的运行方案。
因此实际优化时,通过试验的方法获得各个机组在不同条件的运行数据,并通过全面分析、综合计算,获得最优运行方式,给火电厂运行提供指导与参考。
发电机的数学建模

发电机使用计划的数学模型四川理工学院组员:薛倩王军周春花2011-4-23发电机使用计划的数学模型摘要本文讨论如何合理计划使用发电机,使每天发电机的总成本最少的问题,是一个分段优化的问题。
对这个问题时间分段较少时,所求出的最终值才会更精确,建立数学模型,利用软件编程求解。
对于问题一建立以发电机每天总成本最小值作为目标函数的整数规划模型1,从题目所给的已知条件、数据以及合理的假设条件,分析确定数学模型的约束条件,然后对此数学模型1利用lingo软件编程,求解该数学模型,找出最优解,得到每天发电机最小成本为xxxx元。
问题二在问题一的基础上,改变相应约束条件,同样运用模型1,修改lingo程序,求解找出最优解,解得发电机每天总成本为xxxx元。
问题三,要求在任意时刻,发电机组必须流出20%的发电能力力量,也即是要求实际输出功率的80%用于满足每日电力需求量,同样运用问题一中建立的模型,在lingo变成时对约束条件中的数据稍作修改,解得发电机每天总成本为xxxx元。
关键词: 分段优化整数规划最优解最小总成本一、问题的重述为了满足每日电力的需求(单位:兆瓦),可以选用四种不同类型的发电机。
每日电力需求如下表示:表一每日用电需求(兆瓦)小输出功率。
所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
这些数据均列于下表中。
表二发电机相关数据只有在某个时间段启动或者关闭发电机。
与启动发电机不同,关闭发电机不需要付出任何代价。
以此,有如下几个问题:(1)在每个时间段应分别使用哪些发电机方能使每天的总成本最小?(2)如果型号2的发电机的可用数量变为6,则发电机的使用计划是否会发生变化?(3)如果要求在任意时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升,问发电机的使用计划如何?(选做)二、问题的分析此题主要是考虑的是一个最优解问题,也就是说此问题是一个分段优化的问题。
发电机机组最优组合数学模型
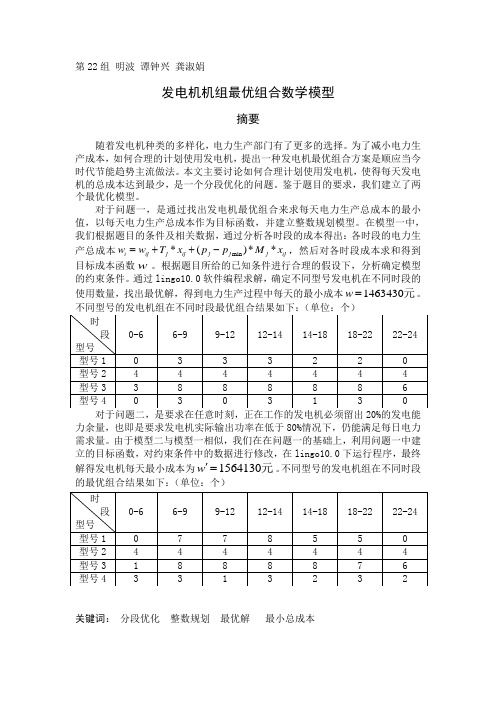
第22组 明波 谭钟兴 龚淑娟发电机机组最优组合数学模型摘要随着发电机种类的多样化,电力生产部门有了更多的选择。
为了减小电力生产成本,如何合理的计划使用发电机,提出一种发电机最优组合方案是顺应当今时代节能趋势主流做法。
本文主要讨论如何合理计划使用发电机,使得每天发电机的总成本达到最少,是一个分段优化的问题。
鉴于题目的要求,我们建立了两个最优化模型。
对于问题一,是通过找出发电机最优组合来求每天电力生产总成本的最小值,以每天电力生产总成本作为目标函数,并建立整数规划模型。
在模型一中,我们根据题目的条件及相关数据,通过分析各时段的成本得出:各时段的电力生产总成本min *()**i ij j ij j j j ij w w T x p p M x =++-,然后对各时段成本求和得到目标成本函数w 。
根据题目所给的已知条件进行合理的假设下,分析确定模型的约束条件。
通过lingo10.0软件编程求解,确定不同型号发电机在不同时段的使用数量,找出最优解,得到电力生产过程中每天的最小成本1463430w =元。
力余量,也即是要求发电机实际输出功率在低于80%情况下,仍能满足每日电力需求量。
由于模型二与模型一相似,我们在在问题一的基础上,利用问题一中建 立的目标函数,对约束条件中的数据进行修改,在lingo10.0下运行程序,最终解得发电机每天最小成本为1564130w '=元。
不同型号的发电机组在不同时段的最优组合结果如下:(单位:个)关键词: 分段优化 整数规划 最优解 最小总成本1. 问题重述为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。
每日电力需求如下表1。
每种发电机都有一个最大发电能力,当接入电网时,其输出功率不应低于某一最小输出功率。
所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A题院系______________参赛队员__________________联系电话______________题目发电机组的优化配置摘要本文针对不同种类发电机,不同时段的实际用电情况,建立了如何合理安排发电机使用的模型。
对于问题(一),该模型灵活运用二次规划,整体考虑一天中的各个阶段,并利用lingo求得一天中最小费用为997790(元)。
在问题(二)中,应用经济学模型和统计学中线性回归分析的原理,并利用excel中丰富的统计函数和lingo软件求得结果。
问题(三),仿照问题(一)的方法,但发现最小费用没变。
正文一、问题重述电是我们生活中不可缺少的一部分,现考虑发电机组优化配置问题。
某发电厂负责某地区的供电任务,已知该地区夏季一天的电力需求如下:现电厂有三种类型发电机可投入运转:一型12台;二型6台;三型5台;各个型号机组相关数据如下:正常情况下,在满足估计的负荷要求之外,每一时刻运转的发电机组应足够多,使得当负荷增加不超过15%时,能够通过调高运转的发电机组的输出来满足增载的要求。
请你建立该问题的数学模型,通过求解模型回答以下问题:(1)在一天中各个时间段应安排使用那些发电机组运转可以使得在满足负荷要求的情况下总的费用最低?总的费用为多少?(2)在一天中每段时间,电力生产的边际费用是多少?即应为用电定什么价格?(3)将后备输出保障的15%降低为10%,运转费用节省的情况如何?可以降为多少?二、问题的基本假设1.假设每个阶段不会变更设备。
2.不考虑设备需要维护与修理。
3.假设用电需求相对稳定,不会发生突变。
4.关闭和启动发电机时均是瞬时完成,不计相应使用的时间。
5.发电机输出过程其功率始终保持不变。
三、符号说明四、模型建立与求解 问题(一)模型分析此题研究的是每天在第j 个阶段如何合理分配各种类型的发电机,使每日的成本Q 最低的数学模型,建立如下二次规划模型[3]。
发电机组运转的费用可以分成两部分:第一部分与其输出功率和运行时间紧密相连,即:53(,)(,)11((min )*)**i j j i j i j i j pp f a n t ==-+∑∑;第二部分与其输出功率和运行时间无关,即开机时费用其中,0()0,0x x g x x >⎧=⎨≤⎩,还有当i=1时,(1,)(5,)n i j n j -=。
模型的建立 确定目标函数在满足需求量的情况下,为了使每天发电成本最低,我们建立如下目标函数53(,)(,)(,)(1,)11((min )*)***()i j j i j i j i j i j i j i j pp f a n t b g n n -==-++-∑∑其中 约束条件模型的求解通过lingo 编程[2](见附录)得到结果Q 为997790.0元结果分析由上述表格可知,第一种机型在所有阶段里全部使用;第二种机型在各阶段几乎全部使用;第三种机型则几乎没用。
经分析,考虑到需求量与使用成本的关系,第三种机型不适合用来在该地区供电。
问题(二)模型的分析此题要求一天中每段时间电力生产的边际费用(即边际成本)。
首先给出边际成本[1]的定义:MC 是厂商在短期内增加一单位产量是所增加的成本。
经过lingo 试验,?Q ?30时,发电机组的类型和数量都保持不变。
所以启动费不变,不予考虑。
模型的建立由问题(一)可知不能直接求出各阶段用电价格与需求电量之间的关系,所以不能直接求导。
只能通过0∆→逐渐逼近才能求出边际成Q本。
并用线性回归分析MC与?Q的关系。
MC=β0+β1?Q模型的求解±±±±±兆瓦;通过运行lingo(程序见本题分别设?Q=7,10,16,21,27附录)和excel中的INTERCEPT函数求解拟合直线的截距和LINEST函数求解拟合直线的斜率可获得各阶段边际成本价格MC(Q)(表格见附录)模型的结果由上表格β1相对于β0为零,每个阶段边际成本逼近于一个常数,且阶段三与阶段五的拟合曲线相近,阶段二与阶段四相近。
结果见下表:结果分析用影子价格【5】的方法对上述结果进行检验,可以看出结果正确。
问题(三)模型分析这里的目标函数同问题一相同,建立单目标最优模型。
只需在约束条件中将后备输出保障的15%降低为10%。
目标函数53(,)(,)(,)(1,)11((min )*)***()i j j i j i j i j i j i j i j pp f a n t b g n n -==-++-∑∑其中 约束条件 模型的结果通过lingo 编程(见附录)得到结果Q 为997790.0元结果分析由上表可知将后备输出保障的15%降低为10%后,总费用Q 不变,且各阶段每种机型的使用台数也不变。
五、误差分析发电机输出过程其功率始终保持不变是在理想情况下才存在的,有一定的误差,还有在开启以及关闭发电机时不仅有功率损耗方面的误差,而且还有时间方面的误差,这些都会对模型的建立有一定程度上的影响。
此外lingo 的运算结果只保留小数点后3位数字,所以也存在无误差。
六、模型评价模型的优点:(1)模型的结构简洁明了,可移植性好;(2)问题(一)的模型可操作性强,适用范围广;(3)本模型中使用了lingo和excel软件,大大减少了计算量。
模型的缺点:(1)由于软件等原因,存在误差;(2)问题(二)模型的操作较为复杂。
七、参考文献【1】高鸿业.西方经济学.中国人民大学出版社.【2】宋来忠.数学建模与实验.科学出版社.【3】姜启源,谢金星,叶俊.数学建模.高等教育出版社.【4】茆诗松,程依明,濮晓龙.概率论与数理统计教程.高等教育出版社.【5】胡运权.运筹学基础及应用.高等教育出版社.附录程序(问题一)model:sets:Time_slot/1..5/:t,w;Generator_type/1..3/:a,f,b,minp,maxp;Link(Time_slot,Generator_type):n,p;endsetsdata:t=6,3,6,3,6;w=15000,30000,25000,40000,27000;minp=850,1250,1500;maxp=2000,1750,4000;a=1000,2600,3000;f=2,1.3,3;b=2000,1000,500;enddatamin=@sum(Link(i,j):n(i,j)*a(j)*t(i)+n(i,j)*(p(i,j )-minp(j))*t(i)*f(j)+@if(n(@if(i#eq#5,1,i+1),j) #gt#n(i,j),n(@if(i#eq#5,1,i+1),j)-n(i,j),0)*b(j ));@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))>=w(i););@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))<=w(i)*1.15;);@for(Time_slot(i):@bnd(0,n(i,1),12););@for(Time_slot(i):@bnd(0,n(i,2),6););@for(Time_slot(i):@bnd(0,n(i,3),5););@for(Link(i,j):@bnd(minp(j),p(i,j),maxp(j));); @for(Link(i,j):@gin(n(i,j)););end程序(问题二):以 Q=7为例:model:sets:Time_slot/1..5/:t,w,q;Generator_type/1..3/:a,f,b,minp,maxp;Link(Time_slot,Generator_type):n,p;endsetsdata:t=6,3,6,3,6;q=7?;w=15000,30000,25000,40000,27000;minp=850,1250,1500;maxp=2000,1750,4000;a=1000,2600,3000;f=2,1.3,3;b=2000,1000,500;enddatamin=@sum(Link(i,j):n(i,j)*a(j)*t(i)+n(i,j)*(p(i,j )-minp(j))*t(i)*f(j)+@if(n(@if(i#eq#5,1,i+1),j) #gt#n(i,j),n(@if(i#eq#5,1,i+1),j)-n(i,j),0)*b(j ));@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))>=w(i)+q;);@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))<=(w(i)+q)*1.15;);@for(Time_slot(i):@bnd(0,n(i,1),12););@for(Time_slot(i):@bnd(0,n(i,2),6););@for(Time_slot(i):@bnd(0,n(i,3),5););@for(Link(i,j):@bnd(minp(j),p(i,j),maxp(j)););@for(Link(i,j):@gin(n(i,j)););end程序(问题三)model:sets:Time_slot/1..5/:t,w;Generator_type/1..3/:a,f,b,minp,maxp;Link(Time_slot,Generator_type):n,p;endsetsdata:t=6,3,6,3,6;w=15000,30000,25000,40000,27000;minp=850,1250,1500;maxp=2000,1750,4000;a=1000,2600,3000;f=2,1.3,3;b=2000,1000,500;enddatamin=@sum(Link(i,j):n(i,j)*a(j)*t(i)+n(i,j)*(p(i,j )-minp(j))*t(i)*f(j)+@if(n(@if(i#eq#5,1,i+1),j) #gt#n(i,j),n(@if(i#eq#5,1,i+1),j)-n(i,j),0)*b(j ));@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))>=w(i););@for(Time_slot(i):@sum(Generator_type(j):n(i,j)*p (i,j))<=w(i)*1.10;);@for(Time_slot(i):@bnd(0,n(i,1),12););@for(Time_slot(i):@bnd(0,n(i,2),6););@for(Time_slot(i):@bnd(0,n(i,3),5););@for(Link(i,j):@bnd(minp(j),p(i,j),maxp(j)););@for(Link(i,j):@gin(n(i,j)););end表格(问题二)。
