Z变换收敛域总结及习题
Z变换习题(1)

k k
1 2
.... ....
2 1
k
3
k
2
1
1 j
3
j
e 3,
1 j
3
j
e 3
2
2
2
2
jn
j
n
f (n) 2 u(n) e 3 u (n) e 3 u(n)
2 u ( n ) cos( n ) u ( n )
3
[ 2 cos( n )] u ( n )
3
10
z 1)( z 2
1)
1 | z | 2 | z | 1 | z | 1
8
Z反变换
解:
(1)
F(z)
z
1
2
3 3
z ( z 1)( z 2) z 1 z 2
F(z) 1 z 2 z 3 z 1 3 z 2
f (n) 1 (1)n u(n) 2 2n u (n 1)
3
3
1| z|2 f (n) 是双边序列
1 ( 1 )n z n
n 2
n 2
2z 1 2z
收敛域:2z 1 即:z 1 2
极点为:z 1 零点为:z 0 2
3
Z变换
3.求以下序列的z 变换并画出零极点图和收敛域:
x(n)
1 2
n
u(n)
解:
ZT
x(n)
x(n)zn
n
n0
1 2
n
zn
零点:
1 1 1 z1 2
11
Z反变换
7已知 X (z)
2z2 3z
,若收敛域分别为1 z 2和 2 z 3
(z 1)(z 2)(z 3)
双边z变换定义及收敛域
n2 ≤ 0
7
(4)双边序列
n为任意值时皆有值
其z变 换:X (z) = x(n)z−n + ∑x(n)z−n ∑
n=0 −1 ∞
n=−∞
前式Roc: 0 ≤ z < Rx+ 后式Roc: Rx− < z ≤ ∞
∴当Rx− ≥ Rx+时,Roc : ∅ 当Rx− < Rx+时,Roc : Rx− < z < Rx+
0
Rx −
Re[z]
n1 ≥ 0
包括z =5∞处
因果序列 • n1≥0的右边序列 的右边序列 • Roc: Rx− ≤| z |≤ ∞ • 因果序列的z变换必在∞处收敛 因果序列的z变换必在∞ 收敛域一定是某个圆的外部
Rx −
j Im[z]
Re[z] n1 ≥ 0
0
包括z =∞处
6
(3)左边序列
n=−∞
∞
P( z ) 令X ( z ) = Q( z)
j Im z] [
Re[z]
则X(z)的零点:使X(z)=0的点, 即P( z ) = 0和当Q ( z )阶次高于P ( z )时 Q ( z ) → ∞ X(z)的极点:使X(z) → ∞的点, 即Q ( z ) = 0和当P ( z )阶次高于Q ( z )时P ( z ) → ∞
2
(1)有限长序列 1)有限长序列
x(n), n ≤ n ≤ n2 1 x(n) = 其 n 他 0,
其Z变换 X (z) = ∑x(n)z−n :
n=n1 n2
j Im[z]
Roc至 为 0 < z < ∞ 少 :
有限z平面 有限 平面
复习 z变换

总结 • 给定z变换X(z)不能唯一地确定一个序列,只有 给定z变换X(z)不能唯一地确定一个序列, X(z)不能唯一地确定一个序列 同时给出收敛域才能唯一确定。 同时给出收敛域才能唯一确定。
• X(z)在收敛域内解析,不能有极点,故: X(z)在收敛域内解析,不能有极点, 在收敛域内解析 –右边序列的z变换收敛域一定在模最大的有 右边序列的z变换收敛域一定在模最大的有 右边序列的 限极点所在圆之外 –左边序列的z变换收敛域一定在模最小的有 左边序列的z变换收敛域一定在模最小的有 左边序列的 限极点所在圆之内
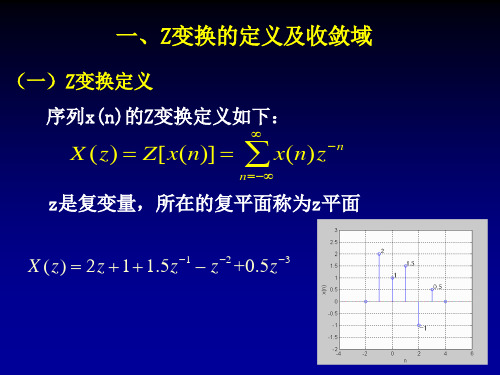
一、 Z变换的定义 变换的定义
双 z 换 X(z) = 边变
n= ∞ -
x(n)z−n ∑
∞
二、z变换的收敛域 变换的收敛域
对于任意给定的序列x(n) ,能使 X(z) = ∑ (n)z−n x
n=− ∞ ∞
收敛的所有z 值之集合为收敛域。
即 足 满
n=− ∞
x(n)z−n < ∞ 的 域 R C 区 (O ) ∑
z反变换 反变换
部分分式展开法 部分分式展开法
1.z变换式的一般形式 . 变换式的一般形式
N(z) b +b z +b z2 +L b −1zr−1 +b zr + r 2 r X(z) = = 0 1 D z) a0 +a z +a2z2 +L ak−1zk−1 +ak zk ( + k− 1
anu(n) z >a z 换 基 形 z变 的 本 式 ↔ n z −a −a u(−n−1 z < a )
同理[ຫໍສະໝຸດ ]∞a−nx(n) ↔X(az)
(R
z变换的收敛域

z变换的收敛域
z变换的收敛域是指在哪些复平面上的z值,使得z变换的级数或积分收敛。
z变换的收敛域通常按照其包含在复平面第一象限
(Re(z)>0,Im(z)>0)还是全平面(包括虚轴)来分类,分别称为单边收敛和双边收敛。
对于时域信号x(n)的z变换X(z),其收敛域的判断方法为:
1.通过分析x(n)的极限,确定z变换的极点和零点,并求出其可能的收敛域。
2.通过柯西收敛原理,判断z变换的收敛域。
3.对于一些标准的信号,比如因果序列、双边指数信号等,可以直接列出其z变换并判断收敛域。
在工程应用中,通常只需关注z变换的最小收敛域,即最小包含其所有极点的收敛域。
最小收敛域也称为“ROC”,表示因果性和稳定性的限制条件。
信号系统Z变换习题讲解

信号系统Z 变换习题讲解7-1 分别绘出下列各序列的图形。
(1)[](1/2)[]n x n u n = (2)[]2[]n x n u n = (3)[](1/2)[]n x n u n =- (4)[](2)[]n x n u n =- 解:7-2 分别绘出下列各序列的图形。
(1)[][]x n nu n =-- (2)[]2[]n x n u n -= (3)[](1/2)[]n x n u n -=- (4)[](1/2)[]n x n u n =-- 解:1234(1)01234(2)(3)[n ](2)(1)(4)7-3 分别绘出下列各序列的图形。
(1)[]sin 5n x n π⎛⎫= ⎪⎝⎭ (2)[]cos 105n x n ππ⎛⎫=- ⎪⎝⎭ 解:7-5 序列x [n ]如图题7-5所示,把x [n ]表示为δ[n ]的加权与延迟之线性组合。
图 题7-5解: []2[3][]3[1]2[3]x n n n n n δδδδ=-+-+-+-7-7 求下列序列的z 变换X (z ),并注明收敛域,绘出X (z )的零极点图。
(1)(1/2)nu [n ] +δ [n ] (4)(1/2)n {u [n ] - u [n -8]} (5)δ [n ] -15δ [n -2]解:1011(1)()[()[][]]()[]221212111222n n n nn n n X z u n n z z n z z z z z z δδ∞∞∞---=-∞==-∞=+=+-=+=>--∑∑∑(2)∞--=-∞=--=--=--==>--∑∑718881711(4)()()([][8])()22111()()220111()22n n n nn n X z u n u n z z z z z z z zδδ∞-=-∞-=--=->∑21(5)()([][2])51105n n X z n n z z z7-8 求双边序列x [n ] =||(1/2)n 的z 变换,标明收敛域及绘出零极点图。
信号分析第六章第一节z变换及收敛域

说明:相同的z 变换,对不同的收敛域,其时域信 号不同,故在确定 z 变换时,必须指明收敛域。
X
11
(3)双边序列的收敛
第
j Im[z]
页
x k b k k b 0
Re[ z ]
或xkb k kb k k 1
k0
k0
0b1
xk b k
bkkz
zb
zb
1
Z变换 存在
离散系统的Z变换分析
连续系统的拉氏变换分析
X
4
第
第一节 Z 变 换
页
一.Z变换的提出—由拉氏变换引出
连续信号 等间隔采样 抽样信号
x s(t) x (t)T (t) x (t) (t k)T x (k)T ( t k)T
k 0
k 0
单边拉氏变换
X s (s)
0
x(kT) (t kT)est dt
2.离散时间信号与系统
序列的变换与运算,差分方程求解,包括时 域经典法和卷积和法.
X
3
第
二.变换域分析法
页
1.连续时间信号与系统: 频域分析、复频域分析。 微分方程转化为S(或jw)的代数方程 卷积积分转换为代数乘
2.离散时间信号与系统: Z变换,DFT(FFT)。 Z变换可将差分方程转化为Z代数方程。 卷积和转换为代数乘
bk k 1
b1 k k 1
b 1 xk b k
k
Z变换 不存在
z
z b1
z b1
1
k
若0b1
1b 则RO:Cb z 1
b
b
环状区域
X
12
第
收敛域性质综述 页
★因果序列的ROC为 z R1的圆外区域;
第二章Z变换例题

解: (1)对题中的差分方程两边作z变换,得
Y (z) z1Y (z) z2Y (z) z1X (z)
所以
H (z)
Y (z) X (z)
z 1
1 z1
z 2
(z
z a1)(z
a2 )
可求得零点为 z 0 , z
极点为 z1 a1 0.5(1 5) 1.62, z2 a2 0.5(1 5) 0.62
(1) x(n) a n , a 1
(2) (3) (4)
x(n)
1 2
n
u
n
x(n)
1 2
n
u
n
1
x(n) 1 , n 1
n
分析:Z[x(n)] x(n)zn 中,n的取值范围是 x(n) n
的有值范围,z变换的收敛域是满足
x(n)zn M 的z值范围。
n
解:
(1)由z变换的定义可知:
1 2
z
2
因而,x1(n)为n 0时有值的左边序列,x2 (n)为n 0 时
有值的右边序列。则
x1 (0)
lim
z0
X1
z
lim
z0
1 4
z
z2
0
得
x2
(0)
lim
z
X
2
(z)
lim
z
1 3
z
z
1 2
1 3
x(0)
x1(0)
x2
(0)
1 3
例5 有一信号y(n)与另两个信号 x1(n)和x2 (n) 的关系是
un
式中 a1 1.62, a2 0.62 由于H(z)的收敛域不包括单位圆,故这是个不稳定系统
2第二章-z变换
调用: num [ p0 , p1 , p2 , , pM ]
den [d 0 , d1 , d 2 , , d N ] H freqz(num, den, )
ˆ X a ( s)
X (z )
思考练习
?
X a (s)
2. Z变换与傅里叶变换
s j 的拉普拉斯变换即为傅里叶变换,
ze e
sT
jT
映射为z平面的单位圆
jT
X ( z ) z e jT X (e
ˆ ) X a ( j)
抽样序列在单位圆上的z变换,等于其理想抽 样信号的傅里叶变换。
c
c
| H (e j ) |2 d
c
Parseval定理
序列的傅立叶变换是从频域对离散时间信号和系
统进行分析。它是用{ 变换用{
jt
e
j n
}作为基函数对序
列进行正交展开,这与连续时间信号中的傅立叶
e
}对模拟信号进行展开相似。
4. 序列傅立叶变换的对称性
• 序列的共轭对称性质
xe (n) xe (n) 若序列 xe (n)满足
则称 xe (n)为共轭对称序列
若序列xo (n)满足 xo (n) x
o
( n)
则称 xo (n)为共轭反对称序列
任何序列 x(n)均可表示成上述两种序列之和,
即x(n) xe (n) xo (n) 1 xe ( n) {x( n) x ( n)} 2 其中 1 xo ( n) {x( n) x ( n)} 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Rx− = max { z1 , z2 ,L, z N
}
3)左边序列
X ( z) =
n =−∞
∑ x ( n) z
n2
−n
⎧n2 > 0, 0 < z < Rx+ ⎪ ⎨ ⎪ ⎩ n2 ≤ 0, 0 ≤ z < Rx+
Rx+ = min { z1 , z2 ,L, z N }
4)双边序列
X ( z) =
1 n ∑ x(k ), n + 1 k =0
n = 0,1,L 。其中, y ( n) 是系统输出, x(k ) 是
n 1 y (n − 1) + x( n) 。它是递推的定常系数差分方程吗?为什么? n +1 n +1
n
(2)已知某系统的单位取样响应 h(n) = a , − 1 < a < 1 , 1)求将 h( n) 分解成左边序列 h1 (n) 和右边序列 h2 (n) 的数学表达式,且 h( n) = h1 (n) + h2 (n) 。 2 )在分别求出 h1 (n) 和 h2 (n) 对应的傅立叶变换 H1 (e jω ) 和 H 2 (e jω ) 后,验证 h(n) 的傅立叶变换满足
1.Z 变换收敛域总结 1)有限长序列
X ( z ) = ∑ x ( n) z − n
n = n1
n2
⎧ n1 ≥ 0, 0 < z ≤ ∞ ⎪ ⎨ ⎪ ⎩n2 ≤ 0, 0 ≤ z < ∞
2)右边序列
X ( z ) = ∑ x ( n, z > Rx− ⎪ z > Rx− ⎨n1 = 0, ⎪ n < 0, R < z < ∞ x− ⎩ 1
n =−∞
∑ x ( n) z
∞
−n
⎧ ⎪ Rx+ > Rx− , ⎨ ⎪ ⎩ Rx+ ≤ Rx− ,
Rx− < z ≤ Rx+ X ( z )无收敛域
2.某年考题 (1)已知某系统输入和输出关系为 y ( n) = 系统输入。 1)判断它是线性系统吗?为什么? 2)试证明 y ( n) 可以表示为 y (n) =
H (e jω ) = H1 (e jω ) + H 2 (e jω ) =
1 − a2 。 1 − 2a cos ω + a 2
