初等数学公式及其函数图像
二基本初等函数及其图像

移
用xh 代替x 是将图像右移h
个单位( h>0),若h 为负数,则左
移.
第二节 初等函数及其图像
三、构建新函数
例
1. 平
已知 f (x) x3,试画出 2 f (x)
移 和 f (x) 2 的图像,并写出该函数的
图像向左平移 5 个单位所得图像的函
函 函数,设第一种产品的销售利润为
数 U1=f(t),第二种产品的销售利润为 的 U2=g(t), 则两种产品的实际利润
和 用函数符号表示即有
差
函数的和
U(t)= U1 +U2 =f(t) +g(t)
第二节 初等函数及其图像
三、构建新函数
函数和的定义
2.
函
两个函数的和是一个函数,其在
数 每一点的函数值都是两个函数在自变 的 量的相同取值点的函数值的和.
例 求函数 y x 的反函数. x2
第二节 初等函数及其图像
一、反函数
想一想
1.一个函数与其反函数的定义域及值域有
什么关系?
2.
f
1(
x)与
1 之间有没有关系? f( x)
3. f 1( f( x))与f( f 1( x))各等于多少?
第二节 初等函数及其图像
二、基本初等函数及其图像
形如 y = x (R)的函数称为幂函数.
y arccos x的图像
4. 反 三 角 函 数 想一想 反余弦函数有什么性质?
第二节 初等函数及其图像
二、基本初等函数及其图像
y arctan x的图像
4. 反 三 角 函 数 想一想 反正切函数有什么性质?
最全高数基本初等函数概念图像及性质完整版

基本初等函数. 幂函数(a 为实数 )要记住最常见的几个幂函数的定义域及图形..指数函数定义域:,值域:,图形过( 0, 1)点, a>1 时,单调增加; a 时,单调减少。
今后用的较多。
.对数函数定义域:,值域:,与指数函数互为反函数,图形过(1, 0)点, a>1 时,单调增加;a<1 时,单调减少。
.三角函数,奇函数、有界函数、周期函数;,偶函数、有界函数、周期函数;,的一切实数,奇函数、周期函数,的一切实数,奇函数、周期函数;,.反三角函数;;;。
以上是五种基本初等函数,关于它们的常用运算公式都应掌握注:( 1)指数式与对数式的性质由此可知,今后常用关系式,如:( 2)常用三角公式积化和差sina*cosb=(sin(a+b)+sin(a-b))/2 cosa*sinb=(sin(a+b)-sin(a-b))/2cosa*cosb=(cos(a+b)+cos(a-b))/2 sina*sinb=-(cos(a+b)-cos(a-b))/2和差化积sinx+siny=2sin((x+y)/2)*cos((x-y)/2) sinx-siny=2cos((x+y)/2)*sin((x-y)/2) cosx+cosy=2cos((x+y)/2)*cos((x-y)/2) cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)赠送以下资料《二次函数的应用》中考题集锦10 题已知抛物线y x2mx 2m 2 (m 0).( 1)求证:该抛物线与x 轴有两个不同的交点;( 2)过点P(0,n)作y 轴的垂线交该抛物线于点 A 和点 B (点 A 在点 P 的左边),是否存在实数 m,n ,使得 AP2PB ?若存在,则求出m,n 满足的条件;若不存在,请说明理由.答案:解:( 1)证法 1:29 m2,y x2mx 2m2x m24当 m0 时,抛物线顶点的纵坐标为9 m20 ,4顶点总在 x 轴的下方.而该抛物线的开口向上,该抛物线与x 轴有两个不同的交点.(或者,当 m 0 时,抛物线与y 轴的交点(0,2m2)在x轴下方,而该抛物线的开口向上,该抛物线与 x 轴有两个不同的交点.)证法 2:m2 4 1 ( 2m2 ) 9m2,当 m0时, 9m20 ,该抛物线与 x 轴有两个不同的交点.( 2)存在实数m,n,使得AP2PB .设点 B 的坐标为(t,n),由 AP2PB 知,y①当点 B 在点 P 的右边时, t0,点 A 的坐标为(2t, n) ,A PBx 且 t, 2t是关于 x 的方程 x2mx2m2n 的两个实数根.O m24( 2m2n) 9m24n 0 ,即 n9 m2.4且 t ( 2t )m (I), t ( 2)t2(II)m n由( I)得,t m,即m 0.将 t m代入(II)得, n0 .y 当 m0且 n0 时,有 AP2PB .②当点 B 在点 P 的左边时, t0,点 A 的坐标为(2 t,n),且 t,2t 是关于x的方程 x 2mx2m2n 的两个实数根.xOm24( 2m2n) 9m24n 0 ,即 n9 m2.4AB P且 t 2t m (I),t 2t2m2n (II)由( I)得,t m0 .3,即m将 t m代入( II )得,n20 m2且满足 n9 m2.32094当 m0 且n m2时,有AP2PB9第 11 题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间t (秒)间的关系式为S 10t t 2,若滑到坡底的时间为 2 秒,则此人下滑的高度为()A.24米B.12米C. 12 3 米D.6米答案:B第 12 题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月 25日起的 180 天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图( 1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.y (天)z(元 )16060140( 180, 92)5012040100858036020401020140160100120O20 40 6080 100 120150 180t(天)O204060 80110140160 180t(天 )( 1)直接写出图(1)中表示的市场销售单价y (元)与上市时间t (天)(t0)的函数关图 (1)图 (2)系式;( 2)求出图( 2)中表示的种植成本单价z(元)与上市时间t (天)(t 0)的函数关系式;( 3 )认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(说明: 市场销售单价和种植成本单价的单位:元/500 克.)答案:解:( 1)依题意,可建立的函数关系式为:2 t 160 (0t,3 120)y 80 (120 ≤ t,150)2 20 (150 ≤t ≤ .5( 2)由题目已知条件可设za(t 110) 220 .85图象过点 (60, ) ,385 a(60 110) 2 20. a1 . 3300z1(t 110) 2 20 (t 0 ). 300( 3)设纯收益单价为W 元,则 W =销售单价 成本单价.2 1601110) 220 (0 t,t(t120)3300故W 801 (t 220(120 ≤t,300 110)150)2 201 220 (150 ≤ t≤.5300化简得1 2100(0,300W1(t 110)2 60 (120≤ t 150), 30012 56 (150 ≤ t ≤.300①当 W1 (t 10)2 100(0 t 120) 时,有 t 10时, W 最大,最大值为 100;300②当 W1 (t 110)2 60(120 ≤ t 150) 时,由图象知,有 t 120 时, W 最大,最大300值为 59 2 ;3③当 W1 (t 170)2 56(150 ≤ t ≤ 180) 时,有 t 170 时, W 最大,最大值为 56.300综上所述,在 t 10 时,纯收益单价有最大值,最大值为100 元.第 13 题如图,足球场上守门员在O 处开出一高球,球从离地面1 米的 A 处飞出( A 在 y 轴上),运动员乙在距O 点6 米的B 处发现球在自己头的正上方达到最高点M,距地面约 4 米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.( 1)求足球开始飞出到第一次落地时,该抛物线的表达式.( 2)足球第一次落地点 C 距守门员多少米?(取 43 7)( 3)运动员乙要抢到第二个落点D ,他应再向前跑多少米?(取26 5)y4 M2 1 AOBCDx答案:解:( 1)( 3 分)如图,设第一次落地时,抛物线的表达式为ya(x6) 2 4.y由已知:当 x 0 时 y 1.即 1 36a 4, a1 . 4M12E FN表达式为 y124. 2 ( x 6)1 A1 x2 12OBCDx(或 yx 1 )12 1( 2)(3 分)令 y0, ( x6)2 4 0.12(x6)2 48. x 4 3 6 ≈ 13,x4 3 6 0 (舍去).12足球第一次落地距守门员约 13 米.( 3)(4 分)解法一:如图,第二次足球弹出后的距离为CD根据题意: CDEF (即相当于将抛物线 AEMFC 向下平移了 2 个单位)21( x 6) 24解得 x6 2 6,x2 6 26.121CD x 1 x 2 4 6 ≈10.BD 13 6 1017 (米).解法二: 令1( x 6) 2 4 0.12解得x 1 6 4 3 (舍), x 26 4 3 ≈13.点 C 坐标为( 13, 0).设抛物线 CND 为 y1( x k) 2 2.12将 C 点坐标代入得:1(13 k) 2 2 0.12解得:k 1 13 2 613 (舍去),k 2 6 4 3 2 6 ≈ 6 7 5 18.y1( x 18)2 212 令 y0, 01( x 18)2 2.12x 118 2 6 (舍去), x 2 18 2 6≈23.BD 23 6 17 (米).解法三:由解法二知, k 18,所以 CD 2(18 13) 10, 所以 BD(136) 10 17.答:他应再向前跑17 米.第 14 题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费 2.7 万元;购置滴灌 设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为 0.9 ;另外每公顷种植蔬菜需种子、化肥、农药等开支 0.3 万元.每公顷蔬菜年均可卖7.5 万元.y (万元),( 1)基地的菜农共修建大棚 x (公顷),当年收益(扣除修建和种植成本后)为写出 y 关于 x 的函数关系式.( 2)若某菜农期望通过种植大棚蔬菜当年获得 5 万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)( 3)除种子、化肥、农药投资只能当年受益外, 其它设施 3 年内不需增加投资仍可继续使用. 如果按 3 年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:( 1) y 7.5x2.7x 0.9x 20.3x0.9x 2 4.5x .( 2)当 0.9x 24.5x5 时,即 9x 245x 50 0 , x 15 , x 2 1033从投入、占地与当年收益三方面权衡,应建议修建5公顷大棚.(3)设3Z (万元)3年内每年的平均收益为Z 7.5x0.9x 0.3x20.3x0.3x2 6.3x20.3 x 10.5 33.075(10分)不是面积越大收益越大.当大棚面积为10.5 公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益.②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当 0.3x2 6.3x0时, x10 , x2 21.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第 15 题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18 元,按定价 40元出售,每月可销售 20 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价 1元,月销售量可增加 2 万件.(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写x的取值范围);(2)求出月销售利润z(万元)(利润=售价-成本价)与销售单价x(元)之间的函数关系式(不必写 x 的取值范围);(3)请你通过( 2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于 480 万元.答案:略.第 16 题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为 2m ,隧道最高点P 位于 AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?yPA BO Cx答案:( 1)由题意可知抛物线经过点A0,2 ,P 4,6 ,B 8,2设抛物线的方程为y ax2bx c将 A,P,D 三点的坐标代入抛物线方程.解得抛物线方程为y1x22x 24( 2)令 y4 ,则有 1 x 2 2x2 44解得x 14 2 2, x 2 4 2 2x 2 x 14 2 2货车可以通过.( 3)由( 2)可知1x 2 x 1 2 2 22 货车可以通过.第 17 题如图,在矩形ABCD 中, AB 2 AD ,线段 EF 10 .在 EF 上取一点 M ,分别以EM , MF 为一边作矩形 EMNH 、矩形 MFGN ,使矩形 MFGN ∽ 矩形 ABCD .令 MN x ,当 x 为何值时,矩形 EMNH 的面积 S 有最大值?最大 D C值是多少?ABHN GEMF答案:解:矩形 MFGN ∽ 矩形 ABCD ,MN MF .AD ABAB2 AD , MN x ,MF 2x .EMEFMF 10 2x .Sx(10 2x) 2 x 2 10x22 52 x52.2当 x5时, S 有最大值为25.22第 18 题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润 y A (万元)与投资金额 x (万元)之间存在正比例函数关系: y A kx ,并且当投资 5 万元时,可获利润 2 万元.信息二:如果单独投资B 种产品,则所获利润y B (万元)与投资金额 x (万元)之间存在二次函数关系:y B ax 2 bx ,并且当投资2 万元时,可获利润 2.4 万元;当投资4 万元时,可获利润 3.2 万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对A,B两种产品共投资 10 万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?答案:解:(1)当x 5 时,y1,,0.4 ,2 25k ky A0.4x ,当x 2 时,y B 2.4 ;当x 4 时,y B 3.2.2.44a2b3.216a4ba0.2解得1.6by B0.2x2 1.6 x .( 2)设投资B种商品x万元,则投资 A 种商品(10x) 万元,获得利润W万元,根据题意可得W0.2x2 1.6 x0.4(10 x)0.2 x2 1.2x4W0.2( x3)2 5.8当投资 B 种商品 3 万元时,可以获得最大利润 5.8 万元,所以投资A种商品7万元, B种商品 3 万元,这样投资可以获得最大利润 5.8 万元.第 19 题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱 A3 B3 50m , 5 根支柱 A1 B1, A2 B2, A3 B3, A4 B4,A5 B5之间的距离均为15m ,B1B5∥ A1 A5,将抛物线放在图( 2)所示的直角坐标系中.(1)直接写出图( 2)中点 B1, B3, B5的坐标;(2)求图( 2)中抛物线的函数表达式;( 3)求图( 1)中支柱 A2 B2, A4 B4的长度.B3yB2B430m B3B1B5B1B5A1A2 A3 A4 A5O l图 (1)图(2)答案:B1 ( 30, 0) , B3 (0,30) , B5 (30,0) ;(1)( 2)设抛物线的表达式为y a(x 30)( x30) ,把 B3 (0,30) 代入得 y a(030)(030)30 .∴ a 1.301( x∵ 所求抛物线的表达式为:y30)( x30) .30( 3)∵B4点的横坐标为15,∴ B4的纵坐标 y41(1530)(1530)45.302∵ A3B350 ,拱高为30,∴立柱 A4B4 204585(m) .2285(m) 。
高等数学公式大全以及初等函数图像

高等数学公式导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式:三角函数:正弦函数sin x ;余弦函数cos x ;正切函数sin tan cos x x x =;余切函数cos cot sin xx x =; 正割函数1sec cos x x =;余割函数1csc sin x x=·诱导公式:函数 角A sincostg ctg -α -sinα cosα -tgα -ctgα 90°-α cosα sinαctgαtgα 90°+α cosα -sinα -ctgα -tgα 180°-α sinα-cosα -tgα-ctgα 180°+α -sinα -cosα tgα ctgα 270°-α -cosα -sinα ctgα tgα 270°+α -cosα sinα -ctgα -tgα360°-α -sinα cosα -tgα -ctgα 360°+αsinαcosαtgαctgα常用三角函数公式:22cos sin 1x x += 22cos sin cos 2x x x -= 2s i n c o s s i n x x x= 21cos 22sin x x -= 21c o s 22c o sx x +=22211tan sec cos x x x +== 22211cot csc sin x x x+== xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x1sin sin [cos()cos()]2x y x y x y =-+-- 1c o s c o s [c o s ()c o s ()]2x y x y x y =++- 1sin cos [sin()sin()]2x y x y x y =++-·和差角公式: ·和差化积公式:反三角函数: a r c s i n a r c c o s 2x x π+= a r c t a n a r c c o t 2x x π+= arcsin x :定义域[1,1]-,值域[,]22ππ-;arccos x :定义域[1,1]-,值域[0,]π; arctan x :定义域(,)-∞+∞,值域(,)22ππ-;arccot x :定义域(,)-∞+∞,值域(0,)π·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( αααααααααα23333133cos 3cos 43cos sin 4sin 33sin tg tg tg tg --=-=-=αααααααααααααα222222122212sin cos sin 211cos 22cos cos sin 22sin tg tg tg ctg ctg ctg -=-=-=-=-==33223()33a b a a b ab b ±=±+± 3322()()a b a b a a b b ±=±+ 123221()()n n n n n n n a b a b a a b a b ab b ------=-+++++122(1)(1)(1)()2!!n n n n n k kn n n n n n k a b a na b a b a b b k ------++=++++++高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
高数总结:基本初等函数图像及其性质
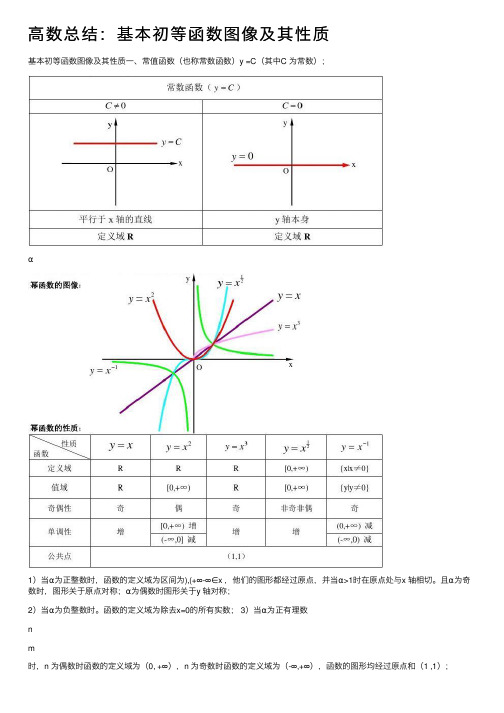
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。
6类基本初等函数以及三角函数(考研数学基础)
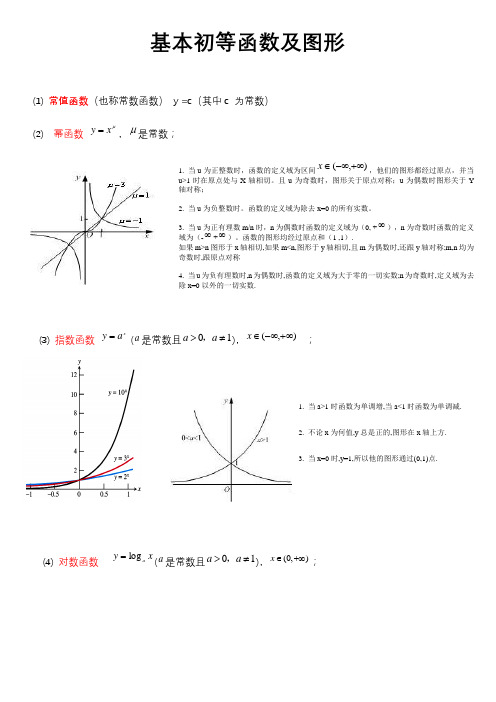
基本初等函数及图形(1) 常值函数(也称常数函数) y =c (其中c 为常数)(2) 幂函数 μx y =,μ是常数;(3) 指数函数 xa y = (a 是常数且01a a >≠,),),(+∞-∞∈x ;(4) 对数函数x y a log =(a是常数且01a a >≠,),(0,)x ∈+∞;1. 当u 为正整数时,函数的定义域为区间),(+∞-∞∈x ,他们的图形都经过原点,并当u>1时在原点处与X 轴相切。
且u 为奇数时,图形关于原点对称;u 为偶数时图形关于Y 轴对称;2. 当u 为负整数时。
函数的定义域为除去x=0的所有实数。
3. 当u 为正有理数m/n 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n 均为奇数时,跟原点对称4. 当u 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数.1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(5) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数. a<1在实用中很少用到/(6)反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .小结:(a 为任意实数)(正弦函数)正弦函数是奇函数且三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x=αcos 正切:xy=αtan 余切:y x =αcot正割:xr=αsec 余割:y r =αcsc注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
考研数学必备函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$ $cos(pi/2+a)=-sin(a)$ $sin(pi-a)=sin(a)$ $cos(pi-a)=-cos(a)$ $sin(pi+a)=-sin(a)$ $cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$$1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数直角坐标系中的定义。
高等数学公式大全以及初等函数图像

高等数学公式导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹()公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
初等函数图像知识点总结

初等函数图像知识点总结在学习初等函数的过程中,图像是一个非常重要的概念。
初等函数的图像可以帮助我们更直观地理解函数的性质和特点。
在本文中,我们将总结初等函数图像的相关知识点,包括函数图像的基本形状、对称性质、特殊点以及常见的初等函数图像等内容。
一、函数图像的基本形状1. 直线函数的图像直线函数的图像是一条直线,其一般方程为y = kx + b,其中k和b分别代表斜率和截距。
斜率k决定了直线的倾斜方向和程度,当k>0时,直线向右上方倾斜;当k<0时,直线向右下方倾斜。
截距b决定了直线与y轴的交点,当b>0时,直线与y轴的交点在y轴上方;当b<0时,直线与y轴的交点在y轴下方。
2. 平方函数的图像平方函数的图像是一个开口向上或向下的抛物线,其一般方程为y = ax^2 + bx + c,其中a决定了抛物线的开口方向和程度。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
二次函数的顶点坐标为(-b/2a, c),可以通过顶点坐标确定抛物线的位置。
3. 绝对值函数的图像绝对值函数的图像是一条V形的折线,其一般方程为y = |x|,表示x的绝对值。
函数图像在原点处有一个拐点,称为折点,折点是函数图像的特殊点之一。
4. 根号函数的图像根号函数的图像是一条从原点开始的曲线,其一般方程为y = √x,函数图像在x轴的正半轴上。
根号函数的图像是一个开口向右的半圆形曲线。
5. 指数函数的图像指数函数的图像是一条增长或衰减的曲线,其一般方程为y = a^x,其中a>0且a≠1。
指数函数的图像在坐标轴之间没有交点,增长函数的图像是向上的曲线,衰减函数的图像是向下的曲线。
6. 对数函数的图像对数函数的图像是一条先增后减的曲线,其一般方程为y = log_ax,其中a>0且a≠1。
对数函数的图像在x轴的正半轴上,对数函数的图像与指数函数的图像是关于y=x对称的。
二、函数图像的对称性质1. 奇偶性奇函数的图像关于原点对称,即f(-x)=-f(x),即图像关于原点对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (a) b f 1 (b) a .
27. 若 函 数 y f ( kx b) 存 在 反 函 数 , 则 其 反 函 数 为 y
1 [f k
1
( x ) b] , 并 不 是
y [ f 1 (kx b) ,而函数 y [ f 1 (kx b) 是 y
者的一个必要而不是充分条件.特别地, 方程 ax bx c 0(a 0) 有且只有一个实根在
2
(k1 , k 2 ) 内,等价于 f (k1 ) f (k 2 ) 0 ,或 f (k1 ) 0 且 k1
k1 k 2 b k2 . 2 2a
9.闭区间上的二次函数的最值
A CU B CU A B R
4.容斥原理
card ( A B) cardA cardB card ( A B ) card ( A B C ) cardA cardB cardC card ( A B ) card ( A B) card ( B C ) card (C A) card ( A B C ) .
1
ab 对称. 2m
( x) 的图象关于直线 y=x 对称. 25.若将函数 y f ( x) 的图象右移 a 、上移 b 个单位,得到函数 y f ( x a ) b 的图 象;若将曲线 f ( x, y ) 0 的图象右移 a 、上移 b 个单位,得到曲线 f ( x a, y b) 0 的图
11.定区间上含参数的二次不等式恒成立的条件依据 (1)在给定区间 (,) 的子区间 L (形如 , , , , , 不同)上含参数 的二次不等式 f ( x, t ) 0 ( t 为参数)恒成立的充要条件是 f ( x, t )min 0( x L) . (2)在给定区间 (,) 的子区间上含参数的二次不等式 f ( x, t ) 0 ( t 为参数)恒成立 的充要条件是 f ( x, t )man 0( x L) .
b p, q , f ( x)max max f ( p), f (q) , f ( x)min min f ( p), f (q) . 2a b p, q , 则 f ( x)min min f ( p), f (q) , 若 (2) 当 a<0 时 , 若 x 2a x
反设词 一个也没有 至少有两个 至多有( n 1 )个 至少有( n 1)个
p 且 q p 或 q
p 且q
14.四种命题的相互关系 原命题 若p则q 互 互 否 否 否命题 若非p则非q 互逆 为 逆 为 逆 否 逆否命题 若非q则非p 互逆 互 互 否 逆命题 若q则p
15.充要条件 (1)充分条件:若 p q ,则 p 是 q 充分条件. (2)必要条件:若 q p ,则 p 是 q 必要条件. (3)充要条件:若 p q ,且 q p ,则 p 是 q 充要条件. 注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然. 16.函数的单调性 (1)设 x1 x2 a, b, x1 x2 那么
(2)函数 y f ( x) 的图象关于直线 x
f (a b mx) f (mx) .
ab 对称 f (a mx) f (b mx) 2
24.两个函数图象的对称性 (1)函数 y f ( x) 与函数 y f ( x ) 的图象关于直线 x 0 (即 y 轴)对称. (2)函数 y f ( mx a ) 与函数 y f (b mx) 的图象关于直线 x (3)函数 y f ( x) 和 y f
ab ab ;两个函数 y f ( x a) 与 y f (b x) 的图象关于直线 x 对称. 2 2 a 21. 若 f ( x) f ( x a) , 则 函 数 y f ( x) 的 图 象 关 于 点 ( ,0) 对 称 ; 若 2 f ( x) f ( x a) ,则函数 y f ( x) 为周期为 2a 的周期函数. n n 1 22.多项式函数 P( x) an x an 1 x a0 的奇偶性 多项式函数 P ( x ) 是奇函数 P ( x ) 的偶次项(即奇数项)的系数全为零. 多项式函数 P ( x ) 是偶函数 P ( x ) 的奇次项(即偶数项)的系数全为零. 23.函数 y f ( x) 的图象的对称性 (1)函数 y f ( x) 的图象关于直线 x a 对称 f (a x) f (a x ) f (2a x) f ( x) .
x
b p, q ,则 f ( x)max max f ( p), f (q) , f ( x)min min f ( p), f (q) . 2a
10.一元二次方程的实根分布 依据:若 f (m) f (n) 0 ,则方程 f ( x ) 0 在区间 (m, n) 内至少有一个实根 . 设 f ( x) x2 px q ,则
初等数学常用公式及常用结论
1. 元素与集合的关系 x A x CU A , x CU A x A . 2.德摩根公式
CU ( A B) CU A CU B; CU ( A B) CU A CU B .
3.包含关系
A B A A B B A B CU B CU A
2
b k1 k 2 , 或 f (k 2 ) 0 且 2a 2
二次函数 f ( x) ax bx c(a 0) 在闭区间 p, q 上的最值只能在 x 间的两端点处取得,具体如下: (1)当 a>0 时, 若x
b 处及区 2a
b b ), f ( x) max max f ( p), f (q) ; p , q , 则 f ( x) min f ( 2a 2a
5. 集合 {a1 , a2 ,
, an } 的子集个数共有 2 n 个;真子集有 2 n –1 个;非空子集有 2 n –1
n
个;非空的真子集有 2 –2 个. 6.二次函数的解析式的三种形式 (1)一般式 f ( x) ax bx c(a 0) ;
2
(2)顶点式 f ( x) a( x h) k (a 0) ;
2
(3)零点式 f ( x) a( x x1 )( x x2 )(a 0) . 7.解连不等式 N f ( x) M 常有以下转化形式
N f ( x) M [ f ( x) M ][ f ( x) N ] 0 M N M N f ( x) N | | f ( x) 0 2 2 M f ( x) 1 1 . f ( x) N M N 8.方程 f ( x ) 0 在 (k1 , k 2 ) 上有且只有一个实根,与 f (k1 ) f (k 2 ) 0 不等价,前者是后
a 0 a 0 (3) f ( x) ax bx c 0 恒成立的充要条件是 b 0 或 2 . b 4 ac 0 c 0
4 2
12.真值表 p q 非p p或q p且q 真 真 假 真 真 真 假 假 真 假 假 真 真 真 假 假 假 真 假 假 13.常见结论的否定形式 原结论 反设词 原结论 是 不是 至少有一个 都是 不都是 至多有一个 大于 不大于 至少有 n 个 小于 不小于 至多有 n 个 对所有 x , 存在某 x , p 或q 成立 不成立 对任何 x , 不成立 存在某 x , 成立
f (0) 1, lim
x 0
g ( x) 1. x
29.几个函数方程的周期(约定 a>0) (1) f ( x) f ( x a ) ,则 f ( x ) 的周期 T=a; (2) f ( x) f ( x a) 0 ,
f ( x1 ) f ( x2 ) 0 f ( x)在a, b 上是增函数; x1 x2 f ( x1 ) f ( x2 ) 0 f ( x)在a, b 上是减函数. ( x1 x2 ) f ( x1 ) f ( x2 ) 0 x1 x2 (2) 设函数 y f ( x) 在某个区间内可导,如果 f ( x ) 0 ,则 f ( x ) 为增函数;如果 f ( x ) 0 ,则 f ( x ) 为减函数. 17.如果函数 f ( x ) 和 g ( x ) 都是减函数,则在公共定义域内,和函数 f ( x) g ( x) 也是减 函 数 ; 如 果 函 数 y f (u ) 和 u g ( x) 在 其 对 应 的 定 义 域 上 都 是 减 函 数 , 则 复 合 函 数 y f [ g ( x)] 是增函数.
1 [ f ( x) b] 的反函数. k
28.几个常见的函数方程 (1)正比例函数 f ( x) cx , f ( x y ) f ( x) f ( y ), f (1) c .
x (2)指数函数 f ( x) a , f ( x y ) f ( x) f ( y ), f (1) a 0 .
p 2 4q 0 (1)方程 f ( x ) 0 在区间 (m,) 内有根的充要条件为 f ( m) 0 或 p ; m 2 f ( m) 0 f ( n) 0 (2)方程 f ( x ) 0 在区间 (m, n) 内有根的充要条件为 f (m) f (n) 0 或 p 2 4q 0 m p n 2 f ( m) 0 f ( n ) 0 或 或 ; af (n) 0 af (m) 0 p 2 4q 0 (3)方程 f ( x ) 0 在区间 ( , n) 内有根的充要条件为 f ( m) 0 或 p . m 2
