八年级最短路径问题归纳
八年级数学最短路径题型归纳

八年级数学中的最短路径问题,通常涉及到几何图形中的点、线、面等元素,需要利用一些基本的几何知识和数学原理来求解。
以下是一些常见的最短路径题型及其解题方法:1.两点之间的最短距离:题型描述:在平面上给定两点A和B,求A到B的最短距离。
解题方法:直接连接A和B,线段AB的长度即为最短距离。
2.点到直线的最短距离:题型描述:在平面上给定一点P和一条直线l,求P到l的最短距离。
解题方法:作点P到直线l的垂线,垂足为Q,则PQ的长度即为最短距离。
3.直线到直线的最短距离:题型描述:在平面上给定两条直线l1和l2,求l1到l2的最短距离。
解题方法:如果l1和l2平行,则它们之间的距离即为最短距离;如果l1和l2不平行,则作l1到l2的垂线,垂足所在的线段即为最短4.点到圆的最短距离:题型描述:在平面上给定一点P和一个圆O,求P到圆O的最短距离。
解题方法:如果点P在圆O内,则最短距离为P到圆心的距离减去圆的半径;如果点P在圆O外,则最短距离为P到圆心的距离;如果点P在圆O上,则最短距离为0。
5.圆到圆的最短距离:题型描述:在平面上给定两个圆O1和O2,求O1到O2的最短距离。
解题方法:如果两圆外离,则它们之间的最短距离为两圆的半径之和;如果两圆外切,则它们之间的最短距离为两圆的半径之差;如果两圆相交或内切,则它们之间的最短距离为0;如果两圆内含,则它们之间的最短距离为两圆的半径之差减去两圆半径之和的绝对值。
6.多边形内的最短路径:题型描述:在一个多边形内给定两个点A和B,求A到B的最短解题方法:通常需要将多边形划分为多个三角形,然后利用三角形内的最短路径(即连接两点的线段)来求解。
7.立体几何中的最短路径:题型描述:在立体图形中给定两点A和B,求A到B的最短路径。
解题方法:通常需要将立体图形展开为平面图形,然后利用平面几何中的最短路径原理来求解。
在解决最短路径问题时,需要注意以下几点:准确理解题目要求,确定需要求的是哪两点之间的最短距离。
最短路径(八年级最短路径问题归纳)

原创不容易,【关注】店铺,不迷路!2019年中考数学大结局分析——最短路径问题4:费马点费马点问题一个等边三角形是在三角形的三条边的每一条边上向外形成的。
三个等边三角形的外接圆相交于一点T,称为托里切利点,而三个等边三角形的外接圆称为托里切利圆。
在一定条件下,托里切利点与等中心和费马点相同。
托里切利点是意大利物理学家托里切利发现的。
这个问题是费马(1601-1665)向意大利物理学家托里切利(1608-1647)提出的,作为一个著名的“寻找一个点使它到三角形三个顶点的距离最小”的极值问题,托里切利解决了这个问题。
当三角形的内角都小于120时,K为期望点,所以K称为托里切利点,也称为费马点。
后来德国的施泰纳(1796-1863)独立提出并推广,所以也叫施泰纳问题。
本篇文章中介绍的问题主要是以大家熟知的费马点为背景。
平时大家一听这名字感觉很神奇,学过之后可能感觉也就那回事。
很多数学问题、数学知识都是经历几代数学家的努力之后的成果。
除了做题,有空的时候可以多了解一些数学文化、数学史,领略数学的魅力。
话不多说,直接上题。
【题1】(武汉,2019)问题背景:如图1所示,绕a点逆时针转动ABC,得到ADE,其中DE和BC在p点相交,可以推导出结论:paPC=PE。
解题:如图2,在MNG中,Mn=6,m=75,mg=42。
如果点o是MNG中的一个点,则从点o到MNG三个顶点的距离之和的最小值为。
回答之前,可以先看一下前面的文章:旋转结构的几何最大值【分析】三角形内确定一点到三个顶点的距离和最小值,就是我们前面说的问题。
上辅助线先。
怎么做,圆内任取一点并连接三个顶点,再将其中一个三角形如MOG绕点M 逆时针旋转60度得MOG,连接OO。
易得四点共线时距离和最小。
点G是定点,所以NG的长度为定值。
NMG为135,所以容易求得NG为229。
(备注:过点G作MN的垂线即可解得。
)下面是菁优网的答案。
29。
下面是陕西省的中考压轴题【题2】(2018陕西)问题提出(1)如图所示,在ABC中,a=120,ab=AC=5,那么ABC的外接圆半径r为。
人教八年级数学上册最短路径问题

如图,点A,B是直线l同侧不重合的两点,在直线l上求作一点C,使得
AC+BC的长度最短.作法:①作点B关于直线l的对称点B′;②连接AB′,与直
线l相交于点C,则点C为所求作的点.在解决这个问题时没有用到的知识或方
法是( )
A.转化思想 B.三角形两边之和大于第三边
∙B A∙
C.两点之间,线段最短
l
∙B
题转化为“两点之间,线段最短”来解决,该
A∙
过程用到了“转化思想”,“两点之间,线段
l
C
最短”,验证是否为最短距离时利用了三角形
两边之和大于第三边.
B′
随堂练习 2
两棵树的位置如图所示,树的底部分别为点A,B,有一只昆虫沿着A至B的路径在 地面爬行,小树的树顶D处有一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C 处,问小虫在AB之间何处被小鸟抓住时,小鸟飞行路程最短,在图中画出该点的 位置.
1、直线异侧的两点到直线上一点距离和最短的问题.
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C使得AC+BC的值最 小,此时点C就是线段AB与直线l的交点.
A∙
C l
∙B
新知探究
知识点2
2、直线同侧的两点到直线上一点距离和最短的问题.
如图,点A,B分别是直线l同侧的两个点,在直线l上找一点C使得AC+BC的值 最小,这时先作点B关于直线l的对称点的B′,连接AB′交直线l于点C(也可以作 点A关于直线l的对称点A′,连接A′B交直线l于点C),此时点C就是所求作的点.
C
∵A′C=AC=BD,
在△A′CE和△BDE中, ∠A′CE=∠B′C=BD,
则△A′CE≌△BDE(AAS),CE=DE,A′E=BE.
2020年八年级数学上册第十三章13.4 课题学习 最短路径问题

16
2
详细答案 点击题序
3
详细答案 点击题序
1.如图,∠AOB=30°,点 M、N 分别是射线 OA、 OB 上的动点,OP 在∠AOB 内,且 OP=6,则△ PMN 周长的最小值为 6 .
2.尺规作图(保留作图痕迹):如图,已知直线 l 及 其两侧两点 A、B.
(1)在直线 l 上求一点 Q,使到 A、B 两点距离之和 最短;
(2)在直线 l 上求一点 P,使 PA=PB. 解:(1)如图,连接 AB 与直线 l 的交点 Q 即为所求. (2)作线段 AB 的垂直平分线 MN,直线 MN 与直线 l 的 交点 P 即为所求.
3.(1)如图①,在直线 AB 一侧有 C、D 两点,在 AB 上找一点 P,使 C、D、P 三点组成的三角形的周长 最短; 解:如图所示.
(1)若要使自来水厂到A,B两村的 距离相等,则应选择在哪建厂(要 求:尺规作图,保留作图痕迹, 不必写文字说明)?
分析:(1)欲求到A、B两村的距离相等的厂址,即 作出线段AB的垂直平分线与EF的交点即可; 解:(1)如图,点M即为所求.
(2)若要使自来水厂到A,B两村的距离之和最短, 应建在什么地方? 分析:(2)作出A点关于直线EF的对称点A′,再连 接A′B,找到A′B与EF的交点即可. (2)如图,点N即为所求.
(2)如图②,在∠AOB 内部有一点 P,在 OA、OB 上 分别存在点 E、F,使得 E、F、P 三点组成的三角 形的周长最短,请找出 E、F 两点. 解:如图所示.
知识要点 最短路径问题
定义
关于“两点的所有连线中, 线段 最短
”“连接直线外一点与直线上各点的所 有线段中, 垂线段最短”等的问题,
八年级上册最短路径知识点

八年级上册最短路径知识点在学习数学中,最短路径是一个重要的概念。
在八年级上册中,我们会学习到最短路径的相关知识。
本文将系统地介绍最短路径的概念、算法和应用。
1、最短路径的概念最短路径是指从一个起点到达一个目标点的路径中,使得路径上的边权值之和最小的路径。
在最短路径的计算中,边权值常常代表距离或花费等。
最短路径可以用图表示,通常被称为权重图。
在权重图中,每个节点代表一个地点,每条边代表两个地点之间的路径。
边上的权重可以是任何非负实数。
2、最短路径算法在计算最短路径时,存在多种算法可供选择。
以下是几种较常见的最短路径算法:A、Dijkstra算法:Dijkstra算法通过计算起点到其他点的最短路径,找到整个图的最短路径。
该算法适用于边权值为非负数的图。
B、Bellman-Ford算法:Bellman-Ford算法通过对边进行松弛操作,多次更新起始点到其他点的最短路。
该算法适用于边权值非负的图。
C、Floyd算法:Floyd算法通过迭代计算任意两点之间的距离来找到最短路径。
该算法适用于边权值可以是任何实数的图。
3、最短路径的应用最短路径的应用十分广泛,以下是几个实际应用场景的例子:A、导航:最短路径可用于帮助我们规划驾车或步行路线。
例如,谷歌地图利用最短路径算法帮助用户寻找最合适的路线。
B、运输:最短路径可用于计算货车或船只的最佳路线。
例如,国家邮政公司使用最短路径算法优化邮递路线。
C、电器布线:最短路径可帮助我们规划电气线路。
例如,一个高层建筑物中,我们需要通过最短路径算法来找到电路的最佳路径。
D、金融:最短路径可用于计算银行间的最佳借贷路线。
例如,银行可以使用最短路径算法来计算最优的借贷方案。
4、总结最短路径是一个十分有用的数学概念,可以应用于各个领域。
在八年级上册,我们学习了最短路径的定义、计算方法和应用场景。
希望本文能够帮助大家更好地理解最短路径的相关知识。
(完整版)八年级最短路径问题归纳小结.doc
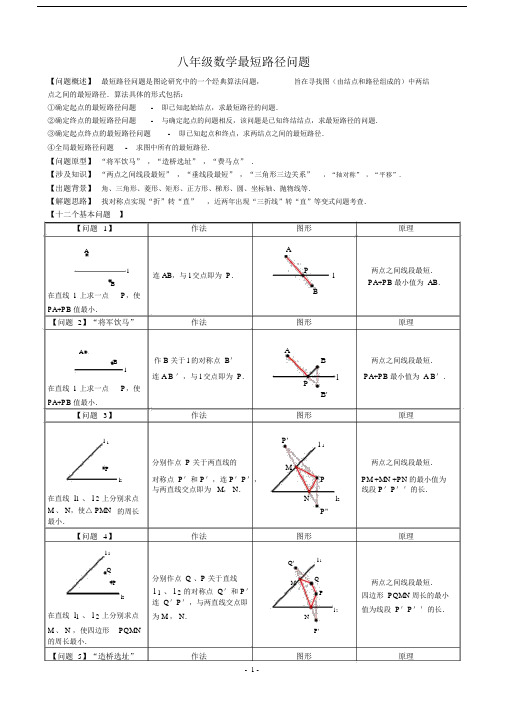
八年级数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址” ,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短” ,“三角形三边关系”,“轴对称” ,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】【问题1】作法图形原理A Al连 AB,与 l 交点即为 P.Pl两点之间线段最短.B PA+PB 最小值为 AB.B在直线 l 上求一点P,使PA+PB 值最小.【问题 2】“将军饮马”作法图形原理A AB 作 B 关于 l 的对称点 B' B 两点之间线段最短.l连 A B ',与 l 交点即为 P.l PA+PB 最小值为 A B'.P在直线 l 上求一点P,使B'PA+PB 值最小.【问题3】作法图形原理l 1 P' l1P分别作点 P 关于两直线的M两点之间线段最短.对称点 P'和 P',连 P'P',PM +MN +PN 的最小值为l2 P在直线 l1、 l 2上分别求点与两直线交点即为 M, N.N l2线段 P'P''的长.M 、 N,使△ PMN 的周长P''最小.【问题4】作法图形原理l 1lQ' 1Q分别作点 Q 、P 关于直线P MQ 两点之间线段最短.l 1、 l 2的对称点Q'和P'l2 P 四边形 PQMN 周长的最小连 Q'P',与两直线交点即l 2 值为线段 P'P''的长.在直线 l1、 l 2上分别求点为 M , N.NM 、 N ,使四边形PQMN P'的周长最小.【问题 5】“造桥选址”作法图形原理- 1 -AM Nmn将点 A 向下平移MN 的长度单位得A',连 A'B,交 nAA' M 两点之间线段最短.mB直线 m ∥ n ,在 m 、 n ,上分别求点 M 、N,使 MN ⊥m ,且 AM+ MN+ BN 的值最小.【问题 6】ABlM a N在直线 l 上求两点M、N(M 在左),使 MN a ,并使AM + MN+ NB 的值最小.【问题 7】l1Pl 2在l 1上求点A,在 l 2上求点 B,使 PA+ AB 值最小.于点 N,过 N 作 NM ⊥ m 于M.作法将点 A 向右平移 a 个长度单位得 A',作 A'关于l的对称点 A',连 A'B,交直线l 于点N,将N点向左平移a 个单位得 M.作法作点 P 关于l1的对称点P ',作 P'B⊥l2于 B,交l2于A.AM +MN +BN 的最小值为NnA'B+MN .B图形原理A A'B两点之间线段最短.lM N AM +MN +BN 的最小值为A'B+ MN.A''图形原理l1P'P 点到直线,垂线段最短.APA+ AB 的最小值为线段P'l 2 B的长.B【问题 8】作法l 1NAMl2 作点 A 关于l2的对称点BA ',作点B 关于l1的对称A 为l1上一定点,B 为l2上点 B',连 A'B'交l2于 M,一定点,在 l 2上求点M,交 l 1 于 N.在 l 1 上求点N ,使AM + MN+ NB 的值最小.【问题 9】作法图形原理B'l 1N两点之间线段最短.AAM +MN +NB 的最小值为M B l 2线段 A'B'的长.A'图形原理ABl在直线l 上求一点 P,使 PA PB 的值最小.连AB ,作 AB 的中垂线与直线 l 的交点即为 P.A垂直平分上的点到线段两B端点的距离相等.lP PA PB = 0.【问题 10】作法图形原理- 2 -A三角形任意两边之差小于A Bl作直线 AB ,与直线 l 的交第三边. PA PB ≤AB .B点即为 P .l在直线 l 上求一点 P ,使PPA PB 的最大值 = AB .PA PB 的值 最大 .【问题 11】作法 图形原理AAl 作 B 关于 l 的对称点 B ' B'B作直线 A B ',与 l 交点即lP为 P .B在直线 l 上求一点 P ,使PA PB 的值 最大 .三角形任意两边之差小于第三边. PA PB ≤ AB '.PA PB 最大值 = AB '.【问题 12】“费马点”作法图形原理ABC所求点为“费马点” ,即满足∠ APB =∠ BPC =∠APC = 120 °.以 AB 、 ACDAE两点之间线段最短.为边向外作等边△ ABD 、PPA+ PB+ PC 最小值 = CD .△ ABC 中每一内角都小于120°,在△ ABC 内求一点P ,使 PA+PB+PC 值最小.△ ACE ,连 CD 、 BE 相交于 P ,点 P 即为所求.BC【精品练习 】 1.如图所示,正方形ABCD 的面积为 12,△ ABE 是等边三角形,点一点 P ,使 PD +PE 的和最小,则这个最小值为( )A . 23 B . 2 6C . 3D . 62.如图,在边长为 2 的菱形 ABCD 中,∠ ABC = 60 °,若将 △ ACD交于点 E 、 F ,则 △ CEF 的周长的最小值为( )E 在正方形 ABCD 内,在对角线 AC 上有ADPEB C绕点 A 旋转,当 AC ′、 AD ′分别与 BC 、 CDA . 2B . 2 3C . 2 3D . 4- 3 -3.四边形 ABCD 中,∠ B=∠ D = 90 °,∠ C= 70 °,在 BC 、 CD 上分别找一点M、 N,使△ AMN 的周长最小时,∠ AMN + ∠ ANM 的度数为()A DA . 120°B. 130°C.110 °D. 140 °NBMC 4.如图,在锐角△ ABC 中, AB = 4 2 ,∠ BAC = 45 °,∠ BAC 的平分线交 BC 于点D , M、 N 分别是 AD 和 AB上的动点,则 BM +MN 的最小值是C.DMAN B5.如图, Rt△ ABC 中,∠ C= 90 °,∠ B= 30 °,AB= 6,点 E 在 AB 边上,点 D 在 BC 边上(不与点B、C 重合),且 ED = AE,则线段AE 的取值范围是.AEC D B 6.如图,∠AOB = 30 °,点 M、 N 分别在边OA、 OB 上,且OM = 1, ON= 3,点 P 、 Q 分别在边OB、 OA 上,则 MP + PQ+ QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt△ABC 中,∠ C= 90°,则有AC 2BC 2AB2)7.如图,三角形△ ABC中,∠OAB=∠AOB=15°,点B在x轴的正半轴,坐标为B( 6 3 , 0).OC 平分∠ AOB ,点 M 在 OC 的延长线上,点N 为边 OA 上的点,则MA + MN 的最小值是 ______.- 4 -8.已知 A( 2, 4)、 B (4, 2). C 在y轴上, D 在 x 轴上,则四边形ABCD 的周长最小值为,此时 C、 D 两点的坐标分别为.yABO x 9.已知A( 1, 1)、 B (4, 2).y( 1) P 为 x 轴上一动点,求PA+PB 的最小值和此时P 点的坐标;BAO x( 2) P 为 x 轴上一动点,求PA PB 的值最大时P 点的坐标;yBAO x( 3) CD 为 x 轴上一条动线段, D 在 C 点右边且CD = 1,求当AC+ CD+ DB 的最小值和此时 C 点的坐标;yBAO C D x10 .点 C 为∠ AOB 内一点.( 1)在 OA 求作点 D , OB 上求作点 E ,使△ CDE 的周长最小,请画出图形;( 2)在( 1)的条件下,若∠AOB = 30°, OC= 10,求△ CDE 周长的最小值和此时∠DCE 的度数.ACO B- 5 -11.( 1)如图①,△ ABD 和△ ACE 均为等边三角形,BE、 CE 交于 F,连 AF,求证: AF +BF +CF = CD ;( 2)在△ ABC 中,∠ ABC = 30°, AB= 6, BC= 8,∠ A ,∠ C 均小于 120°,求作一点 P,使 PA+PB+PC 的值最小,试求出最小值并说明理由.DAAEFB C图①B C图②12 .荆州护城河在CC'处直角转弯,河宽相等,从 A 处到达 B 处,需经过两座桥DD '、 EE ',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使 A 到 B 点路径最短?- 6 -。
初中八年级数学最短路径问题

八年级数学最短路径问题一、两点在一条直线异侧例:已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
练习、如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A 到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)二、两点在一条直线同侧例:图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.练习:如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
三、一点在两相交直线内部例:已知:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形ABC,使三角形周长最小.练习1:已知:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形ABC周长最小值为OA.求∠MON的度数。
练习2:某班举行晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB 桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?提高训练一、题中出现一个动点。
1.当题中只出现一个动点时,可作定点关于动点所在直线的对称点,利用两点之间线段最短,或三角形两边之和小于第三边求出最值.例:如图,在正方形ABCD中,点E为AB上一定点,且BE=10,CE=14,P为BD上一动点,求PE+PC最小值。
二、题中出现两个动点。
当题中出现两个定点和两个动点时,应作两次定点关于动点所在直线的对称点.利用两点之间线段最短求出最值。
例:如图,在直角坐标系中有四个点, A(-8,3),B(-4,5)C(0,n),D(m,0),当四边形ABCD周长最短时,求C、D的坐标。
练习1如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是.三、题中出现三个动点时。
数学八年级_轴对称_最短路径问题

三角形第3节多边形及其内角和【知识梳理】路径最短问题:运用轴对称,将分散的线段集中到两点之间,从而运用两点之间线段最短,来实现最短路径的求解。
所以最短路径问题,需要考虑轴对称。
典故:相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A地出发,到一条笔直的河边l 饮马,然后到B地.到河边什么地方饮马可使他所走的路线全程最短?精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马问题”.这个问题提炼出数学问题为:设C 为直线l上的一个动点,当点C 在l 的什么位置时,AC 与CB 的和最小(如图)作法:(1)作点B 关于直线l 的对称点B′;(2)连接AB′,与直线l 交于点C.则点C 即为所求.证明:如图,在直线l上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.由轴对称的性质知,BC =B′C,BC ′=B′C′.∴ AC +BC = AC +B′C = AB′,AC ′+BC′= AC′+B′C′.在△AB′C′中,AB ′<AC′+B′C′,∴ AC +BC <AC′+BC′.即 AC +BC 最短.预备知识:在直角三角形中,三边具有的关系如下:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC =+【诊断自测】1、如图,直线l 是一条河,A 、B 两地相距5km ,A 、B 两地到l 的距离分别为3km 、6km ,欲在l 上的某点M 处修建一个水泵站,向A 、B 两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )A .B .C .D .2、如图所示,四边形OABC 为正方形,边长为3,点A ,C 分别在x 轴,y 轴的正半轴上,点D 在OA 上,且D 的坐标为(1,0),P 是OB 上的一动点,则“求PD+PA 和的最小值”要用到的数理依据是( )A .“两点之间,线段最短”B.“轴对称的性质”C.“两点之间,线段最短”以及“轴对称的性质”D.以上答案都不正确3.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)()A.B.C.D.【考点突破】例1、如图,在矩形ABCD中,点E为BC的中点,点F在CD上,要使△AEF的周长最小时,确定点F的位置的方法为.答案:作点E关于DC的对称点E′,连接AE′交CD于点F.解析:根据题意可知AE的长度不变,△AEF的周长最小也就是AF+EF有最小值.作点E关于DC的对称点E′,连接AE′交CD于点F.故答案为:作点E关于DC的对称点E′,连接AE′交CD于点F.例2、如图所示,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.(1)若MN=20 cm,求△PEF的周长;(2)若∠AOB=35°,求∠EPF的度数.答案:见解析解析:(1)∵M与P关于OA对称∴OA垂直平分MP.∴EM=EP.又∵N与P关于OB对称∴OB垂直平分PN.∴FP=FN.∴△PEF的周长=PE+PF+EF=ME+EF+FN=MN=20(cm).(2)连接OM,ON,OP,∵OA垂直平分MP,∴OM=OP.又∵OB垂直平分PN,∴ON=OP.∴△MOE≌△POE(SSS),△POF≌△NOF(SSS).∴∠MOE=∠POE,∠OME=∠OPE,∠POF=∠NOF,∠OPF=∠ONF.∴∠MON=2∠AOB=70°∴∠EPF=∠OPE+∠OPF=∠OME+∠ONF=180°-∠MON=110°.例3、如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是()A.2B. C.20 D.2答案:A解析:作M关于OB的对称点M′,作N关于OA的对称点N′,如图所示:连接M′N′,即为MP+PQ+QN的最小值.根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°,∴在Rt△M′ON′中,M′N′==2.故选:A.例4、如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.50° B.60° C.70° D.80°答案:D解析:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,∵∠C=50°,∴∠DAB=130°,∴∠HAA′=50°,∴∠AA′E+∠A″=∠HAA′=50°,∵∠EA′A=∠EAA′,∠FAD=∠A″,∴∠EAA′+∠A″AF=50°,∴∠EAF=130°﹣50°=80°,故选:D.例5、如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A.2 B.2 C.4 D.4答案:B解析:由于点B与D关于AC对称,所以连接BD,与AC的交点即为F点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.连接BD,与AC交于点F.∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.∵正方形ABCD的面积为12,∴AB=2.又∵△ABE是等边三角形,∴BE=AB=2.故所求最小值为2.故选B.例6、如图,荆州古城河在CC′处直角转弯,河宽均为5米,从A处到达B处,须经两座桥:DD′,EE′(桥宽不计),设护城河以及两座桥都是东西、南北方向的,A、B在东西方向上相距65米,南北方向上相距85米,恰当地架桥可使ADD′E′EB的路程最短,这个最短路程是多少米?答案:见解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级最短路径问题归纳
最短路径问题是图论中的一个经典问题,也是计算机科学中的重要研究领域之一。
在八年级的学习中,我们也会接触到最短路径问题,并且通过一些简单的算法来解决这个问题。
本文将对八年级最短路径问题进行归纳总结,希望能够帮助大家更好地理解和应用这个问题。
一、最短路径问题的定义
最短路径问题是指在一个给定的图中,找出两个顶点之间的最短路径,即路径上的边权之和最小。
其中,图由顶点和边组成,顶点表示路径中的点,边表示路径中的通路或连接。
二、最短路径问题的应用
最短路径问题在生活中有着广泛的应用,比如导航系统中的最短路径规划、货物运输中的最短路径选择等等。
通过寻找最短路径,可以帮助我们节省时间和资源,提高效率。
三、最短路径问题的解决方法
1. 迪杰斯特拉算法
迪杰斯特拉算法是解决最短路径问题的一种常用算法。
该算法通过不断更新起点到各个顶点的最短路径,直到找到终点的最短路径为
止。
迪杰斯特拉算法的具体步骤如下:
- 初始化起点到各个顶点的距离为无穷大,起点到自身的距离为0;- 选择一个未访问的顶点,更新起点到其他顶点的距离;
- 重复上述步骤,直到找到终点的最短路径或所有顶点都被访问过。
2. 弗洛伊德算法
弗洛伊德算法是解决最短路径问题的另一种常用算法。
该算法通过不断更新任意两个顶点之间的最短路径,直到更新完所有顶点对之间的最短路径为止。
弗洛伊德算法的具体步骤如下:
- 初始化任意两个顶点之间的距离,如果两个顶点之间有直接的边,则距离为边的权值,否则距离为无穷大;
- 选择一个顶点作为中转点,更新任意两个顶点之间的距离;
- 重复上述步骤,直到更新完所有顶点对之间的最短路径。
四、最短路径问题的注意事项
在解决最短路径问题时,需要注意以下几点:
1. 图的表示方式:可以使用邻接矩阵或邻接表来表示图,根据具体的问题选择合适的表示方式。
2. 边的权值:边的权值可以表示两个顶点之间的距离、时间、花费等等,根据具体的问题选择合适的权值。
3. 起点和终点:确定问题中的起点和终点,以便找到起点到终点的最短路径。
五、最短路径问题的例题分析
下面通过一个例题来分析最短路径问题的解题过程:
例题:在一个有向图中,求出顶点A到顶点B的最短路径。
解题步骤:
1. 确定图的表示方式,选择邻接矩阵来表示图。
2. 初始化起点到各个顶点的距离,起点到自身的距离为0,其他顶点的距离为无穷大。
3. 选择一个未访问的顶点,更新起点到其他顶点的距离。
4. 重复上述步骤,直到找到终点的最短路径或所有顶点都被访问过。
5. 输出顶点A到顶点B的最短路径。
六、总结
最短路径问题是图论中的一个重要问题,通过寻找最短路径可以帮助我们节省时间和资源。
在八年级的学习中,我们介绍了最短路径问题的定义、应用、解决方法和注意事项,并通过一个例题进行了分析。
希望通过本文的归纳总结,大家能够更好地理解和应用最短路径问题。
