管道输气能力理论计算
管道输气能力理论计算

计算管道输气能力的经验公式:
设输气管线为水平,无高程变化,故忽略考虑流速增大引起的动能压降较摩阻压降则:总压降梯度为摩阻压降梯度:
dp/dz=f*ρ*v^2/2/D
已知参数有:
D 管道直径m q
sc 流量,m 3/d
γg 气体比重f 摩阻系数
用平均压力和平均温度计算平均
计算步骤:
1、计算气体平均Z、粘度μ和比
2、假定一个流量,计算雷诺数
3、计算摩阻系数f
4、计算流量qsc
式:
,无高程变化,故忽略重位压降;
的动能压降较摩阻压降下,一般可忽略。
摩阻压降梯度:
ρ*v^2/2/D
L管道长度,m
p1、p2分别为管道起点和终点压力,Mpa T1、T2分别为管道起点和终点温度,℃
均温度计算平均Z。
气体平均Z、粘度μ和比重γg
一个流量,计算雷诺数Re。
一般常用管道输气能力计算公式

一般常用管道输气能力计算公式
管道容积计算
V=AL=πD2L/4
其中:V:管道的体积,m3
L:管道的长度,m
D:管道的内径,m
圆周长公式:C=πD或者C=2πR
圆面积公式:S=πR2或者S=πD2/4
C:圆周长,m
D:圆直径,m
R:圆半径,m
标准状态下天然气体积计算
根据理想气体状态方程式公式计算标准状态下天然气体积。
PnVn/Tn=P1V1/T1=常数(理想气体状态方程式)
其中:Pn:气体在标准状态下的压力Mpa
Vn:气体在标准状态下的体积Nm3
Tn:气体在标准状态下的温度K
P1:气体在工作状态下的压力Mpa
V1:气体在工作状态下的体积Nm3
T1:气体在工作状态下的温度K
一般输气管线的通过能力公式
管线吹扫所用天然气量的计算可按一般输气管线的通过能力公式计算。
Q=5033.11D8/3[(P12-P22)/GTZL]1/2
管线放空能力的近似计算公式:
Q=382.78D8/3[(P12-P22)/L]1/2
其中:Q:天然气的体积Nm3
D:输气管道内径cm
P1:输气管道起点压力Mpa
P2:输气管道终点压力Mpa G:天然气的真实相对密度
T:天然气的绝对温度
Z:天然气的压缩因子
L:输气管道长度Km。
输气管径计算

一般常用管道输气能力计算公式
管道容积计算
V=AL=πD2L/4
其中:V:管道的体积,m3.
L:管道的长度,m
D:管道的内径,m
圆周长公式:C=πD或者C=2πR
圆面积公式:S=πR2或者S=πD2/4
C:圆周长,m
D:圆直径,m
R:圆半径,m
标准状态下天然气体积计算
根据理想气体状态方程式公式计算标准状态下天然气体积。
PnVn/Tn=P1V1/T1=常数(理想气体状态方程式)
其中:Pn:气体在标准状态下的压力Mpa
Vn:气体在标准状态下的体积Nm3
Tn:气体在标准状态下的温度K
P1:气体在工作状态下的压力Mpa
V1:气体在工作状态下的体积Nm3
T1:气体在工作状态下的温度K
一般输气管线的通过能力公式
管线吹扫所用天然气量的计算可按一般输气管线的通过能力公式计
算。
Q=5033.11D8/3[(P12-P22)/GTZL]1/2管线放空能力的近似计算公式:
Q=382.78D8/3[(P12-P22)/L]1/2
其中:Q:天然气的体积Nm3
D:输气管道内径cm
P1:输气管道起点压力Mpa
P2:输气管道终点压力Mpa
G:天然气的真实相对密度
T:天然气的绝对温度
Z:天然气的压缩因子
L:输气管道长度Km。
常用公式

一、输气常用计算公式1. 输气量计算用公式:当管段起终点得相对高差小于200米时[]51.053.2961.0222111522ZTLGP P EdQ -=当管段起终点得相对高差大于200米时()51.01)1(53.2112961.0222111522⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∑=⎥⎥⎦⎤⎢⎢⎣⎡-+∆+-=-ni i i i L aL h h ZTLG h a P P Ed Q式中:Q :气体流量(P 0=0.101325Mpa,T 0=293.15K ),m 3/d ; d :输气管内径,cm ;P 1,P 2:输气管计算段起点、终点的气体压力(绝),MPa ; Z :气体的压缩系数;T :气体的平均温度,非精确计算时可简化为加权平均值; L :计算段长度,km ; G :气体的相对密度;E :输气管的效率系数,DN 为300~800时,E=0.8~0.9; a :系数,a=0.0683(G/ZL),m -1; Δh :输气管段终点和起点的在日常运行管理过程中,针对鄯乌线当前实际(管线长度 L=301.625Km ;管径457×6mm ;),因此,此公式可简化为:Q输 = 7967538⎥⎦⎤⎢⎣⎡-TL PP 22210.51(Nm 3/h )2. 管道储气量计算公式式中:Q 储=管道的储气量,Nm3; V —管道的容积,m3; T 0—293.15K; P 0—0.101325Mpa; T —气体的平均温度;P 1m —管道计算段内气体的最高平均压力(绝),Mpa ; P 2m —管道计算段内气体的最低平均压力(绝),Mpa ; Z 1、Z 2—对应P1m 、P2m 时的气体压缩系数。
3.平均压力P m 及管道任意点气体压力P x 计算公式:⎪⎪⎭⎫- ⎝⎛=221100Z m P Z m P T P VT Q储)(3221221P P P P P m ++= (MPa )LXP P P P x )(222121--=(MPa)4.管道内气体平均温度t 、沿线任意点温度t X 计算式:t X =t 0+( t 0+t 0)e -aX式中:t —管道计算段内气体平均温度,℃; t 0—管道周围介质温度,℃; t 1—管道计算段内起点气体温度,℃; t X —管道任意点气体温度,℃; e —自然对数底数,e=2.718; L —管道计算段的实际长度,Km ; X —管道计算段起点至任意点的长度,Km;⎪⎭⎫⎝⎛--+=aL -1010e QL t t t t PQGC KDa610256.225⨯=a—计算常数;K—管道内气体到土壤的总传热系数,W/m2〃℃;D—管道外直径,m;Q—气体流量(p0=0.101325Mpa,T0=293.15K),m3/d;G—气体的相对密度;C P—气体的定压比热,J/kg〃℃。
管存气计算方法

如何计算管道气存储能力例题:压力在2MPa-3MPa之间.管径为300,长度约15.6KM.如何计算管内的气量.1、管容=0.3*0.3*3.14/4*15.6*1000气量(标准立方米)=压力(bar)*管容(立方米)1MPa=10bar一般这样就可以了,再精确点就再除以一个压缩因子。
2、长输管线距离长、管径大、输送压力较高,管线具有一定的储气能力,长输管线中间设有加压站时,按最末一个加压站至城市配气站的管段计算其储气能力;设有中间加压站的长输管线,可按全线计算其储气能力。
城市天然气输配系统往往利用大口径输气管线储存一定气量作为高峰负荷时增加用户气量之用,其储气能力为储气终了时与储气开始时输气管中存气量之差、一条已投产的输气干管的长度、容积、管线起点允许最高工作压力、终点允许最高工作压力、终点用户要求的最低供气压力及该管线正常输气量等都是已知的,可按下列步骤计算其储气量:(1)根据压气站的最高工作压力或管线强度允许压力,确定储气终了时管线起点压力。
由起点压力和正常输气量按下式算出储气终了时的管线终点压力:式中Q——天然气通过能力(m3/d);(20℃,101,3kPa)D——输气管内径(cm);P1——输气管线的起点绝对压力(106Pa);P2——输气管线的终点绝对压力(106Pa);S——天然气相对密度;Tf——天然气平均绝对温度(K);L——输气管线长度(km);Z——天然气平均压缩因子。
(2)求储气开始时起点压力式中P1min——储气开始时起点绝对压力(106Pa);P2min——储气开始时终点绝对压力(106Pa);P1max——储气终了时起点绝对压力(106Pa);P2max——储气终了时终点绝对压力(106Pa);(3)计算管线的容积V=(Л/4)D2L(4)储气开始时的平均压力(5)储气终了时的平均压力(6)储气量式中Q。
——输气管线储气量(m3);(20℃,101.3kPa)V——输气管线容积(m3);To——293(K);Tm——天然气平均温度(K);Po——标准状态下的压力(101.3kPa);Z1、Z2——在Pm2、Pm2下的压缩因子;Pm1——储气终了时的平均压力(106Pa);Pm2——储气开始时的平均压力(106Pa)。
常用管道输气能力计算公式

常用管道输气能力计算公式1.经验公式经验公式是根据工程实践总结得出的近似计算公式,适用于一般的管道输气能力估算。
常用的经验公式有德阿雷斯经验公式、斯皮洛经验公式和希尔经验公式等。
a)德阿雷斯经验公式:Q = kA(P1-P2) / Pavg其中,Q为管道的体积流量(m³/s),A为管道截面积(m²),P1和P2分别为管道两端的压力(Pa),Pavg为两端压力的平均值(Pa),k为经验系数。
b)斯皮洛经验公式:Q = k(ApA + BpB)(P1^2 - P2^2)^(1/2) / Pavg其中,Q为管道的体积流量(m³/s),Ap和Bp为管道两端的面积因素(一般等于1),P1和P2分别为管道两端的压力(Pa),Pavg为两端压力的平均值(Pa),k为经验系数。
c)希尔经验公式:Q = kA(V1 - V2) / Vavg其中,Q为管道的体积流量(m³/s),A为管道截面积(m²),V1和V2分别为管道两端的速度(m/s),Vavg为两端速度的平均值(m/s),k为经验系数。
这些经验公式在实际应用中可以根据具体情况选用合适的公式,并根据实际工程进行修正。
2.一般计算公式一般计算公式是基于流体力学基本理论的计算方法,适用于复杂的管道系统分析。
常用的一般计算公式有杨氏方程、科尔布恩方程和魏斯巴赫方程等。
这些公式考虑了流体的密度、粘度、弥散和压力损失等综合因素,能够较准确地估算管道的输气能力。
a)杨氏方程:Q=kD^2ΔP/(μL)其中,Q为管道的体积流量(m³/s),D为管道的内径(m),ΔP为管道两端的压力差(Pa),μ为流体的粘度(Pa·s),L为管道的长度(m),k为经验系数。
b)科尔布恩方程:Q=kCvD^2ΔP/(ϱμL)其中,Q为管道的体积流量(m³/s),Cv为流量系数(与流量阀门有关),D为管道的内径(m),ΔP为管道两端的压力差(Pa),ϱ为流体的密度(kg/m³),μ为流体的粘度(Pa·s),L为管道的长度(m),k为经验系数。
输气管道适应能力模拟计算_蔡志刚
-2-
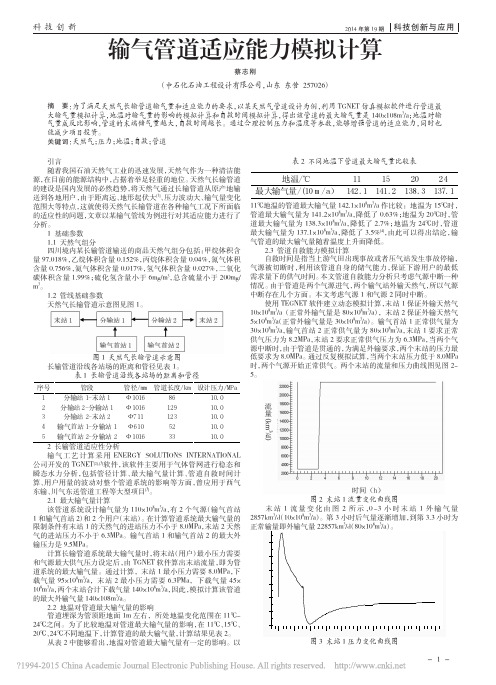
图 4 末站 2 流量变化曲线图 末 站 2 流 量 变 化 由 图 4 所 示 ,0 ~3 小 时 末 站 1 外 输 气 量 1428km3/d(5×108m3/a),第 3 小时后气量逐渐增加,到第 3.3 小时为 正常输量即外输气量 8571km3/d(30×108m3/a)。 从图 5 中可以看出,气源中断后,压力由正常压力的 7.77MPa 逐渐增加,1.2 小时达到最大值 8.38MPa,此后压力逐渐降低,在 7.5 小时压力最低 7.68MPa。此时气源一直在供气,压力逐渐向正常压 力接近,因此末站 2 能满足天然气输送要求。 4 结束语
ÁÁÂÃÄÅÆÇÈÆÈÁÃÂÄÆÃÈÁÄÂ 1基础参数
1.1 天然气组分 四川境内某长输管道输送的商品天然气组分包括:甲烷体积含 量 97.018%,乙烷体积含量 0.152%,丙烷体积含量 0.04%,氮气体积 含量 0.756%,氦气体积含量 0.017%,氢气体积含量 0.027%,二氧化 碳体积含量 1.99%;硫化氢含量小于 6mg/m3,总含硫量小于 200mg/ m3。 1.2 管线基础参数 天然气长输管道示意图见图 1。
容将此充磁后的电能储存,供退磁时使用。在吸合后的保持阶段不消耗
电能,铁芯依靠通电时充磁产生的剩磁保持吸合,与普通接触器相比,
节能 90%以上。节能接触器的线圈每次通电一时间小于 1 秒,故温升仅
为普通产品的一千分之一,没有因发热过流等造成损坏现象线圈寿命
比普通产品延长 1000 倍以上,接近自然氧化的极限值。
图 5 末站 2 压力变化曲线图
通过对天然气长输管道的最大输气能力、末端储气、地温对输 气量的影响、管道自救时间的模拟计算和分析,可以得出结论,设定 合理的设计参数,可以提高管道的多种工况下的适应能力,以便于 满足用户的需求。
一般常用管道输气能力计算公式

一般常用管道输气能力计算公式在石油和天然气工业中,管道输气能力的计算是一个重要的工程问题。
管道输气能力指的是单位时间内通过管道的气体流量,通常以标准立方米/小时或者百万标准立方英尺/天来表示。
下面介绍一些常用的管道输气能力计算公式。
1.伯努利方程伯努利方程是流体动力学中的一个基本定律,它描述了在不同位置的管道中液体或气体的速度、压力和高度之间的关系。
对于稳态、定常流动的压缩气体,可以利用伯努利方程计算管道的输气能力。
伯努利方程可以表示为:P1 + ρv1^2/2 + ρgh1 = P2 + ρv2^2/2 + ρgh2其中,P1和P2分别表示管道两端的压力,ρ表示气体的密度,v1和v2分别为两端气体的流速,g为重力加速度,h1和h2分别为两端气体的高度。
2.克法方程克法方程是由德国科学家克法于1850年提出的,用来计算流体在管道中的流动速度、流量和压力损失。
克法方程是基于能量守恒和质量守恒定律推导出来的,在管道输气能力的计算中也经常被使用。
克法方程可以表示为:Q=A*v其中,Q表示单位时间内通过管道的气体流量,A表示管道的横截面积,v表示气体的流速。
3.柯西相似理论柯西相似理论是流体力学中的一个经验规律,用来描述流体在不同尺寸的管道中的流动特性。
根据柯西相似理论,当两个相似的管道中的流速分布和流量分布相同时,它们的压降也相同,可以通过典型模型的试验数据来推导出管道输气能力的计算公式。
柯西相似理论可以表示为:Q=k*(ΔP*L/D)^n其中,Q表示单位时间内通过管道的气体流量,ΔP表示管道两端的压降,L表示管道的长度,D表示管道的内径,k和n是经验系数。
需要注意的是,以上介绍的公式仅适用于理想情况下,实际工程中还需要考虑多种因素,如管道材料、温度、湍流效应等。
另外,有时需要使用更复杂的模型和方法来计算管道输气能力。
对于大型工程项目,通常会进行更为详细和精确的计算和模拟。
综上所述,管道输气能力的计算公式涵盖了伯努利方程、克法方程和柯西相似理论等基本原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管道输气能力理论计算
管道输气能力是指管道在一定的压力、温度和流量条件下,所能输送
的天然气或其他气体的最大量。
管道输气能力的理论计算依赖于流体力学
和热力学原理,以及管道的几何特征、材料性质等因素。
以下是关于管道
输气能力理论计算的一些主要内容。
首先,管道输气能力的计算需要确定流体的压力、温度和密度等参数。
在计算之前,需要根据设计要求和现场实际情况确定管道的内径、长度、
输送气体的物理性质以及管道的工作条件等参数。
其次,根据流体力学原理,可以利用连续方程和能量方程来计算管道
内气体的速度和压力变化。
连续方程用来描述流体的连续性原理,即单位
时间内流过管道截面的质量必须相等。
能量方程则用来描述气体的能量变化,包括气体的压力、温度和速度等参数的关系。
通过连续方程和能量方程的计算,可以得到管道内气体的流速、压力
分布和温度分布等参数。
根据这些参数可以进一步计算输气能力。
然后,根据管道的几何特征和气体的流动性质,可以采用一些经验公
式或者理论模型来计算管道的输气能力。
其中最常用的是Colebrook公式
和Weymouth公式。
Colebrook公式用来计算流体在光滑管道中的摩擦阻力系数,该公式
基于实验数据和经验关系,可以准确地计算管道内气体的摩擦阻力。
根据Colebrook公式,可以计算出管道的摩擦系数,并据此计算管道的压力损失。
Weymouth公式是一种经验公式,可以用于计算管道中天然气的流量和压力降。
该公式基于气体的流动特性和管道的几何参数,根据Weymouth公式可以计算出管道的流量系数和压力降。
利用上述公式和模型,可以计算出管道的输气能力,即单位时间内通过管道的气体质量或体积。
除了上述方法,还可以采用数值模拟方法,如计算流体力学(CFD)方法来计算管道的输气能力。
CFD方法可以更准确地模拟管道内气体的流动和压力变化,从而得到更准确的输气能力计算结果。
总之,管道输气能力的理论计算是一个复杂的过程,需要考虑诸多因素,如管道的几何特征、气体的物理性质、流体力学原理等。
通过上述方法可以得到较为准确的管道输气能力计算结果,对于管道系统的设计和运行具有重要意义。
