最新生活中的轴对称现象
《轴对称现象》生活中的轴对称优质课件

鼓励学生将所学的轴对称知识应用到实际 生活中,如设计具有对称美的图案、分析 工程结构的稳定性等。
THANKS
谢谢您的观看
例子
正方形、圆形、等腰三角形等都是 常见的轴对称图形。
解析几何中的轴对称
定义
在解析几何中,如果一个点关于 原点对称,那么这个点被称为关
于x轴、y轴或z轴的对称点。
性质
关于x轴对称的点,横坐标相等 ,纵坐标互为相反数;关于y轴 对称的点,横坐标互为相反数, 纵坐标相等;关于z轴对称的点 ,横、纵坐标都互为相反数。
02
生活中的轴对称现象
自然界中的轴对称现象
蝴蝶
蝴蝶的翅膀在飞行时呈现明显的轴对 称,这种对称性有助于保持飞行稳定 。
植物叶子
许多植物的叶子在生长过程中呈现出 轴对称的特点,如枫叶、银杏叶等。
雪花
雪花是自然界中轴对称的典型例子, 其形状由冰晶按照一定规律生长而成 。
建筑中的轴对称现象
01
02
03
轴对称现象的特性
详细描述
轴对称现象具有以下特性
2. 轴线唯一性
每个轴对称现象都有一个唯一 的对称轴,且对称轴两侧的形 状、大小等完全一致。
总结词
全面、深入
1. 对称性
物体或图形在轴对称下,其两 侧形状、大小、排列等完全相 同。
3. 旋转不变性
若将物体或图形绕对称轴旋转 180度,其形状、大小等不会 发生变化。
雕塑
许多雕塑作品采用轴对称 的设计,如罗丹的《思想 者》雕塑,呈现出优雅的 平衡感。
音乐
音乐作品中的旋律和和声 有时会采用轴对称的结构 ,使音乐听起来更加和谐 和平衡。
03
轴对称现象的数学解释
平面几何中的轴对称
《轴对称现象》生活中的轴对称PPT教学课件教学课件

观察
轴对称图形
成轴对称
轴对称图形和成轴对称的关系: 联系:都是沿一条直线折叠后能够互相重合。 区别:轴对称图形是一个图形。
成轴对称是两个图形之间的关系。
(说明:轴对称图形与图形成轴对称并非能够严格区分)
思考
观察下列图形,哪些是轴对称图形?若是轴对 称图形,请找出他们的对称轴。
例题1
(1)
(2)
活动探究
观察下面每对图形(如图),你能类比前面的内容概括出它们的共同特征吗?
共同特征: 每一对图形沿着虚线折叠,左边的图形都能与右边的图形重合.
活动探究
你能结合具体的图形说明轴对称图形和两个图形成轴对称有什么区别与联系吗? 两者的联系: 把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图 形沿对称轴分成两个图形,这两个图形关于这条轴对称.
观察 观察下面的图形有什么共同的特征?
将上图中的每一个图形沿某条直线对折后,直 线两旁的部分能够完全重合。
1.轴对称图形: 如果一个平面图形沿一条直线折叠后,直
线两旁的部分能够完全重合,那么这个图形 叫做轴对称图形。
这条直线叫这个图形的对称轴。
观察 观察每组图案,你发现了什么?
2. 两个图形成轴对称: 如果两个平面图形沿一条直线折叠后能够 完全重合,那么这两个图形成轴对称。 这条直线叫这两个图形的对称轴。
举一反三
随堂检测
1、下列英文字母中,哪些是轴对称图形?
ACDEFGHI JLMNOPQR STUVWXYZ
随堂检测
2、猜字游戏
随堂检测
3.下列各图形是轴对称图形吗?如果是,请说出它们分别有几条对称轴?你能 说出它们各是什么标志吗?
课堂小结
本节课都学到了什么?
《利用轴对称进行设计》生活中的轴对称

2023-11-06•轴对称的定义与性质•生活中的轴对称•轴对称在设计中的应用目录•轴对称的计算机实现•总结与展望01轴对称的定义与性质轴对称是指一个物体关于某一直线(称其为对称轴)对称,也就是说,物体在对称轴的两侧是镜像对称的。
在几何学中,轴对称是一种基本的对称形式,它反映了物体的空间位置关系。
轴对称性是一种等价关系,即如果一个图形关于某一直线对称,则它具有一些特殊的性质。
例如,对于一个关于y轴对称的图形,其关于y轴的垂线是对称的。
轴对称的应用在日常生活中,轴对称的应用非常广泛。
例如,在建筑设计中,许多建筑物都利用了轴对称的概念来设计它们的外观和内部布局。
在自然界中,许多物体也具有轴对称性,例如雪花、蝴蝶翅膀等。
02生活中的轴对称建筑中的轴对称故宫01故宫是中国著名的古建筑群,其主体建筑群具有明显的轴对称特点,从午门到神武门,左右两边的建筑完全对称,体现了中国古代建筑的和谐之美。
雅典卫城02希腊雅典卫城是欧洲最古老、最杰出的古建筑之一,其建筑风格具有典型的轴对称特点,尤其是卫城的中心建筑帕台农神庙,其布局与周围的建筑群呈轴对称。
印度泰姬陵03泰姬陵是印度最著名的古建筑之一,也是世界遗产之列。
它以完美的轴对称和精湛的白色大理石雕刻技术而闻名于世。
雕塑雕塑作品也经常利用轴对称来表现形式美。
例如,古希腊雕塑家经常使用轴对称来创作人体雕塑,以表现人体的平衡和和谐。
绘画在绘画中,轴对称经常被用来创造和谐、平衡和稳定的感觉。
例如,在肖像画中,人物的脸部特征通常会以鼻子为中心,左右两边对称分布。
音乐在音乐中,轴对称也被广泛运用。
例如,在交响乐中,乐章之间往往会有明显的轴对称结构,以表现音乐的形式美和平衡感。
艺术中的轴对称蝴蝶的翅膀通常是轴对称的,这种对称性不仅使蝴蝶看起来更加美观,还帮助它们在飞行时保持平衡和稳定。
自然界中的轴对称蝴蝶雪花是自然界中最具代表性的轴对称物体之一。
每个雪花都有六个分支,每个分支都呈现出完美的轴对称形态。
生活中的轴对称教案(完成版)

生活中的轴对称教案(最新完成版)第一章:轴对称的基本概念1.1 轴对称的定义解释轴对称的概念,让学生理解轴对称图形的特点。
通过实际例子,如剪纸、图片等,让学生直观地感受轴对称。
1.2 轴对称的性质介绍轴对称图形的性质,如对应点的连线与对称轴垂直,对应点相等等。
引导学生通过实际操作,验证这些性质。
第二章:生活中的轴对称现象2.1 生活中的轴对称实例举例说明生活中常见的轴对称现象,如衣服的领子、房间的布置等。
让学生观察并描述这些轴对称现象。
2.2 制作轴对称图形引导学生利用纸张、剪刀等材料,制作自己喜欢的轴对称图形。
鼓励学生发挥创意,设计独特的轴对称图形。
第三章:轴对称与几何图形的变换3.1 轴对称与对称轴解释对称轴的概念,让学生理解对称轴在轴对称中的作用。
引导学生通过实际操作,找出给定图形的对称轴。
3.2 轴对称与旋转介绍轴对称与旋转的关系,让学生理解旋转是轴对称的一种特殊情况。
引导学生通过实际操作,观察旋转对图形的影响。
第四章:轴对称在实际应用中的例子4.1 轴对称在设计中的应用举例说明轴对称在设计中的应用,如标志设计、服装设计等。
让学生欣赏并分析这些设计中的轴对称元素。
4.2 轴对称在建筑中的应用举例说明轴对称在建筑中的应用,如宫殿、教堂等。
引导学生观察并描述这些建筑中的轴对称特点。
第五章:轴对称的练习与拓展5.1 轴对称的练习题提供一些轴对称的练习题,让学生巩固所学知识。
包括找对称轴、判断轴对称图形等类型的题目。
5.2 轴对称的拓展活动引导学生进行轴对称的拓展活动,如设计轴对称的图案、制作轴对称的手工作品等。
鼓励学生发挥创意,展示自己的作品。
第六章:轴对称与坐标系6.1 坐标系中的轴对称介绍坐标系中轴对称的概念,让学生理解在坐标系中如何表示轴对称图形。
引导学生通过实际操作,找出给定图形在坐标系中的对称轴。
6.2 轴对称图形的对称点解释坐标系中轴对称图形的对称点如何计算,让学生掌握对称点的求法。
新北师大版七年级数学下第五章《生活中的轴对称》学案及答案

第五章生活中的轴对称第一课时 5.1 轴对称现象一、学习目标:1、经历观察、分析现实生活实例和典型图案的过程,认识轴对称和轴对称图形培养学生探索知识的能力与分析问题、思考问题的习惯。
2、会找出简单对称图形的对称轴,了解轴对称和轴对称图形的联系与区别。
二、学习重点:通过对现实生活实例和典型图案的观察与分析,认识轴对称和轴对称图形,会找出简单的轴对称图形的对称轴.三、学习难点:找出简单轴对称图形的对称轴与理解轴对称和轴对称图形的联系与区别(一)预习准备(1)预习书115~117页(2)预习作业:1.如图所示的几个图案中,是轴对称图形的是()2.如图所示,下面的5个英文字母中是轴对称图形的有()A.2个 B.3个 C.4个 D.5个3.如图所示的图案中,是轴对称图形的有()A.1个 B.2个 C.3个 D.4个(二)学习过程:1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做_______图形,这条直线叫做_______.2、对称轴是一条_______,有些轴对称图形可能有几条,甚至无数条对称轴.3、把一个图形沿着一条直线翻折过去,如果它能够与另一个图形重合,那么就说这_______图形成轴对称,这条直线就是对称轴,两个图形中的对应点叫做对称点。
4、轴对称图形与轴对称的区别:区别:轴对称是_______图形的位置关系,而轴对称图形是_______具有特殊形状的图形. 5.你认识世界上各国的国旗吗?如图7-4所示,观察下面的一些国家的国旗,是轴对称图形的有( )A.甲乙丙丁戊 B.甲乙丁戊 C.甲乙丙戊 D.甲乙戊6.小红将一张正方形的红纸沿对角线对折后,得到等腰直角三角形,然后在这张重叠的纸上剪出一个非常漂亮的图案,她拿出剪出的图案问小冬,打开后的图案的对称轴至少有( )A.0条 B.1条 C.2条 D.无数条7.如图所示,从轴对称的角度来看,你觉得下面哪一个图形比较独特?简单说明你的理由.8.观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.9.如图所示的四个图形中,从几何图形的性质考虑哪一个与其他三个不同?•请指出这个图形,并简述你的理由.拓展:1.如图所示,以虚线为对称轴画出图形的另一半.回顾小结:1.如果一个图形沿某一条直线折叠后,直线两旁的部分能够,那么这个图形叫做轴对称图形,这条直线叫做。
生活中的轴对称教案(最新完成版)

第五章第五章 生活中的轴对称生活中的轴对称重点1 1 轴对称现象轴对称现象轴对称现象 ………………………………………………………………………………………… 99 99 重点2 2 探索轴对称的性质……………………………………探索轴对称的性质……………………………………探索轴对称的性质…………………………………… 102 重点3 3 简单的轴对称图形……………………………………简单的轴对称图形……………………………………简单的轴对称图形…………………………………… 106 106 重点4 4 利用轴对称设计图案…………………………………利用轴对称设计图案…………………………………利用轴对称设计图案………………………………… 110 1101、经历观察、分析现实生活实例和典型图案的过程,认识轴对称和轴对、经历观察、分析现实生活实例和典型图案的过程,认识轴对称和轴对 称图形培养学生探索知识的能力与分析问题、思考问题的习惯。
称图形培养学生探索知识的能力与分析问题、思考问题的习惯。
2、会找出简单对称图形的对称轴,了解轴对称和轴对称图形的联系与区别。
例1你认识世界上各国的国旗吗?如图7-4所示,观察下面的一些国家的国旗,是轴对称图形的有(国旗,是轴对称图形的有( ))A .甲乙丙丁戊.甲乙丙丁戊B B B.甲乙丁戊.甲乙丁戊.甲乙丁戊C C C.甲乙丙戊.甲乙丙戊.甲乙丙戊D D D.甲乙戊.甲乙戊.甲乙戊 例2观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.在图中画出所有的对称轴.例3如图所示的图案中,是轴对称图形的有(如图所示的图案中,是轴对称图形的有(如图所示的图案中,是轴对称图形的有( ))A A..1个B B..2个C C..3个D D..4个随堂检测1、如图所示的几个图案中,是轴对称图形的是(、如图所示的几个图案中,是轴对称图形的是( ))2、如图所示,下面的5个英文字母中是轴对称图形的有(个英文字母中是轴对称图形的有( ))A A..2个B B..3个C C..4个D D..5个3、如图所示,从轴对称的角度来看,你觉得下面哪一个图形比较独特?简单说明你的理由.简单说明你的理由.4、下列图形中对称轴最多的是、下列图形中对称轴最多的是( ) ( )A 、圆、圆B B B、正方形、正方形、正方形C C C、等腰三角形、等腰三角形、等腰三角形D D D、线段、线段、线段一、线段垂直平分线的概念和性质一、线段垂直平分线的概念和性质1、垂直平分线的定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也称之为中垂线。
生活中的轴对称(经典例题)
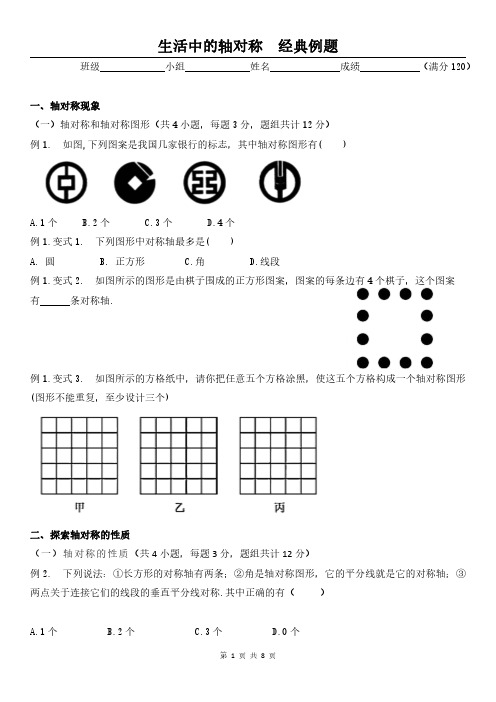
班级小组姓名成绩(满分120)一、轴对称现象(一)轴对称和轴对称图形(共4小题,每题3分,题组共计12分)例1.如图,下列图案是我国几家银行的标志,其中轴对称图形有()A.1个B.2个C.3个D.4个例1.变式1.下列图形中对称轴最多是()A.圆B.正方形C.角D.线段例1.变式2.如图所示的图形是由棋子围成的正方形图案,图案的每条边有4个棋子,这个图案有条对称轴.例1.变式3.如图所示的方格纸中,请你把任意五个方格涂黑,使这五个方格构成一个轴对称图形(图形不能重复,至少设计三个)二、探索轴对称的性质(一)轴对称的性质(共4小题,每题3分,题组共计12分)例2.下列说法:①长方形的对称轴有两条;②角是轴对称图形,它的平分线就是它的对称轴;③两点关于连接它们的线段的垂直平分线对称.其中正确的有()A.1个B.2个C.3个D.0个例2.变式1.如图,△ABC与△A'B'C'关于直线l对称,且∠A=78°,∠C'=48°,则∠B的度数为()A.48°B.54°C.74°D.78°例2.变式2.如图所示,AC垂直平分线段BD,若AB=3cm,CD=5cm,则四边形ABCD的周长是()A.11cmB.13cmC.16cmD.18cm例2.变式3.如图,把一张长方形纸ABCD折叠,使点C与点A重合,折痕为EF.如果∠DEF=123°,那么∠BAF=.(三)轴对称的性质及应用(共4小题,每题3分,题组共计12分)例3.轴对称图形对应点连线被,对应角、对应线段都.例3.变式1.如图,∠AOB内有一点P,分别画出P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为多少?例3.变式2.如图,将长方形纸片ABCD沿其对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为()A.16B.19C.22D.25例3.变式3.如图,在△ABC中,∠ACB=90°,点D在边AB上,连接CD,将△BCD沿CD翻折得到△ECD,使DE∥AC,CE交AB于点F,若∠B=α,则∠ADC的度数是(用含α的代数式表示).三、简单的轴对称图形(一)等腰三角形的性质(共4小题,每题3分,题组共计12分)例4.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高C.腰上的高所在的直线D.顶角平分线所在的直线例4.变式1.等边三角形对称轴的条数是()A.1B.2C.3D.4例4.变式2.如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是()A.6B.7C.8D.9例4.变式3.等腰三角形中有一个角是50°,那么这个等腰三角形的底角是.(二)等腰三角形的性质二(共4小题,每题3分,题组共计12分)例5.下列说法中正确的是()A.关于某条直线对称的两个三角形是全等三角形B.全等三角形一定是关于某条直线对称的C.两个图形关于某条直线对称,则这两个图形一定分别位于这条直线的两侧D.若A,B两点关于直线MN对称,则AB垂直平分MN例5.变式1.如图,BD是△ABC的角平分线,∠ABD=36°,∠C=72°,则图中的等腰三角形有个.例2.变式2.如图,在△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=.例5.变式3.有一个三角形的支架如图所示,AB=AC,小明过点A和BC边的中点D又架了一个细木条,经测量∠B=30°,你在不用任何测量工具的前提下,能得到∠BAD和∠ADC的度数吗?(三)线段和角的轴对称性(共4小题,每题3分,题组共计12分)例6.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E,已知PE=3,则点P到AB的距离是()A.3B.4C.5D.6例6.变式1.如图所示,下列推理中正确的个数是()①因为OC平分∠AOB,点P,D,E分别在OC,OA,OB上,所以PD=PE;②因为P在OC上,PD⊥OA,PE⊥OB,所以PD=PE;③因为P在OC上,PD⊥OA,PE⊥OB,且OC平分∠AOB,所以PD=PE.A.0B.1C.3D.4例6.变式2.小明把一张长方形的纸对折了两次,如图所示,使A,B都落在DC上,折痕分别是DE,DF,则∠EDF的度数为.例6.变式3.如图,已知△ABC中,DE垂直平分AC,且交AC于点E,交BC于点D,△ABD的周长是20,AC=8,你能计算出△ABC的周长吗?(四)等腰(边)三角形的性质的综合应用(共4小题,每题3分,题组共计12分)例7.在△ABC中,若BC=AC,∠A=58°,则∠C=,∠B=.例7.变式1.等边三角形的两条中线相交所成的钝角度数是.例7.变式2.如图P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=.例7.变式3.如图,已知△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连接AD,若∠B=37°,求∠CAD的度数.(五)轴对称图形的综合运用(共4小题,每题3分,题组共计12分)例8.如图所示,△ABC中,∠B与∠C的平分线相交于点O,过点O作MN∥BC,分别交AB,AC于点M,N,若AB=6cm,AC=9cm,BC=12cm,则△AMN的周长为.例8.变式1.如图所示,将两个全等的有一个角为30°的直角三角形拼在一起,其中两条较长直角边在同一条直线上,则图中等腰三角形有个.例8.变式2.如图所示,在△ABC中,AB=AC,AD⊥BC于D,AB+AC+BC=50cm,AB+BD+AD=40cm,则AD=cm.例8.变式3.如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;照这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=.(六)轴对称图形的综合运用二(共4小题,每题3分,题组共计12分)例9.如图,D,E是△ABC的BC边上的两点,且BD=DE=EC=AD=AE,求∠BAC的度数.例9.变式1.如图,∠1=∠2,AE⊥OB于点E,BD⊥OA于点D,AE,BD交于点C,试说明AC=BC.例9.变式2.如图所示,△ABC是等边三角形,点D是AC的中点,DE∥AB,AE∥BC,DE与AE交于点E,点G是AE的中点,GF∥DE,EF∥AC,EF交GF于点F,若AB=4cm,则图形ABCDEFG的外围的周长是多少?例9.变式3.如图,△ABC中,AB=2AC,∠1=∠2,DA=DB,你能说明DC⊥AC吗?四、利用轴对称进行设计(共4小题,每题3分,题组共计12分)例10.如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是()A.正三角形B.正方形C.正五边形D.正六边形例10.变式1.如左下图,将一张正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个大小相等的圆洞,最后将正方形纸片展开,得到的图案是右下图中的()例10.变式2.当你面对镜子的时候,右手拿笔向左挥动,对于镜子中的像来说是()A.右手拿笔,向右挥动B.左手拿笔,向左挥动C.右手拿笔,向左挥动D.左手拿笔,向右挥动例10.变式3.某一车牌在平面镜中的像是,则这辆车的实际号码是()。
生活中的轴对称

生活中的轴对称
生活中的轴对称:生活上有书本,飞机,蝴蝶,排球,足球,篮球,羽毛球拍,灯,柜子,风扇,凳子,桌子,床,被子,沙发,对联,笔盒。
轴对称图形平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
生活作用
1、为了美观。
比如天安门,对称就显的美观漂亮。
2、保持平衡。
比如飞机的两翼。
3、特殊工作的需要。
比如五角星,剪纸。
扩展资料:
实际区别时轴对称图形要像折纸一样折叠能重合的是轴对称图形;中心对称图形只需把图形倒置,观察有无变化,没变的是中心对称图形。
现将小学课本中常见的图形归类如下:既是轴对称图形又是中心对称图形的有:长方形,正方形,圆,菱形等。
只是轴对称图形的有:角,五角星,等腰三角形,等边三角形,等腰梯形等等。
只是中心对称图形的有:平行四边形。
既不是轴对称图形又不是中心对称图形有:不等边三角形,非等腰梯形等。
一个图形既轴对称又中心对称一定有两条或两条以上的对称轴。
