小学奥数圆面积的典型题和解法知识讲解
二年级圆形的面积及解答

二年级圆形的面积及解答
圆形的面积公式
圆形的面积用于描述圆的大小。
面积的计算可以使用以下公式:
$$
面积= π * 半径^2
$$
其中,π是一个常数,约等于3.14,半径是指从圆心到圆周任
意点的距离。
面积计算示例
假设一个圆的半径是5厘米,我们可以通过以下步骤来计算该
圆的面积:
1. 首先,将半径的值代入面积公式中:
面积 = 3.14 * 5^2
2. 其次,计算半径的平方:
面积 = 3.14 * 25
3. 最后,计算面积:
面积 = 78.5 平方厘米
因此,该圆的面积为78.5平方厘米。
解答示例
以下是一些与圆形面积相关问题的解答示例:
问题1
圆的直径是10厘米,求其面积。
解答:
1. 首先,计算半径:
半径 = 直径 / 2 = 10 / 2 = 5厘米
2. 其次,将半径的值代入面积公式中:
面积 = 3.14 * 5^2 = 3.14 * 25 = 78.5平方厘米因此,圆的面积是78.5平方厘米。
问题2
圆的面积是153.86平方厘米,求其半径。
解答:
1. 首先,将面积公式变形为:
半径= √(面积/ π)
2. 其次,代入面积的值:
半径= √(153.86 / 3.14)
3. 最后,计算半径:
半径≈ √49 ≈ 7厘米
因此,圆的半径约为7厘米。
希望以上内容对你有帮助!如有其他问题,请随时咨询。
小升初奥数第十讲 圆的周长和面积

第十讲 圆的周长和面积【知识概述】圆的认识:圆中心的一点叫做圆心,圆心一般用字母“o ”表示;连接圆心和圆上任意一点的线段叫做半径,半径一般用字母“r ”表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母“d ”表示。
d圆心决定圆的位置, O r 半径决定圆的大小。
圆的特征:(1)在同圆或等圆中,半径的长度都相等,直径的长度都相等,直径长度是半径长度的2倍,用字母表示是:d =2r 或r =2d。
(2)圆是轴对称图形,圆有无数条对称轴。
圆的对称轴是直径所在的直线。
圆的周长:围成圆的曲线的长。
周长一般用字母“C ”表示,C=πd=2πr .圆周率:圆的周长和直径的比值,用字母π表示。
(π≈)圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr 2. 圆环的面积计算公式:S =πR2-πr2=π(R2-r2)扇形的面积公式: 360nr S n 360r S 22⨯=⨯=ππ或【典型例题】例1 求下面各圆的周长。
【学大名师】圆的周长是直径的π倍,是半径的2π倍。
解:(1) cm 3r = (2)d = 7dm84.18=(cm ) 98.21=(cm )例2 求下面各圆的面积。
(1)r = 4cm (2)d = 10dm (3)C = 18.84m【学大名师】圆的面积公式是2r S π=,要想求面积,要先求出半径。
解: (1)r=4cm24.501614.3414.32=⨯=⨯(平方厘米)(2)d=10dm10÷2=5(dm )5.782514.3514.32=⨯=⨯(2dm )(3)已知圆的周长,要先求出圆的半径,再利用2r S π=求面积。
C=18.84m3214.384.18=÷÷(m )26.28914.3314.32=⨯=⨯(2m )例3 小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。
六年级奥数上_第13讲__面积计算(一)——圆

例2. 已知图5中,三角形ABC是等腰直角三角形, BC=20厘米,DE为圆的一条直径。求图中阴影部 分的面积。 A
D E
B
F
图5
C
1 1 20 (20 2) (20 2) (20 2 2) 2 2 2 100 50
(平方厘米) 50
A
分析与解:如图6把上面阴影平移到下面,只要从三角 形ABC中减去正方形ADFE的面积就可以了。因为ABC和 ADE都是等腰直角三角形,所以它们的高都是底边的一半, 又知BC=20厘米,DE=10厘米,可以分别求出三角形 ADE和ABC的面积了。
答:阴影部分的面积是50平方厘米。
D E
B
F
图6
C
例2. 如下图,已知圆内正方形的面积是20平 方厘米,求圆外接正方形的面积?
O
分析与解: 圆外接正方形面积是圆内接正方形面积的2倍
20 2 40(平方厘米)
例3. 如下图,圆的周长是16.4厘米,圆的面积与 长方形的面积正好相等。阴影部分的周长是多少 厘米?
O D C
A
Bห้องสมุดไป่ตู้
分析与解:
1 16.4 4.1(厘米) 4 16.4 4.1 20.5(厘米)
小学奥数圆面积的典型题和解法知识讲解

圆面积的典型题和解法一、半径r 2替代法题的特点:一般将正方形,三角形和圆放到一起,一般已知条件是正方形或三角形面积,求圆的面积。
解法:一般设法求出r ,或者求出r 2,★注意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍。
例1:已知下图阴影部分面积为8平方米,求圆的面积:解:由已知条件可得r 2 =8,因此,圆的面积为:814.32⨯=r π例2:ABCD 为正方形,已知AC 长6m ,求阴影部分面积:解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡AD=DC=rAD*DC/2=9因此,r 2 =18, 扇形DAC 的面积为:4/1814.34/2⨯=r π 因此,阴影部分面积为:18-4/1814.34/2⨯=r π例3:求圆与圆内最大正方形的面积比值。
解:△ABC 为等腰直角三角形,则S △ABC=22/2r r r =⨯正方形的面积是两个三角形面积和,为:22r圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π练习题:1、已知下图阴影部分面积为5平方米,求圆的面积:2:、在右图扇形中,正方形面积为30平方米,求阴影部分面积:3:求正方形与正方形内最大圆的面积比值。
题的特点:一般圆内由多个阴影部分面积构成,阴影由弧线和弧线构成,或者由弧线和直线构成。
解法:注意观察面积相同的部分,将相同的部分移动替换,若遇到轴对称图形可尝试旋转图形,记住常见的面积平移图例。
,例1:求阴影部分的面积:解:正方形外三角形底为6,和正方形内三角形底相同,由于顶角相同,所以两个三角形可以互换。
阴影部分面积则为:正方形面积-1/4圆的面积例2:求阴影部分的面积:解:平移得到下图:则阴影部分面积为扇形面积-三角形面积2562π⨯-=.82/244/4cm例3:求阴影部分的面积:解:注意观察,:阴影部分面积为:1*1-1*1/2=1/2练习题:求阴影部分面积:题的特点:图有好几个部分组合而成,各部分之间存在着一定的关系。
奥数专题平面图形之圆的面积(有例题讲解和相应的练习)
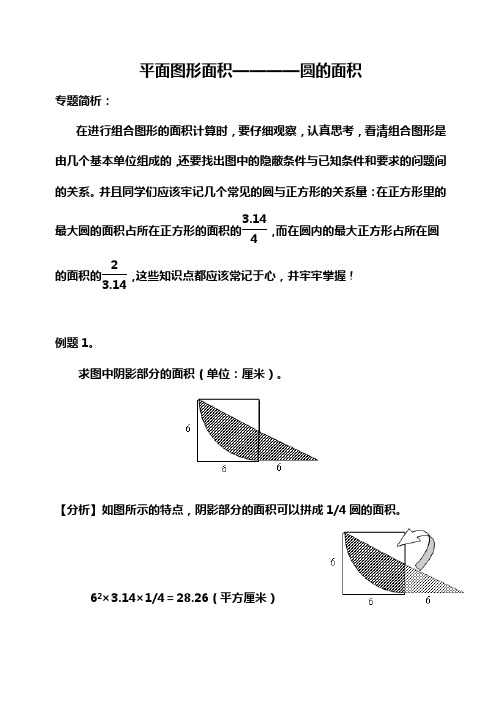
平面图形面积————圆的面积专题简析:在进行组合图形的面积计算时,要仔细观察,认真思考,看清组合图形是由几个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
并且同学们应该牢记几个常见的圆与正方形的关系量:在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心,并牢牢掌握!例题1。
求图中阴影部分的面积(单位:厘米)。
【分析】如图所示的特点,阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4=28.26(平方厘米)练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答例题2。
求图中阴影部分的面积(单位:厘米)。
【分析】阴影部分通过翻折移动位置后,构成了一个新的图形(如图所示)。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4-4×4÷2÷2=8.56(平方厘米)练习21、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2例题3。
如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相O的面积。
等。
求长方形ABO1【分析】因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×1/4×2=1.57(平方厘米)练习31、如图所示,圆的周长为12.56厘米,AC两点把圆分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD的面积。
答2、如图所示,AB=BC=8厘米,求阴影部分的面积。
六年级上册数学培优奥数讲义-第12讲 圆的面积

第12讲 圆的面积知识装备1、圆的面积公式:S =πr 2; 扇形的面积公式:S =360nπr 2。
2、在与圆有关的面积计算中,经常需要添加辅助线,根据圆的特征进行面积转化,使之变成有利于计算的图形,再计算。
初级挑战1求下面图形中阴影部分的面积。
(单位:厘米)思维点拨 :阴影部分面积=( )的面积-( )的面积,半圆直径是8厘米,正方形边长是( )厘米。
答案:正方形的面积:8×8=64(cm ²) 圆的面积:3.14×(8÷2)²=50.24(cm ²) 阴影部分的面积:64-50.24=13.76(cm ²)能力探索11、求下面图形中阴影部分的面积。
(单位:厘米) (1) (2)答案:(1)大半圆的面积:3.14×[(30+50)÷2]²÷2=2512(cm ²) 小半圆的面积:3.14×(30÷2)²÷2=353.25(cm ²) 中半圆的面积:3.14×(50÷2)²÷2=981.25(cm ²) 阴影部分的面积:2512-353.25-981.25=1177.5(cm ²) (2)大半圆的面积:3.14×(8÷2+2)²÷2=56.52(cm ²) 小半圆的面积:3.14×(8÷2)²÷2=25.12(cm ²) 阴影部分的面积:56.52-25.12=31.4(cm ²)2、下图是半径为24厘米的扇形,求图中阴影部分的面积。
答案:两个相同的图形拼成一个四分之一扇形。
3.14×24²÷4-24×24÷2=616.32(平方厘米) 616.32÷2=308.16(平方厘米)初级挑战2如图,等腰直角三角形直角边长为14厘米,两个半圆的直径是三角形的直角边,求图中阴影部分的面积。
六年级奥数上 第13讲 面积计算(一)——圆

A
D
B
图7 分析与解: 分析与解:从图上看要求得阴影部分的面积,就要用四 分之一圆面积减去它所包含的小三角的面积,然而要求出 小三角形的面积仅用同学们现有的知识是做不到的,而要 根据圆的特性,利用图形的旋转变换将图7变成图8的样子 (即沿CD裁开,以D为轴旋转,使AD边与BD边重合), 此时阴影面积就等于半圆面积减去所含三角形AEF的面积。 三角形ABC是等腰直角三角形,所以
1 1 20 × (20 ÷ 2) × − (20 ÷ 2) × (20 ÷ 2 ÷ 2) × × 2 2 2 = 100 − 50
= 50 (平方厘米)
答:阴影部分的面积是50平方厘米。
A E
D
B
F
图6
C
如图7 三角形ABC为等腰直角三角形, ABC为等腰直角三角形 例4. 如图7,三角形ABC为等腰直角三角形,为直 AB的中点 AB=20厘米 圆弧GD HD是分 的中点, 厘米, GD、 角,D是AB的中点,AB=20厘米,圆弧GD、HD是分 别以A 为圆心所作,求图中阴影部分的面积? 别以A、B为圆心所作,求图中阴影部分的面积? 3.14) (取3.14)
O B
图4
已知图5 三角形ABC是等腰直角三角形, ABC是等腰直角三角形 例3. 已知图5中,三角形ABC是等腰直角三角形, BC=20厘米 DE为圆的一条直径 厘米, 为圆的一条直径。 BC=20厘米,DE为圆的一条直径。求图中阴影部 分的面积。 分的面积。 A
D E
B
F
图5
C
分析与解: 分析与解:如图6把上面阴影平移到下面,只要从三角 形ABC中减去正方形ADFE的面积就可以了。因为ABC和 ADE都是等腰直角三角形,所以它们的高都是底边的一半, 又知BC=20厘米,DE=10厘米,可以分别求出三角形 ADE和ABC的面积了。
六年级上册奥数题圆的面积

小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆面积的典型题和解法
一、半径r 2替代法
题的特点:一般将正方形,三角形和圆放到一起,一般已知条件是正方形或三角形面积,求圆的面积。
解法:一般设法求出r ,或者求出r 2,
★注意:园内直角三角形一般为等腰直角三角形,两腰等长,斜边是斜边上高的2倍。
例1:已知下图阴影部分面积为8平方米,求圆的面积:
解:由已知条件可得r 2 =8,
因此,圆的面积为:814.32⨯=r π
例2:ABCD 为正方形,已知AC 长6m ,求阴影部分面积:
解:△ACD 为等腰直角三角形,则S △ACD=6*3/2=9㎡
AD=DC=r
AD*DC/2=9
因此,r 2 =18, 扇形DAC 的面积为:4
/1814.34/2⨯=r π 因此,阴影部分面积为:18-4/1814.34/2⨯=r π
例3:求圆与圆内最大正方形的面积比值。
解:△ABC 为等腰直角三角形,则S △ABC=22/2r r r =⨯
正方形的面积是两个三角形面积和,为:22r
圆的面积为:2r π,则圆与圆内最大正方形的比为:2/π
练习题:
1、已知下图阴影部分面积为5平方米,求圆的面积:
2:、在右图扇形中,正方形面积为30平方米,求阴影部分面积:
3:求正方形与正方形内最大圆的面积比值。
题的特点:一般圆内由多个阴影部分面积构成,阴影由弧线和弧线构成,或者由弧线和直线构成。
解法:注意观察面积相同的部分,将相同的部分移动替换,
若遇到轴对称图形可尝试旋转图形,记住常见的面积平移图例。
,
例1:求阴影部分的面积:
解:正方形外三角形底为6,和正方形内三角形底相同,
由于顶角相同,所以两个三角形可以互换。
阴影部分面积则为:正方形面积-1/4圆的面积
例2:求阴影部分的面积:
解:平移得到下图:
则阴影部分面积为扇形面积-三角形面积
256
2
π
⨯
-
=
.8
2/2
4
4/
4cm
例3:求阴影部分的面积:
解:注意观察,:
阴影部分面积为:1*1-1*1/2=1/2
练习题:求阴影部分面积:
题的特点:图有好几个部分组合而成,各部分之间存在着一定的关系。
解法:注意观察图形,将图形分开或者联合起来考虑问题。
可以尝试补充图形或者删减图形。
例1:甲比乙的面积大6cm2,求阴影部分面积。
解:甲和乙单独考虑难解决问题,将甲、乙和直角梯形放到一起考虑
甲=乙+6,甲+直角梯形面积=乙+直角梯形面积+6。
可得,S长方形ABEF=S三角形BDF+6
S长方形ABEF=4*6=24 所以S△BDF=18
BF*DF/2=18 DF=6
BF=DF 所以S△BDF为直角等腰三角形
S扇形DFG=3.14*6*6/8
阴影部分面积为:S△BDF-S扇形DFG
例2:正方形边长为10cm,求阴影部分面积。
解:直接难以求解,可尝试将图形分解开解决问题,如下图:
可以看小正方形两块空白区域相等。
因此,大正方形外部空白区域和内部空白区域相等
空白区域的面积:(10*10-3.14*5*5)*2
阴影部分面积:10*10-(10*10-3.14*5*5)*2
例3、求阴影部分面积
解:观察,阴影部分面积需要用两个小半圆面积-两个空白圆弧面积。
两个空白圆弧面积=空白半圆的面积-三角形面积。
因此:两个空白圆弧面积=3.14*2.52/2- 3*4/2
阴影部分面积=3.14*22/2+3.14*1.52/2-两个空白圆弧面积
练习题:
1、△ABC为直角三角形,1比2小28cm2,AB长40cm,BC长多少?
的度数。
2、扇形ABC的面积是半圆ADB面积的4/3倍,求CAB
3、求阴影部分面积:。
