图形之间的关系PPT课件
合集下载
《圆与圆位置关系》课件
《圆与圆位置关系》ppt课件
CONTENTS
• 圆与圆的位置关系概述 • 圆与圆的相切关系 • 圆与圆的相交关系 • 圆与圆的分离关系 • 圆与圆位置关系的性质和判定
01
圆与圆的位置关系概述
圆与圆的基本概念
圆心
圆的中心点，通常用大写 字母O表示。
圆
一个平面内，到定点的距 离等于定长的所有点组成 的图形。
平行。
相交关系的性质和判定
总结词
相交关系是圆与圆之间的一种常见位置关系 ，其性质和判定方法对于理解圆与圆的位置 关系同样重要。
详细描述
当两圆相交时，它们的交点数取决于两圆的 相对位置。一般情况下，两圆相交于两个不 同的交点，但有时也可能只有一个交点或没 有交点。此外，相交关系还有对称相交和倾 斜相交两种特殊情况，对称相交时两圆心连 线与两圆的交点连线垂直，倾斜相交时两圆
7
7
04
内切关系在几何图形中常用于
7
构造旋转对称图形和等分图形
。
相切关系的判定
9字
判定两圆是否相切的方法有 多种，其中一种是利用圆心 距和两圆半径的关系进行判 定。
9字
另一种判定方法是利用两圆 在某点相切的性质进行判定 ，即如果两圆在某点相切， 则该点到两圆心的距离相等 。
9字
当两圆的圆心距等于两圆半 径之和时，两圆外切；当圆 心距等于较大圆的半径减去 较小圆的半径时，两圆内切 。
数学公式
d>r1+r2
04
圆与圆的分离关系
圆心距大于两圆半径之和
两圆外离 当两圆的圆心距大于两圆的半径之和时，两圆处于分离状态，没有交点。
圆心距等于两圆半径之和
两圆外切
当两圆的圆心距恰好等于两圆的半径之和时，两圆处于外切状态，仅有一个交点。
CONTENTS
• 圆与圆的位置关系概述 • 圆与圆的相切关系 • 圆与圆的相交关系 • 圆与圆的分离关系 • 圆与圆位置关系的性质和判定
01
圆与圆的位置关系概述
圆与圆的基本概念
圆心
圆的中心点，通常用大写 字母O表示。
圆
一个平面内，到定点的距 离等于定长的所有点组成 的图形。
平行。
相交关系的性质和判定
总结词
相交关系是圆与圆之间的一种常见位置关系 ，其性质和判定方法对于理解圆与圆的位置 关系同样重要。
详细描述
当两圆相交时，它们的交点数取决于两圆的 相对位置。一般情况下，两圆相交于两个不 同的交点，但有时也可能只有一个交点或没 有交点。此外，相交关系还有对称相交和倾 斜相交两种特殊情况，对称相交时两圆心连 线与两圆的交点连线垂直，倾斜相交时两圆
7
7
04
内切关系在几何图形中常用于
7
构造旋转对称图形和等分图形
。
相切关系的判定
9字
判定两圆是否相切的方法有 多种，其中一种是利用圆心 距和两圆半径的关系进行判 定。
9字
另一种判定方法是利用两圆 在某点相切的性质进行判定 ，即如果两圆在某点相切， 则该点到两圆心的距离相等 。
9字
当两圆的圆心距等于两圆半 径之和时，两圆外切；当圆 心距等于较大圆的半径减去 较小圆的半径时，两圆内切 。
数学公式
d>r1+r2
04
圆与圆的分离关系
圆心距大于两圆半径之和
两圆外离 当两圆的圆心距大于两圆的半径之和时，两圆处于分离状态，没有交点。
圆心距等于两圆半径之和
两圆外切
当两圆的圆心距恰好等于两圆的半径之和时，两圆处于外切状态，仅有一个交点。
图形的相似图形的位似ppt
。
工程制图
02
在工程制图中，可以利用位似图形来表示物体的形状和大小，
提高制图精度和效率。
艺术创作
03
艺术家可以利用位似图形创造出具有特殊效果的绘画作品，增
强艺术表现力。
03
图形的相似与图形的位似之间的关系
两者之间的联系
图形相似和图形位似都是图形变换的形式，它们都涉及到图 形形状和大小的变化。
图形的相似和位似都涉及到图形的形状和大小，它们都是图 形变换的基本概念。
性质
位似图形的对应线段、对应点所连线段平行（或在同一
图形的位似的判定方法
定义法
根据位似图形的定义进行判定 。
特征法
利用位似图形的性质进行判定 。
合同法
通过合同变换将两个图形转化 为位似图形。
图形的位似的应用
摄影
01
利用位似原理进行摄影，可以得到具有相同形状和大小的图片
在几何证明中的应用
证明定理
在几何证明中，图形的相似可以帮助证明几何定理。例如，通过使用相似图 形的性质，可以证明勾股定理或毕达哥拉斯定理。
推导公式
在几何中，图形的相似可以帮助推导重要的公式。例如，通过使用相似图形 的性质，可以推导出圆的面积公式或球的体积公式。
05
图形的相似与图形的位似在生活中的应 用
图形的相似的应用
艺术领域
在艺术领域中，人们经常利用相似图形的性质进行创作和设计，如相似三角 形在绘画中的应用。
实际生活
在日常生活中，我们也经常遇到相似图形的应用，如相似图形在广告、宣传 海报等方面的应用。
02
图形的位似
定义与性质
定义
如果两个图形形状相同，大小成比例，那么这两个图形称为位似图形。
数学九年级下册位似—两个位似图形坐标之间的关系课件PPT公开课
（4）若五边形ABCDE与五边形A1B1C1D1E1位似，则其中⊿ABC与⊿A1B1C1也是位似图形. 利用位似中心将△ABC三边扩大为原来的2倍 1、在△ABC外任取一点P 作出下列位似图形的位似中心
1、在△ABC外任取一点P 如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，像这样的两个图形叫位似图形，这个点叫做位似中心，这时的相似 比又叫位似比。
H
如4、图依，次D连，接ED分D、别EA、B，F AC上的点. E
把一个图形变换成一个与原来的图形的形状和大小都相同的图形。
2作、出判下断列位位似似图图形形时的要位注似意中首心先它们必须是相似形，其次每一对对应点所在直线都经过同一点。O
()
( B)
DE BC
F
C
B
G C
2.如图所示,四边形OABC与四边形OA1B1C1 是位似图形, AB与A1B1一定平行吗?为什么?
（3）两个位似图形若全等，则位似中心在两个图形之间； １．位似图形的对应点和位似中心在同一条直线上
利用位似，可以将一个图形放大或缩小
❖ 如图，将四边形ABCD缩小为原来的一半。
A D
C B
练习
❖ 1、教材第2题 ❖ 2、将下列图形放大一倍，使位似中心在图形
内：
❖ 将下列图形放大一倍：
课堂小结
应用位似图形概念作图
利用位似中心作图将△ABC的三边缩小为原来的1/2
A
1、在△ABC外任取一点P D
C
2、分别连接PA、PB、PC
F
P
3、分别取PA、PB、PC的中点D、E、EF
B
4、依次连接D、E、F
小 结
实际上△ABC与△DEF是位似图形，位似中心是点P
1、在△ABC外任取一点P 如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，像这样的两个图形叫位似图形，这个点叫做位似中心，这时的相似 比又叫位似比。
H
如4、图依，次D连，接ED分D、别EA、B，F AC上的点. E
把一个图形变换成一个与原来的图形的形状和大小都相同的图形。
2作、出判下断列位位似似图图形形时的要位注似意中首心先它们必须是相似形，其次每一对对应点所在直线都经过同一点。O
()
( B)
DE BC
F
C
B
G C
2.如图所示,四边形OABC与四边形OA1B1C1 是位似图形, AB与A1B1一定平行吗?为什么?
（3）两个位似图形若全等，则位似中心在两个图形之间； １．位似图形的对应点和位似中心在同一条直线上
利用位似，可以将一个图形放大或缩小
❖ 如图，将四边形ABCD缩小为原来的一半。
A D
C B
练习
❖ 1、教材第2题 ❖ 2、将下列图形放大一倍，使位似中心在图形
内：
❖ 将下列图形放大一倍：
课堂小结
应用位似图形概念作图
利用位似中心作图将△ABC的三边缩小为原来的1/2
A
1、在△ABC外任取一点P D
C
2、分别连接PA、PB、PC
F
P
3、分别取PA、PB、PC的中点D、E、EF
B
4、依次连接D、E、F
小 结
实际上△ABC与△DEF是位似图形，位似中心是点P
《看图找关系》课件PPT(5篇)
公共汽车行驶时间和速度的关系图
纵 轴
横轴
（1）公共汽车从解放路站到商场站之间共行驶了__4_分。 （2）在第1分钟内，汽车行驶速度从0提高到_4_0_0_米／分。 （3）从__0_分到_1__分，汽车行驶速度在增加。 （4）从__3_分到_4__分，汽车行驶速度在减少。 （5）从__1_分到_3__分，汽车行驶速度保持不变，是_4_0_0_米／分。
公共汽车从解放路到商场站之间共行驶了6分钟， 从0分到1分，汽车速度…… 从1分到2分，汽车速度…… …… 试一试 1离家的距离
离家的距离
（1）
时间
（2）
时间
试一试 2
楼层
楼层
楼层
时间 （1）
时间 （2）
时间 （3）
xs 试一试 3
王老师上午有3节课，上课的教室在同一个教学楼。 下面这幅图描述了她上午上课直至中午吃饭的情形。
试一试 2.
学校教学楼有四层。五（1）班的同学第一 节课到三楼上数学课，第二节课到二楼上美术 课，第三节课到四楼上音乐课，第四节课回到 三楼上语文课，中午到一楼食堂吃饭。下面哪 一幅图比较准确地描述了这一过程？
楼层
楼层
楼层
时间 （1）
时间 （2）
时间 （3）
xs 试一试 3.
王老师上午有3节课，上课的教室在同一个教学楼。下 面这幅图描述了她上午上课直至中午吃饭的情形。请你根据 这幅图，编一个故事，在小组或全班交流。
感谢您的阅读！ 为 了 便于学习和使用， 本文档下载后内容可 随意修改调整及打印。
学习永远不晚。 JinTai College
北师大版五年级数学上册
教学目标
1. 能读懂一些用来表示数量关系的图表，能 从图表中获取有关信息。
图底关系PPT课件
a.垂直界面图底关系
营业时立面图底关系
b.平面组织图底关系
多数为两层层高，另有一部分为一层，临江部分点缀三层 建筑。店铺尺寸基本上在2.4米—4.2米之间,基本上是历史 原态尺寸.入口一般居中,兼具与外界联系、采光通风的功 能。因为商业的关系,入口一般等同于或者略小于店铺尺 寸，与开窗面积结合形成尺寸较大洞口，洞口面积超过立 面的1/2，成为立面构图的“底”，而白色墙体成为 “图”。夜间商业功能转换成单纯的居住功能时，图底关 系反转，入口的洞口关闭，与墙体结合成为“底”，洞口 虚体“图”的部分只剩下窗户，加上灯光的关系，使得图 底关系更为明显。
12
13
良好的图底关系特征
■ 意大利建筑的内部与街道的外部空
间,在质量上是相近的,街道,广场与建 筑之间没有什么不明确的空间,因此 将图反转没有什么不妥。
■ 日本江户古版地图,内容表示为用
地与道路划分的关系,而非表示建筑 与街道的关系,道路与建筑之间有大 量用途不明确的剩余空间,因此反转 失去意义。
■ 如图:重庆某区商业中心的城市设计,设计着为 了或得空间的趣味性和丰富性,同时配合商业步行 系统的特点,将建筑与空间同时纳入考虑的范围中, 建筑的整体感比较强,除建筑外的剩余空间也得到 了刻意的设计,从图形学的观点来看,建筑和空间基 本可以互换,图底关系明显。
26
图底关系的适用性
五、其他高密度城市建设项目:
9
“图底关系” 理论的适应性： 1、对传统城市空间特征的解析 2、旧城的改造和更新的项目 3、城市商业中心或大型商业步 行系统(核心地带,低价高,建筑 性质导致其层数较低,建筑向水 平发展,建筑密度高,同时为了加 强城市各商业建筑之间的相互 联系,强化商业空间的活力,空间 的性强,尺度较小) 4、城市中心区大型,复杂的城 市公共建筑综合体 5、其他高密度城市建设项目
人教版九年级下册位似—两个位似图形坐标之间的关系课件
A
y
D
A′
B
D′
B′
C
C′ o
x
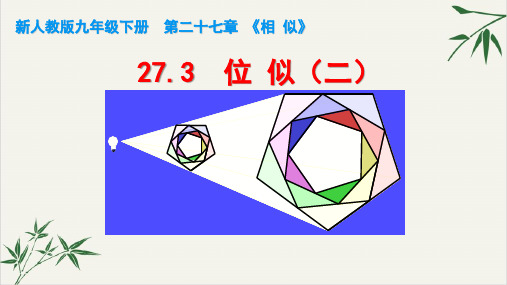
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
A′′ (3,-3 ), B′′ ( 4,-1 ), C′′ ( 2,0 ), D′′ ( 1,-2 )
A
y
D
B
C ′′
Co
x
B ′′
D ′′
A ′′
巩固训练
1. 在平面直角坐标系中，四边形 OABC 的顶点 坐标分别为 O (0，0)，A (6，0)，B (3，6)，C (－3，3). 以原点 O 为位似中心，画出四边形 OABC 的位似图形，使它与四边形 OABC 的相 似是 2 : 3.
A′(-3,3)，B′(-4,1)，C′(-2,0)，D′(-1,2).
或 A′′(3,-3)，B′′(4,-1)，C′′(2,0)，D′′ (1,-2).
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的
坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出
它的一个以原点O为位似中心,位似比为1:2的位似图形.
投影—“动” 悉重难点
解：画法一：将四边 形 OABC 各顶点的坐
标都乘 2 ；在平面 3
直角坐标系中描点O
(0，0)，A' (4，0)，B'
(2，4)，C′ (－2，2)，
用线段顺次连接O，
A'，B'，C'.
y 6
4 C
C' 2
－4
O
－2
－4
B B'
A' A 6x
第六单元 图形之间的关系
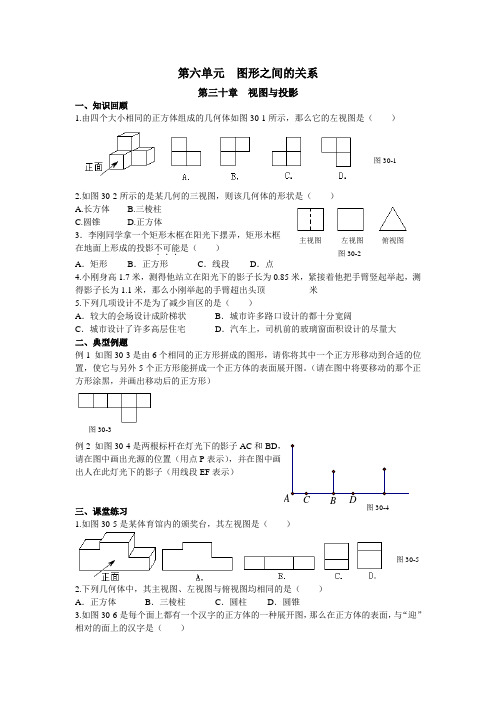
第六单元 图形之间的关系第三十章 视图与投影一、知识回顾1.由四个大小相同的正方体组成的几何体如图30-1所示，那么它的左视图是（ ）2.如图30-2所示的是某几何的三视图，则该几何体的形状是（ ） A.长方体 B.三棱柱 C.圆锥 D.正方体3．李刚同学拿一个矩形木框在阳光下摆弄，矩形木框在地面上形成的投影不可能．．．是（ ） A ．矩形 B ．正方形 C ．线段 D ．点4.小刚身高1.7米，测得他站立在阳光下的影子长为0.85米，紧接着他把手臂竖起举起，测得影子长为1.1米，那么小刚举起的手臂超出头顶__________米5.下列几项设计不是为了减少盲区的是（ ） A ．较大的会场设计成阶梯状 B ．城市许多路口设计的都十分宽阔 C ．城市设计了许多高层住宅 D ．汽车上，司机前的玻璃窗面积设计的尽量大二、典型例题例1 如图30-3是由6个相同的正方形拼成的图形，请你将其中一个正方形移动到合适的位置，使它与另外5个正方形能拼成一个正方体的表面展开图。
（请在图中将要移动的那个正方形涂黑，并画出移动后的正方形）例2 如图30-4是两根标杆在灯光下的影子AC 和BD ， 请在图中画出光源的位置（用点P 表示），并在图中画 出人在此灯光下的影子（用线段EF 表示） 三、课堂练习1.如图30-5是某体育馆内的颁奖台，其左视图是（ ）2.下列几何体中，其主视图、左视图与俯视图均相同的是（ ） A ．正方体 B ．三棱柱 C ．圆柱 D ．圆锥3.如图30-6是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面，与“迎”相对的面上的汉字是（ ）图30-1 主视图 左视图 俯视图图30-2图30-3图30-4图30-5A ．文B ．明C ．奥D ．运 4.如图30-7，箭头表示投影的方向，则图中圆柱体的 投影是（ ） A ．圆 B ．矩形 C ．梯形 D ．圆柱5.如图30-8表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，请你画出该几何体的主视图。
九下数学课件相似图形 课件(共27张PPT)
为 AA'BB'=BB'CC'=AA'CC'
＝ k′，因此k ＝
1 k'
.
感悟新知
要点提醒： 判断两个三角形相似的条件： (1)三角形的三组角分别对应相等； (2)三角形的三组边对应成比例. ●相似三角形的性质：相似三角形的对应角相等，对
应边成比例. ●在相似多边形中，最简单的就是相似三角形.
感悟新知
感悟新知
特别解读 ： ①“形状相同”是判定相似图形的唯一条件. ②两个图形相似是指它们的形状相同，与它们的位置、
大小无关.
感悟新知
例 1
[模拟·南通] 下列图形不是相似图形的是(
C)
A. 同一底片打印出来的两张大小不同的照片
B. 用放大镜将一个细小物体图案放大过程中原图案
和放大图案
C. 某人的侧身照片和正面照片
相似多边 形的性质
相似图形 相似图形
相似三角 形的定义
相似三角 形的性质
感悟新知
新知二 相似多边形
1. 相似多边形的定义 各角分别相等，各边成比例的两个多边形，它们的形状相
同，称为相似多边形. 2. 相似比的定义 相似多边形的对应边的比叫做相似比.
感悟新知
3. 相似多边形的性质 相似多边形的对应边的比相等，对应 角相等.
(1)相似比与两个多边形的先后顺序有关. (2)相似多边形的定义可用来判断两个多边形是否相似. (3)相似多边形的性质常用来求相似多边形未知边的长度或
感悟新知
(1)求梯形ABCD与梯形A′B′C′D′ 的相似比k；
解题秘方：紧扣“相似多边形的性质及相似比的定义”
进行计算.
解：相似比k=
AD 4 2 A'D'=6=3.