原子核 磁矩 毕奥沙法拉定律
毕奥-萨伐尔定律介绍

en
S
I
13
物理学
第五版
7-4
毕奥-萨伐尔定律
例3 载流直螺线管内部的磁场. 如图所示,有一长为l ,半径为R的载 流密绕直螺线管,螺线管的总匝数为N, 通有电流I. 设把螺线管放在真空中,求管 内轴线上一点处的磁感强度.
R
*
P
×× × ×× × ×× × ×× ×× ×
第七章 恒定磁场
1
r
x
C
o r0
P
y
B 的方向沿 x 轴负方向
5
0 I (cos1 cos 2 ) 4 π r0
第七章 恒定磁场
物理学
第五版
7-4
毕奥-萨伐尔定律
B
0 I
4 π r0
(cos1 cos 2 )
z
D
无限长载流长直导线
1 0 2 π
×
2
B
0 I
2 π r0
1
物理学
第五版
7-4
毕奥-萨伐尔定律
任意载流导线在点 P 处的磁感强度 磁感强度 叠加原理 B dB
dB
r
Idl
0 I dl r 4 π r3
dB
P*
I
Idl
r
第七章 恒定磁场
2
物理学
第五版
7-4
毕奥-萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
第五版
7-4
毕奥-萨伐尔定律
2
x Rcot
B dB
2
dx R csc d
0 nI
2
2 2
毕奥 萨伐尔定律

1 0 2
B
I 0
oa
B
+
1
p
2πa
A
I
B
I
X B
太原理工大学大学物理
2)半无限长载流长直导线的磁场
B
0I
4πa
(cos1
cos2
)
I
2
B
1
2
2
B
I 0
4πa
3)载流长I 直导线延长线rr上的*磁p 场
A
1
a
B=0
B
+P
A
太原理B工大学大学物理
2. 圆形载流导线的磁场
真空中 ,半径为R 的载流导线,通有电流I,称圆电流.
求其轴线上一点 p 的磁感强度的方向和大小.
Idl
R
r
dB
o
x
*p x
解:根据对称性分析
B 0
B Bx
太原理工大学大学物理
Idl sin 900
dB 0
dBx dB sin
4π
r2
Idl
rv0
毕奥—萨伐尔定律
4π r2
思考: 判断下列各点磁感强度的方向和大小.
1
1、5 点 :dB 0
8 7
+2
Idl + 3
3、7点
:dB
0 Idl
4π R2
2、4、6、8 点 :
R
6
+ 4
5
dB
0 Idl
4π R2
sin
450
太原理工大学大学物理
2,毕沙定理

0
q
i
i
静电场中高斯定理反映静电场是有源场;
m B dS 0
S
稳恒磁场的高斯定理反映稳恒磁场是无源场。
例题: 在一无限长载流直导线旁有一矩形回路, 求通过该回路的磁通量.
d
I
a
l
2 2
2 R (1 cot )
3 2
3
2
0 R2 nIR csc2 d μ μ0 nId 3 3 2 R csc 2 csc
μ0 nI sin d 2
积分得:
μ0 nI B 2
2
sin d
1
1 μ0 nI (cos 2 cos 1 ) 2
B
μ0 I
2R
即得
例题5 : 如下列各图示,求圆心 o 点的磁感应强度。
解: I
B
O
R
2 3
O
R
I
μ0 I
4R
I
0 I 3 B (1 ) 6R R 2
0 I
R
O
I
O
R
I B 0 4 R 2 R
0 I
B
μ0 I
8R
例题6 : 有限长载流螺线管轴线上任一 点p处的磁场
S
④S 为任意闭合曲面 m BdS cos θ B dS
S
S
规定:dS正方向为曲面上由内向外的法线方向。 则
磁感应线穿入, m 为负;穿出, m 为正。
3.磁场中的高斯定理 由于磁感应线为封闭曲线.因此,通过任意封闭 曲面的磁感应强度通量恒为零.
m B dS 0
毕奥-萨伐尔定律
×
2
×3
7
Idl
R
6
×
4
0 Idl r dB 4 π r3
5
1、5点 :dB 0 0 Idl 3、7点 :dB 4 π R2 2、4、6、8 点 : 0 Idl dB sin 45 0 4 π R2 毕奥-萨伐尔定律
3
第19章 稳恒磁场
大学 物理
1
大学 物理
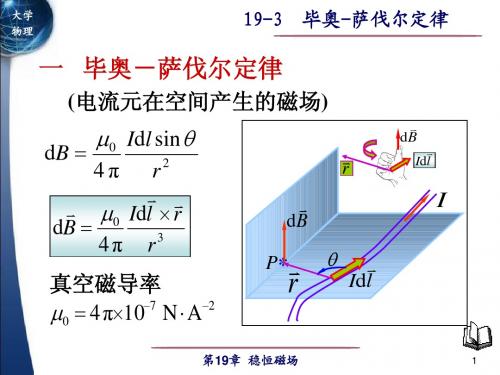
19-3
毕奥-萨伐尔定律
任意载流导线在点 P 处的磁感强度
磁感强度 叠加原理 B dB
dB
r
Idl
0 I dl r 4 π r3
dB
P*
I
Idl
r
第19章 稳恒磁场
2
大学 物理
19-3
毕奥-萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
第19章 稳恒磁场
16
大学 物理
19-3
毕奥-萨伐尔定律
0 nI cos 2 cos 1 B 讨 论 2 (1)P点位于管内轴线中点 1 π 2
cos1 cos2
cos 2 l/2
l / 2
2
R
2
R
1 * P
2
x
×× × ×× × ×× × ×× ×× ×
1 0 nI 2
B
0 nI
x
O
第19章 稳恒磁场
21
大学 物理
19-3
毕奥-萨伐尔定律
四 运动电荷的磁场
0 Idl r dB 3 4π r Idl j Sdl nSdlqv 0 nSdlqv r dB 4π r3
电磁学 毕奥-萨伐尔定律

I 2 dl
e
er
38
L2单位长度受到的力的大小是
f dF12 0 I1I 2
dz
2r0
(2.2-19)
令I1 = I2 = I , 当 r0 = 1米,并且测得f = 2×10 –7牛顿/ 米时,两导线中的电流强度I 就定义为“1安培”.
0
2r0
I2
f
2
1m 2 10 7 1A2
N
/
m
25
A
若两电流元关于平面A镜像对
称,证明:它们在A上的合磁 场B必垂直于A(除非B=0)
Idl r
Idl '
r'
z
dB dB'
0I 4
dl
r
r
3
0I 4
dl'r' r'3
0I 4r 3
(dl r dl 'r ')
dl
(lx
,
l
Hale Waihona Puke y,lz)
dl ' (lx ,ly ,lz )
11
2.安培定律(Amperes’ Law)
真空中,两个稳恒的电流回路L1和L2 ,
电d流F1元2 I1dIl21d对l2I2dlk2的I1作d用lr1122力e为12
在MKSA单位制中,比例常数
k 0 4
(2.2-2)
(2.2-1)
e12 I1dl1 r12
L1
I2dl2 L2
12
其中,0称为真空磁导率,它与真空介电常数e0
36
电磁相互作用宇称守恒
dB( x)
0 4
Idl e r
r2
毕奥萨伐尔定律

磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律,当导体在磁场中运动时,会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动,使定子绕组中产生感应电流,实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域,为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出,运动电荷或电流会产生磁场,这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关,当电荷或电流运动时,会激发周围的磁场 ,磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景,同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时,利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中,拇指指向电流的方向 ,四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m),国际单位制中,磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性,即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组,其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论,它描述 了磁场与电流之间的关系。此外,麦克斯韦方程组还 预言了电磁波的存在,即光、无线电波等。
毕奥萨伐尔定律

毕奥萨伐尔定律毕奥-萨伐尔定律指出: 磁场的是电流元,磁场随场点到电流元的距离平方而衰减,磁场遵从叠加原理,由任意形状通电导线所激发的总磁感应强度B 是由电流元所激发的磁感应强度dB 的矢量积分,任意形状的载流导线都可以看成由许多电流元Idl 组成,只要知道了电流元激发磁场的规律,再用叠加原理就可以求得任意载流导线激发的磁场分布。
载流导线的任一电流元Idl 在给定点P 所产生的磁感应强度dB 的大小与电流元的大小成正比,与电流元和由电流元到P 点的矢径r 之间夹角的正弦成正比,并与电流元到P 点的距离的平方成反比; dB 的方向垂直于dl 与r 所决定的平面,指向由右手螺旋法则决定,即当右手螺旋由Idl 经小于180°的角转向r 时螺旋前进的方向,如附图-1 所示。
其数学表达式为附图-1 电流元到P 点dB 的方向地球磁场起源理论式中: k 为比例系数,在真空中k =107T·m·A-1,不同的磁介质k 值不同。
为了使dB 的公式有理化,取k = μ/4π,μ为介质的磁导率,真空中μ= 4π×107T·m·A-1,这样,式( 附-1) 改为:地球磁场起源理论毕奥-萨伐尔定律的矢量表达式为:地球磁场起源理论任意形状载流导线在P 点产生的磁感应强度B,等于导线上各个电流元Idl 在该点处所产生的磁感应强度矢量和,即:地球磁场起源理论毕奥-萨伐尔定律给出了电流元Idl 对距离r 处的空间某一点P 处产生dB 的大小与方向,但由于电流元不可能单独存在,所以毕奥-萨伐尔定律不可能由实验直接加以验证。
毕奥-萨伐尔定律的正确性是通过间接的方法被证实的,因为由毕奥-萨伐尔定律推出的所有结果都能很好地与实验结果相符合。
大学物理课件-毕-沙-拉定律

×
O
x
Bx
dBx
0 2R
I
0
sind
0 I 2R
dBy
0 2R
I
cosd
By
dBy
0 2R
I
cosd 0
0
例7 四條相互平行的載流長直導線如圖所示,電流均為I,正方形
邊長為2a,求正方形中心的 B
1
2
B4 B3
4 B1 B2 3
B 0I 0I 2 x 2 2a
Bo 0
I
I1
U Ii R
U R li
2rU
Rli
2r
B0
Bi
0li 4r 2
2rU
Rli
0U
2rR
例2 一無限長直載流導線被彎成如圖所示的形狀,通以
電流I,則 Bo
3
1
2 R
3
I
I
2
R
1
B1 B3 0
Bo
B2
0I
2R
3
2
0I
12R
Bo
0I
2R
0I 2 R
(5) x>>R
B
0 IR 2
2(x2 R2)32
則每個運動電荷產生的電流元在P點產生的磁感應強度為:
運動電荷的磁場:
B
dB dN
0 4
qv r0 r2
適用條件:
v <<C
運動電荷的磁場
B
0
4π
qv
r2
r0
大小:
B 0 4
q v sin(v , r0 ) r2
方向:垂直於
v
和
r0所確定的平面,右手螺旋
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
原子核磁矩毕奥沙法拉定律原子核的磁矩与毕奥-萨伐尔定律之间存在关联。
首先,让我们分别了解这两个概念。
原子核的磁矩是原子核的一个基本属性,它是由原子核内的质子和中子的磁矩以及它们的自旋产生的。
磁矩是一个矢量,既有大小又有方向,它描述了原子核在磁场中的行为。
毕奥-萨伐尔定律,又称为毕奥-萨伐尔-拉普拉斯定律,是一个描述电流元在空间任意点产生的磁场的定律。
这个定律指出,电流元Idl在空间某点P处产生的磁感应强度dB的大小与电流元Idl的大小成正比,与电流元Idl所在处到P点的位置矢量和电流元Idl之间的夹角的正弦成正比,而与电流元Idl到P 点的距离的平方成反比。
在原子核物理中,毕奥-萨伐尔定律经常用于计算原子核产生的磁场。
因为原子核由带正电的质子和不带电的中子组成,它们在核内运动产生的电流会导致一个磁矩,这个磁矩可以用毕奥-萨伐尔定律来计算。
