超大整数乘法运算
整数的乘法运算

整数的乘法运算整数的乘法运算是数学中基本的运算之一,它是将两个整数进行相乘的操作。
在日常生活和数学领域中,我们经常会遇到整数的乘法运算,因此了解和掌握整数乘法是非常重要的。
1. 整数的乘法规则在进行整数的乘法运算时,有以下几个规则需要注意:1.1 同号相乘为正,异号相乘为负当两个整数具有相同的符号时,它们的乘积为正数;当两个整数的符号不同时,它们的乘积为负数。
例如,正数5乘以正数3等于15,而负数-4乘以负数2等于8。
1.2 乘法的交换律不变整数的乘法满足交换律,即a乘以b等于b乘以a。
例如,2乘以3等于3乘以2,都等于6。
1.3 乘法的结合律不变整数的乘法满足结合律,即a乘以(b乘以c)等于(a乘以b)乘以c。
例如,2乘以(3乘以4)等于(2乘以3)乘以4,都等于24。
2. 整数乘法的计算方法根据整数乘法的规则,我们可以使用多种方法来计算整数的乘法。
下面介绍两种常用的计算方法:竖式乘法和分配律。
2.1 竖式乘法竖式乘法是一种逐位相乘的计算方法,它将两个整数的每一位进行乘法运算,并将结果相加得到最终的乘积。
例如,计算123乘以45的结果,可以按照以下步骤进行计算:1 2 3× 4 5---------6 1 5 <- 123乘以5的结果4 9 2 0 <- 123乘以40的结果---------5 5 3 5 <- 最终结果2.2 分配律分配律是指将一个整数和另外两个整数的乘法分别进行计算,然后将结果相加得到最终的乘积。
例如,计算3乘以(8加4)的结果,可以按照以下步骤进行计算:3乘以8等于24;3乘以4等于12;将24和12相加,得到最终结果36。
3. 实际应用整数乘法在实际生活和数学应用中有广泛的应用。
以下是一些整数乘法的实际应用场景:3.1 计算商品总价在购物过程中,我们经常需要计算商品的总价。
如果知道商品的单价和数量,可以使用整数的乘法来计算商品的总价。
例如,商品A的单价为10元,购买数量为3个,可以使用10乘以3得到商品A的总价为30元。
整数的乘法运算法则

整数的乘法运算法则整数的乘法运算是数学中非常基础和重要的运算之一,它有一些独特的规则和性质。
在这篇文章中,我们将深入探讨整数的乘法运算法则,包括乘法的交换律、结合律、分配律等内容。
首先,我们来回顾一下整数的乘法定义。
对于任意的整数a和b,它们的乘积记作a*b,表示a和b相乘得到的结果。
例如,2*3=6,-4*5=-20。
在整数的乘法运算中,有一些特殊的规则需要我们特别注意。
首先是乘法的交换律。
乘法的交换律指的是,对于任意的整数a和b,a*b=b*a。
换句话说,整数的乘法满足交换律,乘数的顺序不影响乘积的结果。
这一性质可以通过具体的例子来验证,比如2*3=6,3*2=6,-4*5=-20,5*(-4)=-20。
接下来是乘法的结合律。
乘法的结合律指的是,对于任意的整数a、b和c,(a*b)*c=a*(b*c)。
换句话说,整数的乘法满足结合律,乘法的结合顺序不影响乘积的结果。
这一性质也可以通过具体的例子来验证,比如(2*3)*4=24,2*(3*4)=24,(-4*5)*2=-40,-4*(5*2)=-40。
最后是乘法的分配律。
乘法的分配律指的是,对于任意的整数a、b和c,a*(b+c)=a*b+a*c。
换句话说,整数的乘法满足分配律,乘法对加法的分配性质成立。
这一性质同样可以通过具体的例子来验证,比如2*(3+4)=14,2*3+2*4=14,-4*(5+6)=-44,-4*5+(-4*6)=-44。
通过以上的讨论,我们可以得出结论:整数的乘法运算满足交换律、结合律和分配律。
这些性质是整数乘法运算的基本规则,也是我们在进行乘法运算时必须遵守的规则。
在实际的数学运算中,这些性质可以帮助我们简化计算,准确求得乘积的结果。
总之,整数的乘法运算法则是数学中的重要内容,它包括乘法的交换律、结合律、分配律等多个方面。
这些规则和性质在我们的日常数学运算中起着至关重要的作用,帮助我们准确进行乘法运算,得到正确的结果。
整数的乘法及简便运算

整数的乘法及简便运算概览本文档旨在介绍整数的乘法运算及一些简便运算方法。
我们将讨论基本的乘法规则,并介绍一些用于简化计算的技巧和窍门。
1.整数的乘法规则整数的乘法是指将两个整数相乘得到一个新的整数的操作。
下面是整数乘法的基本规则:正数乘以正数,结果为正数。
正数乘以负数,结果为负数。
负数乘以正数,结果为负数。
负数乘以负数,结果为正数。
例如,3乘以4等于12,-3乘以4等于-12,-3乘以-4等于12.2.简便运算方法2.1 分解法分解法是一种简化大数字乘法的方法。
它的基本原理是将一个大的乘法运算分解成多个小的乘法运算,然后将这些小的乘积相加得到最终结果。
例如,我们要计算36乘以23.我们可以将36分解为30和6,将23分解为20和3.然后我们计算30乘以20得到600,30乘以3得到90,6乘以20得到120,6乘以3得到18.最后将这些乘积相加得到最终结果:600+90+120+18=828.因此,36乘以23等于828.2.2 简便乘法法则简便乘法法则是一种快速计算乘法的方法。
它基于一些数学性质和技巧,可以帮助我们在头脑中进行乘法计算,而不需要借助计算器或纸笔。
以下是一些常见的简便乘法法则:乘以10的幂:将被乘数后面加上相应的0.例如,5乘以100等于500.乘以整十或整百:将被乘数乘以整十或整百后,再除以10或100.例如,25乘以40可以计算为(25乘以4)除以10,即20.乘以9:将被乘数乘以10,然后减去被乘数。
例如,9乘以7等于70减去7,即63.3.总结本文介绍了整数的乘法运算及一些简便运算方法。
了解整数乘法的基本规则是掌握乘法运算的基础,而掌握简便运算方法可以帮助我们更高效地进行计算。
通过练习和熟练掌握这些技巧,我们可以在数学和日常生活中更自信地应用整数的乘法和简便运算。
整数乘法的运算法则

整数乘法的运算法则整数乘法的运算法则是数学中最基本的原则之一,它描述了两个整数相乘的计算方式。
在本文中,我们将详细介绍整数乘法的运算法则,包括它的定义、性质、应用以及一些常见的乘法规律。
一、整数乘法的定义整数乘法的定义是:对于任意两个整数a和b,它们的积ab是一个整数,满足以下条件:1. 若a和b同号,则ab为正数;2. 若a和b异号,则ab为负数。
例如,当a=2,b=3时,它们的积为6;当a=-2,b=3时,它们的积为-6。
二、整数乘法的性质整数乘法具有以下性质:1. 交换律:对于任意两个整数a和b,有ab=ba。
2. 结合律:对于任意三个整数a、b和c,有a(bc)=(ab)c。
3. 分配律:对于任意三个整数a、b和c,有a(b+c)=ab+ac和(b+c)a=ba+ca。
4. 零乘性质:如果存在一个整数a不等于0,另一个整数b等于0,则ab=0。
5. 单位元:整数1是乘法的单位元,即对于任意整数a,有a×1=a。
三、整数乘法的应用整数乘法在数学中有着广泛的应用,例如:1. 计算面积和体积:在计算面积和体积时,需要用到整数乘法。
例如,矩形的面积可以用它的长和宽相乘得到。
2. 计算工资和奖金:在计算工资和奖金时,需要用到整数乘法。
例如,如果一名员工每小时赚10美元,他工作了8个小时,那么他今天的工资就是10×8=80美元。
3. 解决方程式:在解决一些方程式时,需要用到整数乘法。
例如,如果要解决方程式2x=8,就需要用到乘法,将2乘以x得到x=4。
四、常见的乘法规律除了整数乘法的基本原则外,还存在一些常见的乘法规律,如下所示:1. 乘法交换律:对于任意两个整数a和b,有ab=ba。
2. 乘法结合律:对于任意三个整数a、b和c,有a(bc)=(ab)c。
3. 乘法分配律:对于任意三个整数a、b和c,有a(b+c)=ab+ac 和(b+c)a=ba+ca。
4. 乘法消零律:如果存在一个整数a不等于0,另一个整数b等于0,则ab=0。
整数的乘法整十整百与整千整万的乘法

整数的乘法整十整百与整千整万的乘法整数的乘法可以通过各种方法进行计算,其中一种常见的方法是利用整十、整百、整千和整万来进行乘法运算。
本文将详细介绍整数的乘法,并探讨如何利用整十、整百、整千和整万来简化乘法运算。
一、整数的乘法整数的乘法是基本的数学运算之一,它指的是将两个整数相乘得到一个结果。
例如,将整数5乘以整数3,结果为15(5×3=15)。
在进行整数乘法运算时,有以下几个要点需要注意:1. 相乘的两个整数的符号相同时,结果为正数;符号不同时,结果为负数。
2. 任何整数与0相乘,结果都为0。
3. 乘法满足交换律,即a×b=b×a。
二、整十、整百与整千的乘法在进行整数的乘法运算时,我们常常可以利用整十、整百和整千的特性来简化计算。
例如,将整数26乘以整数30,我们可以将乘法分解为两步:1. 先将整数26乘以10(整十),得到260。
2. 再将260乘以3(整十的个位数),得到780。
同样的方法也可以应用于整百和整千的乘法运算。
例如,将整数432乘以整数500,我们可以分解为三步:1. 先将整数432乘以100(整百),得到43,200。
2. 再将43,200乘以5(整百的个位数),得到216,000。
通过这种分解的方法,我们可以大大简化乘法的计算过程,提高计算的准确性和效率。
三、整万的乘法整万是指位于一万的整数,例如10,000、20,000等。
利用整万的特性,我们可以进一步简化乘法运算。
例如,将整数24,000乘以整万10,我们只需要将24,000与10相乘的结果后添加四个0即可,即24,000乘以10等于240,000。
同样地,将整数8,000乘以整万5,只需要将8,000与5相乘的结果后添加四个0即可,即8,000乘以5等于40,000。
通过利用整十、整百、整千和整万来简化乘法运算,我们可以在保持计算准确性的前提下,提高计算的速度和效率,尤其在大数乘法运算时,这种方法可以帮助我们更加方便地进行计算。
整数的乘法整十整百整千与整十整百整千的乘法

整数的乘法整十整百整千与整十整百整千的乘法整数的乘法中,常常涉及到整十、整百和整千的乘法运算。
这种运算方式,在实际生活中具有广泛的应用和重要的意义。
本文将以实例分析的方式,介绍整数的乘法中整十、整百和整千的乘法规律。
一、整十的乘法整十的乘法是指一个整数与10的乘法运算。
具体来说,整十的乘法有以下几个特点:1. 一个整数乘以 10,结果将比原来的整数增加一个零。
例如:5 × 10 = 50,20 × 10 = 200。
2. 一个整数乘以整十的倍数,结果也是将原数后面添上相应数目的零。
例如:5 × 20 = 100,20 × 30 = 600。
3. 整十的乘法在实际问题中,常常出现在货币计算、衡量单位转换等方面。
例如:购买10个价格为50元的商品,需支付500元。
二、整百的乘法整百的乘法是指一个整数与100的乘法运算。
对于整百的乘法,我们可以得出以下规律:1. 一个整数乘以 100,结果将比原来的整数后面增加两个零。
例如:5 × 100 = 500,20 × 100 = 2000。
2. 一个整数乘以整百的倍数,结果也是将原数后面添上相应数目的零。
例如:5 × 200 = 1000,20 × 300 = 6000。
3. 整百的乘法常见于数据统计、报告编制等领域。
例如:统计某年全国GDP达到20000亿元。
三、整千的乘法整千的乘法是指一个整数与1000的乘法运算。
整千的乘法规律如下:1. 一个整数乘以 1000,结果将比原来的整数后面增加三个零。
例如:5 × 1000 = 5000,20 × 1000 = 20000。
2. 一个整数乘以整千的倍数,结果也是将原数后面添上相应数目的零。
例如:5 × 2000 = 10000,20 × 3000 = 60000。
3. 整千的乘法常用于数量计算、面积计算等场景。
整数乘除法运算法则
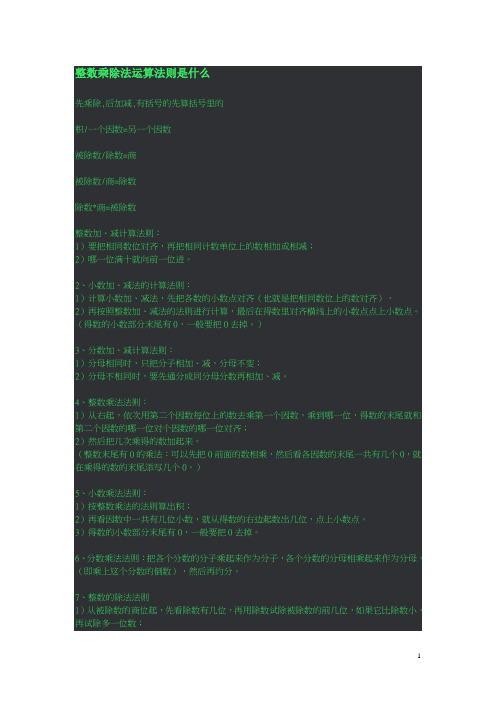
整数乘除法运算法则是什么先乘除,后加减,有括号的先算括号里的积/一个因数=另一个因数被除数/除数=商被除数/商=除数除数*商=被除数整数加、减计算法则:1)要把相同数位对齐,再把相同计数单位上的数相加或相减;2)哪一位满十就向前一位进。
2、小数加、减法的计算法则:1)计算小数加、减法,先把各数的小数点对齐(也就是把相同数位上的数对齐),2)再按照整数加、减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点。
(得数的小数部分末尾有0,一般要把0去掉。
)3、分数加、减计算法则:1)分母相同时,只把分子相加、减,分母不变;2)分母不相同时,要先通分成同分母分数再相加、减。
4、整数乘法法则:1)从右起,依次用第二个因数每位上的数去乘第一个因数,乘到哪一位,得数的末尾就和第二个因数的哪一位对个因数的哪一位对齐;2)然后把几次乘得的数加起来。
(整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0。
)5、小数乘法法则:1)按整数乘法的法则算出积;2)再看因数中一共有几位小数,就从得数的右边起数出几位,点上小数点。
3)得数的小数部分末尾有0,一般要把0去掉。
6、分数乘法法则:把各个分数的分子乘起来作为分子,各个分数的分母相乘起来作为分母,(即乘上这个分数的倒数),然后再约分。
7、整数的除法法则1)从被除数的商位起,先看除数有几位,再用除数试除被除数的前几位,如果它比除数小,再试除多一位数;2)除到被除数的哪一位,就在那一位上面写上商;3)每次除后余下的数必须比除数小。
8、除数是整数的小数除法法则:1)按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;2)如果除到被除数的末尾仍有余数,就在余数后面补零,再继续除。
9、除数是小数的小数除法法则:1)先看除数中有几位小数,就把被除数的小数点向右移动几位,数位不够的用零补足;2)然后按照除数是整数的小数除法来除10、分数的除法法则:1)用被除数的分子与除数的分母相乘作为分子;2)用被除数的分母与除数的分子相乘作为分母。
整数的乘除运算

整数的乘除运算整数的乘除运算是数学中基本的运算方式,我们常常在日常生活和学习中会遇到这种类型的运算。
本文将对整数的乘法和除法进行详细的介绍和讨论。
一、整数的乘法运算整数的乘法运算是指将两个整数进行相乘的操作。
乘法运算通常使用乘号(×)表示,乘号前后的两个整数称为乘法的因数。
整数的乘法遵循以下规则:1. 同号相乘得正,异号相乘得负。
当两个整数同为正或同为负时,它们的乘积为正数;当两个整数异号时,它们的乘积为负数。
例如,2 × 3 = 6,(-2) × (-3) = 6,(-2) × 3 = -6。
2. 乘法满足交换律和结合律。
乘法满足交换律,即 a × b = b × a。
乘法还满足结合律,即 (a × b) ×c = a × (b × c)。
例如,3 × 4 = 4 × 3,(2 × 3) × 4 = 2 × (3 × 4)。
3. 乘法有零元素。
任何整数乘以 0 的结果都为 0。
即 a × 0 = 0。
例如,3 × 0 = 0,(-2) × 0 = 0。
二、整数的除法运算整数的除法运算是指将一个整数除以另一个整数的操作。
除法运算通常使用除号(÷)表示,除号前的整数称为被除数,除号后的整数称为除数。
整数的除法遵循以下规则:1. 同号相除得正,异号相除得负。
当被除数和除数的符号相同时,它们的商为正数;当被除数和除数的符号不同时,它们的商为负数。
例如,6 ÷ 2 = 3,(-6) ÷ (-2) = 3,(-6) ÷ 2 = -3。
2. 除数不为零。
除数不能为零,即在除法运算中除数不能为 0。
例如,6 ÷ 0 是没有定义的。
3. 除法可能存在余数。
当被除数不能被除数整除时,除法运算可能存在余数。
