4850改为5800锥坡放样程序
5800边坡放样程序

直线段边坡超欠挖检查及开口线放样程序程序名:BPFY 程序:A“QX":B“QY":C“QZ”:E“ZX”:F“ZY”:G“ZZ”:P“PB”:K“XP”:L“YP”:M“ZP":Fixm:Pol(E-A,F—B:J ≤0=〉J=J 360⊿D=Abs((K—A)*CosJ (L—B)*SinJ):S=Abs((L-F)*CosJ-(K—E)*SinJ): X=A D*CosJ:Y=B D*SinJ:Z=(G-C)/I*D C:W=AbS(M—Z):V=S/P—W:V<0=〉O“Hcw"=V◢⊿V≥0=〉O“Hqw”=V◢⊿U=W*P-S:U<0=〉N“Scw”=U◢⊿U≥0=>N“Sqw”=U◢⊿“END" 说明:A、B、C为边坡底线的起点,显示为: QX?QY?QZ?依次输入地线起点的X,Y,Z;E、F、G为边坡底线的终点,显示为: ZX?ZY?ZZ?依次输入地线终点的X,Y,Z;P 为坡比,无正负条件; K、L、M为测量点,显示为: XP?YP?PZ?依次输入测量点的X,Y,Z;中间计算测量点至边坡底线的垂足点,保存变量为X、Y、Z。
O为边坡的高程超欠挖值,显示为Hcw或Hqw,分别表示超挖或欠挖,即测点高程设计高程减实测高程;N为边坡的距离超欠挖值,显示为Scw或Sqw,分别表示超挖或欠挖,按高差计算的设计距离减实测点到垂足点距离.圆弧段边坡超欠挖检查及开口线放样程序程序名:YFFY 程序:A“YX":B“YY”:X “XP”:Y“YP”:Z“ZP”:Fixm:Pol(A—X,B—Y):T=Abs(I-R):W=Abs(H-Z):S=W*P-T:V=T/P —W:S〈0=>M“Scw”=S◢⊿S≥0=>M“Sqw”=S◢⊿V〈0=>K“Hcw”=V◢⊿V≥0=〉K“Hqw"=V ◢⊿“END”说明:A、B为圆心坐标,显示为YX?YY?,依次输入圆心点的X、Y;X、Y、Z为测点坐标,显示为XP?YP?ZP?依次输入测点的X、Y,Z;R为到边坡底线的距离(半径);H为边坡底线的高程(马道或平台的高程);I不用管它,直接按“EXE",显示下一个输入;P为坡比,无须输入正负号; M为计算的边坡距离超欠值,显示为Scw或Sqw,分别表示超挖或欠挖,距离超欠值为:设计距离减测量距离;K为计算的边坡高程超欠值,显示为Hcw或Hqw,分别表示超挖或欠挖,高程超欠值为:设计高程减测量高程。
锥坡放样计算程序5800
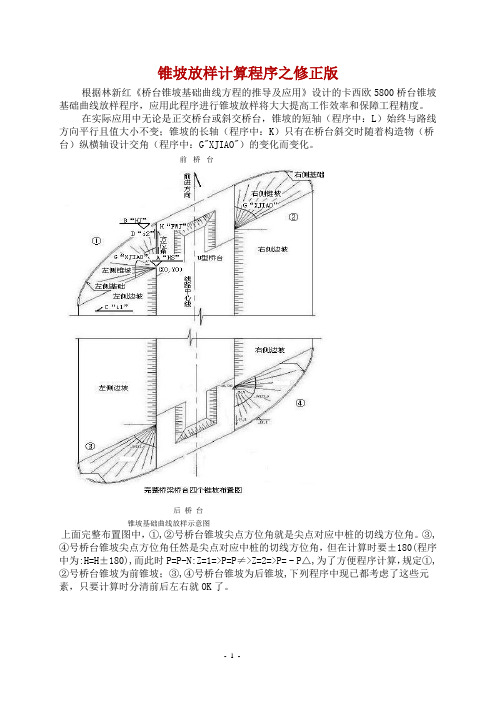
锥坡放样计算程序之修正版根据林新红《桥台锥坡基础曲线方程的推导及应用》设计的卡西欧5800桥台锥坡基础曲线放样程序,应用此程序进行锥坡放样将大大提高工作效率和保障工程精度。
在实际应用中无论是正交桥台或斜交桥台,锥坡的短轴(程序中:L)始终与路线方向平行且值大小不变;锥坡的长轴(程序中:K)只有在桥台斜交时随着构造物(桥台)纵横轴设计交角(程序中:G"XJIAO")的变化而变化。
前桥台后桥台锥坡基础曲线放样示意图上面完整布置图中,①,②号桥台锥坡尖点方位角就是尖点对应中桩的切线方位角。
③,④号桥台锥坡尖点方位角任然是尖点对应中桩的切线方位角,但在计算时要±180(程序中为:H=H±180),而此时P=P-N:Z=1=>P=P≠>Z=2=>P= - P△,为了方便程序计算,规定①,②号桥台锥坡为前锥坡;③,④号桥台锥坡为后锥坡,下列程序中现已都考虑了这些元素,只要计算时分清前后左右就OK了。
程序名: ZPFYJSLbl 0 : "XC"? U: "YC"? V :"HS"?A: "HJ" ?B: "i1"? C: "i2" ?D: "X0" ?E: "Y0" ?F: "XJIAO" ?G: "FWJ" ?H: "QZP-1,HZP-2" ?R: "L-1,R-2":?Z: "JMD" ?S:If R=2:Then H-180→H:IfEnd:(A-B)C÷cos(90-G)→K◢………显示锥坡长半轴长度值(如果去掉黑三角,K值不显示) (A-B)D →L◢……………………显示锥坡短半轴长度值(如果去掉黑三角,L值不显示) 0→T: 0→N:(注意,这里是数字0,而不是字母O)Lbl 1:T+1→T:"n":T◢……显示坐标值的组数If N≥G:Then G→N:IfEnd: G-N→P:KLsin(G)÷√((Ksin(N))²+(Lsin(P))²)→M◢…………显示随着加密递增变化而变化的极轴长度值(可去掉黑三角,M值不显示)If R=1:Then Goto 2:IfEnd: If R=2:Then Goto 3:IfEnd:………判断是前桥台锥坡还是后桥台锥坡Lbl 2: If Z=1:Then -P→P:Goto 4:IfEnd:If Z=2:Then P→P:Goto 4:IfEnd(回车EXE)………判断是前桥台锥坡的左侧锥坡还是右侧锥坡Lbl 3: If Z=1 Then -P→P:Goto 4:IfEnd:If Z=2:Then P→P:Goto 4:IfEnd(回车EXE)……………判断是后桥台锥坡的左侧锥坡还是右侧锥坡Lbl 4:E+Mcos(H+P)→X: "X=":X◢……显示随着加密递增变化而变化的极轴末端的X 坐标F+Msin(H+P)→Y: "Y=":Y◢……显示随着加密递增变化而变化的极轴末端的Y坐标Pol(X-U,Y-V)→J:If J<0 Then J+360→J: IfEnd:“FWJ=”:J►DMS◢……显示随着加密递增变化而变化的放样极坐标方位角“S=”:I◢………………显示随着加密递增变化而变化的放样极坐标距离If N=G: Then Goto 0: IfEnd(回车EXE)…程序自动跳回主程序表示锥坡基础曲线计算放样完毕N+S→N:Goto 1说明:程序中各注释文的涵义"XC"、"YC"--测站点横纵坐标"HS"--锥坡尖点的标高"HJ"--锥坡基础顶面标高"i1"--路基横坡度(椎体长半轴方向),如果为1:1.5则输入为1.5"i2"--锥坡迎水面坡度(路线方向,短半轴方向),如果为1:1则输入为1"X0"、"Y0"--锥坡尖点的横、纵坐标"XJIAO"--桥台横纵轴之间的夹角"FWJ"--锥坡尖点沿路线前进方向的方位角"QZP-1,HZP-2"--输1计算前桥台锥坡,输2计算后桥台锥坡"L-1,R-2"--输1计算左侧桥台锥坡,输2计算右侧桥台锥坡"JMD" --把需要加密点而设置的平分角度值,如要求曲线精度更高,可将角度划分更细加密即可,一般可以设置取S值为:5度、4度或者3度。
5800公路放样程序

FX-5800计算器公路测量常用程序一、程序功能本程序由6个主程序、5个次子程序及5个参数子程序组成。
主要用于公路测量中坐标正反算,设计任意点高程及横坡计算,桥涵放样,路基开挖口及填方坡脚线放样。
程序坐标计算适应于任何线型.二、源程序1.主程序1:一般放样反算程序(①正算坐标、放样点至置仪点方位角及距离;②反算桩号及距中距离)程序名:1ZD-XYLb1 0:Norm 2F=1:(正反算判别,F=1正算,F=2反算,也可以改F前加?,改F为变量)Z[1]=90(与路线右边夹角)Prog"THB":F=1=>Goto 1:F=2=>Goto 2Lb1 1:Fix 3:"X=":Locate 6,4,X◢"Y=":Locate 6,4,Y◢Prog"3JS”:Goto 0:Lb1 2:Fix 3:"KM=":Locate 6,4,Z◢"D=":Locate 6,4,D◢Goto 02.主程序2:高程序横坡程序(设计任意点高程及横坡)程序名:2GCLbI 0:Norm 2“KM”?Z:?D:Prog”H”:Fix 3:”H=”:Locate 6,4,H◢“I=”: Locate 6,4,I◢Goto 03.主程序3:极坐放样计算程序(计算放样点至置仪点方位角及距离)程序名:3JSX:Y:1268.123→K(置仪点X坐标)2243.545→L(置仪点Y坐标,都是手工输入,也可以建导线点数据库子程序,个人认为太麻烦)Y-L→E:X-K→F:Pol(F,E):IF J<0:Then J+360→J:Int(J)+0.01Int(60Frac(J))+0.006Frac(60Frac(J)) →J:(不习惯小数点后四位为角度显示的,也可以用命令J◢DMS◢来直接显示) Fix 4:” FWJ=”: Locate 6,4,J◢(不习惯小数点后四位为角度显示的,也可以用命令J◢DMS◢来直接显示)Fix 3:”S=”:Locate 6,4,I◢4.主程序4:涵洞放样程序(由涵中心桩号计算出各涵角坐标、在主程序3中输入置仪点坐标后计算放样点至置仪点方位角及距离)程序名:4JH-XYLbI 0:Norm 290→Z[1](涵洞中心桩与右边夹角,手工输入,也可以修改成前面加?后变为变量)1→F:Prog”THB”:?L:Z[2]-Z[1] →E:X+Lcos(E) →X:Y+Lsin(E) →Y:Fix 3: "X=":Locate 6,4,X◢"Y=":Locate 6,4,Y◢Prog"3JS”:Goto 0:5.主程序5:路基开挖边线及填方坡脚线放样程序(输入大概桩号及测量坐标、地面标高计算出偏移距离、桩号、距中距离、填挖高度)程序名:5FBXLbI 0:Norm 2: 18→DimZ:2→F:90→Z[1]:Prog “THB”:Z:D:”M0”?M:M→Z[4]:D→Z[3]:Prog”6GD”:L→Z[6]:If D<0:Then 0.75-L→D:Goto H:Else L-0.75→D:Goto H:IfEndLbI H:Prog”H”:H-0.03-Z[4] →Z[5]:Z[6] →L:If Z[5]<0:Then –z[5] →G:Goto W:Else Z[5] →G:Goto T:LbI W:Prog “W0”:Z[10]+Z[11] →A: If G>A:Then Goto 1:Else If G>Z[10]:Then Goto 2:Else Goto 3:IfEnd:LbI 1:L+Z[12]+Z[13]+Z[14]+(G-A)×Z[9]+Z[11]×Z[8]+Z[10]×Z[7]:Goto Z:LbI 2:L+Z[12]+Z[13]+(G-Z[10])×Z[8]+Z[10]×Z[7]:Goto Z:LbI 3:L+Z[12]+G×Z[7]:Goto z:LbI T:L+0.5→N:If G>Z[17]:Then (N+Z[18]+(G-Z[17])×Z[16]+Z[17]×Z[15])→S:Goto Z:Else (N+G×Z[15])→S:Goto z:LbI Z:Z[3]→D:Fix 2:Abs(D)-S→T:”L0=”:L Locate 6,4,T◢"KM=":Locate 6,4,Z◢"D=":Locate 6,4,D◢“TW=”: Locate 6,4,Z[5]◢Goto 06.主程序6:路基标准半幅宽度计算程序(对于设计有加宽渐变的有用,如路基宽度无变化,则把此程序直接输入半幅宽度值至L)程序名:6GDProg “G0”Z-C→E:(B-A)×E/S+A→L:L:7.坐标计算次程序(THB)程序名:THB18→DimZ:"KM"?Z:Prog "X0"1÷P→C:(P-R)÷(2HPR) →S:180÷π→E:F=1=>Goto 1:F=2=>Goto 2←┘Lbl 1:?D:Abs(Z-O) →W:Prog "A":X:Y:Goto 3LbI 2:X:Y:X→I:Y→J:Prog "B":O+W→Z:D→D:Goto 3LbI 3:IF F=1Then X:Y:Else Z:D8. 正算子程序(A)程序名:A0.1184634425→A:0.2393143352→B:0.2844444444→N 0.046910077→K:0.2307653449→L:0.5→M:U+W(Acos(G+QEKW(C+KWS))+Bcos(G+QELW(C+LW S))+Ncos(G+QEMW(C+MWS))+Bcos(G+QE(1-L)W(C+(1-L)WS))+Acos(G+QE(1-K)W(C+(1-K)WS))) →X:V+W(Asin(G+QEKW(C+KWS))+Bsin(G+QELW(C+LW S))+Nsin(G+QEMW(C+MWS))+Bsin(G+QE(1-L)W(C+(1-L)WS))+Asin(G+QE(1-K)W(C+( 1-K)WS))) →Y:G+QEW(C+WS)+Z[1]→Z[2]:X+Dcos(Z[2])→X:Y+Dsin(Z[2])→Y9. 反算子程序(B)程序名:BG-90→T:Abs((Y-V)cos(T)-(X-U)sin(T)) →W:0→D:Lbl 0:Prog "A":T+QEW(C+W S) →L:(J-Y)cos(L)-(I-X)sin(L)→D:IF Abs(D)<0.01:Then Goto1:Else W+D→W:Goto 0←┘Lbl 1:0→D:Prog "A":(J-Y)÷sin(Z[2]) →D:10.高程计算子程序(H)程序名:HProg “S0”:R:T:C:G:I:C-T→F:Z-F→L:C+T→E:G-TI→Q:If T=O:Then Q+LI→H:Goto 0:Else If Z<F:Then Q+LI→H:Goto 0:Else If Z≤E:Then Q+LI+L2÷2÷R→H:Goto 0:LbI 0:H:If D=0:Then Goto I:Else Prog “I”:H+V→H:Goto I:LbI I:H:I:11.高程超高计算程序(I)程序名:IProg”I0”:W=1=> Goto 0:W=2=>Goto 1:LbI 0:If L=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×((N-M)×(Z-C)÷L+M)→V:Goto 2:IfEnd:LbI 1:If L=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×(((3((Z-C)÷L)2-2((Z-C)÷L)∧(3))×(N-M))+M)→V:Goto 2:IfEnd:LbI 2:Abs(D)→E:V÷E→I:I(E-K)→V:12.数据子程序(附后示例)①程序名:X0(坐标计算要素程序)If Z≥25900 And Z≤26615.555:Then 25900→O:11587.421→U:1847.983→V:101。
卡西欧5800边坡测量放样程序隧道测量

卡西欧5800边坡测量程序U″XO″:V″YO″:A″X1″:B″Y1″:POL(G″X2″-A,D″Y2″-B:W=J:I:LBI1:{LKM}:X″XA="=A+LCOSW+KCOS(W+M)◢Y"YA="=B+LSinW+Ksin(W+M)◢POL(S-U),Y-U:J <0=>J=J+36O⊿X″DIX=″=I◢FiX3:O″FW=″=J◢Goto15800边坡测量程序″XO=″?U:″YO=″?V:″X1=″?A:″Y1″?B:″X2″?G:″Y2″?D↙POL(G-A,D-B):J→W:Fix 3:CLS↙Lbi 1 ↙″L=″?L:″K=″?K:″M=″?M↙A+LCOSW+KCOS(W+M)→X↙B+LSinW+Ksin(W+M)→Y↙Cls↙"XA=":Locate 5,1,X:"YA=":Locate 5,2,Y◢Pol(X-U,Y-V):If J <0:Then J+36O→J :Else J→J↙Cls↙″DIX=″:Locate 5,1,I:″FW=″:J▲DMS◢Goto 1程序特点:全线标高数据一次性程序化输入,扩充变量数据库,无需修改程序内容;全线贯通计算,标高计算时将全线数据分为4等分,首先判断待求点在哪个区间,再循环选择,提高运算时间;傻瓜操作,适用初级用户。
一、程序:M CW“1.BG 2.SZ ”:W=1=> Goto 1ΔO“KOU LING”:O≠1 23456=>O=0:Goto 5ΔO=0:Z[1]=0: Goto 0←┘Lbi 0←┘”No.”:Z[1]+1◢{ZHPR}:Z“D0” :H“BG” :P“PD” :R“R0” :Z[Z[1]×4+ 3]=Z:Z[Z[1]×4+4]=H:Z[Z[1]×4+5]=P:Z[Z[1]×4+6]=R:“NEXT”◢Isz Z[1]:Goto0←┘Lbi 1←┘Z[2]= Z[1]←┘{D}:D≤Z[Int(Z [2]÷4+1)×4+3]=>Z[2]= Int(Z [2]÷4) :Goto2ΔD≤Z [Int (Z[2] ÷2+1)×4+3]=>Z[2]=Int(Z[2]÷2):Goto2ΔD≤Z [Int (Z[2]×.75+1)×4+3]=>Z[2]=Int (Z[2]×.75):Goto2ΔGoto 2←┘Lbi 2←┘D<Z[Z[2]×4+3]=>Dsz Z[2]:Goto 2ΔGoto 3←┘Lbi 3←┘Z[Z[2]×4+6]≠0=>G=Z[Z[2]×4+4]+(D-Z[Z[2]×4+3])×Z[Z[2]×4+ 5]÷100+(D-Z[Z[2]×4+3]) ^2÷2÷Z[Z[2]×4+6]:Goto 4ΔG=Z[Z [2]×4+4]+(D-Z[Z[2]×4+3])×Z[Z[2]×4+5]÷100:Goto 4←┘Lbi 4←┘{Z}:Z:G=G-0.02Abs(Z):“G”: G◢(4850输出){Z}:Z:G=G-0.02Abs(Z): G“G”◢(4800输出)Goto 1←┘Lbi 5←┘“OUT”◢程序操作说明程序分为两部分:1.BG为标高计算,2.SZ为参数设置。
卡西欧4500、4800、5800高程程序

竖曲线高程的计算公式1.在直线段上的计算公式:H=G±(K-B)*I2.在曲线段上的计算公式:H=G±(K-B)*I+N(K-Z)2/2R式中:K—待求点的桩号Z—直圆点桩号R—曲线半径H—待求点的高程G—变坡点的高程B—变坡点的桩号I —纵坡度N—常数(凸为-1,凹为+1)4500竖曲线计算实例Lbl 0{K}Lbl 1K≤A→H=G1+(K-变坡点1桩号)*I▲≠→Goto 2△Goto 最后一行Lbl 2K≤B→H=G1+(K-变坡点1桩号)*I-(K-A)2/2R ▲≠→Goto 3△Goto 最后一行Lbl 3K≤C→H=GJD1+(K-JD1桩号)*I▲≠→Goto 4△Goto 最后一行Lbl 4K≤D→H=GJD1+(K-JD1桩号)*I+(K-C)2/2R ▲≠→Goto 5△Goto 最后一行以此类推············Lbl 最后一行U=Y-(H-0.7+1.25*0.18+1.1*0.02) ▲V=U+0.02*14.03 ▲Goto04800竖曲线计算实例Lbl 0{k}Lbl 1K≤A→H=G1+(变坡点1桩号-K)*I▲≠→Goto 2△Goto 最后一行Lbl 2K≤B→H=G2+(变坡点2桩号-K)*I-(K-A)2/2R ▲≠→Goto 3△Goto 最后一行Lbl 3K≤C→H=GJD1+(K-JD1桩号)*I▲≠→Goto4△Goto最后一行Lbl 4K≤D→H=GJD1+(K-JD1桩号)*I+(K-C)2/2R ▲≠→Goto5△Goto最后一行以此类推············Lbl 最后一行U=Y-(H-0.7+1.25*0.18+1.1*0.02) ▲V=U+0.02*14.03 ▲Goto 05800竖曲线计算实例“SQXJSCX”↙Lb1 1↙CLs:Fix 3↙“K=”?k◢(计算点里程输入)If k<67549.755 AND K≥66894.3 :Then -0.00052→A : 0→B : 67394.3→S : 67.37→G : 600000→R : Goto 2 : IfEnd↙If k<68708.391 AND K≥67549.755 :Then -0.0048→A : -0.00052→B : 68494.3→S :66.8→G : 100000→R : Goto 2 : IfEnd↙If k<本段竖曲线终点里程AND K≥前一竖曲线终点里程:Then -0.0048→前坡(大里程向)A : -0.00052→后坡(小里程向)B : 68494.3→竖曲线交点里程S :66.8→交点高程G : 100000→曲率半径R : Goto 2 : IfEnd↙………依次类推,计算原始数据完成输入,坡度换算成小数。
5800线元法修正版程序编写

5800线元法修正版程序编写1.2版本,添加了遗漏的标点符号,修改了竖曲线与隧道,让隧道测量步骤简化一些。
此程序根据4850线元法程序改编,本人第一次编写程序内容可能有些不尽人意敬请谅解.程序名称不可更改,包括符号,也不要擅自删减子程序,如需更改必须与各子程序相呼应,否则将无法调动程序进行计算。
1~16页为程序说明与应用步骤具体解释,17~26页为程序编写,所有S开头后面有横杠的为各项数据库,如换线路更改数据库即可完成各项计算。
注意:程序编写时有下划线字符为一次性输入字符,不可拆分。
置仪点X坐标输入时必须输入小数,如果无小数将默认调动导线点数据库(例如3843.000那么请输入3843.0001并不影响计算)程序名(0-0)主程序目录(U=1):数据库输入原始数据计算中边桩*(U=2): 数据库输入原始数据反算线外点垂桩距状态(线路任一点坐标反算桩号及偏距)*(U=3):计算平面位置检查记录表(U=4):人工输入原始数据计算中边桩(数据库计算线元方位角)* (U=5):人工输入原始数据推算开挖、填筑桩状态(不常用)(U=6):数据库输入原始数据推算开挖、填筑桩状态*(U=7/7.1):计算斜交斜做涵洞单跨桥、斜交正做涵洞七点放样状态并能避免曲线内单跨桥涵进出水口长度不一致,同时适用于曲线桥扇形布桩的盖梁放样,曲线桥扇形布桩的支座放样。
*(U=8): 数据库输入原始数据计算锥坡放样(U=9): 后方交会(U=10): 数据库输入原始数据求线外两点交路线的桩号与夹角(U=11): 圆心辐射法隧道断面超欠挖(适合各种隧道线型)*(U=12): 手动输入原始数据求多边型面积、亩数*(U=13): 数据库输入原始数据求设计高程(竖曲线)*(U=14): 坐标正反算小程序(U=1)数据库输入原始数据计算中边桩(Y)置仪点X坐标(也可输入导线点编号,输入导线点编号即可使用导线点数据库)(O)置仪点Y坐标(当X坐标输入导线点编号后则此行不显示,因数据库已装入X和Y坐标)(B)步长(步长就是间隔长度,当要计算大量有相同距离间隔且相同中边桩,步长就是好东西了,输入数量每次计算自动加减桩号距离)(Q)所求桩号(计算第二个桩开始Q已经自动加入步长不用手动输入,但仍然会显示给你看,并可修改成别的桩号)(V)中桩到边桩的方位角,即与中桩前进方向方位角的夹角(注意:左转为负数,右转为正数)(D)中桩到边桩的距离(中桩输入0)计算完成会显示四个成果:DMS放样方位角(置仪点与所求桩号的放样方位角)I放样距离(置仪点与所求桩号的放样距离)所求桩号的X坐标所求桩号的Y坐标按—号继续下一步放样计算(U=3)数据库输入原始数据计算中边桩(偏差检测、资料编写)(B)步长(步长就是间隔长度,当要计算大量有相同距离间隔且相同中边桩,步长就是好东西了,输入数量每次计算自动加减桩号距离)(MM)所允许的最大误差(毫米为单位,比如高速的中线最大误差是20MM,就输入20)(Q)所求桩号(计算第二个桩开始Q已经自动加入步长不用手动输入,但仍然会显示给你看,并可修改成别的桩号)(V)中桩到边桩的方位角,即与中桩前进方向方位角的夹角(注意:左转为负数,右转为正数)(D)中桩到边桩的距离(中桩输入0)计算完成会显示四行成果:DMS放样方位角(置仪点与所求桩号的放样方位角)I放样距离(置仪点与所求桩号的放样距离)所求桩号的X坐标所求桩号的Y坐标按(—)号显示偏差检测成果:所求桩号的X坐标所求桩号的Y坐标所求桩号的双轴偏差X轴偏差Y轴偏差按-号下一步计算(U=4)人工输入原始数据计算中边桩(线元角计算)(Y)置仪点X坐标(O)置仪点Y坐标(B)步长(H+)起算点桩号(E)起算点X坐标(F) 起算点Y坐标(A)起算点方位角(+-C)起算点曲率(即为半径分之一,也就是1/半径,直线为0,左转为负,右转为正)(+-Z)终算点曲率(即为半径分之一,也就是1/半径,直线为0,左转为负,右转为正)(G)终算点桩号(Q)所求桩号(既是起算点桩号,因程序内字符转换冲突只好再输入) (V)左右夹角(左转为负,右转为正,中桩输入0)(D)中边桩距离(中桩输入0)计算完成会显示四个成果:(此处可忽略,参照U=1计算成果)计算完成按(AC/on)一次,然后按(EXIT)将内容(Prog 0-0)清除输入字母(R),再按(EXE)显示为线元方位角数字(注:必须用度,分,秒抄记,因为计算结果为百进位,度分秒为60进位)注:此计算成果谨适用于数据库线元角输入(即:数据库曲线段线元角ZH~HY、HY~YH、YH~HZ段)(U=5):人工输入原始数据推算开挖、填筑桩状态(不常用)(Y)置仪点X坐标(O)置仪点Y坐标(H+)起算点桩号(E)起算点X坐标(F) 起算点Y坐标(A)起算点方位角(+-C)起算点曲率(即为半径分之一,也就是1/半径,直线为0,左转为负,右转为正)(+-Z)终算点曲率(同上)(G)终算点桩号(W)实测大地高程(S)变坡点设计高程(I) =变坡点设计高程与实测大地高程之高差(正为填方、负为挖方)(P) 填方或挖方的坡比(若1:0.75则输入0.75填挖坡比全为正)(B)中桩到变坡点的宽度(D)=推算的中桩到开挖、填筑桩距离(D?)采用的中桩到开挖、填筑桩距离(Q)所求开挖、填筑桩号(V)左右夹角(注:只能输入线路右边90和左边-90因为开挖、填筑桩总是垂直的)计算完成显示四个结果:(同U=6显示结果相同,按—号下一步计算)(U=6):数据库输入原始数据推算开挖、填筑桩状态(Y)置仪点X坐标(O)置仪点Y坐标(W)实测大地高程(S)变坡点设计高程(距离地面最近的那个平台或路面高程)(I)=变坡点设计高程与实测大地高程之高差(自动计算所得结果,此处不需输入。
CASIO-fx-4850P-4800p-5800P-9750GⅡ程序运行示例及说明

程序运行示例及说明运行主程序“LQXJS”一、任意点坐标计算(道路、桥、涵)第一步:Z? 1(进入道路、桥、涵任意点坐标计算).第二步:A? 742589.425(输入起点的“X”坐标).第三步:B? 463404.387(输入起点的“Y”坐标).第四步:C? 15°23′31.7″(输入起点的方位角).第五步:D?1÷340 (输入起点曲率).第六步:E? 1÷2286.5(输入终点曲率).第七步:F? 714.188(输入起点桩号).第八步:G? 890.019 (输入终点桩号)第九步:H? 800 (输入待求点桩号)第十步:S? 0((输入待求点至中桩的距离(中心桩为“0”、左为“-”右为“+”) 第十一步:U=26°50′56.17″ (待求点所计算的切线方位角).第十二进步:X=742669.0657 (显示待求点所计算的“X”坐标).Y=463435.9536(显示待求点所计算的“Y”坐标).第十三步:Q? 1(输入“1”时返回第九步,再重复步骤第十步~十三步计算各点的道路坐标;当输入“0”时进入桥、涵坐标计算,再继续下面步骤).第十四步:P? 135(输入桥、涵中心点处纵向轴线(路线前进方向)与横向轴线(从左到右方向)之间的夹角.如图).第十五步:K? 0(输入桥、涵中心点处纵向轴线(路线前进方向)偏离切线方向的偏角(左“-”右“+”)如图). 第 107頁第十六步:J? 8(输入桥、涵的垂直跨距(桥、涵各点至中心处横向轴线的垂直距离的2倍)).第十七步:W? 20 (输入桥、涵上各点至纵向轴线(路线前进方向)的垂直距离(左“-”右“+”)如图). 第十八步: M? 1(计算以桥涵中心处横轴线为界在前面各点的坐标;(M=1为前面、M=-1为后面、M=0 为横轴线)如图).第十九步:L=742647.2359(显示待求点所计算的“X”坐标).N=463447.3197(显示待求点所计算的“Y”坐标).第二十步:返回第十六步,再根据需要计算各点坐标.第二十一步:J、W同时输入“0”则可以退出桥、涵坐标计算,并返回到程序第九步状态.二、坐标反算桩号、距离第一步:Z? 2(进入坐标反算桩号、距离).第二步:A? 742589.425(输入起点的“X”坐标).第三步:B? 463404.387(输入起点的“Y”坐标).第四步:C? 15°23′31.7″(输入起点的方位角).第五步:D?1÷340 (输入起点曲率).第六步:E? 1÷2286.5(输入终点曲率).第七步:F? 714.188(输入起点桩号).第八步:G? 890.019 (输入终点桩号)第九步:J? 742669.0657(输入已知点X坐标).第十步:P? 463435.9536(输入已知点Y坐标).第十一步:H=800(显示待求点所计算的里程桩号)..第十二步:S=0 (显示待求点所计算的距离左为“-”、右为“+”)第十三步:返回第九步.三.曲率判断方法1.直线段计算时: D=0:E=02.圆曲线段计算时:D=1÷R:E=1÷R(左“-”,右“+”)3.直缓段计算时: D=0:E=1÷R(左“-”,右“+”)4.缓直段计算时: D=1÷R:E=0(左“-”,右“+”)5.非完整型缓和曲线段计算时:D=1÷R1:E=1÷R2(左“-”,右“+”)H H(X、Y)N=1 时U ZCR纵向轴线横向轴线KPM=1M=-1M=OJS(J、P)N=2 时H UUw(L、N)起点(A,B)FD G E。
卡西欧计算器5800测量放样程序

卡西欧5800程序(修改于湘桂)R(主程序,通过里程求中桩、边桩坐标,在输入测站坐标后并求极坐标放样要素)1→M :“NEWZ CIRCLE”?M : If M=-1: Then “JD”?U :“1-TR-1-TL” ? N : “AT ” ? O : “JX” ? S : “JY ” ? P : “L0 ” ? H : “R” ? R : “ZJ” ? A : IfEnd↙“OPP NAME ”?W : If W=-1 : Then “OPPX”?B : “OPPY”?C : Else Prog“CONTREL”:IfEnd↙Lbl 0: “C”?K : If Int(K÷1000)>0 : Then Int(K÷1000)→V :Else “V”?V :K+1000V→K:IfEnd↙If M=1:Then Prog“CIRCLE” IfEnd↙H÷2-H^(3)÷(240R2)+(R+H2÷(24R))tan(A÷2)→T:πR(A-180H÷π÷R)÷180+2H→L↙U-T→G:K→Q↙If Q≤G+L÷2:Then Q-G→Q: Else G+L-Q→Q: IfEnd↙If Q<0:Then Prog “L”:Goto1: IfEnd↙If Q≤H:Then Q-Q^(5)÷(40R2H2)→X:Q^(3)÷(6RH)-Q^(7)÷(336R^(3)H^(3)) →Y:90Q2÷(πRH) →F: Else 180(Q-H÷2)÷(πR) →F:Rsin(F)+H÷2-H^(3)÷(240R2) →X:R(1-Cos(F))+H2÷(24R) →Y: IfEnd↙Pol(T-X,Y) ↙If K≤G+L÷2:Then O-180-NJ→E:NF+O→F: “F=”:F▲DMS◢ ElseNA+NJ+ O→E: O+NA-NF→F: “F=”:F▲DMS◢IfEnd↙“X=”:S+Icos(E)→X◢“Y=”:P+Isin(E)→Y◢If F<0:Then 360+F→F: IfEnd↙If F≥360:Then F-360→F: IfEnd↙Lbl1: “÷1”?Z: If Z=1:Then Prog “I”: IfEnd↙If Z=2:Then Prog “LD”: IfEnd↙If Z=-1:Then Prog “Q”: “X=”:X◢“Y=”: Y◢IfEnd↙Prog “P”↙Goto 0↙P(子程序,受主程序R调用,求极坐标放样要素:方位角及平距)Pol(X-B,Y-C): “D=”:I◢If J<0:Then 360+J→J: Else 0+J→J: IfEnd↙“AQ=”:J▲DMS◢L(子程序,受主程序R调用,求直线上点位坐标及切线方位角)T-Q→Q:If K<G:Then O+180→E: O→F: “X=”:S+Qcos(E)→X◢“Y=”:P+Qsin(E) →Y◢ Else O+NA→F: “X=” S+Qcos(F) →X◢“Y=”:P+Qsin(F) →Y◢IfEnd↙I(子程序,受主程序R调用,求边桩坐标)“RA”?E:“D”?D:E+F→E: If E≥360:Then E-360→E: IfEnd↙X+Dcos(E)→X: Y+Dsin(E)→Y: “X=”: X◢“Y=”: Y◢E→F↙Q(子程序,受主程序R调用,求副线边桩坐标)“1A”?E:“1D”?D:E+F→E↙X+Dcos(E)→X: Y+Dsin(E)→Y:E→F↙“2R”?E: “2D”?D: E+F→E↙X+Dcos(E)→X: Y+Dsin(E)→Y↙E→F↙LD(子程序,受主程序R调用,通过坐标反求里程和偏距)40→DimZ↙O→Z[1]:U→Z[2]:S→Z[3]: P→Z[4] ↙H÷2-H^(3)÷(240R2)→M: H2÷(24R)-H^(4)÷(2688R^(3))→V:90H2÷(πR)→D:(R+V)Tan(A÷2)+M→T: πRA÷180+H→K:O+NA→J:Prog“JD”:J→Z[21]:U-T+K→Z[22]: S-Tcos(O)→Z[5]:P-Tsin(O)→Z[6]:Z[5]+Mcos(O)+(R+V)cos(O+90N)→Z[7]:Z[6]+Msin(O)+ (R+V)sin(O+90N)→Z[8] ↙H-H^(5)÷(40R2H2)→Z:H^(3)÷(6RH)-H^(7)÷(336R^(3)H^(3))→C: Pol(C,Z):90-J→J:Prog“JD”: O+JN→J:Prog“JD”↙Z[5]+Icos(J)→Z[9]:Z[6]+Isin(J)→Z[10]:S+Tcos(Z[21])→Z[11]: P+Tsin(Z[21])→Z[12] ↙Pol(Z[10]-Z[8],Z[9]-Z[7]):90-J→J:Prog“JD”:J→Z[13] ↙J+(A-2D)N→J: Prog“JD”: J→Z[14] ↙“CEDIAN”◢Lbl 0: ↙“B”?B:If B=0:Then Prog “R”: IfEnd↙“XN=”?X: “YN=”?Y:Pol(Y-Z[8],X-Z[7]) ↙90-J→J: Prog“JD”:J→W:J-Z[13]→J↙Prog“JD”:J→Z[15] ↙W-Z[14]→J↙Prog“JD”:J→Z[16] ↙If N=1:Then Goto 1: IfEnd↙If N=-1:Then Goto 2: IfEnd↙Lbl 1: ↙If Z[15]>180:Then Goto 3: IfEnd↙If Z[16]≤180:Then Goto 5:Else Goto 4 : IfEnd↙Lbl 2: ↙If Z[15]<180:Then Goto 3: IfEnd↙If Z[16] >180:Then Goto 5:Else Goto 4 : IfEnd↙Lbl 3: ↙“H1”◢Pol(Y-Z[6],X-Z[5]):90-J→J: Prog“JD”↙J-Z[1]+90→J: Prog“JD”↙Isin(J)→G↙If G>0:Then 0→L:Goto 6: IfEnd↙If G≤0:Then “DK=”:Z[2]-T+G→Z[19]◢If N=1:Then “LD=”:-NIcos(J)→Z[20]◢Else “LD=”:NIcos(J) →Z[20]◢IfEnd↙“SD=1,LD≠1”?D:If D=1:Then Prog “SDCQJC”: IfEnd↙Goto 0↙Lbl 4: ↙“Y”◢If N=-1:Then 360-Z[15]→Z[15]: IfEnd: “DK=”:Z[2]-T+H+πR(Z[15])÷180→Z[19]◢If N=1:Then “LD=”:-(I-R)→Z[20]◢Else “LD=” :I-R→Z[20]◢IfEnd↙“SD=1,LD≠1”?D:If D=1:Then Prog “SDCQJC”: IfEnd↙Goto 0↙Lbl 5: ↙“H2”◢Pol(Y-Z[12],X-Z[11]):90-J→J: Prog“JD”:J→W:Z[21]-90→J: Prog“JD”:W-J→J: Prog“JD”:Isin(J)→G:If G<0:Then 0→L: -G→G↙Goto 7: IfEnd↙If G≥0:Then “DK=”:Z[22]+G→Z[19]◢IfEnd: If N=1:Then “LD=”:-NIcos(J)→Z[20]◢Else “LD=”:NIcos(J)→Z[20]◢IfEnd↙“SD=1,LD≠1”?D:If D=1:Then Prog “SDCQJC”: IfEnd↙Goto 0↙Lbl 6: ↙L+G→L:L-L^(5)÷(40R2H2)→Z:L^(3)÷(6RH)-L^(7)÷(336R^(3)H^(3)) →C:Pol(C,Z):90-J→J: Prog“JD”:J→W:Z[1]+WN→J: Prog“JD”:Z[5]+Icos(J)→Z[17]: Z[6]+Isin(J) →Z[18] ↙J+2WN→J: Prog“JD”:J-90→J: Prog“JD”:J→W↙Pol(Y-Z[18],X-Z[17]):90-J→J: Prog“JD”↙J-W→J: Prog“JD”:Isin(J)→G:If Abs(G)>0.001:Then Goto 6: IfEnd↙“DK=”:Z[2]-T+L+G→Z[19]◢If N=1:Then “LD=”:-Ncos(J) →Z[20]◢Else“LD=”:NIcos(J) →Z[20]◢IfEnd↙“SD=1,LD≠1”?D:If D=1:Then Prog “SDCQJC”: IfEnd↙Goto 0↙Lbl 7: ↙L+G→L:L-L^(5)÷(40R2H2)→Z:L^(3)÷(6RH)-L^(7)÷(336R^(3)H^(3)) →C:Pol(C,Z):90-J→J: Prog“JD”:J→W:Z[21]-180-WN→J: Prog“JD”↙Z[11]+Icos(J)→Z[17]:Z[12]+Isin(J)→Z[18]:J-2WN→J: Prog“JD”↙J-90→J: Prog“JD”:J→W↙Pol(Y-Z[18],X-Z[17]):90-J→J: Prog“JD”↙J-W→J:Prog “JD”↙Isin(J)→G: If Abs(G)>0.001:Then Goto 7:IfEnd↙“DK=”:Z[22]-L-G→Z[19]◢If N=1:Then “LD=”:NIcos(J)→Z[20]◢Else“LD=”:-NIcos(J) →Z[20]◢IfEnd↙“SD=1,LD≠1”?D:If D=1:Then Prog “SDCQJC”: IfEnd↙Goto 0↙JD(子程序,受LD程序调用,计算角度归化值)If J<0:Then J+360→J: IfEnd↙If J≥360:Then J-360→J: IfEnd↙CIRCLE(子程序,线路平面曲线要素,受主程序R调用)If K≤缓直点里程:Then 交点里程→U:交点X坐标→S:交点Y坐标→P:转角值→A:-1(曲线段左偏)或1(曲线段右偏)→N:圆曲线半径→R:缓和曲线长→H:直线段起始方位角→O:Goto 1: IfEnd↙If K≤……(同上输完全部曲线要素为止)Lbl 1↙CONTREL(控制点坐标数据库子程序,受主程序R和ZBFS调用)If W=控制点点号:Then 控制点X坐标→B:控制点Y坐标→C: IfEnd↙If W=……(同上输完全部控制点数据为止)ZBFS(主程序,求两已知点方位角及平距,或已知两点求后方交会点坐标)Lbl 0:1→W: “NEW OPP”?W:If W=1:Then “OPPX”?X: “OPPY”?Y:Else Prog “CONTREL”:B→X:C→Y: IfEnd↙Lbl 1:-1→W: “NEW CPP”?W: If W=-1:Then “CPPX”?S: “CPPY”?T: Else Prog “CONTREL”:B→S:C→T: IfEnd↙Pol(S-X,T-Y): “D=”:I◢If J<0:Then J+360→J: Else 0+J→J: IfEnd↙“AQ=”:J▲DMS◢Lbl 2:0→W: “ZBFS=0,SQS≠0”?W:If W=0:Then Goto 1: Else Prog “SQS”: IfEnd↙Goto 0↙SQS(子程序,受主程序ZBFS调用,通过角度边长求交会点坐标值)Lbl 0: “S1=”?A: “J1=?M: “J2=”?N: “S2=?D:N-M→Q: If Q <0:Then Q+360→Q: IfEnd↙If Q<45°0′0″:Then “ERROR PLEASE REPEAT”◢Goto 0: IfEnd↙√(A2+D2-2ADos(Q))→E: “S3=”:E◢If Abs(A-D)≥60:Then “ERROR PLEASE REPEAT”◢Goto 0: IfEnd↙If Abs(I-E)<0.01:Then cos-1((A2+E2-D2)÷(2AE))→R: cos-1((D2+E2-A2) ÷(2DE))→G: Else “ERROR PLEASE REPEAT”◢Goto 0: IfEnd↙If J<0:Then J+360→J:IfEnd↙(X+Acos(J+R)+S+Dcos(J+180-G))÷2→F: “X=”:F◢(Y+Asin(J+R)+T+Dsin(J+180-G))÷2→P: “Y=”:P◢SQX(主程序,竖曲线求线路各里程点中桩设计高程)1→S:“NEWZ SQXK”?S: If S=-1:Then ?U:?R:?T:?N:?I:?F: “HB”?B: IfEnd↙Lbl 0: “C”?K : If Int(K÷1000)>0 : Then Int(K÷1000)→V :Else “V”?V :K+1000V→K:IfEnd↙If S≠-1:Then Prog “SQXK”: IfEnd↙U-T→G:K→Q: If Q≤G:Then Q-U→Q: Else Q-G→W: IfEnd↙If Q≤G:Then “H=”:B+QN÷1000→H◢Goto 1↙Else If Q≤U+T:Then “H=”:B+(Q-U)N÷1000+FW2÷(2R)→H◢Goto 1↙Else If Q≥U+T:Then “H=”:B+(Q-U)I÷1000→H◢Goto 1:IfEnd↙Lbl 1: “P”?P: “O=”:H-P→O◢Goto 0↙SQXK(子程序,受主程序SQX调用,竖曲线要素)If K≤竖曲线圆直点里程:Then 变坡点里程→U:变坡点设计高程→B:竖曲线圆曲线半径→R:竖曲线切线长→T:竖曲线直线段坡度常数(上、下坡有正负之分)→N:变坡点常数(凸为-1,凹为1)→F: Goto 0: IfEnd↙If K≤……(同上输完全部竖曲线要素为止)Lbl 0↙SDCQJC(子程序,受LD程序调用,采集隧道支护位置坐标高程数据一次性计算出该支护位置的超欠挖量)40→DimZ↙Lbl 0:Z[19]→Z[23]:Prog “SQXZ”↙Z[24]-Z[27]→Z[30]: Z[23]→Z[31] ↙If Z[31]≤Z[30]:Then Z[31]-Z[24]→Z[31]:Else Z[31]-Z[30] →Z[32]: IfEnd↙If Z[31]≤Z[30]:Then Z[25]+(Z[31])×(Z[28])÷1000→Z[33]: Goto 1↙Else If Z[31]≤Z[24]+Z[27]:Then Z[25]+(Z[31]-Z[24])×(Z[28])÷1000+(Z[29])×(Z[32])2÷(2×Z[26])→Z[33]: Goto 1↙Else If Z[31]≥Z[24]+Z[27]:Then Z[25]+(Z[31]-Z[24])×I÷1000→Z[33]: Goto 1: IfEnd↙Lbl 1: “H0=”:Z[33]+内轨面至圆心高差常数→Z[33]◢“HN”?K: “Δh=”:K-Z[33]→Z[34]◢If Z[20]≥隧道中心线与设计中心线的偏移量ω:Then Z[20]-ω→Z[35]:Else ω- Z[20]→Z[35] : IfEnd↙“RN=”:√((Z[34])2+(Z[35])2)→Z[36]◢“R0”?Z: “RCQ=”: Z[36]-Z→Z[37]◢SQXZ(子程序,受主程序SDCQJC调用,竖曲线要素)40→DimZ↙If Z[23]≤竖曲线圆直点里程:Then 变坡点里程→Z[24]:变坡点设计高程→Z[25]:竖曲线圆曲线半径→Z[26]:竖曲线切线长→Z[27]:竖曲线直线段坡度常数(上、下坡有正负之分)→Z[28]:变坡点常数(凸为-1,凹为1)→Z[29]:IfEnd↙If Z[23]≤……(同上输完全部竖曲线要素为止)Lbl 0↙。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
功能与应用
在锥坡施工放样中,不少人还在用“拉线法”、“图解等比例量距法”等原始方法进行放样。
本节介绍了一种全新的锥坡放样方法,可用下述程序配合全站仪对各种正、斜交锥坡放样。
大大减轻了放样人员的内外业劳动强度,减小了出错机率。
特别是对斜交锥坡放样,其先进性和便捷性更是无与伦比。
基本原理与基本公式
基本原理:为使路堤与桥台或挡土墙墙面等构造物连接处圆滑过渡,并使水流通畅,需在构造物两侧构筑呈锥体型土坡体,且为了保证构造物靠流水一侧不受冲刷侵蚀,故在其表面砌石防护,称为锥坡。
锥坡的形状为四分之一个椭圆截锥体,当锥坡的填土高度小于6m时,锥坡的纵向即平行于路线方向的坡度一般为1:1;横向即垂直于路线方向的坡度一般为1:,与路基边坡一致。
当锥坡的填土高度超过6m时,路基面以下超过6m的坡体纵向由1:1变为1:,横向由1:变为1:。
因为锥坡程序在本书中为非重点内容,故本程序中未考虑“二级变坡”,请使用者注意,如果在应用中出现“二级变坡”的情况,可先计算出椭圆的长、短半轴后,再将其换算成一个直坡,运行本程序,同样可精确求解。
锥坡的常用测量方法有:椭圆曲线内侧支距法、椭圆曲线外侧支距法、纵横等分图解法、双点双距图解法、双圆垂直投影图解法等,本书中是采用的椭圆曲线内侧支距法计算椭圆纵横支距参数,然后用坐标转化公式将其转化为大地坐标,可以将全站仪置于导线点上直接施测。
基本公式:
椭圆方程为:
图6-3 椭圆内侧支距法(正交)
根据坡比,椭圆长半轴为a=i1×(H S-H J),短半轴为b=i2×(H S-H J)。
令长半轴a上某点到锥尖的距离为n,如果构造物为斜交时,令斜角为α0。
如图6-3所示,正交时α0=0,于是在长半轴上距锥尖na处的横、纵支距分别为:
再用坐标转换公式
将其转换成施工坐标。
式中X、Y——在长半轴上距锥尖na处的大地坐标
x zj、y zj——锥尖处大地坐标(作起算值)
x、y——在长半轴上距锥尖na处的横、纵支距
α——锥尖沿短半轴方向的方位角
源程序
程序名:【CONIC PITCHING】
Lbl0
Norm:Deg
"X0" D : "Y0" G: "AZIMUTH"A:"α0"B : "HS"H : "HJ" I: "i1" K: "i2" L: " " Z
0→ J: 0→ N:Goto2
Lbl1
“N”N
N<0=>Goto0
N>1=>Goto0
Lbl2
J+1→J◢………………………………显示坐标值的组数
K(H-I)N÷cosB→E: L(H-I)√(1-N2)→ F………计算纵横支距值
Z=2=>E→(-E)……………………判定锥坡在桥台的左右方向
Fix3
D+Ecos(A+90+B)+FcosA→ X◢………将支距转换成X坐标并显示
G+Esin(A+90+B)+FsinA→ Y◢………将支距转换成Y坐标并显示
J≥15=>Goto1……如果算完第15组,N=1则转到标记1处运行
If N≥.9:ThenN+.02→ N: Goto2 :IfEnd…………………………如果在~1之间则以为步长加密并转到标记2处运行
If N≥0:ThenN+.1→ N:Goto2:IfEnd……………………………如果在0~之间则以为步长计算并转到标记2处运行
程序说明
一、程序中各注释文的涵义
X0、Y0——锥坡尖点的横、纵坐标
HS——锥坡尖点的标高
HJ——锥坡基础顶面标高
i1——路基坡度,如果为1:则输入为
i2——锥坡迎水面坡度,如果为1:1则输入为1
AZIMUTH——锥尖沿短半轴方向指向锥坡边缘方向的方位角
α0——构造物与路基法线方向交角,左斜为正,右斜为负。
如图6-5。
——如果要放样的锥坡为左侧锥坡则输为1,反之输为2
n——为椭圆长半轴等分数,其值应在0~1之间。
当n值输入的间隔越密集,则测出的点就越密集。
二、程序应用注意事项
在程序运行后,将直接输出按椭圆长半轴上到锥尖的距离十等分后每个等分点对应在椭圆弧上的坐标,即自动得出从0a、……到、、、、、对应的椭圆弧上共15组坐标值。
考虑到n值在~之间时输出的点间隔较大,
该程序已在~之间按的步长自动加密。
当15组点输出后考虑到有的点位需要复核重放或局部加密的需要,程序还可以根据用户输入的n值任意加密,例如,想在处加密,则输入n=,即可得出椭圆弧上对应于长半轴上处的大地坐标值。
在计算正交时可将α0输入为0,斜交时按图6-5中所示角度输入,当锥坡左斜时,α0应输入为正值,反之为负值。
图6-4 正交桥台锥坡示意图
图6-5 斜交桥台锥坡示意图
应用实例
因为本程序不考虑两级放坡,但可以计算两级放坡。
关于一级放坡的例子就此略过,现在就看看两级放坡用本程序如何计算。
例6-3:有一右斜U型桥台,斜角为30°,锥坡尖点设计标高为HS=,锥坡基础顶面设计标高为HJ=,锥坡尖点在施工坐标系内的坐标(x0,y0)为(,),方位角AZIMUTH=125°39′36″,以6m为变坡点设置两级放坡。
第一级放坡为1:i1=1:;1:i2=1:1,第二级放坡为1:i12=1:;1:i22=1:。
试计算左侧锥坡的放样数据。
解:对于两级放坡的情况,我们可以通过计算将其转化为一单向坡面。
先分别计算椭圆的长、短半轴长。
第一级:a1=i1×6=×6=9m
b1=i2×6=×6=6m
第二级: a2=i12×(H S-H J-6)=× b2=i22×(H S-H J-6)=×故长、短半轴长分别为a=a1+a2=;b=b1+b2=10m
根据单坡面时长半轴a=i1×(H S-H J),短半轴b=i2×(H S-H J)故可得到,在将其折算为单坡面时i1和 i2分别为:i1=÷=;i2=10÷=
再将HS=、HJ=、X0=、Y0=、α0=-30、AZIMUTH=125°39′36″、i1=、i2=、=1逐一输入程序当中,即可算得基础内缘的椭圆弧上各点的坐标值。
其值如下:
POInt=1;X=;Y= POInt=8;X=;Y=
POInt=2;X=;Y= POInt=9;X=;Y=
POInt=3;X=;Y= POInt=10;X=;Y=
POInt=4;X=;Y= POInt=11;X=;Y=
POInt=5;X=;Y= POInt=12;X=;Y=
POInt=6;X=;Y= POInt=13;X=;Y=
POInt=7;X=;Y= POInt=14;X=;Y=
POInt=15;X=;Y=。
