八年级数学等边三角形
人教版八年级数学上册《等边三角形》PPT

探索星空:探究一
等腰三角形有“三线合一”的性质, 等边三角形有“三线合一”的性质吗?
A
那它共有几条中线、高和角平分线?
它们之间有什么关系?
FE
B DC
结论:等边三角形每条边上的中线,高和所对角的
平分线都互相重合。
探索星空:探究二
等边三角形是轴对称图形吗? 有几条对称轴?
对称轴是什么?
A
F
E
B C
= 60°
∴∠A= ∠ B=∠C ∴ AB=AC=BC
A
几何语言:
几何语言:
在△ABC中 ∵AB=AC ∠A= 60° ∴ AB=AC=BC
在△ABC中 ∵AB=AC ∠B= 60° ∴ AB=AC=BC
B
C
练习与巩固
判断对错,并说明理由: 1三条边都相等的三角形是等边三角形。 2有两个角等于60°的三角形是等边三角形。 3有一个角是60°的等腰三角形是等边三角形。 4等腰三角形是等边三角形。
求证:∠A=
∠
B=∠C=
。
60
证明:∵AB=AC (已知)
∴ ∠ B=∠C(等边对等角)
B
C
几何语言:
∵AC=BC (已知) ∴ ∠A= ∠ B(等边对等角)
在△ABC中
∴ ∠A= ∠ B=∠C(等量代换)
∵AB=AC=BC
∵∠A+∠ B+∠C=180 。
∴∠A=
∠
B=∠C=
。
60
∴∠A= ∠ B=∠C= 60。
例4:如图△ABC是等边三角形,DE‖BC,交AB,AC于点D,E。
求证:△ADE是等边三角形。
证明:∵△ABC是等边三角形
A
八年级数学人教版(上册)第1课时等边三角形的性质与判定

C
∴ △ADE 是等边三角形.
侵权必究
讲授新课
变式3 上题中,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由. A
证明:∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
D
E
∵ AD=AE,
B
C
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
等边三角形 三条边都相等的三角形 是等边三角形
三个角都相等的三角形 是等边三角形
小明等认边为三还角有形第的三种判方定法方“法两:条边相等且有一个角是60°的三角 形也是等有边一三个角角形”是,60你°同的意等吗腰?三角形是等边三角形.
侵权必究
讲授新课
归纳总结
等边三角形的判定方法:
三边都相等的三角形是等边三角形.
A.①②③ B.①②④
C.①③
D.①②③④
侵权必究
当堂练习
6.如图,点A,B,C在一条直线上,△ABD,
△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于
点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①
△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;
④MB平分∠AMC,其中结论正确的有( D )
A.1个 B.2个
C.3个
D.4个
侵权必究
当堂练习
7.如图,在△ABC中,∠ACB=90°,∠CAB=30°, 以AB为边在△ABC外作等边△ABD,E是AB的中点, 连接CE并延长交AD于F.求证:△AEF≌△BEC.
证明:∵△ABD是等边三角形, ∴∠DAB=60°, ∵∠CAB=30°,∠ACB=90°, ∴∠EBC=180°-90°-30°=60°, ∴∠FAE=∠EBC. ∵E为AB的中点, ∴AE=BE. 又∵ ∠AEF=∠BEC, ∴△AEF≌△BEC(ASA).
八年级数学上册知识点归纳:等边三角形

八年级数学上册知识点归纳:等边三角形等边三角形英文:equilateraltriangle,“等边三角形”也被称为“正三角形”。
若是一个三角形知足以下任意一条,那么它必知足另一条,三边相等或三角相等的三角形为等边三角形:三边长度相等。
2三个内角度数均为60度。
3一个内角为60度的等腰三角形等边三角形尺规作法其作法相当简单:先用尺画出一条任意长度的线段,等边三角形的尺规作图再别离以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原先线段的两个端点画线段,那么这二条线段和原先线段即组成一正三角形。
等边三角形的性质⑴等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。
⑵等边三角形每条边上的中线、高线和所对角的平分线相互重合⑶等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或对角的平分线所在的直线。
⑷等边三角形的重要数据空间对称群二面体群角和边的数量3施莱夫利符号{3}内角的大小60°⑸等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。
⑹等边三角形内任意一点到三边的距离之和为定值等边三角形的判定⑴三边相等的三角形是等边三角形⑵三个内角都相等的三角形是等边三角形⑶有一个角是60度的等腰三角形是等边三角形两个内角为60度的三角形是等边三角形说明:可第一考虑判定三角形是等腰三角形。
等边三角形的性质与判定明白得:第一,明确等边三角形概念。
三边相等的三角形叫做等边三角形,也称正三角形。
第二,明确等边三角形与等腰三角形的关系。
等边三角形是特殊的等腰三角形,等腰三角形不必然是等边三角形。
等边三角形概念:三条边都相等的三角形叫做等边三角形,“等边三角形”也被称为“正三角形”。
是特殊的等腰三角形。
若是一个三角形知足以下任意一条,那么它必知足另一条,三边相等或三角相等的三角形叫做等边三角形:三边长度相等;2三个内角度数均为60度;3一个内角为60度的等腰三角形。
八年级上册数学等边三角形

八年级上册数学等边三角形一、轴对称图形1. 把一个图形沿着一条直线折叠,如果直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
这时我们也说这个图形关于这条直线(成轴)对称。
2. 把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图关于这条直线对称。
这条直线叫做对称轴。
折叠后重合的点是对应点,叫做对称点3、轴对称图形和轴对称的区别与联系4.轴对称的性质①关于某直线对称的两个图形是全等形。
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
③轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
④如果两个图形的对应点连线被同条直线垂直平分,那么这两个图形关于这条直线对称。
二、线段的垂直平分线1. 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点,在线段的垂直平分线上三、用坐标表示轴对称小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为______.点(x, y)关于y轴对称的点的坐标为______.2.三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等四、(等腰三角形)知识点回顾1.等腰三角形的性质①.等腰三角形的两个底角相等。
(等边对等角)②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
(三线合一)2、等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(等角对等边)五、(等边三角形)知识点回顾1.等边三角形的性质:等边三角形的三个角都相等,并且每一个角都等于600 。
2、等边三角形的判定:①三个角都相等的三角形是等边三角形。
②有一个角是600的等腰三角形是等边三角形。
八年级上册数学-等边三角形
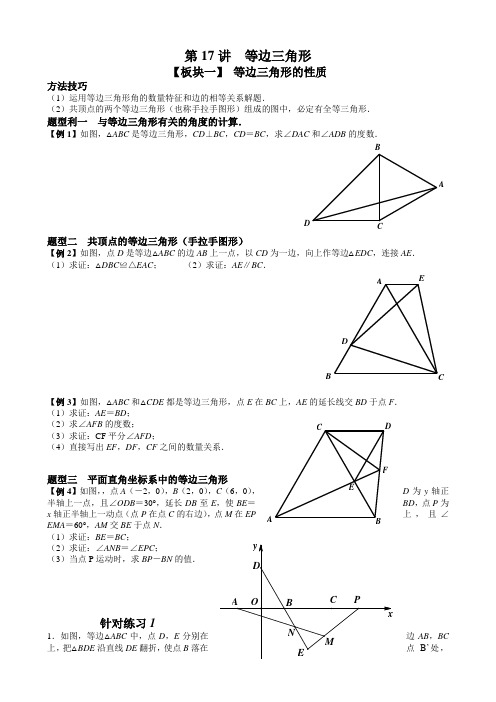
A第17讲 等边三角形【板块一】 等边三角形的性质方法技巧(1)运用等边三角形角的数量特征和边的相等关系解题.(2)共顶点的两个等边三角形(也称手拉手图形)组成的图中,必定有全等三角形.题型利一 与等边三角形有关的角度的计算.【例1】如图,△ABC 是等边三角形,CD ⊥BC ,CD =BC ,求∠DAC 和∠ADB 的度数.AD题型二 共顶点的等边三角形(手拉手图形)【例2】如图,点D 是等边△ABC 的边AB 上一点,以CD 为一边,向上作等边△EDC ,连接AE . (1)求证:△DBC ≌△EAC; (2)求证:AE ∥BC .B【例3】如图,△ABC 和△CDE 都是等边三角形,点E 在BC 上,AE 的延长线交BD 于点F . (1)求证:AE =BD ; (2)求∠AFB 的度数; (3)求证:CF 平分∠AFD ;(4)直接写出EF ,DF ,CF 之间的数量关系.题型三 平面直角坐标系中的等边三角形【例4】如图,,点A (-2,0),B (2,0),C (6,0),D 为y 轴正半轴上一点,且∠ODB =30°,延长DB 至E ,使BE =BD ,点P 为x 轴正半轴上一动点(点P 在点C 的右边),点M 在EP 上,且∠EMA =60°,AM 交BE 于点N .(1)求证:BE =BC ;(2)求证:∠ANB =∠EPC ;(3)当点P 运动时,求BP -BN 的值.针对练习11.如图,等边△ABC 中,点D ,E 分别在边AB ,BC上,把△BDE 沿直线DE 翻折,使点B 落在点B’处,D EDB ’,EB ’分别交AC 于点F ,G ,若∠ADF =80°,求∠EGC 的度数.B'B2.如图,△ABD 和△ACE 都是等边三角形, DC 于BE 交于点M . (1)求证:BE =CD ;(2)求∠AMD 的度数.3.如图1,等边△ABC 中,点D 是AB 上一点,以CD为一边,向上作等边△EDC ,向下作等边△DCF ,连接AE ,BF . (1)求证:AB =AE +BF ;(2)当点D 在BA 延长线上时,如图2,若AE =10,BF =4,求AC 的长.B图1 图24.已知点D ,E 分别是等边△ABC 的边BC ,AB 上的点,∠ADE =60°. (1)如图1,当点D 是BC 的中点时,求证:AE =3BE ; (2)如图2,当点M 在AC 上,满足∠ADM =60°,求证:BE =CM ;(3)如图3,过C 作CF ∥AB 交ED 延长线于点F ,探究线段BE ,CF ,CD 之间的数量关系,并给出证明.BCBCBC图1 图2 图35.在平面直角坐标系中,已知点A 在y 轴的正半轴上,点B 在第二象限,AO =a ,AB =b ,BO 与x 轴正方向的夹角150°,且220a -b a-b . ⑴判断△ABO 的形状;⑵如图1,若BC ⊥BO ,BC =BO ,点D 为CO 的中点,AC 、BD 交于点E ,求证:AE = BE +CE ;图 1⑶如图2,若点E 为y 轴的正半轴上一动点,以BE 为边作等边△BEG ,延长GA 交x 轴于点P ,AP 与AO 之间有何数量关系?试证明你的结论.图 26.△ABC 为等边三角形,BC 交y 轴于点D ,A (a ,0),B (b ,0),且a ,b 满足230a+ . (1)如图1,求点A ,B 的坐标及CD 的长;图 1(2)如图2,P是AB的延长线上一点,点E是CP右侧一点,CP=PE,且∠CPE=60°,连接EB,求证:直线EB必过点D关于x轴对称的对称点;E(3)如图3,若点M在CA的延长线上,点N在AB的延长线上,且∠CMD=∠DNA,求AN-AM的值.【板块二】60°角的用法◆方法技巧◆合理利用60°角构造等边三角形得到相等线段,再进行推理.题型一过60°角一边上一点作平行线构造等边三角形.方法技巧:过60°角一边上一点,作平行线构造等边三角形,转化边与角.【例5】如图,△ABC是等边三角形,点D是AC的中点,点E,F分别在BC,AB的延长线上,∠EDF=120°.(1)求证:DE=DF;(2)若AB=5,求CE-BF的值.A题型二 在60°角的两边上截取两条相等线段构造等边三角形 方法技巧:在60°角的边上截取两条相等线段后构成等边三角形,然后产生新的全等三角形,从而找到解决问题的突破口.【例6】如图,△ABC 为等边三角形,∠ADB =60°. (1)如图1,当∠DAB =90°时,直接写出DA ,DC ,DB 之间的数量关系_______;图 1ABCD(2)如图2,当∠DAB ≠90°时,①中的关系式是否成立?说明理由.图 1ABCD题型三 利用60°角的一边上的点向另一边做垂线构造30°,60°,90°的直角三角形 方法技巧:利用30角所对的直角边等于斜边的一半,作高. 【例7】如图,在△ABC 中,∠B =60°,∠C =45°,AB =2,BC =1 ,求△ABC 的面积.ABC題型四 利用60°角延长构造等边三角形方法技巧;向外延长60”角的一边,在外部构造等边三角形.【例8】已知点D ,点E 分別等边△ABC 边BC ,AC 上的点,CD =AE ,AD 与BE 交于点F .(1)如图1,求∠AFE 的度数;图 1BCAD(2)点G 边AC 中点,∠BFG =120° ,如图2,求证:AF =2FG .图 2BCAD针对练习21.如图,在等边△ABC 中,AC =9,点O 在AC 上,且AO =3,点P 是AB 上一动点,连接OP ,以O 为圆心,OP 长为半径画弧交BC 于点D ,连接PD ,如果PO =PD ,求AP 的长.ABCP2.如图.在等边△ABC 中,∠ABC 与∠ACB 的平分线相交于点O ,且OD ∥AB ,OE ∥AC . (1)试判定△ODE 的形状,并说明你的理由;(2)线段BD ,DE ,EC 三者有什么关系?请说明理由.E DBCA3.点D 为BC 上任一点,∠ADE =60°,边ED 与∠ACB 外角的平分线交于点E ,求证:AD =DE ;BCAD4.已知△ABC 是边长为5的等边三角形.(1)如图1,若点P 是BC 上一点,过点C ,点P 分别作AB ,AC 的平行线,两线相交于点Q ,连接BQ ,AP 的延长线交BQ 于点D .试问:线段AD ,BD ,CD 之间是否存在某种确定的数量关系?若存在,请写出它们之间数量关系并证明你的结论;若不存在,说明理由;图 1QBCA(2)如图2,若点P 是BC 延长线上一点,连接AP ,以AP 为边作等边△APE (点E 、点A 在直线BC 同侧),连接CE 交AP 于点F ,求CE -CP 的值.图 2BCDE5.如图,在△ABC 中,∠BAC =60°,以BC 为边在△ABC 的同侧作等边△DBC ,BD ,AC 相交于点E ,连结AD .(1)如图1,若A 2ACAB,求证:△ABC ≌△ADC图 1CAD(2)如图2,若3AC AB,求ABAD的值. 图 2CAD6.如图1,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE =BD ,连接CE 、DE . ⑴求证:EC =ED ;图 1BDE⑵如图2,EO ⊥CD 于点O ,点N 在EO 上,△DNM 为等边三角形,CM 交EO 于F ,若FO =1,求FM -FN 的值.图 1BDE[板块三) 30°角的用法方法技巧构造30°角的直角三角形,算边长与面积.题型一 已知30°角连线巧得隐直角.【例9】如图,在△ABC 中,AB =AC ,∠C =30°,AB 的垂直平分线交AB 于点D ,交BC 于点E ,试探究BE 与CE 之间的数量关系.BC题型二 利用30°作高构造直角三角形.【例10】如图,CD 是△ABC 的中线,CD ⊥CB ,∠ACD =30°,求证:AC =2BC.DABC题型三 已知30°和90°角补形构造直角三角形 【例11】如图,四边形ABCD 中,∠C =30°,∠B =90°,∠ADC =120°,若AB =2,CD =8,求AD 的长.ACBD题型四 利用底角为15°的等腰三角形构造30°角的直角三角形 【例12】如图,∠AOC =15°,OC 平分∠AOB ,点P 为OC 上一点,PD /∥OA 交OB 于点D ,PE ⊥OA 于点E ,若OD =4cm ,求PE 的长.EOA题型五 利用150°构造30°角的直角三角形【例13】如图,在△ABC 中,AB =AC ,点D 为BC 上一点,以AD 为腰作等腰△ADE ,且AD =AE ,∠BAC =∠DAE =30°,连接CE ,若BD =2,CD =5,求△DCE 的面积.BCADE题型六30°直角三角形斜边上的高方法技巧:30°角的直角三角形斜边上的高中,有3个30°的直角三角形,选取最小的和最大的两个直角三角形进行计算.【例14】如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为点D ,∠A =30°,AD =6,求BC 的长.DABC针对练习31.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米的售价为a 元,求购买这种草皮至少需要多少元?BCA2.在△ABC 中,∠B =30°,AB =AC =8,P 为BC 上一点,求AP 的最小值.ABCP3.如图,在等边△ABC 中,点D 为AC 上一点,CD =CE ,∠ACE =60°. (1)求证:△BCD ≌△ACE ;图1EBCA(2)延长BD 交AE 于点F ,连接CF ,若AF =CF ,猜想线段BF ,AF 的数量美系,并证明你的猜想.图 2BCAE4.如图,在△ABC 中,∠BAC =90°,点D 为三角形内一点,且AB =AC =BD ,∠ABD =30°.求证:AD =CD ,AB C。
人教版八年级数学上册等边三角形

反过来怎么样——逆向思维
命题:在直角三角形中, 如果一条直角边等于斜边 的一半,那么它所对的锐角等于300.是真命题吗? 如果是,请你证明它.
已知:如图,在△ABC中,∠ACB=900,BC= 1 AB.
求证:∠A=300.
2
A
B
C
反过来怎么样——逆向思维
证明:如图, 延长BC至D,使CD=BC,连接AD.
概念 性 质
等 有二 腰 条边 三 角 相等 形
等 有三 边 条边 三 角 轴一条 1、等边对等角 2、三线合一 3、对称轴三条
判定
1、定义 2等角对等边
1定义 2两个角是600 3等腰三角形有一个 600
我能行 3
将两个含有板有30°的三角尺如图摆放在 一起,你能借助这个图形,找到Rt△ABC的直
A 300
C
这是一个通过线段之间的关系来判定 一个角的具体度数(300)的根据之一.
比一比:看 谁 算 的 快
1.如图:在Rt△ABC中 ∠A=300,AB+BC=12cm 则AB=__8___cm B
300
C
A
2.如图:△ABC是等边三角形,
A
AD⊥BC,DE⊥AB,若AB=8cm,
BD=4_c_m_, BE=_2__c_ m E
∴∠A=300(直角三角形两锐角互余).
回顾反思 4
几何的三种语言
定理:在直角三角形中, 如果一条直角边等于 斜边的一半,那么它所对的锐角等于300.
在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直
B
′ 角边等于斜边的一半,那么它所对的锐角
等于300).
人教版数学八年级上册 等边三角形

∵在Rt△ABC 中, ∠C =90°,∠A=30°, ∴
例题 下图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱 BC、 DE 垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC 、 DE 要多长?
答案:3.7m,1.85m.
练习 在Rt△ABC 中,∠C =90° ,∠B=2∠A ,∠B 和∠A各是多少度 ,边AB 和BC 之间有什么关系?
∵∠B=60°
∴∠B=∠C=60°,
∴∠A=60°, ∴∠A=∠B=∠C, ∴△ABC 是等边三角形.
归纳
要判定一个三角形是等边三角形有哪几种方法?
方法一
方法二
方法三
三边相等的 三角相等的 三角形是等 三角形是等 边三角形 边三角形
有一个角是60°的等腰 三角形是等边三角形
例题
如图,△ABC 是等边三角形,DE∥BC, 分别交AB,AC 于点D ,E.求证:△ADE 是等边三角形. 证明: ∵△ABC 是等边三角形, ∴∠A =∠B =∠C =60°. ∵DE∥BC, ∴∠B =∠ADE,∠C =∠AED. ∴∠A=∠ADE =∠AED. ∴△ADE 是等边三角形. 想一想,还有其他证法吗?
证明
等边三角形的每条边上的中线、高和这 条边所对的角的平分线都分别重合.
∵AB=AC,BD=DC ∴∠BAD=∠CAD,AD⊥BC ∵BA=BC,EA=EC ∴∠ABE=∠CBE,BE⊥AC ∵CA=CB,AF=BF ∴∠CAF=∠BAF,CF⊥AB
结论
等边三角形的每条边上的中线、高和这 条边所对的角的平分线都分别重合.
证明
三个角都相等的三角形是等边三角形
已知:△ABC 中,∠A=∠B=∠C. 求证:△ABC 是等边三角形.
人教版八年级数学上册第十三章 等边三角形的性质与判定

3.如何证明“等边三角形每条边上的中线、高和所对角的平分线 都相互重合”.
(借助等腰三角形“三线合一”的性质推理可证)
1.请同学们思考: (1)一个三角形满足什么条件是等边三角形? (①从边看:三条边都相等;②从角看:三个角都相等) (2)一个等腰三角形满足什么条件是等边三角形?
(有一个角是60°的等腰三角形是等边三角形)
3.请同学们完成课本80页例4.
知识点1.等边三角形的定义及性质(重难点)
1.定义:三边都相等的三角形叫做等边三角形,也叫正三角形. 2.性质:(1)等边三角形的三个内角都相等,并且每一个角都
等于60°. (2)等边三角形每条边上的中线、高和所对角的平分 线都相互重合. (3)等边三角形是轴对称图形,它有3条对称轴,分别 为三边的垂直平分线.
1.本节课我们从哪些方面对等边三角形进行了研究? (从等边三角形的性质和判定角度进行研究)
13.3等腰三角形
13.3.2等边三角形
第1课时 等边三角形的性质与判定
1.通过学生自主探究,掌握等边三角形的性质与判定,感受数学的严谨性,发展 学生推理能力.
2.经历“猜想—验证—总结归纳—应用拓展”的探究过程,采用自主探索与合作 交流相结合的方式,亲历“做数学”的过程,培养探究数学问题的能力.
【题型一】等边三角形的性质
例1:如图,等边三角形ABC的两条角平分线BD和CE交于点O,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结核性胸膜炎治疗时应用乙胺丁醇,最易出现的不良反应是A.皮疹B.药物热C.胃肠道刺激D.肾功能损害E.球后视神经炎 加强能源、交通、水利和信息等基础设施建设,增强对的保障能力是我国产业结构调整的方向和重点之一。A.产业技术水平B.资源优化配置C.经济社会发展D.投资政策 急性化脓性腹膜炎的手术指征中,不正确的是()A.原发性腹膜炎B.非手术治疗无效C.中毒症状明显伴休克D.弥漫性腹膜炎无局限趋势E.观察12小时症状及体征加重 难以确诊的急性腹膜炎,最有价值的检查是A.白细胞计数和分类B.血、尿淀粉酶C.直肠指诊D.腹部X线平片E.腹腔穿刺 美国心理学家WoodWorth提出的行为表示式"S-O-R"分别指A.S-see,O-organize,R-respondB.S-sense,O-organize,R-reactC.S-stimulus,O-organism,R-reactionD.S-stimulate,O-organize,R-respondE.S-sensory,O-organism,R-response 脑断层显像所用OM线,是指()A.前额-小脑连线B.眼-枕骨连线C.眼-小脑连线D.眼-耳连线E.垂直于身体长轴的连线 苯巴比妥特殊杂质检查中,中性或碱性物质是指()A.苯巴比妥钠盐B.苯巴比妥酸C.苯基丙二酰脲D.尿素E,2—苯基丁二酰胺和2—苯基丁二酰脲 合同法律关系由哪些要素构成? 关于日本血吸虫的描述下列不正确的是A.是一种人畜共患病B.雌雄异体,合抱寄生C.分布于长江沿岸及以南地区D.钉螺为中间宿主E.成虫及分泌物致病,虫卵不致病 献血者有下列哪种情况不能判定为暂缓献血。A.妇女月经期前后三天B.近五年内输注全血或血液成分者C.分娩未满一年者D.感冒病愈未满一周者E.肺结核未满一年者 深Ⅱ度烧伤创面处理不正确的是。A.1:2000氯己定清洗创面,去除异物B.去除水泡皮C.油质纱布包扎创面D.面部创面不包扎E.创面使用抗生素预防全身感染 VHF是否有麦克风堵塞检查装置A.正确B.错误 马血清抗毒素是A.是抗体,不是抗原B.是抗原,不是抗体C.即是抗体,又是异种抗原D.即非抗原,又非抗体E.是异嗜性抗原 按胸部虚里,其动之微弱者,属A.虚损劳瘵B.心肺气绝C.小儿食滞D.宗气内虚E.痘诊将发 治疗肝性脑病的措施中,下列不属防治氨中毒的一项是A.低蛋白饮食B.使用左旋多巴C.口服抗生素D.服用乳果糖E.滴注乙酰谷酰胺 [单选,案例分析题]女,25岁,左乳痛7天,体温39.5~4℃,局部明显压痛、红肿。如乳腺病灶形成脓肿,最重要的诊断依据为A.局部检查有波动B.穿刺抽出脓液C.局部皮温高D.局部疼痛E.全身症状重 失血性休克的处理原则是A.补充血容量B.尽快止血C.根据微循环状态,选择合适的血管活性药D.使用强心剂E.对难以暂时止血者边补充血容量,边进行根本止血措施 低钾血症心电图最早的改变是A.ST段降低B.T波降低、变平或倒置C.Q-T间期延长D.U波E.QRS增宽 患者,男,36岁,工人,体温40.5℃,面色潮红,皮肤灼热,无汗,呼吸、脉搏增快,自诉在高温下工作5小时。护士此时处置最好的降温方法是()A.用冰槽头部冷敷B.化学冰袋头部冷敷C.用冰袋冷敷足底部D.30%乙醇全身擦浴,快速降温E.10℃温水全身擦浴 下列属于化学变化的是。A.氯化钠溶解在水中B.液态氧受热放出氧气C.金属导电D.氧化钠溶解在水中 下列有关公务员法定条件说法正确的是。A、具有正常履行职责的身体条件B、拥护社会主义的外籍人士C、具有良好品行D、大专以上文化程度 疲劳会使船员.A.体力下降,反应迟钝B.体力不支,大脑不听使唤C.记忆、判断、感知失误D.以上都是 煤气设备及管道检修化验进人标准和。 主动安全带和被动安全带各使用个安全带卷收器。A.1和2B.2和1C.1和1 患者,女,胃癌手术前需插导尿管,患者有顾虑不配合,护士应()A.解释插管的目的,取得患者配合B.术前时间紧张,强行插入C.与医生联系,叫医生处理D.不置屏风遮挡,不解释插管目的E.不请同室患者离开后再插管 骨性关节炎的临床表现不包括A.晨僵>30分钟B.关节肿胀C.粘着感D.关节活动受限E.疼痛 以实物消耗量反映建筑工程经济效益的施工预算编制方法是。A.工料单价法B.实物法C.总合单价法D.实物金额法 按任务的横向划分而确立的各制造或安装单位的分包工作目标称为进度目标中的。A.阶段性目标B.分项目标C.短期目标D.长期目标 感染人的禽流感病毒有、、三种亚型毒株,均为甲型流感病毒的成员A.H5N1、H9N2、H7N7B.H5N2、H9N2、H7N2C.H5N1、H9N1、H7N1D.H5N2、H9N2、H7N2E.H5N7、H9N7、H7N7 关于医学模式的观点错误的是A.是一种哲学观在医学上的反映B.随历史的发展而不断发展变化C."生物-心理-社会"医学模式的提出并不排斥生物医学的研究D.新的医学模式以身心一元论为基本指导思想,坚持病因一元论的观点E.医学心理学促进和推动了医学模式的转化 二氧化碳不能用水同时扑救.A.正确B.错误 我行接受委托,按照一定的程序、办法和标准,对委托人履行经济承诺的能力及其可信任程度进行调查、审核和测定,确定委托人资信状况的业务叫?A、资信评级B、资信证明C、资信调查D、信息咨询 从国家赔偿立法的发展历史来看,各国国家赔偿法最初都以为主要规范对象。A、行政活动B、立法活动C、司法活动 沥青底涂层的优点是能消音和预防飞石的冲击,目前在车身上使用这种防腐蚀材料。A.钢板B.铝板C.玻璃纤维塑料板 上课是整个教学工作的()。A.中心环节B.起始环节C.终止环节D
