非稳定流达西实验
5地下水运动的基本规律
第五章地下水运动的基本规律5. 1 港流基本概念渗流一地卞水在岩石空隙中的运动称为渗流(渗透,地下径流)。
渗流场一发生渗流的区域。
层流运动——水的质点作有秩序的、互不混杂的流动。
紊流运动——水的质点无秩序的、互相混杂的流动。
稳定流一各个运动要素(水位、流速、流向等)不随时间改变的水流运动。
非稳定流——运动要素随时间变化的水流运动。
地卜•水总是从能量校高处流向能量较低处。
能态差异是地卜水运动的驱动力。
地下水的机械能包括动能和势能,水力学中用总水头(hydiaulic head)H表示,水总是从总水头高的地方流向总水头低的地方。
5. 2重力水运动的基本规律1.达西定律(Darcy'sLaw)1856年达西通过实验得到达西定律。
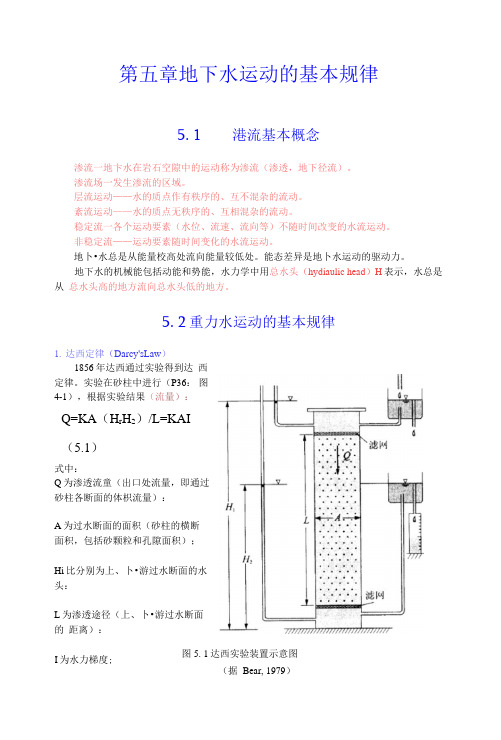
实验在砂柱中进行(P36:图4-1),根据实验结果(流量):Q=KA(H r H2)/L=KAI(5.1)式中:Q为渗透流童(出口处流量,即通过砂柱各断面的体枳流量):A为过水断面的面积(砂柱的横断面积,包括砂颗粒和孔隙面积);Hi比分别为上、卜•游过水断面的水头:L为渗透途径(上、卜•游过水断面的距离):图5. 1达西实验装置示意图I为水力梯度;(据Bear, 1979)K 为渗透系数。
由水力学:Q=vA达西定律也可以另一种形式表达(流速): 由公式(5.1)及Q=\A 得:v=KI式中:£ --- 渗透流速,m/d, cm/s ;K ----- 渗透系数,nVd, cm/s :I —水力梯度,无量纲(比值)。
具体到实际问题:计算流最:H _ HQ =川F ---------- (单位一•般为:m 3/d, L/s)L微分形式:式中:负号表示水流方向与水力梯度方向相反,水流方向(坐标方向):由水位高一 低:而水力梯度方向:由等水位线低一高。
在三维空间中(向量形式):■\v = -K x ^-i-K v ^- j-K,-51k = -KgradH dy dz或V = -KVH ,式中:K 一为渗透系数张量:gradH =更 i +更* 更 Amdy dz若用标量表示,V 的三个分最分别为:得到 v=Q/A(对地下水也适用)(5.2) (5.3)v=-KdH £Vy= ~K - dy—呻**■ dz2. 渗透流速(V ) (seepage velocity, Daicy velocity )与实际流速(u )渗透流速一水流通过整个过水断面(包括砂砾和孔隙)的流速。
安建工 地下水动力学 第一章(xiu)

渗流场(flow field)由固体骨架和岩石空隙中的水两
部分组成。渗流只发生在岩石空隙中。
多孔介质概念与特性
我们把孔隙岩层称为多孔介质(porous media).
•多孔介质特性:
彼此连通的网络,几何形态及连通情况异
常复杂,难以用精确的方法来描述。
由固体骨架和孔隙组成,孔隙通道是不连
续的。
nd 32
2
J
K
nd 32
渗透系数的表达式
裂隙介质(概化为走向和缝宽相同的平行板)
k nB 12 K k
2
nB 12
2
v KJ
nB 12
2
J
K
nB 12
2
六、渗流分类
1. 按运动要素(v,p,H)是否随时间变化,分:稳定流与非稳定流 2. 按地下水质点运动状态的混杂程度,分:
微分形式:
五、渗透系数(hydraulic conductivity)
是重要的水文地质参数,它表征在一般正常条
件下对某种流体而言岩层的渗透能力
(permeability)
v=KJ;
当J=1时,K=v
K在数值上是当J=1时的渗透流速,量钢[L/T];
常用单位cm/s;m/d。
渗透系数与哪些因素有关呢?
: 比重;:动力粘滞性系数;
K k
渗透率k:反映介质几何特性,量纲[L2];
常用单位:cm2; 石油地质中用达西: 1 达西=9.8697*10-9cm2.
渗透系数的表达式
多孔介质(概化为等径的平行毛细管束):
多孔介质中的非达西流

多孔介质中的非达西流多孔介质是指在内部具有复杂通道结构、具有许多微小孔隙或通道的材料。
在此种材料中流体的运动受到宏观介质结构及介质微观孔隙结构的影响,因此,产生了许多非达西流现象。
以下,我们将为大家详细介绍多孔介质中的非达西流。
首先,让我们先来了解一下达西流。
达西流是一种在管道或孔隙中流动的不可压缩流动,其流速不同区域相等,且不受介质内微小细节的影响。
达西流是我们学习流体力学的重要基础。
而在多孔介质中,介质内部的复杂通道结构和孔隙分布会导致流体的流动变得非常复杂。
在这样的情况下,达西流的假设已经不能满足多孔介质中的流动规律。
接下来,我们来看看多孔介质中的几种非达西流现象。
首先是分层流。
当介质内部存在大小不同的孔隙或通道时,介质内流动的速度会在不同大小的孔隙或通道中产生差异。
因此,当多孔介质中的流体从一种介质到另一种介质时,会在交界处发生分层现象,即速度不同的不同层流发生相互作用。
其次是回流现象。
在通道非常复杂的多孔介质中,流动可能会形成由于反向运动和回流现象导致的混沌流动。
再次是非线性渐进现象。
当流体在多孔介质中流动时,在开始的时候,流动可能是线性的,但是随着速度的增加和压强的变化,流动的速度难以线性地跟随变化,从而出现了非线性渐进现象。
如何解决多孔介质中的非达西流呢?对于多孔介质中的非达西流,我们可以使用多种方法进行研究和解决。
其中一种方法是通过建立复杂的数学模型来模拟多孔介质中的流动规律。
另一种方法是通过实验的方式来研究多孔介质中的非达西流现象。
最近几年,随着物理学和数学学科的发展,计算方法已经成为研究多孔介质中非达西流的一种重要工具。
总之,多孔介质中的非达西流现象是流体力学学科中重要的研究内容。
通过对多孔介质中的非达西流进行深入的研究,我们可以更好地理解和掌握多孔介质中的力学规律,对于解决工业、环境和生物等领域中的实际问题有着重要的指导意义。
达西定律

三、达西定律的适用条件
适用条件
雷诺数(Re)小于1-10之间某一数值的层流才符合达西定律;
Vd Vd Re
天然条件下地下水的渗流速度通常很缓慢,绝大部分为层流运动,一般 可用线性定律描述其运动规律。
当地下水流速相当大时,呈紊流运动,此时的渗透服从非线性渗透定 律称为哲才(A.Chezy)定律:
V——I 曲线
V
1
砂样
2
O
I
V=K· I ——(3)
思考:1和2哪个代表砾样和砂砾混合样的V-I曲线?
二、达西公式各物理量的含义
过水断面ω 与实际过水断面ω ' 过水断面ω :砂柱的横切面积,是指水流通过的包括岩石 骨架与空隙在内的整个断面。 实际过水断面ω ′:扣除结合水所占据范围以外的空隙面积, 也就是重力水所占据的空隙面积 。
影响渗透系数的因素—— 以松散岩石
,等径孔隙为例来分析
V u ne K I I
多孔介质(概化为等径的平行毛细管束):
I d u 32
K
2 0
32
d ne
2 0
K k
K表示渗透率
K与液体的物理性质有关,与液体的容重γ成正比,与动 力粘滞系数μ成反比。 K与岩石的性质有关,与空隙大小(d0)成2次方,与空 隙多少(ne)成一次方。
中间内插,画其它流线 等单宽流量控制流线根数; 等水头差绘制等水头线
以河间地块为例,考虑稳定均匀降雨条件下,均质 各向同性介质稳定信手流网的绘制。
思考题:河流完全切割含水层至隔水底板,其它条件不 变时流网形态?
流网的应用
确定任意点的水头值(H)及变化规律; 确定水力梯度 I 的大小及变化规律; 等水头线愈密, 水力梯度愈大! 确定渗透流速V的大小及变化规律; V KI 确定流量Q的大小及变化规律。 流线愈密,径流愈强!
实验一达西定律验证实验

实验一 达西定律验证实验1 实验目的和要求(1)测定均质沙柱的渗透系数K 值;(2)测定通过沙柱的渗流量与水头损失的关系,验证渗流的达西定律。
2 实验原理液体在孔隙介质中流动时,由于粘滞性作用将会产生能量损失。
达西(Henry Darcy )在1852-1855年间通过实验,总结得出渗流能 量损失与渗流速度成一次方的线性规律,后人称为达西定律。
由于渗流速度很小,故速度水头可以忽略不计。
因此总水头H 可用测压水头h 来表示,水头损失w h 可用测压水头差来表示,即,于是,水力坡度J 可用测管水头坡度来表示:12w h h h hJ L L L-∆===式中:L 为两个测压管孔之间距离;1h 与2h 为两个测压孔的测压水头。
达西通过大量实验,得到砂柱内渗流量Q 与过水断面面积A 和水力坡度J 成正比,并和砂的透水性能有关,所建立基本关系式如下:12h h Q KAKAJ L-==或者式中v 为渗流简化模型的断面平均流速,即渗流速度;系数K 为反映孔隙介质透水性能的综合系数,即渗透系数。
实验中的渗流区为一圆柱形的均质砂体,属于均匀渗流,可以认为各点的流动状态是相同的,任意点的渗流流速v 等于断面平均渗流流速,因此达西定律也可以表示为:v KJ =。
渗流雷诺数用下列经验公式求:10.750.23ee vd R n υ=⋅+式中e d 为砂样有效粒径、v 为渗流速度、υ为流体的运动粘滞系数、n 为孔隙率。
3 实验仪器或设备直立圆筒沙柱;供水箱;量筒;测压管;秒表等。
4 实验步骤(1)记录基本常数,包括实验圆筒内径D 、测孔间距L及砂样有效粒径d e、孔隙率n 与水温T。
(2)开启供水管注水,让水浸透圆筒内全部砂体并使圆筒充满水;一般按流量从大到小顺h),通过调节出水口位置高度(即序进行实验。
本次实验采用固定供水箱以及该测压水头(1h)来改变测压水头差。
待水流稳定后,即可用体积法测定渗流量。
2(3)依次调整水头,待水流稳定后进行上述测量,共测10次。
地下水向完整井的非稳定流运动

地下水向完整井的非稳定流运动研究有助 于深入了解地下水系统的动态变化,为地 下水资源的管理和保护提供科学依据。
它涉及到地下水在土壤、岩石等介质 中的流动规律,以及与地下水开采、 污染、自然流动等相关的实际问题。
研究目的和意义
研究目的
探讨地下水向完整井的非稳定流运动 规律,建立相应的数学模型,并开展 数值模拟和分析。
特点
完整井的边界条件简单,便于数学建模和数值模拟。在地下 水动力学中,完整井模型广泛应用于研究地下水向井的非稳 定流运动。
完整井的模型建立过程
01 确定研究区域和井的位置,明确研究目标。
02
根据实际地质和水文条件,选择合适的数学 模型和方程。
03
根据边界条件和初始条件,建立数学方程的 定解问题。
04
研究展望
需要进一步深入研究地下水向完整井 的非稳定流运动的机理和影响因素, 提高对其本质的认识。
需要加强地下水与地表水、土壤水等 水体的相互关系研究,以全面了解水 资源的循环和利用过程。
针对不同地区和不同条件的地下水系统,需 要开展更为细致和深入的实验和数值模拟研 究,以揭示其非稳定流运动的规律和特点。
07 结论与展望
研究结论
地下水向完整井的非稳定流运 动是一个复杂的过程,涉及到
多个物理和化学因素。
通过实验和数值模拟,我们发 现地下水位、渗透性、孔隙度 等因素对非稳定流运动有显著
影响。
在特定条件下,非稳定流运动 可能导致地下水污染或资源枯 竭等问题,需要引起重视。
针对不同地区和不同条件的地 下水系统,需要采取相应的管 理和保护措施,以保障地下水 资源的安全和可持续利用。
污染程度评估
评估地下水污染程度,了解污染物在地下水中的扩散和迁移情况。
渗流的基本定律(达西定律)

影响渗透系数大小的因素
f(孔隙大小 多少、液体性质) 孔隙大小、 K= f(孔隙大小、多少、液体性质) 岩层空隙性质(孔隙大小、多少) 岩层空隙性质(孔隙大小、多少) 由流体的物理性质决定, 由流体的物理性质决定,与γ成正比,与μ成 成正比, 反比.流体的物理性质与所处的温度、压力有关。 反比.流体的物理性质与所处的温度、压力有关。
vx = Kxx Jx + Kxy Jy vy = Kyx Jx + Kyy Jy
v = Kε Jε ε ε v = K η Jη η η
si θ n co θ s
o c sθ 设R为旋转矩阵 R = −si θ n
设R为旋转矩阵
vx v ε =[R ] v η vy Jx Jε =[R ] J η Jy
多孔介质概念与特性
我们把孔隙岩层称为多孔介质(porous media). 我们把孔隙岩层称为多孔介质 •多孔介质特性 多孔介质特性: 多孔介质特性 8彼此连通的网络,几何形态及连通情况异常复杂, 彼此连通的网络,几何形态及连通情况异常复杂, 彼此连通的网络 难以用精确的方法来描述。 难以用精确的方法来描述。 8由固体骨架和孔隙组成,孔隙通道是不连续的。 由固体骨架和孔隙组成,孔隙通道是不连续的。 由固体骨架和孔隙组成
z
a. 一维流:仅沿一个方向存在流速 一维流: b. 二维流:沿两个方向存在分流速 二维流: 分:平面二维流、剖面二维流) 平面二维流、剖面二维流) c. 三维流: 三维流: 三个方向均存在分流速
图 1-2-8a
x y
一维流
岩层按渗透性分类
6. 按岩层渗透性随空间和方向变化特点,分 均质各向同性、均质各向异性、 均质各向同性、均质各向异性、 非均质各向同性、 非均质各向同性、非均质各向异性 几个概念: 各向同性、各向异性、均质、非均质
《非达西渗流实验研究及数学描述》范文

《非达西渗流实验研究及数学描述》篇一一、引言渗流现象在地质学、石油工程、地下水动力学等多个领域具有重要应用价值。
传统上,达西定律被广泛用于描述渗流过程,但在某些特殊情况下,如高流速、多孔介质、非均匀流等复杂条件下的渗流行为,其应用效果可能会受到一定程度的限制。
为了更好地理解并描述这些复杂的渗流过程,非达西渗流理论逐渐引起了学界和工业界的广泛关注。
本文通过实验方法对非达西渗流现象进行研究,并对其数学描述进行探讨。
二、非达西渗流实验研究1. 实验设备与材料实验设备主要包括高压渗透仪、多孔介质材料(如砂石、玻璃珠等)、测量仪器等。
其中,多孔介质材料的选择对实验结果具有重要影响,应尽量选择具有不同孔径、孔隙率等特性的材料。
2. 实验方法与步骤(1)制备不同特性的多孔介质样品;(2)在高压渗透仪中设置不同流速和压力条件;(3)观察并记录渗流过程中的流量、压力变化等数据;(4)对实验数据进行处理和分析。
3. 实验结果与分析通过实验,我们观察到在非达西渗流条件下,流量与压力之间的关系不再遵循传统的线性关系。
随着流速的增加,渗流过程表现出明显的非线性特征。
此外,多孔介质的特性对渗流过程具有显著影响,如孔径大小、孔隙率等都会影响渗流速度和压力分布。
三、非达西渗流的数学描述为了更好地描述非达西渗流过程,我们引入了非线性渗流模型。
该模型考虑了多孔介质特性、流速、压力等多种因素,能够更准确地反映实际渗流过程中的非线性特征。
通过对实验数据的拟合和分析,我们可以得到模型中的相关参数,从而对渗流过程进行定量描述。
四、结论本文通过实验方法对非达西渗流现象进行了研究,并对其数学描述进行了探讨。
实验结果表明,在非达西渗流条件下,流量与压力之间的关系表现出明显的非线性特征。
为了更好地描述这一过程,我们引入了非线性渗流模型。
该模型能够考虑多种因素,包括多孔介质特性、流速、压力等,从而更准确地反映实际渗流过程中的非线性特征。
通过对模型参数的拟合和分析,我们可以对渗流过程进行定量描述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 变水头达西流渗流实验
一、实验目的
通过非稳定流条件下的渗流实验,加深对达西定律的理解。
从而认识到达西定律既适用 于稳定流条件也适用于非稳定流条件。
二、实验装置
如图1-1所示,圆管A 下段装有待测定的砂样,底端为铜丝网,砂样表层铺放薄层细 砾。
实验开始时,圆管上部装满水,水便通过砂样渗流,圆管上部水位则逐渐下降。
圆管下端放在盛水器皿B 中,通过砂样渗流到器皿中的水会自动溢出,以固定渗流段下游水位。
排水容器E 通过排水管随时排走盛水器皿溢出的水。
三、实验原理
利用达西定律和水均衡原理可以证明图1-1所示的装置中,水头H 与时间呈半对数关 系(详见《地下水动力学》第一章),即 H K
L
H K L H K L H K L t lg 3.2lg 3.2ln ln 00-=-=
式中:t - 时间;
0H - 实验的初始水头(即当t =0时的水头); H - 对应不同时间t 的水头; K - 渗透系数。
因此,实验过程中,可测定对应不同时间的水头值,作出t ~H lg 直线关系图(图3-3)。
利用该直线的斜率m 求渗透系数K 。
四、实验步骤
(1)熟悉仪器结构以及秒表操作方法与读数。
进行实验分工,建议一人观察水头变化,一人看秒表,一人记录。
(2)将盛水器皿充满水,并将渗透管的下端放入盛水器皿B 的水面之下约1cm 。
(3)用量杯对试样充水,使其自由渗透2~3次,以饱和砂土,排除空气。
(4)记下初始水头0H ,对透明管充水到渗透管零点上方。
待水位下降至零刻度,开动秒表记时。
(5)水位下降到预先设计的降深值(1,2,3,……,10cm )时,记录对应的时间(表3-2)。
(6)重复实验步骤(4)~(5)1~2次,进行核对。
(7)改变渗透管下端没入盛水器皿的深度(离器皿底部约1cm)进行同样实验,记录读数。
(8)与不同砂样的小组交换仪器重复上述步骤(4)~(7)的实验,做好记录。
图3-3 实验装置图
A -带刻度的透明圆管(下部装有砂样);
B -盛水皿;
C -支架;
D -排水管口;
E -排水容器
五、实验成果
1.提交实验数据记录(表3-2)。
2.数据处理
lg曲线。
(1)在坐标纸上绘制两种砂样的t~H
lg直线关系图
图3-4 t~H
(2)计算渗透系数K(表3-2)。
表3-2 渗透系数计算简表
3.问题讨论
(1)达西定律的应用条件是什么?
(2)渗透管出口端放在盛水器皿不同深度时,渗流速度有何变化?为什么?(对比实验资料说明)
(3)本实验中测定水位H的基准面在何处?
表3-3 实验数据记录。
