113多边形及其内角和-江西省南昌市第二中学八年级数学上册课件(共26张PPT)
合集下载
人教版八年级数学上册课件 11.3.2 多边形的内角和(共27张PPT)

17、儿童是中心,教育的措施便围绕他们而组织起来。上午11时23分57秒上午11时23分11:23:5721.8.12
You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
试想:三角形内角和为180°, 四边形内角和为360 °, 任意多边形的内角和等于多少?
(2分)
5、一个多边形的各内角都等于120°,它是_六__
边形。 (2分)
闯关三:综合应用
6、 一个多边形内角和是外角和的2倍,它是几 边形?(2分)
解: 设多边形的边数为n,根据题意可得 (n-2)•180° = 360°×2 解得:n = 6
答: 它是六边形。
最后一关:我的学习收获(2分)
1.n边形的内角和: (n-2)×180° 2.多边形的外角和是 360° 3.数学思想方法:转化
2011人教版八年级上册
11.3.2多边形的内角和
三角形的内角和等于180°
长方形,正方形的内角和 都是360°
猜猜看:任意四边形的内角和等于多少?
活动1:探索任意四边形的内角和等于多
少度?你是怎样得到的?
A
B
D C
180°×2=360°
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。21.8.1221.8.12Thursday, August 12, 2021
10、阅读一切好书如同和过去最杰出的人谈话。11:23:5711:23:5711:238/12/2021 11:23:57 AM
11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。21.8.1211:23:5711:23Aug-2112-Aug-21
初中数学人教版八年级上册11.3.2多边形的内角和 教学课件(共23张PPT)

=360°-180°=180°.
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做 六边形的外角和.六边形的外角和等于多少? 问题1:任意一个外角和它相邻的内角有什么关系?
互补 问题2:六边形的6个外角加上与它们 相邻的内角,所得总和是多少?
解得:n=10,∴ 这个多边形的边数是10. 故答案为:10.
练习6(1)根据图中的相关数据,求出x 的值:
(2)一个多边形内角和的度数比外角和的度数的4倍多180度, 求多边形的边数.
解:(1)(x+9)°+115°+90°+x°=(4-2)×180°, 解得:x=73.
(2)设多边形的边数为n, ∵多边形的外角和是360°,内角和的度数比外角和的度数的4倍多180度, ∴可得方程(n-2)180°=4×360°+180° 解得n=11,
练习4一个多边形的内角和是外角和的2倍,则这个多边形是(C )
A.四边形
B.五边形
C.六边形
D.八边形
解析:设所求正n 边形边数为n ,由题意得 (n-2) ·180°=360°×2 解得n=6. 则这个多边形是六边形.故选C.
练习5一个多边形的内角和是其外角和的4倍,则这个 多边形的边数是10 . 解析:设这个多边形的边数为n, 则该多边形的内角和 为(n-2)×180°,依题意得:(n-2)×180°=360°×4,
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫 做
六边形的外角和.六边形的外角和等于多少? 问 题 3 :上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和 因此六边形的外角和
如果一个四边形的一组对角互补,那么另一组对角也互补.
如图,在六边形的每个顶点处取一个外角,这些外角的和叫做 六边形的外角和.六边形的外角和等于多少? 问题1:任意一个外角和它相邻的内角有什么关系?
互补 问题2:六边形的6个外角加上与它们 相邻的内角,所得总和是多少?
解得:n=10,∴ 这个多边形的边数是10. 故答案为:10.
练习6(1)根据图中的相关数据,求出x 的值:
(2)一个多边形内角和的度数比外角和的度数的4倍多180度, 求多边形的边数.
解:(1)(x+9)°+115°+90°+x°=(4-2)×180°, 解得:x=73.
(2)设多边形的边数为n, ∵多边形的外角和是360°,内角和的度数比外角和的度数的4倍多180度, ∴可得方程(n-2)180°=4×360°+180° 解得n=11,
练习4一个多边形的内角和是外角和的2倍,则这个多边形是(C )
A.四边形
B.五边形
C.六边形
D.八边形
解析:设所求正n 边形边数为n ,由题意得 (n-2) ·180°=360°×2 解得n=6. 则这个多边形是六边形.故选C.
练习5一个多边形的内角和是其外角和的4倍,则这个 多边形的边数是10 . 解析:设这个多边形的边数为n, 则该多边形的内角和 为(n-2)×180°,依题意得:(n-2)×180°=360°×4,
6×180°=1080°
如图,在六边形的各个顶点处取一个外角,这些外角的和叫 做
六边形的外角和.六边形的外角和等于多少? 问 题 3 :上述总和六边形的内角和、外角和有什么关系?
六边形的外角和加上内角和等于这个总和 因此六边形的外角和
人教版八年级数学上册课件 11.3.2 多边形的内角和(共25张PPT)

E
F
E
A B
D
A
C
B
D C
A B
E
1
2
5
3
4
5边形
180 45 360 540
D
C
6边形
F E 180 64 360 720
O6 5
1
D
A
2
4 3
B
C
E
A
D
5边形
2
180 34 180 540
3
1
4
BO
C
E
D
6边形
180 35 180 720
C F
2 34
5
1
AO
B
O
2 3 45
5边形
180 34180 540
2 3
1
4
BO
C
6边形
E
D
180 35 180 720
F
C
………………
2
3 4
5
n边形
1
A
O
B
180
(
nn-11))
180
(n 2)180
Hale Waihona Puke GAD4边形
180 3 180 360
B
C
在外部O取一点
2 3 45
E1
6D
5边形
180 34180 540
A
C
BP
3、长方形内角和是_____°,正方形内角和是_____°
画出一个四边形,利用手中的工具猜想 这个四边形的内角和。
演 示
1、你是怎么得到的,分享一下方法。
2、你认为上述的哪些方法更科学、 准确的说明四边形的内角和是360° 呢?
最新人教部编版八年级数学上册《11.3多边形及其内角和【全套】》精品PPT优质课件

∠3 +∠ACD =180°,
得 ∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD =540°.
综合应用 5.某学校七年级六个班举行篮球比赛,比赛
采用单循环积分制(即每两个班都进行一次比 赛).一共需要多少场比赛?
解:一共需要15场 比赛.如图:
课堂小结
在平面内,由一些线段首尾顺次相接组成的 封闭图形叫做多边形.
A
A
B C
C
DB
凸四边形
D 正三角形 正方形 正五边形 正六边形
课后作业
1.从教材课后习题中选取; 2.从练习册中选取。
底面为六边 形的螺母
底面为八边 形的螺母
如果一个多边形由 n 条线段组成,那么这个
多边形就叫做 n 边形.
多边形__相__邻__两__边___组成的角叫做它的内角. A
B E
C
D
多边形的边与它__的__邻__边__的__延__长__线__组成的 角叫做它的外角.
A
B E
C
D
练习1 下列图形包含了哪些多边形?
从n 边形的一个顶点出发,可以作(n -3)条 对角线,它们将n 边形分为(n -2)个三角形,这 (n -2)个三角形的内角和就是n 边形的内角和, 所以,n 边形的内角和等于(n -2)×180°.
练习
填空: (1)十边形的内角和为 1 440 度. (2)已知一个多边形的内角和为1 080°, 则它的边数为___8___.
11.3 多边形及其内角和
11.3.1 多边形
R·八年级上册
新课导入
你能从图中想象出几个由一些线段围成的 图形吗?
• 学习目标: 1.能叙述多边形、多边形的内角、外角和对角 线的意义. 2.知道什么是凸多边形和正多边形.
人教版八年级数学上册 11.3.2 多边形的内角和 课件(共29张PPT)
5
知识点一:多边形的内角和
新知探究
四边形内角和
D
4
C
如图,在四边形ABCD中,连接 对角线AC,则四边形ABCD被分为
△ABC和△ACD两个三角形.
2
A
1
3 B
你能推出五
由此可得:∠DAB+∠B+∠BCD+∠D
边形和六边形
=∠1+∠2+∠B+∠3+∠4+∠D 的内角和吗?
=(∠1+∠B+∠3)+(∠2+∠4+∠D)
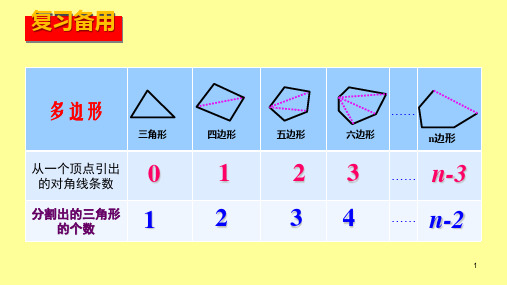
复习备用
多边形
三角形
四边形
五边形
……
六边形
n边形
从一个顶点引出 的对角线条数
0
1
2 3 …… n-3
1 分割出的三角形 的个数
2
3 4 …… n-2
1
激情引入
1.看完这些图案你能抽象出哪些几何图形? 2.生活中有如此多的几何图形,你对它们了 解多少?
我们知道三角形的内角和是180度,正方 形、长方形的内角和是360度,那么四边形、 五边形、六边形的呢?
2
人教版八年级数学上册 第十一章 三角形
11.3 多边形及内角和
11.3.2 多边形的内角和
3
学习目标 1.会通过不同方法探索多边形的内角和与外角和
公式,并会用它们进行有关计算. 2.通过将多边形问题转化为三角形问题解决,体 会化归思想的应用方法,提高分析问题和解决问 题的能力.
重点难点
重点:多边形的内角和与外角和. 难点:多边形的内角和公式的推导.
A.360° B.540° C.720° D.900°
14
八年级数学上册第十一章11.3《多边形及其内角和》PPT课件

探究新知
素养考点 1 多边形的截角问题
例1 凸六边形纸片剪去一个角后,得到的多边形的边 数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况, ∴新多边形的边数为7、5、6三种情况, 如图所示.
探究新知
归纳总结
一个多边形截去一个角后,多边形的边数可能 增加了一条,也可能不变或减少了一条.
正三角形 正方形
正五边形 正六边形
探究新知 想一想 下列多边形是正多边形吗?如不是,请说明为什么?
(四条边都相等)
(四个角都相等)
答:都不是,第一个图形不符合四个角都相等;第二个图形不 符合各边都相等.
注意 判断一个多边形是不是正多边形,各边都相等,各角 都相等,两个条件必须同时具备.
巩固练习
4.下列属于正多边形的特征的有( B )
解析:从某个多边形的一个顶点出发的对角线共有2条, 则将多边形分割为3个三角形. 所以该多边形的内角和是3×180°=540°.
课堂检测
基础巩固题
1.下列多边形中,不是凸多边形的是( B )
A
B
C
D
2. 九边形的对角线有( C ) A. 25条 C. 27条
B. 31条 D. 30条
课堂检测
基础巩固题
11.3 多边形及其内角和 11.3.1 多边形
导入新知
在实际生活当中,除了三角形,还有许多由线段围 成的图形.观察图片,你能找到由一些线段围成的图形吗?
导入新知
导入新知
中国某一村远景图
五角大楼
素养目标
3. 掌握多边形对角线的定义及公式,并能运 用公式解决相关问题. 2. 了解什么是凸多边形和正多边形.
探究新知 思考 比较多边形的定义与三角形的定义,为什么要 强调“在平面内”呢?怎样命名多边形呢? 这是因为三角形中的三个顶点肯定都在同一个平面内,
人教版八年级上册 11.3 多边形及其内角和 课件(共21张PPT)

12x = 240, x=20,
∴ 3x = 60, 4x = 80, 5x = 100. 答:∠B,∠C,∠D的度数分别为60°,80°,100°.
按角分类
锐角三角形 直角三角形 钝角三角形
按边分类
等腰三角形 等边三角形
j-腰
k -腰
1-底角
2-底角
l-底边
每个角都是锐角 两个锐角互余 有一个角是钝角 两腰相等,两底角相等 三边都相等,三个角都是60°
在 n 边形的每个顶点处各取一个外角,这些外角 的和叫做n边形的外角和.
n边形外角和= n个平角-n边形内角和 =n×180°-(n-2) × 180° =360°. n边形的外角和等于360°.
B
2 C
1
A n
F 5
3 D 4
E
知识点及时练
1.(肇庆·中考)一个多边形的内角和是外角和的2倍,
则这个多边形是( C )
知识点及时练
6 、已知两个多边形的内角和为 1440°,且两多 边形的边数之比为 1︰3,求它们的边数分别是 多少? 解:设它们的边数分别是x,y.由题意得:
180+( y -2)· 180=1440 (x-2)· x : y=1 : 3 解之得 x =3 y =9 答:它们的边数分别是3和9。
教材知识点精讲
教材知识点精讲
1. 认识多边形
对角线
读出图中所有的对角线 A E
B
C 对角线——— 连接多边形不相邻的两个顶点的线段.
D 对角线
教材知识点精讲
2. 多边形的内角和
画出多边形中从一个顶点出发的对角线,写出它的条数. 1 0
2
3
5
从n边形的一个顶点出发能画出多少条对角线? (1) (n-3) (n≥3)
八年级上册11.3.2多边形的内角和(共26张PPT)

12 ∴∠FAB+∠BCD+∠DEF= ×720°=360°
拓展:一个六边形如图,已知 BA∥DE ,∠B= ∠ E,∠C=∠F
(1)求证:CD∥AF (2)求∠A+∠C+∠E的度数.
E F
D
1 2
C
43
A
B
这节课你学到了什么? 还有什么困惑?
小结:
1.“三个一”(一个定义、一个公式和一个性质)
三角形的内角和是180°,那么四边 形的内角和是多少呢?五边形呢?你 是如何得到这个结论的?
探究
请你利用分割的方
A
法探索五边形的内
角是多少?
E
B D
C 5边形内角和=3×180°=540°
方法2
B
A
180°× 5=900°? 五边形内角和540°??
O
E
D C 180°× 5 – 360°= 540°
3、填空(求边数)
1、已知一个多边形的内角和为1080°, 则它的边数为_8_。
2、已知一个多边形的每一个内角都是 156°,则它的边数为_15_。
例: 一个六边形如图,已知AB∥DE,BC∥EF,
CD∥AF,求∠A+∠C+∠E的度数。
解:如图所示,连结AD,
E
∵AB∥DE, CD∥AF(已知)
(2)已知一个多边形的内角和为720o ,则这个 多边形是__6____边形 (3)在五边形ABCDE中,若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为__8_0_o___
过多边形一个顶点的所有对角线将这个 多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.
D
1 2Biblioteka ∴∠1=∠3,∠2=∠4(两 F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探究
有一天老王闲的没事,把一个五边形锯去一个 内角后会得到几边形呢?
①
②
③
解:五边形锯去一个内角后得到的图形可能是六边 形,如图①;五边形,如图②;四边形,如图③
总结
多边形的锯内角(三角形)规律
n边形锯去一个内角后得到的图形可能是n-1 边形,n边形或n+1边形。
例1
下列图形中,多边形有( A )
内角
E 外个顶点的线段。
分类
多边形的分类
如图,画出四边形ABCD的任何一条边所在直线,
整个四边形都在这条直线的同一侧,这样的四边形叫
做凸四边形。反之则叫做凹四边形。
A
A
B
C
D
C
B
D
正多边形
各个角都相等,各条边都相等的多边形 叫做正多边形.
正三角形 正方形
正五边形 正六边形
边 n边形外角和
形 的 =n个平角-n边形内角和
B
外 2 = n×180 °-(n-2) × 180°
1A n
F 45
角 =360 °
C
E
和
3D
结论:n边形的外角和等于360°.
定理
多边形内角和:n边形内角和等于(n-2)·180° 多边形外角和:多边形外角和等于360°
正n边形每个内角的度数是 n 2 •180
n
360
正n边形每个外角的度数是 n
注意
多边形边数与内外角和关系
(1)多边形内角和与边数相关:边数增加,内角 和增加,边数减少,内角和减少,每增加一条边, 内角和增加180°,反之也成立; (2)多边形外角和恒等于360°,与边数多少无关
例1
若一个正n边形的每个内角为156°,则这个正n边 形的边数是( C ) A.13 B.14 C.15 D.16
例2
如图,长方形纸片EFGH可以绕着长方形纸片ABCD上 的点O自由的旋转,当边EH与AB相交时,形成了∠1, ∠2,求∠1+∠2的度数
例3
如图,在五边形 ABCDE 中,∠A+∠B+∠E=300°,
DP、CP 分别平分∠EDC、∠BCD,则∠P 的度数是
()
A.60° B.65°
C.55° D.50°
关 1 过关条件
目标
多边形的定义与分类
多边形
多边形的内角和与外角和
多边形的对角线 正多边形的相关计算
定义
多边形的定义
在同一平面内,由不在同一条直线上 的一些线段首尾顺次相接组成的图形叫做 多边形。
……
五边形
六边形 七边形
可表示为:五边形ABCDE或五边形AEDCB
A
多
边
顶点
形
的 相
B
关
概
念边
C
探究
【例2】如图,在五边形的每个顶点处各取一个外角,
多 这些外角的和叫做五边形的外角和.五边形的外角和
边
等于多少?
五边形外角和
形 的
=5个平角 -五边形内角和 B
1A 6
5
外 =5×180°-(5-2) × 180°
2
E
角 =360 °
C
4
和 结论:五边形的外角和等于360°. 3
D
探究
多 边 形 的 外 角 和
公式
多 边 形 的 内 角 和
n边形内角和=(n-2) ·180°
A
G
F
E B
D C
问题
如果一个四边形的一组对角互补, B
那么另一组对角有什么关系?
C
A
D
如果四边形一组对角互补,那么另一组对角也互补.
如果一个角的两边与另一个角的两边分别垂直, 那么这两个角的关系是_相__等_或__者__互_补_
A.2个 B.3个
C.4个 D.5个
例2
把一个多边形纸片沿一条直线截下一个三角形后,
变成一个18边形,则原多边形纸片的边数不可能是
(A )
A.16
B.17
C.18
D.19
探究
多 边 形 的 内 角 和
四边形的内角和 (4-2)× 180° = 360° 五边形的内角和 (5-2)× 180° = 540° 六边形的内角和 (6-2)× 180° =720° 七边形的内角和 (7-2)× 180° = 900°
例4
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+ ∠K的度数为( )
探究
……
三角形
四边形
五边形
六边形
从同一顶点引出的对角线的条数:
n边形
0 1 23
分割出的三角形的个数:
n-3
1 2 3 4 n-2
总结
n边形从一个顶点出发的对角线条数 为:_(_n_-_3_)_条(n≥3)
分割出的三角形的个数:n-2
n边形共有对角线 n(n 3) 条(n≥3)
2
例1
十边形共有__3_5__条对角线
解: 10(120−3ሻ=35
例2
已知一个多边形的内角和等于1440°,求此多边形 对角线的条数
解:(n−2)·180° =1440° n=10
10(120−3ሻ=35 答:此多边形对角线条数为10条
如图,在六边形的每个顶点处各取一个外角, 这些外角的和叫做六边形的外角和.六边形 的外角和等于多少?
=6个平角 -六边形内角和
=6×180°-(6-2) × 180°
=360 °
A6 B1
2
C
3
D4
F
5
E
n边形外角和是多少度?
多 探究 在n边形的每个顶点处各取一个外角,这些外角 的和叫做n边形的外角和.
