波动图象的应用
波动图象与振动图象的综合应用

波动图象与振动图象在物理实验中的应用
波动光学实验
波动图象可以用于光学实验中, 例如干涉和衍射实验,通过观察 光波的干涉和衍射现象,验证光 的波动理论。
振动实验
在物理实验中,可以利用振动图 象研究物体的振动规律和特性, 例如固有频率、阻尼系数等。
物理过程模拟
通过模拟物理过程的波动和振动 行为,可以深入理解物理现象的 本质和规律,为科学研究和技术 开发提供支持。
在图象上标注出坐标轴,以便更好地观察和分析 振动的变化规律。
波动图象与振动图象的绘制技巧
突出关键信息
在绘制波动图象和振动图象时,应突出关键信息,如波峰、波谷、 振动最大位移等。
保持图象清晰
在绘制波动图象和振动图象时,应保持图象清晰,避免过多的噪声 和干扰。
比较不同图象
在绘制波动图象和振动图象时,可以比较不同图象的特点和规律, 以便更好地理解和分析波动和振动的本质。
01
揭示物理现象的本质
通过综合应用波动图象和振动图象,可以更深入地理解物理现象的本质,
如波动和振动的相互作用和转化。
02
提高解决实际问题的能力
在实际工程和科学研究中,许多问题涉及到波动和振动的相互作用。综
合应用波动图象和振动图象,有助于更准确地分析和解决这些问题。
03
促进多学科交叉融合
波动图象和振动图象的综合应用涉及到多个学科领域,如物理学、工程
振动图象在机械故障诊断中的应用
故障识别
01
振动图象可以用于机械故障的识别,通过分析机械设备的振动
信号,判断设备的运行状态和故障类型。
故障定位
02
结合振动图象和传感器网络技术,可以定位机械设备的故障位
置,提高维修效率。
波动图象与振动图象

在交叉学科领域的应用拓展
生物医学工程
波动和振动图象在生物医学工程中具有广泛的应用前景,如生物 力学、生物医学材料等。
环境科学
在环境科学领域,波动和振动图象可用于监测地质结构、地震活 动等,为灾害预警和环境保护提供支持。
航空航天
在航空航天领域,波动和振动图象可用于研究飞行器结构的动态 特性,提高飞行器的安全性和性能。
特点
波动图象通常以时间和空 间为坐标轴,呈现波动能 量的传播和变化规律。
表现形式
波动图象通常以波形曲线 表示,可以反映波的振幅、 频率、相位等信息。
振动图象的定义与特点
定义
振动图象是指描述振动现 象的图象,如机械振动、 电磁振动等。
特点
振动图象通常以时间和位 移为坐标轴,呈现物体振 动的规律和变化。
02
波动图象的绘制与分析
波动图象的绘制方法
直接绘制法
根据实验或观测数据,直接在坐 标纸上绘制波动图象。这种方法 需要手工操作,精度较低,但简
单易行。
计算机绘图法
利用计算机软件进行波动图象的绘 制。这种方法精度高,可以绘制复 杂波动图象,但需要一定的计算机 绘图技能。
数学模型法
通过建立波动方程,利用数学软件 求解,并绘制波动图象。这种方法 适用于理论研究和模拟分析。
在人工智能与大数据分析中的应用前景
人工智能算法
利用人工智能算法对波动和振动图象进行自动识别、分类和预测, 提高数据处理和分析的效率和准确性。
数据挖掘技术
通过数据挖掘技术,可以从大量的波动和振动图象数据中提取有价 值的信息,为相关领域的研究和应用提供支持。
机器学习模型
利用机器学习模型对波动和振动图象进行学习和预测,实现自适应的 监测和控制。
波动图解析
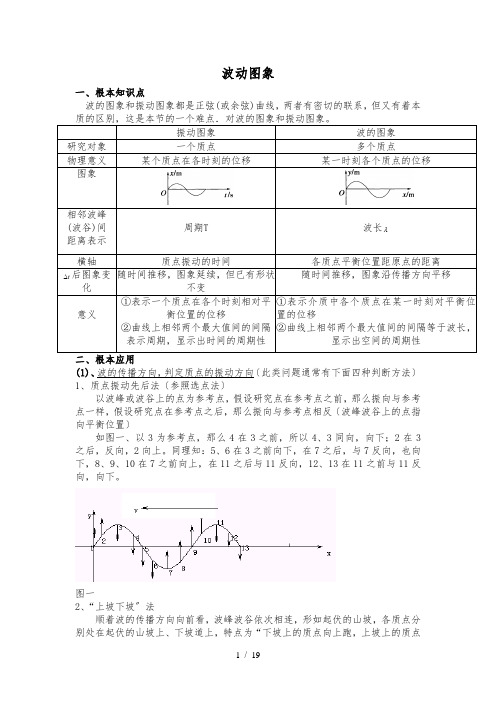
波动图象一、根本知识点波的图象和振动图象都是正弦(或余弦)曲线,两者有密切的联系,但又有着本振动图象波的图象研究对象一个质点多个质点物理意义某个质点在各时刻的位移某一时刻各个质点的位移图象相邻波峰(波谷)间距离表示周期T 波长λ横轴质点振动的时间各质点平衡位置距原点的距离t∆后图象变化随时间推移,图象延续,但已有形状不变随时间推移,图象沿传播方向平移意义①表示一个质点在各个时刻相对平衡位置的位移②曲线上相邻两个最大值间的间隔表示周期,显示出时间的周期性①表示介质中各个质点在某一时刻对平衡位置的位移②曲线上相邻两个最大值间的间隔等于波长,显示出空间的周期性(1)、波的传播方向,判定质点的振动方向〔此类问题通常有下面四种判断方法〕1、质点振动先后法〔参照选点法〕以波峰或波谷上的点为参考点,假设研究点在参考点之前,那么振向与参考点一样,假设研究点在参考点之后,那么振向与参考点相反〔波峰波谷上的点指向平衡位置〕如图一、以3为参考点,那么4在3之前,所以4、3同向,向下;2在3之后,反向,2向上。
同理知:5、6在3之前向下,在7之后,与7反向,也向下,8、9、10在7之前向上,在11之后与11反向,12、13在11之前与11反向,向下。
图一2、“上坡下坡〞法顺着波的传播方向向前看,波峰波谷依次相连,形如起伏的山坡,各质点分别处在起伏的山坡上、下坡道上,特点为“下坡上的质点向上跑,上坡上的质点往下钻。
如图二、波向左传扩,所以由右向左看,13、12、6、5、4、均为上坡的质点〔往下钻〕故振向向下,10、9、8、2、1均为下点坡上的质点〔向上跑〕故振向向上。
图二3、逆复波形法就是逆着波的传扩方向复描波形,但凡复描时笔尖向上所经过的质点此刻振向均向上,但凡复描时笔尖向下所经过的质点,此刻振向均向下。
〔注意,此法除波谷和波峰点〕如图三、波各左传播,用笔尖从左向右复描波形,那么在1、2、8、9、10时笔尖向上,所以振向向上,在4、5、6、12、13时笔尖向下,所以振向向下。
波动图像常见题型及常用方法

波动图像常见题型及常用方法1.由波的传播方向确定质点振动方向(或由质点振动方向确定波的传播方向).①特殊点法:在质点P 靠近波源一方附近图像上找另一点P ',若P '在下方,则P 向下运动. ②微平移法:作出经微小时间△t 后的波形,就知道了各质点经过△t 后到达的位置,运动方向就知道了.2.由波的传播方向及某时刻的波形图线画出另一时刻的波形图线.①平移法:先算出经过△t 时间波传播距离△s =v △t =λ△t/T ,再把波形往波传播方向推进λ△t/T 即可,当波形推进波长整数倍时,波形和原来重合,所以实际处理时通常采用去整留零头的方法处理.②特殊点法:取几个特殊点,根据他们的振动方向,判断经△t 后的位置,连接这些位置画出相应的正弦(或余弦)曲线即可得.③根据两个时刻的波形图像判断可能出现的波动情况.④根据两个质点的位置,判断可能出现的波动情况.例一 一列简谐波某时刻的波形图如图1甲所示,图1乙表示该波传播介质中某质点此后一段时间内的振动图像,则( )A.若波沿x 轴正方向传播,图乙为a 点的振动图像B.若波沿x 轴正方向传播,图乙为b 点的振动图像C.若波沿x 轴负方向传播,图乙为c 点的振动图像D.若波沿x 轴负方向传播,图乙为d 点的振动图像解析:设图甲对应t =0时刻,由图知图乙对应的质点在t =0时刻,在平衡位置,则向上振动.若波向正向传,a 、b 、c 、d 中,只有b 质点符合;若波向负向传,只有d 符合,所以选B 、D.例二 如图2所示,画出了一列向右传播的横波在某个时刻的波形图像,由图像可知( )A.质点b 此时位移为零B.质点b 此时向-y 方向运动C.质点d 的振幅是2cmD.质点a 再经过T/2通过的路程是4cm ,偏离平衡位置的位移是4cm解析:由图像可知质点b 此时位于平衡位置,故其位移为零,A 正确.根据带动法,在质点b靠近波源一侧的附近,选参考质点b ',由于质点b '在质点b 上方,所以此刻质点b 向+y 方向运动,B 错误.简谐波在介质中传播时,介质中各质点振幅都相同,故C 正确.再经过T/2,质点a 运动到负最大位移处,其路程为2A ,即4cm ,位移为-2cm ,故D 错误.例三 如图3甲表示一列简谐波在介质中传播时,某一质点a 的振动图像,请你在乙图中作出这列简谐波在t =0时刻的波形图(质点a 画在坐标原点上).解析:t =0时刻质点a 正处于平衡位置且沿+y 方向运动,经T/4达正向最大位移处.设x 轴正向为波传播的方向,利用波形与振动方向关系的判断方法,得出t =0时的波形图如乙图所示.例四 图4甲中有一条均匀的绳,1,2,3,4,…是绳上一系列等间距的点.现有一列简谐横波沿此绳传播.某时刻,绳上9,10,11,12四点的位置和运动方向如图乙所示(其他电的运动情况未画出),其中点12的位移为零,向上运动,点9的位移达到最大值.画出再经过3/4周期时的波形图.解析:从题中的图乙可以看出,在图乙所示的某时刻,该均匀绳上点9正达位移最大时,而点12正通过平衡位置向上运动.因而由图乙中点9、10、11、12所在的位置点连成的那段曲线,代表在该均匀绳上传播的简谐横波在图乙所示的某时刻的从0至点12的波形图.由图乙中表示的这段波形图的形状和点9、10、11、12四个点的运动方向,可以判断出在均匀绳上传播的简谐横波是向右传播的.由于介质中各质点都围绕各自平衡位置往复运动,所以再经过3/4周期,质点9在平衡位置,而质点12到负的最大位移处.由此可得出点9到点12间的波形.由这段波形也就知道了这一时间整条绳上的波形,如图丙所示.图4。
一波动图象与波速公式的应用

一、波动图象与波速公式的应用1.波的图象反映了在某时刻介质中的各质点离开平衡位置的位移情况,图象的横轴表示各质 点的平衡位置,纵轴表示该时刻各质点的位移,如图3所示.图象的应用:(1)直接读取振幅A 和波长λ,以及该时刻各质点的位移.(2)确定某时刻各质点加速度的方向,并能比较其大小.(3)结合波的传播方向可确定各质点的振动方向或由各质点的振动方向确定波的传播方向.2.波速与波长、周期、频率的关系为:v =λT=λf . 1.一列沿x 轴正方向传播的简谐机械横波,波速为4 m/s.某时刻波形如图4所示,下列说法正确的是 ( )A.这列波的振幅为4 cmB.这列波的周期为1 sC.此时x =4 m 处的质点沿y 轴负方向运动D.此时x =4 m 处的质点的加速度为02. 在O 点有一波源,t =0时刻开始向上振动,形成向右传播的一列横波.t 1=4 s 时,距离O 点为3 m 的A 点第一次达到波峰;t 2=7 s 时,距离O 点为4 m 的B 点第一次达到波谷.则以下说法正确的是( )A.该横波的波长为2 mB.该横波的周期为4 sC.该横波的波速为1 m/sD.距离O 点5 m 的质点第一次开始向上振动的时刻为6 s 末二、振动图像和波动图像1.一列简谐横波沿x 轴传播,t =0时刻的波形如图5甲所示,此时质点P 正沿y 轴负方向运动,其振动图象如图乙所示,则该波的传播方向和波速分别是( )A.沿x 轴负方向,60 m /sB.沿x 轴正方向,60 m/sC.沿x 轴负方向,30 m /sD.沿x 轴正方向,30 m/s2. 如图6甲为一列简谐横波在t =0.10 s 时刻的波形图,P 是平衡位置为x =1 m 处的质点,Q 是平衡位置为x =4 m 处的质点,图乙为质点Q 的振动图象,则 ( )A.t =0.15 s 时,质点Q 的加速度达到正向最大B.t =0.15 s 时,质点P 的运动方向沿y 轴负方向C.从t =0.10 s 到t =0.25 s ,该波沿x 轴正方向传播了6 mD.从t =0.10 s 到t =0.25 s ,质点P 通过的路程为30 cm三、波的干涉,衍射,多普勒效应1.波的干涉(1)产生稳定干涉的条件:频率相同的两列同性质的波相遇. (2)现象:两列波相遇时,某些区域振动总是加强,某些区域振动总是减弱,且加强区和减弱区互相间隔.(3)对两个完全相同的波源产生的干涉来说,凡到两波源的路程差为一个波长的整数倍时,振动加强;凡到两波源的路程差为半个波长的奇数倍时,振动减弱.2.产生明显衍射现象的条件:障碍物或孔(缝)的尺寸跟波长相差不多,或者比波长更小.3.多普勒效应(1)波源不动⎩⎪⎨⎪⎧ 观察者向波源运动,接收频率增大观察者背离波源运动,接收频率减小 (2)观察者不动⎩⎪⎨⎪⎧波源向观察者运动,接收频率增大波源背离观察者运动,接收频率减小 1.如图7表示两个相干波源S 1、S 2产生的波在同一种均匀介质中相遇.图中实线表示波峰,虚线表示波谷,c 和f 分别为ae 和bd 的中点,则:图7(1)在a 、b 、c 、d 、e 、f 六点中,振动加强的点是__________.振动减弱的点是____________.(2)若两振源S 1和S 2振幅相同,此时刻位移为零的点是________.答案 (1)a 、c 、e b 、d 、f (2)b 、d2.如图8甲所示,男同学站立不动吹口哨,一位女同学坐在秋千上来回摆动,下列关于女同学的感受的说法正确的是( AD )甲乙A.女同学从A向B运动过程中,她感觉哨声音调变高B.女同学从E向D运动过程中,她感觉哨声音调变高C.女同学在C点向右运动时,她感觉哨声音调不变D.女同学在C点向左运动时,她感觉哨声音调变低3.利用发波水槽得到的水面波形如图9甲、乙所示,则 ()A.图甲、乙均显示了波的干涉现象B.图甲、乙均显示了波的衍射现象C.图甲显示了波的干涉现象,图乙显示了波的衍射现象D.图甲显示了波的衍射现象,图乙显示了波的干涉现象《课后训练》1.关于振动和波的关系,下列说法中正确的是 ()A.振动是波的成因,波是振动的传播B.振动是单个质点呈现的运动现象,波是许多质点联合起来呈现的运动现象C.波的传播速度就是质点振动的速度D.波源停止振动时,波立即停止传播2.关于波的形成和传播,下列说法正确的是()A.质点的振动方向与波的传播方向平行时,形成的波是纵波B.质点的振动方向与波的传播方向垂直时,形成的波是横波C.波在传播过程中,介质中的质点随波一起迁移D.波可以传递振动形式和能量3.如图1所示是一列简谐波在t=0时刻的波形图,介质中的质点P沿y轴方向做简谐运动的表达式为y=10sin 5πt cm.关于这列简谐波,下列说法中正确的是()A.这列简谐波的振幅为20 cmB.这列简谐波的周期为5.0 sC.这列简谐波在该介质中的传播速度为25 cm/sD.这列简谐波沿x轴正向传播4.如图2所示为观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个小孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间的距离表示一个波长,则对波经过孔后的传播情况,下列描述不正确的是()A.此时能明显观察到波的衍射现象B.挡板前后波纹间距相等C.如果将孔AB 扩大,有可能观察不到明显的衍射现象D.如果孔的大小不变,使波源的振动频率增大,能更明显地观察到衍射现象5.沿x 轴正方向传播的一列简谐横波在t =0时刻的波形如图4所示,M 为介质中的一个质点,该波的传播速度为40 m/s ,则t =140 s 时 ( )A.质点M 对平衡位置的位移一定为负值B.质点M 的速度方向与对平衡位置的位移方向相同C.质点M 的加速度方向与速度方向一定相同D.质点M 的加速度方向与对平衡位置的位移方向相反6. 一列简谐波沿x 轴正方向传播,在t =0时波形如图5所示,已知波速为10 m/s.则t =0.1 s 时正确的波形应是下图中的 ( )图57. 如图6所示,实线是沿x 轴传播的一列简谐横波在t =0时刻的波形图,虚线是这列波在t =0.2 s 时刻的波形图.该波的波速为0.8 m/s ,则下列说法正确的是 ( )A.这列波的波长是14 cmB.这列波的周期是0.5 sC.这列波可能是沿x 轴正方向传播的D.t =0时,x =4 cm 处的质点速度沿y 轴负方向8. 如图7所示为一列简谐横波在t =0时刻的波形图,波的传播方向平行于x 轴.质点A 位于x A =2 m 处,质点B 位于x B =3 m 处,t =2 s 时,质点B 第一次出现在波峰位置;t =3 s 时,质点A 第一次出现在波峰位置.则 ( )A.波速为1 m/sB.波的周期为4 sC.波沿x轴正方向传播D.t=1 s时,质点A的振动速度小于质点B的振动速度9.一列简谐横波在某一时刻的波形图如图9甲所示,图中P、Q两质点的横坐标分别为x=1.5 m和x=4.5 m.P点的振动图象如图乙所示.在下列四幅图中,Q点的振动图象可能是10.质点O振动形成的简谐横波沿x轴正方向传播,t时刻的波形图如图10甲所示,当波传到x=3 m处的质点P时开始计时,质点P的振动图象如图乙所示,则()A.该波的频率为25 HzB.该波的传播速度为2 m/sC.质点O开始振动时沿y轴正方向D.从t时刻起,经过0.015 s,质点P回到平衡位置。
波动图象专题课件

在波动图象中,异常值通常表现为离群点或极端值。为了识别异常值,可以使用一些统计学方法,如 Z-score、IQR等,来计算每个数据点与平均值或中位数的偏离程度。此外,还可以使用可视化手段, 如箱线图、散点图等,来直观地展示异常值并对其进行筛选和处理。
对比分析
总结词
对比分析是通过比较不同数据集或不同时间点的波动图象来发现它们之间的差异和相似 之处的方法。
。
信号处理
用于分析信号的特性、频率和 相位等信息,如音频、图像等
信号处理领域。
物理实验
用于展示物理实验的波形和数 据,如振动、波动等实验。
工程应用
用于监测和控制工程设备的运 行状态,如机械振动、电气信
号等。
02
波动图象的绘制方法
数据准备
01
02
03
数据收集
收集与波动相关的数据, 如时间序列数据、价格数 据等。
波动图象的分类
时间序列图
以时间为横轴,表示某 一变量随时间变化的趋
势。
频谱图
以频率为横轴,表示某 一信号在不同频率下的
强度分布。
波形图
以时间为横轴,表示某 一信号的实时波形。
相图
以相角为横轴,表示某 一信号的相位变化。
波动图象的应用场景
01
02
03
04
数据分析
用于分析数据的变化趋势和规 律,如股票价格、气候变化等
未来需要进一步探索波动图象在不同领域的应用,挖掘其更大的潜力,同时需要 解决如何提高图象的准确性和可读性问题,以及如何更好地与其他技术进行集成 和应用等挑战。
THANKS
感谢观看
详细描述
周期性波动通常表现为图象中的规律性波峰和波谷。通过观察波动图象,我们可以发现一些具有周期性的模式。 为了更好地识别和利用周期性波动,可以使用一些统计方法,如傅里叶变换和小波变换,来分析图象中的频率成 分和周期性特征。
如何区分振动图象和波动图象

如何区分振动图象和波动图象
振动图象和波动图象是描述物理系统振动和波动的图形表示,它们在描述对象和所涉及的物理过程上有一些区别:
1. 振动图象:
•振动图象通常用来描述单个物体或系统的振动行为,例如弹簧振子、单摆等。
•振动图象通常包含一个时间轴和一个物体的位置或速度随时间的变化图。
•振动图象中通常只显示一个振动物体的运动状态,不涉及物理量的空间分布。
2. 波动图象:
•波动图象用于描述波在介质中的传播行为,可以是机械波、电磁波等。
•波动图象通常包含一个时间轴和一个或多个空间位置随时间的变化图,用来描述波在空间中的传播情况。
•波动图象中显示了波的传播方向、波的波长、振幅等波的特征。
因此,区分振动图象和波动图象的关键是看图象所描述的物理对象和物理过程。
振动图象主要描述个别物体或系统的振动行为,而波动图象主要描述波在空间中的传播行为。
1/ 1。
振动图像和波动图像的综合应用

强化训练:
4、一列沿着x轴正方向传播的横波,在t=0时刻的 波形如图甲所示.图甲中某质点的振动图象如图乙
所示.质点N的振幅是
图乙表示质点
m,振动周期为
m/s.
s,
(从质点K、L、M、N中选填)
的振动图象.该波的波速为
y/m y/m 0.8 0.8 K L N 0 0 0.5 1.01.5 2.0 1 2 3 4 x/m -0.8 -0.8 M 乙 甲
例1、图2为图1所示波的振源的振动图像。根据图 示信息回答下列问题:该波的波长为 0.4m 、波 20m/s 速是_________ 。
y/cm 15 x/cm 0 -15 10 20 30 40 50 0 -15 5 10 15 20 25 15 t/10-3 s y/cm
图1
图2
练习1、一列简谐横波沿x轴传播,图甲是t = 3s时 的波形图,图乙是波上x=2m处质点的振动图线.则 该横波的速度为 m/s,传播方向 1 为 X轴负方向. y/cm 0 x / 1 2 3 4 5m 图甲 0 y/cm
振幅、周期;任一时刻质点 振幅、波长;该时刻各质点 的位移、加速度、振动方向; 的位移、加速度;波中各质 点的振动方向。 y y T v x
0
t
0
原图象延伸T/4
拍一个人做广播操的录像
图象沿传播方向平移λ/4
拍许多人做广播操的一张照
课堂探究·突破考点
一、已知波动图像和波中某一质点振动图线确定波的传播方向
①波的频率;
②波的传播速度。
y/cm 1 0 -1 1
x1 2
3 4 5
x2
t/s 6
练习4.(2008年高考理综天津卷21)一列简谐横
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主要题型之四: 主要题型之四: 推理问题
例题7: 在XY平面内有一列沿 轴正向传播的简谐横波, 平面内有一列沿X轴正向传播的简谐横波 例题 平面内有一列沿 轴正向传播的简谐横波, 波速为3.0m/s,频率为 频率为2.5Hz,振幅为 振幅为8.0x10-2m,已知 已知t=0 波速为 频率为 振幅为 已知 的位移为y=4.0x10-2m,速度沿 轴正向 点在 点的 速度沿Y轴正向 点在P点的 时,P的位移为 的位移为 速度沿 轴正向,Q点在 右方9.0x10-1m处,对于 点来说 对于Q点来说 右方 处 对于 点来说: A.在t=0时,位移为 -4.0x10-2m 在 时 位移为 位移为y= B.在t=0时,速度沿 轴负方向 在 时 速度沿 速度沿y轴负方向 C.在t=0.1s时,位移为 -4.0x10-2m 在 位移为y= 时 位移为 D.在t=0.1s时,速度沿 轴正方向 在x
例⒌如图,一根张紧的水平绳上有相距14m 的a、 如图,一根张紧的水平绳上有相距14m 14 两点, 点在a点的右方, b两点,b点在a点的右方,当一列简谐波沿此绳 向右传播时, 点处于波峰位置时, 向右传播时,若a点处于波峰位置时,b点恰处 于平衡位置,且向下运动,经过1.00秒后, 1.00秒后 于平衡位置,且向下运动,经过1.00秒后,a位 于平衡位置,且向下运动, 于平衡位置,且向下运动,而b点恰处于波谷位 求这列波可能的波速? 置,求这列波可能的波速?
主要题型之二: 主要题型之二: 求波在任意时刻的波形图
例题一: 例题一: 如图所示为一列向右传播的简谐波在某时刻的波 形图, 试画出再经过T/4、 形图, 试画出再经过 、3T/4和5T/4时的波形图 和 时的波形图
Y O
波的传播方向
X
试画出该时刻前T/4、 试画出该时刻前 、3T/4和5T/4时刻的波形图 和 时刻的波形图
波 动 图 象 的 应 用
三、振动图象与波的图象的比较
振 动 图 O 象 图 t 象 X 波 的 O X Y
1.
图象的 O 波的 的 的 的 的
的 的
2.振动图象的 波的图象的 3. 图象的 4.振动图象 波的图象
波
四、波的图象的应用(一) 波的图象的应用 一
主要题型之一: 主要题型之一: 波的传播方向、质点的振动方向以及 波的传播方向、质点的振动方向以及 波形图三者知其二 而求其一。 三者知其二, 波形图三者知其二,而求其一。 例题一: 例题一: 如图所示为一列向右传播的简谐波在某时刻的 更多资源 更多资源 波形图 试求出波形图上A、 、 、 四个质点的振动方向 试求出波形图上 、B、C、D四个质点的振动方向
更多资源 更多资源
主要题型之四: 主要题型之四: 两种图象的综合应用 时的波形如图, 例6:一列简谐横波在 :一列简谐横波在t=1s时的波形如图,这 时的波形如图 列波中的P点的振动图象 点的振动图象, 列波中的 点的振动图象,那么该波的传播速 度和传播方向可能为: 度和传播方向可能为: Y/cm A、25cm/S,向左 、 , A、50cm/S,向左 、 , A、25cm/S,向右 、 , A、50cm/S,向右 、 ,
主要题型之三: 主要题型之三:
波动问题的多解性 波在传播过程中由于波动问题的多解性时间上的 周期性、空间上的周期性、 周期性、空间上的周期性、及传播方向的双向性 是导致波动问题的多解性的原因,若加限定条件, 是导致波动问题的多解性的原因,若加限定条件, 可使无限解转化为有限解或唯一解,具体表现在: 可使无限解转化为有限解或唯一解,具体表现在: ⒈波的传播方向不确定必有两种可能解 ⒉波形变化时间与周期关系不确定必有系列解 ⒊波形移动距离与波长关系不确定必有系列解
Y O
A
波的传播方向 C B D
X
例题二: 例题二: 如图所示为一列简谐波在某时刻的波形图, 如图所示为一列简谐波在某时刻的波形图, 已知图形上某点的振动方向如图所示。 已知图形上某点的振动方向如图所示。试求这列波 的传播方向
Y O
V
X
如果这个质点的振动方向向上,则波的传播方向又如何? 如果这个质点的振动方向向上,则波的传播方向又如何? 如果已知这个质点做减速运动,则波的传播方向又如何? 如果已知这个质点做减速运动,则波的传播方向又如何?
例 ⒋ 一列波在t1 时刻的波形图如图中的实线所示,t2 时 一列波在t 时刻的波形图如图中的实线所示, 刻的波形图如图中的虚线所示,已知Δt=t 刻的波形图如图中的虚线所示 , 已知 Δt=t2- t1=0.5S, 求 ①这列波可能的波速? 这列波可能的波速? 这列波向哪个方向传播? ②若波速为68m/s ,这列波向哪个方向传播? 若波速为68m/s 68 y/cm 5 0 -5 2 4 6 8 1012 X/m/S
