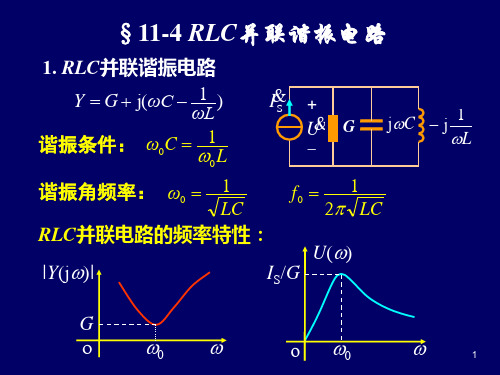
RLC并联谐振电路
RLC并联谐振电路 、 波特图 、 滤波器简介
2. 电感线圈与电容器的并联谐振 实际的电感线圈总是存在电阻,因此电感线圈与 电容器的并联电路如图所示:
R C L
Y jC
1 R jL
L R 2 j C 2 2 2 R (L) R (L)
谐振时:
ω0 L ω0C 2 0 2 R (ω0 L)
2 0
1 当 C2 0 时,发生并联谐振,0 L1
1 L1C2
7
§11-5 波特图
对电路和系统的频率特性进行分析时,为了直观 地观察频率特性随频率变化的趋势和特征,工程上常 采用对数坐标来作频响曲线,这种用对数坐标描绘的 频率响应图就称为频响波特图。
例 画出网络函数的波特图。
200j H ( j ) ( j +2)(j +10)
H ( ) H ( )
1 0 1 2 0 1 0 低通 高通 带通
1 2 带阻
12
典型无源滤波器
1)低通滤波器
2)高通滤波器
13
3)带通滤波器
4)带阻滤波器
14
下次课内容:
• 第十二章 三相电路
• 12.1 三相电路
• 12.2 线电压(电流)与相电压
(电流)的关系
作业:11-6(c,d),11-10,11-12
15
2
I S
+
U
_
I G
G
I I L C 1 jC j
L
当 Q >>1,IC=IL=QIS >>IS,过电流
3)=cos=1,P=U0IS 达到最大,Q = 0。
2 IS P U 0 IS G
RLC串并联交流电路及其谐振

知识小结
1.总电压U U R 2 (U L U C )2IR 2 (X LX C )2IZ
电抗
X
XL
XC
L
1 C
总阻抗 Z R 2 ( X L X C )2
总电压与电流的相位差 arctanXLXC
R
知识小结
2.交流电路的性质
当 XL >XC 时, > 0 ,u 超前 i , 呈感性 当 XL < XC 时 , < 0 , u 滞后 i ,呈容性 当 XL = XC 时 , = 0 , u. i 同相 ,呈纯电阻性
u u R u L u C U m s in (t )
+_ຫໍສະໝຸດ Cu_C
设 i Im sinωt
:则 uR I m R sin ω t
为同频率 正弦量
uL = Imω Lsin ( ω t 90)
uC
= Im
1 sin (ω t 90) ωC
相量图
参考相量
I
+
+
UL
UL
R U XL
_ XC
2)电路参数一定时,频率与电路性质的关系:
如:当频率 增加时, X L 增加、X c 减小,电路的感
性增加,容性减弱。
相量图
UL UC
UC
U
UL
I
UR UL UC
UL
UR UC I
U I
U
UR UC
(a) X>0
(b) X<0
(c) X=0
呈感性
呈容性
呈纯电阻性
2.电路的功率
i
+
+
R u_ R
电路的总电流最小。 (3)总电流与电源电压同
RLC串联和并联谐振电路谐振时的特性

具有电感、电容和电阻元件旳单口网络,在 某些工作频率上,出现端口电压和电流波形相位 相同旳情况时,称电路发生谐振。能发生谐振旳 电路,称为谐振电路。谐振电路在电子和通信工 程中得到广泛应用。本节讨论最基本旳RLC串联和 并联谐振电路谐振时旳特征。
一、RLC串联谐振电路
图12-15(a)表达RLC串联谐振电路,图12-15(b)是它 旳相量模型,由此求出驱动点阻抗为
图12-20
由以上各式和相量图可见,谐振时电阻电流与电流源 电流相等 IR IS 。电感电流与电容电流之和为零, 即 IL IC 0 。电感电流或电容电流旳幅度为电流源电 流或电阻电流旳Q倍,即
I L IC QIS QI R
并联谐振又称为电流谐振。
(8 47)
3.谐振时旳功率和能量
IL= IC增长一倍。总之,由 R、L和C旳变化引起 Q值变化
旳倍数与IL= IC变化旳倍数相同。
例12-8 图12-22(a)是电感线圈和电容器并联旳电路模型。 已知R=1, L=0.1mH, C=0.01F。试求电路旳谐振 角频率友好振时旳阻抗。
图12-22
解:根据其相量模型[图12-22((b)]写出驱动点导纳
(12 42)
电路谐振时电压到达最大值,此时电阻、电感和电容 中电流为(见下页)
IR GU IS
IL
1 U
j0 L
j
R
0L
IS
jQIS
IC j0CU j0 RCIS jQIS
(12 43) (12 44) (12 45)
其中
Q
R
0L
R 0 C
R
C L
(12 46)
称为RLC并联谐振电路旳品质因数,其量值等于谐振 时感纳或容纳与电导之比。电路谐振时旳相量图如图1220(b)所示。
rlc并联谐振电路实验报告

rlc并联谐振电路实验报告一、实验目的二、实验原理三、实验器材和仪器四、实验步骤五、实验结果分析六、实验结论一、实验目的本次实验旨在掌握并理解RLC并联谐振电路的基本原理及其特性,通过对电路参数的调整和观察,加深对谐振电路的认识和理解。
二、实验原理1. RLC并联谐振电路的基本原理RLC并联谐振电路由一个电感L、一个电容C和一个固定阻值R组成。
当该电路被接到交流源上时,如果交流源频率等于该电路的共振频率,则该电路会出现共振现象。
此时,整个电路中流动的电流将达到最大值,并且在L和C之间形成一个高阻抗区域。
2. 共振频率计算公式RLC并联谐振电路的共振频率f0可以通过以下公式进行计算:f0 = 1 / (2π√LC)3. 实验器材和仪器本次实验所需器材和仪器如下:- RLC并联谐振电路板- 信号发生器- 示波器- 万用表四、实验步骤1. 连接电路将RLC并联谐振电路板、信号发生器和示波器进行连接。
具体连接方式如下:- 将信号发生器的正极接到电路板上的“+”端口,负极接到“-”端口。
- 将示波器的探头分别接到电路板上的“Vout”和“GND”端口。
2. 测量电路参数使用万用表测量电路板上的电感L、电容C和阻值R,并记录下来。
3. 调节信号发生器频率将信号发生器输出频率调整为从几百Hz开始逐渐增加,直到观察到示波器上出现共振现象为止。
记录下此时的频率f0。
4. 观察示波器曲线观察示波器上的曲线,包括幅度和相位。
通过调整信号发生器频率,观察曲线幅度和相位随着频率变化而变化的情况。
5. 改变电路参数改变电路板上的L、C或R值,再次进行步骤3和4,并记录下观察结果。
五、实验结果分析在本次实验中,我们成功地制作了一个RLC并联谐振电路,并通过实验观察到了电路的共振现象。
通过调整信号发生器频率,我们成功地找到了该电路的共振频率f0,并观察到了示波器上的曲线幅度和相位随着频率变化而变化的情况。
在改变电路参数后,我们发现电路的共振频率和曲线幅度、相位等特性会发生变化。
RLC并联谐振电路

返回 上页 下页
11-5 波特图
对电路和系统的频率特性进行分析时,为了直观
地观察频率特性随频率变化的趋势和特征,工程上常
采用对数坐标来作频响曲线,这种用对数坐标描绘的
频率响应图就称为频响波特图。
例 画出网络函数的波特图。H ( j) 200 j ( j+2)(j+10)
解 改写网络函数为
H ( j)
-20lg 1+j/2
幅频(a) 波幅特频波图特图
100 200
-20lg 1+j/10
返回 上页 下页
相位(单位度)
90 arctan( ) arctan( )
2
10
。
。
90
90
O0。 0.1 0.2
12
-90。
ar-cttaann-(12 ) 2
a-rcttaann-1(10 ) 10
10 20
相频(b)波相特频波图特图
100 200
返回 上页 下页
11-6 滤波器简介
滤波器
工程上根据输出端口对信号频率范围的要求,设 计专门的网络,置于输入-输出端口之间,使输出端口 所需要的频率分量能够顺利通过,而抑制或削弱不需 要的频率分量,这种具有选频功能的中间网络,工程 上称为滤波器。
0
0
1 ( R)2 LC L
返回 上页 下页
注意 ① 电路发生谐振是有条件的,在电路参
数一定时,满足
1 (R)2 0 R LC L
L C
时, 可以发生谐振
② 一般线圈电阻R<<L,则等效导纳为
Y
R2
R
(L)2
j[C
R2
L (L)2
实验7RLC串`并联谐振电路

6
3.确定通频带宽度△f、并计算Q值:
Q
f0 f
4.由公式: 计算Q值,并与上述两个Q值进 行比较。
表1 RLC串联电路
L =0.1H( r0 = ) C = 0.5 μf R = 100 保持Vab=5伏
100 200 300
f (HZ) U( 伏 )
× 500 700 1000
Q 0L
谐振时: IL =
R
IC =
9
R2 (L CR 2 3CL2 )2
Z并
(CR)2 ( 2 LC 1)2
tg 1 L C(R 2 2 L2 )
R
谐振频率:
1 LC
(R)2 L
0
1
1 Q2
式中ω 为串联谐振的角频率
0
5
[实验内容与步骤]
1.测定串联电路的谐振曲线
(1)按图接好电路, 根据R、L和C的数据, 大致估计 电路谐振频率f 0 , 然后, 调节信号源的频率, 按表1进 行测试, 当R两端的电压降最大时, 处于谐振状态, 在 谐振频率附近可多测几次, 以能正确确定谐振频率。 按测试值作出谐振曲线。
f ( Hz) 700 800 900 950 x
1050 1100 1200 1300
U(R)
I
7
2.测定并联电路谐振曲线
只要找到主回路电流最小 时的对应频率, 就是改变信 号源频率, 测出Rs上的压降 最小时的频率, 即为并联电 路的谐振频率。
8
表2 RLC并联电路
rlc并联谐振电路的谐振频率

RLC并联谐振电路的谐振频率1. 引言RLC并联谐振电路是一种重要的电路结构,它在电子工程和通信领域中广泛应用。
谐振频率是RLC并联谐振电路的一个重要参数,它决定了电路的特性和性能。
本文将围绕任务名称:RLC并联谐振电路的谐振频率,详细介绍RLC并联谐振电路的基本原理、公式推导和计算方法。
2. RLC并联谐振电路RLC并联谐振电路由一个电感器(L)、一个电容器(C)和一个阻抗(R)组成,并且它们是并联连接的。
如图所示:在这个电路中,R代表负载阻抗,L代表电感,C代表电容。
当该电路处于谐振状态时,其频率达到最大值,此时称为谐振频率。
3. 谐振频率公式推导为了推导出RLC并联谐振电路的谐振频率公式,我们需要先分析电路的特性。
3.1 电感器电感器是由线圈或绕组构成的元件,它具有储存和释放电磁能量的能力。
其单位是亨利(H)。
3.2 电容器电容器是由两个导体之间的绝缘介质隔开的元件,它具有储存和释放电荷的能力。
其单位是法拉(F)。
3.3 阻抗阻抗是指在交流电路中对电流流动的阻碍程度,其单位是欧姆(Ω)。
在RLC并联谐振电路中,阻抗可以表示为:Z = R + jX其中,R为阻抗的实部,X为阻抗的虚部。
虚部X可以表示为:X = XL - XCXL为电感器的感抗,XC为电容器的感抗。
感抗可以分别表示为:XL = ωLXC = 1 / (ωC)其中,ω为角频率。
3.4 谐振频率公式当RLC并联谐振电路处于谐振状态时,其阻抗Z达到最小值。
根据以上推导可得:Z = R + j(XL - XC)当XL = XC时,阻抗Z达到最小值。
即:ωL = 1 / (ωC)解方程可得谐振频率:ω = 1 / sqr t(LC)由于谐振频率与角频率之间有关系:ω = 2πf其中,f为谐振频率。
综上所述,RLC并联谐振电路的谐振频率公式为:f = 1 / (2πsqrt(LC))4. 谐振频率计算方法根据上述推导的公式,我们可以计算RLC并联谐振电路的谐振频率。
电路设计--RLC并联谐振电路

电路设计--RLC并联谐振电路
RLC并联谐振电路是一种重要的电路类型,它由电感、电容和电阻元件组成。
当这些
元件被正确地连接在一起时,它们可以形成一个谐振电路,产生一个特定的频率响应。
在RLC并联谐振电路中,电容和电感是并联的,它们共享相同的输入信号,并形成一
个共振电路。
电容和电感的并联使得电路在共振频率下,具有较高的电感和电容值,从而
导致较低的复阻抗。
在这个频率点,电路的耗散功率最小。
如果电路中有电阻元件存在,
那么电路的损耗将会变大,共振频率也会发生变化。
在设计RLC并联谐振电路时,需要确定电容和电感的合适值以确保它们在所需的共振
频率下具有适当的阻抗。
可以通过计算共振频率、品质因数和带宽等参数来确定电路的性能,进而选择合适的元件。
在实际应用中,RLC并联谐振电路被广泛应用于各种领域,如无线电收发器、滤波器、功率放大器、音频放大器、电视机、雷达、天线等。
例如,在收音机中,谐振电路是用来
选择和放大无线电信号的。
总之,RLC并联谐振电路是一种重要的电路类型,它在电子学和通信领域具有广泛的
应用。
设计一个合适的RLC并联谐振电路需要综合考虑电路的参数、元件和应用要求,以
确保电路能够满足实际需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RLC 并联谐振电路
电路课程设计举例:?以R L C并联谐振电路
1.电路课程设计目的
(1)验证屉C并联电路谐振条件及谐振电路的待点;
(2)学习使用EWB仿真软件进行电路模拟。
2.仿真电路设计原理
本次设计的屉C串联电路图如下图所示。
图1屉C并联谐振电路原理图
理论分析与计算:
根据图1所给出的元件参数具体计算过程为
发生谐振时满足0()C =」一,则RLC并联谐振角频率0°和谐振频率/[分别是RLC并联谐振电路的待点如下。
(1)谐振时Y二G,电路呈电阻性,导纳的模最小|丫卜J G'+ J B'G•
(2)若外施电流人一定,谐振时,电压为最大,[J丄,且与外施电流同相。
G
(3)电阻中的电流也达到最大,且与外施电流相等,W
(4)谐振时// +/c = 0,即电感电流和电容电流大小相等,方向相反。
3.谐振电路设计内容与步骤
(1)电路发生谐振的条件及验证方法
这里有儿种方法可以观察电路发生串联谐振:
(1)利用电流表测量总电流人和流经R的电流人,两者相等时即为并联谐振。
(2)利用示波器观察总电源与流经R的电流波形,两者同相即为并联谐振。
例题:已知电感L为0. 02H,电容C为50uf,电阻R为2000。
由f =一计算得,f = 157.1Hz
J 02兀亦」°
按上图进行EWB的仿真,得到下图。
流经电阻R的电流和总电流I相等为10mA,流进电感L和电容C的总电流为5. 550uF,儿乎为零,所以电路达到谐振状态。
总电源与流经R的电流波形同相,所以电路达到并联谐振状态。
4.实验体会和总结
这次实验我学会了运用EWB仿真RLC并联谐振电路,并且运用并联谐振的特点判断达到谐振状态。
尤其是观察总电源与流经R的电流波形,两者同相即为并联谐振。
这种方法我们只能在实验中看到,平时做题试卷上是不可能观察到的。
这加深了我对谐振电路的理解。
