圆的基本性质测试题

合集下载

《圆的基本性质》单元测试题s-shuc302

《圆的基本性质》单元测试题王立根一、选择题：（28分）1、三角形外接圆的圆心是（）（A）三内角平分线的交点，（B）三边中垂线的交点，（C）三中线的交点，（D）三高线的交点，2、在①平行四边形，②菱形，③等腰梯形，④矩形，⑤正方形中，一定有外接圆的是（）（A）①②③（B）②③④（C）③④⑤（D）②④⑤3、一条弦把半径为r的圆分成1：2的两条弧，则弦长为（）（A ）（B）（C）（D）4、⊙O的直径为10cm，P是⊙O内一点，OP=3，则过点P的最短弦长为（）（A）4 （B）6 （C）8 （D）105、等腰三角形ABC中，AB=AC，∠A=30°，BC=6，则△ABC的外接圆直径为（）（A）（B）6 （C）（D）126、如图，⊙O中，AB=AD=CD，∠A=138°，则∠E=（）（A）48°（B）52°（C）58°（D）63°7、已知扇形的圆心角为120°，弧长等于半径为5cm的圆周长，则扇形的面积为（）（A）75cm2 (B)75πcm2 (c)150cm2 (D)150πcm2二、填空题：（21分）1、在⊙O中，直径为10cm，一条弦长为6cm，则这条弦的弦心距为---------cm.2、△ABC内接于以BC为直径的圆，且AB=8，AC=6，则△ABC的外接圆半径为--------。

3、已知四边形ABCD内接于⊙O，∠A：∠B：∠C=2：3：4，则∠D=---------。

4、如图，△ABC中，AB=AC，∠C=68°，以AB为直径的⊙O交AC于D，交BC于E，则∠DOE=--------度。

5、已知扇形面积为15πcm2,弧长为6πcm，则扇形半径为------- cm.6、弓形的半径为10cm，弦长为12cm，则弓高为---------cm.7、已知扇形面积为12cm2,半径为6cm,则扇形周长为--------cm三、如图，△ABC的外接圆直径AB交CD于E，已知∠C=65°，∠D=47°，求∠CEB的度数。

圆的基本性质单元能力测试(含答案)

第7题第8题第三章圆的基本性质能力提升测试卷一、选择题（共10小题，每小题3分，共30分）1. 如图，在⊙O 中，弦AB ∥CD ,若︒=∠40ABC ，则=∠BOD （） A. ︒20 B. ︒40 C. ︒50 D. ︒802.如图，点A 、B 、C 在⊙O 上，∠ACB =30°，则sin ∠AOB 的值是（） A ． B ．C ．D ．3.用圆心角为120°，半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（） A ．cm B ．3cm C ．4cm D ．4cm4.如图，AD 为⊙O 的直径，作⊙O 的内接正三角形ABC ，甲、乙两人的作法分别是：甲：1、作OD 的中垂线，交⊙O 于B ，C 两点，2、连接AB ，AC ，△ABC 即为所求的三角形乙：1、以D 为圆心，OD 长为半径作圆弧，交⊙O 于B ，C 两点。

2、连接AB ，BC ，CA ．△ABC 即为所求的三角形。

对于甲、乙两人的作法，可判断（）A ．甲、乙均正确B ．甲、乙均错误C ．甲正确、乙错误D ．甲错误，乙正确第4题第5题 5.如图，已知BD 是⊙O 直径，点A 、C 在⊙O 上，⌒AB =⌒BC，∠AOB =60°，则∠BDC 的度数是（）A.20°B.25°C.30°D. 40°6.如图，AB 为⊙O 的直径，弦CD ⊥AB 于E ，已知CD =12，则⊙O 的直径为（） A. 8 B. 10 C.16 D.20第1题第2题第3题DCB AO第9题7.如图所示，扇形AOB的圆心角为120︒，半径为2，则图中阴影部分的面积为( )334.-πA2334.-πB3234.-πC34.πD8.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（）A．CM=DM B．CB=DB C．∠ACD=∠ADC D．OM=MD9.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（）A．CM=DM B．CB=DB C．∠ACD=∠ADC D．OM=MD10.如图所示，圆O的弦AB垂直平分半径OC，则四边形OACB（）A、是正方形B、是长方形C、是菱形D、以上答案都不对二、填空题（共6小题，每小题4分，共24分）如图所示的圆面图案是用相同半径的圆与圆弧构成的．若向圆面投掷飞镖，则飞镖落在黑色区域的概率为．12．如图，AB是⊙O的弦，OC⊥AB于C．若AB=23，0C=1，则半径OB的长为________．13.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2．将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置，B，A，C′三点共线，则线段BC扫过的区域面积为．14．如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1，则凸轮的周长等于_________．15.如图所示，AB为⊙O的直径，AC为弦，OD∥BC交AC于点D，若AB=20cm，∠A=30°，则AD=cm．16.如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交AB于E，交⊙O于D．则AD=_____________．三、解答题（共7题，共66分）17、（本题8分）如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的A BCO第10题第11题第12题第13题第14题第15题第16题中点,AD ⊥BC 于点D .求证:AD =12BF .18（本题8分）.如图,⊙O 的直径AB 和弦CD 相交于点E ,∠CEA =30°, 求CD 的长.19．（本题8分）如图所示,OA 、OB 、OC都是圆O 的半径,∠AOB =2∠BOC ．求证:∠ACB =2∠BAC .20、（本题10分）如图，弧AC 是劣弧，M 是弧AC 中点，B 为弧AC 上任意一点，自M 向BC 弦引垂线，垂足为D ，求证：AB +BD =DC 。

浙教版圆的基本性质测试卷

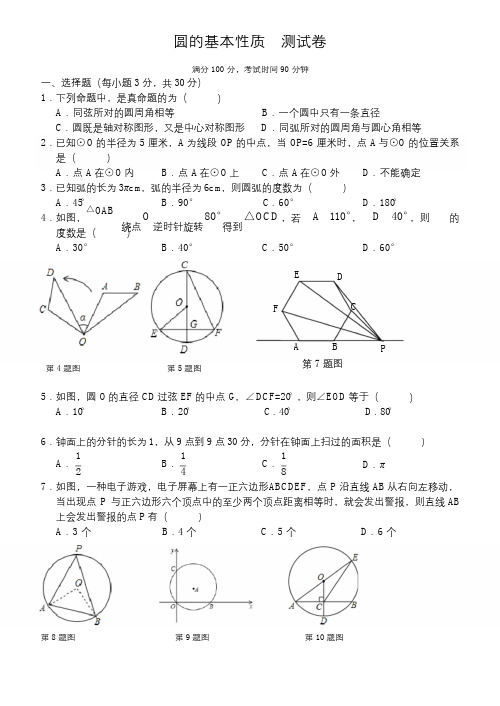
圆的基本性质测试卷满分 100 分，考试时间 90 分钟一、选择题（每小题 3 分，共 30 分） 1．下列命题中，是真命题的为（ A ．同弦所对的圆周角相等） B ．一个圆中只有一条直径C ．圆既是轴对称图形，又是中心对称图形D ．同弧所对的圆周角与圆心角相等2．已知⊙O 的半径为 5 厘米，A 为线段 OP 的中点，当 OP=6 厘米时，点 A 与⊙O 的位置关系是（ A ．点 A 在⊙O 内 3．已知弧的长为 3πcm ，弧的半径为 6cm ，则圆弧的度数为（） B ．点 A 在⊙O 上 C ．点 A 在⊙O 外 D ．不能确定） A ．45° 4．如图，△O AB度数是（ B ．90 ° O 绕点逆时针旋转 C ．60 ° D ．180°A 110° D 40° 80° △O C D 得到，若，，则的） A ．30° B ．40° C ．50° D ．60°E D CFABP第 7 题图第 4 题图第 5 题图5．如图，圆 O 的直径 C D 过弦 EF 的中点 G ，∠D C F =20°，则∠E O D 等于（ A ．10° B ．20° C ．40° D ．80° ） 6．钟面上的分针的长为 1，从 9 点到 9 点 30 分，分针在钟面上扫过的面积是（）1 A ．2 1 4 1 8B ．C ．D ．π7．如图，一种电子游戏，电子屏幕上有一正六边形ABC D E F ，点 P 沿直线 AB 从右向左移动，当出现点 P 与正六边形六个顶点中的至少两个顶点距离相等时，就会发出警报，则直线 AB 上会发出警报的点 P 有（ A ．3 个 B ．4 个） C ．5 个 D ．6 个第 8 题图第 9 题图第 10 题图8．如图，A、B、P是半径为2 的⊙O上的三点，∠APB=45°，则弦AB的长为（A．B．2 C．D．4 ）2 2 29．如图，在平面直角坐标系中，⊙A经过原点O，并且分别与x轴、y轴交于B、C两点，已知（8，0），（0，6），则⊙的半径为（）B C AA．3 B．4 C．5 D．810．如图，⊙O的半径O D⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，C D=2，则的长为（）E CA．2 15 B．8 C．2 10 D．2 13二、填空题（每小题3 分，共30分）11．一条弧所对的圆心角为72°，则这条弧所对圆周角为12．已知⊙O的面积为36π，若PO＝7，则点P在⊙O 13．一纸扇柄长30cm，展开两柄夹角为120°，则其面积为°．．cm ．214．如图，AB为⊙O的直径，弦CD⊥AB于点E，若C D=6 ，且AE：BE=1：3，则AB= ．第14题图第15题图第16题图第17题图15．如图，AB是⊙O的直径，点C是圆上一点，∠BA C=70°，则∠O CB= 16．已知：如图，圆内接四边形AB C D中，∠BCD=110°，则∠BAD=°．°．17．如图，O C是⊙O的半径，AB是弦，且O C⊥AB，点P在⊙O上，∠AP C=26°，则∠B O C= ．18．如图，⊙O中，弦AB、D C的延长线相交于点P，如果∠A O D=120°，∠BD C=25°，那么∠P= °．第18题图第19题图第20题图19．如图，A D、AC分别是直径和弦，∠CA D=30°，B是AC上一点，BO⊥A D，垂足为O，B O=5c m，则C D等于cm．20．如图：在⊙O中，AB、AC为互相垂直且相等的两条弦，O D⊥AB，OE⊥AC，垂足分别为D、E，若AC＝2 cm，则⊙O的半径为cm．三、解答题（共40分）21．（6分）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．(1)请你补全这个输水管道的圆形截面；(2)若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．22．（6分）如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连结E D、BE．(1)试判断DE与B D是否相等，并说明理由；(2)如果BC＝6，AB＝5，求BE的长．AE OC D B23．（6分）如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，A D，B D的长．24．（6分）如图，将小旗AC D B放于平面直角坐标系中，得到各顶点的坐标为A（－6，12），BC D B（－6，0），（0，6），（－6，6）．以点为旋转中心，在平面直角坐标系内将小旗顺时针旋转90°．(1)画出旋转后的小旗A′C′D′B′，写出点C′的坐标；(2)求出线段BA旋转到B′A′时所扫过的扇形的面积．25．（8分）如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使D C=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．(1)求证：∠B=∠D；(2)若AB=4，BC－AC=2，求CE的长．26．（8分）在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦A C翻折交AB于点D，连结．C D(1)如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；(2)如图2，若点D与圆心O不重合，∠BAC=25°，请直接写出∠DC A的度数．圆的基本性质测试卷6．A7．C10．D11．3612．外13．300π315．2016．7017．52°18．3519．520．3221．(1)图略；(2)10cm．22．(1)连结A D．∵AB是⊙O的直径，∴A D⊥BC，BE⊥AC．∵AB=AC，∴B D=C D，∴D E=B D．(2)由勾股定理，得BC－CE=BE=AB－AE．设AE=x，则6－(5－x)=5－x，解得222222222 7524x=．∴=BE AB A E2．2523．∵AB是直径．∴∠ACB＝∠A DB=90°．在Rt△ABC中，BC=AB2AC2102682（cm）．∵平分∠ACB，∴．∴=．又在△A DB D中，A D2B D2AB2=＋，C D A D B D Rt AB D∴A D=B D=5（cm）．224．(1)图略，C′（0，－6）；(2)∵A（－6，12），B（－6，0），∴AB=12．∴线段BA旋转到B′A′时所扫过的扇形的面积90122=36．36025．(1)∵AB 为⊙O 的直径，∴∠AC B =90°，∴AC ⊥B C ，∵D C=CB ，∴A D=AB ，∴∠B=∠D ；(2)解：设 BC=x ，则 AC=x －2，在 Rt △ AB C 中，AC +B C =AB ，∴（x －2） +x =4 ，解得：2 2 2 2 2 2 x =1+ 7 x ， =1－（舍去），∵∠ =∠ ，∠ =∠ ，∴ ∠ =∠ ，∴ = ，∵ = ， B E B D D E C D CE C D CB 7 1 2 ∴CE=CB=1+ ．7 1 1 126．(1)过点 O 作 O E ⊥A C 于 E ，则 AE= AC= ×2=1，∵翻折后点 D 与圆心 O 重合，∴OE= r ，2 2 22 3 1 在 △Rt A OE中， A O 2 AE 2 OE 2 + = r ，即 =1 +（），解得 = 3 ； r 2 2 r 2 2 (2)连接 BC ，∵AB 是直径，∴∠ACB =90°，∵∠BAC =25°，∴∠B =90°－∠BA C =90°－25°=65°，根据翻折的性质，⌒所对的圆周角等于 A C 所对的圆周角，∴∠D CA =∠ －∠ =65°－ B A A D C 25°=40°．圆的基本性质测试卷6．A7．C10．D11．3612．外13．300π315．2016．7017．52°18．3519．5 20．3 221．(1)图略；(2)10cm．22．(1)连结A D．∵AB是⊙O的直径，∴A D⊥BC，BE⊥AC．∵AB=AC，∴B D=C D，∴D E=B D．(2)由勾股定理，得BC－CE=BE=AB－AE．设AE=x，则6－(5－x)=5－x，解得2222222227 524x=．∴=BE AB A E2．2523．∵AB是直径．∴∠ACB＝∠A DB=90°．在Rt△ABC中，BC=AB2AC2102682（cm）．∵平分∠ACB，∴．∴=．又在△A DB D 中，A D2B D2AB2=＋，C D A D B D Rt AB D∴A D=B D=5（cm）．224．(1)图略，C′（0，－6）；(2)∵A（－6，12），B（－6，0），∴AB=12．∴线段BA旋转到B′A′时所扫过的扇形的面积90122=36．36025．(1)∵AB 为⊙O 的直径，∴∠AC B =90°，∴AC ⊥B C ，∵D C=CB ，∴A D=AB ，∴∠B=∠D ；(2)解：设 BC=x ，则 AC=x －2，在 Rt △ AB C 中，AC +B C =AB ，∴（x －2） +x =4 ，解得：2 2 2 2 2 2 x =1+ 7 x ， =1－（舍去），∵∠ =∠ ，∠ =∠ ，∴ ∠ =∠ ，∴ = ，∵ = ， B E B D D E C D CE C D CB 7 1 2 ∴CE=CB=1+ ．7 1 1 126．(1)过点 O 作 O E ⊥A C 于 E ，则 AE= AC= ×2=1，∵翻折后点 D 与圆心 O 重合，∴OE= r ，2 2 22 3 1 在 △Rt A OE中， A O 2 AE 2 OE 2 + = r ，即 =1 +（），解得 = 3 ； r 2 2 r 2 2 (2)连接 BC ，∵AB 是直径，∴∠ACB =90°，∵∠BAC =25°，∴∠B =90°－∠BA C =90°－25°=65°，根据翻折的性质，⌒所对的圆周角等于 A C 所对的圆周角，∴∠D CA =∠ －∠ =65°－ B A A D C 25°=40°．圆的基本性质测试卷6．A7．C10．D11．3612．外13．300π315．2016．7017．52°18．3519．5 20．3 221．(1)图略；(2)10cm．22．(1)连结A D．∵AB是⊙O的直径，∴A D⊥BC，BE⊥AC．∵AB=AC，∴B D=C D，∴D E=B D．(2)由勾股定理，得BC－CE=BE=AB－AE．设AE=x，则6－(5－x)=5－x，解得2222222227 524x=．∴=BE AB A E2．2523．∵AB是直径．∴∠ACB＝∠A DB=90°．在Rt△ABC中，BC=AB2AC2102682（cm）．∵平分∠ACB，∴．∴=．又在△A DB D 中，A D2B D2AB2=＋，C D A D B D Rt AB D∴A D=B D=5（cm）．224．(1)图略，C′（0，－6）；(2)∵A（－6，12），B（－6，0），∴AB=12．∴线段BA旋转到B′A′时所扫过的扇形的面积90122=36．36025．(1)∵AB 为⊙O 的直径，∴∠AC B =90°，∴AC ⊥B C ，∵D C=CB ，∴A D=AB ，∴∠B=∠D ；(2)解：设 BC=x ，则 AC=x －2，在 Rt △ AB C 中，AC +B C =AB ，∴（x －2） +x =4 ，解得：2 2 2 2 2 2 x =1+ 7 x ， =1－（舍去），∵∠ =∠ ，∠ =∠ ，∴ ∠ =∠ ，∴ = ，∵ = ， B E B D D E C D CE C D CB 7 1 2 ∴CE=CB=1+ ．7 1 1 126．(1)过点 O 作 O E ⊥A C 于 E ，则 AE= AC= ×2=1，∵翻折后点 D 与圆心 O 重合，∴OE= r ，2 2 22 3 1 在 △Rt A OE中， A O 2 AE 2 OE 2 + = r ，即 =1 +（），解得 = 3 ； r 2 2 r 2 2 (2)连接 BC ，∵AB 是直径，∴∠ACB =90°，∵∠BAC =25°，∴∠B =90°－∠BA C =90°－25°=65°，根据翻折的性质，⌒所对的圆周角等于 A C 所对的圆周角，∴∠D CA =∠ －∠ =65°－ B A A D C 25°=40°．。

(完整版)圆的基本性质检测试题

圆的基本性质测试题班级姓名得分一：选择题（每题3分，共30分）（）1.下列语句中不正确的有①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③圆是轴对称图形，对称轴是任意一条直径所在的直线， ④半圆是弧，⑸直径是圆内最长的弦，⑥等弧所对的圆周角相等. A ．3个Ｂ．4个 C ．5个Ｄ．6个（）2. 如图，已知⊙O 的半径为5，弦AB=6，M 是AB 上任意一点，则线段OM 的长可能是：A ．2.5B ．3.5C ．4.5D ．5.5 （）3．如图，，已知AB 是⊙O 的直径，∠BOC=400，那么∠AOE=A.400B. 600C.800D.1200（）4．如图，将圆沿AB 折叠后，圆弧恰好经过圆心，则 ∠AOB 等于:A ．60°B ．90°C ．120°D ．150°(第3题) (第4题) （第5题）（第6题）（）5. 两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为A ．(45)+ cmB ．9 cmC ．45cmD ．62cm（）6. 如图，BD 是⊙O 的直径，圆周角∠A = 30︒，则∠CBD 的度数是 A ．30︒ B ．45︒ C ．60︒ D ．80︒（）7．AB 为⊙O 的直径，C 、D 是⊙O 上的两点，∠BAC ＝30º，AD ＝CD ，则∠DAC 的度数是:A ．30ºB ．60ºC ．45ºD ．75º（第7题）（第8题）（第9题）（第10题）（）8．如图，在⊙O 中，CD 是直径，弦AB ⊥CD ，垂足为E ，连接BC ，若AB =2cm ，∠BCD =22°30′，则⊙O 的半径为: A .4cm B.2cm C.1cm D.0.5cm （）9. 已知⊙O 的直径AB=12，弦AC=6，AD=62，则∠CAD=A. 60°B. 450C.1050 或150D. 60°或 450（）10．如图，AB 是⊙O 的直径，AB=2，点C 在⊙O 上，∠CAB=30°，D 为的中点，P 是直径AB 上一动点，则PC+PD 的最小值为: Ａ．22 Ｂ.2 Ｃ.1 Ｄ.2二：填空题（每题3分，共18分）11. 如图，⊙O 的半径OA=10cm ，弦AB=16cm ，P 为AB 上一动点，则点P 到圆心O 的最短距离为。

圆基本性质测试

圆的基本性质小测一、选择题（30）（）1、如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE的长为A、10 B、8 C、6 D、4（）2、一条排水管的截面如图所示.已知排水管的截面圆半径10O B=，截面圆圆心O到水面的距离O C是6，则水面宽A B是A.16B.10C.8D.6（）3、如图，⊙O是△A BC的外接圆，∠OCB＝40°，则∠A的度数等于A．60° B．50° C．40° D．30°（）4、如图，⊙O过点B、C，圆心O∠BAC=90°，OA=1，BC=6。

则⊙O的半径为 A．6D．（）5、如图，若AB是⊙0的直径，ABD=58°，则∠BCD =A 116°B 32°C 58°D 64°（）6、如图，⊙O是△ABC的外接圆，∠BAC=60°,若⊙O的半径OC为2，则弦BC的长为 A．1 B C．2 D．（）7、矩形ABCD中，AB＝8，BC=P在边AB上，且BP＝3AP，如果圆P是以点P为圆心，PD为半径的圆，那么下列判断正确的是A 点B、C均在圆P外；B 点B在圆P外、点C在圆P内；C 点B在圆P内、点C在圆P外D 点B、C均在圆P内．（）8、如图，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD ＝105°，则∠DCE的大小是A． 115° B． 105°C． 100°D． 95°（）9、如图，已知E F是⊙O的直径，把A∠为60 的直角三角板ABC的一条直角边B C放在直线E F上，斜边A B与⊙O交于点P，点B与点O重合．将三角板ABC沿O E方向平移，使得点B与点E重合为止．设POF x∠= ，则x的取值范围是 A．3060x≤≤ B．3090x≤≤C．30120x≤≤ D．60120x≤≤（）10、下列说法正确的是A、三点确定一个圆B、直径所对的圆周角是直角C、度数相等的弧是等弧D、相等的圆心角所对的弧相等二、填空题11、若O为ABC∆的外心，且60=∠BOC,则__________=∠BAC12、点P是⊙O所在平面上一定点，点P到圆上的最大距离和最小距离分别为10和2，则该圆的直径为13、在⊙O中，AB为直径，CD为弦，AB⊥CD，P为圆周上与C，D不重合的任意一点，若∠COB=50°，则∠CPD是______________度14、在半径为1的⊙O中，弦AB、AC的长分别为3和2，则∠BAC的度数是___________15、圆的弦长等于它的半径，那么这条弦所对的圆周角的度数是____16、在半径为5cm的⊙O中，弦AB＝6cm，弦CD＝8cm，且AB∥CD，求AB与CD之间的距离是_________17、在同一平面内有三条公路两两相交，一供电站到这三条公路的距离都相等，则这样的供电站可以建___个18、点M是半径为5的⊙O内一点，且OM=4，在过M点的所有⊙O的弦中，你认为弦长为整数的弦的条数有_____条19、已知点A（2，0），B(-2,0),圆D的圆心为（0，3），半径为2.5。

圆的基本性质练习题

圆的基本性质练习题姓名______________学号__________一．选择题：（本题共10小题，每小题3分，共30分）1. 已知扇形的弧长为π8，扇形的圆心角为060，则这个扇形的半径为（）A. 12B. 24C. 62D. 482．如图，△ABC 的顶点A 、B 、C 均在⊙O 上，若∠ABC+∠AOC=90°，则∠AOC 的大小是（）A. 030B. 045C. 060D. 0703．下列说法正确的是（）A ．半圆是弧，弧也是半圆B ．三点确定一个圆C ．平分弦的直径垂直于弦D ．直径是同一圆中最长的弦4．如图，DC 是⊙O 直径，弦AB ⊥CD 于F ，连接BC ，DB ，则下列结论错误的是（）A ．弧AD=弧BDB ．AF=BFC ．OF=CFD D ．∠DBC=90°5．已知⊙O 的直径为10，若PO=5，则点P 与⊙O 的位置关系是（）A ．点P 在⊙O 内B ．点P 在⊙O 上C ．点P 在⊙O 外D ．无法判断6.如图，A 、B 、C 、D 四个点均在⊙O 上，∠AOD=70°，AO ∥DC ，则∠B 的度数为（）A.40°B.45°C.50°D.55°7．如图，⊙O 的半径为10，若OP=8，则经过点P 的弦长可能是（）A ．10B ．6C ．19D ．228. 如图，在半径为13cm 的圆形铁片上切下一块高为8cm 的弓形铁片，则弓形弦AB 的长为（）A 、10cmB 、16cmC 、24cmD 、26cm9.如图，点C 是以AB 为直径的半圆O 的三等分点，AC=2，则图中阴影部分的面积是（）A 、334-πB 、3234-πC 、332-πD 、332-π 10．如图，Rt △ABC 中，AB ⊥BC ，AB=6，BC=4，P 是△ABC 内部的一个动点，且满足∠PAB=∠PBC ，则线段CP 长的最小值为（）A ．23 B ．2 C ．13138 D ．131312 二．填空题（本题共6小题，每题4分，共24分）温馨提示：填空题必须是最简洁最正确的答案！ 11．一正六边的边长为8，则它的外接圆的直径为_______________12．四边形ABCD 内接于⊙O ，弧AB ：弧BC ：弧CD=2：3：5，∠BAD=120°，则∠ABC=_____13．如图，将弧AC 沿弦AC 折叠交直径AB 于圆心O ，则弧AC= 度．14．在半径为2的圆中，弦AC 长为1，M 为AC 中点，过M 点最长的弦为BD ，则四边形ABCD 的面积为15．如图，⊙O 是△ABC 的外接圆，AO ⊥BC 于点F ，D 为弧AC 的中点，且弧CD 的度数为70°，则∠BAF=16．如图，⊙O 的半径OD ⊥弦AB 于点C ，连结AO 并延长交⊙O 于点E ，连结EC ．若AB=8，CD=2，则EC 的长为________________17．已知△ABC 的边BC=23cm ，且△ABC 内接于半径为2cm 的⊙O ，则∠A= 度．18.如图，C 、D 是以AB 为直径的圆O 上的两个动点（点C 、D 不与A 、B 重合），在运动过程中弦CD 始终保持不变，M 是弦CD 的中点，过点C 作CP ⊥AB 于点P ．若CD=3，AB=5，PM=x ，则x 的最大值是_________.19.如图，△ABC 内接于⊙O ，∠B=90°，AB=BC ，D 是⊙O 上与点B关于圆心O 成中心对称的点，P 是BC 边上一点，连接AD 、DC 、AP ．已知AB=8，CP=2，Q 是线段AP 上一动点，连接BQ 并延长交四边形ABCD 的一边于点R ，且满足AP=BR ，则=QRBQ ______ 三．解答题（共6题，共66分）温馨提示：解答题应将必要的解答过程呈现出来！20（本题6分）如图，AB ，CD 是⊙O 的两条直径，过点A 作AE ∥CD 交⊙O 于点E ，连接BD ，DE ，求证：BD=DE ．21（本题8分）．如图所示，AB=AC ，AB 为⊙O 的直径，AC 、BC 分别交⊙O 于E 、D ，连结ED 、BE ．（1）求证：BE ⊥AC ；（2）求证：BD=DE ；22（本题8分）．如图，在直角坐标系中，⊙E 的半径为5，点E （1，﹣4）．（1）求弦AB 与弦CD 的长；（2）求点A ，B 坐标．23（本题10分）．如图，AB 是⊙O 的直径，弦CD⊥AB 于点E ，点P 在⊙O 上，PB 与CD 交于点F ，∠PBC=∠C．（1）求证：CB∥PD；（2）若∠PBC=22.5°，⊙O 的半径R=2，求劣弧AC 的长度．24.如图，在⊙O 中，两弦AB 与CD 的中点分别是P 、Q ，且⋂⋂=CD AB ，连结PQ ，求证：∠APQ ＝∠CQP 。

圆的基本性质-测试题

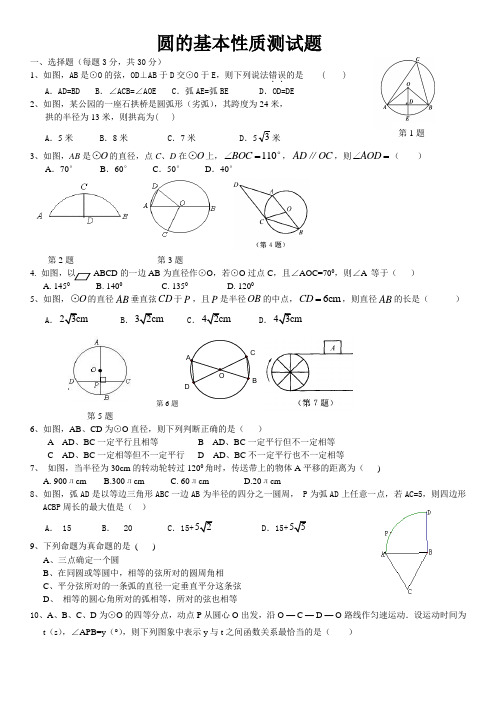
CBOAD圆的基本性质测试题一、选择题（每题3分，共30分）1、如图，AB 是⊙O 的弦，OD ⊥AB 于D 交⊙O 于E ，则下列说法错误．．的是 ( ) A ．AD=BD B ．∠ACB=∠AOE C ．弧AE=弧BE D ．OD=DE2、如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为( )A ．5米B ．8米C ．7米D ．53米3、如图，AB 是O ⊙的直径，点C 、D 在O ⊙上，110BOC ∠=°，AD OC ∥，则AOD ∠=（）A ．70°B ．60°C ．50°D ．40°第2题第3题4. 如图，以 ABCD 的一边AB 为直径作⊙O ，若⊙O 过点C ，且∠AOC=700，则∠A 等于（） A. 1450 B. 1400 C. 1350 D. 12005、如图，O ⊙的直径AB 垂直弦CD 于P ，且P 是半径OB 的中点，6cm CD =，则直径AB 的长是（）A ．23cmB ．32cmC ．42cmD ．43cm第5题6、如图，AB 、CD 为⊙O 直径，则下列判断正确的是（）A AD 、BC 一定平行且相等B AD 、BC 一定平行但不一定相等 C AD 、BC 一定相等但不一定平行 D AD 、BC 不一定平行也不一定相等7、如图，当半径为30cm 的转动轮转过1200角时，传送带上的物体A 平移的距离为（ ) A. 900лcm B.300лcm C. 60лcm D.20лcm8、如图，弧AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周， P 为弧AD 上任意一点，若AC=5，则四边形ACBP 周长的最大值是（）A ． 15B ． 20C ．15+52D ．15+55 9、下列命题为真命题的是 ()A 、三点确定一个圆B 、在同圆或等圆中，相等的弦所对的圆周角相C 、平分弦所对的一条弧的直径一定垂直平分这条弦D 、相等的圆心角所对的弧相等，所对的弦也相等10、A 、B 、C 、D 为⊙O 的四等分点，动点P 从圆心O 出发，沿O — C — D — O 路线作匀速运动．设运动时间为t （s ），∠APB=y （°），则下列图象中表示y 与t 之间函数关系最恰当的是（）第6题第1题OAC B第16题第14题图ECDAB二、填空题（每题4分，共32分）11、已知⊙O 的周长为6π，当PO 时，点P 在⊙O 上。

第3章圆的基本性质浙教版数学九年级上册测试(含答案)

浙教版数学九年级上册第三章圆的基本性质一、选择题1．下列说法正确的是（）A．三个点可以确定一个圆B．半圆（或直径）所对的圆周角是直角C．相等的圆心角所对的弧相等D．长度相等的弧是等弧2．已知一个扇形的面积是24π，弧长是2π，则这个扇形的半径为（）A．24B．22C．12D．63．如图，点A、B、C在⊙O上，∠C=40∘，则∠AOB的度数是（）A．50∘B．60∘C．70∘D．80∘4．如图，AB是⊙O的直径，弦CD⊥AB于点E，若BE=5，AE=1，则弦CD的长是（）A．5B．5C．25D．65．将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A，B的读数分别为86°，30°，则∠ACB的度数是（）A．28°B．30°C．36°D．56°6．如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则BC的长为（）A ．103πB ．109πC ．59πD ．518π7．如图， AB 是半圆O 的直径，点C ，D 在半圆O 上．若 ∠ABC =50° ，则 ∠BDC 的度数为（）A ．90°B ．100°C ．130°D ．140°8．如图，正六边形ABCDEF 内接于⊙O ，若⊙O 的周长等于6π，则正六边形的边长为（）A ．3B ．6C ．3D ．239．如图，正五边形ABCDE 内接于⊙O ，阅读以下作图过程：①作直径AF ；②以点F 为圆心，FO 为半径作圆弧，与⊙O 交于点M ，N ；③连接AM ，MN ，AN ．结论Ⅰ：△AMN 是等边三角形；结论Ⅱ：从点A 开始，以DN 长为半径，在⊙O 上依次截取点，再依次连接这些分点，得到正十八边形．对于结论Ⅰ和结论Ⅱ，下列判断正确的是（）A ．Ⅰ和Ⅱ都对B ．Ⅰ和Ⅱ都不对C．Ⅰ不对Ⅱ对D．Ⅰ对Ⅱ不对10．如图，抛物线y＝x2﹣8x+15与x轴交于A、B两点，对称轴与x轴交于点C，点D（0，﹣2），点E （0，﹣6），点P是平面内一动点，且满足∠DPE＝90°，M是线段PB的中点，连接CM．则线段CM的最大值是（）A．3B．412C．72D．5二、填空题11．如图，在⊙O中，弦AB，CD相交于点P．若∠A＝40°，∠APD＝75°，则∠B＝ °．12．如图，AB、AC是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N．如果MN=2.5，那么BC= ．13．如图，四边形ABCD内接于⊙O ，若四边形ABCD的外角∠DCE=65°，则∠BAD的度数是．14．如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝70°，则∠EAC的度数为 .15．我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术：“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率π的近似值为3.1416．如图，⊙O的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计⊙O，若用圆内接正十二边形作近似估计，可得π的估计值为．的面积，可得π的估计值为33216．如图，点M(2,0)、N(0,4)，以点M为圆心5为半径作⊙M交y轴于A、B两点，点C为⊙M上一动点，连接CN，取CN中点D，连接AD、BD，则A D2+B D2的最大值为．三、解答题17．如图，四边形ABCD为⊙O的内接四边形，AC是⊙O的直径，AD=BD，∠CAB=32°．求∠ACD的度数．18．如图，OC为⊙O的半径，弦AB⊥OC于点D，OC＝10，CD＝4，求AB的长．19．如图，正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求解答下列问题：（1）△A1B1C1与△ABC关于坐标原点O成中心对称，则B1的坐标为__________；（2）BC与B1C1的位置和数量关系为___________；（3）将△ABC绕某点逆时针旋转90°后，其对应点分别为A2(―1,―2)，B2(1,―3)，C2(0,―5)，则旋转中心的坐标为___________．20．如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于点D，（1）求∠ACB的度数；（2）求BC的长；（3）求AD，BD的长．21．如图，AB是⊙O的直径，C是⏜BD的中点，CE⊥AB于点E，BD交CE于点F．（1）求证：CF=BF．（2）若CD=6，AC=8，求⊙O的半径及CE的长．22．如图所示，AB为☉O的直径，AC是☉O的一条弦，D为BC的中点，作DE⊥AC于点E，交AB的延长线于点F，连接DA.（1）若AB=90 cm，则圆心O到EF的距离是多少?说明你的理由.（2）若DA=DF=63，求阴影部分的面积(结果保留π).23．如图，AB是⊙O的直径，弦CD⊥AB与点E，已知AB=10，AE=8，点P为AB上任意一点，（点P不与A､B重合），连结CP并延长与⊙O交于点Q，连QD，PD，AD．（1）求CD的长．（2）若CP=PQ，直接写出AP的长．（3）①若点P在A，E之间（点P不与点E重合），求证：∠ADP=∠ADQ．②若点P在B，E之间（点P不与点E重合），求∠ADP与∠ADQ满足的关系．答案解析部分1．【答案】B2．【答案】A3．【答案】D4．【答案】C5．【答案】A6．【答案】B7．【答案】D8．【答案】C9．【答案】D10．【答案】C11．【答案】3512．【答案】513．【答案】65°14．【答案】15°15．【答案】316．【答案】49217．【答案】61°18．【答案】1619．【答案】（1）(2,2)；（2）平行且相等；（3）(0,―1)．20．【答案】（1）∠ACB=90°（2）BC=8cm（3）BD=AD=52cm21．【答案】（1）证明：∵AB是⊙O的直径，∴∠ACB=90°，∴∠A=90°-∠ABC．∵CE⊥AB，∴∠ECB=90°-∠ABC，又∵C是BD的中点，∴CD=BC，∴∠DBC=∠A，∴∠ECB=∠DBC，∴CF= BF；（2）解：∵BC=CD，∴BC=CD=6．在Rt△ABC中，AB= BC2+AC2=62+82=10，∴⊙O的半径为5；∵S△ABC= 12AB×CE= 12BC×AC，∴CE= BC×ACAB =6×810=245.22．【答案】（1）解：如图所示，连接OD，∵D为BC的中点，∴∠CAD=∠BAD.∵OA=OD，∴∠BAD=∠ADO.∴∠CAD=∠ADO.∴OD∥AE.∵DE⊥AC，∴OD⊥EF.∴OD的长是圆心O到EF的距离.∵AB=90 cm，∴OD=12AB=45 cm.（2）解：如图所示，过点O作OG⊥AD交AD于点G.∵DA=DF，∴∠F=∠BAD.由(1)，得∠CAD=∠BAD，∵∠F+∠BAD+∠CAD=90°，∴∠F=∠BAD=∠CAD=30°.∴∠BOD=2∠BAD=60°，OF=2OD.∵在Rt△ODF中，OF2-OD2=DF2，∴(2OD)2-OD2=(63)2，解得OD=6.在Rt△OAG中，OA=OD=6，∠OAG=30°，AG=OA2―O G2=33，AD=23，S△AOD=1×63×3=93.2+93=6π+93.∴S阴影=S扇形OBD+S△AOD=60π×6236023．【答案】（1）解：连接OD，∵直径AB=10，AE=8，∴BE=2.∴OE=5-2=3.又∵AB⊥CD，在Rt△PED中，P D2=P E2+E D2∴ED=52―32=4∴CD=2ED=8（2）解：若CP=PQ，则点P与点O重合，或点P与点E重合．所以AP=5或8（3）解：①连接AC，由图可知∠ACQ=∠ADQ，因为AB是⊙O的直径，AB⊥CD，所以CE=DE，即AB是CD的垂直平分线，所以AC=AD，PC=PD，因为AP=AP，所以∠ACP=∠ADP ，所以∠ADP=∠ADQ ．②∠ADP+∠ADQ=180°．理由如下：连接AC ，因为AB 是直径，AB ⊥CD ，所以AC=AD ，CE=DE ，所以△ACP ≌△ADP （SSS ），所以∠ACP=∠ADP ，因为∠ACP=12ADQ ，∠ADQ=12ACQ ，所以∠ACP+∠ADQ=12（ADQ +ACQ ）=180°．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

内容：满分：100分
一、选择题（本大题共10小题，每小题3分，共30分） 1．⊙O 中，直径AB ＝a ，弦CD ＝b,,则a 与b 大小为（）
A ．a ＞b
B ．a ≥b
C ．a ＜b
D ． a ≤b
2.下列语句中不正确的有（）
①相等的圆心角所对的弧相等； ②平分弦的直径垂直于弦； ③圆是轴对称图形，任何一条直径都是它的对称轴； ④半圆是弧。

A ．1个Ｂ．2个 C ．3个Ｄ．4个
3．已知⊙O 的半径为5，点O 到弦AB 的距离为3，则⊙O 上到弦AB 所在直线的距离为2的点有（） A ．1个
B ．2个
C ．3个
D ．4个
4．如图，已知⊙O 的半径为5，弦AB=6，M 是AB 上任意一点，则线段OM 的长可能是（）
A ．
B ．3.5
C ．
D ．
5．如图，
，已知AB 是⊙O 的直径，∠BOC=400，那么∠AOE=（）
B. 600
C.800
6．如图，将圆沿AB 折叠后，圆弧恰好经过圆心，则等于（） A ．60° B ．90° C ．120° D ．150°
(第4题) (第5题) (第6题)
7．已知⊙O 的半径是5cm ，弦AB ∥CD ，AB ＝6cm ，CD ＝8cm ，则AB 与CD 的距离是（） A ．1 cm B ．7 cm C.1 cm 或7 cm D.无法确定 8．如图，BD 是⊙O 的直径，圆周角∠A = 30，则∠CBD 的度数是（） A ．30
B ．45
C ．60
D ．80
9．如图，AB 为⊙O 的直径，C 、D 是⊙O 上的两点，∠BAC ＝30º，AD ＝CD ，则∠DAC 的度数是（） A ．30º
B ．60º
C ．45º
D ．75º
10．如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为（）
A ．(45) cm
B ．9 cm
C ．45cm
D ．62cm
(第8题) (第9题) (第10题)
二、填空题（本大题共4小题，每小题３分，共12分）
11．如图，⊙O 的半径OA=10cm ，弦AB=16cm ，P 为AB 上一动点，则点P 到圆心O 的最短距离为。

12．如图，AB 为⊙O 的弦，⊙O 的半径为5，OC ⊥AB 于点D ，交⊙O 于点C ，且CD ＝1，则弦AB 的长是。

（11）（12）（13）（14）
13．如图，CD 是⊙O 的直径，弦AB ⊥CD ，连接OA ，OB ，BD ，若∠AOB ＝100°，则∠ABD ＝度。

14．如图，点A 、B 是⊙O 上两点，AB=10，点P 是⊙O 上的动点（P 与A ，B 不重合）连结AP ，PB ，过点O 分别作OE ⊥AP 于点E ，OF ⊥PB 于点F ，则EF= 。

三、（本题共2小题，每小题5分，满分10分）
15．如图所示，AB 是⊙O 的弦，半径OC 、OD 分别交AB 于点E 、F ，且AE=BF ，请你找出线段
OE 与OF 的数量关系，并给予证明。

16．如图是一块圆形砂轮破碎后的部分残片,试找出它的圆心, 并将它还原成一个圆．要求：
１、尺规作图；２、保留作图痕迹。

（可不写作法。

）
四、（本题共2小题，每小题5分，满分10分）
O P
B
A A
D B
C
O
_ O _E
_ D
_ C _ B
_ A
A
B
O M
A E
O
F
B P
AmB O 30
D
B
C
A
O
D C
B
A
17.如图，在⊙O 中，＝2 ，试判断AB 与CD 的大小关系，并说明理由。

18．如图所示，⊙O 的直径AB 和弦CD 交于E ，已知AE=6cm ，EB=2cm ，∠CEA ＝30°，求CD 。

五、（本题共2小题，每小题6分，满分12分）
19．如图，OA 和OB 是⊙O 的半径，并且OA ⊥OB ，P 是OA 上任一点，BP 的延长线交⊙O 于Q ，
过Q 的⊙O 的切线交OA 的延长线于R 。

求证：RP ＝RQ 。

20. 如图，BC 为⊙O 的直径，AD ⊥BC ，垂足为D 。

＝，BF 和AD 相交于E 。

试猜
想AE 与BE 的长度之间的关系，并请说明理由。

六、（本大题满分8分）
21．如图所示，AB 是⊙O 的一条弦，OD AB ⊥，垂足为C ，交⊙O 于点D ，点E 在⊙O 上。

（1）若52AOD ∠=，求DEB ∠的度数；（2）若3OC =，5OA =，求AB 的长。

七、（本大题满分8分）
22．如图所示，已知AB 为⊙O 的直径，CD 是弦，且AB ⊥CD 于点E 。

连接AC 、OC 、BC 。

（1）求证：∠ACO=∠BCD 。

（2）若EB=8cm ，CD=24cm ，求⊙O 的直径。

八、（本大题满分10分）
23．如图所示，已知O 是∠EPF 的平分线上的一点，以O 为圆心的圆与角的两边分别交于点A 、B 和C 、D 。

⑴求证：PB=PD 。

⑵若角的顶点P 在圆上或圆内，⑴中的结论还成立吗若不成立，请说明理由；若成立，请加以证明。

#
O
R
B
Q
A
P
C
B
A
O
D
O
E C
B
E B
C A
O
E
D B
O C
AB AF。