双闭环比值控制系统仿真
三级液位仿真系统双闭环比值控制系统实验报告
三级液位仿真系统双闭环比值控制系统实验报告实验目的：研究三级液位仿真系统的双闭环比值控制系统的控制性能。
实验原理：三级液位仿真系统由三个互相连接的水罐组成，每个水罐包含一个水泵和一个液位传感器。
具体地说，第一个水罐是输入罐，第二个水罐是中间罐，第三个水罐是输出罐。
输入罐和中间罐之间通过一个水泵连接，中间罐和输出罐之间通过另一个水泵连接。
每个水罐的液位传感器用于测量液位。
控制目标是使输出罐的液位与输入罐的液位的比值保持特定的设定值。
为了实现这个目标，可以采用双闭环控制策略。
外环控制器根据输出罐的液位误差来调整中间罐的液位设定值，内环控制器根据中间罐的液位误差来调整输出罐的液位设定值。
这样，中间罐的液位将根据外环控制器的输出、输出罐的液位将根据内环控制器的输出来调节。
实验步骤：1. 搭建三级液位仿真系统并连接控制器。
2. 设定输入罐的液位设定值，进行稳定步变响应实验，记录输出罐的液位波动情况。
3. 分析实验结果，评估控制性能。
4. 重复步骤2和步骤3，分别设定不同的输入罐的液位设定值，比较不同设定值下的控制性能。
实验结果：根据实验步骤进行实验后，记录并分析实验结果，得出如下结论：1. 在稳定步变响应实验中，输出罐的液位波动较小，表明双闭环比值控制系统具有较好的控制性能。
2. 随着输入罐的液位设定值的增加，输出罐的液位波动增加，说明双闭环比值控制系统对于高液位设定值下的控制性能稍有不足。
实验结论：通过这个实验，我们得出了三级液位仿真系统双闭环比值控制系统的控制性能。
实验结果表明，双闭环比值控制系统能够实现较好的液位控制性能，但在高液位设定值下稍有不足。
这个实验为进一步研究和改进液位控制系统提供了参考依据。
双闭环控制仿真报告
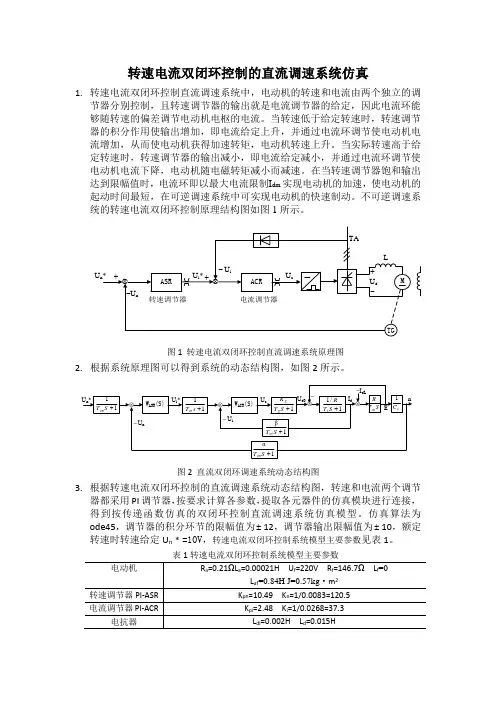
转速电流双闭环控制的直流调速系统仿真1. 转速电流双闭环控制直流调速系统中，电动机的转速和电流由两个独立的调节器分别控制，且转速调节器的输出就是电流调节器的给定，因此电流环能够随转速的偏差调节电动机电枢的电流。
当转速低于给定转速时，转速调节器的积分作用使输出增加，即电流给定上升，并通过电流环调节使电动机电流增加，从而使电动机获得加速转矩，电动机转速上升。
当实际转速高于给定转速时，转速调节器的输出减小，即电流给定减小，并通过电流环调节使电动机电流下降，电动机随电磁转矩减小而减速。
在当转速调节器饱和输出达到限幅值时，电流环即以最大电流限制I dm 实现电动机的加速，使电动机的起动时间最短，在可逆调速系统中可实现电动机的快速制动。
不可逆调速系统的转速电流双闭环控制原理结构图如图1所示。
U 图1 转速电流双闭环控制直流调速系统原理图2. 根据系统原理图可以得到系统的动态结构图，如图2所示。
图2 直流双闭环调速系统动态结构图3. 根据转速电流双闭环控制的直流调速系统动态结构图，转速和电流两个调节器都采用PI 调节器，按要求计算各参数，提取各元器件的仿真模块进行连接，得到按传递函数仿真的双闭环控制直流调速系统仿真模型。
仿真算法为ode45，调节器的积分环节的限幅值为±12，调节器输出限幅值为±10，额定转速时转速给定U n ﹡=10V ，转速电流双闭环控制系统模型主要参数见表1。
1） 电流环仿真图3 电流环仿真模型设置好参数后，设定仿真时间为0.1s ，启动仿真过程，用示波器观察仿真结果。
图4-a 和图4-b 分别是以KT=0.25和KT=1.0的关系式按典型I 型系统设计PI 调节器得到的电流环的阶跃响应仿真结果，图a 无超调，但上升时间长，图b 超调大，但上升时间短。
a 无超调的仿真结果b 超调量较大的仿真结果图4 电流环仿真波形从图4的仿真结果中可以看出，在直流电动机的恒流升速阶段，电流值低于λI N =200A ，其原因是电流调节器系统受到电动机反电势的扰动，如图3所示，它是一个线性渐增的扰动量，所以系统做不到无静差，而是I d 略低于I dm 。
三级液位仿真系统双闭环比值控制系统实验报告
三级液位仿真系统双闭环比值控制系统实验报告实验报告:三级液位仿真系统双闭环比值控制系统一、引言液位控制是工业自动化中的重要应用之一、液位控制系统的目标是使液位保持在设定值附近，并且在输入条件发生变化时能够快速恢复到稳定状态。
本实验针对三级液位仿真系统，设计了双闭环比值控制系统，旨在通过控制液位流量比值来实现液位的稳定控制。
二、实验原理在三级液位仿真系统中，通过给定流量值控制输入泵的流量，控制出口泵的速度以满足液位控制要求。
传感器采集液位信号并反馈给控制系统，经过控制计算得到输出调节量，控制输入泵和出口泵的流量值。
双闭环比值控制系统将比例控制器、积分控制器和比例-积分二次控制器结合起来，通过对输入泵和出口泵的流量进行控制，实现液位的稳定控制。
其中，比例控制器通过控制出口泵的速度来调节液位；积分控制器通过控制输入泵的流量来增加系统的稳定性。
比例-积分二次控制器结合了比例控制器和积分控制器的优点，既能快速响应输出，又能保持系统的稳态。
三、实验步骤1.连接实验系统：将液位传感器和流量传感器分别连接到控制系统进行信号采集。
2.设置参数：根据实际系统，设置合适的参数，包括液位传感器和流量传感器的量程、比例控制器和积分控制器的参数等。
3.运行系统：启动实验系统，并设置液位的设定值。
4.控制开关：根据实验要求，打开或关闭比例控制器、积分控制器和比例-积分二次控制器。
5.实验记录：记录实验系统的响应速度、稳态误差和稳定性等参数，并与理论预期进行对比分析。
四、实验结果通过实验控制系统成功实现了液位稳定控制。
实验结果表明，比例-积分二次控制器的控制效果最好，能够快速响应输出，且稳定性较好。
比例控制器的控制效果次之，响应速度较快，但稳定性较差。
积分控制器的控制效果最差，响应速度相对较慢。
五、实验总结本实验通过三级液位仿真系统的双闭环比值控制系统，成功实现了液位的稳定控制。
实验结果表明，比例-积分二次控制器是一种有效的控制方法，能够在保证系统响应速度的同时保持稳态。
“双闭环控制直流电动机调速系统”数字仿真实验
实验指导书“双闭环控制直流电动机调速系统”数字仿真实验一、实验目的1.熟悉Matlab/Simulink仿真环境；2.掌握Simulink图形化建模方法；3.验证“直流电动机转速/电流双闭环PID控制方案”的有效性。
二、实验内容1.“双闭环直流电动机调速系统”的建模2.电流环／调节器设计3.电流环动态跟随性能仿真实验4.转速环／调节器设计5.转速环动态抗扰性能仿真实验6.系统动态性能分析（给出仿真实验结果与理论分析结果的对比／分析／结论）三、实验步骤1、系统建模A．控制对象的建模建立线性系统动态数学模型的基本步骤如下：（1）根据系统中各环节的物理定律，列写描述据该环节动态过程的微分方程；（2）求出各环节的传递函数；（3）组成系统的动态结构图并求出系统的传递函数。
下面分别建立双闭环调速系统各环节的微分方程和传递函数。
B．额定励磁下的直流电动机的动态数学模型图1给出了额定励磁下他励直流电机的等效电路，其中电枢回路电阻R 和电感L 包含整流装置内阻和平波电抗器电阻与电感在内，规定的正方向如图所示。
图1 直流电动机等效电路由图1可列出微分方程如下：0dd d dI U RI LE dt=++ （主电路，假定电流连续） e E C n = （额定励磁下的感应电动势）2375e L GD dnT T dt-=⋅ （牛顿动力学定律，忽略粘性摩擦）e m d T C I = （额定励磁下的电磁转矩）定义下列时间常数：l LT R=——电枢回路电磁时间常数，单位为s ；2375m e mGD R T C C =——电力拖动系统机电时间常数，单位为s ； 代入微分方程，并整理后得：0()dd d ldI U E R I T dt -=+ m d d L T dE I I R dt-=⋅ 式中，/dL L m I T C =——负载电流。
在零初始条件下，取等式两侧得拉氏变换，得电压与电流间的传递函数0()1/()()1d d l I s R U s E s T s =-+（1）电流与电动势间的传递函数为()()()d dL m E s R I s I s T s=-（2）d Ua) b)Uc)图2 额定励磁下直流电动机的动态结构图 a) 式（1）的结构图 b)式（2）的结构图c)整个直流电动机的动态结构图C ．晶闸管触发和整流装置的动态数学模型在分析系统时我们往往把它们当作一个环节来看待。
基于MATLAB的直流电机双闭环调速系统的设计与仿真
基于MATLAB的直流电机双闭环调速系统的设计与仿真直流电机双闭环调速系统是一种常见的控制系统，常用于工业生产中对电机速度的精确控制。
本文将基于MATLAB软件进行直流电机双闭环调速系统的设计与仿真，包括系统设计、参数设置、控制策略选择、系统仿真以及性能分析等方面。
文章将以1200字以上的篇幅进行详细阐述。
一、系统设计直流电机双闭环调速系统由速度环和电流环构成。
速度环控制系统的输入为速度设定值和电机实际速度，输出为电机期望电压；电流环控制系统的输入为速度环输出的电压和电机实际电流，输出为电机实际电压。
通过控制电机的期望电压和实际电压，达到对电机速度的调控。
二、参数设置在进行系统仿真之前，需要确定系统中各个参数的值。
包括电机的额定转矩、额定电压、电感、电阻等参数，以及控制环节的比例增益、积分增益、微分增益等参数。
这些参数的选择会影响系统的稳定性和动态性能，需要根据实际情况进行调整。
三、控制策略选择常见的控制策略包括PID控制、PI控制、PD控制等。
在直流电机双闭环调速系统中，可以选择PID控制策略。
PID控制器由比例环节、积分环节和微分环节组成，可以提高系统的稳定性和响应速度。
四、系统仿真在MATLAB中进行直流电机双闭环调速系统的仿真，可以使用Simulink模块进行搭建。
根据系统设计和参数设置，搭建速度环和电流环的控制器，连接电机实际速度和电机实际电流的反馈信号，输入速度设定值和电机期望电流，输出电机期望电压。
通过仿真可以得到系统的动态响应曲线，评估系统的性能。
五、性能分析在仿真结果中，可以分析系统的静态误差、超调量、调整时间等指标，评估系统的控制性能。
通过参数调整和控制策略更改等方式，可以优化系统的控制性能，使系统达到更好的调速效果。
总结：本文基于MATLAB软件对直流电机双闭环调速系统进行了设计与仿真。
通过系统设计、参数设置、控制策略选择、系统仿真以及性能分析等步骤，可以得到直流电机双闭环调速系统的动态响应曲线，并通过参数调整和控制策略更改等方式，优化系统的控制性能。
SPWM波控制逆变器双闭环PID调节器的建模与仿真
SPWM波控制逆变器双闭环PID调节器的建模与仿真随着电力行业的快速发展，逆变器的应用越来越广泛，逆变器的好坏会直接影响整个系统的逆变性能和带载能力。
逆变器的控制目标是提高逆变器输出电压的稳态和动态性能，稳态性能主要是指输出电压的稳态精度和提高带不平衡负载的能力；动态性能主要是指输出电压的THD(Total Hannonic Distortion) 和负载突变时的动态响应水平。
在这些指标中对输出电压的THD 要求比较高，对于三相逆变器，一般要求阻性负载满载时THD 小于2%,非线性满载(整流性负载)的THD 小于5%.这些指标与逆变器的控制策略息息相关。
文中主要介绍如何建立电压双环SPWM 逆变器的数学模型，并采用电压有效值外环和电压瞬时值内环进行控制。
针对UPS 单模块10 kVA 单相电压型SPWM 逆变器进行建模仿真。
通过仿真，验证了控制思路的正确性以及存该控制策略下的逆变器所具有的鲁棒性强，动态响应快，THD 低等优点。
并以仿真为先导，将其思想移植到具体开发中，达到预期效果。
1 三电平逆变器单相控制模型的建立带LC 滤波器的单相逆变器的主电路结构如图1 所示。
图1 中L 为输出滤波电感，C 为滤波电容，T1,T2,T3,T4 分别是用来驱动IGBT 的三电平的SPWM 波，U0 为输出负载两端的电压。
在建立控制系统的仿真模型时，需要采集负载两端的电压与实际要求的电乐值做比较，然后通过调节器可以得到所需要调节的值。
在此仿真模型中，驱动波形采用的是三电平的SPWM 波形，具体的产生原理在这不做详细描述。
在Matlah 的Simlink 库中SPWM 波的产生如图2 所示，这里调制比设为0.8。
图1 三电平逆变器单相主电路图2 四相SPWM 产生电路。
“双闭环控制直流电动机调速系统”数字仿真实验2
“双闭环控制直流电动机调速系统”数字仿真实验24、SIMULINK建模我们借助SIMULINK，根据上节理论计算得到的参数，可得双闭环调速系统的动态结构图如下所示：图7 双闭环调速系统的动态结构图（1）系统动态结构的simulink建模①启动计算机，进入MATLAB系统检查计算机电源是否已经连接，插座开关是否打开，确定计算机已接通，按下计算机电压按钮，打开显示器开关，启动计算机。
打开Windows开始菜单，选择程序，选择MATAB6.5.1，选择并点击MATAB6.5.1，启动MATAB程序，如图8，点击后得到下图9：图8选择MATAB程序图9 MATAB6.5.1界面点击smulink 中的continuous,选择transfor Fc n（传递函数）就可以编辑系统的传递函数模型了，如图10。
图10 smulink界面②系统设置选择smulink界面左上角的白色图标既建立了一个新的simulink模型，系统地仿真与验证将在这个新模型中完成，可以看到在simulink目录下还有很多的子目录，里面有许多我们这个仿真实验中要用的模块，这里不再一一介绍，自介绍最重要的传递函数模块的设置，其他所需模块参数的摄制过程与之类似。
将transfor Fc n（传递函数）模块用鼠标左键拖入新模型后双击transfor Fc n（传递函数）模块得到图11，开始编辑此模块的属性。
图11参数表与模型建立参数对话栏第一和第二项就是我们需要设置的传递函数的分子与分母，如我们需要设置电流环的控制器的传递函数：0.01810.0181()0.2920.0180.062ACR s s W s s s++=⋅=，这在对话栏的第一栏写如：[0.018 1]，第二栏为：[0.062 0]。
点击OK ，参数设置完成。
如图12。
图12传递函数参数设置设置完所有模块的参数后将模块连接起来既得到图7所示的系统仿真模型。
在这里需要注意的是，当我们按照理论设计的仿真模型得到的实验波形与理想的波形有很大的出入。
“双闭环控制直流电动机调速系统”数字仿真实验
“双闭环控制直流电动机调速系统”数字仿真实验24、SIMULINK建模我们借助SIMULINK，根据上节理论计算得到的参数，可得双闭环调速系统的动态结构图如下所示：图7 双闭环调速系统的动态结构图（1）系统动态结构的simulink建模①启动计算机，进入MATLAB系统检查计算机电源是否已经连接，插座开关是否打开，确定计算机已接通，按下计算机电压按钮，打开显示器开关，启动计算机。
打开Windows开始菜单，选择程序，选择MATAB6.5.1，选择并点击MATAB6.5.1，启动MATAB程序，如图8，点击后得到下图9：图8选择MATAB程序图9 MATAB6.5.1界面点击smulink 中的continuous,选择transfor Fc n（传递函数）就可以编辑系统的传递函数模型了，如图10。
图10 smulink界面②系统设置选择smulink界面左上角的白色图标既建立了一个新的simulink模型，系统地仿真与验证将在这个新模型中完成，可以看到在simulink目录下还有很多的子目录，里面有许多我们这个仿真实验中要用的模块，这里不再一一介绍，自介绍最重要的传递函数模块的设置，其他所需模块参数的摄制过程与之类似。
将transfor Fc n（传递函数）模块用鼠标左键拖入新模型后双击transfor Fc n（传递函数）模块得到图11，开始编辑此模块的属性。
图11参数表与模型建立参数对话栏第一和第二项就是我们需要设置的传递函数的分子与分母，如我们需要设置电流环的控制器的传递函数：0.01810.0181()0.2920.0180.062ACR s s W s s s++=⋅=，这在对话栏的第一栏写如：[0.018 1]，第二栏为：[0.062 0]。
点击OK ，参数设置完成。
如图12。
图12传递函数参数设置设置完所有模块的参数后将模块连接起来既得到图7所示的系统仿真模型。
在这里需要注意的是，当我们按照理论设计的仿真模型得到的实验波形与理想的波形有很大的出入。
直流电动机双闭环控制系统的设计仿真毕业设计(Word最新版)
直流电动机双闭环限制系统的设计仿真毕业设计通过整理的直流电动机双闭环限制系统的设计仿真毕业设计相关文档，渴望对大家有所扶植，感谢观看！摘要传统的直流电机始终在电机驱动系统中占据主导地位，但由于其本身固有的机械换向器和电刷导致电机容量有限、噪音大和牢靠性不高，因而迫使人们探究低噪音、高效率并且大容量的驱动电机。
随着电力电子技术和微限制技术的迅猛发展成熟起来的直流无刷电机具有体积小、重量轻、效率高、噪音低、容量大且牢靠性高的特点，从而使其极有渴望代替传统的直流电机成为电机驱动系统的主流。
首先，从电机本体和限制角度动身，阐述了直流无刷电机在实际应用中须要解决的关键性问题：电磁转矩脉动。
具体分析了电磁转矩脉动产生的各种缘由，特殊是分析了相电流换向所产生的纹波转矩脉动。
其次，本文对无刷直流电动机的工作原理进行了详尽的分析，建立了三相无刷直流电动机的数学模型。
并利用MATLAB ／SIMULINK软件建立了三相无刷直流电动机的限制系统仿真模型。
仿真模型采样的是电机限制系统中常用的双环系统(转速一电流双闭环限制)。
为了提高系统的静动态特性，转速外环接受PI调整器，电流内环接受PI调整器。
转子位置通过直流无刷电机感应电势检溺，仿真结果表明白该仿真模型限制系统与理论分析完全吻合，从而证明白模型的有效性。
然后，初步设计了伺服系统的原理图。
以PID限制器作为整个限制电路的核心，一台40w的直流无刷电机作为被控对象，完成了伺服系统的转速限制。
最终，对将来的工作赐予了展望，并对全文的内容进行了总结。
关键词：无刷直流电动机；转矩脉动；PID限制器Abstract Conventional DC motor always takes up dominant position in driving system，butits inherent mechanical commutator and brush bring on limited capability，low reliability and big noise．These shortcoming necessitate US to develope lower noise，high efficiency and big capability driving motor．With the development of the power electronicsand micro—control technique，permanent—magnet brushless DC motor possesses small volume，light weight，high efficiency，low noise，big capability and reliability，so it is hopeful to become main motor in drive system．Fuzzy controller has the advantage of robust trait and strong anti-jamming merit．First，from the point of view of motor and control，the paper expounds all kinds of cause of brushless dc motor’s ripple toque．Especially，analyzes the cause of commutation ripple torque．Second，mathematical model is presented based on the the operating principle of BLDCM，which is analyzed in detail．This paper introduces software matlab／simulink and how to use it．Simulation model of three—phase BLDCM is set up and performed．The controlsystem is virtually a dual closed—loop system with current controller’s inner loop and speed controller as outer loop．speed controller adopts fuzzy。
直流电动机双闭环调速系统MATLAB仿真实验报告
直流电动机双闭环调速系统MATLAB仿真实验报告
实验目的：
本实验旨在设计并实现直流电动机的双闭环调速系统，并使用MATLAB进行仿真实验，验证系统的性能和稳定性。
实验原理：
直流电动机调速系统是通过改变电机的输入电压来实现调速的。
双闭环调速系统采用了速度环和电流环两个闭环控制器，其中速度环的输入为期望转速和实际转速的误差，输出为电机的电流设定值；电流环的输入为速度环输出的电流设定值和实际电流的误差，输出为电机的输入电压。
实验步骤：
1.建立直流电动机的数学模型。
2.设计速度环控制器。
3.设计电流环控制器。
4.进行系统仿真实验。
实验结果：
经过仿真实验，得到了直流电动机双闭环调速系统的性能指标，包括上升时间、峰值过渡性能和稳态误差等。
同时，还绘制了调速曲线和相应的控制输入曲线，分析了调速系统的性能和稳定性。
实验结论：
通过对直流电动机双闭环调速系统的仿真实验，验证了系统的性能和
稳定性。
实验结果表明，所设计的双闭环控制器能够实现快速且稳定的直
流电动机调速，满足了实际工程应用的需求。
实验心得：
本实验通过使用MATLAB进行仿真实验，深入理解了直流电动机的双
闭环调速系统原理和实现方式。
通过实验，我不仅熟悉了MATLAB的使用，还掌握了直流电动机的调速方法和控制器设计的原则。
同时，实验中遇到
了一些问题，比如系统的超调过大等，通过调整控制器参数和优化系统结
构等方法，最终解决了这些问题。
通过本次实验，我对直流电动机调速系
统有了更加深入的理解，为之后的工程应用打下了坚实的基础。
直流双闭环调速系统设计与仿真
直流双闭环调速系统设计与仿真一、直流双闭环调速系统的基本原理电流环用于控制电机的电流，通过测量电机的电流反馈信号与给定的电流信号进行比较，得到误差信号，然后经过PID控制器计算控制信号，最后通过逆变器输出给电机控制电流。
二、直流双闭环调速系统的设计1.确定系统参数：包括电机的转矩常数，转矩惯量，电感，电阻等参数。
2.设计速度环控制器：根据转速信号和转速误差信号，设计速度环控制器的传递函数。
可以选择PID控制器，也可以选择其他类型的控制器。
3.设计电流环控制器：根据电流信号和电流误差信号，设计电流环控制器的传递函数。
同样可以选择PID控制器或其他类型的控制器。
4.进行系统仿真：将设计好的速度环和电流环控制器加入电机模型，进行系统仿真。
通过调整控制器参数，观察系统的响应特性，可以优化系统性能。
5.调整控制参数：根据仿真结果，调整控制器的参数，使系统响应更加快速、稳定。
三、直流双闭环调速系统的仿真1.定义系统模型：建立直流电机的状态方程，包括速度环和电流环的动态方程。
2.设定系统初始条件和输入信号：设置电机的初始状态和给定的转速信号以及电流信号。
3.选择控制器类型和参数：根据设计要求，选择控制器类型和参数。
可以选择PID控制器，并根据调试经验选择合适的参数。
4.搭建控制系统模型：将速度环和电流环的控制器模型和电机模型连接在一起，构建闭环控制系统模型。
5.进行系统仿真：利用MATLAB或其他仿真软件进行系统仿真，根据给定的转速信号和电流信号，观察系统的响应特性。
四、直流双闭环调速系统的优化1.参数调整：根据仿真结果，调整控制器的参数，使系统的性能得到优化。
可以通过试探法或自适应调节方法进行参数调整。
2.饱和处理：考虑到电机的饱和特性，可以在控制器中添加饱和处理模块，以提高系统的稳定性和抗干扰能力。
3.鲁棒性设计：考虑到系统参数的不确定性，可以采用鲁棒控制方法，提高系统的鲁棒性能。
4.死区补偿：在电机控制中常常会出现死区现象，可以在控制器中添加死区补偿模块，以减小死区对系统性能的影响。
直流电机双闭环PID调速系统仿真设计
目录直流电机双闭环PID调速系统仿真 (1)1 转速、电流双闭环直流调速系统的组成及工作原理 (2)2 双闭环调速系统的动态数学模型 (2)3 调节器的设计 (4)3.1 电流调节器的设计 (4)3.2 转速调节器的设计 (6)4 搭建模型 (8)5 参数计算 (10)5.1 参数的直接计算 (10)5仿真具体参数 (13)6 仿真结果 (13)7 结束语 (14)8 参考文献 (16)直流电机双闭环PID调速系统仿真摘要在工程的应用中，直流电动机的占有很大的比例，同时对于直流系统的调速要求日益增长。
在直流调速系统中比较成熟并且比较广泛的是双闭环调速系统，本文对于直流双闭环的PID调速系统作简要的设计，同时利用Matlab/Simulink 仿真软件进行仿真处理。
关键词: 直流双闭环 PID调速在现代化的工业生产过程中，许多生产机械要求在一定的范围内进行速度的平滑调节，并且要求有良好的稳态、动态性能。
而直流调速系统调速范围广、静差率小、稳定性好，过载能力大，能承受频繁的冲击负载，可实现频率的无级快速起制动和反转等良好的动态性能，能满足生产过程自动化系统中各种不同的特殊运行要求。
在高性能的拖动技术领域中，相当长时期内几乎都采用直流电力拖动系统。
开环直流调速由于自身的缺点几乎不能满足生产过程的要求，在应用广泛地双闭环直流调速系统中，PID控制已经得到了比较成熟的应用。
Matlab是目前国际上流行的一种仿真工具，它具有强大的矩阵分析运算和编程功能，建模仿真可视化功能Simulink是Matlab五大公用功能之一，他是实现动态系统仿真建模的一个集成环境，具有模块化、可重载、图形化编程、可视化及可封装等特点，可以大大提高系统仿真的效率和可靠性。
Simulink提供了丰富的模型库供系统仿真使用，它的仿真工具箱可用来解决某些特定类型的问题，也包括含有专门用于电力电子与电气传动学科仿真研究的电气系统模型库。
此外，用户可根据自己的需要开发并封装模型以扩充现有的模型库。
双闭环比值控制系统仿真
学号：01课程设计报告题双闭环比值系统仿真目学计算机科学与信息工程学院院专自动化业班2013级自动化3级学生刘博姓名指导教师吴诗贤2016年11月26日摘要 (3)一、课程设计任务 (5) (5)(1) ....................................................................PID控制原理及PID参数整定概述.. (5)(2) ....................................................................基于稳定边界法的PID控制器参数整定算法. (7)(3) ....................................................................利用Simulink建立仿真模型. (9)(4) ····································································参数整定过程 (14)(5) ....................................................................调试分析过程及仿真结果描述 (20)三、总结 (20)参考文献21双闭环比值控制系统仿真摘要：双闭环比值控制系统的特点是在保持比值控制的前提下，主动量和从动量两个流量均构成闭环回路，这样克服了自身流量的干扰，使主、从流量都比较平稳,并使得工艺总负荷也较稳定。
双闭环比值控制
过程控制工程课程设计报告设计题目：双闭环比值控制目录一.双闭环比值控制系统简介 (3)二.双闭环比值控制系统仿真综合实例 (4)三.双闭环比值控制系统实例步骤及仿真图 (5)四.参考历史文献 (12)五.心得体会 (15)一．双闭环比值控制系统双闭环比值控制系统的特点是在保持比值控制的前提下，主动量和从动量两个流量均构成闭环回路，这样克服了自身流量的干扰，使主、从流量都比较平稳,并使得工艺总负荷也较稳定。
从动量控制回路是随动控制系统，期望系统响应快些，一般按单回路整定；主动量控制回路是定值控制系统，反应速度较慢时有利于从动控制回路的快速跟踪，一般整定为周期过程。
主、从控制回路均选择PI 控制方式。
二.双闭环比值控制系统系统仿真综合实例双闭环比值控制系统的工艺图及控制框图如下图所示。
假设主动控制量控制系统的数学模型和从动控制量控制系统的数学模型为t e s s G 5.1153)(-+=和s e s s s G 5.)120)(110(3)(-++=。
三.双闭环比值控制系统实例及仿真图（1）分析主动量控制系统和从动量控制系统稳定性。
执行该系统的Bode 图得，系统开环稳定，幅值稳定裕量7.05dB ，对应增益为2.25。
（2)选择控制系统结构和调节器形式。
控制系统框图如图下图1所示。
其中k 代表比值，在此设定为4.)(1s GC 和)(2s GC 分别为主动量控制环和从动控制环的控制器，按前述分析取PI 形式。
图1控制系统框图（3)整定主动量回路控制器参数。
仍采用稳定边界法整定系统参数。
设定停止时间为60.0，Relative tolerance设定为1e-5。
仿真图如下图2。
图2主动量回路控制器参数整定仿真图控制Kp不断减小为8.2时，得到等幅振荡图如下图3，放大图为图4，估计出临界振荡周期Tk为4。
Ki=Kp*T/Ti。
图3图4由稳定边界法临界振荡计算公式得Kp=2.2*8.2/10=1.804；Ki=8.2*（4/1.2）/1000=0.333。
基于matlab的直流电机双闭环调速系统仿真
基于Matlab的直流电机双闭环调速系统仿真本文将介绍使用Matlab软件进行直流电机双闭环调速系统的仿真。
直流电机调速系统是工业控制领域中常见的一种控制系统，通过控制电机的输入电压，调节电机的转速。
双闭环调速系统在传统的单闭环调速系统的基础上增加了速度环和电流环，提高了系统的稳定性和响应速度。
1. 直流电机调速系统介绍直流电机调速系统主要包括电机、电机功率器件、传感器和控制器等组成部分。
其中，电机是被控对象，通过控制电机功率器件的输入电压，可以调节电机的转速。
传感器用于实时测量电机的转速和转矩，将测量值反馈给控制器。
控制器根据测量值和设定值的差异，生成控制信号，控制输入电压，使得电机的转速达到设定值，并保持在设定值附近。
2. 双闭环调速系统结构双闭环调速系统在传统的单闭环调速系统的基础上增加了速度环和电流环，使得系统的控制更加精确。
速度环对电机的速度进行控制，根据速度误差生成调节电压；电流环则对电机的电流进行控制，根据电流误差生成最终的控制信号。
双闭环调速系统的结构如下所示：_______ _______| | e1 | |r +--+ | |---+-->| C |---+--> u| | | | |_____| |+--->| P1 | | | +-------+| | | _______ | | |y <---+ |_____| _|_ | | | | |_______ | | C1 | | | P2 || | | |_____| | | |--| P0 |--+ +--> | |t |_____| | +-------+y其中，r为输入信号（设定值），y为输出信号（测量值），e1为速度误差，e2为电流误差，P1为速度环比例控制器，P2为电流环比例控制器，C1为电流环输入限幅器，C为速度环输入限幅器，u为控制信号（调节电压）。
3. 双闭环调速系统仿真实现步骤步骤一：建立模型在Matlab软件中，建立直流电机的数学模型。
直流电动机双闭环调速系统的仿真模拟
直流电动机双闭环调速系统的仿真模拟摘要：本文介绍了利用MATLAB软件中的Simulink组件对直流电动机双闭环调速系统进行仿真模拟，获得了直流电动机双闭环调速系统的相关曲线。
可知，在该调速系统中运用双闭环调速系统能够显著改善系统的静态与动态性能，以及应用MATLAB软件对系统进行仿真具有便捷、高效等优点。
关键词：MATLAB；直流电动机；双闭环调速系统；仿真引言目前大多数以直流电动机作为动力源的生产设备都对直流电动机的转速和快速启动能力有较高的要求，如工业机器人等设备，为了提高效率和质量，还要求其系统本身具有自我调节的能力，以实现其系统的自动化功能，这就对调速系统有了较高的要求。
本文通过一个基于MATLAB的系统实例做一些分析，其对相似的设计具有一定的参考意义。
1.直流电动机双闭环调速控制系统1.1转速、电流双闭环调速系统的构成[1]双闭环调速系统的控制电路包括：给定环节、转速调节器ASR、电流调节器ACR、限幅装置、电流反馈环节、转速反馈环节等。
1.2直流电动机双闭环调速系统的动态特性[2]建立双闭环调速控制系统的动态结构图，应用软件MATLAB提供的Simulink 组件动态仿真工具，如图1所示。
在下图控制系统中，PI调节器控制电流和转速；将晶闸管整流环节及电动机环节分别近似成一阶惯性环节和二阶传递函数模型。
图1动态结构图2.直流电动机双闭环调速系统的仿真实例2.1直流电动机双闭环调速系统的设计[3]首先设计系统内部电流环，确定电流调节器的组成电路与电路元件。
将电流环作为一个惯性环节；同理，根据已知模型的参数要求采用同样的方法设计出转速调节环节。
系统参数设置如下：电势常数：转矩常数：电磁时间常数：机电时间常数：晶闸管整流装置滞后时间常数：选取转速调节器的输出限幅值为通过计算可以得出：晶闸管装置放大系数：启动电流：选取电流调节器的输出限幅值为可以得到：电流反馈系数：选取电流反馈滤波时间常数：选取转速最大给定值：可以得到转速反馈系数：选取转速反馈滤波时间常数：反馈调节系统的设计：电流调节器的数学模型为：。
双闭环直流调速系统设计及仿真
双闭环直流调速系统设计及仿真———————————————————————————————— 作者：———————————————————————————————— 日期：1绪论直流调速是现代电力拖动自动控制系统中开展较早的技术。
在20世纪60年代，随着晶闸管的出现，现代电力电子和控制理论、计算机的结合促进了电力传动控制技术研究和应用的繁荣。
晶闸管-直流电动机调速系统为现代工业提供了高效、高性能的动力。
尽管目前交流调速的迅速开展，交流调速技术越趋成熟，以及交流电动机的经济性和易维护性，使交流调速广泛受到用户的欢送。
但是直流电动机调速系统以其优良的调速性能仍有广阔的市场，并且建立在反响控制理论根底上的直流调速原理也是交流调速控制的根底[1]。
现在的直流和交流调速装置都是数字化的，使用的芯片和软件各有特点，但根本控制原理有其共性。
对于那些在实际调试过程中存在很大风险或实验费用昂贵的系统，一般不允许对设计好的系统直接进展实验。
然而没有经过实验研究是不能将设计好的系统直接放到生产实际中去的。
因此就必须对其进展模拟实验研究。
当然有些情况下可以构造一套物理装置进展实验，但这种方法十分费时而且费用又高，而且在有的情况下物理模拟几乎是不可能的。
近年来随着计算机的迅速开展，采用计算机对控制系统进展数学仿真的方法已被人们采纳。
但是长期以来，仿真领域的研究重点是仿真模型的建立这一环节上，即在系统模型建立以后要设计一种算法。
以使系统模型等为计算机所承受，然后再编制成计算机程序，并在计算机上运行。
因此产生了各种仿真算法和仿真软件[2]。
由于对模型建立和仿真实验研究较少，因此建模通常需要很长时间，同时仿真结果的分析也必须依赖有关专家，而对决策者缺乏直接的指导，这样就大大阻碍了仿真技术的推广应用。
MATLAB提供动态系统仿真工具Simulink，那么是众多仿真软件中最强大、最优秀、最容易使用的一种。
它有效的解决了以上仿真技术中的问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学号：2013133301课程设计报告题目双闭环比值系统仿真学院计算机科学与信息工程学院专业自动化班级2013级自动化3学生姓名刘博指导教师吴诗贤2016年11月26日摘要 (3)一、课程设计任务 (5) (5)(1)PID控制原理及PID参数整定概述 (5)(2)基于稳定边界法的PID控制器参数整定算法 (7)(3)利用Simulink建立仿真模型 (9)(4)参数整定过程 (14)(5)调试分析过程及仿真结果描述 (20)三、总结 (20)参考文献21双闭环比值控制系统仿真摘要：双闭环比值控制系统的特点是在保持比值控制的前提下，主动量和从动量两个流量均构成闭环回路，这样克服了自身流量的干扰，使主、从流量都比较平稳,并使得工艺总负荷也较稳定。
从动量控制回路是随动控制系统，期望系统响应快些，一般按单回路整定；主动量控制回路是定值控制系统，反应速度较慢时有利于从动控制回路的快速跟踪，一般整定为周期过程。
主、从控制回路均选择PI控制方式。
MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。
MATLAB的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似，故用MATLAB来解算问题要比用C、FORTRAN等语言完成相同的事情简捷得多，并且mathwork也吸收了像Maple等软件的优点，使MATLAB成为一个强大的数学软件。
Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。
同时有大量的第三方软件和硬件可应用于或被要求应用于Simulink。
Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。
Simulink可以用连续采样时间、离散采样时间或两种混合的采样时间进行建模，它也支持多速率系统，也就是系统中的不同部分具有不同的采样速率。
为了创建动态系统模型，Simulink提供了一个建立模型方块图的图形用户接口，这个创建过程只需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且用户可以立即看到系统的仿真结果。
Simulink是用于动态系统和嵌入式系统的多领域仿真和基于模型的设计工具。
对各种时变系统，包括通讯、控制、信号处理、视频处理和图像处理系统，Simulink提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试。
构架在Simulink基础之上的其他产品扩展了Simulink多领域建模功能，也提供了用于设计、执行、验证和确认任务的相应工具。
Simulink与MATLAB紧密集成，可以直接访问MATLAB大量的工具来进行算法研发、仿真的分析和可视化、批处理脚本的创建、建模环境的定制以及信号参数和测试数据的定义。
关键词：双闭环比值控制系统、MATLAB、Simulink一、课程设计任务要求已知双闭环比值控制系统如图所示其中，a=4，Gc1(S)和Gc2(S)均为PI控制器。
请采用稳定边界法整定两个PI控制器的参数，并对整个系统进行仿真。
二、课程设计主要内容(1) PID控制原理及PID参数整定概述2.1.1 PID控制原理当今的闭环自动控制技术都是基于反馈的概念以减少不确定性。
反馈理论的要素包括三个部分：测量、比较和执行。
测量关键的是被控变量的实际值，与期望值相比较，用这个偏差来纠正系统的响应，执行调节控制。
在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节。
PID控制器（比例-积分-微分控制器）是一个在工业控制应用中常见的反馈回路部件，由比例单元P、积分单元I和微分单元D组成。
PID控制的基础是比例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快大惯性系统响应速度以及减弱超调趋势。
PID（比例（proportion）、积分（integral）、导数（derivative））控制器作为最早实用化的控制器已有近百年历史，现在仍然是应用最广泛的工业控制器。
PID控制器简单易懂，使用中不需精确的系统模型等先决条件，因而成为应用最为广泛的控制器。
PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。
比例（P）控制比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差。
积分（I）控制在积分控制中，控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统。
为了消除稳态误差，在控制器中必须引入“积分项”。
积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。
这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。
因此，比例+积分（PI）控制器，可以使系统在进入稳态后无稳态误差。
微分（D）控制在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。
其原因是由于存在有较大惯性组件（环节）或有滞后（delay）组件，具有抑制误差的作用，其变化总是落后于误差的变化。
解决的办法是使抑制误差的作用的变化“超前”，即在误差接近零时，抑制误差的作用就应该是零。
这就是说，在控制器中仅引入“比例”项往往是不够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项”，它能预测误差变化的趋势，这样，具有比例+微分的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。
所以对有较大惯性或滞后的被控对象，比例+微分（PD）控制器能改善系统在调节过程中的动态特性。
2.1.2 PID参数整定PID控制器的参数整定是控制系统设计的核心内容。
它是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。
PID控制器参数整定的方法很多，概括起来有两大类：一是理论计算整定法。
它主要是依据系统的数学模型，经过理论计算确定控制器参数。
这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改。
二是工程整定方法，它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。
PID控制器参数的工程整定方法，主要有临界比例法、反应曲线法和衰减法。
三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式对控制器参数进行整定。
但无论采用哪一种方法所得到的控制器参数，都需要在实际运行中进行最后调整与完善。
①临界比例法：临界比例度参数整定法是ontrnlfcrtuning hacd on criticalprFxmtionxl band控制器的一种参数整定方法。
临界比例度参数整定法。
先在单纯比例作用(P)下，将比例增益逐步增加(亦即将比例度逐步减小)，肖到被控变最出现等幅振荡为止。
此时的比例度称为临界比例度，振荡周期称为临界周期。
然后按照一定的公式，由临界比例度和临界周期计算出在采用f,PI或F'ILl控制算法时应选取的比例增益(或比例度)、再调时间和顶调时间的参数值。
②衰减曲线法：衰减曲线参数整定法controller tuning based }n attenua-ring eurvc控制器参数整定方法的一种。
先在单纯比例作用(P)下调整比例增益Kr，使在阶跃输人下的过渡过程呈现规定的衰减曲线形式，通常是使相邻两个周期曲线幅值之比为4:1或LU:1衰减，并测出过渡过程的振荡周期只。
然后按照一定的公式，由测得的K:和上值计算出在采用P、PI或P I17控制算法时应选取的比例增益、再调时间和预调时间的参数值③反应曲线法：前三种整定调节器参数的方法，都是在预先不知道控制对象特性的情况下进行的。
如果知道控制对象的特性参数，即时间常数T、时间迟延ξ和放大系数K，则可按经验公式计算出调节器的参数。
利用这种方法整定的结果可达到衰减率φ=0.75的要求。
现在一般采用的是临界比例法。
利用该方法进行PID控制器参数的整定步骤如下：1）首先预选择一个足够短的采样周期让系统工作；2）仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例放大系数和临界振荡周期；3）在一定的控制度下通过公式计算得到PID控制器的参数。
(2) 基于稳定边界法的PID控制器参数整定算法稳定边界法是一种闭环的整定方法。
它基于纯比例控制系统临界振荡试验所得数据，即临界比例带δcr和临界振荡周期Tcr，利用一些经验公式，求取PID 控制器最佳参数值。
具体求取步骤如下。
①置PID控制器积分时间Ti到最大值（Ti=∞），微分时间Td为零（Td=0），比例带δ置较大值，使控制系统投入运行。
②待系统运行稳定后，逐渐减小比例带，直到系统出现如图2-1所示的等幅振荡，即所谓临界振荡过程。
记录下此时的比例带δcr（临界比例带），并计算两个波峰的时间Tcr（临界振荡周期）。
图2-1系统的临界振荡响应③利用δcr和Tcr值，按表2-1给出的相应计算公式，求PID控制器各整定参数δ、Ti、Td的数值。
表2-1稳定边界法参数整定计算公式注意：在采用这种方法时，控制系统应工作在线性区，否则得到的持续震荡曲线可能是极限环，不能依据此数据来计算整定。
应当指出，由于被控制对象特性的不同，按上述经验公式求得的控制器整定参数不一定都能获得满意的结果。
实践证明，对于无自平衡特性的对象，用稳定边界法求得的控制器参数往往使系统响应的衰减率偏大（Ψ>0.75）；而对于有自平衡特性的高阶等容对象，用此法整定控制器参数，系统响应的衰减率大多偏小（Ψ<0.75）。
为此，上述求得的控制器参数，需要针对具体系统在实际运行过程中作在线校正。
稳定边界法适用于许多过程控制系统。
但对于如锅炉水位控制系统那样的不允许进行稳定边界试验的系统，或者某些事件常数较大的单容对象，采用纯比例控制时系统本质稳定。
对于这些系统是无法用稳定边界法来进行参数整定的。
(3) 利用Simulink建立仿真模型Simulink建模具体步骤：打开MATLAB R2014a会出现如下界面点击启动Simulink库点击Simulink库后会弹出如图所示的模块窗口界面点击New model建立一个新的空白模型仿真窗口如下图所示，只有先建立一个空白模型窗口才能将上图所示的各种仿真模块添加到该窗口，通过模块之间的连接来建立Simulink仿真模型。