2.8牛顿运动定律之降落伞下落的规律
降落伞的下降过程
解出,mg-kSV=C'*e^(-kSt/m)
当t=0时,V=0(因为刚开始下落时,降落伞的速度为0)
解出,C'=mg
得到,V=mg/
1.分三阶段:未打开伞时，重力大于空气阻力，加速下落，而f=kv方，故随着速度的增大，空气阻力整大，加速度变小，但此时仍在加速下落;二阶段，在打开伞前，由于重力还大于空气阻力，故有一定加速度G0，刚打开伞时，空气阻力突然增大，但仍然小于重力，故有加速度G1，不过小于G0.由于惯性思维我们认为它仍应以原来加速度下落，加速度突然减小，在电视上看来就仿佛像上运动了;三，当空气阻力增大到等于重力时，人就匀速落下，仿佛飘下来
2.设空气阻力f=kSV
下落过程中,降落伞的加速度a=(mg-f)/m=g-kSV/m
根据加速度的定义,a=dV/dt(加速度的微分表达式)
这样,dV/dt=g-kSV/m
mdV/(mg-kSV)=dt
积分得到:∫mdV/(mg-kSV)=∫dt
-m/kS*∫d(-kSV)/(mg-kSV)＝∫dt
《降落伞》 讲义
《降落伞》讲义一、降落伞的定义与基本原理降落伞，这一神奇的装置，是一种利用空气阻力使人或物体从空中缓慢下降的工具。
它的基本原理其实并不复杂，主要基于空气动力学。
当降落伞打开时，其巨大的伞面会与空气产生强烈的相互作用。
空气在伞面的阻挡下被迫分流，从而产生阻力。
这个阻力与下降速度的平方成正比，也就是说，下降速度越快，阻力就越大。
通过合理设计降落伞的形状、面积和材质，可以控制阻力的大小，从而实现安全、平稳的下降。
二、降落伞的主要组成部分降落伞主要由伞衣、伞绳和背带系统这几个关键部分组成。
伞衣是降落伞中最为关键的部分，它承担着产生阻力的主要任务。
伞衣的形状通常为圆形或椭圆形，其面积大小直接影响着降落伞的阻力和下降速度。
一般来说，面积越大，阻力越大，下降速度就越慢。
伞绳则将伞衣与背带系统连接起来，起到传递力量和稳定伞衣的作用。
伞绳的数量、长度和强度都经过精心设计，以确保在使用过程中能够承受巨大的拉力。
背带系统是与使用者或承载物相连的部分，它要保证舒适、牢固地将使用者固定在降落伞上，并均匀地分配拉力，避免对使用者造成伤害。
三、降落伞的分类降落伞的分类方式多种多样，常见的有以下几种：1、按用途分类空降兵用降落伞：这是军事领域中常见的类型，用于士兵从飞机上跳伞并安全着陆。
运动降落伞：供跳伞爱好者在娱乐和体育活动中使用。
救生降落伞：用于紧急情况下拯救人员生命，如飞行员在飞机故障时使用。
2、按结构分类圆形降落伞：结构简单，阻力较大，下降速度相对较慢。
方形降落伞：具有更好的操控性和稳定性。
翼型降落伞：外形类似飞机的机翼，能够提供更大的滑翔能力。
3、按控制方式分类被动式降落伞：无需使用者主动控制，打开后自动按照预定的方式下降。
主动式降落伞：使用者可以通过操纵装置来改变降落伞的姿态和下降轨迹。
四、降落伞的制作材料降落伞的制作材料对于其性能和安全性至关重要。
伞衣通常采用高强度、轻质的尼龙或聚酯纤维材料，这些材料具有良好的抗拉强度和耐磨损性能，同时重量较轻，有助于减轻整体重量。
牛顿运动定律之降落伞下落的规律
牛顿第三定律
解释了空气阻力对降落伞 下落的影响，指导设计更 合理的降落伞形状和结构。
THANKS
感谢观看
空气阻力
空气阻力越大，降落伞下落速度越慢。
降落伞质量
质量越大，降落伞下落速度越快。
形状和结构
降落伞的形状和结构对空气阻力有显著影响，从而影响下落速度。
牛顿运动定律在降落伞下落中的综合应用
01
02
03
牛顿第一定律
解释了降落伞在无外力作 用时保持静止或匀速直线 运动的原因。
牛顿第二定律
解释了降落伞下落加速度 与作用力、质量之间的关 系，指导设计更轻便、阻 力更小的降落伞。
03
牛顿第二定律：力与加速度的关系
定义与概念
01
牛顿第二定律：物体受到的力与它的加速度成正比，用公式表 示为F=ma，其中F代表物体受到的合外力，m代表物体的质量，
a代表物体的加速度。
02
牛顿第二定律是经典力学中的基本定律之一，它描述了力、质 量和加速度之间的基本关系，是物体运动规律的基础。
03
04
牛顿第三定律：作用与反作用定律
定义与概念
定义
作用力和反作用力大小相等、方向相 反、作用在同一条直线上。
概念
作用与反作用定律是牛顿运动定律中 的一个基本原理，它描述了物体间相 互作用的关系。
降落伞下落中的作用与反作用表现
01
降落伞受到重力的作用，同时产 生一个向上的反作用力，即空气 阻力。
02
牛顿第二定律适用于宏观低速的物体，即物体速度远小于 光速的情况。
降落伞下落中的力与加速度关系
降落伞下落过程中，受到重力和空气阻力的作用。重力方向向下，空气阻力方向向上。随着下落速度的增加，空气阻力逐渐 增大，直到空气阻力与重力平衡时，降落伞达到稳定下落状态。
简易降落伞的科学原理
简易降落伞的科学原理
简易降落伞的科学原理主要涉及到重力、空气阻力和牛顿第二定律。
首先，重力是指地球对物体的吸引力。
当一个人或物体处于高处时，存在着下落的趋势，即重力会使人或物体向下加速。
第二，空气阻力是指空气对物体运动产生的阻碍力。
当一个人或物体向下运动时，空气会与其相互作用，产生一个向上的阻力，阻碍其下坠的速度。
最后，牛顿第二定律指出，力等于质量乘以加速度。
根据这个定律，如果一个降落伞打开，人或物体就会受到空气阻力的作用，产生一个向上的力。
根据牛顿第二定律，当物体受到一定的空气阻力时，它的加速度会减小，最终达到平衡状态，即物体的下降速度变为匀速下降。
简易降落伞的原理是利用空气阻力来减缓下降的速度。
当降落伞打开时，伞布会增大人或物体与空气之间的接触面积，从而增加空气阻力。
这个阻力会逐渐减小下降的速度，使人或物体以一个较慢的速度下降，实现较为安全的降落。
需要注意的是，简易降落伞并不适用于高空或极端天气条件下的降落。
在这些情况下，需要较为复杂的降落伞系统和更加精确的设计和制造。
降落伞的原理是什么
降落伞的原理是什么
降落伞的原理是借助阻力减缓下落速度的装置。
当一个人从高空跳伞时，会因为地心引力作用而加速下落，直到达到一个稳定的下落速度。
为了降低下落速度，减少着地时的冲击力，降落伞起到了重要的作用。
降落伞的设计基于两个关键原理：空气阻力和重力。
降落伞的主要部分是伞面和伞线。
伞面由坚韧而轻便的材料制成，通常是尼龙或涤纶。
伞线连接伞面和降落伞跳伞者的身体，用于操纵和控制降落伞。
当跳伞者打开降落伞时，伞面迅速展开，并开始收集空气。
空气的进入使得伞面周围形成高压区域，而下方形成低压区域。
这种气压差导致了一个向上的力，称为升力。
升力的产生使得降落伞能够产生阻力，减缓下落速度。
重力和升力之间的平衡决定了下落速度。
当降落伞下落速度变慢到达稳定状态时，降落伞跳伞者能够以相对缓慢而安全的速度下降。
控制下落速度的关键是伞面的大小和形状、伞线的张力以及降落伞者的体重。
更大的伞面和更紧张的伞线可以产生更大的阻力，从而降低下降速度。
此外，降落伞跳伞者可以通过操作伞线来改变降落伞的飞行方向和速度。
通过拉动或松开不同的伞线，可以实现转向、加速或减速等操作，以适应不同的飞行需求和情况。
总体来说，降落伞的原理是利用空气阻力产生升力，减缓下落速度，为跳伞者提供安全的着陆方式。
初二物理降落伞实验课堂笔记2024人教版
初二物理降落伞实验课堂笔记2024人教版引言降落伞是一种利用空气阻力减缓物体下落速度的装置。
它在航空、航天、军事和救援等领域有着广泛的应用。
在初二物理课程中，我们通过制作和实验降落伞，深入了解了空气阻力、重力和运动的基本原理。
一.降落伞的基本原理降落伞的工作原理主要依靠空气阻力。
当降落伞展开时，伞面增大了物体的表面积，从而增加了空气阻力，减缓了物体的下落速度。
根据牛顿第二定律，物体的加速度与作用力成正比，与质量成反比。
因此，降落伞通过增大空气阻力来减小物体的加速度，使其以较慢的速度安全着陆。
二.制作降落伞的材料和步骤材料：1.轻质布料（如尼龙布）2.细绳3.小重物（如砝码）4.剪刀5.尺子6.胶带步骤：1.制作伞面：将布料剪成一个正方形或圆形，确保边缘平整。
2.固定伞绳：在伞面的四个角（或圆周的等距点）打孔，穿过细绳并打结固定。
3.连接重物：将细绳的另一端绑在小重物上，确保连接牢固。
4.测试降落伞：从一定高度（如3米）处释放降落伞，观察其下落过程。
三.实验设计与数据记录在实验中，我们通过改变降落伞的伞面面积、伞绳长度和重物质量，探究这些因素对降落伞下落时间的影响。
实验变量：1.伞面面积：使用不同面积的伞面（如0.5平方米、1平方米、1.5平方米），观察其对下落时间的影响。
2.伞绳长度：使用不同长度的伞绳（如1米、1.5米、2米），记录下落时间。
3.重物质量：使用不同质量的重物（如20克、30克、40克），比较下落时间。
数据记录表：四.实验结果与分析通过实验数据分析，我们得出以下结论：1.伞面面积：伞面面积越大，降落伞在空中滞留的时间越长。
这是因为较大的伞面提供了更大的空气阻力，减缓了下落速度。
2.伞绳长度：伞绳长度对降落伞的下落时间影响不大。
在相同伞面面积和重物质量的情况下，伞绳长度的变化对下落时间的影响较小。
3.重物质量：重物质量越大，降落伞在空中滞留的时间越短。
较重的物体在重力作用下下落速度更快，因此滞留时间较短。
牛顿运动定律之降落伞下落的规律
t )
vT g
2
ln [c o s h (
gt vT
)] C 2
当t = 0时，x = 0， C 可得常数
vT g
2
2
vT g
2
ln [c o s h ( )]
降落伞下落的高度为 当v > vT时，可得 积分 即
x
cosh g d x v d t v T c o th ( t ) d t vT
当Kv > 1时，即v > vT，积分上式
g t C 1 1 2K ln Kv 1 Kv 1
设当t = 0时，v = v0，C 可得常数为
1
1 2Kபைடு நூலகம்
1 Kv
ln
K v0 1 K v0 1
利用反双曲正切函数可得 速度为 其中
v 1 K c o th ( K g t K C 1 )
x
ln
co sh ( g t / vT )
x vT
vT g
2
c o th (
gt vT
g vT
t ) d t
vT g
2
c o s h ( g t / v T ) s in h ( g t / v T )
d(
g vT
t )
ln [s in h (
gdt dv 1 K v
2 2
分离变 量得
].
1
2 1 Kv
(
dv
dv 1 Kv
)
1 2K
[
d (1 K v ) 1 Kv
d (1 K v ) 1 Kv
5、降落伞
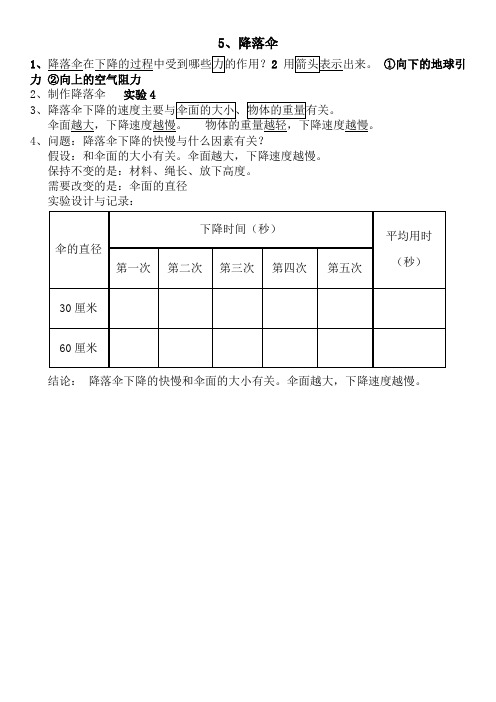
1、降落伞在下降的过程中受到哪些力的作用？2 用箭头表示出来。 ①向下的地球引 力 ②向上的空气阻力 2、制作降落伞 实验 4 3、降落伞下降的速度主要与伞面的大小、物体的重量有关。 伞面越大，下降速度越慢。 物体的重量越轻，下降速度越慢。 4、问题：降落伞下降的快慢与什么因素有关？ 假设：和伞面的大小有关。伞面越ห้องสมุดไป่ตู้，下降速度越慢。 保持不变的是：材料、绳长、放下高度。 需要改变的是：伞面的直径 实验设计与记录： 下降时间（秒） 伞的直径 第一次 30 厘米 60 厘米 结论： 降落伞下降的快慢和伞面的大小有关。伞面越大，下降速度越慢。 第二次 第三次 第四次 第五次 （秒） 平均用时
降落伞下降原理
降落伞下降原理
下降原理：
降落伞的原理是利用空气的阻力，降低下降速度。
用比较大的伞面增加自由落体下降时的阻力，减小下降时的速度，使人下降到地面的速度成为人体能自够承受的速度，也就是人体下降的速度和体重形成的动量是人体尤其是双腿能够承受和克服的，避免由于速度过高摔伤致残，甚至危及生命。
主要用途：
降落伞又称“保险伞”，其广泛用于航空航天领域，主要功能如下：
1)应急救生：要用于飞机失事时拯救飞行员的性命。
2)稳定作用：持飞机弹射椅的姿态稳定，空中加油机的加油器稳定。
3)减速作用：机着陆时的刹车减速以及各种航弹伞的滞空减速。
降落伞能使飞机着陆滑
行由2000多米缩短至800～900米。
4)回收作用：于飞机器的空中回收，诸如无人驾驶飞机、试验导弹、运载火箭助推器、
高速探测器以及返回式航天飞行器的回收等。
还有宇宙飞船和热气球探测器上设备的回收。
5)空降空投：兵空降，以及各种物资和武器的空投。
6)航空运动：空中跳伞、山坡滑翔、悬挂翼滑翔、动力飞行以及牵引升空等运动。
大班科学教案降落伞的原理
大班科学教案降落伞的原理大班科学教案：降落伞的原理一、引言降落伞作为一种常见的空气动力学装置，被广泛应用于军事、航空、救援等领域。
它的原理是以空气阻力为基础，能够减缓物体的下坠速度，确保人或物品在空中得到较为平稳的下降。
本文将介绍降落伞的基本原理以及在科学教学中的应用。
二、降落伞的原理1. 空气阻力原理降落伞利用空气阻力原理来减缓物体下降的速度。
当降落伞展开后，伞面与空气相互作用，产生了垂直于下降方向的阻力。
根据牛顿第二定律，物体所受到的阻力与它的运动速度成正比，因此阻力的作用可以降低物体的下降速度。
2. 伞面结构降落伞的伞面通常由防水材料制成，具有一定的弹性和耐磨性。
伞面上通常有许多小孔，用来调整伞面内外的气压差异，确保伞面展开后的稳定性和平衡性。
此外，降落伞上还配备有绳索，用于连接伞面和背带，使降落伞与使用者相连。
3. 降落伞的设计原则降落伞的设计需要考虑安全、稳定性和可控性等多个因素。
在设计中，需要合理选择伞面的面积和形状，以及绳索的长度和数量。
同时，还需要根据具体使用场景来调整降落伞的重量和材料选择，以满足不同环境下的需求。
三、降落伞在科学教学中的应用降落伞作为一种实践性强、直观性好的装置，可以在科学教学中发挥重要作用。
以下是降落伞在大班科学教学中的应用示例：1. 降落伞实验通过制作简易的降落伞模型，引导学生进行实验，了解降落伞的原理和空气阻力的作用。
学生可以通过改变伞面的面积、改变物体的质量等方式，观察和比较不同情况下的降落速度和降落过程。
通过实践感受和观察，学生能够更好地理解和掌握空气阻力的基本原理。
2. 降落伞制作工艺引导学生通过手工制作降落伞，锻炼他们的动手能力和创造力。
教师可以准备一些简单的材料和工具，如纸张、胶水、剪刀等，让学生在指导下进行降落伞的制作。
通过实际操作，学生能够更好地理解伞面形状和材料选择对降落伞性能的影响，并培养他们的动手创造能力和团队合作意识。
3. 降落伞模拟实验借助科技手段，可以进行降落伞的模拟实验。
降落伞的运动趋势
降落伞的运动趋势降落伞作为一种人类控制下的运动装备，具有独特的运动趋势。
在回答这个问题时，我将结合物理学的相关理论和实际运动实验，逐步解析降落伞的运动趋势。
首先，降落伞的运动趋势与重力、空气阻力和操纵方式密切相关。
当降落伞从高空往下运动时，重力是主导因素，其大小与质量和速度有关。
根据物理学的万有引力定律，降落伞所受到的重力随着海拔高度的减小而减小，重力是以9.8米/秒²进行逐渐增大的。
因此，降落伞在初始时将以一个较大的下降速度向下运动。
然而，空气阻力的作用逐渐增大，开始抵消降落伞下落的速度。
空气阻力是与速度的平方成正比的，即阻力大小与速度的平方成正比。
当速度增大时，降落伞所受到的空气阻力也随之增大，逐渐抵消重力的作用。
当空气阻力与重力相等时，降落伞将进入稳定状态，速度将不再发生变化，此时称为终端速度。
终端速度是降落伞的一个重要参数，它受到降落伞的形状、面积和重量的影响。
较大的降落伞通常具有较小的终端速度，因为空气阻力较大。
而较小的降落伞则具有更大的终端速度。
降落伞的其他设计要素，如线的张力、切线夹角等也影响降落伞的终端速度。
一般情况下，终端速度通常在每小时40到60公里之间。
在降落伞的运动趋势中，操纵方式也起着至关重要的作用。
通过改变降落伞的展开面积、调整降落伞与地面夹角等方法，可以实现对降落伞运动的控制。
例如，通过拉紧或放松降落伞绳索，可以改变降落伞的形状和展开面积，从而改变降落伞的速度和下降角度。
操纵者还可以利用降落伞的侧滑效应，改变降落伞的飞行方向。
此外，降落伞的运动趋势在实际运动中还受到其他因素的影响。
例如，风速和风向对降落伞的运动轨迹有重要影响。
如果风速较大，则降落伞可能会被吹离原先计划的着陆区域，并且风向的变化也会改变降落伞的运动方向。
因此，在进行降落伞运动时，准确判断风速和风向是非常关键的。
总结起来，降落伞的运动趋势是受到重力和空气阻力的相互作用的结果。
初始时，重力是主导因素，使降落伞迅速下降。
降落伞的工作原理10字
降落伞的工作原理10字降落伞是一种人们常用的救生装备，它能确保人们在高空中安全降落。
降落伞的工作原理可以概括为：通过空气阻力与重力的平衡来减缓下降速度，使人们能够安全着陆。
具体来说，降落伞的工作原理主要包括以下几个方面：1. 初始状态：当人们从高空跳出或飞行器失事时，降落伞处于合拢状态。
合拢状态时，降落伞的展开面积较小，能够减小下降速度，提供一定的减速效果。
2. 伞盖展开：当降落伞保险结构打开后，伞盖开始展开。
伞盖展开的过程中，有多个驱动包和伞帽等细节展开，逐步放大了伞盖的面积。
3. 空气阻力：伞盖展开后，面对空气的阻力会逐渐增大。
空气阻力是降落伞工作的关键，它通过与重力相互平衡，减缓下降速度。
当空气阻力与重力平衡时，下降速度将稳定在一个安全范围内。
4. 背带与抬头绳：降落伞上有背带和抬头绳等结构。
背带固定在身体上，可以帮助保持平衡和稳定。
抬头绳则通过调整来改变伞盖的角度，以适应不同的风速和风向。
5. 着陆：当降落伞的下降速度减缓到安全水平时，人们将开始准备着陆。
此时，需要根据实际情况选择适当的着陆点，并通过调整抬头绳等手段来控制降落伞的下降轨迹。
最终，人们将安全地着陆在地面上。
总体来说，降落伞的工作原理是通过空气阻力与重力平衡，来减缓下降速度并确保人们在高空中安全着陆。
降落伞的设计和结构使得它能够适应不同的环境和情况，并提供最佳的安全保护。
降落伞的工作原理可以说是基于物理学的重力与空气阻力原理，并通过工程设计和制造来实现。
无论是在军事、空中救援还是极限运动等领域，降落伞都起到了至关重要的作用，为人们提供了可靠的生命保护。
牛顿第二定律应用(雨滴下落)
v=g .t
实际的雨滴的竖直下落过程 加速度a逐渐减小的加速运动
o
t/sΒιβλιοθήκη F阻F =？
合
G=mg
根据牛顿第二定律:F合=mg—f阻 =m*a ；综上分析 可知：雨滴在竖直下落过程中，合力竖直向下并且 大小逐渐减小；加速度a竖直向下逐渐减小；雨滴做 竖直向下的加速度逐渐减小的加速运动，直到f =mg 时， F =0， a=0，此后速度不再增加。
阻
合
实际情景中雨滴的竖直下落和理想的自由落体 运动的不同，可以从下图的v-t图像中体现：
从动力学看竖直下落的雨滴
在现实中，雨滴大约在1.5km左右的高空形成并开始 下落。 计算一下，若该雨滴做自由落体运动，到达地面时的 速度是多大？ 【思考】你遇到过这样快速的雨滴吗？据资料显示， 落到地面的雨滴速度一般不超过8m/s，这是为什么呢？
分析受力：重力 G=mg ; 空气阻力f（实际物体下落时都 要受到空气阻力，速度越快，阻力越大）
降落伞基本直径及下降速度的设计计算
在无人机或四轴、航模上安装降落伞，以免除炸鸡的风险，还有模友玩水火箭，水火箭的回收也需要用到降落伞，那么降落伞的直径应该取多大合适，下降速度又是多少呢，网上基本没有这方面的文章，smurfjack查阅了一些资料，给大家讲解一下：
降落伞的下落速度和空气密度、伞的形状特性、载重量等因素有关，总体上可以用降落伞拉力方程来表述：
当载重的重力与降落伞拉力相等时，降落伞匀速下降，即有方程：
这就是最终结论。
全尺寸降落伞在不同下降模式和速度下的典型风阻系数
设计例子：
设降落伞风阻系数Cd=2.4，载重1.8kg，期望其下降速度为4 m/s(四轴的话最好不要超过5m/s,否则撞击太剧烈)求降落伞直径？。
降落伞的原理
降落伞的原理
降落伞是一种利用空气阻力来减缓物体下落速度的装置，广泛应用于空降、救援、运输等领域。
它的原理主要是利用空气的阻力来平衡重力，从而减缓物体下落的速度，保障人员或物资的安全。
下面我们来详细了解一下降落伞的原理。
首先，降落伞的原理是基于牛顿第二定律和空气阻力的。
根据牛顿第二定律，物体所受的合外力等于物体的质量乘以加速度，而空气阻力是与物体下落速度的平方成正比的。
当物体下落时，空气阻力会逐渐增大，最终与重力平衡，使物体达到稳定的下降速度。
其次，降落伞的结构也是实现原理的重要组成部分。
降落伞通常由伞面、伞架和连接绳组成。
伞面是由轻而坚固的材料制成，能够承受空气阻力并展开成伞状，增加阻力面积；伞架则是支撑伞面的骨架，使伞面保持稳定的展开状态；而连接绳则是将伞面与下降物体连接在一起，使得伞面能够随着物体下落而展开，起到减速作用。
此外，降落伞的原理还涉及到空气动力学的知识。
空气动力学是研究空气对物体运动的影响的学科，通过空气动力学的原理，我
们可以更好地理解降落伞的运行机理。
当降落伞展开后，伞面与空气之间形成了一个大的阻力面积，空气被迫通过伞面，由于空气的阻力，使得下降物体的速度逐渐减缓，最终达到安全的着陆速度。
总的来说，降落伞的原理是基于空气阻力和牛顿第二定律，通过合理的结构设计和空气动力学的原理，使得下降物体能够平稳地减速下降，保障人员和物资的安全。
在实际应用中，不同类型的降落伞会根据具体的需求和环境进行设计，以最大程度地发挥其减速作用。
因此，了解降落伞的原理对于提高其设计和使用的效率和安全性具有重要意义。
自由落体的规律
自由落体的规律
自由落体是指物体在没有受到空气阻力的情况下，从静止开始沿竖直方向下落的运动。
自由落体运动的规律可以用牛顿第二定律和重力加速度公式来表示。
牛顿第二定律表明，物体所受合力等于其质量乘以加速度。
在自由落体运动中，物体所受合力为重力，方向向下。
因此，可以得出以下公式：
F = mg
其中，F表示物体所受合力，m表示物体的质量，g表示重力加速度，约为9.8米/秒²。
根据牛顿第二定律，物体的加速度与所受合力成正比，与物体的质量成反比。
因此，在自由落体运动中，物体的加速度恒定，为重力加速度g。
这意味着，物体在自由落体运动中的速度会随着时间的推移而不断增加，且速度的增加是均匀的。
根据运动学公式，物体在自由落体运动中的位移可以用以下公式表示：
h = 1/2 gt²
其中，h表示物体下落的位移，t表示物体下落的时间。
综上所述，自由落体运动的规律为：物体所受合力为重力，方向向下；物体的加速度恒定，为重力加速度g；物体的速度会随着时间的推移而不断增加，且速度的增加是均匀的；物体下落的位移与时间的平方成正比。
高空跳伞为什么重物会下落
高空跳伞为什么重物会下落高空跳伞是一项极具刺激和冒险精神的运动，对于勇敢的人来说是一次终身难忘的体验。
在进行高空跳伞时，我们经常会观察到一个有趣的现象，那就是重物总是会下落。
为什么重物会下落呢？这涉及到物体在空气中受力和运动的原理。
首先，我们来了解一下物体受力的基本原理。
根据牛顿第一定律，物体在没有外力作用时将保持静止或匀速直线运动。
而物体在自由下落时，重力是其唯一的作用力，没有其他外力对其产生影响。
重力是地球吸引物体的力，它的方向始终指向地球的中心。
因此，根据重力的作用，引起物体下落。
其次，了解物体在空气中的运动阻力。
当物体在空气中运动时，空气会对其产生一定的阻力。
这是由于空气分子与物体表面发生碰撞，产生了阻力。
这种阻力与物体的速度成正比，速度越快，阻力就越大。
因此，在高空跳伞过程中，重物受到的阻力比轻物要大，正因为阻力较大，所以重物下落速度较慢。
再次，重物的质量对其下落速度也有影响。
根据牛顿第二定律，物体的加速度与作用力成正比，与质量成反比。
加速度是物体的速度变化率，作用力是推动物体运动的力。
因此，重物由于质量较大，所受到的重力也较大，从而加速度较大，下落速度较快。
最后，我们来总结一下高空跳伞为什么重物会下落的原因。
首先，重物受到的重力大于空气阻力，因此向下运动。
其次，重物的质量较大，受到的重力较大，加速度大，速度快。
而轻物受到的重力较小，加速度小，速度慢。
这就是为什么重物会下落而轻物会漂浮在空中的原因。
总结起来，高空跳伞中重物下落的原因是由于重力大于空气阻力，以及重物的质量较大，加速度较大的结果。
这一现象符合牛顿力学定律的基本原理。
了解这些物理原理，我们可以更好地理解和欣赏高空跳伞这项壮丽而极富挑战性的运动。
降落伞动量定理
当人打开绳子的瞬间绳子的拉力会瞬间增大，而后减小。
因此应考虑绳子因为冲量获得的瞬间拉力。
此时应根据动量定理（mg-ksv ）Δt=m Δv 和微积分方法计算出绳子的最大拉力。
先把人单独作为研究对象：1． 当打开伞前的一瞬间，伞和人还未分离，具有相同的速度，且人与伞包之间的连接绳之间没有拉力，即Ft=0;此时人受的合力为mg-ks1v1,方向竖直向下。
2． 当伞打开后的一瞬间，伞和人分离，很快在Δt 的时间内，伞和人由于绳的拉力又具有相同的速度开始减速下降，人的空气阻力相当于降落伞的空气阻力可以忽略不计，Ft= ks2v2；此时人受的合力为ks2v2-mg ，方向竖直向上。
在这很短的时间间隔内，人的动量发生很大的改变。
假设，降落伞打开到和人一起稳定下降的时间间隔Δt=1s. 3． 计算：t0时刻打开伞。
则1001ks t mt mgv eks -=-（1）1秒钟后：220122ks t mt mg ks v mg v eks ks --=-则运用动量定理：()t dvF m g dt=-即：10[()]t t t F m g v v =--且限制条件为：11304cos tF θ≤但又根据()t mg F t m v -∆=∆取时间和速度的微元，有：t dvmg F m dt-=即()t dvF m g dt=-由上式可知，绳的最大拉力出现在速度V 变化率最大的时刻，而这一最大时刻出现在刚刚完全打开伞的一刹那。
由于我们简化模型的效果，我们忽略了开始打开伞到伞完全打开的这一过称，而直接把第一阶段的末速度作为第二阶段的初速度，所以导致在刚刚完全打开伞的一刹那时的瞬时速度不可导，所以求不出最大速度V 变化率，因此我们用打开伞后的一瞬间绳的拉力作为最大拉力，往后由于速度逐渐减小，而拉力也逐渐减小，这是一个比较好的近似。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
其中
= KC1′ arc coth( α′ =
v0 ). vT
v
g vT tanh( t + α ) vT
{范例2.8} 降落伞下降的规律
g = (v < vT) v vT coth( t + α ′) vT
(v > vT)
g t + α )dt vT
当v < vT时，利用关系v =
= dt dx/dt，可得 dx v= vT tanh(
可得常数
ln
降落伞下落的高度为 x = v
2 T
g
sinh( gt / vT + α ′) . sinh α ′
不论降落伞的初速度是小于极限速度还是大 于极限速度，最后的速度都趋近于极限速度。
在初速度较大的情况下，在相同的时间内， 降落伞下落的高度要大些，所以速度较大的 高度曲线在速度较小的高度曲线上面。
1 g tanh( Kgt += vT tanh( t + α ) KC1 ) vT K
v0 α = 其中 = KC1 arctanh( ). vT
{范例2.8} 降落伞下降的规律
= gdt 1 d(1 + Kv) d(1 − Kv) [ − ] 2 K 1 + kv 1 − Kv
当Kv > 1时，即v > vT，积分上式
2 vT cosh( gt / vT + α ) 降落伞下落的高度为 x = ln g cosh α g = dt dx v= vT coth( t + α ′)dt 当v > vT时，可得 vT 2 vT cosh( gt / vT + α ′) g g = α ′)dt 积分 x vT ∫ coth( v t + = g ∫ sinh( gt / v + α ′) d( v t + α ′) T T T 2 2 vT gt 当t = 0时，x = 0， ′ = − vT ln[sinh(α ′)] ′)] + C2 ′ = ln[sinh( + α 即x C2 g + Kv) d(1 − Kv) gdt = = ( + )= [ − ]. 2 2 1− K v 2 1 + Kv 1 − Kv 2 K 1 + Kv 1 − Kv
{范例2.8} 降落伞下降的规律
1 d(1 + Kv) d(1 − Kv) [ ] = gdt − 2 K 1 + kv 1 − Kv
不论初速度是大还是小，加速度最后都趋于0。 初速度较小时，其加速度的方向与速度方向相同，并随 着速度的增加而减少；初速度较大时，其加速度的方向 与速度的方向相反，大小也随着速度的增加而减少。
2 vT g = = 积分 x vT ∫ tanh( t + α )dt vT g
sinh( gt / vT + α ) g d( ∫ cosh( gt / vT + α ) vT t + α )
2 2 vT gt v ln[cosh( + α )] + C2 当t = 0时，x = 0， C = − vT ln[cosh(α )] = 即 2 g vT g 可得常数
1 Kv + 1 gt + C1′ = ln 2 K Kv − 1
设当t = 0时，v = v0，C1′ = 1 ln Kv0 + 1 2 K Kv0 − 1 可得常数为
Kv
1 利用反双曲正切函数可得 Kgt + KC1′ = arc tanh
= 速度为 v 1 g coth( Kgt + KC1′) = vT coth( t + α ′) K v
当Kv < 1时，即v < vT，例如初速度为0的情况，积分上式
1 1 + Kv gt + C1 = ln 2 K 1 − Kv
设当t = 0时，v = v0， C = 1 ln 1 + Kv0 1 2 K 1 − Kv0 可得常数为
利用反双曲 1 1 + x ln = arc tanh x 可得 Kgt + KC1 = arc tanh Kv 正切函数 2 1− x 速度为 v =
{范例2.8} 降落伞下降的规律
物体在空气中运动时，阻力的大小可以表示为f = CρAv2/2。 其中ρ是空气的密度，A是物体的有效横截面积，C为阻力 系数。一降落伞和人组成系统的极限速度为vT = 5m/s，当 系统从静止开始下落时，求它的速度和下落的高度随时间 的变化关系。如果该降落伞开始没有打开，当速度达到v0 = 10m/s时才打开，系统的运动规律是什么？ [解析]伞和人受到重力mg，方向竖直向下； 空气阻力f，方向竖直向上。 其中k = CρA/2，k 取向下为正方向，根据牛顿第二定律 是比例系数。 可列人和伞的运动方程mg - kv2 = ma， 由于a = dv/dt，可得微分方程 其中K2 = k/mg。 dv 当dv/dt→0时，v→vT，vT是 = g (1 − K 2 v 2 ) dt 极限速度，因此K = 1/vT。 分离变 量得