minitab应用实例
MINITAB应用案例
MINITAB应用案例就近一个文章说:对2010 年全国大学生调查的分析。
该调查利用随机分层法,抽取了19 所的5000 多名大四学生进行调查。
在这19 所高校中,有10 所“211 工程”的重点大学和9 所普通大学。
调查中搜集了学生的来源省份、家庭背景、高考成绩和高中表现等多项数据。
统计结果发现,如果其父母在政府、国企和事业单位有干部身份,那么这些学生有更大几率上“211”。
而如果其父母是工人,农民,文员,技术员或企业家,那么这些学生上重点大学的几率则会降低。
统计结果说明,在控制了父母教育水平和家庭收入两个变量之后,父母职业这个变量的影响还是显著。
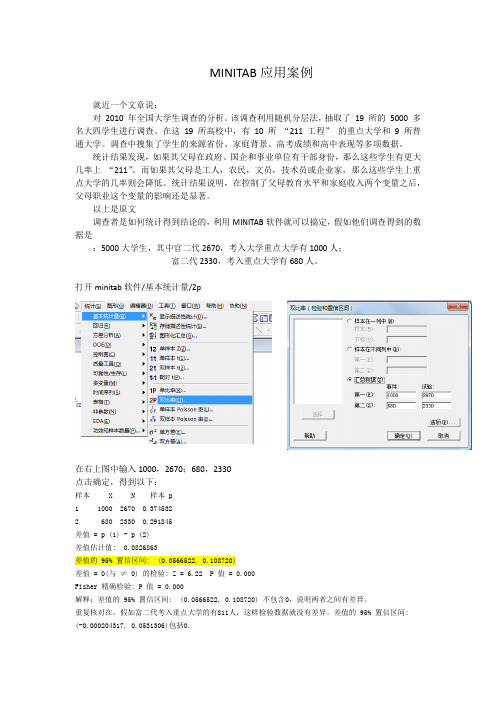
以上是原文调查者是如何统计得到结论的,利用MINITAB软件就可以搞定,假如他们调查得到的数据是:5000大学生,其中官二代2670,考入大学重点大学有1000人;富二代2330,考入重点大学有680人。
打开minitab软件/基本统计量/2p在右上图中输入1000,2670;680,2330点击确定,得到以下:样本 X N 样本 p1 1000 2670 0.3745322 680 2330 0.291845差值 = p (1) - p (2)差值估计值: 0.0826863差值的 95% 置信区间: (0.0566522, 0.108720)差值 = 0(与≠ 0) 的检验: Z = 6.22 P 值 = 0.000Fisher 精确检验: P 值 = 0.000解释:差值的 95% 置信区间: (0.0566522, 0.108720) 不包含0,说明两者之间有差异。
重复核对在,假如富二代考入重点大学的有811人,这样检验数据就没有差异。
差值的 95% 置信区间: (-0.000204317, 0.0531306)包括0.样本 X N 样本 p1 1000 2670 0.3745322 811 2330 0.348069差值 = p (1) - p (2)差值估计值: 0.0264632差值的 95% 置信区间: (-0.000204317, 0.0531306)差值 = 0(与≠ 0) 的检验: Z = 1.94 P 值 = 0.052Fisher 精确检验: P 值 = 0.055以上用实际生活案例来引发MINITAB的应用。
minitab doe案例

minitab doe案例
以下是一个使用Minitab进行DOE(实验设计)的案例:
案例:PCB板的镀铜线质量优化
1. 确定每个因子的高低水平,例如温度、时间、电流等。
2. 打开Minitab软件,创建一个新的DOE计划。
3. 选择合适的因子数、区组中心点数、角点仿行数和区组数,以满足实验需求。
4. 生成正交试验矩阵,并按照计划进行实验。
5. 将实验数据复制到Minitab中进行DOE分析。
6. 选择因子和响应,进行效应图和方差分析。
7. 根据分析结果,优化因子水平,以提高镀铜线的质量。
通过以上步骤,可以使用Minitab进行DOE,优化PCB板的镀铜线质量。
Minitab教程案例

(#)
8
Minitab菜单(Manip)
从活动 Worksheet 中复制数据,制作 subsetWorksheet。 把活动 Worksheet 分成两个以上新的 Worksheet 把多个Worksheet合并为一个Worksheet
把列上内容复制到其它列上 把一列以上的数据移到多个列上 把多个列上的数据合成一个列 交换行和列的位置
恢复已删除资料 清除 Cell(s)的数据 删除 Cell(s)的数据– 下端的cell移动 复制 Cell(s) 粘贴 Cell(s) LinK粘贴 Link管理
选择所有cell 编辑最后操作的对话框 打开命令编辑器
一般选项
练习)在AUTO.MTW上 1)删除 4,5Row后把 C4,C5的DATA变更为 234 2) 把C2 Col移动到C5 3)把C4 ColumnSize变更为 12
1. Minitab 的操作
(#)
1
什么是Minitab ?
Minitab
MINITAB= Mini +Tabulator =小型 +计算机
介绍
于1972年,美国宾夕法尼亚 州立大学用来作统计分析、教育用而开发,目前已 出版Window用版本Vesion12.2,并且已在工学、社会学等所有领域被广泛使用。 特别是与Six-sigma关联,在GE、AlliedSignal等公司已作为基本的程序而使用。
方法1.利用开始菜单运行Minitab的方法
方法2.利用Minitab图标运行的方法
Minitab初始画面
(#)
4
Minitab画面构成
Minitab
▪Sessionwindow:直接输入Minitab的命令或显示类似统计表的文本型结果文 件的窗口 ▪WorKsheets:用于直接输入数据或可以修改的窗口,具有类似Excel中的 spreadsheet功能
minitab19 excel 实例

Minitab 19 Excel实例是一个用于数据分析的软件工具,它提供了多种数据导入选项,包括直接从Excel中导入数据、从数据库导入数据以及从其他数据文件格式导入数据等。
一旦数据导入完成,接下来的一步是对数据进行清洗。
Minitab 19 Excel实例提供了多种数据清洗工具,如去除空值、去除重复值、纠正数据格式等。
通过使用这些工具,可以确保数据完全准确且适合进行后续的分析。
在Minitab 19 Excel实例中,可以进行基本统计分析。
Minitab 19 Excel实例提供了广泛的统计分析工具,包括描述性统计、频率分析、方差分析等。
通过使用这些工具,可以获得数据的基本统计特征,如中位数、平均数、标准差等。
此外,Minitab 19 Excel实例还提供了图形和图表功能,可以帮助用户更好地理解和解释数据。
例如,可以使用柱状图、折线图、散点图等来展示数据的分布和趋势。
总之,Minitab 19 Excel实例是一个功能强大的数据分析工具,可以帮助用户更好地管理和分析数据,为决策提供支持。
doe(实验设计)与minitab培训doe案例

doe(实验设计)与minitab培训doe案例实验设计(DOE,Design of Experiments)是一种系统化的方法,用于确定和优化实验参数以实现特定的目标或解决特定的问题。
在制造业、工程、科学研究和其他领域中,DOE被广泛用于提高产品质量、降低成本、改进生产过程等。
Minitab是一款流行的统计软件,用于数据分析、假设检验、回归分析等。
它提供了丰富的工具和功能,帮助用户轻松地分析和解释数据。
以下是一个关于DOE和Minitab培训的案例:假设一家制造公司想要提高其产品的抗拉强度。
通过实验设计,该公司确定了以下几个因素可能影响产品的抗拉强度:温度、压力和材料类型。
目标是找到最佳的温度、压力和材料类型组合,以最大化产品的抗拉强度。
为了解决这个问题,公司使用Minitab软件进行实验设计。
首先,Minitab 帮助确定因素和水平,并生成一个实验矩阵,其中包括每个实验的条件和结果。
然后,公司按照实验矩阵进行实验,并记录每个实验的结果。
在收集完数据后,Minitab帮助进行数据分析。
通过分析结果,公司确定了最佳的温度、压力和材料类型组合。
此外,Minitab还提供了其他有用的统计信息,如因素对结果的影响程度、因素的交互作用等。
通过这个案例,Minitab培训的目标是使参与者能够:1. 了解实验设计的基本概念和方法;2. 使用Minitab软件进行实验设计和数据分析;3. 掌握如何解释和分析实验结果;4. 应用实验设计的方法来解决实际问题。
总之,通过DOE和Minitab培训,参与者可以学习如何系统地设计和分析实验,并使用统计软件来分析和解释数据。
这将有助于提高产品质量、改进生产过程和提高企业的竞争力。
minitab应用实例

Minitab应用实例引言Minitab是一款流行的统计分析软件,可用于数据分析、质量管理和过程改进。
它提供了广泛的功能和工具,使用户能够轻松地进行数据探索、统计分析和报告生成。
本文将通过介绍几个实际应用实例,展示Minitab的一些主要功能和应用场景。
这些实例将涵盖数据探索、假设检验、回归分析和质量控制等方面。
数据探索数据探索是数据分析的第一步,它可以帮助我们了解数据的特征和结构。
Minitab提供了多种方式来进行数据探索,包括数据摘要、描述性统计、数据可视化等。
例如,我们有一组销售数据,想要了解销售额的分布和趋势。
我们可以使用Minitab的柱状图和直方图功能,绘制销售额的分布图。
这样可以直观地看到销售额在哪个区间的数据更多,是否存在异常值等。
另外,Minitab还提供了箱线图、散点图等图表类型,可以帮助我们分析数据间的相关性和趋势。
假设检验假设检验是统计学中常用的技术,用于验证关于总体参数的假设。
Minitab提供了多种假设检验的功能,可以帮助我们进行参数估计和假设检验。
举个例子,我们有一份某公司员工的薪资数据,我们想要检验该公司的平均薪资是否高于行业平均水平。
我们可以使用Minitab的t检验功能来进行假设检验,得出结论是否拒绝原假设。
除了t检验,Minitab还支持多种其他假设检验方法,如方差分析、卡方检验等。
回归分析回归分析是用于建立因果关系模型的一种统计技术。
Minitab提供了强大的回归分析功能,可以帮助我们建立和评估回归模型。
例如,我们有一份汽车销售数据,想要预测汽车销售量与价格、广告费用和促销活动等变量之间的关系。
我们可以使用Minitab的多元线性回归功能来建立回归模型,并通过分析回归系数和显著性水平来评估模型的拟合优度。
此外,Minitab还提供了其他回归分析方法,如逐步回归、逻辑回归等。
质量控制质量控制是制造业中重要的环节,用于监控和改善产品的质量。
Minitab提供了一系列用于质量控制的统计工具和方法。
Minitab在品管常用作图中的应用

1、双击Minitab运行程序图标‘
’打开Minitab软件;
2、在Excel电子文档中输入的‘钢板厚度的数据列表’然后将表
格复制到Minitab的工作表中。
3、在主菜单栏,选择选择‘统计/质量工具/能力分析/正太’ ,打
开
‘能力分析(正太分布)’对话框;
4、勾选对话框中的‘单列’选项,包含回归’ 将光标放置在其
1、Minitab作图(柏拉图)的一般步骤
1、双击Minitab运行程序图标‘
’打开Minitab软件;
2、在电子文档的C1与C2列中输入各种不良原因与不良数
3、在主菜单栏,选择‘Stat(统计)/Quality Tools(质
量工具)/Pareto (柏拉图)’打开柏拉图 对话框;
4、 勾选‘已整理成表格的数据缺陷’栏,将光标置‘标签位
右边的空白栏,选择对话框左上角的‘C12 其它’行,再点击 ‘选
择’,选择分支‘其它’; 11 .在‘因果图’对话框的‘效应’右边的空白栏输入‘假焊’;在 ‘标题’右
边的空白栏输入‘假焊不良原因的因果图’; 12. 点击‘确定’,完成作图。
详细步骤参见下页截图:
5
2、Minitab作图(因果图)的一般步骤
Cpm CL 下限
2100.. 08
1 9
Minitab作图有何优点? 最关键是什么?
Minitab作图的优点:简单、高效,图形直观、 一目了然;无与伦比的易学性。
最关键是:分类整理好数据列; 选择所要做图的类别; 逐步勾选进行运算。
21 2024/4/3
复制到Minitab的工作表中。
3、在主菜单栏,选择‘统计/控制图/单值的变量控制图/单值’
,打开‘控制图’对话框;
minitab应用实例

PIVs
客户经理 经验 每月工作时间 客户类型 销售区域
KPOV
} 每周销售拜访数量
小结一下这个“研究”是为了确保收集到正确的数据!
如何测量拜访次数?
收集数据前...
• 记录销售拜访的指导方针:
-与客户面对面 -至少有30分钟 -讨论客户的问题,新产品报价,客户产品需求,促销等。
•测量系统分析:
•说明客户的交互作用 •要求销售员给一些情形分类,用“销售拜访”或“无” •培训所有客户经理直到他们能100% 正确分类 •销售员用数据收集表记录调查结果
抽取样本!
抽样
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
观察少数 . . . 以估计总体
第1步
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
收集数据的目标或期望结果是什么? 一般来讲,为了达到目的需要收集什么数据? 为收集数据,你将监测什么过程和产品?
• 数据来源: 销售拜访登记簿
• 问题的具体化:
– 情况: 根据客户调查,销售拜访在月初时很少,且间隔很长;而在月末时戏剧性地 增加很多。
– 程度: 至少有3个客户由于LLC缺乏与他们的联系而降低了交易量,并主要由此原 因将生意转给了其竞争对手。
– 现状: 测量单位是每周的拜访数量。以前我们只有来自客户经理们关于每周拜访数 的估计。这样,我们将需要收集数据以了解每周实际拜访数。
销售l 拜访
是否达到销售拜访的目标 (35个/周)?
•• •• •
时间序列图或趋势图
为什么使用? • 研究一段时间内的数据是否有一定的趋势
如何使用? • 随着时间变化的线图. • 图形可能反映出过程的变化.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a. 美国的所有人 b. 俄亥俄州的所有学生 c. 俄亥俄州的所有人
a. 所有的GEL C&I 客户 b. 所有的 GEL SPAs c. 所有的 GEL C&I SPAs
a. 荧光灯灯丝盘 b. 60瓦白炽灯灯丝盘 c. 所有的白炽灯灯丝盘
唉! 我没有测量资源
– 俄亥俄州每个学生的阅读水平 – 对每一个C&I SPA的处理时间 – 每盘白炽灯灯丝的长度
Who is the Customer? What’s Important? (CTQ) What’s the Defect? What re the Units of Measurement?
• 问题宏观陈述: 每周销售拜访的平均数低于要求的35个以上,造成LLC丢 失销售机会和客户。
•输出变量 & 单位: 每周销售拜访数
应采取什么方法从总体或过程抽样?
大多数的统计工具需要使用随机的和有代表性的数据。不论你是从一个过程 还是从一个总体收集数据,你必须选定正确的抽样方法,以确保你的样本从 统计角度看是有效的。
总体
过程
过程抽样
过程在运动
总体抽样
样本
有助于理解过程的特性和状况
样本
决定总体的特征
总体
当从总体抽样时,运用随机或分组随机抽样法有助于确保获得一个 有效的数据系列或样本。在许多情况下,从一批中抽样可以被认为 是从总体中抽样,并且适用于同样的规则。随机抽样最适用于只包 含通常原因连续变量的总体。当一个总体具有明显的分类特征时, 应用分组随机抽样法,或分区抽样,可清晰地了解每一个类别的表 现。
第3步
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
测量工具
当决定使用测量工具时,首先检查该工具是否存在; 如果不存在, 你将需要 重新选择一个工具。下列是一些工具的例子:秒表,量具,眼睛,直尺, 千分尺,计算机,测量图,温度计,天平,调查表和X-射线仪器。
例如,如果你决定测量一个拜访电话打了多长时间,合适的测量工具可能 是一只秒表,或者储存在拜访系统里的计时软件。
样本必须具有代表性。 在一个有代表性的样本里,收集的数据应该精确地反应一个总体 或过程。有代表性的抽样有助于避免偏颇于调查中的总体或过程 的某一特定区域。
样本必须是随机的。 在一个随机的样本里,数据的收集无序进行,每一个元素都有相等 的机会被选来测量。随机抽样有助于避免偏颇于收集数据的特定时 间和顺序,操作员,或数据收集员。
例子:如果从一批单据中抽样以检查其正确度,被检查 的单据应是可从这批单据的任何地方获取的。
从一个分类总体中抽样
加工的轴
总体
样本
2组的样本
加工的直径
过程抽样
过程在运动
总体抽样
样本
有助于理解过程的特性和状况
样本
决定总体的特征
抽样的方法
随机抽样
分组随机抽样
每个元素被选中的可能性相 等
系统随机抽样
每第 n 个元素
第2步
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
决定测量对象时,思考下列问题:
• 我们需要什么数据? 决定具体的测量数据(将被集中 起来)以满足第1步所述的目标。确认所需的每一个Y 或X.
• 对每一个测量,其操作定义是什么? 写下每一个定 义,以确保所有团队成员对于收集的数据有一个共同 的理解.
• 对任何项目,必须平衡样本尺寸和风险 等级以满足数据收集目标的要求。
小样本 高风险
大样本 低风险
好样本的特质:
无偏颇
•有代表性 •随机的
总体
无代表性
有代表性
样本必须是无偏颇的。 一个样本的偏颇是指任何这种因素的出现或影响,这种因素使得被取样的 总体或过程显得与其实际不同。 当收集的数据与影响总体或过程的关键因 素无关时,就产生了偏颇。
总体被分成若干组,在每组内随机选 择
子群抽样
过程在运动
在该点每小 时3个样品
大约需要抽取多少样品来计算置信区间?
统计工具 平均值 标准偏差 缺陷率 (P) 直方图或柏拉图 散点图 控制图
最小样本尺寸 5-10 25-30
100 and nP5 50 25 20
Minitab软件包简介和图表演示
问题陈述
抽取样本!
抽样
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
观察少数 . . . 以估计总体
第1步
起草项目数据收集计划
建立数据 收集目标
决定 测量对象
决定 如何测量
• 收集数据的目标或期望结果是什么? • 一般来讲,为了达到目的需要收集什么数据? • 为收集数据,你将监测什么过程和产品?
– 时间段: 每周的销售拜访数的历史记录一直不同。然而,客户抱怨在最近6个月内 一直在增加,并且客户在上个月已经采取了行动。
• 数据来源: 销售拜访登记簿
• 问题的具体化:
– 情况: 根据客户调查,销售拜访在月初时很少,且间隔很长;而在月末时戏剧性地 增加很多。
– 程度: 至少有3个客户由于LLC缺乏与他们的联系而降低了交易量,并主要由此原 因将生意转给了其竞争对手。
– 现状: 测量单位是每周的拜访数量。以前我们只有来自客户经理们关于每周拜访数 的估计。这样,我们将需要收集数据以了解每周实际拜访数。
总体
样本
警告
当决定抽样方案时,你应确保谨记数据收集目标。随机抽样可以提供一个总体的好样本,但是它可能不能 让你发现罕见的或偶然的情况(特殊原因造成的数据点)。为了发现这样的缺陷,运用随机抽样法时你可能 需要收集很大的样本。
从一个统一总ቤተ መጻሕፍቲ ባይዱ中抽样
例子:如果从一箱材料中抽样,箱子的每个地方都有相 等的机会被抽取为样品。
第三章 测量阶段
第二节 测量什么--对象
什么是总体?
“总体” 代表着. . .所有的信息 (人员, 物品,事件,活动,等.)
它构成一个我们感兴趣或关心的特定
的集合。
在这个世界上,并不 是每个人都如此!
“如果我想了解 . . .”
“我的总体是 . . .” 1. 俄亥俄州的学生平均阅读水平
2. 对于GEL C&I客户平均的特殊 价格审批(SPA)处理时间
准备抽样方案 抽样方案决定数据收集的频率和数量。
总体
样本
• 运用选取的样本,你能获得关于一个总
体或过程的结论;这就是所谓的“统计推
论”。
• 如果样本是总体的代表,在实践就没有 风险或不确定。
• 然而,当样本尺寸被缩小到只有总体的 一小小部分时,出现样本不能表达总体或 者得出错误的结论的风险随之增加。
