【8A版】槽钢矩形管方管规及载荷计算
矩形方管的重量计算方法

矩形方管的重量计算方法
矩形方管的重量计算方法可以通过以下步骤进行:
1. 确定矩形方管的尺寸,包括宽度、高度和壁厚。
假设宽度为W,高度为H,壁厚为T。
2. 计算矩形方管的截面积,即A = (W - T) * (H - T)。
3. 确定矩形方管的长度,假设长度为L。
4. 根据截面积和长度来计算矩形方管的体积,即V = A * L。
5. 根据矩形方管的材料密度来计算其重量,假设矩形方管的材料密度为ρ。
6. 矩形方管的重量可以通过W = ρ * V来计算。
注意:在实际应用中,密度的单位通常是千克/立方米,长度的单位可以是米或者厘米。
根据需要进行单位换算。
方管载荷计算公式

方管承载力计算公式比如50*30*1.5的方管二个端点架起,中间悬空1米的跨度,在这1米的跨度上50*30*1.5的方管能放多重的物品。
M=Pac/L(M:弯矩,P集中力,a集中力距支座距离,c集中力距另一支座距离,L跨度,L=a+c)W=b*h*h*h/12(仅用于矩形截面)f=M/W≤材料的许用应力(弹性抗拉强度/安全系数)。
钢材力学性能是保证钢材最终使用性能(机械性能)的重要指标,它取决于钢的化学成分和热处理制度。
在钢管标准中,根据不同的使用要求,规定了拉伸性能(抗拉强度、屈服强度或屈服点、伸长率)以及硬度、韧性指标,还有用户要求的高、低温性能等。
①抗拉强度(σb)试样在拉伸过程中,在拉断时所承受的最大力(Fb),出以试样原横截面积(So)所得的应力(σ),称为抗拉强度(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:式中:Fb--试样拉断时所承受的最大力,N(牛顿);So--试样原始横截面积,mm2。
②屈服点(σs)具有屈服现象的金属材料,试样在拉伸过程中力不增加(保持恒定)仍能继续伸长时的应力,称屈服点。
若力发生下降时,则应区分上、下屈服点。
屈服点的单位为N/mm2(MPa)。
上屈服点(σsu):试样发生屈服而力首次下降前的最大应力;下屈服点(σsl):当不计初始瞬时效应时,屈服阶段中的最小应力。
屈服点的计算公式为:式中:Fs--试样拉伸过程中屈服力(恒定),N(牛顿);So--试样原始横截面积,mm2。
③断后伸长率(σ)在拉伸试验中,试样拉断后其标距所增加的长度与原标距长度的百分比,称为伸长率。
以σ表示,单位为%。
计算公式为:式中:L1--试样拉断后的标距长度,mm;L0--试样原始标距长度,mm。
④断面收缩率(ψ)在拉伸试验中,试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比,称为断面收缩率。
以ψ表示,单位为%。
计算公式如下:式中:S0--试样原始横截面积,mm2;S1--试样拉断后缩径处的最少横截面积,mm2。
槽钢载荷性能计算

907.2 mm2 即 9.072 cm2
I1= 849700.4544 mm4 即 84.97005 cm4 I2= 440899.2 mm4 即 44.08992 cm4 I3= 1887416.496 mm4 即 188.7416 cm4 I4= 980254.4976 mm4 即 98.03 cm4
∑f=(mm)
3.09 mm
11.59 mm
14.68
<
L/100= 20
Байду номын сангаас
f=5p1l4/( 384× EI)=
f=p2l3/(3 ×EI)=
∑f=(mm)
0.32 mm
mm
0.32
<
L/200= 10
77005.012 mm3 即 77.00501 cm3
kN/m2 kN
集中荷载标 准值 梁弯矩设计 值
型钢应力 σ
=M/1.05W x=(N/mm2
)
Q235焊缝抗
拉压剪设计
215
值flw= N/mm2
723.37
>
kN 46.4 kN.m
160
N/mm f= 215 2
3.364528
挠度验算
均布荷载 标准值 p1= 型钢参数 构件长度
4158270.648 mm4 即 415.8271 cm4
焊缝最外 边缘的抵 抗矩 Ww1=2*I/ H 焊缝翼缘 和腹板连 接处的抵 抗矩 Ww2=2*I/h
1
杆件验算 荷载输入
均布荷载 标准值 梁端剪力 设计值 钢材参数 Q235抗拉 压弯设计 值f= N/mm2
61879.0275 mm3 即 61.87903 cm3
槽钢方钢矩形管矩形钢管的尺寸公差规格表参考
矩形钢管重量计算-矩形钢管尺寸规格表
矩形钢管理论重量计算方法(边长+边长)×2×壁厚×0.00785×长度
型焊接空心结构型材JIS G 3466 (日标)
一般构造用角型钢管产品材质:Q235、Q345(16Mn)、20#、合金钢、不锈钢。产品用途:机械设备、太阳能设备、钢结构用,汽车部件、桥梁地桩、护栏、船舶内部结构用。产品规格:
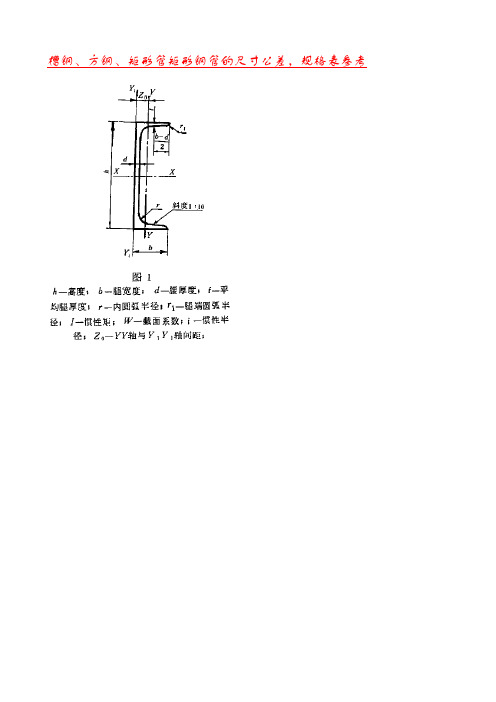
槽钢、方钢、矩形管矩形钢管的尺寸公差,规格表参考
产品执行标准:GB/T3094-2000 (国标)
冷压异型钢管 GB/T6728-2002 (国标)
矩形钢管尺寸规格表
矩形钢管重量计算-矩形钢管尺寸规格表
矩形钢管理论重量计算方法
(边长+边长)×2×壁厚×0.00785×长度
结构用冷弯空心型钢 ASTM A500 (美标)
产品执行标准:GB/T3094-2000 (国标)冷压异型钢管GB/T6728-2002 (国标)
70
80
矩形钢管尺寸规格表
矩
[重点]方管载荷计算公式
![[重点]方管载荷计算公式](https://img.taocdn.com/s3/m/6d79f26826284b73f242336c1eb91a37f1113234.png)
方管承载力计算公式比如50*30*1.5的方管二个端点架起,中间悬空1米的跨度,在这1米的跨度上50*30*1.5的方管能放多重的物品。
M=Pac/L(M:弯矩,P集中力,a集中力距支座距离,c集中力距另一支座距离,L跨度,L=a+c) W=b*h*h*h/12(仅用于矩形截面)f=M/W≤材料的许用应力(弹性抗拉强度/安全系数)。
钢材力学性能是保证钢材最终使用性能(机械性能)的重要指标,它取决于钢的化学成分和热处理制度。
在钢管标准中,根据不同的使用要求,规定了拉伸性能(抗拉强度、屈服强度或屈服点、伸长率)以及硬度、韧性指标,还有用户要求的高、低温性能等。
①抗拉强度(σb)试样在拉伸过程中,在拉断时所承受的最大力(Fb),出以试样原横截面积(So)所得的应力(σ),称为抗拉强度(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:式中:Fb--试样拉断时所承受的最大力,N(牛顿);So--试样原始横截面积,mm2。
②屈服点(σs)具有屈服现象的金属材料,试样在拉伸过程中力不增加(保持恒定)仍能继续伸长时的应力,称屈服点。
若力发生下降时,则应区分上、下屈服点。
屈服点的单位为N/mm2(MPa)。
上屈服点(σsu):试样发生屈服而力首次下降前的最大应力;下屈服点(σsl):当不计初始瞬时效应时,屈服阶段中的最小应力。
屈服点的计算公式为:式中:Fs--试样拉伸过程中屈服力(恒定),N(牛顿);So--试样原始横截面积,mm2。
③断后伸长率(σ)在拉伸试验中,试样拉断后其标距所增加的长度与原标距长度的百分比,称为伸长率。
以σ表示,单位为%。
计算公式为:式中:L1--试样拉断后的标距长度,mm;L0--试样原始标距长度,mm。
④断面收缩率(ψ)在拉伸试验中,试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比,称为断面收缩率。
以ψ表示,单位为%。
计算公式如下:式中:S0--试样原始横截面积,mm2;S1--试样拉断后缩径处的最少横截面积,mm2。
方管载荷计算公式

方管承载力计算公式比如50*30*1.5的方管二个端点架起,中间悬空1米的跨度,在这1米的跨度上50*30*1.5的方管能放多重的物品。
M=Pac/L(M:弯矩,P集中力,a集中力距支座距离,c集中力距另一支座距离,L跨度,L=a+c)W=b*h*h*h/12(仅用于矩形截面)f=M/W≤材料的许用应力(弹性抗拉强度/安全系数)。
钢材力学性能是保证钢材最终使用性能(机械性能)的重要指标,它取决于钢的化学成分和热处理制度。
在钢管标准中,根据不同的使用要求,规定了拉伸性能(抗拉强度、屈服强度或屈服点、伸长率)以及硬度、韧性指标,还有用户要求的高、低温性能等。
①抗拉强度(σb)试样在拉伸过程中,在拉断时所承受的最大力(Fb),出以试样原横截面积(So)所得的应力(σ),称为抗拉强度(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:式中:Fb--试样拉断时所承受的最大力,N(牛顿);So--试样原始横截面积,mm2。
②屈服点(σs)具有屈服现象的金属材料,试样在拉伸过程中力不增加(保持恒定)仍能继续伸长时的应力,称屈服点。
若力发生下降时,则应区分上、下屈服点。
屈服点的单位为N/mm2(MPa)。
上屈服点(σsu):试样发生屈服而力首次下降前的最大应力;下屈服点(σsl):当不计初始瞬时效应时,屈服阶段中的最小应力。
屈服点的计算公式为:式中:Fs--试样拉伸过程中屈服力(恒定),N(牛顿);So--试样原始横截面积,mm2。
③断后伸长率(σ)在拉伸试验中,试样拉断后其标距所增加的长度与原标距长度的百分比,称为伸长率。
以σ表示,单位为%。
计算公式为:式中:L1--试样拉断后的标距长度,mm;L0--试样原始标距长度,mm。
④断面收缩率(ψ)在拉伸试验中,试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比,称为断面收缩率。
以ψ表示,单位为%。
计算公式如下:式中:S0--试样原始横截面积,mm2;S1--试样拉断后缩径处的最少横截面积,mm2。
方管载荷计算

方管承载力计算公式比如50*30*1.5的方管二个端点架起,中间悬空1米的跨度,在这1米的跨度上50*30*1。
5的方管能放多重的物品。
M=Pac/L(M:弯矩,P集中力,a集中力距支座距离,c集中力距另一支座距离,L跨度,L=a+c)W=b*h*h*h/12(仅用于矩形截面)f=M/W≤材料的许用应力(弹性抗拉强度/安全系数)。
强度计算=M/W (其中,弯矩M=0.125qL*2,W为截面模量)刚度计算=(5qL*4)/ 384EI钢材力学性能是保证钢材最终使用性能(机械性能)的重要指标,它取决于钢的化学成分和热处理制度。
在钢管标准中,根据不同的使用要求,规定了拉伸性能(抗拉强度、屈服强度或屈服点、伸长率)以及硬度、韧性指标,还有用户要求的高、低温性能等.①抗拉强度(σb)试样在拉伸过程中,在拉断时所承受的最大力(Fb),出以试样原横截面积(So)所得的应力(σ),称为抗拉强度(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:式中:Fb-—试样拉断时所承受的最大力,N(牛顿);So—-试样原始横截面积,mm2。
②屈服点(σs)具有屈服现象的金属材料,试样在拉伸过程中力不增加(保持恒定)仍能继续伸长时的应力,称屈服点.若力发生下降时,则应区分上、下屈服点。
屈服点的单位为N/mm2(MPa)。
上屈服点(σsu):试样发生屈服而力首次下降前的最大应力;下屈服点(σsl):当不计初始瞬时效应时,屈服阶段中的最小应力。
屈服点的计算公式为:式中:Fs-—试样拉伸过程中屈服力(恒定),N(牛顿);So--试样原始横截面积,mm2。
③断后伸长率(σ)在拉伸试验中,试样拉断后其标距所增加的长度与原标距长度的百分比,称为伸长率。
以σ表示,单位为%。
计算公式为:式中:L1—-试样拉断后的标距长度,mm;L0——试样原始标距长度,mm.④断面收缩率(ψ)在拉伸试验中,试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比,称为断面收缩率。
矩形管承载力计算公式

矩形管承载力计算公式矩形管承载力计算公式是用来计算矩形管在承受力的情况下的最大承载能力的公式。
矩形管是一种常见的结构材料,广泛应用于建筑、桥梁、机械等领域。
了解和正确应用矩形管承载力计算公式对于设计和工程师来说至关重要。
矩形管承载力计算公式可以通过以下方式进行计算:1. 首先,确定矩形管的几何属性,包括长、宽和厚度等。
这些参数将用于计算矩形管的截面面积和惯性矩。
2. 其次,确定矩形管的材料属性,如弹性模量和抗拉强度等。
这些参数将用于计算矩形管的弯曲和屈服。
3. 然后,根据矩形管所受力的类型,选择适当的承载力计算公式。
常见的承载力类型包括弯曲、屈服和剪切等。
4. 最后,将矩形管的几何属性和材料属性代入所选的承载力计算公式,进行计算。
计算结果将给出矩形管所能承受的最大力量。
需要注意的是,矩形管承载力计算公式是基于理论和实验研究得出的,并且假设矩形管在承受力的情况下是完全均匀的。
实际情况可能会受到诸多因素的影响,如温度、湿度和材料的质量等。
因此,在应用矩形管承载力计算公式时,需要根据具体情况进行适当的修正和调整。
除了矩形管承载力计算公式,还有其他与矩形管承载力相关的参数和公式。
例如,矩形管的弯曲刚度可以通过弯曲刚度公式进行计算。
矩形管的应力分布可以通过应力分布公式进行计算。
这些公式和参数可以帮助工程师更好地理解和分析矩形管的承载力情况。
矩形管承载力计算公式是工程设计和分析中必备的工具。
正确应用这些公式可以帮助工程师评估矩形管的承载能力,从而确保结构的安全和可靠。
然而,需要注意的是,矩形管承载力计算公式是理论模型,实际情况可能存在差异,因此在设计和分析中需要结合实际情况进行合理调整和修正。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
槽钢规格表大全20XX(最新)槽钢规格表大全20XX(最新)国际标准槽钢规格,槽钢规格表20XX年最新更新版!C160G60G20是槽钢腹板高160翼缘板宽60钢板厚20槽钢规格表大全20XX(最新)500G300G8.0--12.0mm 450G250G6.0--12.0mm 400G300G6.0--12.0mm 400G200G6.0--12.0mm 350G250G6.0--12.0mm 350G150G6.0--12.0mm 300G200G6.0--12.0mm 300G150G6.0--12.0mm 300G100G4.0--10.0mm 280G180G4.0--10.0mm 250G150G4.0--10.0mm 250G100G4.0--10.0mm 200G150G4.0--10.0mm 200G100G4.0--10.0mm 200G95G4.0--10.0mm 160G80G4.0--10.0mm 150G100G3.0--10.0mm 150G90G3.0--10.0mm 150G75G3.0--8.0mm 140G80G3.0--10.0mm 120G100G3.0--10.0mm 120G80G2.0--8.0mm 120G60G2.0--5.0mm 120G50G2.0--5.0mm 120G40G2.0--4.0mm 100G80G2.0--8.0mm100G60G2.0--5.0mm100G50G1.0--5.0mm100G40G2.0--3.0mm90G60G2.0--4.0mm80G60G1.4--4.0mm80G50G1.2--3.0mm80G40G0.9--4.0mm70G50G1.2--4.0mm70G30G1.5--3.0mm60G40G0.8--4.0mm60G30G0.8--3.0mm50G40G0.8--3.0mm50G30G0.7--4.0mm50G25G0.7--3.0mm50G20G0.7--1.7mm40G30G0.7--3.0mm40G25G0.7--2.5mm40G20G0.6--3.0mm30G20G0.6--2.0mm20G14G0.5--1.2mm20G10G0.5--1.2mm方管承载力计算公式比如50G30G1.5的方管二个端点架起,中间悬空1米的跨度,在这1米的跨度上50G30G1.5的方管能放多重的物品。
M=Pac/L(M:弯矩,P集中力,a集中力距支座距离,c集中力距另一支座距离,L跨度,L= a+c)W=bGhGhGh/12(仅用于矩形截面)f=M/W≤材料的许用应力(弹性抗拉强度/安全系数)。
强度计算=M/W(其中,弯矩M=0.125qLG2,W为截面模量)刚度计算=(5qLG4)/384EI钢材力学性能是保证钢材最终使用性能(机械性能)的重要指标,它取决于钢的化学成分和热处理制度。
在钢管标准中,根据不同的使用要求,规定了拉伸性能(抗拉强度、屈服强度或屈服点、伸长率)以及硬度、韧性指标,还有用户要求的高、低温性能等。
①抗拉强度(σb)试样在拉伸过程中,在拉断时所承受的最大力(Fb),出以试样原横截面积(So)所得的应力(σ),称为抗拉强度(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:式中:Fb--试样拉断时所承受的最大力,N(牛顿);So--试样原始横截面积,mm2。
②屈服点(σs)具有屈服现象的金属材料,试样在拉伸过程中力不增加(保持恒定)仍能继续伸长时的应力,称屈服点。
若力发生下降时,则应区分上、下屈服点。
屈服点的单位为N/mm2(MPa)。
上屈服点(σsu):试样发生屈服而力首次下降前的最大应力;下屈服点(σsl):当不计初始瞬时效应时,屈服阶段中的最小应力。
屈服点的计算公式为:式中:Fs--试样拉伸过程中屈服力(恒定),N(牛顿);So--试样原始横截面积,mm2。
③断后伸长率(σ)在拉伸试验中,试样拉断后其标距所增加的长度与原标距长度的百分比,称为伸长率。
以σ表示,单位为%。
计算公式为:式中:L1--试样拉断后的标距长度,mm;L0--试样原始标距长度,mm。
④断面收缩率(ψ)在拉伸试验中,试样拉断后其缩径处横截面积的最大缩减量与原始横截面积的百分比,称为断面收缩率。
以ψ表示,单位为%。
计算公式如下:式中:S0--试样原始横截面积,mm2;S1--试样拉断后缩径处的最少横截面积,mm2。
⑤硬度指标金属材料抵抗硬的物体压陷表面的能力,称为硬度。
根据试验方法和适用范围不同,硬度又可分为布氏硬度、洛氏硬度、维氏硬度、肖氏硬度、显微硬度和高温硬度等。
对于管材一般常用的有布氏、洛氏、维氏硬度三种。
A、布氏硬度(HB)用一定直径的钢球或硬质合金球,以规定的试验力(F)压入式样表面,经规定保持时间后卸除试验力,测量试样表面的压痕直径(L)。
布氏硬度值是以试验力除以压痕球形表面积所得的商。
以HBS(钢球)表示,单位为N/mm2(MPa)。
其计算公式为:式中:F--压入金属试样表面的试验力,N;D--试验用钢球直径,mm;d--压痕平均直径,mm。
测定布氏硬度较准确可靠,但一般HBS只适用于450N/mm2(MPa)以下的金属材料,对于较硬的钢或较薄的板材不适用。
在钢管标准中,布氏硬度用途最广,往往以压痕直径d来表示该材料的硬度,既直观,又方便。
举例:120HBS10/1000130:表示用直径10mm钢球在1000Kgf(9.807KN)试验力作用下,保持30s(秒)测得的布氏硬度值为120N/mm2(MPa)。
B、洛氏硬度(HK)洛氏硬度试验同布氏硬度试验一样,都是压痕试验方法。
不同的是,它是测量压痕的深度。
即,在初邕试验力(Fo)及总试验力(F)的先后作用下,将压头(金钢厂圆锥体或钢球)压入试样表面,经规定保持时间后,卸除主试验力,用测量的残余压痕深度增量(e)计算硬度值。
其值是个无名数,以符号HR表示,所用标尺有A、B、C、D、E、F、G、H、K等9个标尺。
其中常用于钢材硬度试验的标尺一般为A、B、C,即HRA、HRB、HRC。
硬度值用下式计算:当用A和C标尺试验时,HR=100-e当用B标尺试验时,HR=130-e式中e--残余压痕深度增量,其什系以规定单位0.002mm表示,即当压头轴向位移一个单位(0.002mm)时,即相当于洛氏硬度变化一个数。
e值愈大,金属的硬度愈低,反之则硬度愈高。
上述三个标尺适用范围如下:HRA(金刚石圆锥压头)20-88HRC(金刚石圆锥压头)20-70HRB(直径1.588mm钢球压头)20-100洛氏硬度试验是目前应用很广的方法,其中HRC在钢管标准中使用仅次于布氏硬度HB。
洛氏硬度可适用于测定由极软到极硬的金属材料,它弥补了布氏法的不是,较布氏法简便,可直接从硬度机的表盘读出硬度值。
但是,由于其压痕小,故硬度值不如布氏法准确。
C、维氏硬度(HV)维氏硬度试验也是一种压痕试验方法,是将一个相对面夹角为1360的正四棱锥体金刚石压头以选定的试验力(F)压入试验表面,经规定保持时间后卸除试验力,测量压痕两对角线长度。
维氏硬度值是试验力除以压痕表面积所得之商,其计算公式为:式中:HV--维氏硬度符号,N/mm2(MPa);F--试验力,N;d--压痕两对角线的算术平均值,mm。
维氏硬度采用的试验力F为5(49.03)、10(98.07)、20(196.1)、30(294.2)、50(490.3)、100(980.7)Kgf(N)等六级,可测硬度值范围为5~1000HV。
表示方法举例:640HV30/20表示用30Hgf(294.2N)试验力保持20S(秒)测定的维氏硬度值为640N/mm2(MPa)。
维氏硬度法可用于测定很薄的金属材料和表面层硬度。
它具有布氏、洛氏法的主要优点,而克服了它们的基本缺点,但不如洛氏法简便。
维氏法在钢管标准中很少用。
⑥冲击韧性指标冲击韧性是反映金属才来哦对外来冲击负荷的抵抗能力,一般由冲击韧性值(ak)和冲击功(Ak)表示,其单位分别为J/cm2和J(焦耳)。
冲击韧性或冲击功试验(简称"冲击试验"),因试验温度不同而分为常温、低温和高温冲击试验三种;若按试样缺口形状又可分为"V"形缺口和"U"形缺口冲击试验两种。
冲击试验:用一定尺寸和形状(10×10×55mm)的试样(长度方向的中间处有"U"型或"V"型缺口,缺口深度2mm)在规定试验机上受冲击负荷打击下自缺口处折断的实验。
A、冲击吸收功Akv(u)--具有一定尺寸和形状的金属式样,在冲击负荷作用下折断时所吸收的功。
单位为焦耳(J)或Kgf.m。
B、冲击韧性值akv(u)--冲击吸收功除以试样缺口处底部横截面积所得的商。
单位为焦耳/厘米2(J/cm2)或公斤力.米/厘米2(Kgf.m/cm2)。
计算公式为:式中:Akv(u)--试样折断时所吸收的功,Kgf.m(J);S--试样缺口处底部横截面面积,cm2。
常温冲击试验温度为20±50C;低温冲击试验温度范围为<15~-1920C;高温冲击试验温度范围为35~10000C。
低温冲击试验所用冷却介质一般为无毒、安全、不腐蚀金属和在试验温度下不凝固的液体或气体。
如无水乙醇(酒精)、固态二氧化碳(干冰)或液氮雾化气(液氮)等。
